
神经网络变得简单(第 57 部分):随机边际扮演者-评论者(SMAC)
概述
在构建自动交易系统时,我们开发了制定后续决策的算法。强化学习方法正是为了解决这些问题。强化学习的关键问题之一是如同智能体学习与环境交互那般的探索过程。在这种前后呼应情况下,经常运用最大熵原理,这促使智能体按最大随机度执行动作。然而,在实践中,这种算法只能训练简单的智能体学习单个动作周围的局部变化。这是因为需要计算智能体政策的熵值,并将其用作训练目标的一部分。
同时,提高扮演者政策表现力的一种相对简单的方式是使用潜在变量,其为智能体提供了自己的模型随机性推理过程,手段则是观察、环境和未知奖励。
将潜在变量引入智能体的政策,令其能够涵盖更多样化的场景,且与历史观测兼容。这里应该注意的是,具有潜在变量的政策不允许使用简单的表达式来判定它们的熵。朴素的熵估值可能会导致灾难性的政策优化失败。此外,熵最大化的高方差随机更新无法轻易区分局部随机效应和多模态探索。
在《潜在状态边际化作为改进探索的低成本方法》一文中提出了解决这些潜在可变政策缺陷的方案之一。作者提出了一种《简单而有效的政策优化算法,能够在完全可观察和部分可观察的环境中提供更高效和更强大的探索。
本文的主要贡献可以简要归纳为以下几点:
- 在部分可观测性条件下使用潜在变量政策来改进探索和健壮性的动机。
- 提出了若干种随机估算方法,这些方法注重研究效率和方差降低。
- 将方法应用于扮演者-评论者方法导致了随机边际扮演者-评论者(SMAC)算法的创生。
1. SMAC 算法
随机边际扮演者-评论者算法的作者提出使用潜在变量来构建分布式扮演者政策。这是提高智能体动作模型和政策灵活性的一种简单有效的方式。该方式需要运用随机智能体行为政策在现有算法基础上进行少量修改。
潜在变量政策可以表达如下:
![]()
其中 st 是取决于当前观测值的潜在变量。
引入 q(st|xt) 潜在变量通常会增加扮演者政策的表达能力。这令政策能够捕获更广范围的最优动作。这在早期研究阶段特别有用,因为此刻缺乏有关未来奖励的信息。
为了把随机模型进行参数化,该方法的作者建议 针对 π(at|st) 扮演者政策,以及 q(st|xt) 潜在变量函数两者使用分解高斯分布。成果是计算效率高的潜在变量政策,因为抽样和密度估算仍旧很划算。此外,它还允许我们应用拟议的方式,基于遵照随机政策和单一高斯分布的现有算法构建模型。我们只需添加一个新的 st 随机节点。
请注意,由于马尔可夫(Markov)的假设过程,π(at|st) 仅取决于当前的潜在状态,尽管所拟议的算法可以很容易地扩展为非马尔可夫状况。然而,归因于不停复发,我们根据完整的隐藏历史观察到边际化,因为当前的潜在状态 st,以及 π(at|st) 政策是在智能体所执行动作的影响下从初始状态发生一系列转变的结果。
![]()
同时,拟议的潜在变量处理方式并不依赖于 q 的影响。
潜在变量的存在令最大熵训练变得相当困难。毕竟,这需要对熵分量进行准确估算。由于边际化的困难,潜在变量模型的熵极难估值。此外,使用潜在变量会增加梯度的方差。此外,可以在 Q-函数中使用潜在变量,从而不确定性收敛更佳。
在每一种情况下,《随机边际扮演者-评论者》的作者都推导出了处理潜在变量的合理方法。最终结果非常简单,相比没有潜在变量的政策,增加的额外资源成本最少。
反过来,由于概率对数的不可解性,使用潜在变量令熵(或边际熵)不可用。
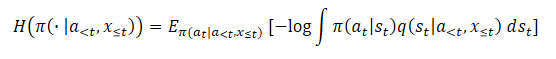
使用朴素估算器将导致标的最大熵泛函的上限最大化,从而导致误差最大化。这刺激了变异分布尽可能远离 q(st|a<t,x≤t) 真实后验估算。此外,这个误差是无边界的,可以变得任意大,且不会实际影响我们想要最大化的真实熵,从而导致严重的数值不稳定问题。
文章展示了一个初步实验的结果,其中,政策优化期间估算熵值的方式生出了极端巨大的数值,明显高估了真实熵,并导致未经训练的政策。以下是上述文章中的可视化效果。
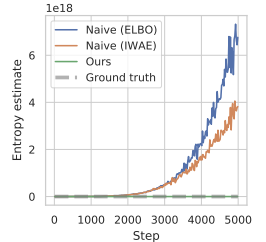
为了克服高估问题,方法作者提出构建边际熵下限的估算器。
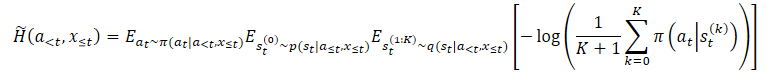
其中 p(st|a≤t,x≤t) 是政策的未知后验分布。
不过,我们可以很容易地从中选取 st⁰,然后在 st⁰ 条件下选择 t。成果则是一个嵌套估值器,我们实际上从 q(st|a<t,x≤t) 中选择了 K+1 次。为了选择动作,我们只使用第一个 st⁰ 潜在变量。所有其它潜在变量都用于估算边际熵。
注意,这并不等同于用独立样本替换对数中的期望值。所拟议的估算器随 K 单调增加,在极限下变为一个无偏边际熵估算器。
上述方法可以应用于普通的熵最大化算法。但该方法的作者创建了一种称为随机边际扮演者-评论者(SMAC) 的特殊算法。SMAC 的特征是利用具有潜在变量的扮演者政策,并将边际熵目标函数的下限最大化。
该算法遵循普遍接受的扮演者-评论者样式,并使用经验回放缓冲区来存储数据,并基于该缓冲区更新扮演者和评论者两方的参数。
评论者依据最小化误差来学习:
![]()
其中:
(x, a, r, x') — 来自 D 回放缓存区,
a' — 扮演者动作,根据 π(·|x') 政策,
Q ̅ — 评论者的目标函数,
H ̃ — 政策熵估值。
此外,我们还依据潜在变量估算政策熵。
此外,按最小化误差来更新扮演者:
![]()
注意,在更新评论者时,我们在后续状态下依据扮演者政策的熵估值,而在更新扮演者政策时 — 按当前那个。
总体上,SMAC 在强化学习方法的算法细节方面与朴素 SAC 基本相同,但主要通过结构化探索行为获得改进。这是通过潜在变量建模达成的。
2. 利用 MQL5 实现
以上是作者的随机边际扮演者-评论者方法的理论计算。在本文的实践部分,我们将利用 MQL5 实现所提出的算法。唯一的例外是我们不会完全重复原始的 SMAC 算法。所述文章研究了在几乎所有强化学习算法中使用提议方法的可能性。我们将利用这个机会,实现在上一篇文章中讨论的 NNM 算法中所提出的方法。
将对模型的架构进行第一次更改。我们从上面的方程式中可以看出,SMAC 算法基于三个模型:
- q — 表示潜在状态的模型;
- π — 扮演者;
- Q — 评论者。
我认为,最后两个模型不会出任何问题。第一个潜在状态模型是输出端具有随机节点的编码器。扮演者和评论者都用编码器操作结果作为源数据。于此,回顾一下变分自动编码器是合适的。
我们已开发的部分允许我们不将编码器移到单独的模型中,而是像以前一样将其保留在扮演者模型的架构之中。因此,为了实现所提出的算法,我们必须对扮演者架构进行更改。也就是说,我们需要在数据预处理模块(编码器)的输出端添加一个随机节点。
模型架构的结构在 CreateDescriptions 方法中指定。本质上,我们对扮演者架构进行了最小的更改,同时保留数据预处理块不变。价格走势和指标的历史数据被馈送到一个完全连接神经层。然后它们在批量常规化神经层进行初级处理。
bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic, CArrayObj *convolution) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; } if(!convolution) { convolution = new CArrayObj(); if(!convolution) return false; } //--- Actor actor.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1000; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
然后,常规化的数据经由两个连续卷积层验算,我们尝试从数据结构中提取某些形态。
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = BarDescr; descr.window = HistoryBars; descr.step = HistoryBars; int prev_wout = descr.window_out = HistoryBars / 2; descr.activation = LReLU; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = prev_count; descr.window = prev_wout; descr.step = prev_wout; descr.window_out = 8; descr.activation = LReLU; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
我们用两个完全连接层将环境状态边际化。
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.optimization = ADAM; descr.activation = LReLU; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
接下来,我们将收到的数据与有关帐户状态的信息相结合。在此,我们对模型架构进行了第一次更改。在随机模块之前,我们需要创建一个层,大小是潜在表象的两倍:我们需要以均值和方差的形式衡量分布。因此,我们将串联层的大小指定为潜在表象的两倍。紧随其后的是变分自动编码器的潜在状态层。正是依据这一层,我们创建了一个随机节点。
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = 2 * LatentCount; descr.window = prev_count; descr.step = AccountDescr; descr.optimization = ADAM; descr.activation = SIGMOID; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronVAEOCL; descr.count = LatentCount; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
请注意,我们提升了数据预处理单元(编码器)的大小。在安排模型之间的数据传输时,我们必须要考虑到这一点。
我保留了扮演者的决策模块不变。它包含三个全连接层,和一个变分自动编码器的潜在状态层,该层创建扮演者的随机行为。
//--- layer 8 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 9 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 10 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 2 * NActions; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 11 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronVAEOCL; descr.count = NActions; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
现在我们来看看评论者的架构。初看,SMAC 方法作者的建议不包含对评论者架构的要求。我们可以轻易保留它不变。您也许还记得,我们使用分解的奖励函数。问题来了:我们应该在哪里给添加的随机节点分配熵值?我们可以将其添加到任何现有的奖励元素之中。但在奖励函数分解的上下文中,在评论者的输出端再添加一个元素更合乎逻辑。因此,我们提升了奖励元素数量的常数。
#define NRewards 5 //Number of rewards
除此之外,评论者模型的架构保持不变。
//--- Critic critic.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = LatentCount; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = LatentCount; descr.window = prev_count; descr.step = NActions; descr.optimization = ADAM; descr.activation = LReLU; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NRewards; descr.optimization = ADAM; descr.activation = None; if(!critic.Add(descr)) { delete descr; return false; }
我们已经指定了实现 SMAC 算法所需的所有模型。不过,不要忘记,我们正在 NNM 算法中实现所提议的方法。因此,我们保留了所有以前使用的模型,从而保留算法的全部功能。沿用随机卷积编码器模型,不作任何更改。我就不再多聊它了。您可在附件中找到它。本文中用到的所有程序也都出现在那里。
我们回到模型之间的数据传输问题。为了能让评论者引用扮演者的潜在状态,我们使用 LatentLayer 常量中指定的潜在状态层 ID。因此,为了根据扮演者架构的变化将评论者重定向到所需的神经层,我们只需要更改指定常量之中的数值即可。在此上下文中,不需要对程序代码进行其它调整。
#define LatentLayer 7
现在我们来讨论用算法来计算奖励函数中的熵分量。方法作者针对理论部分中出现的问题提出了他们的观点。不过,我们扩展了 NNM 方法的实现,其中我们使用核范数(nuclear norm)作为扮演者的熵分量。为了令奖励函数的各种元素值具有可比性,针对编码器运用类似的方式是合乎逻辑的。
SMAC 方法的作者建议使用 K+1 编码器样本来估算潜伏状态的熵。很明显,对于编码器训练过程中的单个环境状态,我们将很快得出一些平均值。在进一步优化编码器参数的过程中,我们将努力减小方差值,最大化独立状态的分离。当离散度在极限内递减到 “0” 时,熵值也将趋于 “0”。使用核范数,我们会得到同样的效果吗?
为了回答这个问题,我们可以深入研究数学方程式,或可以参考实践。当然,我们不会在很长一段时间内创建和训练模型,以此测试使用核范数的可能性。我们将令它变得更容易、更迅捷。我们来创建一小段 Python 脚本。
首先,我们导入两个函数库:numpy 和 matplotlib。我们将使用第一个进行计算,第二个 — 则是用于可视化结果。
# Import libraries import numpy as np import matplotlib.pyplot as plt
为了创建样本,我们需要分布的统计指标:平均值,和相应的方差。它们将由模型在训练期间生成。我们只需要随机值来测试该方式。
mean = np.random.normal(size=[1,10]) std = np.random.rand(1,10)
请注意,任何数字都可以用作平均值。我们从正态分布生成它们。不过,方差只能是正数,我们在 (0, 1] 范围内生成它们。
我们将使用类似于随机节点的分布重新参数化技巧。为此,我们将从正态分布生成一个随机值矩阵。
data = np.random.normal(size=[20,10])
我们将准备一个向量来记录我们的内部奖励。
reward=np.zeros([20])
该思路如下:在降低方差但其它条件相同的情况下,我们需要使用核范数来测试内在奖励的行为。
为了降低方差,我们将创建一个折减因子的向量。
scl = [2**(-k/2.0) for k in range(20)]
接下来,我们创建一个循环,于其中我们将针对具有恒定均值和方差递减的随机数据使用分布重新参数化技巧。基于获得的数据,我们将用核范数来计算内部奖励。将获得的结果保存到准备好的奖励向量当中。
for idx, k in enumerate(scl): new_data=mean+data*(std*k) _,S,_=np.linalg.svd(new_data) reward[idx]=S.sum()/(np.sqrt(new_data*new_data).sum()*max(new_data.shape))
可视化脚本结果。
# Draw results
plt.plot(scl,reward)
plt.gca().invert_xaxis()
plt.ylabel('Reward')
plt.xlabel('STD multiplier')
plt.xscale('log',base=2)
plt.savefig("graph.png")
plt.show() 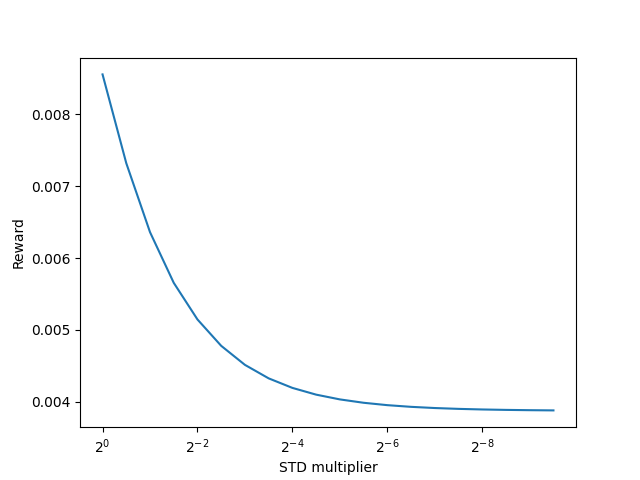
获得的结果清晰地表明,依据核范数的内部奖励降低,分布方差降低,所有其它条件等同。这意味着我们可以安全地使用核范数来估算潜伏状态的熵。
我们回到利用 MQL5 实现算法。现在我们能够开始实现潜在状态熵估算了。首先,我们需要判定要抽取的潜在状态的数量。我们将通过 SamplLatentStates 常量来定义此指标。
#define SamplLatentStates 32
下一个问题是:我们真的需要经由编码器(在我们的例子中是扮演者)模型进行完整的前向验算,从而对每个潜在状态进行抽样吗?
很明显,在不改变初始数据和模型参数的情况下,所有神经层的结果在每次后续验算中都是相同的。唯一的区别依赖随机节点的结果。因此,对于每个单独的状态来说,扮演者模型的一次直接验算就足够了。接下来,我们将使用分布重新参数化技巧,并对我们需要的隐藏状态的数量进行取样。我认为,这个思路很明确,且我们正在转入实现。
首先,我们据均值为 “0”,且方差为 “1” 的正态分布生成一个随机值矩阵。这种分布指标最便于重新参数化。
float EntropyLatentState(CNet &net) { //--- random values double random[]; Math::MathRandomNormal(0,1,LatentCount * SamplLatentStates,random); matrix<float> states; states.Assign(random); states.Reshape(SamplLatentStates,LatentCount);
然后,我们将从扮演者模型中加载已训练过的分布参数,其存储在倒数第二个编码器层之中。这里应该注意的是,我们的模型提供了一个数据缓冲区,其中按顺序存储已学习分布的所有均值,随后是所有方差。不过,若要执行矩阵运算,我们需要两个行值重复的矩阵,而非一个向量。此处,我们要用到一个小技巧。首先,我们创建一个含有所需行数和双倍列数的大型矩阵,以零值填充。在第一行中,我们将来自分布参数数据缓冲区的数据写入。然后,我们将调用按列累积矩阵值求和的函数。
技巧是,所有字符串,除第一个之外,都以零填填充。作为执行累积求和运算的结果,我们只需将数据从第一行复制到所有后续行。
现在我们只需将矩阵垂直分成两个相等的矩阵,即可得到分裂矩阵的数组。它将包含索引为 0 的平均值矩阵。方差矩阵的索引为 1。
//--- get means and std vector<float> temp; matrix<float> stats = matrix<float>::Zeros(SamplLatentStates,2 * LatentCount); net.GetLayerOutput(LatentLayer - 1,temp); stats.Row(temp,0); stats=stats.CumSum(0); matrix<float> split[]; stats.Vsplit(2,split);
现在,我们就能非常简单地从正态分布中重新参数化随机值,并获得所需的样本数量。
//--- calculate latent values states = states * split[1] + split[0];
在矩阵的底部,我们将添加一个含有当前编码器值的字符串,在扮演者和评论者的前向验算期间作为输入数据使用。
//--- add current latent value net.GetLayerOutput(LatentLayer,temp); states.Resize(SamplLatentStates + 1,LatentCount); states.Row(temp,SamplLatentStates);
在这个阶段,我们已为计算核范数准备好了所有数据。我们计算奖励函数的熵分量。结果将返回给调用程序。
//--- calculate entropy states.SVD(split[0],split[1],temp); float result = temp.Sum() / (MathSqrt(MathPow(states,2.0f).Sum() * MathMax(SamplLatentStates + 1,LatentCount))); //--- return result; }
筹备工作已经完成。我们转入 EA 与环境和训练模型进行交互的工作。
EA 与环境交互(Research.mq5 和 Test.mq5)保持不变,我们现在不再赘述它们。本文中用到的所有程序的完整代码可在附件中找到。
我们转入模型训练 EA,并专注于 Train 训练方法。在方法伊始,我们将判定经验回放缓冲区的总体大小。
//+------------------------------------------------------------------+ //| Train function | //+------------------------------------------------------------------+ void Train(void) { int total_tr = ArraySize(Buffer); uint ticks = GetTickCount();
然后,我们将调用随机卷积编码器对经验回放缓冲区中的所有现有样本进行编码。该过程已被完全从以前的实现转移。
int total_states = Buffer[0].Total; for(int i = 1; i < total_tr; i++) total_states += Buffer[i].Total; vector<float> temp, next; Convolution.getResults(temp); matrix<float> state_embedding = matrix<float>::Zeros(total_states,temp.Size()); matrix<float> rewards = matrix<float>::Zeros(total_states,NRewards); int state = 0; for(int tr = 0; tr < total_tr; tr++) { for(int st = 0; st < Buffer[tr].Total; st++) { State.AssignArray(Buffer[tr].States[st].state); float PrevBalance = Buffer[tr].States[MathMax(st,0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(st,0)].account[1]; State.Add((Buffer[tr].States[st].account[0] - PrevBalance) / PrevBalance); State.Add(Buffer[tr].States[st].account[1] / PrevBalance); State.Add((Buffer[tr].States[st].account[1] - PrevEquity) / PrevEquity); State.Add(Buffer[tr].States[st].account[2]); State.Add(Buffer[tr].States[st].account[3]); State.Add(Buffer[tr].States[st].account[4] / PrevBalance); State.Add(Buffer[tr].States[st].account[5] / PrevBalance); State.Add(Buffer[tr].States[st].account[6] / PrevBalance); double x = (double)Buffer[tr].States[st].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_MN1); State.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_W1); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_D1); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(!Convolution.feedForward(GetPointer(State),1,false,NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); ExpertRemove(); return; } Convolution.getResults(temp); state_embedding.Row(temp,state); temp.Assign(Buffer[tr].States[st].rewards); next.Assign(Buffer[tr].States[st + 1].rewards); rewards.Row(temp - next * DiscFactor,state); state++; if(GetTickCount() - ticks > 500) { string str = StringFormat("%-15s %6.2f%%", "Embedding ", state * 100.0 / (double)(total_states)); Comment(str); ticks = GetTickCount(); } } }
经验回放缓冲区中的所有样本编码完成后,从矩阵中删除多余的行。
if(state != total_states)
{
rewards.Resize(state,NRewards);
state_embedding.Reshape(state,state_embedding.Cols());
total_states = state;
}
接下来是直接模型训练模块。在此,我们初始化局部变量,并创建一个模型训练循环。循环迭代次数由外部 Iterations 变量确定。
vector<float> rewards1, rewards2; int bar = (HistoryBars - 1) * BarDescr; for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++) { int tr = (int)((MathRand() / 32767.0) * (total_tr - 1)); int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2)); if(i < 0) { iter--; continue; }
在循环的主体中,我们对环境的轨迹和单独状态进行取样,以便更新当前迭代的模型参数。
然后,我们检查使用目标模型的阈值。如有必要,我们将后续状态数据加载到相应的数据缓冲区当中。
target_reward = vector<float>::Zeros(NRewards); reward.Assign(Buffer[tr].States[i].rewards); //--- Target TargetState.AssignArray(Buffer[tr].States[i + 1].state); if(iter >= StartTargetIter) { float PrevBalance = Buffer[tr].States[i].account[0]; float PrevEquity = Buffer[tr].States[i].account[1]; Account.Clear(); Account.Add((Buffer[tr].States[i + 1].account[0] - PrevBalance) / PrevBalance); Account.Add(Buffer[tr].States[i + 1].account[1] / PrevBalance); Account.Add((Buffer[tr].States[i + 1].account[1] - PrevEquity) / PrevEquity); Account.Add(Buffer[tr].States[i + 1].account[2]); Account.Add(Buffer[tr].States[i + 1].account[3]); Account.Add(Buffer[tr].States[i + 1].account[4] / PrevBalance); Account.Add(Buffer[tr].States[i + 1].account[5] / PrevBalance); Account.Add(Buffer[tr].States[i + 1].account[6] / PrevBalance); double x = (double)Buffer[tr].States[i + 1].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_MN1); Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_W1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_D1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); //--- if(Account.GetIndex() >= 0) Account.BufferWrite();
准备好的数据用于执行扮演者和两个目标评论者模型的前向验算。
if(!Actor.feedForward(GetPointer(TargetState), 1, false, GetPointer(Account))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } //--- if(!TargetCritic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)) || !TargetCritic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
基于贯穿目标模型的直接验算结果,我们将准备后续状态值的向量。此外,我们将根据 SMAC 算法添加潜在状态的熵估值。
TargetCritic1.getResults(rewards1); TargetCritic2.getResults(rewards2); if(rewards1.Sum() <= rewards2.Sum()) target_reward = rewards1; else target_reward = rewards2; for(ulong r = 0; r < target_reward.Size(); r++) target_reward -= Buffer[tr].States[i + 1].rewards[r]; target_reward *= DiscFactor; target_reward[NRewards - 1] = EntropyLatentState(Actor); }
在准备好后续状态的成本向量后,我们转入操控选定的环境状态,并用相应的源数据填充必要的缓冲区。
//--- Q-function study State.AssignArray(Buffer[tr].States[i].state); float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; Account.Clear(); Account.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); Account.Add(Buffer[tr].States[i].account[1] / PrevBalance); Account.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); Account.Add(Buffer[tr].States[i].account[2]); Account.Add(Buffer[tr].States[i].account[3]); Account.Add(Buffer[tr].States[i].account[4] / PrevBalance); Account.Add(Buffer[tr].States[i].account[5] / PrevBalance); Account.Add(Buffer[tr].States[i].account[6] / PrevBalance); double x = (double)Buffer[tr].States[i].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_MN1); Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_W1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_D1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(Account.GetIndex() >= 0) Account.BufferWrite();
然后,我们执行扮演者的前向验算,生成环境的潜在状态。
if(!Actor.feedForward(GetPointer(State), 1, false, GetPointer(Account))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
在更新评论者参数阶段,我们仅使用潜伏状态。我们从经验回放缓冲区中获取扮演者的动作,并调用两个评论者的前向验算。
Actions.AssignArray(Buffer[tr].States[i].action); if(Actions.GetIndex() >= 0) Actions.BufferWrite(); //--- if(!Critic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions)) || !Critic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
评论者的参数会参考来自环境的实际奖励进行更新,并根据当前扮演者政策调整。扮演者更新政策的影响参数已在后续环境状态的成本向量中考虑在内。
我要提醒您,我们应用了分解的奖励函数,并调用 CAGrad 方法来优化梯度。这导致每个评论者的引用值向量不同。首先,我们准备一个引用值向量,并执行一次贯穿第一个评论者的逆向验算。
Critic1.getResults(rewards1); Result.AssignArray(CAGrad(reward + target_reward - rewards1) + rewards1); if(!Critic1.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) || !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
然后我们针对第二个评论者重复操作。
Critic2.getResults(rewards2); Result.AssignArray(CAGrad(reward + target_reward - rewards2) + rewards2); if(!Critic2.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) || !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
注意,在更新每个评论者参数后,我们执行逆向验算,以便更新编码器参数。另外,不要忘记在每个阶段控制过程。
更新评论者参数后,我们继续优化扮演者模型。为了判定扮演者级别的误差梯度,我们将使用评论者来预测扮演者动作成本的最小移动平均误差。该方式会让我们更准确地估算扮演者政策生成的动作,作为结果,分布误差梯度更准确。
//--- Policy study CNet *critic = NULL; if(Critic1.getRecentAverageError() <= Critic2.getRecentAverageError()) critic = GetPointer(Critic1); else critic = GetPointer(Critic2);
我们之前已经运作了扮演者的前向验算。现在,我们将制定环境的预测性后续状态。“预测性”是此处的一个关键词。毕竟,经验回放缓冲区包含有关价格走势和指标的历史数据。它们不依赖于扮演者动作,因此我们可以安全地使用它们。不过,账户的状态直接取决于扮演者执行的交易操作。扮演者当前政策中的动作也许与经验回放缓冲区中存储的动作不同。在这个阶段,我们必须形成一个描述账户状态的预测向量。为了方便我们行事,此功能已在上一篇文章中讨论的 ForecastAccount 方法中实现。现在我们只需要调用它,并传输正确的初始数据。
Actor.getResults(rewards1); double cl_op = Buffer[tr].States[i + 1].state[bar]; double prof_1l = SymbolInfoDouble(_Symbol, SYMBOL_TRADE_TICK_VALUE_PROFIT) * cl_op / SymbolInfoDouble(_Symbol, SYMBOL_POINT); vector<float> forecast = ForecastAccount(Buffer[tr].States[i].account,rewards1,prof_1l, Buffer[tr].States[i + 1].account[7]); TargetState.AddArray(forecast);
现在我们已有所有必要的数据,我们执行选定评论者和随机卷积编码器的前向验算,以便生成预测性后续状态的嵌入。
if(!critic.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)) || !Convolution.feedForward(GetPointer(TargetState))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
基于获得的数据,我们形成奖励函数的引用值向量,更新扮演者参数。此外,我们确保调用 CAGrad 方法校正误差梯度。
next.Assign(Buffer[tr].States[i + 1].rewards); Convolution.getResults(rewards1); target_reward += KNNReward(KNN,rewards1,state_embedding,rewards) + next * DiscFactor; if(forecast[3] == 0.0f && forecast[4] == 0.0f) target_reward[2] -= (Buffer[tr].States[i + 1].state[bar + 6] / PrevBalance); critic.getResults(reward); reward += CAGrad(target_reward - reward);
之后,我们禁用评论者参数更新模式,并执行其逆向验算,然后执行扮演者的完整逆向验算。
Result.AssignArray(reward); critic.TrainMode(false); if(!critic.backProp(Result, GetPointer(Actor)) || !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); critic.TrainMode(true); break; } critic.TrainMode(true);
确保监控整个过程。成功完成两个模型的逆向验算之后,我们返回到评论者训练模式。
在此阶段,我们更新了评论者和扮演者的参数。我们所要做的就是更新评论者目标模型的参数。在此,我们取在 EA 外部参数中设置的 Tau 比率软性更新模型参数。
//--- Update Target Nets TargetCritic1.WeightsUpdate(GetPointer(Critic1), Tau); TargetCritic2.WeightsUpdate(GetPointer(Critic2), Tau);
在模型训练循环主体中的操作结束时,我们通知用户训练过程的进度,并进入循环的下一次迭代。
if(GetTickCount() - ticks > 500) { string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic1", iter * 100.0 / (double)(Iterations), Critic1.getRecentAverageError()); str += StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic2", iter * 100.0 / (double)(Iterations), Critic2.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } }
模型训练循环的所有迭代成功完成之后,我们清除图表上的注释字段。在日志中显示训练结果,并启动 EA 终止。
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic1", Critic1.getRecentAverageError()); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic2", Critic2.getRecentAverageError()); ExpertRemove(); //--- }
您也许已经注意到,在训练扮演者时,我跳过了 SMAC 方法提供的潜在状态熵分量的计算。我决定不把奖励向量分解为单独的部分。在构建 NNM 算法时,此过程已移至单独的 KNNReward 方法。正是在该方法中,我进行了必要的调整。
如前,我们首先检查方法主体中预测性状态嵌入的大小,与经验回放缓冲区中环境状态嵌入矩阵的对应关系。
vector<float> KNNReward(ulong k, vector<float> &embedding, matrix<float> &state_embedding, matrix<float> &rewards ) { if(embedding.Size() != state_embedding.Cols()) { PrintFormat("%s -> %d Inconsistent embedding size", __FUNCTION__, __LINE__); return vector<float>::Zeros(0); }
控制模块成功通过之后,我们初始化必要的局部变量。
ulong size = embedding.Size(); ulong states = state_embedding.Rows(); k = MathMin(k,states); ulong rew_size = rewards.Cols(); vector<float> distance = vector<float>::Zeros(states); matrix<float> k_rewards = matrix<float>::Zeros(k,rew_size); matrix<float> k_embeding = matrix<float>::Zeros(k + 1,size); matrix<float> U,V; vector<float> S;
准备工作阶段至此完毕,我们直接转入计算操作。首先,我们判定自预测性状态至来自经验回放缓冲区实际样本的距离。
for(ulong i = 0; i < size; i++) distance+=MathPow(state_embedding.Col(i) - embedding[i],2.0f); distance = MathSqrt(distance);
定义 k-最近邻,并填充嵌入矩阵。此外,我们将相应的奖励转移到预先准备好的矩阵当中。同时,我们按与状态向量之间的距离成反比的比率调整奖励向量。指定的比率将根据更新的行为政略,判定经验回放缓冲区中的奖励对扮演者所选动作的结果影响。
for(ulong i = 0; i < k; i++) { ulong pos = distance.ArgMin(); k_rewards.Row(rewards.Row(pos) * (1 - MathLog(distance[pos] + 1)),i); k_embeding.Row(state_embedding.Row(pos),i); distance[pos] = FLT_MAX; }
将环境预测性状态的嵌入添加到嵌入矩阵的最后一个字符串之中。
k_embeding.Row(embedding,k);
求解结果嵌入矩阵的奇异值向量。使用内置矩阵操作即可轻松执行此操作。
k_embeding.SVD(U,V,S);
我们形成奖励向量,作为相应的针对参与率调整的 k-最近邻奖励的平均值。
vector<float> result = k_rewards.Mean(0);
分别使用扮演者政策的核范数和潜在状态,以熵分量填充奖励向量的最后两个元素。
result[rew_size - 2] = S.Sum() / (MathSqrt(MathPow(k_embeding,2.0f).Sum() * MathMax(k + 1,size))); result[rew_size - 1] = EntropyLatentState(Actor); //--- return (result); }
生成的奖励向量将返回给调用程序。所有其它 EA 方法均已转移,未进行任何更改。
模型训练 EA 的工作到此结束。本文中用到的所有程序的完整代码可在附件中找到。到了测试时间了。
3. 测试
在本文的实践部分,我们已做了大量实现工作,把随机边际扮演者-评论者方法并入到之前实现的 NNM 算法 EA 当中。现在,我们转入测试已完成工作的阶段。始终如一,这些模型在 EURUSD H1 上进行训练和测试。所有指标采用默认参数。
现在已经是 9 月份了,故我把训练期提升至 2023 年的 7 个月。我们将使用 2023 年 8 月的历史数据测试该模型。
我已经提到了 NNM 方法的功能,且在创建 “...\NNM\Study.mq5” 训练 EA 时经验回放缓冲区中缺少生成的状态。然后我们决定降低一个训练循环的迭代次数。我们将坚持与训练模型相关的相同方法。
与上一篇文章中使用的训练过程类似,我们不会从整体上降低经验回放缓冲区。但同时,我们将逐步填充经验回放缓冲区。在第一次迭代中,我们启动训练数据收集 EA,执行 100 次验算。在指定的历史间隔内,这已经为我们提供了近 360K 的训练模型状态。
在模型训练的第一次迭代之后,我们用另外 50 次验算来补充样本数据库。因此,我们逐渐用训练政策框架内相应扮演者行为的新状态填充经验重放缓冲区。
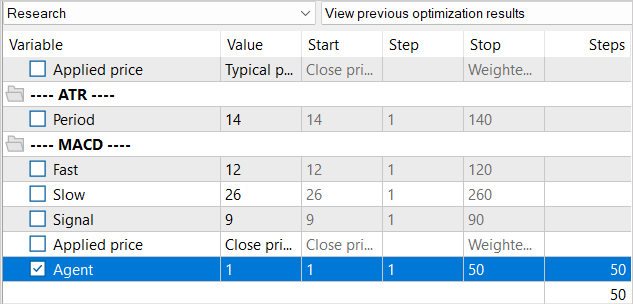
我们重复训练模型的过程,并多次收集其它样本,直到达到训练扮演者政策的预期结果。
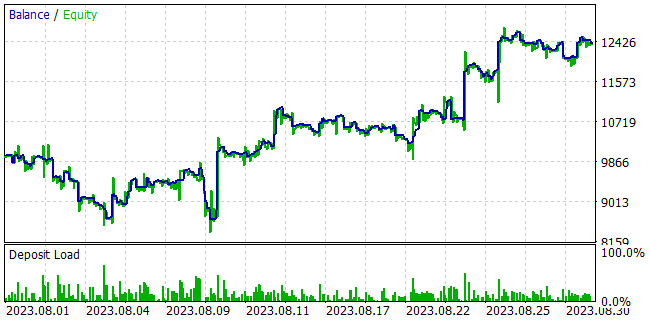
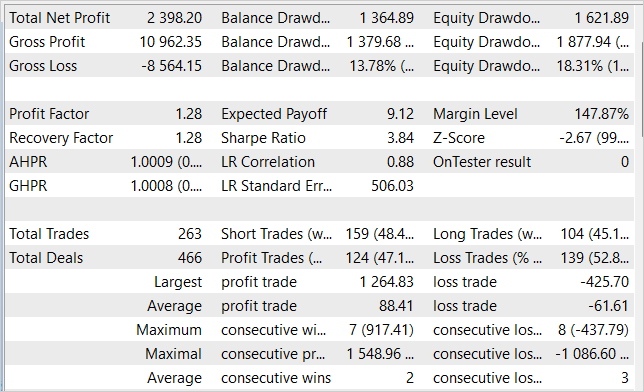
在训练模型时,我们设法获得了一个扮演者政策,其能够在训练样本上产生利润,并将获得的知识推广到后续环境状态。例如,在策略测试器中,我们训练的模型能够在训练样本之后的一个月内产生 23.98% 的盈利。在测试期间,该模型执行了 263 次交易操作,其中 47% 以盈利了结。每笔交易的最大盈利几乎是最大亏损交易的 3 倍。每笔交易的平均盈利比平均亏损高 44%。所有这些加在一起令我们能够获得 1.28 的盈利因子。该图形展示了余额线的明显上升趋势。
结束语
本文认为随机边际扮演者-评论者方法为解决强化学习问题提供了一种创新方法。基于最大熵原理,SMAC 允许智能体更有效地探索环境,并更稳健地学习,这是通过引入额外的随机潜在变量节点来实现的。
在智能体的政策中使用潜在变量,可显著提高其表现力,以及在观察和奖励中对随机性进行建模的能力。
然而,在训练含有潜在变量的政策方面存在一些困难。方法作者提供了应对这些困难的解决方案。
在实践部分,我们成功地将 SMAC 集成到 NNM 方法架构当中,创建了一种简单有效的政策优化方法,并经测试结果得以验证。我们已能够训练每月产生高达 24% 回报的扮演者政策。
考虑到这些结果,SMAC 方法是解决实际问题的有效解决方案。
然而,请记住,本文中讲述的所有程序都只是为了演示该方法而创建的,不适合在真实帐户上工作。它们需要额外的功能配置和优化。
我要提醒您,金融市场是一种高风险的投资类型。您或您的电子交易工具执行的交易,其所有风险完全由您自行承担。
链接
文中所用程序
| # | 名称 | 类型 | 说明 |
|---|---|---|---|
| 1 | Research.mq5 | 智能交易系统 | 样本收集 EA |
| 2 | Study.mq5 | 智能交易系统 | 智能体训练 EA |
| 3 | Test.mq5 | 智能交易系统 | 模型测试 EA |
| 4 | Trajectory.mqh | 类库 | 系统状态定义结构 |
| 5 | NeuroNet.mqh | 类库 | 创建神经网络的类库 |
| 6 | NeuroNet.cl | 代码库 | OpenCL 程序代码库 |
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/13290
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 开发回放系统(第31部分):EA交易项目——C_Mouse类(五)
开发回放系统(第31部分):EA交易项目——C_Mouse类(五)
测试 EA 的每一次通过都会产生截然不同的结果,就好像该模型与之前的所有模型都不同一样。很明显,模型在每次通过测试时都会发生变化,但该 EA 的行为几乎没有发生变化,那么其背后的原因是什么呢?
下面是一些图片:
该模型采用随机政治行为。因此,在研究的开始阶段,我们可以看到每一次交易都是随机的。我们收集这些通行证,然后重新开始模型研究。然后重复这个过程若干次。当行动者找到好的行动策略时,我们就可以开始研究了。
让我们换一种方式来回答这个问题。在收集(研究)样本并对其进行处理(研究)后,我们运行测试脚本。在没有任何 "研究 "或 "学习 "的情况下,连续运行几次后得到的结果完全不同。
测试脚本在 OnInit 子程序(第 99 行)中加载经过训练的模型。在这里,我们为 EA 提供了一个在测试处理过程中不应发生变化的模型。据我所知,它应该是稳定的。这样,最终结果就不会改变。
在此期间,我们不进行任何模型训练。测试 "只会收集更多样本。
随机性是在研究模块中观察到的,也可能是在优化策略时在研究模块中观察到的。
Actor 在第 240 行被调用,以计算前馈结果。如果它在创建时不是随机初始化的,我相信情况就是这样,它的行为不应该是随机的。
您是否发现上述推理中有任何误解?
让我们换一种方式来回答这个问题。在收集(研究)样本并对其进行处理(研究)后,我们运行测试脚本。在没有进行任何研究的情况下,连续运行几次后,得到的结果完全不同。
测试脚本在 OnInit 子程序(第 99 行)中加载经过训练的模型。在这里,我们为 EA 提供了一个在测试处理过程中不应发生变化的模型。据我所知,它应该是稳定的。那么,最终结果也不应该发生变化。
在此期间,我们不进行任何模型训练。测试只会收集更多样本。
随机性在 "研究 "模块中观察到,也可能在 "学习 "模块优化策略时观察到。
Actor 在第 240 行被调用,以计算前馈结果。如果在创建时没有随机初始化(我认为是这样的),那么它的行为就不应该是随机的。
您是否发现上述推理中有任何误解?
Actor 使用随机策略。我们通过VAE 实现了它。
层 CNeuronVAEOCL 使用前一层的数据作为高斯分布的均值和 STD,并从该分布中采样相同的动作。一开始,我们在模型中加入随机权重。因此,它会产生随机均值和 STD。最后,我们在模型测试的每一关都有随机动作。在研究时,模型会为每个状态找到一些均值,而 STD 则趋向于零。