Kombinatorik und Wahrscheinlichkeitsrechnung für den Handel (Teil IV): Bernoulli-Logik

Inhalt

• Einführung
• Die Bedeutung einer korrekten Datenrepräsentation bei der Analyse
• Doppelte Zustände
• Mehrere Zustände
• Software-Implementierung der Mehrfachzustände
• Schlussfolgerung
• Referenzen

Einführung

In den vorangegangenen Artikeln dieser Reihe habe ich Fraktale als ein Instrument zur Beschreibung von Märkten und insbesondere der Preisbildung beschrieben. Dieses Modell beschreibt den Markt perfekt — dies wurde durch Berechnungen und Simulationen bestätigt. Ursprünglich sollte es nicht nur die einfachsten Formen der Preisbildung beschreiben, sondern auch die weitere Beschreibung beliebiger Vektorreihen ermöglichen, die einen Parametersatz haben, der dem der Preisbildung ähnelt. Nun, im allgemeinen Fall stellt sich heraus, dass ein Handel auch ein Teil des Marktes ist, der durch eine zeitliche Dauer und eine Wahrscheinlichkeit des Auftretens im Handelsprozess gekennzeichnet ist. Beliebige Kurven können sowohl aus Preisen als auch aus Handelspositionen erstellt werden. Bei den Kursen ist diese Kurve die Kurshistorie, bei den Handelspositionen ist es die Handelshistorie.

Der Fall mit den Kursen ist viel klarer, da alle Elemente einer solchen Reihe eindeutig aufeinander folgen. Natürlich ist es möglich, solche Preisreihen zu erstellen, die sich gegenseitig überschneiden, aber diese Analyse wäre absolut nutzlos, da sie keinen praktischen Nutzen hätte. Der Fall der Backtests oder der Handelshistorie ist komplizierter. Bei der Untersuchung dieser Prozesse bin ich zu dem Schluss gekommen, dass es einen viel einfacheren und korrekteren Weg zu profitablem und stabilem Handel gibt — durch die Analyse der Handelshistorie oder der der Backtests. Es wird einen abschließenden Artikel geben, in dem einer dieser Ansätze beschrieben wird, aber dafür ist es im Moment noch zu früh.

Die Bedeutung einer korrekten Datenrepräsentation bei der Analyse

Wenn wir uns mit der Analyse der Möglichkeiten befassen, Handelshistorie und Backtests in der Sprache der Mathematik zu beschreiben, müssen wir zunächst den Zweck und das mögliche Ergebnis einer solchen Analyse verstehen. Bringt eine solche Analyse irgendeinen zusätzlichen Nutzen? Tatsächlich ist es unmöglich, auf Anhieb eine klare Antwort zu geben. Aber es gibt eine Antwort, die schrittweise zu einfachen und funktionierenden Lösungen führen kann. Allerdings sollten wir uns zunächst mit mehr Details befassen. Angesichts der Erfahrungen aus früheren Artikeln haben mich die folgenden Fragen interessiert:

1. Ist es möglich, jede Strategie auf eine fraktale Beschreibung des Handels zu reduzieren?
2. Wenn dies möglich ist, wo wäre es sinnvoll?
3. Wenn es nicht immer möglich ist, was sind die Bedingungen für die Reduzierbarkeit?
4. Wenn die Bedingungen für die Reduzierbarkeit erfüllt sind, entwickle Reduktionsalgorithmus.
5. Ziehe andere Möglichkeiten zur Beschreibung der Strategie in Betracht. Verallgemeinerung

Die Antworten auf all diese Fragen lauten wie folgt. Es ist möglich, einige Strategien auf eine fraktale Beschreibung zu reduzieren. Ich habe diesen Algorithmus entwickelt und werde ihn weiter beschreiben. Er ist auch für andere Zwecke geeignet, da es sich um ein universelles Fraktal handelt. Lassen Sie uns nun nachdenken und versuchen, die folgende Frage zu beantworten: Was ist die Handelsgeschichte in der Sprache der Zufallszahlen und der Wahrscheinlichkeitstheorie? Die Antwort ist einfach: Es handelt sich um eine Menge isolierter Entitäten oder Vektoren, deren Auftreten in einem bestimmten Zeitraum eine bestimmte Wahrscheinlichkeit und einen bestimmten Zeitnutzungsfaktor hat. Das Hauptmerkmal jeder dieser Entitäten ist die Wahrscheinlichkeit ihres Auftretens. Der Zeitnutzungsfaktor ist ein Hilfswert, mit dessen Hilfe bestimmt werden kann, wie viel der verfügbaren Zeit für den Handel genutzt wird. Die folgende Abbildung kann helfen, die Idee zu verstehen:

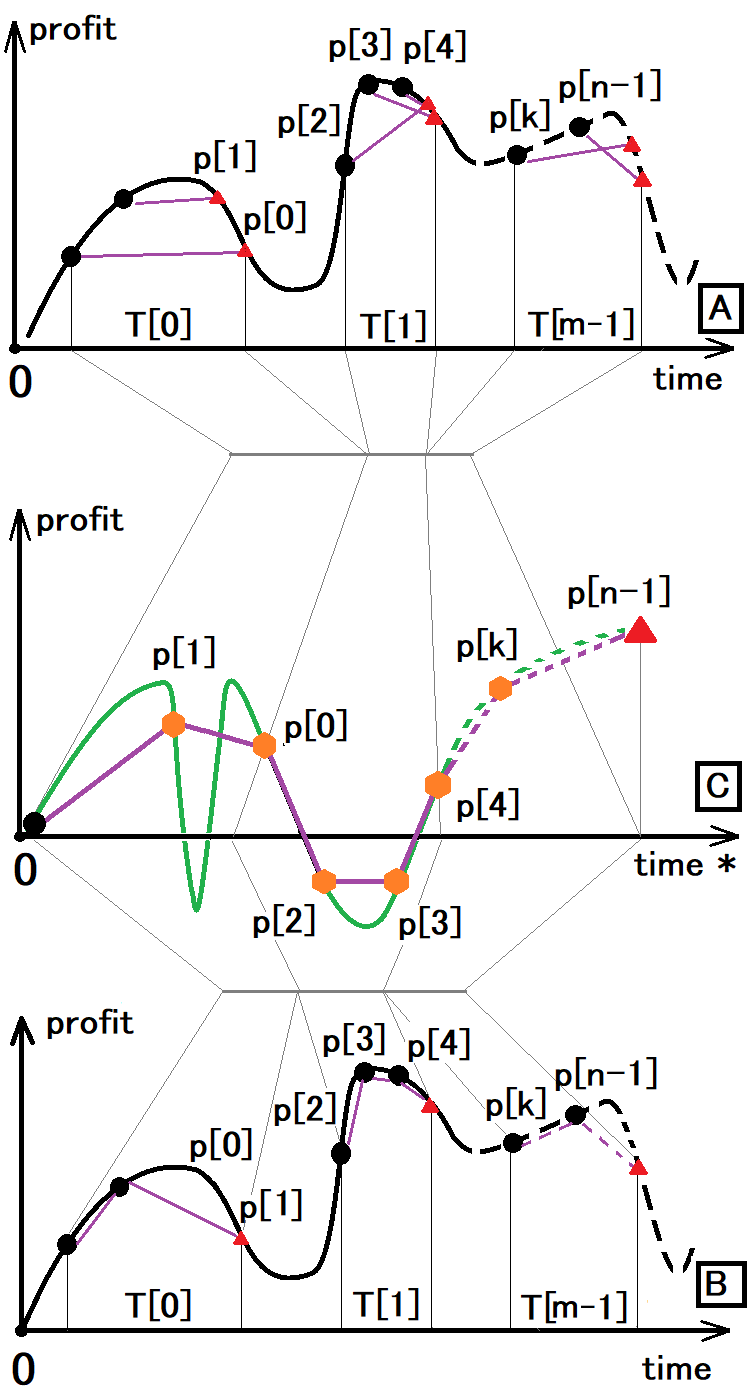
In der Abbildung werden die folgenden Symbole verwendet:

1. Schwarzer Punkt - der Beginn des Handels
2. Rotes Dreieck - das Ende des Handels
3. Orangefarbenes Sechseck - sowohl das Ende des vorherigen Handels als auch der Beginn des nächsten Handels
4. T[i] - Zeitpunkt eines relevanten Handelsfensters
5. p[i] - Gewinn oder Verlust einer relevanten Handelsposition
6. n - Anzahl der Positionen
7. m - Anzahl der Handelsfenster

Die Abbildung zeigt drei Charts, um zu demonstrieren, dass die Optionen A und B auf die Option C reduziert werden können:

1. Option A ist die Art und Weise, wie wir willkürlichen Handel mit allen möglichen Tricks, Geldmanagement usw. sehen.
2. Option B ist die gleiche, nur dass jeweils nur eine Position offen sein darf.
3. Option C zeigt, wie wir den Handel entweder im Signalservice oder im Backtest sehen.

Hier ist Option C die informativste und in den meisten Fällen verlassen wir uns auf diese Darstellung des Handels. Darüber hinaus kann absolut jede Strategie auf diesen Typ reduziert werden, da die Equity-Linie das Hauptmerkmal eines jeden Backtests oder Handelssignals ist. Diese Linie spiegelt den tatsächlichen Gewinn oder Verlust zum aktuellen Zeitpunkt wider.

Die Analyse der Equity-Linie einer beliebigen Strategie würde zeigen, dass die Eröffnungs- und Schlusspunkte des Handels an absolut beliebigen Positionen liegen können, wenn die Linie unverändert bleibt. Das bedeutet, dass eine Handelsstrategie auf sehr viele verschiedene Arten dargestellt werden kann und alle diese Arten gleichwertig sind, da ihre Equity-Linien gleichwertig sind. Es hat also keinen Sinn, nach allen äquivalenten Möglichkeiten zu suchen. Welchen Sinn hat es, sie zu finden?

Eine Strategie des Typs B kann leicht in den Typ C umgewandelt werden, da wir nur die Zeitintervalle in der gleichen Reihenfolge zusammenkleben müssen, in der sie auftreten. Genau das tun der Tester und der Signaldienst auch. Anders sieht es aus, wenn Sie versuchen, Typ A in C umzuwandeln. Um diese Umwandlung durchzuführen, müssen wir zunächst A in Typ B reduzieren, und dann kann das Ergebnis in Typ C reduziert werden.

Diese Umwandlung an sich hat keinen praktischen Nutzen für den Handel. Sie kann jedoch helfen, die Dinge tiefgründiger zu verstehen. Wir können zum Beispiel feststellen, dass es die folgenden Arten von Strategien gibt:

1. Beschrieben durch zwei Zustände
2. Beschrieben durch mehrere Zustände
3. Beschrieben durch eine unendliche Anzahl von Zuständen

In diesem Artikel zeige ich Ihnen Beschreibungsbeispiele für die ersten beiden Arten von Strategien. Die dritte Art ist komplexer und erfordert einen eigenen Artikel. Ich werde zu gegebener Zeit auf diese Idee zurückkommen. Bevor wir uns mit der dritten Art von Strategien befassen, ist es jedoch notwendig, die ersten beiden zu verstehen. Diese beiden Typen bereiten uns auf den dritten, allgemeinen Strategietyp vor.

Doppelte Zustände

Die in früheren Artikeln beschriebenen Fraktale stellen eigentlich ein Modell mit zwei Zuständen dar. Hier sind die Zustände Aufwärts- und Abwärtsbewegungen. Wenn wir das Modell auf die Handelsbilanzlinie und nicht auf die Preisbildung anwenden, funktioniert dieses Modell auf genau dieselbe Weise. Das Modell basiert auf dem Bernoulli-Schema. Das Bernoulli-Schema beschreibt das einfachste Fraktal mit zwei Zuständen:

• p[k] = C(n,k)*Pow(p,k)*Pow(q,n-k) — Bernoulli-Formel (p[k] ist die Wahrscheinlichkeit für eine bestimmte Kombination)
• p ist die Wahrscheinlichkeit für den Zustand "1" als Ergebnis eines einzelnen Experiments
• q ist die Wahrscheinlichkeit für den Zustand "2" als Ergebnis eines einzelnen Experiments

Mit diesen Formeln lässt sich die Wahrscheinlichkeit berechnen, dass nach "n" Schritten eine Gleichgewichtskurve oder eine beliebige andere Kurve mit "k" ersten Zuständen und "n-k" zweiten Zuständen vorliegt. Diese müssen nicht unbedingt Handelsgewinne sein. Diese Zustände können jeden beliebigen Parametervektor symbolisieren, in dem wir Einzigartigkeit sehen. Die Summe aller Wahrscheinlichkeiten einer bestimmten Kombination muss eine vollständige Gruppe bilden, was bedeutet, dass die Summe aller dieser Wahrscheinlichkeiten gleich Eins sein muss. Dies symbolisiert die Tatsache, dass in "n" Schritten notwendigerweise eine dieser Kombinationen auftreten muss:

• Summ(0...k...n)[ p[k] ] = 1

In diesem Fall sind wir daran interessiert, diese Dinge zu verwenden, um entweder die Preisbildung oder Backtests und Signale zu beschreiben. Stellen wir sich vor, dass unsere Strategie aus Positionen besteht, die durch äquidistante Stop-Levels geschlossen werden. Gleichzeitig wissen wir, dass es unmöglich ist, die erwartete Preisbewegung in der Zukunft zu berechnen. Die Verteilung dieser Wahrscheinlichkeiten wird wie folgt aussehen:

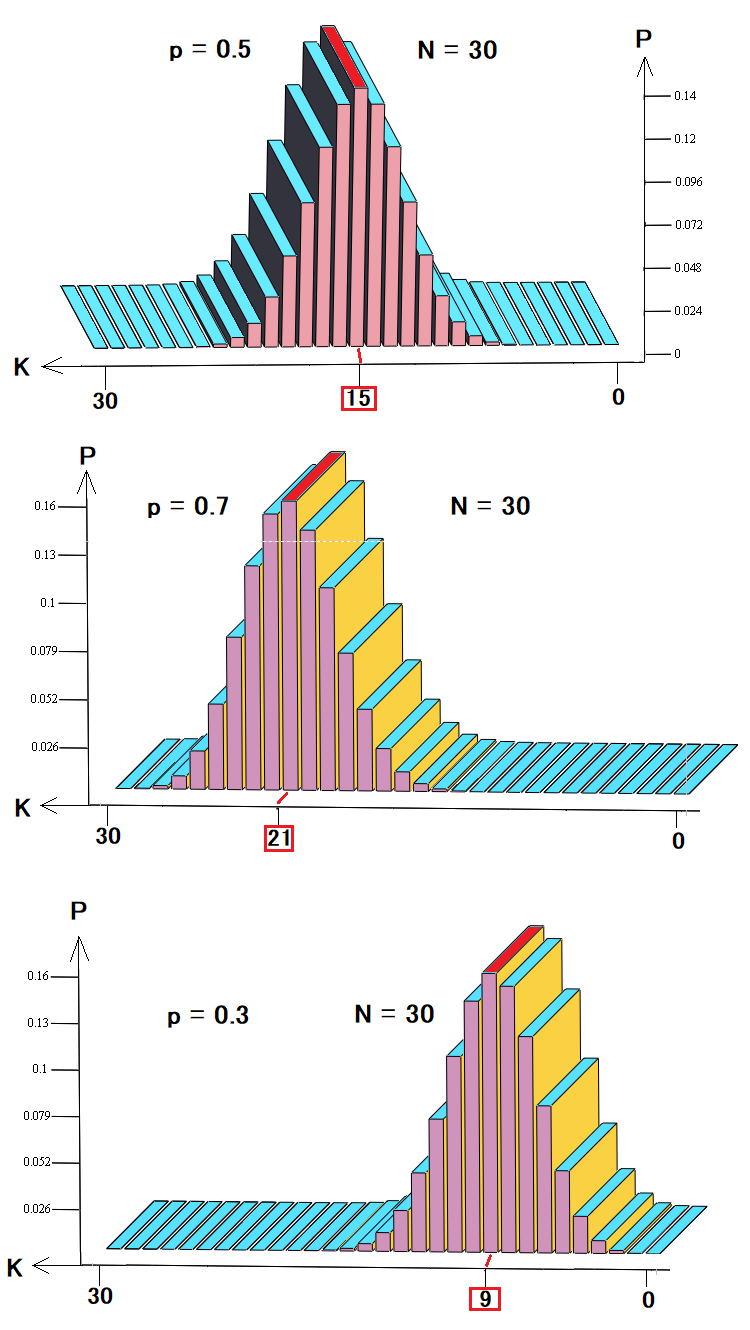
Diese drei Abbildungen zeigen:

1. Wahrscheinlichkeitsverteilung bei einem Random Walk oder dem Handel
2. Wahrscheinlichkeitsverteilung für profitables Handeln oder einen Aufwärtstrend
3. Wahrscheinlichkeitsverteilung für einen verlustreichen Handel oder einen Abwärtstrend

Wie aus den Diagrammen ersichtlich ist, ändern sich je nach Wahrscheinlichkeit eines Anstiegs die Wahrscheinlichkeiten bestimmter Kombinationen und der wahrscheinlichste Fall verschiebt sich nach links oder rechts, wie alle anderen Wahrscheinlichkeiten auch. Diese Backtest- oder Preisdarstellung ist das einfachste und bevorzugte Modell für die Analyse. Ein solches Modell ist völlig ausreichend, um die Preisbildung zu beschreiben; es reicht jedoch nicht aus, um den Handel zu beschreiben. Die Gleichgewichtskurve kann nämlich verschiedene Positionen enthalten, die sich in Bezug auf Dauer und Gewinn/Verlust unterscheiden. Je nachdem, welche Handelsmetriken wichtiger sind, können wir eine beliebige Anzahl von Zuständen festlegen, nicht nur zwei.

Mehrere Zustände

Betrachten wir nun das folgende Beispiel. Nehmen wir an, wir interessieren uns immer noch für Gewinn oder Verlust einer Position. Nun wissen wir, dass der Gewinn- oder Verlustzustand drei streng definierte Werte annehmen kann, und wir kennen die Wahrscheinlichkeiten für jeden der Werte. Wenn dies der Fall ist, können wir sagen, dass wir ein Drei-Zustands-System haben. Ist es möglich, alle möglichen Ereignisentwicklungen wie in einem Zwei-Zustands-System zu beschreiben? Ja, das ist möglich. Ich werde das Bernoulli-Schema leicht verbessern, so dass es mit einem System mit einer beliebigen Anzahl von Zuständen funktionieren kann.

Gemäß der Bernoulli-Logik müssen wir Zustandszähler definieren:

• i[0] ist die Anzahl der Ergebnisse mit dem ersten Zustand in einer Kette unabhängiger Experimenten
• i[1] ist die Anzahl der Ergebnisse mit dem zweiten Zustand in einer Kette unabhängiger Experimente
• . . .
• i[N] ist die Anzahl der Ergebnisse mit dem Nten Zustand
• N ist die Anzahl der Systemzustände
• s ist die Zustandsnummer

Wenn wir die Anzahl der Vorkommnisse eines bestimmten Zustands einzeln bestimmen, dann ist die verfügbare Anzahl für den nächsten Zustand:

• s[i] = N - Summ(0... k ... i - 1) [ s[k] ]

Dies kann vereinfacht werden. Wenn wir die Anzahl der Ergebnisse des vorherigen Zustands gewählt haben, dann bleibt die Anzahl der Ergebnisse für den nächsten Zustand genau gleich wie die Anzahl der Zustände, die für den vorherigen Zustand gewählt wurden. Genau wie im Bernoulli-Schema gibt es Wahrscheinlichkeitsketten, die inkonsistent sind und die gleiche Wahrscheinlichkeit haben. Die Anzahl der Ketten mit der gleichen Anzahl aller Zustände wird dann wie folgt berechnet:

• A[h](N,i[0] ,i[1] ,... i[n]) = C(N , i[0]) * C(N-i[0] , i[1]) *… . C(N-Summ(0...k...n-1)[ i[k] ] , i[n])
• C sind Kombinationen
• h ist eine eindeutige Reihe von Schritten

Natürlich können die Wahrscheinlichkeiten solcher Reihen wie im Bernoulli-Schema berechnet werden. Man multipliziert die Wahrscheinlichkeit einer Reihe mit ihrer Anzahl:

• p[k] = A[h](N,i[0] ,i[1] ,... i[n]) * Pow(p[0], i[0]) * Pow(p[1], i[1]) ... * Pow(1- Summ(0...j...N-1)[ p[j] ] , i[1])
• p[j] ist die Wahrscheinlichkeit für einen bestimmten Zustand

Der Übersichtlichkeit halber habe ich dreidimensionale Graphen erstellt, wie im vorherigen Beispiel für zwei Zustände. Wieder haben wir 30 Schritte, aber hier verwenden wir drei Zustände anstelle von zwei:

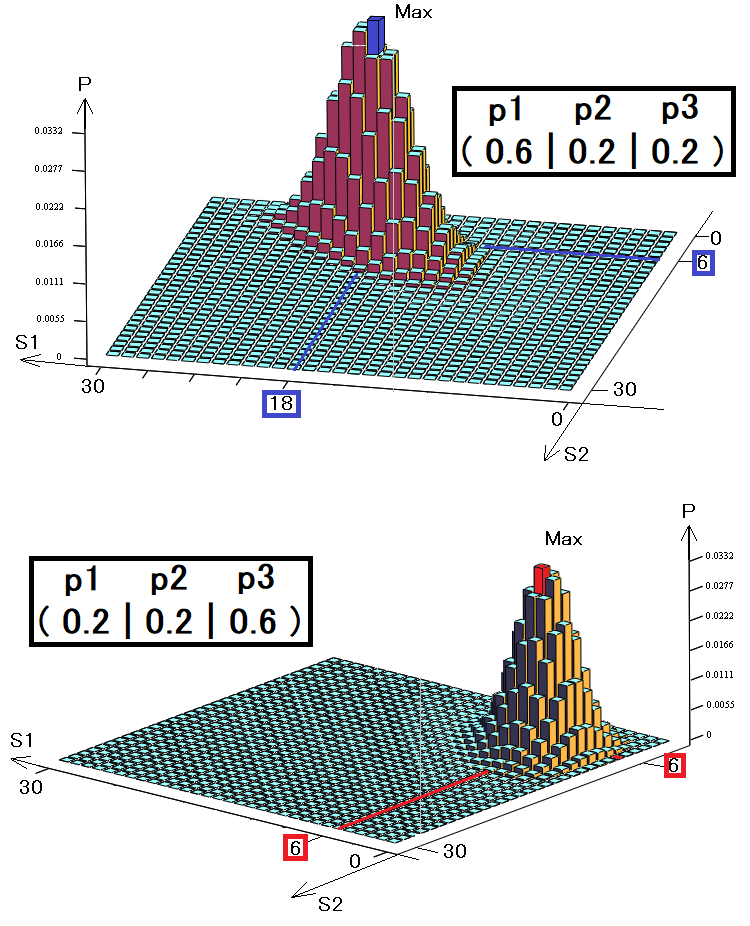
Das Volumen eines solchen Diagramms ist genau gleich eins, da jeder Balken ein unvereinbares Ereignis symbolisiert und alle diese unvereinbaren Ereignisse eine vollständige Gruppe bilden. Die Diagramme zeigen zwei verschiedene Strategien mit unterschiedlichen Wahrscheinlichkeitsvektoren. Diese Wahrscheinlichkeiten symbolisieren die Wahrscheinlichkeit des Eintretens eines der drei Zustände.

• S1 ist die Anzahl des Auftretens des ersten Zustands
• S2 ist die Anzahl des Auftretens des zweiten Zustands
• S3 = 30 - S1 - S2 - die Anzahl des Auftretens des dritten Zustands

Hätte unser System einen vierten Zustand, dann könnte es nur vierdimensional dargestellt werden. Für fünf Zustände bräuchten wir ein fünfdimensionales Diagramm, und so weiter. Für das menschliche Auge stehen nur 3 Dimensionen zur Verfügung, so dass komplexere Systeme nicht grafisch dargestellt werden können. Nichtsdestotrotz sind auch mehrdimensionale Funktionen funktional, genau wie die anderen.

Software-Implementierung der Mehrfachzustände

Die Fälle von zwei Zuständen können durch ein eindimensionales Array dargestellt werden. Was ist mit mehreren Zuständen? Wir können uns ein mehrdimensionales Array vorstellen. Aber soweit ich weiß, verwenden alle Programmiersprachen höchstens zweidimensionale Arrays. Vielleicht bieten einige die Möglichkeit, drei- oder mehrdimensionale Arrays zu erstellen, aber das ist keine praktische Option. Eine bessere Möglichkeit ist die Verwendung von Sammlungen oder Tupeln:

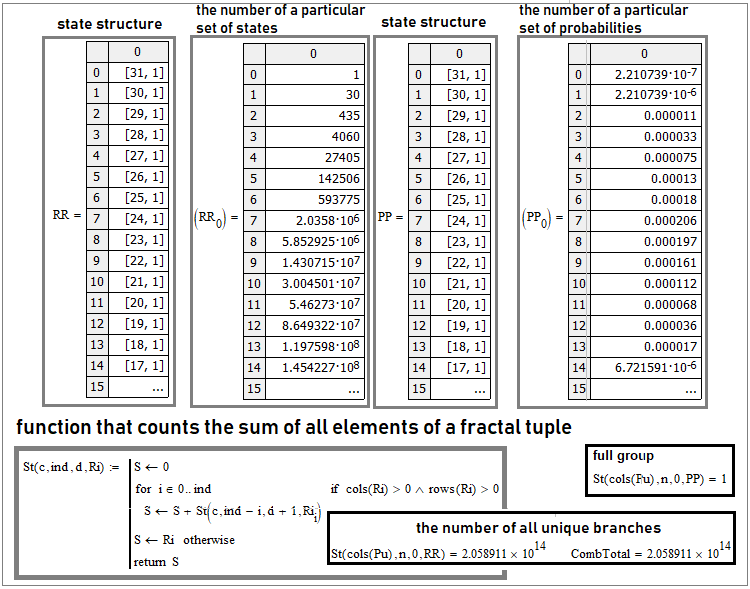
Dies ist der Fall bei "30" Schritten. Die erste und dritte Spalte spiegeln die interne Struktur des Tupels wider. Es handelt sich lediglich um ein Array innerhalb eines Arrays. Wenn zum Beispiel "[31,1]" geschrieben wird, bedeutet dies, dass dieses Matrixelement ebenfalls eine Matrix mit "31" Zeilen und einer Spalte ist. Die Bernoulli-Formel und das gesamte Bernoulli-Schema sind nur ein besonderer Fall dieses allgemeineren Schemas. Wenn zwei Zustände erforderlich sind, werden die Tupel zu eindimensionalen Arrays. In diesem Fall erhalten wir einfache Kombinationen, die in der Bernoulli-Formel die Schlüsselrolle spielen.

Wenn wir uns ansehen, was sich in diesen Feldern befindet, erhalten wir die Spalten "2" und "4". Die zweite Spalte ist die Anzahl der äquivalenten Verzweigungen bestimmter eindeutiger Zustandsgruppen, und die vierte ist die Gesamtwahrscheinlichkeit solcher Verzweigungen, da ihre Wahrscheinlichkeiten gleich sind.

Ein wirklich klares Kriterium zur Validierung der Berechnung solcher Tupel ist die Überprüfung der gesamten Gruppe von Ereignissen und der Gesamtzahl aller eindeutigen Verzweigungen. Zu diesem Zweck können wir eine allgemeine Funktion erstellen, die alle Elemente ihrer komplexen Tupel zusammenfasst, unabhängig davon, wie komplex ihre interne Struktur ist. Ein Beispiel ist im obigen Screenshot zu sehen. Eine solche Funktion muss wiederkehrend sein; sie sollte sich selbst im Inneren aufrufen — in diesem Fall ist sie eine universelle Funktion für eine beliebige Anzahl von Zuständen und eine beliebige Anzahl von Schritten. Die Anzahl der eindeutigen Verzweigungen wird wie folgt berechnet:

• Pow(N,n)

Mit anderen Worten, die Anzahl der Systemzustände muss mit der Anzahl der Schritte potenziert werden — auf diese Weise erhalten wir alle möglichen Kombinationen von eindeutigen Ketten, die aus unseren Zuständen bestehen. In der Abbildung ist diese Zahl als Variable "CombTotal" dargestellt. Die resultierende Summe wird mit dieser Variablen verglichen.

Um die Tupel zu zählen, sollten wir ähnliche Funktionen mit der gleichen, wiederkehrenden Struktur verwenden:

Wie man sehen kann, sind sie sich sehr ähnlich. Es gibt nur ein paar Unterschiede. Auf jeder Stufe müssen wir das Ergebnis zusätzlich mit der Anzahl der Kombinationen auf den verbleibenden freien Stufen multiplizieren. Bei der Berechnung der Wahrscheinlichkeiten muss das Ergebnis zusätzlich mit der Wahrscheinlichkeit des gerade untersuchten Zustands multipliziert werden. Vergessen Sie auch nicht, mit der bereits akkumulierten Wahrscheinlichkeit der Kette zu multiplizieren. Kumulieren Sie nach und nach alle Zustände, bis keine freien Zellen mehr übrig sind, wobei die Zellen die Anzahl der Schritte darstellen.

Wir können auch ein Beispiel für die Extraktion von Zuständen aus den uns bekannten Daten betrachten. Wir haben zum Beispiel eine Handelsstatistik, in der für jede Position die folgenden Informationen gespeichert sind: Laufzeit, Handelsvolumen, Verlust oder Gewinn usw. Da die Stichprobe endlich ist, ist auch die Anzahl der Zustände endlich. So lässt sich beispielsweise feststellen, wie viele Gewinnmöglichkeiten es in der Stichprobe gibt. Jeder einzigartige Gewinnwert kann als einzigartiger Zustand betrachtet werden. Zählen Sie die Anzahl der Vorkommen all dieser Gewinne in der gesamten Stichprobe, teilen Sie durch die Gesamtzahl aller Geschäfte und erhalten Sie die Wahrscheinlichkeit eines bestimmten Zustands. Wiederholen Sie diesen Vorgang für alle Zustände. Wenn wir dann alle diese Wahrscheinlichkeiten zusammenzählen, erhalten wir eins. In diesem Fall ist alles richtig gemacht worden. In ähnlicher Weise können wir den Handel nach der Laufzeit der Order klassifizieren. Mit anderen Worten: Ein Zustand kann jedes eindeutige Merkmal eines Ereignisses sein. In diesem Fall wird ein Handel als ein Ereignis betrachtet, während die Handelsparameter die Merkmale eines bestimmten Ereignisses sind. In unserem Fall können die Zustandsbeispiele wie folgt aussehen:

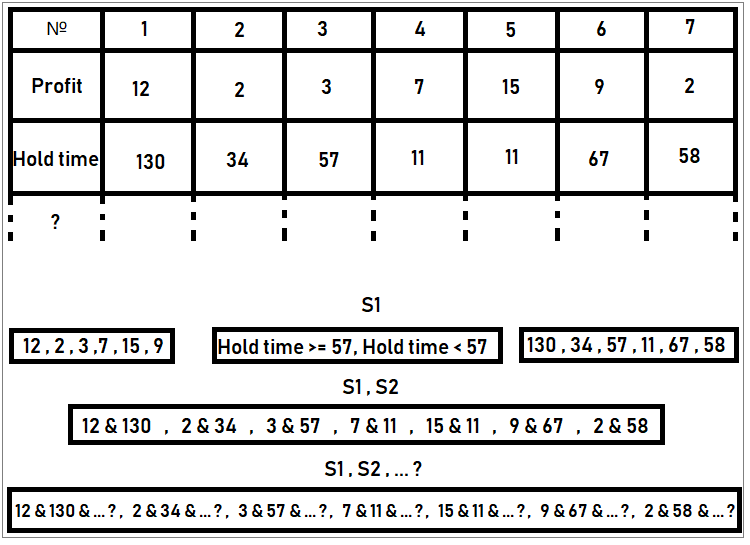
Die Abbildung zeigt ein Beispiel für die Zusammenstellung von Zustandsgruppen. Gemäß den Regeln sollten die Zustände eine vollständige Gruppe von Ereignissen bilden, d. h. es sollten keine gemeinsamen Zustände vorhanden sein. Die Wahrscheinlichkeit dieser Ereignisse kann berechnet werden, indem die Anzahl der Positionen in der Tabelle mit bestimmten Zuständen durch die Anzahl aller Positionen (in unserem Fall 7) geteilt wird. Dies war das Beispiel der Positionen; wir können jedoch auch mit beliebigen anderen Zuständen arbeiten.

Schlussfolgerung

In diesem Artikel habe ich versucht zu zeigen, wie man Datenstichproben auswertet, wie man aus solchen Stichproben neue macht, indem man die Daten klassifiziert und zu Zustandsmengen kombiniert, deren Wahrscheinlichkeiten berechnet werden können. Was Sie mit diesen Daten machen, bleibt Ihnen überlassen. Meiner Meinung nach ist es am besten, mehrere Stichproben zu erstellen und diese auszuwerten — dies wird auch als Stichproben-Clustering bezeichnet. Das Clustering von Stichproben kann als guter Filter dienen, um die Leistung bestehender Systeme im Handel zu verbessern. Es kann auch verwendet werden, um aus einer scheinbar unrentablen Strategie einen Gewinn zu erzielen — einfach die Daten clustern und die gewünschten profitablen Muster finden. Und vor allem können solche Mechanismen als Datenverarbeitungsstufen in skalierbaren Handelssystemen eingesetzt werden. Wir werden diese Mechanismen später in der Praxis anwenden, wenn wir dazu übergehen, ein sich selbst anpassendes Handelssystem zusammenzustellen. Für den Moment ist dies nur ein weiterer Baustein.

Referenzen

• Kombinatorik und Wahrscheinlichkeitsrechnung für den Handel (Teil I): Die Grundlagen
  
• Kombinatorik und Wahrscheinlichkeitsrechnung für den Handel (Teil II): Das universelle Fraktal
  
• Kombinatorik und Wahrscheinlichkeitsrechnung für den Handel (Teil III): Das erste mathematische Modell