取引のための組合せ論と確率論(第IV部): ベルヌーイの定理

目次

• はじめに
• 分析における正しいデータ表現の重要性
• 2ステート
• 複数状態
• ソフトウェアによる複数状態の実装
• 終わりに
• 参照資料

はじめに

連載のこれまでの記事では、市場、特に価格設定を説明するためのツールとしてフラクタルについて説明しました。このモデルが市場を完全に説明するということは、計算とシミュレーションによって確認されています。本来の目的は、最も単純な価格設定形式を説明することだけでなく、パラメータの価格設定セットに類似したパラメータのセットを持つ任意のベクトル系列を詳細に説明できるようにすることでもありました。一般的なケースでは、取引も市場の一部であることがわかります。これは、期間と取引プロセスに現れる確率によって特徴付けられます。価格と取引の両方からは任意の曲線を作成できます。この曲線は、価格の場合は価格履歴で取引の場合は取引履歴です。

価格系列ではすべてのメンバーが明らかにお互いを従っているので、価格の場合ははるかに明確です。もちろん、互いに重なり合うような価格系列を作成することは可能ですが、そのような分析からの実際的な利益がないため、この分析は絶対に役に立たないでしょう。バックテスト、または取引履歴の場合は、より複雑になります。これらのプロセスを研究したとき、私は、取引履歴またはバックテストの分析を通じて、収益性が高く安定した取引へのはるかに簡単で正しい道があるという結論に達しました。これらのアプローチの1つは最後の記事で説明しますが、現時点では時期尚早です。

分析における正しいデータ表現の重要性

取引履歴とバックテストを数学の言語で記述する可能性の分析を検討する場合、まずそのような分析の目的と考えられる結果を理解する必要があります。そのような分析に付加価値はあるのでしょうか。実際、すぐに明確な答えを出すことは不可能ですが、答えは存在し、徐々に単純で実用的な解決策につながる可能性があります。ただし、まず詳細を掘り下げる必要があります。以前の記事での経験から、次の質問に興味を持ちました。

1. ストラテジーを取引のフラクタル記述に単純化することは可能でしょうか。
2. 単純化が可能であれば、それはどこで役に立つのでしょうか。
3. 単純化が常に可能であるとは限らない場合、単純化が可能な条件は何でしょうか。
4. 単純化が可能な条件が満たされている場合は、単純化のアルゴリズムを開発します
5. ストラテジーを説明する他のオプションを検討します - 一般化

これらすべての質問に対する答えは次のとおりです。一部のストラテジーはフラクタル記述に単純化することができます。このアルゴリズムを開発したので、これについてさらに説明します。それはユニバーサルフラクタルであるため、他の目的にも適しています。ここで、取引履歴とは乱数と確率論の言語では何であるかという質問について考えて答えてみましょう。答えは簡単です。取引履歴は孤立したエンティティまたはベクトルのセットであり、特定の期間での発生には特定の確率と時間利用率があります。そのような各エンティティの主な特徴は、その発生の確率です。時間利用率は、利用可能な時間のどれだけが取引に使用されているかを判断するのに役立つ補助値です。次の図は、この概念を理解するのに役立ちます。

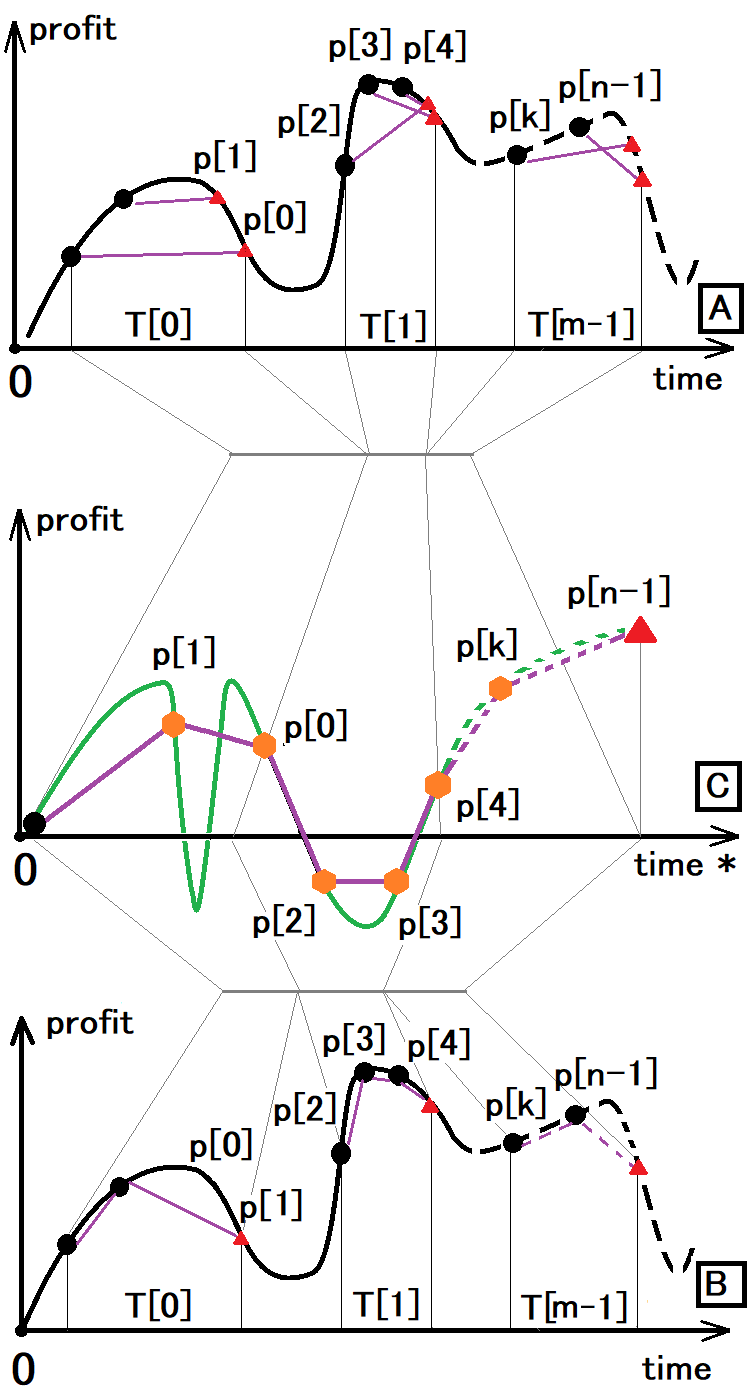
この図では、次の記号が使用されています。

1. 黒い点 - 取引の始まり
2. 赤い三角形 - 取引の終わり
3. 橙色の六角形 - 前の取引の終わりと次の取引の始まりの両方
4. T[i] – 関連する取引ウィンドウの時間
5. P[i] –関連する取引の利益または損失
6. n – 取引数
7. m – 取引ウィンドウの数

この図は、オプションAとBをオプションCに単純化することができることを示す3つのグラフを示しています。次に、これらのオプションが何であるかを見てみましょう。

1. オプションAは、考えられるすべてのトリック、資金管理などを使用して、任意の取引をどのように見るかです。
2. オプションBは同じですが、一度に1つの注文しか持てないことを考慮しています。
3. オプションCは、シグナルサービスまたはバックテストで取引をどのように見るかです。

ここではオプションCが最も有益なものであり、ほとんどの場合、この取引の表現に依存しています。さらに、エクイティラインがバックテストまたは取引シグナルの主な特徴であるため、すべてのストラテジーは絶対的にこのタイプに単純化することができます。このラインは、現時点での実際の利益または損失を反映しています。

任意のストラテジーでのエクイティラインの分析は、ラインが変更されないままである場合、取引の開始点と終了点を絶対的に任意の位置に配置できることを示します。つまり、取引ストラテジーは非常に多くの異なる方法で表すことができるが、それらのエクイティラインが同等であるため、これらすべての方法が同等であるということです。したがって、同等のオプションをすべて検索しても意味がありません。それらを見つける目的は何でしょうか。

タイプBのストラテジーは、発生するのと同じ順序で時間間隔を結合するだけでよいため、タイプCに簡単に変換できます。実際、これはまさにテスターとシグナルサービスが行うことです。タイプAをタイプCに変換しようとすると、状況が異なります。この変換を実装するには、まずAをBに単純化し、次に結果をCに縮小する必要があります。これで、ストラテジーテスターとシグナルサービスがどのように動作するかがわかります。

この変換自体は取引に実用的な価値をもたらすことはありませんが、より深いことを理解するのに役立ちます。たとえば、次のタイプのストラテジーがあると結論付けることができます。

1. 2つの状態によって説明される
2. 複数の状態によって記述される
3. 無限数の状態によって記述される

本稿では、最初の2つのタイプのストラテジーの説明例を示します。3番目のタイプはより複雑で、別の記事が必要です。やがてこの考えに戻ります。何にしても、3番目のタイプのストラテジーを検討する前に、最初の2つを理解する必要があります。これらの2つのタイプは、3番目の一般的なストラテジータイプに進む前に心を整えます。

2ステート

以前の記事で説明されているフラクタルは、実際には2つの状態のモデルを表しています。ここでの状態とは上向きと下向きの動きのことです。価格設定の代わりに取引バランスラインにモデルを適用すると、このモデルはまったく同じように機能します。モデルはベルヌーイスキームに基づいています。ベルヌーイスキームは、2つの状態を持つ最も単純なフラクタルを記述します。

• P[k] = C(n,k)*Pow(p,k)*Pow(q,n-k)   — ベルヌーイの公式(P[kは特定の組み合わせの確率です)
• pは、単一の実験の結果としての状態「1」の確率です。
• qは、単一の実験の結果としての状態「2」の確率です。

これらの式は、「n」ステップ後に、「k」の最初の状態と「n-k」の2番目の状態を持つバランス曲線またはその他の曲線を持つ確率を計算できます。これらは取引の利益である必要はありません。これらの状態は、一意性が見られる任意のパラメーターベクトルを象徴することができます。特定の組み合わせのすべての確率の合計は、完全なグループを形成する必要があります。つまり、そのようなすべての確率の合計は1に等しくなければなりません。これは、「n」ステップでそのような組み合わせの1つが必ず現れる必要があるという事実を象徴しています。

• Summ(0...k…n)[ P[k] ] = 1

この場合、これらを使用して、価格設定またはバックテストとシグナルのいずれかを説明することに関心があります。このストラテジーが等距離のストップレベルで決済された取引で構成されていると想像してください。同時に、将来の予想価格変動を計算することは不可能であることが分かっています。これらの確率の分布は次のようになります。

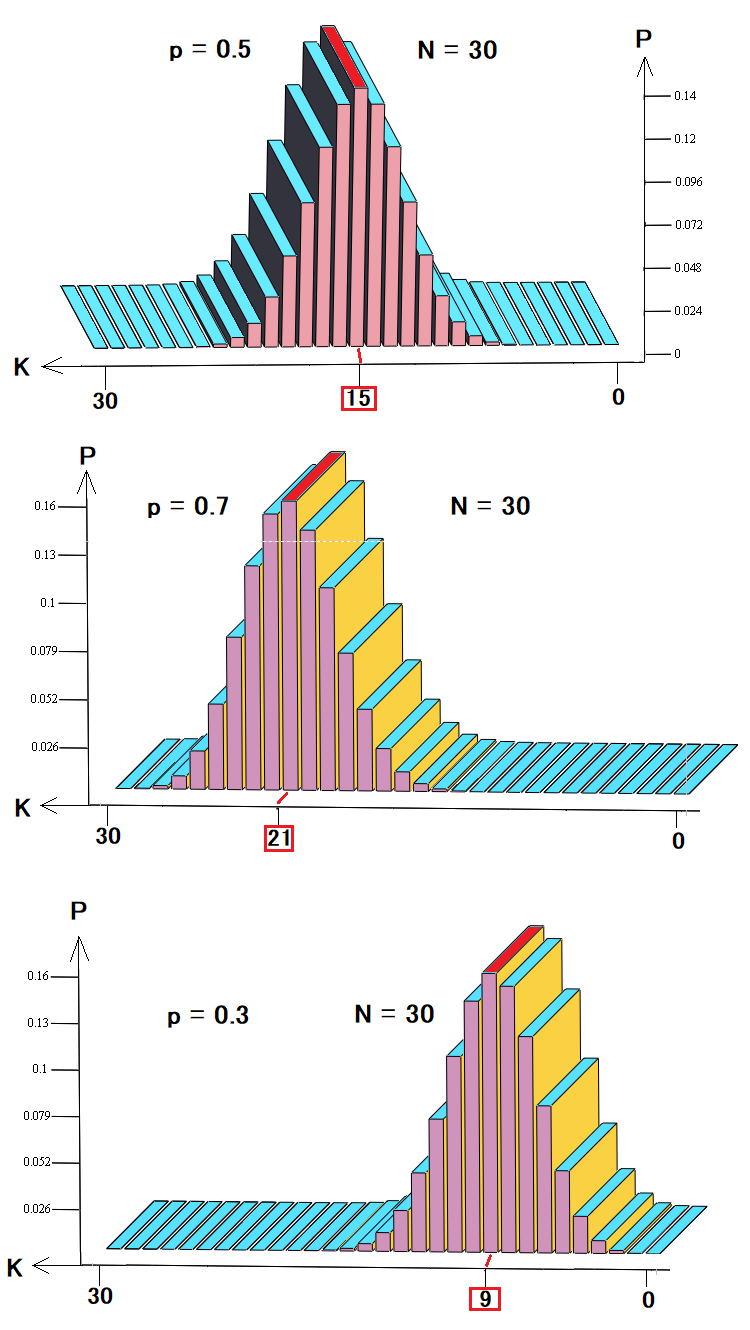
これらの3つの図は、次のことを示しています。

1. ランダムウォークまたは取引における確率分布
2. 収益性の高い取引または上昇トレンドの確率分布
3. 収益性のない取引または下降トレンドの確率分布

図からわかるように、ステップアップの確率に応じて、特定の組み合わせの確率が変化し、他のすべての確率と同様に、最も可能性の高いケースが左または右にシフトします。このバックテストまたは価格設定の表現は、最も単純で分析に好ましいモデルです。このようなモデルは、価格設定を説明するのには十分ですが、取引について説明するには不十分です。実際、バランス曲線には、期間と利益/損失の点で異なるさまざまな取引が含まれる可能性があります。どの取引指標がより重要であるかに応じて、2つだけでなく、任意の数の状態を設定できます。

複数状態

それでは、次の例を考えてみましょう。取引の利益または損失の額にはまだ関心があると仮定します。利益または損失の状態が3つの厳密に定義された値を取ることができることと各値の確率はわかっています。この場合は3ステートシステムがあると言えます。2ステートシステムのように、考えられるすべてのイベントの進展を説明することは可能でしょうか。実は可能です。ベルヌーイスキームを少し改善して、任意の数の状態のシステムで機能できるようにします。

ベルヌーイの定義によって、状態カウンタを定義する必要があります。

• i[0] – 一連の独立した実験の最初の状態での結果の数
• i[1]は、一連の独立した実験における2番目の状態の結果の数です。
• の利用をお勧めします。の利用をお勧めします。の利用をお勧めします。
• i[N]は、N –状態の結果の数です。
• Nはシステム状態の数です
• sは状態番号です

特定の状態の発生数を1つずつ決定すると、次の状態で使用可能な数は次のようになります。

• s[i]  = N - Summ(0… k … i - 1) [ s[k] ]

これは簡略化できます。前の状態の結果の数を選択した場合、次の状態の結果の数は、前の状態に対して選択された状態の数とまったく同じままです。ベルヌーイスキームと同様に、一貫性がなく、同じ確率を持つ確率の連鎖があります。次に、すべての状態の数が同じである連鎖の数は、次のように計算されます。

• A[h](N,i[0]  ,i[1] ,… i[n]) = C(N , i[0]) * C(N-i[0] , i[1]) *…. C(N-Summ(0…k…n-1)[ i[k] ] , i[n])
• Cは組み合わせです
• hは一意の一連のステップです

明らかに、そのようなセットの確率はベルヌーイスキームのように計算できます。1つのセットの確率にそれらの数を乗算します。

• P[k] = A[h](N,i[0]  ,i[1] ,… i[n]) * Pow(p[0], i[0]) * Pow(p[1], i[1]) … * Pow(1- Summ(0…j…N-1)[ p[j] ] , i[1])
• p [j]は特定の状態の確率です

わかりやすくするために、前の2つの状態の例のように、3次元グラフを作成しました。ここでも、30のステップがありますが、ここでは2つではなく3つの状態を使用します。

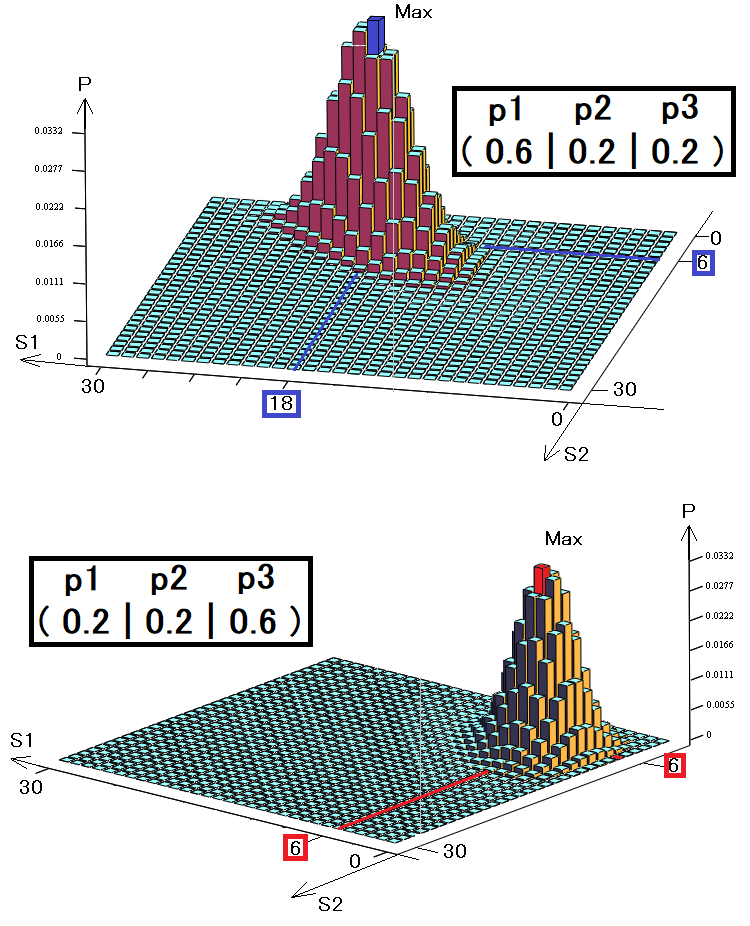
各バーは互換性のないイベントを表し、これらの互換性のないイベントはすべて完全なグループを形成するため、このような図のボリュームは正確に1になります。これらの図は、確率ベクトルが異なる2つの異なるストラテジーを示しています。これらの確率は、3つの状態のうちの1つが発生する可能性を象徴しています。

• S1は、最初の状態の発生数です。
• S2は、2番目の状態の発生数です。
• S3 = 30 – S1 – S2 – 第3の状態の発生数

システムに第4の状態があったならば、4次元でしか提示できません。5つの状態の場合、5次元の図が必要になる..などです。人間の目では、3次元しか使用できないため、より複雑なシステムをグラフィカルに表現することはできません。それにもかかわらず、多次元関数も他の関数と同じように機能します。

ソフトウェアによる複数状態の実装

2つの状態のケースは、1次元配列で表すことができます。複数の状態はどうでしょうか。多次元配列について考えるかもしれません。しかし、私が知る限り、すべてのプログラミング言語は多くても2次元配列を使用します。おそらく、3次元以上の配列を作成する可能性を提供するものもありますが、これは便利なオプションではありません。より良いオプションは、コレクションまたはタプルを使用することです。

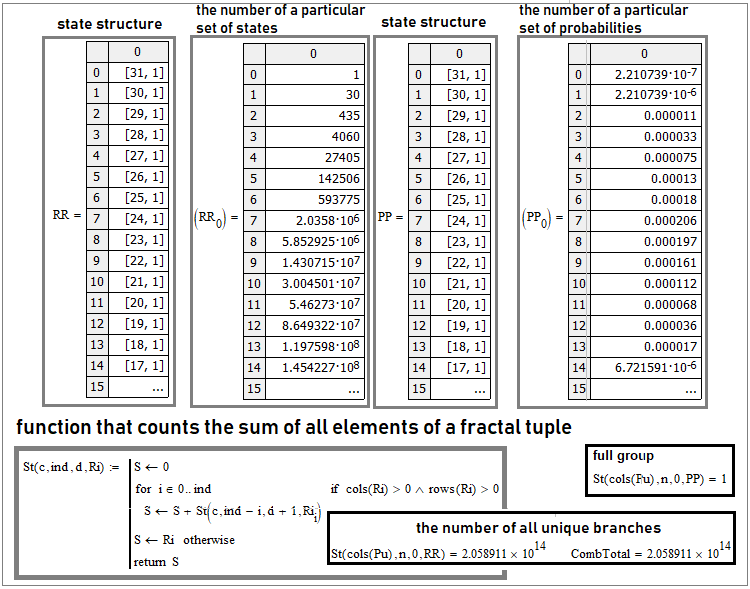
これは「30」ステップの状況です。1列目と3列目は、タプルの内部構造を反映しています。これは、配列内の単なる配列です。たとえば「[31,1]」と書かれている場合、この行列要素は31行と1列の行列です。ベルヌーイの公式とベルヌーイスキーム全体は、このより一般的なスキームの特定のケースにすぎません。2つの状態が必要な場合、タプルは1次元配列に変わります。その場合、ベルヌーイの公式で重要な役割を果たす単純な組み合わせが得られます。

これらの配列の内部には、列「2」と「4」があります。列「2」は、特定の一意の状態セットの同等のブランチの数であり、列「4」は、確率が等しいため、そのようなブランチの合計確率です。

このようなタプルの計算を検証するための真に明確な基準は、イベントの完全なグループとすべての一意のブランチの総数を確認することです。これを行うには、内部構造がどれほど複雑であっても、複雑なタプルのすべての要素を合計する一般的な関数を作成できます。上のスクリーンショットに例を示します。このような関数は再帰的である(内部でそれ自体を呼び出す)必要があります。この場合、それは任意の数の状態と数のステップに対して普遍的な関数になります。一意のブランチの数については、真の値は次のように計算されます。

• Pow(N,n)

言い換えると、システム状態の数をステップ数の累乗で増やす必要があります。そうすれば、状態で構成される一意の連鎖のすべての可能な組み合わせを取得できるようになります。この図では、この数値は「CombTotal」変数として示されています。結果の合計は、この変数と比較されます。

タプルをカウントするには、同じ繰り返し構造を持つ同様の関数を使用します。

ご覧のとおり、それらは非常に似ており、違いは数点のみです。各レベルで、残りの空きステップの組み合わせの数を結果に追加で乗算する必要があります。確率を計算するときは、結果に現在調査中の状態の確率を追加で乗算する必要があります。また、連鎖のすでに蓄積された乗算を掛けることを忘れないでください。セルはステップ数であり、空きセルがなくなるまで、すべての状態を1つずつ蓄積します。

また、既知のデータから状態を抽出する例を検討することもできます。たとえば、取引統計があり、注文ごとに、機嫌、取引量、損失/利益などの情報が格納されます。サンプルは有限であるため、状態の数も有限です。たとえば、サンプルにいくつの利益オプションがあるかを判断できます。それぞれの固有の利益値は、固有の状態と見なすことができます。サンプル全体でそのようなすべての利益の発生数を数え、すべての取引の総数で割って、特定の状態の確率を取得します。すべての状態でこれを繰り返します。その後これらすべての確率を合計すると1になります。この場合、すべてが正しく行われています。同様の方法で、注文の存続期間によって取引を分類できます。言い換えると、状態はイベントの任意の固有の特性である可能性があります。この場合、取引はイベントと見なされますが、取引パラメータは特定のイベントの特性です。状態の例は次のようになります。

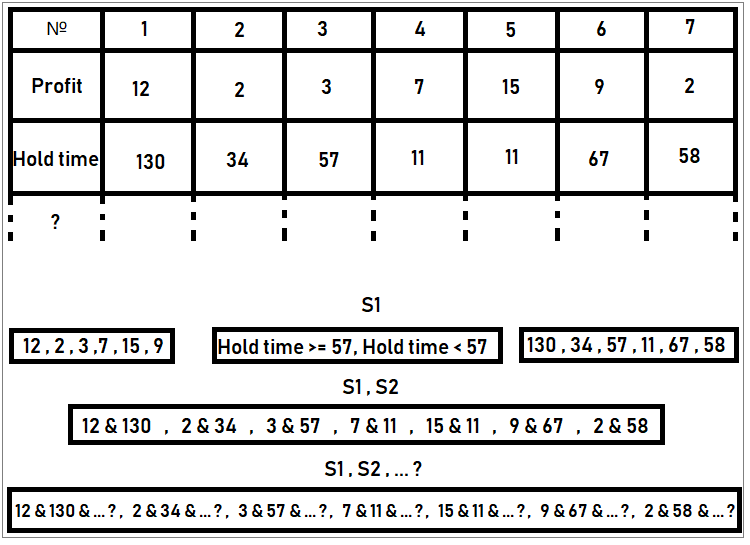
この図は、状態のセットをコンパイルする例を示しています。規則によれば、状態はイベントの完全なグループを形成する必要があります。つまり、そこに共同状態があってはなりません。これらのイベントの確率は、特定の状態のテーブル内の注文数をすべての注文数(この場合は7)で割ることによって計算できます。これは注文の例でしたが、他のどの状態とも連携できます。

終わりに

本稿では、データサンプルを評価する方法と、データを分類して確率を計算できる状態のセットに結合することにより、そのようなサンプルから新しいサンプルを作成する方法を示しました。このデータをどうするかはあなた次第です。複数のサンプルを作成して評価するのが最善の方法だと思います。これはサンプルクラスタリングとも呼ばれます。サンプルクラスタリングは、既存のシステムの取引パフォーマンスを向上させるための優れたフィルタとして機能します。また、データをクラスター化して、目的の収益性の高いサンプルを見つけるだけで、一見収益性の低いストラテジーから利益を得るのにも使用できます。そして最も重要なことに、このようなメカニズムは、スケーラブルな取引システムのデータ処理ステージとして使用できます。これらのメカニズムは、後で自己適応型取引システムの構築に移るときに実際に適用されます。今のところ、これは単なる別のレンガです。

参照資料

• 取引のための組合せ論と確率論(第I部):基本
  
• 取引のための組合せ論と確率論(第II部): ユニバーサルフラクタル
  
• 取引のための組合せ論と確率論(第III部): 初めての数学モデル