Yeniden alma algoritması: Verimliliği artırmak için matematiksel bir model

İçindekiler

• Giriş
• Ortalama alma algoritmasına dayalı alım-satım özelliklerini iyileştirme yöntemleri
• "Düşüşten kurtulmama yardım edin"
• Ortalama alma algoritması hakkında genel düşünceler
• Yeniden alma sistemlerinin daha doğru bir şekilde değerlendirilmesinin incelikleri
• Kârlılığın derinlemesine ve evrensel olarak anlaşılması
• Evrensel değerlendirme
• Netleştirme yöntemlerine örnekler
• Çeşitlendirme ile sistemlerin verimliliğinin artırılması
• Yararlı limitler
• Birden fazla enstrümanın paralel kullanımı açısından faydalı özellikler
• Rastgele bir değişkenin normal dağılımı
• Rastgele değerler dağılımı yasası çerçevesinde kâr eğrisi güzelliği
• Sonuç

Giriş

Bu alım-satım yöntemi, çok çeşitli Uzman Danışmanlarda aktif olarak kullanılmaktadır. Üstelik birçok çeşidi ve melezi vardır. Ayrıca, bu tür sistemlere yapılan atıfların sayısına bakılırsa, bu konunun sadece bu sitede değil, diğer web kaynaklarında da çok popüler olduğu açıktır. Tüm yöntem çeşitleri, piyasa hareketine karşı alım-satımı içeren ortak bir konsepte sahiptir. Başka bir deyişle, Uzman Danışman mümkün olduğunca düşüşten alış yapabilmek ve mümkün olduğunca yüksekten satış yapabilmek için yeniden alımları kullanır.

Bu çok eski, klasik bir alım-satım planıdır. Önceki makalelerimden birinde bu konuya kısmen değinmiş ve bu tür yöntemleri melezleştirmenin olası yollarını vurgulamıştım. Bu makalede, forum kullanıcılarının yaptığından daha derine inerek kavrama daha yakından bakacağız. Bununla birlikte, yeniden alma algoritması bazı çok ilginç ve kullanışlı özellikleri vurgulamak için çok uygun olduğundan, makale daha genel ve çok daha geniş olacaktır.

Ortalama alma algoritmasına dayalı alım-satım özelliklerini iyileştirme yöntemleri

"Düşüşten kurtulmama yardım edin" ("Uzman Danışmanım iyi para kazanıyor, ancak bazen tüm hesabı havaya uçuruyor" yazan kişilerden)

Bu, birçok algoritmik ve manuel yatırımcının ortak sorunudur. Bu makaleyi yazdığım sırada böyle bir kişiyle sohbet ettim, ancak kendisi benim bakış açımı bütünüyle kavrayamadı. Ne yazık ki, bana öyle geliyor ki, böyle bir durumun tüm komedisini anlama şansı neredeyse hiç yok. Ne de olsa benzer bir soruyu daha yaşlı ve deneyimli halime sorsaydım, büyük olasılıkla ben de cevabı anlayamazdım. Kendime vereceğim doğru cevapların beni nasıl hissettireceğini bile biliyorum. Aşağılandığımı ya da algoritmik alım-satımla daha fazla ilgilenmekten caydırıldığımı düşünürdüm.

Gerçekte her şey çok daha basittir. Sadece belli bir yolda yürümek ve biraz bilgelik kazanmak için sabrım vardı, tabii buna bilgelik denebilirse. Bu bir idealleştirme ve kendini övme değil, aksine gerekli bir asgari düzeydir. Bu yolun haftalar ve aylar yerine yıllar sürmesi üzücü.

Burada koca bir hayal ve kendini kandırma dünyası var ve dürüst olmak gerekirse, bazı insanların basitliğinden şimdiden sıkılmaya başladım. Lütfen saçma sapan işler yapmayı ve kendinizi piyasanın kralı sanmayı bırakın. Bunun yerine, deneyimli bir kişiyle iletişime geçin ve ondan bütçenize uygun bir Uzman Danışman seçmesini isteyin. İnanın bana, bu şekilde çok fazla zaman ve para tasarrufu yapacaksınız, akıl sağlığınızdan bahsetmiyorum bile. Bu makaleyi böyle bir kişi yazdı. Kanıtlar aşağıda verilmiştir.

Ortalama alma algoritması hakkında genel düşünceler

Yeniden alma algoritmasına veya "ortalama alma algoritmasına" bir göz atarsak, ilk olarak bu sistemin zarar riski yokmuş gibi görünebilir. Bu tür algoritmalar hakkında henüz hiçbir şey bilmediğim ve her türlü makası yenen büyük matematiksel beklentiler karşısında şaşırdığım zamanlar oldu. Şimdi bunun sadece bir yanılsama olduğu açıktır, yine de bu yaklaşımda rasyonel bir nokta vardır, ancak buna daha sonra değineceğiz. Öncelikle, bu tür sistemleri objektif bir şekilde değerlendirebilmek için, bize artan kârların basit bir görüntüsünden biraz daha fazlasını söyleyebilecek bazı dolaylı parametreleri bilmemiz gerekir.

Strateji sınayıcı raporundaki en alakalı parametreler, bakiye eğrisinin harika görünmesine rağmen sistemin açıkça kaybettiğini anlamaya bile yardımcı olabilir. Zaten anlamış olabileceğiniz gibi, her şey kârlılık eğrisiyle ilgilidir. Aslında, alım-satım sisteminin tüm önemli parametreleri, elbette matematiksel beklenti ve onun birincil özellikleri olan ilk ve en temel matematiksel özelliklere göre ikincildir. Ancak matematiksel beklentinin o kadar esnek bir değer olduğunu belirtmek gerekir ki, her zaman fazla iyimser düşünme tuzağına düşebilirsiniz.

Aslında, matematiksel beklenti gibi bir kavramı doğru bir şekilde kullanabilmek için, öncelikle bunun olasılık teorisinin terminolojisi olduğunu ve bu niceliğin herhangi bir hesaplamasının olasılık teorisinin kurallarına göre yapılması gerektiğini anlamak gerekir:

• Analiz edilen örneklem ne kadar büyük olursa hesaplamalar o kadar doğru olur, ideal olarak tam değer sonsuz bir örneklemden hesaplanır.
• Sonsuzluğu birkaç parçaya bölersek, birkaç sonsuzluk elde ederiz.

Birisi, elimizde yalnızca sınırlı sayıda gerçek fiyat örneklemi varsa, belirli bir stratejinin tam matematiksel beklentisini nasıl hesaplayacağımızı düşünebilir. Ve birileri bu sonsuzluklara neden ihtiyacımız olduğunu düşünecektir. Mesele şu ki, matematiksel beklenti gibi belirli ortalama değerlere ilişkin tüm hesaplamalar, yalnızca bu hesaplamaların yapıldığı alanda bir ağırlığa sahiptir, ancak başka bir alanla hiçbir ilgisi yoktur. Herhangi bir matematiksel özelliğin yalnızca hesaplandığı yerde ağırlığı vardır. Bununla birlikte, belirli bir stratejinin kârlılığının özelliklerini iyileştirmek için bazı teknikler ayırt edilebilir, bu da gerekli parametrelerin gerçek değerlerine en yakın değerlerin elde edilmesini mümkün kılacaktır.

Bu doğrudan bizim görevimizle ilgilidir. Sonsuz uzunluktaki bir stratejinin geleceğini göremeyeceğimizi fark ettikten sonra, ki bu zaten kendi içinde tamamen saçmalık gibi geliyor. Bununla birlikte, bu matematiksel bir gerçektir ve gerçek matematiksel özelliklerin hesaplanması için gerekli ve yeterli bir koşuldur. Sınırlı bir örneklem üzerinde hesaplanan sayıyı, sonsuz bir örneklem üzerinde hesaplanabilecek sayıya nasıl yaklaştırabileceğimiz fikrine geliyoruz. Matematiğe aşina olanlar, sonsuz toplamları hesaplamak için uygulanabilecek iki matematiksel kavram olduğunu bilirler:

• İntegral
• Sonsuz serilerin toplamı

İntegralin ve serilerin toplamının hesaplanabilmesi için, ya integrali hesaplanması gereken fonksiyonun dikkate alınan integral alanı içindeki tüm noktalarının ya da dikkate alınan seri içindeki sayı dizisinin tüm elemanlarının elde edilmesi gerektiğinin herkes için açık olduğunu düşünüyorum. Hala en mükemmel seçenek vardır - integralini alacağımız fonksiyon için uygun matematiksel ifadeleri ve serinin elemanlarını oluşturmak için ifadeyi elde etmek. Birçok durumda, uygun matematiksel ifadelere sahipsek, bitmiş integral veya serilerin toplamı için kesin denklemleri elde edebiliriz, ancak gerçek alım-satım durumunda, diferansiyel hesabı uygulayamayacağız ve genel olarak bu bize çok yardımcı olmayacak, ancak anlamak önemlidir.

Tüm bunlardan çıkan sonuç, herhangi bir sistemin doğrudan değerlendirilmesi için yalnızca sınırlı bir örnekleme ve strateji sınayıcıda elde ettiğimiz belirli parametrelere sahip olduğumuzdur. Aslında, önemleri büyük ölçüde abartılmaktadır. Strateji sınayıcı parametrelerini kullanarak belirli bir stratejinin kârlılığını değerlendirmenin mümkün olup olmadığı, bu parametrelerin kesin bir cevap için yeterli olup olmadığı ve en önemlisi bu parametrelerin nasıl doğru kullanılacağı ve gerçekten doğru kullanıp kullanmadığımız sorusu ortaya çıkmaktadır.

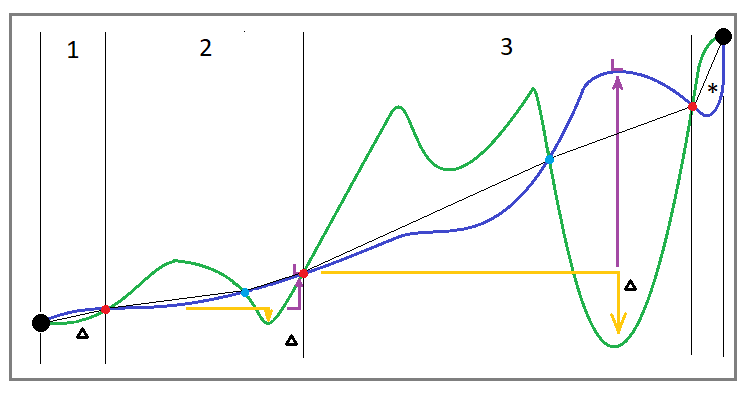
Ayrıca, her strateji için, stratejinin gerçek kârlılığını ve güvenliğini doğru bir şekilde değerlendirebileceğimiz herhangi bir parametrenin tamamen farklı olabileceğini anlamamız gerekir. Bu, kâr eğrisinin değerlendirilmesiyle doğrudan ilgilidir. Bunu anlamak için, öncelikle yeniden alma algoritmasını kullanırken elde ettiğimiz alım-satım eğrisinin yaklaşık genel bir görünümünü çizelim:

Şekil 1

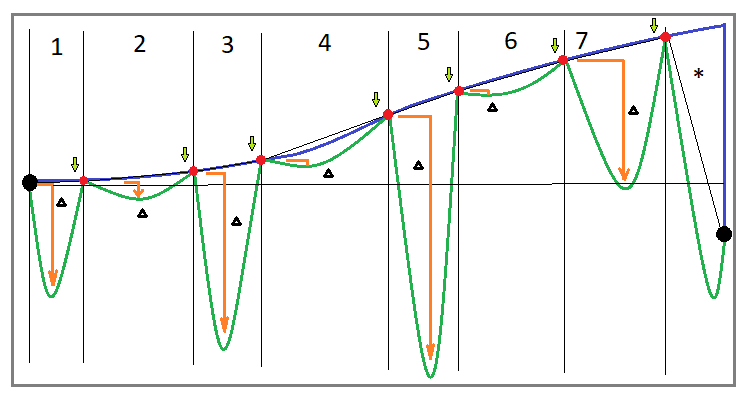
Tek bir enstrüman için yeniden alma algoritmasının uygulanmasıyla başlayalım. Bu algoritmayı doğru bir şekilde uygularsanız, alım-satımınız her durumda döngülerden oluşacaktır. İdeal olarak, tüm döngüler pozitif olmalıdır. Bazı döngüler negatif bölgede kapanıyorsa, ya bu algoritmayı yanlış uyguluyorsunuzdur ya da artık saf bir algoritma değildir ve içinde halihazırda değişiklikler vardır. Ancak biz klasik yeniden almayı ele alacağız. Klasik bir yeniden almayı ifade etmek için alım-satım eğrisinin bazı karakteristik parametrelerini tanımlayalım:

• Bakiye eğrisi büyümeli ve N döngüden oluşmalıdır
• Tüm döngülerin pozitif kârı vardır
• Alım-satım kesildiğinde, kendimizi tamamlanmamış son döngüde bulmamız muhtemeldir
• Tamamlanmamış döngü negatif kârlılığa sahiptir
• Döngülerin karakteristik para düşüşleri vardır.

Görünüşe göre eğrinin genel görünümü ilk bakışta böyle bir sistemin kârlı olduğunu açıkça ortaya koymalıdır, ancak her şey o kadar basit değildir. Başlangıç noktasının altında özellikle kapattığım son bitmemiş alım-satım döngüsüne bakarsanız, bazı durumlarda şanslı olacağınızı ve döngünün başarılı bir şekilde tamamlanmasını bekleyeceğinizi, bazı durumlarda ise sonuna kadar beklemeyebileceğinizi ve büyük bir kayıpla karşılaşabileceğinizi veya bakiyenizi tamamen havaya uçurabileceğinizi göreceksiniz. Bu neden oluyor? Mesele şu ki, görüntü, para düşüşü miktarının mutlak değeriyle sınırlı olduğu ve sonuç olarak bu düşüşte harcanan sürenin de sınırlı olması gerektiği konusunda yanlış bir izlenim verebilir.

Gerçekte, test alanı ne kadar uzun olursa, ortalama düşüş alanı da o kadar uzun olur. Burada kesinlikle bir sınır yoktur. Sınır yalnızca bakiyeniz ve para yönetiminizin kalitesi şeklinde mevcuttur. Bununla birlikte, sisteminizi bu ilkeye dayalı olarak kurmaya yönelik yetkin bir yaklaşım, bakiyenizin nihayetinde havaya uçmadan önce ömrünün artmasına veya en iyi ihtimalle çok az kâr elde etmenize yol açabilir.

Yeniden alma (ortalama alma) algoritmasına dayalı sistemleri test etmek söz konusu olduğunda, hayatta kalma kabiliyetini, güvenilirliğini ve gerçek kârlılığını doğru bir şekilde değerlendirmek için özel bir test yapısına uyulmalıdır. Bütün mesele, bu yaklaşımda tek bir testin değeri basit bir nedenden dolayı en aza inmektedir; herhangi bir “normal” stratejiyi test ederken, strateji sınayıcıdaki tüm test için kârınız “normal” olarak dağılmış değere çok yakındır. Bu, herhangi bir genel stratejiyi uzun süre pozisyon tutmadan test ederken, yaklaşık olarak eşit sayıda kârlı ve kârsız test alanı elde edeceğiniz anlamına gelir; bu, stratejinin istikrarsız olduğunu veya stratejinin piyasayı doğru bir şekilde anladığını ve tüm geçmiş üzerinde çalıştığını çok hızlı bir şekilde size bildirecektir.

Bir yeniden alma stratejisi ile uğraşırken, bu dağılım güçlü bir şekilde deforme olabilir, çünkü bu sistemin doğru testi için mümkün olan maksimum bakiyeyi ayarlamanız gerekir. Buna ek olarak, test sonucu büyük ölçüde test bölümünün uzunluğuna bağlıdır. Aslında, bu yaklaşımda, tüm alım-satım alım-satım döngülerine dayanır ve bu sistemin her bir benzersiz ayarı, hem ortalama düşüşün tamamen farklı bir değerine hem de onunla ilişkili ortalama düşüş süresinin farklı bir değerine sahip olabilir. Bu parametrelere bağlı olarak, çok kısa test bölümleri çok yüksek veya çok düşük test sonucu gösterebilir. Genellikle, bu tür testlerin çok azı yapılmaktadır ve bu da çoğu durumda bu sistemlerin çalışmasına aşırı güven duyulmasına neden olabilmektedir.

Yeniden alma sistemlerinin daha doğru bir şekilde değerlendirilmesinin incelikleri

Şimdi, alım-satım sistemlerinin bilinen parametrelerini uygulayarak yeniden alma algoritmasını kullanan sistemlerin performansını nasıl doğru bir şekilde değerlendireceğimizi öğrenelim. Her şeyden önce, böyle bir değerlendirmede tek bir özelliğin kullanılmasını tavsiye ederim - düzelme faktörü. Nasıl hesaplandığını görelim:

• Recovery Factor = Total Profit / Max Equity Drawdown
• Total Profit - alım-satım alanlarının toplam kârı
  
• Max Equity Drawdown - bakiye ve varlığın bir önceki ortak noktasına (bakiye zirvesi) göre varlıktaki maksimum düşüş
  

Gördüğümüz gibi, bu, nihai kârın maksimum para düşüşüne bölünmesidir. Bu parametrenin klasik anlamda matematiksel anlamı, fikre göre, sistemin varlık düşüşünü düzeltme yeteneğini göstermesidir. Böyle bir özelliği kullanırken bir alım-satım sisteminin kârlılığı için sınır koşulu aşağıdaki gerçektir:

• Recovery Factor > 1
  

Anlaşılabilir bir insan diline çevrilirse, kâr elde etmek için bakiyenin aynı miktarından daha fazla risk alamayacağımız anlamına gelir. Bu parametre çoğu durumda belirli bir sistem için alım-satım kalitesinin doğru bir değerlendirmesini sağlar. Bunu kullanın, ancak çok dikkatli olun, çünkü matematiksel önemi açısından oldukça tartışmalı bir değerdir.

Bununla birlikte, bu parametrenin de çok değişken olduğunu ve matematiksel anlamlılık düzeyinin çok düşük olduğunu anlamanız için size tüm dezavantajlarını açıklamam gerekecek. Elbette, bir şeyi eleştiriyorsan, o zaman bir alternatif sun diyebilirsiniz. Bunu kesinlikle yapacağım, ancak bu parametreyi analiz ettikten sonra. Bu parametre maksimum düşüşe bağlıdır ve bu da alım-satım eğrisi üzerindeki herhangi bir noktaya bağlanabilir, yani bu düşüşü başlangıç bakiyesine göre yeniden hesaplar ve maksimum düşüşün yerine koyarsak, neredeyse her zaman fazla hesaplanmış bir düzelme faktörü elde ederiz. Tüm bunları düzgün bir şekilde formüle edelim:

• Recovery Factor Variation 1 =  Total Profit / Max Equity Drawdown From Start
• Max Equity Drawdown From Start - başlangıç bakiyesinden maksimum düşüş (önceki maksimum bakiyeden değil)
  

Elbette bu klasik düzelme faktörü değildir, ancak özünde aslında genel kabul görmüş sınır koşuluna göre kârlılığı çok daha doğru bir şekilde belirler. Öncelikle bu parametreyi hesaplamanın her iki seçeneği de görsel olarak tasvir edelim - klasik olan ve benimki: 

Şekil 2

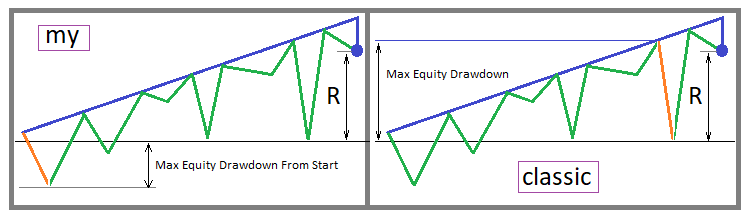
İlk durumda, bu parametrenin daha yüksek değerler alacağı görülebilir, ki elbette istediğimiz de budur. Ancak kârlılık değerlendirmesi açısından iki yaklaşım izlenebilir. Klasik parametre, test bölümünün süresini mümkün olduğunca uzun tutmanın daha iyi olduğu yaklaşıma daha uygundur. Bu durumda, “Max Equity Drawdown” değerinin daha yüksek bir değeri, bu düşüşün alım-satım eğrisinin en başından başlamadığı gerçeğini telafi eder ve bu nedenle bu parametre çoğu durumda gerçek değerlendirmeye yakındır. Benim parametrem çoklu geriye dönük testleri değerlendirirken daha verimlidir.

Başka bir deyişle, stratejiniz üzerinde ne kadar çok test yaparsanız bu parametre o kadar doğru sonuç verir. Stratejinizin testleri mümkün olduğunca çok farklı alanda yapılmalıdır. Bu, başlangıç ve bitiş noktalarının maksimum değişkenlikle seçilmesi gerektiği anlamına gelir. Doğru bir değerlendirme için, en farklı "N" alan seçip test etmek ve ardından tüm test alanları için bu parametrenin aritmetik ortalamasını hesaplamak gerekir. Bu kural, düzelme faktörünün her iki versiyonunu da (hem benimki hem de klasik) iyileştirmemize olanak tanıyacaktır. Tek fark klasik olanı iyileştirmek için daha az bağımsız geriye dönük test yapılması gerekecektir.

Bununla birlikte, bu parametrelerin netleştirilmesi için bu tür açıklayıcı manipülasyonların az olduğunu söylemek yetersiz kalacaktır. Herkesin kendi benzer parametresini bulabileceğini ve hatta MetaTrader'da geriye dönük test için hesaplanan özelliklerden biri olarak eklenebileceğini göstermek için kendi düzelme faktörü versiyonumu gösterdim. Ancak bu parametrelerden herhangi birinin matematiksel bir kanıtı yoktur ve dahası, bu parametrelerden herhangi birinin kendi hataları ve uygulanabilirlik sınırları vardır. Tüm bunlar, şu anda yeniden alma kullanan bir algoritmanın kesinlikle doğru bir şekilde değerlendirilmesi için kesin bir matematiksel parametre olmadığı anlamına gelir. Bununla birlikte, parametrem çeşitli testlerin sayısındaki artışla birlikte mutlak doğruluğa yönelecektir. Bir sonraki bölümde daha fazla ayrıntı vereceğim.

Kârlılığın derinlemesine ve evrensel olarak anlaşılması

Evrensel değerlendirme

Matematiksel kâr beklentisi ve kâr faktörü gibi parametrelerin herhangi bir strateji sınayıcı raporunda veya bir alım-satım sinyalinin özelliklerinde mevcut olduğunu herkesin bildiğine inanıyorum, ancak kimsenin size bu özelliklerin, işlem analizinin yeterli olmadığı bu tür alım-satım sistemlerinin kârlılığını hesaplamak için de kullanılabileceğini söylediğini sanmıyorum. Dolayısıyla, bu parametreleri "pozisyon" birimini "segment üzerinde test" ile değiştirerek kullanabilirsiniz. Bu parametreyi hesaplarken, içerideki herhangi bir yapıyı dikkate almadan birçok bağımsız test yapmanız gerekecektir. Bu yaklaşım, yalnızca en popüler iki parametreyi kullanarak alım-satım sisteminin gerçek beklentilerini değerlendirmenize yardımcı olacaktır. Buna ek olarak, size son derece faydalı bir alışkanlık aşılayabilir - çoklu testler. Bu yaklaşımı kullanmak için sadece aşağıdaki denklemi bilmeniz yeterlidir:

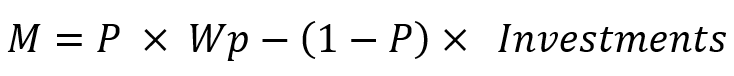
Tanımlamalar:

• M - beklenen getiri değeri
• Wp - istenen kâr
• Investments - gerekli kârı elde etmek için yatırım yapmak istediğiniz miktar
• P - kâr elde edilene kadar yeterli yatırıma sahip olma olasılığı
• (1-P) - kâr elde edilene kadar yeterli yatırıma sahip olmama olasılığı (bakiye kaybı)

Aşağıda kâr faktörü için benzer bir denklem yer almaktadır:

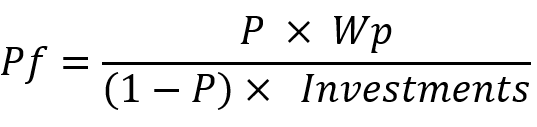
Bilmeniz gereken tek şey, rastgele alım-satımda ve makas, komisyon, swap ve kayma gibi engellerin olmaması durumunda, bu değişkenlerin herhangi bir alım-satım sistemi için her zaman aşağıdaki değerleri alacağıdır:

M = 0

Pf = 1

Bu özellikler ancak öngörülü bir an varsa sizin yönünüzde değişebilir. Bu nedenle, bakiyenizi kaybetmeden kâr elde etme olasılığımız aşağıdaki değeri alacaktır:

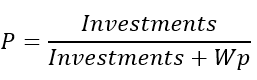
Bu ifadeyi denklemlerimizde olasılık yerine koyarsanız, size verdiğim birimleri elde edersiniz. Makas, komisyon ve swapı dikkate alırsak, aşağıdakini elde ederiz:

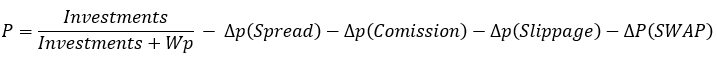
Makas, komisyon ve swap nihai olasılığı azaltmakta, bu da sonuçta birimlerin geçerliliğini yitirmesine neden olmaktadır. Bunun yerine aşağıdaki eşitsizlikler ortaya çıkar:

• M < 0
• Pf < 1

Bu kesinlikle herhangi bir alım-satım sistemi için geçerli olacaktır ve buradaki yeniden alma algoritması kesinlikle diğer sistemlerden daha iyi değildir. Böyle bir sistemi test ederken veya çalıştırırken, sinyalin veya geriye dönük testin nihai kârının rastgele değerinin dağılım fonksiyonunu güçlü bir şekilde deforme edebilir, ancak tipik olarak bu senaryo en sık olarak kısa süreli test veya çalıştırma sırasında ortaya çıkar.

Bunun nedeni, kısa bir bölümde test yaparsanız büyük bir düşüşle karşılaşma olasılığının çok daha az olmasıdır. Ancak bu testleri daha uzun segmentlerde yapmaya başladığınızda, genellikle daha önce görmediğiniz şeyleri göreceksiniz. Ancak eminim ki çoğu kişi bunun sadece bir kaza olduğu ve bu tehlikeli bölgelerin bir şekilde atlanması gerektiği konusunda kendilerini rahatlatabilecektir. Aynı durum genellikle kısa segmentler üzerinde yapılan çoklu testler için de geçerli olacaktır.

Herhangi bir sistemin kârsızlığının üstesinden gelmenin tek bir yolu vardır. Olasılık hesaplama denklemine ek bir bileşen daha ekleyelim:

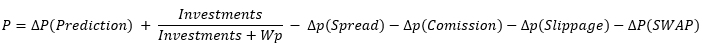
Gördüğümüz gibi, denklemde yeni bir bileşen olan "dP(Prediction)" ortaya çıkmıştır. Artı işaretine sahiptir, bunu sadece bu bileşenin makasların, komisyonların ve swapların etkisini telafi edebileceğini göstermek için bilerek yaptım. Bu, olumsuz etkilerin üstesinden gelmek ve kâra ulaşmak için her şeyden önce yeterli tahmin kalitesine ihtiyacımız olduğu anlamına gelir:

İstediğimiz eşitsizlikleri ancak bu özel eşitsizliği sağlarsak elde edebiliriz:

• M > 0
• Pf > 1

Gördüğünüz gibi, bu ifadelerin anlaşılması çok kolaydır ve eminim ki hiç kimse doğruluklarından şüphe duymayacaktır. Bir sonraki alt bölüm bu denklemler kullanılarak daha kolay anlaşılabilir. Aslında, bunları hatırlamanızı veya en azından mantığını hatırlamanızı tavsiye ederim, böylece gerektiğinde hafızanızda her zaman geri yükleyebilirsiniz. Burada asıl önemli olan onları anlamanızdır. Genel olarak bu denklemlerden biri yeterlidir, ancak bir örnek için iki tane göstermenin daha iyi olacağını düşündüm. Diğer parametrelere gelince, bunların bu bölüm çerçevesinde gereksiz olduğuna inanıyorum.

Netleştirme yöntemlerine örnekler

Bu alt bölümde, size düzelme faktörünün daha doğru bir değerini elde etmenizi sağlayacak bazı ek iyileştirme manipülasyonları sunmak istiyorum. "Şekil 1"e geri dönmenizi ve numaralandırılmış bölümlere bakmanızı öneririm. Düzelme faktörünü iyileştirmek için, bu segmentlerin bağımsız testler olduğunu düşünmek gerekir. Bu şekilde, bu testleri zaten gerçekleştirdiğimiz olduğumuzu göz önünde bulundurarak çoklu testlerden vazgeçebiliriz. Bunu yapabiliriz çünkü bu segmentler hem başlangıç noktası hem de bitiş noktası olan döngülerdir ve bu da geriye dönük test ile eşdeğerlik sağlar. 

Bu bölüm çerçevesinde, aynı anda birkaç enstrüman üzerinde test veya işlem yaptığımız gerçeğini göz önünde bulundurarak ilk görüntüyü eşdeğeriyle tamamlamaya değer olduğunu düşünüyorum. Birden fazla enstrüman üzerinde paralel alım-satım için yeniden alma algoritması kullanıldığında alım-satım eğrisi şu şekilde görünecektir:

Şekil 3

Bu eğrinin yapısının tek bir enstrümandaki yeniden alma eğrisinden farklı olduğunu görebiliriz. Buraya ara mavi noktalar ekledim, bu da düşüşten önce "tersine düşüş" olan segmentler olabileceği anlamına geliyor. Gerçek şu ki, bunu bir düşüş olarak değerlendiremeyiz. Ancak yine de bu kesimleri analizin dışında tutmaya hakkımız yok. Bu yüzden bir döngünün parçası olmalıdırlar.

Her yeni döngünün bir öncekinin bitiminden itibaren ertelenmesinin daha doğru olacağını düşünüyorum. Bu durumda, bir önceki döngünün sonu, varlıktaki son düşüşün düzelme noktası olarak kabul edilmelidir. Resimde bu döngüler kırmızı noktalarla ayrılmıştır. Ancak aslında döngünün bu tanımı yeterli değildir. Sadece varlık düşüşünü tespit etmek yeterli değildir, aynı zamanda mevcut döngünün başlangıcından daha düşük olup olmadığını belirlemek de önemlidir. Aksi takdirde, bu ne tür bir düşüştür?

Bu döngüleri vurguladıktan sonra, bunları ayrı bağımsız testler olarak değerlendirebilir ve her biri için düzelme faktörünü hesaplayabiliriz. Bu aşağıdaki şekilde yapılabilir:

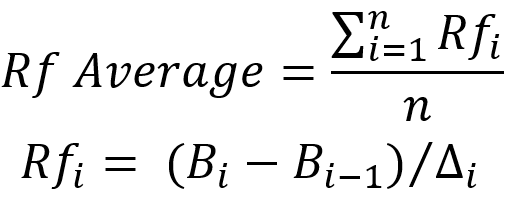
Bu denklemde, bakiye eğrisi üzerindeki karşılık gelen noktalar (bölümdeki bakiyenin son değeri ve başlangıç değeri) "B" olarak kullanılırken, delta düşüşümüzü temsil eder. Ayrıca okuyucunun son şekle geri dönmesini istiyorum. Üzerinde, yukarıda listelediğim nedenlerden dolayı deltayı klasik yöntemde olduğu gibi mavi olandan değil, her döngünün kırmızı başlangıç noktasından çizdim. Ancak orijinal düzelme faktörünü iyileştirmeniz gerekiyorsa, delta mavi noktadan çizilmelidir. Bu durumda, parametreleri iyileştirme yöntemi parametrelerin kendisinden daha önemlidir. Ortalama alma işlemi olarak basit aritmetik ortalama alınır.

Bununla birlikte, bir veya daha fazla özel veya klasik parametreyi netleştirdikten sonra bile, bu parametrenin değerinin birden, hatta iki veya üçten büyük olması kârlı bir alım-satım sisteminin işareti olarak görülmemelidir.

Tam olarak aynı denklem çoklu geriye dönük testle uygulanmalıdır. Mesele şu ki, bu durumda herhangi bir geriye dönük test bir döngüye eşdeğerdir. Hatta önce döngüler için ortalamaları hesaplayabilir ve tüm bunlardan sonra, geriye dönük testlere göre ortalamanın ortalamasını hesaplayabiliriz. Ya da test segmentinin süresini en üst düzeye çıkararak bunu çok daha kolay bir şekilde yapabiliriz. Bu yaklaşım, döngü sayısının maksimumda olması nedeniyle sizi en azından çoklu testten kurtaracaktır, bu da ortalama düzelme faktörünün mümkün olduğunca doğru bir şekilde hesaplanacağı anlamına gelir.

Çeşitlendirme ile sistemlerin verimliliğinin artırılması

Yararlı limitler

Geriye dönük testlerin belirli özelliklerini iyileştirme olasılıklarını gördükten sonra, şüphesiz daha iyi donanımlı hale geldiniz, ancak yine de ana şeyi bilmiyorsunuz. Temel nokta şu sorunun cevabında yatmaktadır - tüm bu çoklu testlerin yapılması veya döngülere bölünmesi neden gereklidir? Benim harcadığım zaman kadar çaba harcamadığınız sürece bu soru gerçekten karmaşık. Ne yazık ki bu gerekli, ancak benim yardımımla bunu yapmanız gereken süreyi büyük ölçüde azaltabilirsiniz.

Bu bölüm, belirli bir parametrenin nesnelliğini değerlendirmenizi sağlayacaktır. Hem teorik olarak hem de denklemleri kullanarak açıklamaya çalışacağım. Genel denklemle başlayalım:

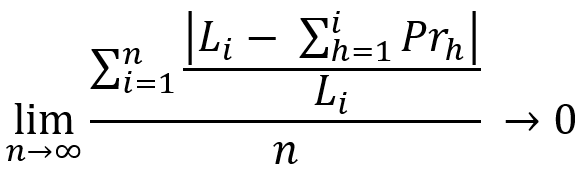
Bazı küçük değişikliklerle benzer bir denkleme bakalım:

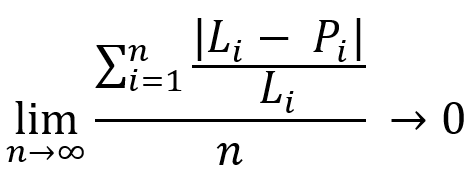
Bu denklemlerin özü aynıdır. Bu denklemler, herhangi bir kârlı alım-satım sisteminde, test bölümünün süresi sonsuza gittiğinde, ortalama kârımızı temsil eden belirli bir çizgi ile bakiye ve mevcut kâr çizgilerinin tam bir birleşmesini elde edeceğimizi göstermektedir. Çoğu durumda, bu çizginin niteliği seçtiğimiz strateji tarafından belirlenir. Daha derin bir anlayış için aşağıdaki resme bakalım:

Şekil 4

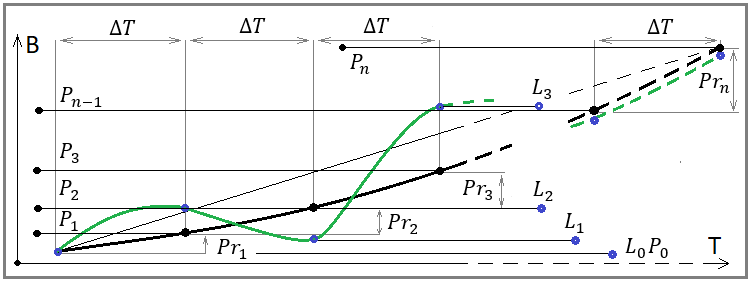
Bu resme dikkatlice bakarsanız, denklemlerimizde bulunan tüm büyüklükleri göreceksiniz. Matematiksel limitlerimizin geometrik anlamını ortaya koymaktadır. Denklemlerimizde eksik olan tek şey dT zaman aralığıdır. Bu aralık ile bakiye adımlarımızı ayrıştırarak bu aralıkların bakiyesi ve kârı için sayı serimizin tüm noktalarını elde ediyor ve aynı noktalarda orta çizgimizin değerlerini hesaplıyoruz. Bu denklemler aşağıdaki ifadenin matematiksel karşılığıdır:

• Çoklu test veya alım-satım eğrisini ne kadar çok bir araya getirirsek, o kadar çok düzgün bir yükselen çizgi gibi görünürler (yalnızca sistem gerçekten kârlıysa)

Başka bir deyişle, herhangi bir kârlı alım-satım sistemi, seçtiğimiz test alanı ne kadar uzun olursa, strateji sınayıcının veya sinyalin sonuç grafiği kısmında daha güzel görünür. Bazıları hiçbir sistemin bu tür parametrelere ulaşamayacağını söyleyebilir, yine de Mağazada çok sayıda örnek var, bu yüzden bunu inkar etmek aptalca olur. Her şey algoritmanın evrenselliğine ve piyasa fiziğini ne kadar iyi anladığınıza bağlıdır. Alım-satım yaptığınız piyasanın doğasında her zaman var olan matematiği biliyorsanız, aslında sonsuza kadar büyüyen bir kâr eğrisi elde edersiniz ve sistemin etkinliğini onaylamak için tüm bir sonsuzluğu beklemenize gerek yoktur. Elbette bunun son derece zor bir görev olduğu açıktır, ancak yine de birçok algoritma çerçevesinde bu görev başarılabilir.

Bu teorik girişi, bu tekniklerin nasıl doğru kullanılacağını öğrenerek bitirelim. Sadece sınırlı örneklemlerimiz ve buna bağlı olarak da kaçınılmaz eksik toplamlarımız varken, bu teknikleri sonsuz toplamlarla nasıl kullanacağımızı sorabilirsiniz.

1. Cevap, tüm geçmişi bölümlere ayırmakta yatıyor
2. Tüm geçmişin olduğu segmente kadar test süresi açısından sürekli artan uzunluklara sahip birkaç segment seçeriz
3. Bir test metodolojisi seçeriz
4. Test ederiz
5. Düzelme faktöründe ve/veya göreceli düşüşte iyileşme ararız

Bu zahmetli test şemasının özü, limitlerimizin sırasıyla gerçekten sonsuza ve sıfıra eğilimli olduğuna dair dolaylı işaretleri ortaya çıkarmaktır. Test şemamızın verimliliğini artırmak için, en uzun test bölümünün en azından en kısa test bölümünden daha güzel görünmesi gerektiğini ve ideal olarak da her bir sonraki bölümün hem daha büyük hem de daha güzel görünmesi gerektiğini anlamalıyız. "Daha güzel" kavramını sadece bunun aslında limitlerimize eşdeğer olduğunu herkese açık hale getirmek için kullanıyorum.

Bununla birlikte, limitlerimiz yalnızca teorik değerlendirmeler veya hazırlıklar (ne derseniz) sırasında iyidir. Bu bağlamda şu soru ortaya çıkmaktadır: "gözle analize" başvurmadan bu gerçekleri nasıl keşfedebiliriz? Limitlerimizi bir şekilde strateji sınayıcı raporunda sahip olduğumuz parametrelere uyarlamamız gerekiyor. Başka bir deyişle, test yapımızın kullanılabilmesi için bazı strateji sınayıcı raporu veya sinyal parametreleri için alternatif limitlere ihtiyacımız var. Size gerekli ve yeterli bir alternatif limitler seti göstereyim:

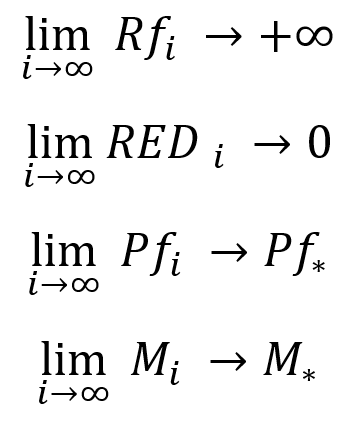
Burada anlamamız gereken şey:

1. Sonsuz bir test sırasında, herhangi bir kârlı stratejinin düzelme faktörü sonsuza yönelir
2. Sonsuz bir test sırasında, herhangi bir kârlı stratejinin varlığa göre göreceli düşüşü sıfıra eğilim gösterir
3. Sonsuz bir test sırasında, herhangi bir kârlı stratejinin işlemlerinin kâr faktörü ortalama değerine eğilim gösterir ve sonlu bir reel limite sahiptir
4. Sonsuz bir test sırasında, herhangi bir kârlı stratejinin otomatik lot etkin olmadan (sabit bir lot ile) matematiksel beklentisi ortalama değerine eğilim gösterir ve sonlu bir reel limite sahiptir

Tüm bunlar sonsuz testlerle ilgilidir, ancak sonlu bir örnekleme uyarlamaya geçmeden önce bu limitlerin matematiksel anlamını anlamakta fayda vardır. Bu ifadelerin metodolojimize uyarlanması, her biri bir öncekinden önemli ölçüde daha büyük, tercihen en az iki kat daha büyük olan birkaç test segmenti seçmemiz gerektiği gerçeğiyle başlamalıdır. Bu, daha kısa ve daha uzun testler arasındaki okuma farkını fark edebilmek için gereklidir. Testlerimizi, indeks arttıkça uzunluğu da zamanla artacak şekilde numaralandırırsak, sonlu örneklemler durumu için aşağıdaki uyarlamayı elde ederiz:

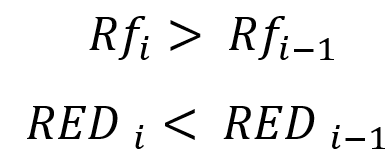
Diğer bir deyişle, düzelme faktöründeki artış ve göreceli düşüşteki azalma, büyük olasılıkla test segmentinin veya sinyal ömrünün daha da artmasının eğrimizi görsel olarak daha güzel hale getirdiğinin dolaylı bir kanıtıdır. Bu, sonsuz limitlerimizin gerçekleştiğini teyit ettiğimiz anlamına gelir. Aksi takdirde, kâr eğrisi daha düz hale gelmiyorsa, elde edilen sonucun rastlantıya çok yakın olduğunu ve gelecekte kayıp olasılığının son derece yüksek olduğunu belirtebiliriz.

Elbette pek çok kişi sistemi daha sık optimize edebileceğimizi ve her şeyin yoluna gireceğini söyleyecektir. Bazı çok nadir durumlarda bu mümkündür, ancak bu yaklaşım tamamen farklı bir test metodolojisi gerektirecektir. Kimseye bu yaklaşıma başvurmasını tavsiye etmiyorum, çünkü bu durumda herhangi bir matematiğiniz yok, burada ise her şey açık ve net bir şekilde var.

Tüm bu nüanslar, yeniden alma algoritmasının test edilmesinin bu yaklaşımın kullanılmasını daha da gerektirdiğine sizi ikna etmelidir. Özellikle, görevi basitleştirebilir ve yeniden alma sistemini maksimum uzunluktaki segment üzerinde hemen test edebiliriz. Bu mantığı tersine çevirebiliriz. En uzun segmentteki alım-satım performansını beğenmezsek, kısa segmentlerdeki daha iyi performans bile eşitsizliklerimizin artık karşılanmadığını ve sistemin bu aşamada alım-satıma hazır olmadığını gösterecektir.

Birden fazla enstrümanın paralel kullanımı açısından faydalı özellikler

Sınırlı bir geçmiş üzerinde test yaparken, şu soru kesinlikle ortaya çıkacaktır - test metodolojimizi doğru bir şekilde kullanmamız için yeterli geçmiş var mı? Mesele şu ki, çoğu durumda stratejinin ağırlığı vardır, ancak kalitesi rahat kullanım için yeterince yüksek değildir. Öncelikle, en azından gerçekten tahmin gücüne sahip olup olmadığını ve modernizasyonuna başlayıp başlayamayacağımızı anlamalıyız. Bazı durumlarda, kelimenin tam anlamıyla yeterli işlem geçmişine sahip değiliz. Peki, ne yapmalıyız? Birçok kişinin tahmin ettiği gibi, alt bölümün başlığına bakılırsa, bu amaç için birden fazla enstrüman kullanmalıyız. 

Bu açık bir gerçek gibi görünebilir, ancak ne yazık ki, her zaman olduğu gibi, hiçbir yerde matematik yoktur. Birden fazla enstrüman üzerinde test yapmanın mantığı, test süresini artırma mantığıyla eşdeğerdir. Tek değişiklik, sisteminizin çok dövizli olması gerektiğidir. Sistem farklı alım-satım enstrümanları için farklı ayarlara sahip olabilir, ancak tüm ayarların benzer olması arzu edilir. Ayarların benzerliği, sistemin mümkün olan maksimum sayıda alım-satım enstrümanı üzerinde çalışan fiziksel ilkeleri kullandığı gerçeğini temsil edecektir.

Bu yaklaşımla ve bu tür testlerin doğru bir şekilde uygulanmasıyla, "i" indeksi, sabit bir test segmentinde aynı anda test edilen enstrümanların sayısı olarak anlaşılmalıdır. O zaman ifadeler aşağıdaki anlama gelecektir:

1. İşlem gören enstrüman sayısı arttıkça, daha fazla enstrüman, kurtarma faktörünü yükseltir
2. İşlem gören enstrüman sayısı arttıkça, daha fazla enstrüman, varlığa göre göreceli düşüşü azaltır

Aslında, test sayısındaki bir artış, basitlik açısından, testlerin toplam süresindeki bir artış olarak yorumlanabilir, sanki her bir enstrüman için her bir testi büyük bir genel testin parçası olarak kabul ediyormuşuz gibi. Bu soyutlama sadece bu yaklaşımın da neden aynı güce sahip olduğunu anlamanıza yardımcı olacaktır. Ancak bu konuyu daha doğru bir şekilde ele alırsak ve birkaç enstrümandan oluşan bir çizginin neden çok daha güzel olacağını daha derinlemesine anlarsak, o zaman aşağıdaki olasılık teorisi kavramlarını kullanmalıyız:

• Rastgele değer
• Rastgele bir değişkenin varyansı
• Rastgele bir değişkenin matematiksel beklentisi
• Rastgele bir değişkenin normal dağılım yasası

Tüm bunlara neden ihtiyaç duyduğumuzu tam olarak açıklamak için öncelikle bir geriye dönük teste veya bir alım-satım sinyaline biraz daha farklı bakmamıza yardımcı olacak bir görüntüye ihtiyacımız var:

Şekil 5

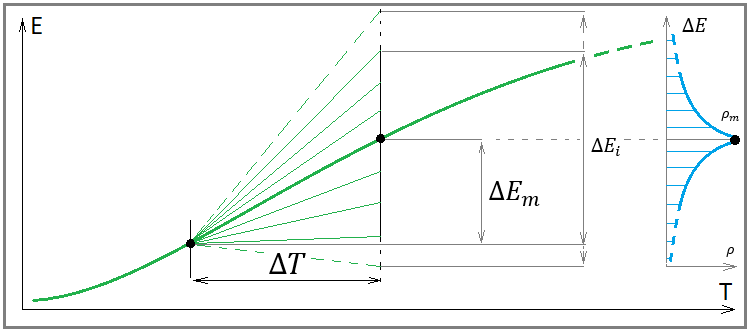
Burada bir bakiye çizgisi çizmiyorum, çünkü burada hiçbir şeyi çözmüyor ve sadece bir kâr çizgisine ihtiyacımız var. Bu görüntünün anlamı, her bir kâr çizgisi için, (kâr çizgisi artışının rastgele bir değişkeninin dağılım yasasını oluşturmanın mümkün olduğu) sabit uzunlukta sonsuz sayıda bağımsız segment seçmenin mümkün olmasıdır. Rastgele bir değişkenin varlığı, gelecekte seçilen alandaki kâr artışının en geniş aralıkta tamamen farklı değerlere sahip olabileceği anlamına gelir.

Kulağa karmaşık geliyor, ama aslında her şey basit. Sanırım pek çok kişi normal dağılım yasasını duymuştur. Doğadaki neredeyse tüm rastgele süreçleri tanımladığı varsayılır. Bence bu, sizin "düşünmenizi" engellemek için icat edilmiş bir illüzyondan başka bir şey değil. Şaka bir yana, dağılım yasasının popüler olmasının nedeni, rastgele bir değişkenin matematiksel beklentisine göre simetrik dağılımları tanımlamak için yapay olarak derlenmiş ve çok uygun bir denklem olmasıdır. Daha ileri matematiksel dönüşümler ve deneyler için bize faydalı olacaktır.

Ancak, bu yasa ile çalışmaya başlamadan önce, rastgele bir değişkenin herhangi bir dağılım yasası için temel özelliği tanımlamalıyız:

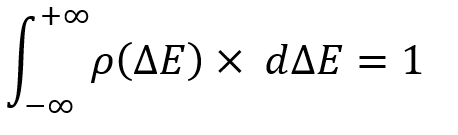
Herhangi bir rastgele değişken dağılım yasası, esasen ortak olmayan olayların tam grubunun analoğudur. Tek fark, bu olaylardan sabit bir sayıya sahip olmamamız ve istediğimiz zaman bu şekilde ilgilendiğimiz herhangi bir olayı seçebilmemizdir:

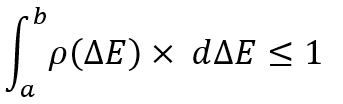
Aslında, bu integral belirtilen rastgele değişken aralığında rastgele bir değişken bulma olasılığını dikkate alır ve doğal olarak birden büyük olamaz. Belirli bir olay uzayındaki hiçbir toplam olayın olasılığı birden büyük olamaz. Ancak, en önemli şey bu değildir. Burada önemli olan tek şey, bu durumda olayın yalnızca iki sayıdan oluşan bir set tarafından belirlendiğini anlamanız gerektiğidir. Bunlar, minimum boyutlu rastgele değişkenler için örneklerdir.

Bir olayın "N*2" sayısıyla belirlenebildiği "N" boyut için bu denklemlerin analogları ve hatta daha karmaşık yapılar (çok boyutlu bölge integralleri çerçevesinde) vardır. Bunlar matematiğin oldukça karmaşık bölümleridir, ancak burada gereksizdirler. Burada elde edilen tüm yasalar tek boyutlu versiyon için kendi kendine yeterlidir.

Daha karmaşık yapılara geçmeden önce, rastgele değer dağılımı yasalarının bazı popüler parametre özelliklerini hatırlayalım:

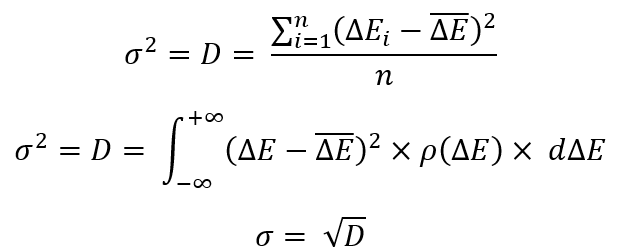
Bu denklemlerden herhangi birini tanımlamak için en önemli şeyi belirlememiz gerekir - rastgele bir değişkenin matematiksel beklentisi. Bizim durumumuzda, aşağıdaki gibi görünür:

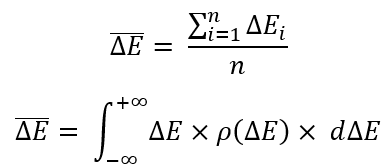
Matematiksel beklenti basitçe aritmetik ortalamadır. Matematikçiler basit şeylere çok zekice isimler vermeyi severler, böylece kimse bir şey anlamaz. İki denklem sundum. Aralarındaki tek fark, ilkinin sonlu sayıda rastgele değişken (sınırlı miktarda veri) üzerinde çalışması ve ikinci durumda "olasılık yoğunluğu" üzerindeki integralin kullanılmasıdır.

İntegral, toplamın eşdeğeridir; tek farkı sonsuz sayıda rastgele değişkeni toplamasıdır. Rastgele bir değişkenin dağılım yasası, integralin altındadır ve rastgele değişkenlerin tüm sonsuzluğunu içerir. Bazı farklılıklar vardır, ancak genel olarak özü aynıdır.

Şimdi önceki denklemlere geri dönelim. Bunlar, çoğu matematikçi için kullanışlı olan rastgele değişken dağılımı yasalarıyla yapılan bazı manipülasyonlardır. Son örnekte olduğu gibi, iki uygulama vardır - biri sonlu bir rastgele değişkenler kümesi için, diğeri sonsuz bir küme için (rastgele değişken dağılımı yasası). "D"nin, tüm rastgele değişkenler ile ortalama rastgele değişken (rastgele değişkenin matematiksel beklentisi) arasındaki farkın ortalama karesi olduğunu belirtir. Bu değere "varyans" adı verilir. Bu değerin kökü "standart sapma" olarak adlandırılır.

Rastgele bir değişkenin normal dağılımı

Rastgele değişkenler matematiğinde genel olarak kabul edilen bu değerlerdir. Rastgele dağılım yasalarının en önemli özelliklerini tanımlamak için en uygun oldukları düşünülür. Bu fikre katılmıyorum, ancak yine de size nasıl hesaplandıklarını göstermek zorundayım. Sonuçta, normal dağılım yasasını anlamak için bu büyüklüklere ihtiyaç duyulacaktır. Bu bilgiyi kolayca bulmanız pek olası değil, ancak size normal dağılım yasasının sadece birkaç amaç doğrultusunda yapay olarak icat edildiğini söyleyeceğim:

• Matematiksel beklentiye göre simetrik dağılım yasasını belirlemenin basit bir yolu
• Dağılım ve standart sapmayı belirleyebilme
• Matematiksel beklentiyi belirleyebilme

Tüm bu seçenekler, normal dağılım yasası olarak adlandırılan rastgele değişken dağılımı yasası için hazır bir denklem elde etmemizi sağlar:

Rastgele değişkenler dağılımı yasalarının başka varyasyonları da vardır. Her biri belirli bir dizi problem için icat edilmiştir, ancak normal yasa en popüler ve en iyi bilineni olduğundan, onu aşağıdaki ifadeleri kanıtlamak ve matematiksel eşdeğerlerini bulmak için bir örnek olarak kullanacağız:

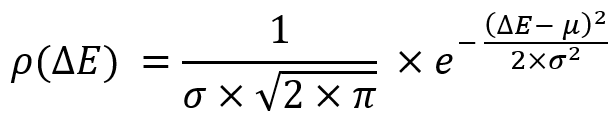
• Kârlı bir sistem için ne kadar çok enstrüman paralel olarak işlem görürse, kâr grafiğimiz o kadar güzel ve düz olur (çeşitlendirmenin özel bir durumu)
• Test veya alım-satım için seçilen alan ne kadar uzun olursa, kâr grafiğimiz o kadar güzel ve düz olur
• Kanıtlanmış kârlılığa sahip ne kadar çok paralel alım-satım sistemi olursa, genel kârlılık grafiğimiz o kadar düz ve güzel olur
• Yukarıdakilerin hepsinin birleşimi ideal çeşitlendirmeyi ve en güzel grafiği ortaya çıkarır

Söylenen her şey yalnızca kârlılığı matematiksel ve pratik olarak kanıtlanmış alım-satım sistemleri için geçerlidir. Matematiksel terimlerle "daha güzel grafiğin" ne anlama geldiğini tanımlayarak başlayalım. Yukarıda denklemini gösterdiğim "standart sapma" bize bu konuda yardımcı olabilir.

Aynı matematiksel beklentiye sahip bir kâr artışı rastgele değişkeni için elimizde bir dağılım yoğunluğu eğrileri ailesi varsa ve bunlar pratikte aynı olan iki grafik için zaman içinde aynı süredeki iki segmenti sembolize ediyorsa, o zaman en küçük standart sapmaya sahip olanı tercih ederiz. Bu ailedeki mükemmel eğri, standart sapması sıfır olan eğri olabilir. Bu eğriye ancak geleceği bilirsek ulaşılabilir, ki bu imkansızdır, yine de bu aileden eğrileri karşılaştırmak için bunu anlamalıyız.

Rastgele değerler dağılımı yasası çerçevesinde kâr eğrisi güzelliği

Bu gerçek, seçilen zaman aralığında aynı matematiksel kâr artışı beklentilerine sahip bir eğri ailesiyle uğraşırken anlaşılabilir bir durumdur, ancak tamamen gelişigüzel dağılım eğrileriyle uğraşırken ne yapmalıyız? Bunların nasıl karşılaştırılacağı net değildir. Bu bağlamda, standart sapma artık mükemmel değildir ve ölçeklendirmeyi dikkate alan daha evrensel başka bir karşılaştırma değerine ihtiyacımız vardır veya bu dağılım yasalarını, tüm dağılımların aynı matematiksel beklentiye sahip olacağı ve dolayısıyla klasik kriterlerin tüm eğriler için geçerli olacağı belirli bir göreceli değere indirgemek için bir algoritma bulmalıyız. Ben böyle bir algoritma geliştirdim. İçindeki tekniklerden biri aşağıdaki dönüşümdür:

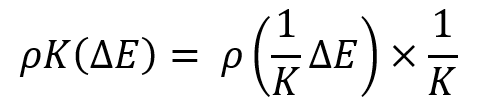
Bu eğrilerin ailesi aşağıdaki gibi görünecektir:

Şekil 6

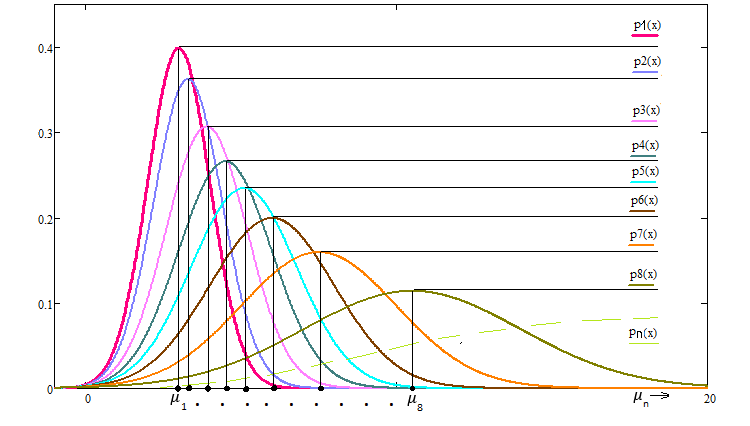
Çok ilginç bir gerçek şu ki, normal dağılım yasasını bu dönüşüme tabi tutarsak, o zaman bu dönüşüme göre değişmezdir ve şöyle görünecektir:

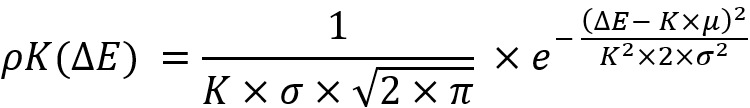
Değişmezlik aşağıdaki ifadelerden oluşur:

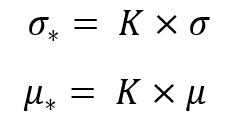
Bu ifadeleri önceki denklemde yerine koyarsak, yıldız işaretli karşılık gelen değerlerle çalışan aynı dağılım yasasını elde ederiz:

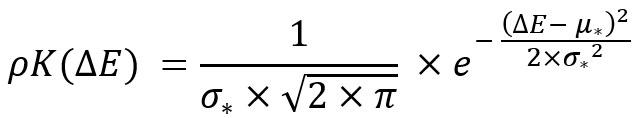
Bu dönüşüm sadece dönüşüm yasasının değişmezliğini değil aynı zamanda aşağıdaki parametrenin değişmezliğini de sağlamak için gereklidir:

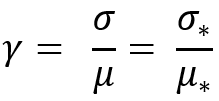
Bu parametreyi icat etmek zorunda kaldım. Normal dağılım yasasını, diğer yasalar gibi, bu olmadan düzgün bir şekilde ölçeklendirmek imkansızdır. Bu parametre başka herhangi bir dağılım yasası için de değişmez olacaktır. Aslına bakarsanız, normal yasanın algılanması ve anlaşılması daha kolaydır. Fikri, farklı matematiksel beklentilere sahip herhangi bir dağılım için kullanılabileceği ve özünün standart sapmaya benzer olacağı, ancak karşılaştırılan tüm dağılımların aynı matematiksel beklentiye sahip olması gerekmediğidir. Görünüşe göre, dönüşümümüz belirli bir parametrenin aynı değere sahip olduğu bir dağılım ailesi elde etmek için tasarlanmıştır. Oldukça kullanışlı görünüyor, değil mi?

Bu, söz konusu grafik güzelliğini tanımlamanın bir yoludur. En küçük parametreye sahip sistem "en güzeldir”. Bunların hepsi iyi, ancak bu parametreye farklı bir amaç için ihtiyacımız var. İki sistemin güzelliğini karşılaştırmak için bir görev belirledik. Birbirinden bağımsız olarak alım-satım yapan iki sistemimiz olduğunu düşünelim. Dolayısıyla amacımız bu sistemleri birleştirmek ve bu birleşmenin bir etkisi olup olmayacağını anlamaktır. Daha doğrusu şunu umuyoruz:

 

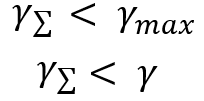
Bunlar, herhangi bir dağılım yasası kullanıldığında gözlemlenecektir. Bu otomatik olarak, paralel olarak işlem gören enstrümanlarımız veya sistemlerimiz benzer kârlılığa sahipse çeşitlendirmenin mantıklı olduğu anlamına gelir. Bu gerçeği biraz farklı bir şekilde kanıtlayacağız. Dediğim gibi, tüm dağılımları göreceli rastgele bir değere indirgemek için bir algoritma buldum. Bunu kullanacağız, ancak önce iki deltanın toplamını temsil eden rastgele bir değişkenin dağılım yasası çerçevesinde birkaç çizginin birleştirilmesinin genel sürecini analiz edeceğiz. Çiftler halinde birleştirme için tekrarlayan mantık kullanacağız. Bunu yapmak için, her biri tanımlanmış bir matematiksel beklentiye sahip "n+1" eğrimiz olduğunu varsayıyoruz. Ancak birleşmeyi simgeleyen rastgele değişkene ulaşmak için şunu anlamamız gerekir:

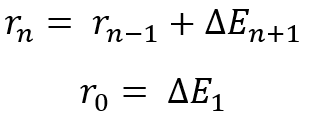
Aslında bu, matematiksel bir anlam ifade etmeyen tekrarlayan bir ifadedir, ancak listede bulunan tüm rastgele değişkenleri birleştirme mantığını gösterir. Basitçe ifade etmek gerekirse, "n" ardışık dönüşüm kullanarak birleştirmemiz gereken "n+1" eğrimiz vardır. Aslında bu, bir tür dönüşüm operatörleri kullanarak her bir adımda toplam rastgele değişkenin dağılım yasasını elde etmemiz gerektiği anlamına gelir.

Uzun açıklamalara girmeyeceğim. Bunun yerine, kendi sonuçlarınızı çıkarabilmeniz için bu dönüştürme operatörlerini basitçe göstereceğim. Bu denklemler, seçilen zaman aralığı içerisinde iki kâr eğrisinin birleştirilmesini uygulamakta ve eğrilerin iki segmentinin toplam kârının "dE1 + dE2" sırasıyla seçilen "r" değerinden düşük (Pl) ve yüksek (Pm) olma olasılığını hesaplamaktadır:

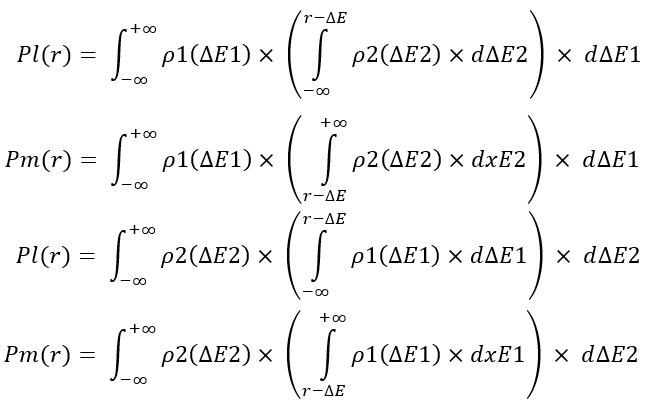
Bu büyüklükleri burada uygulamak için iki seçenek vardır. İkisi de birbirine tamamen benziyor. Bu değerler hesaplandıktan sonra, "r" rastgele değişkeninin dağılım yasasını elde etmek için kullanılabilirler, ki bu da tüm tekrarlayan birleştirme zincirini çözmek için bize gereken şeydir. Rastgele değişken tanımına göre, bu denklemlerden ilgili dağılım yasalarını aşağıdaki gibi elde edebiliriz:

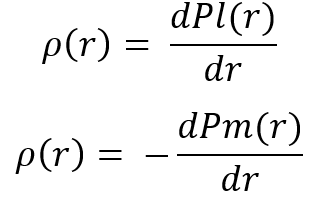
Tahmin edebileceğiniz gibi, dağılım yasasını elde ettikten sonra, tekrarlayan dönüşümler zincirinde bir sonraki adıma geçebiliriz. Tüm zincir boyunca çalıştıktan sonra, tekrarlayan birleştirme zinciri için kullandığımız dağılımlardan biriyle karşılaştırabileceğimiz nihai dağılımı elde ederiz. Elimizdeki yasalara dayanarak birkaç dağılım oluşturalım ve her birleştirmenin "bir öncekinden daha güzel" olduğu gerçeğini göstermek için örnek olarak bir birleştirme adımı gerçekleştirelim:

Şekil 7

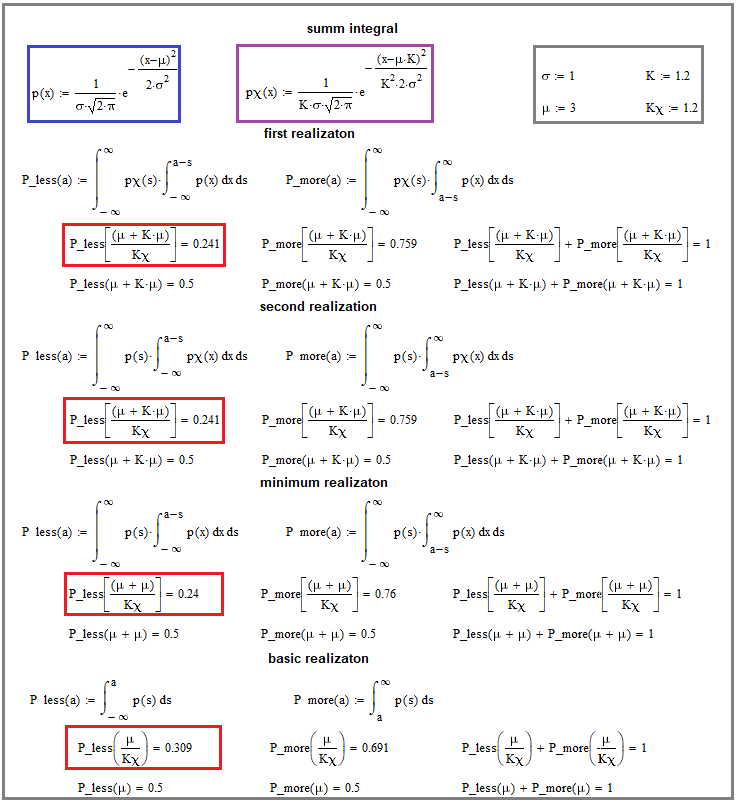
Şekil, birleştirme denklemlerimizi uygulayan matematiksel birleştirmeyi göstermektedir. Burada gösterilmeyen tek şey, integralleri rastgele bir birleşme değeri dağılımının yasalarına dönüştürmek için türevdir. Türevin sonucuna biraz sonra, daha genel bir fikir çerçevesinde bakacağız, ancak şimdilik görüntüde ne olduğuyla ilgilenelim.

Kırmızı dikdörtgenlere dikkat edin. Burada esas olan onlardır. En aşağıdaki integral, rastgele değişkenin "Kx" ile bölünen matematiksel beklentiden daha küçük bir değer alma olasılığını hesaplayacak şekilde orijinal dağılım yasasına göre integral aldığımızı söyler. Yukarıda biraz farklı iki dağılımın birleşmesi için benzer integraller görüyoruz. Her durumda, matematiksel beklenti ile integralin seçilen sınır değeri arasındaki bu oranı (Kx) korumak önemlidir, bu da karşılık gelen "Kx" ile ifade edilir. 

Yukarıda size verdiğim denklemlere göre her iki birleştirme seçeneğinin de orada sunulduğuna dikkat edin. Ayrıca, sanki iki benzer kâr eğrisini birleştiriyormuşuz gibi, temel dağılımın kendisiyle birleşmesi söz konusudur. Benzer ifadesi, görüntüde aynı anlamına gelmez, daha ziyade seçilen zaman aralığındaki kâr eğrisi artışının rastgele değişkeni için aynı dağılım yasalarına sahip olmak anlamına gelir. Bunun kanıtı, birleşen rastgele değişkenin orijinaline göre göreceli sapma olasılığını daha düşük bulmamızdır. Bu, herhangi bir birleşmede rastgele bir kâr değerinin artışı için daha "güzel" bir yasaya sahip olduğumuz anlamına gelir. Elbette konunun daha derinlemesine incelenmesini gerektiren istisnalar vardır, ancak bu yaklaşımın makale için yeterli olduğunu düşünüyorum. Büyük olasılıkla hiçbir yerde daha iyisini bulamazsınız, çünkü bu çok özel bir materyaldir.

Güzelliği karşılaştırmanın alternatif yolu, hem orijinal dağılım yasalarını hem de yukarıda ele alınan tekrarlayan zincirin sonucunu dönüştürmektir. Bunu başarmak için, ölçeklenebilir bir dağılım eğrileri ailesi elde etmemizi sağlayan dönüşümümüzü kullanmamız ve aşağıdaki gibi yapmamız yeterlidir:

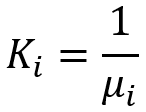
Bu dönüşümün püf noktası, bu yaklaşımla, ilgili dönüşüme tabi tutulan tüm dağılım yasalarının aynı matematiksel beklentiye sahip olacağı ve buna bağlı olarak, herhangi bir egzotik kriter icat etmek zorunda kalmadan "güzelliklerini" değerlendirmek için yalnızca standart sapmayı kullanabileceğimizdir. Size iki yöntem gösterdim. Size en uygun olanı seçmek size kalmış. Tahmin edebileceğiniz gibi, tüm bu göreceli eğrilerin dağılım yasaları şöyle görünecektir:

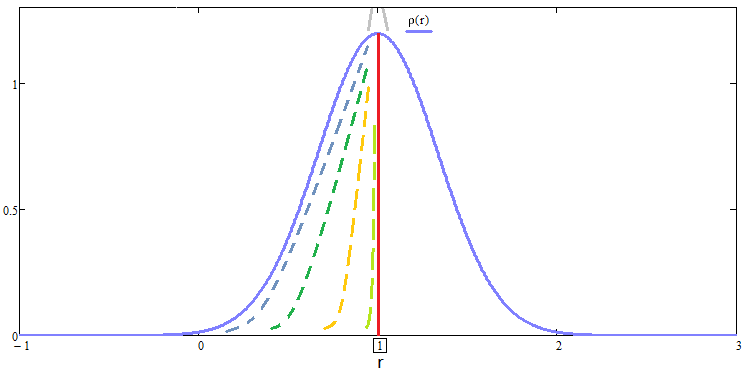
Bu yaklaşım genişletilmiş testler için de geçerlidir. Burada genişletilmiş testler derken daha uzun bir segment üzerinde test yapmayı kastediyoruz. Bu uygulama sadece test ne kadar uzun olursa grafiğin o kadar güzel olacağı gerçeğini doğrulamak için uygundur. Bu kanıt için uygulamanız gereken tek püf noktası, testin süresini artırırsak, bunu bir tam sayının katları şeklinde yaptığımızı, bu sayının katlarında ise 1 adımını değil "n" adımını kullandığımızı ve birleştirme denklemlerini uyguladığımızı dikkate almaktır. Bu birleştirme daha da basit olacaktır, çünkü tekrarlayan birleştirme zinciri sadece çoğaltılan tek bir eleman içerecektir ve sonucu sadece bu elemanla karşılaştırmak mümkün olacaktır.

Sonuç

Makalede, yeniden alma algoritmasının kendisini değil, alım-satım sistemlerinin daha doğru ve verimli bir şekilde değerlendirilmesi için size gerekli matematiksel denklemleri ve yöntemleri veren çok daha önemli bir konuyu ele aldık. Daha da önemlisi, çeşitlendirmenin ne kadar değerli olduğunu, onu neyin etkili kıldığını ve her şeyi doğru yaptığınızdan emin olarak doğal ve sağlıklı bir şekilde onu nasıl artıracağınızın matematiksel kanıtını gördük.

Ayrıca, herhangi bir kârlı sistemin grafiğinin kullandığımız alım-satım alanı ne kadar uzun olursa ve aynı zamanda bir hesapta aynı anda ne kadar çok kârlı sistem işlem yaparsa o kadar güzel olduğunu kanıtladık. Şimdiye kadar her şey bir teori şeklinde çerçevelendi, ancak bir sonraki makalede bu teorinin uygulamalı yönlerini ele alacağız. Basitçe ifade etmek gerekirse, fiyat simülasyonu ve çoklu döviz alım-satımı simülasyonu için çalışan bir matematiksel model oluşturacağız ve tüm teorik sonuçlarımızı doğrulayacağız. Bu teoriyi büyük olasılıkla hiçbir yerde bulamayacaksınız, bu yüzden bu matematiği daha derinlemesine incelemeye veya en azından özünü anlamaya çalışın.