Combinatoria e probabilità per il trading (Parte IV): Logica di Bernoulli

Contenuto

• Introduzione
• L'importanza di una corretta rappresentazione dei dati nell'analisi
• Stati doppi
• Stati multipli
• Implementazione software di stati multipli
• Conclusioni
• Riferimenti

Introduzione

Negli articoli precedenti di questa serie, ho descritto i frattali come uno strumento per descrivere i mercati e, in particolare, i prezzi. Questo modello descrive perfettamente il mercato - questo è stato confermato da calcoli e simulazioni. Lo scopo originario non era solo quello di descrivere le forme di prezzo più semplici, ma anche di consentire un'ulteriore descrizione di qualsiasi serie vettoriale che abbia un insieme di parametri simili all'insieme di parametri del prezzo. Ebbene, nel caso generale, si scopre che un trade è anche un pezzo di mercato, caratterizzato da una durata temporale e da una probabilità di apparire nel processo di scambio. Le curve arbitrarie possono essere create sia dai prezzi che dagli scambi. Per i prezzi, questa curva è la cronologia dei prezzi, mentre per i trade è la cronologia delle negoziazioni.

Il caso del prezzo è molto più chiaro, poiché tutti i membri di questa serie si susseguono chiaramente. Naturalmente, è possibile creare tali serie di prezzi che si sovrappongono l'una all'altra, ma questa analisi sarebbe assolutamente inutile, poiché non si trarrebbe alcun vantaggio pratico. Il caso dei backtest, o della cronologia di trading, è più complicato. Studiando questi processi, sono giunto alla conclusione che esiste un percorso molto più semplice e corretto per un trading profittevole e stabile - l'analisi della cronologia di trading o dei backtest. Ci sarà un articolo finale che descriverà uno di questi approcci, ma per ora è troppo presto per farlo.

L'importanza di una corretta rappresentazione dei dati nell'analisi

Se consideriamo l'analisi delle possibilità di descrivere la cronologia di trading e i backtest nel linguaggio della matematica, dobbiamo innanzitutto comprendere lo scopo e i possibili risultati di tale analisi. C'è un valore aggiunto in questa analisi? In effetti, è impossibile dare subito una risposta chiara. Ma c'è una risposta che può portare gradualmente a soluzioni semplici e funzionanti. Tuttavia, dovremmo prima approfondire i dettagli. Data l'esperienza degli articoli precedenti, ero interessato alle seguenti domande:

1. È possibile ridurre qualsiasi strategia a una descrizione frattale del trading?
2. Se è possibile, dove sarebbe utile?
3. Se non è sempre possibile, quali sono le condizioni per la riducibilità?
4. Se le condizioni di riducibilità sono soddisfatte, sviluppare l'algoritmo di riducibilità.
5. Considerare altre opzioni per descrivere la strategia. Generalizzazione.

Le risposte a tutte queste domande sono le seguenti. È possibile ridurre alcune strategie a una descrizione frattale. Ho sviluppato questo algoritmo e lo descriverò più avanti. È adatto anche ad altri scopi, poiché è un frattale universale. Ora pensiamo e proviamo a rispondere alla seguente domanda: Cos’ è la cronologia di trading nel linguaggio dei numeri casuali e della teoria della probabilità? La risposta è semplice: si tratta di un insieme di entità isolate o vettori, il cui verificarsi in un certo periodo di tempo ha una certa probabilità e un fattore di utilizzo del tempo. La caratteristica principale di ognuna di queste entità è la probabilità che si verifichi. Il fattore di utilizzo del tempo è un valore ausiliario che aiuta a determinare quanto tempo disponibile viene utilizzato per il trading. La figura seguente può aiutare a comprendere l'idea:

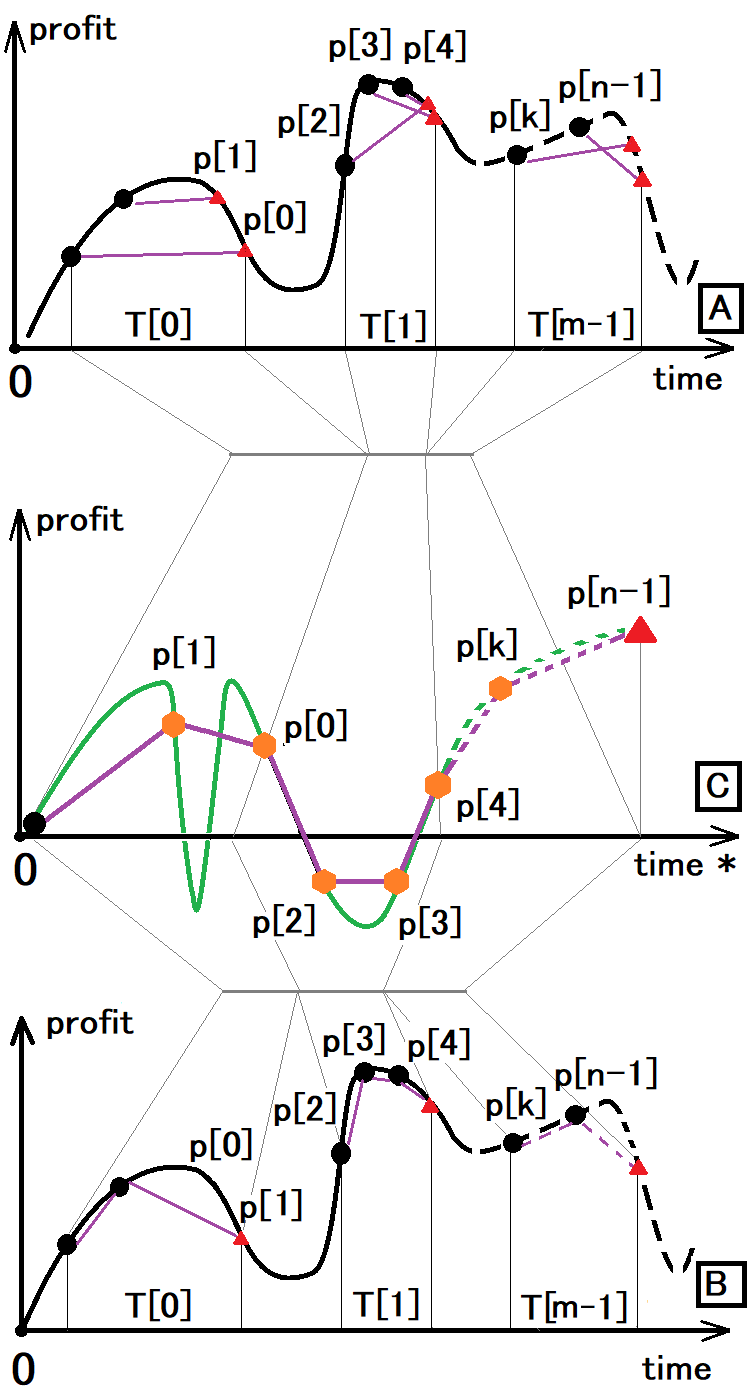
Nella figura sono utilizzati i seguenti simboli:

1. Punto nero - l'inizio del trade
2. Triangolo rosso - la fine del trade
3. Esagono arancione - sia la fine della trade precedente che l'inizio di quello successivo.
4. T[i] - ora di una relativa finestra di trading
5. P[i] - profitto o perdita di un relativo trade
6. n - Il numero di trade
7. m - numero di finestre di trading

La figura mostra tre grafici per dimostrare che le opzioni A e B possono essere ridotte all'opzione C. Vediamo ora quali sono queste opzioni:

1. L'opzione A è il modo in cui vediamo il trading arbitrario utilizzando tutti i trucchi possibili, la gestione del denaro, ecc.
2. L'opzione B è la stessa, ma considerando che può essere aperto un solo ordine alla volta.
3. L'opzione C è il modo in cui vediamo il trading nel servizio Segnali o nel backtest.

L'opzione C è quella più informativa e nella maggior parte dei casi ci si affida a questa rappresentazione del trading. Inoltre, qualsiasi strategia può essere ridotta a questo tipo, perché la equity line è la caratteristica principale di qualsiasi backtest o segnale di trading. Questa riga riflette il profitto o la perdita reale al momento attuale.

L'analisi della equity line di una strategia arbitraria mostrerebbe che i punti di apertura e di chiusura dell'operazione possono essere situati in posizioni assolutamente arbitrarie se la linea rimane invariata. Ciò significa che una strategia di trading può essere rappresentata in un numero enorme di modi diversi e tutti questi modi saranno equivalenti, poiché le loro equity lines sono equivalenti. Pertanto, non ha senso cercare tutte le opzioni equivalenti. Qual’è lo scopo di trovarli?

Una strategia di tipo B può essere facilmente convertita in una di tipo C, perché basta incollare insieme gli intervalli di tempo nello stesso ordine in cui si verificano. In realtà, questo è esattamente ciò che fanno il tester e il servizio segnali. La situazione è diversa se si cerca di convertire il tipo A in C. Per attuare questa conversione, dobbiamo prima ridurre A al tipo B, e poi il risultato può essere ridotto al tipo C. Ora sapete come funzionano il tester di strategia e il servizio Segnali.

Questa trasformazione di per sé non ha alcun valore pratico per il trading. Tuttavia, può aiutare a capire cose più profonde. Ad esempio, possiamo concludere che esistono i seguenti tipi di strategie:

1. Definita da due stati
2. Definita da stati multipli
3. Definita da un numero infinito di stati

In questo articolo vi mostrerò esempi di descrizione per i primi due tipi di strategie. Il terzo tipo è più complesso e richiede un articolo a parte. Tornerò su questa idea a tempo debito. In ogni caso, prima di considerare il terzo tipo di strategie, è necessario comprendere le prime due. Questi due tipi ci prepareranno la mente prima di procedere con il terzo tipo di strategia generale.

Stati doppi

I frattali descritti negli articoli precedenti rappresentano in realtà un modello a due stati. Qui gli stati sono movimenti verso l'alto e verso il basso. Se applichiamo il modello alla linea del saldo di trading anziché al prezzo, questo modello funzionerà esattamente allo stesso modo. Il modello è basato sullo schema di Bernoulli. Lo schema di Bernoulli descrive il frattale più semplice con due stati:

• P[k] = C(n,k)*Pow(p,k)*Pow(q,n-k) - Formula di Bernoulli (P[k] è la probabilità di una combinazione specifica)
• p è la probabilità dello stato "1" come risultato di un singolo esperimento
• q è la probabilità dello stato "2" come risultato di un singolo esperimento

Queste formule possono calcolare la probabilità che dopo "n" passaggi avremo una curva del saldo o qualsiasi altra curva con "k" primi stati e "n-k" secondi stati. Questi non devono essere profitti di trade. Questi stati possono simboleggiare qualsiasi vettore di parametri in cui si riscontra l'unicità. La somma di tutte le probabilità di una particolare combinazione deve formare un gruppo completo, il che significa che la somma di tutte queste probabilità deve essere uguale a uno. Questo simboleggia il fatto che in "n" passaggi deve necessariamente comparire una di queste combinazioni:

• Summ(0...k...n)[ P[k] ] = 1

In questo caso, ci interessa utilizzare questi elementi per descrivere i prezzi o i backtest e i segnali. Immaginiamo che la nostra strategia consista in trade chiusi da livelli di stop equidistanti. Allo stesso tempo, sappiamo che è impossibile calcolare il movimento dei prezzi previsto per il futuro. La distribuzione di queste probabilità sarà simile a questo:

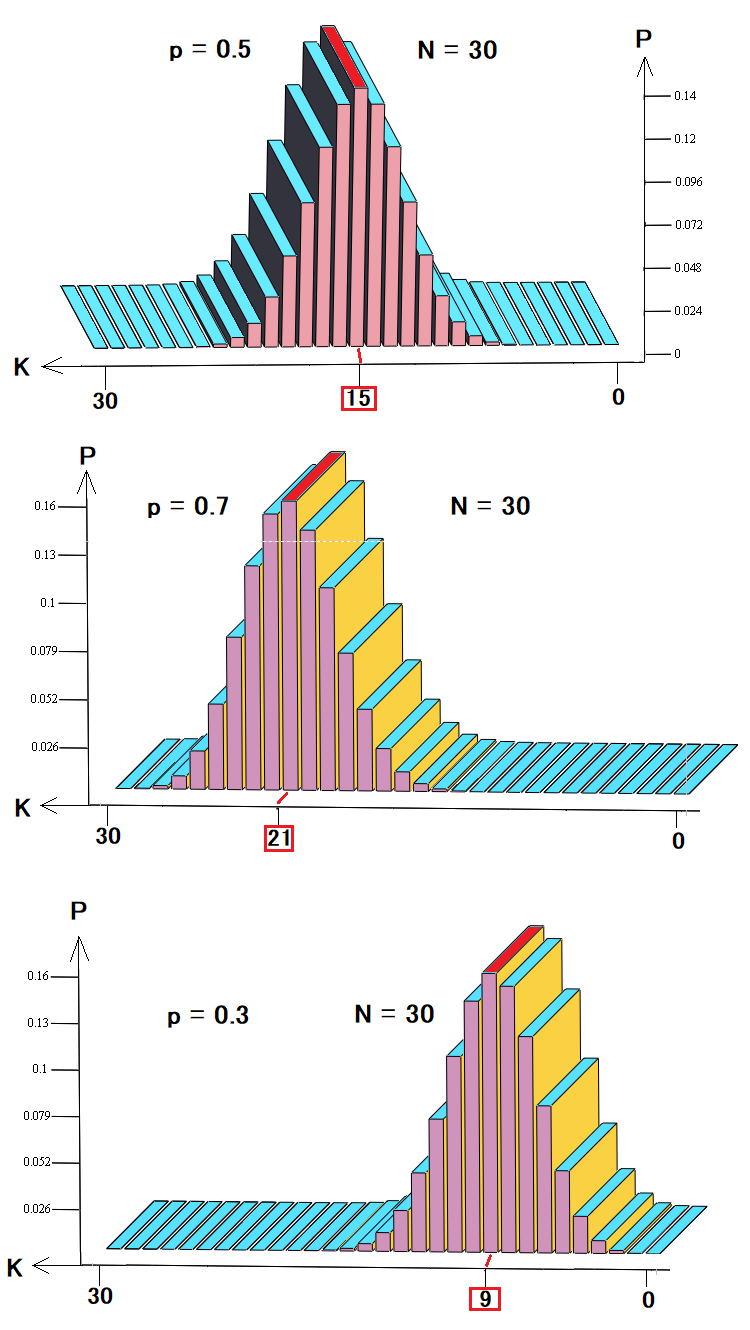
Queste tre figure mostrano:

1. Distribuzione di probabilità in una passeggiata aleatoria o trading
2. Distribuzione di probabilità per trading profittevoli o per un trend rialzista
3. Distribuzione di probabilità per trading perdenti o trend ribassista

Come si può vedere dai diagrammi, a seconda della probabilità di un incremento, le probabilità di alcune combinazioni cambiano e il caso più probabile si sposta verso sinistra o verso destra, come tutte le altre probabilità. Questo backtest o rappresentazione dei prezzi è il modello più semplice e preferito per l'analisi. Un modello di questo tipo è sufficiente per descrivere il prezzo, ma non abbastanza per descrivere il trading. In realtà, la curva del saldo può contenere diverse operazioni, che differiscono in termini di durata e di profitto/perdita. A seconda delle metriche di trading più importanti, possiamo impostare un numero qualsiasi di stati, non solo due.

Stati multipli

Prendiamo in considerazione il seguente esempio. Supponiamo di essere ancora interessati al valore di profitto o perdita di un trade. Ora, sappiamo che lo stato di profitto o perdita può assumere tre valori rigorosamente definiti e conosciamo le probabilità di ognuno di questi valori. Se questo è il caso, allora possiamo dire che abbiamo un sistema a tre stati. È possibile descrivere tutti i possibili sviluppi degli eventi come un sistema a due stati? In realtà, è possibile. Migliorerò leggermente lo schema di Bernoulli in modo che possa funzionare con un sistema con qualsiasi numero di stati.

Secondo la logica di Bernoulli, dobbiamo definire i contatori di stato:

• i[0] - il numero di risultati con il primo stato in una catena di esperimenti indipendenti
• i[1] è il numero di risultati con il secondo stato in una catena di esperimenti indipendenti
• . . .
• i[N] è il numero di risultati con N - stati
• N è il numero di stati del sistema
• s è il numero di stato

Se determiniamo il numero di occorrenze di un certo stato uno per uno, il numero disponibile per lo stato successivo sarà:

• s[i] = N - Summ(0... k ... i - 1) [ s[k] ]

Si può semplificare. Se abbiamo scelto il numero di risultati dello stato precedente, il numero di risultati per lo stato successivo rimane esattamente uguale al numero di stati selezionati per lo stato precedente. Proprio come nello schema di Bernoulli, esistono catene di probabilità incoerenti che hanno la stessa probabilità. Il numero di catene con lo stesso numero di tutti gli stati viene quindi calcolato come segue:

• A[h](N,i[0] ,i[1] ,... i[n]) = C(N , i[0]) * C(N-i[0] , i[1]) *.... C(N-Summ(0...k...n-1)[ i[k] ] , i[n])
• C sono le combinazioni
• h è un insieme unico di passaggi

Ovviamente, le probabilità di tali insiemi possono essere calcolate come nello schema di Bernoulli. Moltiplicare la probabilità di un insieme per il suo numero:

• P[k] = A[h](N,i[0] ,i[1] ,... i[n]) * Pow(p[0], i[0]) * Pow(p[1], i[1]) ... * Pow(1- Summ(0...j...N-1)[ p[j] ] , i[1])
• p[j] è la probabilità di un certo stato

Per chiarezza, ho creato grafici tridimensionali, come nell'esempio precedente per due stati. Anche in questo caso abbiamo 30 passaggi, ma utilizziamo tre stati invece di due:

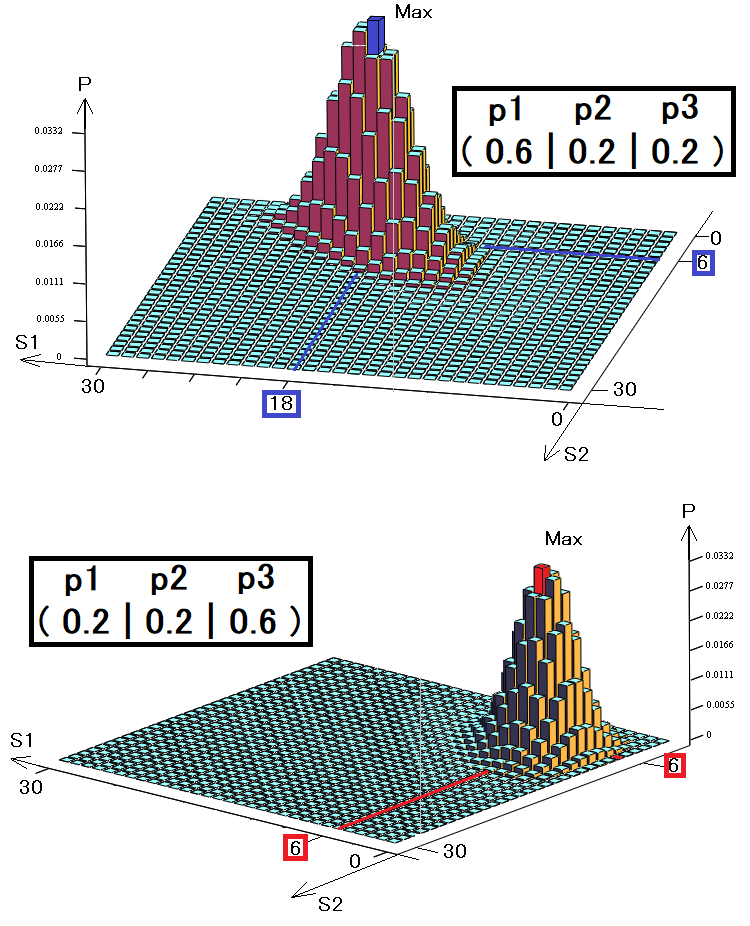
Il volume di tale diagramma sarà esattamente uguale a uno, poiché ogni barra simboleggia un evento incompatibile e tutti questi eventi incompatibili formano un gruppo completo. I diagrammi mostrano due diverse strategie con vettori di probabilità differenti. Queste probabilità simboleggiano la possibilità che si verifichi uno dei tre stati.

• S1 è il numero di occorrenze del primo stato
• S2 è il numero di occorrenze del secondo stato
• S3 = 30 - S1 - S2 – il numero di occorrenze del terzo stato

Se il nostro sistema avesse un quarto stato, allora potrebbe essere presentato solo in modo quadridimensionale. Per cinque stati avremmo bisogno di un diagramma a cinque dimensioni, e così via. Per l'occhio umano sono disponibili solo 3 dimensioni, quindi i sistemi più complessi non possono essere rappresentati graficamente. Tuttavia, anche le funzioni multidimensionali sono funzionali, proprio come le altre.

Implementazione software di stati multipli

I casi a due stati possono essere rappresentati da un array monodimensionale. E per quanto riguarda gli stati multipli? Possiamo pensare a un array multidimensionale. Ma, per quanto ne so, tutti i linguaggi di programmazione utilizzano al massimo array bidimensionali. Forse alcuni offrono la possibilità di creare array a tre o più dimensioni, ma non è un'opzione conveniente. Un'opzione migliore è quella di usare collezioni o tuple:

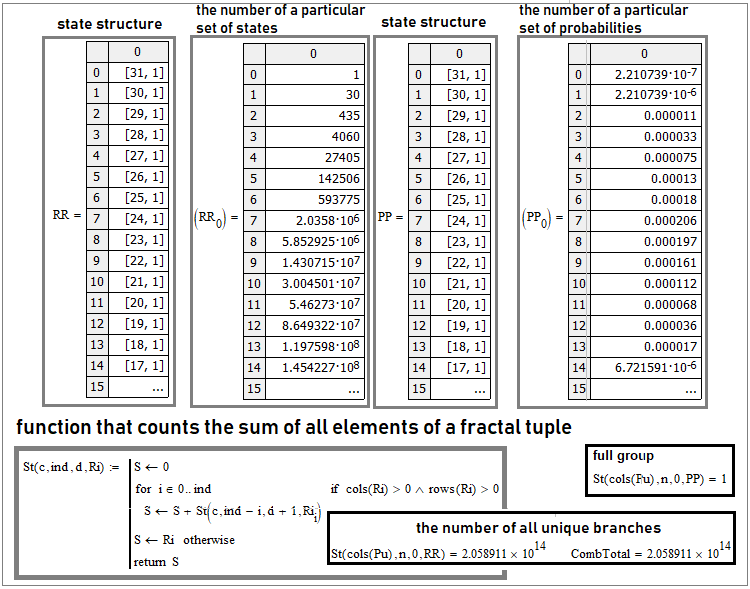
Questa è la situazione con "30" passaggi. La prima e la terza colonna riflettono la struttura interna della tupla. Si tratta di un array all'interno di un array. Dove è scritto, ad esempio, "[31,1]", significa che anche questo elemento della matrice è una matrice con "31" righe e una colonna. La formula di Bernoulli e l'intero schema di Bernoulli sono solo un caso particolare di questo schema più generale. Se sono richiesti due stati, le tuple si trasformeranno in array monodimensionali, nel qual caso otterremo combinazioni semplici che svolgono il ruolo chiave nella formula di Bernoulli.

Se guardiamo cosa c'è all'interno di questi array, otterremo le colonne "2" e "4". La seconda colonna è il numero di rami equivalenti di specifici insiemi unici di stati e la quarta è la probabilità totale di tali rami, poiché le loro probabilità sono uguali.

Un criterio davvero chiaro per convalidare il calcolo di tali tuple è quello di controllare l'intero gruppo di eventi e il numero totale di tutti i rami unici. Per farlo, possiamo creare una funzione generale che sommi tutti gli elementi delle loro tuple complesse, indipendentemente dalla complessità della loro struttura interna. Un esempio è mostrato nella schermata precedente. Una funzione di questo tipo deve essere ricorrente; deve chiamare se stessa all'interno - in questo caso sarà una funzione universale per qualsiasi numero di stati e numero di passaggi. Per quanto riguarda il numero di rami unici, il valore vero è calcolato come segue:

• Pow(N,n)

In altre parole, il numero di stati del sistema deve essere elevato alla potenza del numero di passaggi - in questo modo otterremo tutte le possibili combinazioni di catene uniche costituite dai nostri stati. Nella figura, questo numero è indicato come variabile "CombTotal". La somma risultante sarà confrontata con questa variabile.

Per contare le tuple, dobbiamo usare funzioni simili con la stessa struttura ricorrente:

Come si può vedere, sono molto simili. Ci sono solo un paio di differenze. Ad ogni livello, dobbiamo inoltre moltiplicare il risultato per il numero di combinazioni di passaggi liberi rimanenti. Quando si calcolano le probabilità, il risultato deve essere ulteriormente moltiplicato per la probabilità dello stato attualmente sotto esame. Inoltre, non dimenticate di moltiplicare per la probabilità già accumulata della catena. Uno alla volta accumula tutti gli stati finché non rimangono celle libere, mentre le celle rappresentano il numero di passaggi.

Possiamo anche considerare un esempio di estrazione degli stati dai dati che conosciamo. Ad esempio, disponiamo di statistiche di trading, in cui vengono memorizzate le seguenti informazioni per ogni ordine: durata, volume di trading, perdita o profitto, ecc. Poiché il campione è finito, anche il numero di stati è altrettanto finito. Ad esempio, possiamo determinare quante opzioni di profitto ci sono nel campione. Ogni valore di profitto unico può essere considerato uno stato unico. Contate il numero di occorrenze di tutti questi profitti in tutto il campione, dividetelo per il numero totale di tutte le operazioni e ottenete la probabilità di un particolare stato. Ripetere l'operazione per tutti gli stati. Se poi sommiamo tutte queste probabilità, ne otteniamo una. In questo caso tutto è stato fatto correttamente. In modo analogo, possiamo classificare i trade in base alla durata dell'ordine. In altre parole, uno stato può essere qualsiasi caratteristica unica di un evento. In questo caso, un trade è considerato un evento, mentre i parametri del trade sono le caratteristiche di un particolare evento. Nel nostro caso, gli esempi di stato possono essere i seguenti:

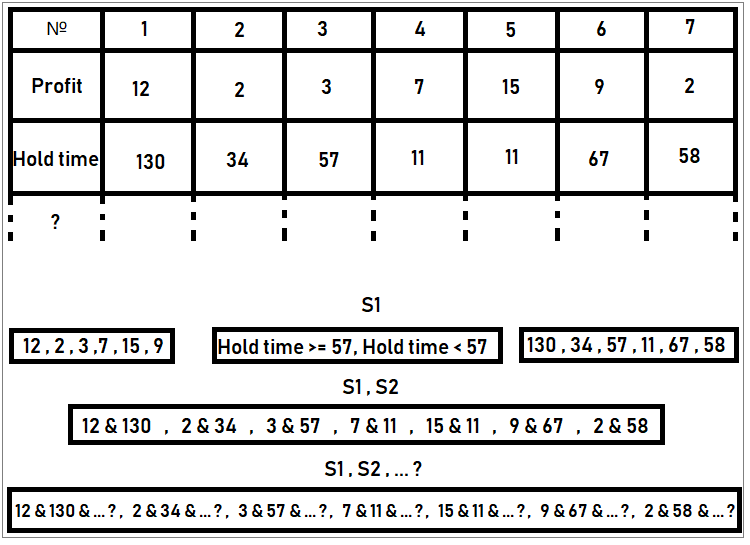
La figura mostra un esempio di compilazione di insiemi di stati. Secondo le regole, gli stati devono formare un gruppo completo di eventi, cioè non ci devono essere stati congiunti. La probabilità di questi eventi può essere calcolata dividendo il numero di ordini nella tabella con stati specifici per il numero di tutti gli ordini (che nel nostro caso è 7). Questo era l'esempio degli ordini; tuttavia, possiamo lavorare con qualsiasi altro stato.

Conclusioni

In questo articolo ho cercato di dimostrare come valutare i campioni di dati, come crearne di nuovi da tali campioni classificando i dati e combinandoli in insiemi di stati, di cui è possibile calcolare le probabilità. Cosa fare con questi dati dipende da voi. Credo che l'uso migliore sia quello di creare più campioni e di valutarli - questo è anche chiamato clustering dei campioni. Il clustering dei campioni può servire come un buon filtro per migliorare le prestazioni di trading dei sistemi esistenti. Può anche essere utilizzato per ottenere profitti da una strategia apparentemente non profittevole — basta raggruppare i dati e trovare i campioni redditizi desiderati. E soprattutto, tali meccanismi possono essere utilizzati come fasi di elaborazione dei dati in sistemi di trading scalabili. Applicheremo questi meccanismi nella pratica più avanti, quando passeremo ad assemblare un sistema di trading auto-adattante. Per ora, questo è solo un altro mattone.

Riferimenti

• Combinatoria e teoria della probabilità per il trading (Parte I): Le basi
  
• Combinatoria e teoria della probabilità per il trading (Parte II): Frattale universale
  
• Combinatoria e teoria della probabilità per il trading (Parte III): Il primo modello matematico