Combinatoires et probabilités pour le trading (Partie IV) : Logique de Bernoulli

Sommaire

• Introduction
• L'importance d'une représentation correcte des données dans l'analyse
• États doubles
• États multiples
• Mise en œuvre logicielle de plusieurs états
• Conclusion
• Références

Introduction

Dans les articles précédents de cette série, j'ai décrit les fractales comme étant un outil permettant de décrire les marchés et, en particulier, les prix. Ce modèle décrit parfaitement le marché, ce qui a été confirmé par des calculs et des simulations. L'objectif initial n'était pas seulement de décrire les formes de prix les plus simples, mais aussi de permettre une description plus poussée de toute série vectorielle dont l'ensemble des paramètres est similaire à celui des prix. Dans le cas général, il s'avère qu'une transaction est également un élément du marché, caractérisé par une durée dans le temps et une probabilité d'apparition dans le processus de trading. Des courbes arbitraires peuvent être créées à partir des prix et des transactions. Pour les prix, cette courbe correspond à l'historique des prix, alors que pour les transactions, il s'agit de l'historique des transactions.

Le cas du prix est beaucoup plus clair, car tous les membres de la série se suivent clairement. Il est bien entendu possible de créer des séries de prix qui se chevauchent. Mais cette analyse serait absolument inutile, car elle ne présenterait aucun avantage pratique. Le cas des backtests, ou historiques de trading, est plus compliqué. En étudiant ces processus, je suis arrivé à la conclusion qu'il existe un chemin beaucoup plus facile et plus correct vers un trading rentable et stable : l'analyse de l'historique des transactions, ou backtests. Un article final décrira l'une de ces approches, mais il est encore trop tôt pour le faire.

L'importance d'une représentation correcte des données dans l'analyse

Si nous envisageons d'analyser les possibilités de décrire l'historique des transactions et les backtests dans un langage mathématique, nous devons tout d'abord comprendre l'objectif et les résultats possibles d'une telle analyse. Une telle analyse apporte-t-elle une valeur ajoutée ? En fait, il est impossible de donner une réponse claire tout de suite. Mais il existe une réponse, qui peut progressivement déboucher sur des solutions simples et efficaces. Mais il convient d'abord d'entrer dans les détails. Compte tenu de l'expérience des articles précédents, je me suis intéressé aux questions suivantes :

1. Est-il possible de réduire toute stratégie à une description fractale du trading ?
2. Si c'est possible, où cela serait-il utile ?
3. Si ce n'est pas toujours possible, quelles sont les conditions de la réductibilité ?
4. Si les conditions de réductibilité sont remplies, développer l'algorithme de réduction
5. Envisager d'autres options pour décrire la stratégie. Généralisation

Les réponses à toutes ces questions sont les suivantes : il est possible de réduire certaines stratégies à une description fractale. J'ai développé cet algorithme et je le décrirai plus loin. Elle peut également être utilisée à d'autres fins, car il s'agit d'une fractale universelle. Réfléchissons maintenant et essayons de répondre à la question suivante : Qu'est-ce que l'historique des transactions dans le langage des nombres aléatoires et de la théorie des probabilités ? La réponse est simple : il s'agit d'un ensemble d'entités isolées ou de vecteurs, dont l'occurrence pendant une certaine période de temps a une certaine probabilité et un facteur d'utilisation du temps. La principale caractéristique de chacune de ces entités est la probabilité qu'elle se produise. Le facteur d'utilisation du temps est une valeur auxiliaire qui permet de déterminer la part du temps disponible utilisée pour le trading. La figure suivante peut aider à comprendre cette idée :

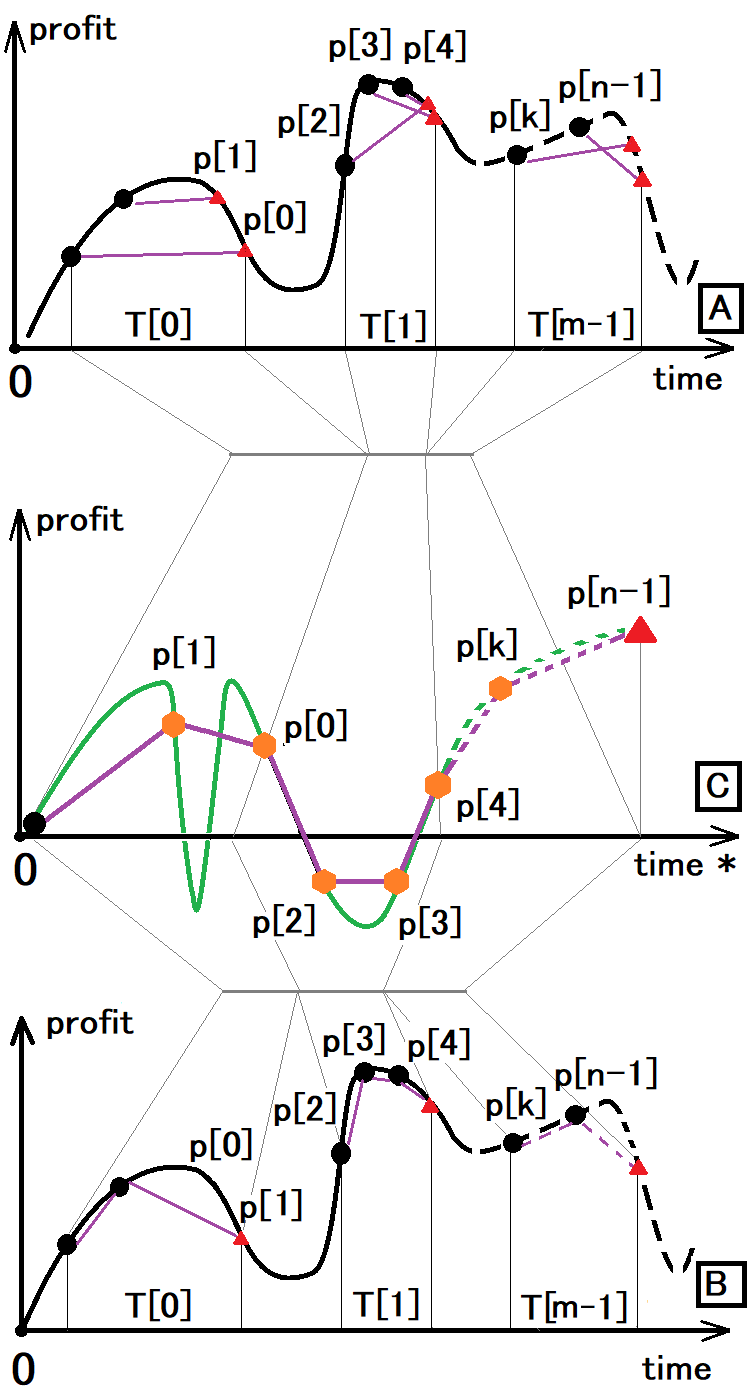
Les symboles suivants sont utilisés dans la figure :

1. Point noir - le début de la position
2. Triangle rouge - la fin de la position
3. Hexagone orange - à la fois la fin de la position précédente et le début de la position suivante
4. T[i] - la période de trading concernée
5. P[i] - le profit ou perte d'une position
6. n - le nombre de positions
7. m - le nombre de fenêtres de trading

La figure présente 3 graphiques qui démontrent que les options A et B peuvent être réduites à l'option C. Voyons maintenant quelles sont ces options :

1. L'option A correspond à la façon dont nous envisageons le trading arbitraire en utilisant toutes les astuces possibles, la gestion de l'argent, etc.
2. L'option B est la même, mais elle tient compte du fait qu'un seul ordre peut être ouvert à la fois.
3. L'option C correspond à la façon dont nous voyons les transactions dans le service des Signaux ou dans le backtest.

L'option C est la plus informative et, dans la plupart des cas, nous nous appuyons sur cette représentation du trading. Toute stratégie peut également être réduite à ce type, car la ligne d'équité est la principale caractéristique de tout backtest et de tout signal de trading. Cette ligne reflète le bénéfice ou la perte réel(le) à l'instant présent.

L'analyse de la ligne d'équité d'une stratégie arbitraire montrerait que les points d'ouverture et de clôture de la transaction peuvent être situés dans des positions absolument arbitraires si la ligne reste inchangée. Cela signifie qu'une stratégie de trading peut être représentée d'un très grand nombre de façons différentes et que toutes ces façons seront équivalentes car leurs lignes d'équité sont similaires. Il est donc inutile de rechercher toutes les options équivalentes. Quel est l'intérêt de les trouver ?

Une stratégie de type B peut être facilement convertie en stratégie de type C, car il suffit de coller les intervalles de temps dans l'ordre où ils se produisent. C'est exactement ce que font le testeur et le service Signals. La situation est différente si vous essayez de convertir le type A en C. Pour mettre en œuvre cette conversion, nous devons d'abord réduire le type A en type B, puis le résultat peut être réduit en type C. Vous savez maintenant comment fonctionnent le testeur de stratégie et le service Signals.

Cette transformation n'a en soi aucune valeur pratique pour le trading. Mais elle peut aider à comprendre des choses plus profondes. Par exemple, nous pouvons conclure qu'il existe les types de stratégies suivants :

1. Décrit par 2 états
2. Décrit par plusieurs états
3. Décrit par un nombre infini d'états

Dans cet article, je vous présenterai des exemples de description pour les deux premiers types de stratégies. Le troisième type est plus complexe et nécessite un article distinct. Je reviendrai sur cette idée en temps voulu. Quoi qu'il en soit, avant d'envisager le troisième type de stratégies, il est nécessaire de comprendre les deux premiers. Ces deux types de stratégies préparent notre esprit avant d'aborder le troisième type de stratégie générale.

États doubles

Les fractales décrites dans les articles précédents représentent en fait un modèle à 2 états. Ici, les états sont les mouvements haussiers et les mouvements baissiers. Si nous appliquons le modèle à la courbe du solde du trading plutôt qu'aux prix, ce modèle fonctionnera exactement de la même manière. Le modèle est basé sur le schéma de Bernoulli. Le schéma de Bernoulli décrit la fractale la plus simple avec 2 états :

• P[k] = C(n, k) * Pow(p, k) * Pow(q, n - k) - Formule de Bernoulli (P[k] est la probabilité d'une combinaison spécifique)
• p est la probabilité de l'état "1" comme étant le résultat d'une seule expérience
• q est la probabilité de l'état "2" comme étant le résultat d'une seule expérience

Ces formules permettent de calculer la probabilité qu'après "n" étapes, nous ayons une courbe d'équilibre ou toute autre courbe ayant "k" premiers états et "n-k" seconds états. Ces états peuvent symboliser n'importe quel vecteur de paramètres pour lequel nous constatons une unicité. La somme de toutes les probabilités d'une combinaison particulière doit former un groupe complet, ce qui signifie que la somme de toutes ces probabilités doit être égale à 1. Cela symbolise le fait qu'en "n" étapes, une de ces combinaisons doit nécessairement apparaître :

• Somme(0...k...n)[ P[k] ] = 1

Dans le cas présent, nous souhaitons utiliser ces éléments pour décrire soit les prix, soit les backtests et les signaux. Imaginons que notre stratégie consiste en des positions fermées par des niveaux d'arrêt équidistants. En même temps, nous savons qu'il est impossible de calculer l'évolution attendue des prix dans le futur. La distribution de ces probabilités se présente comme suit :

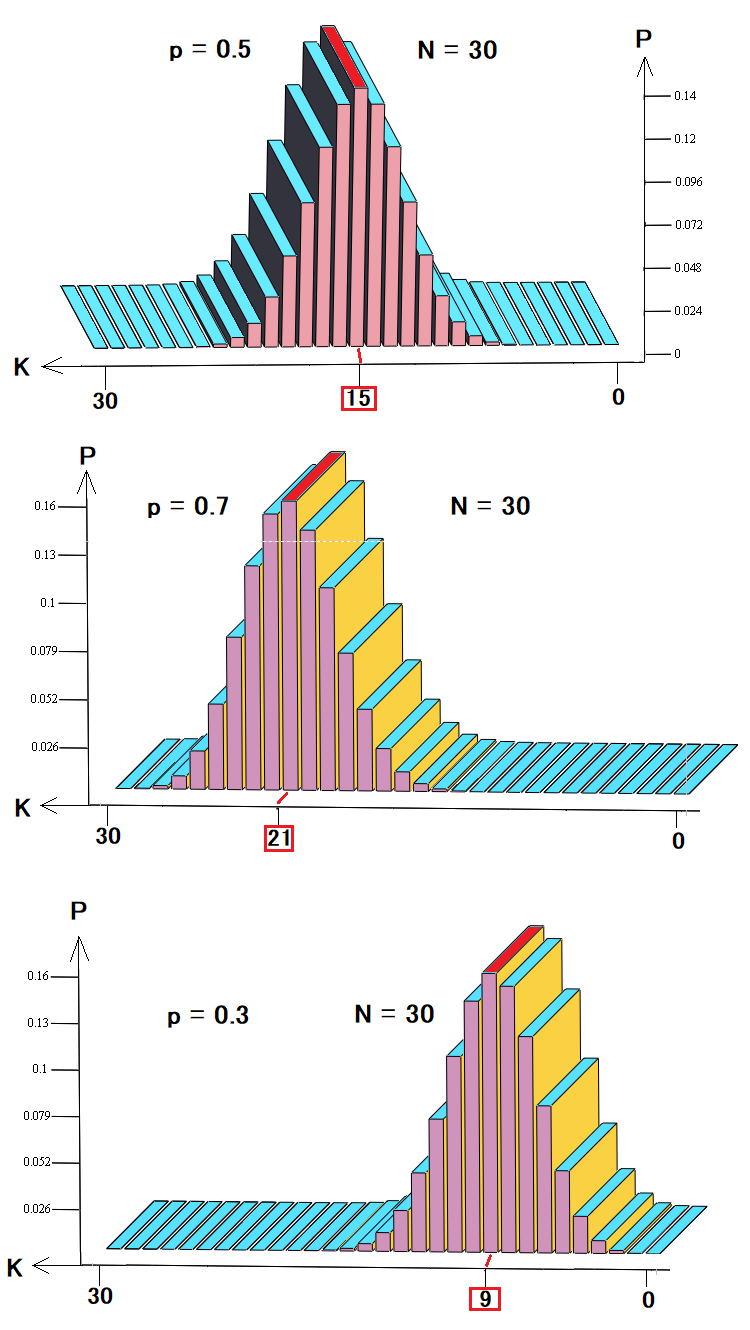
Ces 3 chiffres montrent :

1. La distribution de probabilité dans une marche ou un trading aléatoire
2. La distribution de probabilités pour un trading rentable ou une tendance haussière
3. La distribution de probabilité pour les positions perdantes ou les tendances baissières

Comme le montrent les diagrammes, en fonction de la probabilité d'un pas en avant, les probabilités de certaines combinaisons changent et le cas le plus probable se déplace vers la gauche ou vers la droite, comme toutes les autres probabilités. Ce backtest ou cette représentation des prix est le modèle d'analyse le plus simple et le plus adapté. Un tel modèle est tout à fait suffisant pour décrire la fixation des prix, mais il n'est pas suffisant pour décrire le trading. La courbe d'équilibre peut en fait contenir plusieurs transactions, qui diffèrent en termes de durée et de profit/perte. En fonction des paramètres de trading les plus importants, nous pouvons définir un nombre quelconque d'états, et pas seulement deux.

États multiples

Prenons maintenant l'exemple suivant : supposons que nous soyons toujours intéressés par la valeur du profit ou de la perte d'une position. Nous savons maintenant que l'état de profit ou de perte peut prendre 3 valeurs strictement définies, et nous connaissons les probabilités de chacune de ces valeurs. Si c'est le cas, nous pouvons dire que nous avons un système à 3 états. Est-il possible de décrire tous les événements possibles comme un système à 2 états ? En fait, c'est possible. Je vais légèrement améliorer le schéma de Bernoulli afin qu'il puisse fonctionner avec un système comportant un nombre quelconque d'états.

Selon la logique de Bernoulli, nous devons définir des compteurs d'état :

• i[0] - le nombre de résultats avec le premier état dans une chaîne d'expériences indépendantes
• i[1] est le nombre de résultats avec le deuxième état dans une chaîne d'expériences indépendantes
• . . .
• i[N] est le nombre de résultats avec l'état N.
• N est le nombre d'états du système
• s est le numéro de l'état

Si nous déterminons le nombre d'occurrences d'un certain état un par un, alors le nombre disponible pour l'état suivant sera :

• s[i] = N - Somme(0... k ... i - 1) [ s[k] ]

Elle peut être simplifiée. Si nous avons choisi le nombre de résultats de l'état précédent, le nombre de résultats de l'état suivant reste exactement le même que le nombre d'états sélectionnés pour l'état précédent. Tout comme dans le schéma de Bernoulli, il existe des chaînes de probabilités qui ne sont pas cohérentes et qui ont la même probabilité. Le nombre de chaînes ayant le même nombre d'états est alors calculé comme suit :

• A[h](N, i[0] , i[1] , ... i[n]) = C(N , i[0]) * C(N - i[0] , i[1]) *.... C(N - Somme(0...k...n-1)[ i[k] ] , i[n])
• C sont des combinaisons
• h est un ensemble unique d'étapes

Il est évident que les probabilités de ces ensembles peuvent être calculées comme dans le schéma de Bernoulli. Multipliez la probabilité d'une série par leur nombre :

• P[k] = A[h](N, i[0] , i[1] , ... i[n]) * Pow(p[0], i[0]) * Pow(p[1], i[1]) ... * Pow(1 - Somme(0...j...N-1)[ p[j] ] , i[1])
• p[j] est la probabilité d'un certain état

Pour plus de clarté, j'ai créé des graphiques en 3 dimensions, comme dans l'exemple précédent pour 2 états. Là encore, nous avons 30 étapes, mais nous utilisons ici 3 états au lieu de 2 :

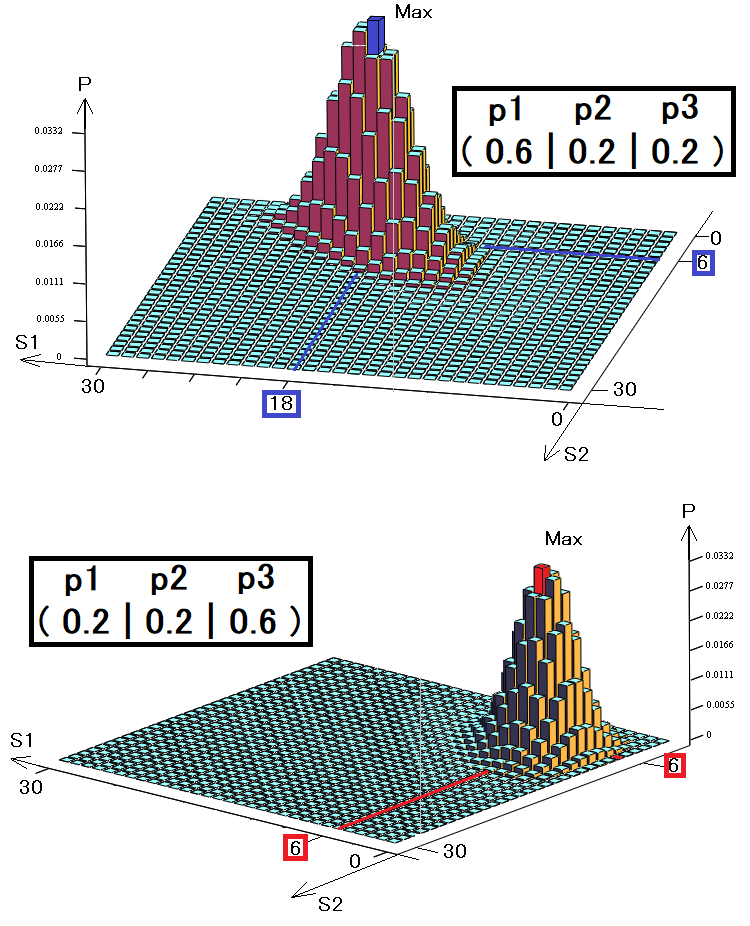
Le volume de ce diagramme sera exactement égal à 1, puisque chaque barre symbolise un événement incompatible, et que tous ces événements incompatibles forment un groupe complet. Les diagrammes montrent deux stratégies différentes avec des vecteurs de probabilité différents. Ces probabilités symbolisent la probabilité d'apparition de l'un des trois états.

• S1 est le nombre d'occurrences du premier état
• S2 est le nombre d'occurrences du deuxième état
• S3 = 30 - S1 - S2 - nombre d'occurrences du troisième état

Si notre système avait un quatrième état, il ne pourrait être présenté que de manière quadridimensionnelle. Pour 5 états, nous aurions besoin d'un diagramme à 5 dimensions, et ainsi de suite. L'œil humain ne dispose que de 3 dimensions, de sorte que les systèmes plus complexes ne peuvent pas être représentés graphiquement. Néanmoins, les fonctions multidimensionnelles sont également fonctionnelles, tout comme les autres.

Mise en œuvre logicielle de plusieurs états

Les cas à 2 états peuvent être représentés par un tableau à 1 dimension. Qu'en est-il des états multiples ? On peut penser à un tableau multidimensionnel. Mais, pour autant que je sache, tous les langages de programmation utilisent au maximum des tableaux à 2 dimensions. Certains offrent peut-être la possibilité de créer des tableaux à 3 dimensions ou plus, mais cette option n'est pas très pratique. Il est préférable d'utiliser des collections ou des tuples :

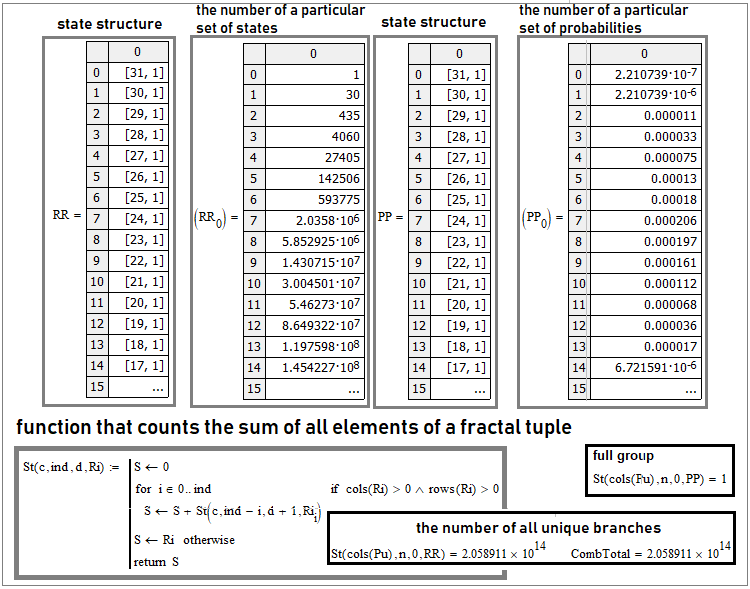
C'est le cas des "30" étapes. Les première et troisième colonnes reflètent la structure interne du tuple. Il s'agit simplement d'un tableau dans un tableau. Lorsqu'il est écrit par exemple "[31,1]", cela signifie que cet élément de la matrice est également une matrice avec "31" lignes et 1 colonne. La formule de Bernoulli et l'ensemble du schéma de Bernoulli ne sont qu'un cas particulier de ce schéma plus général. Si deux états sont nécessaires, les tuples se transformeront en tableaux unidimensionnels, auquel cas nous obtiendrons des combinaisons simples qui jouent un rôle clé dans la formule de Bernoulli.

Si nous regardons ce qui se trouve à l'intérieur de ces tableaux, nous obtiendrons les colonnes "2" et "4". La deuxième colonne est le nombre de branches équivalentes d'ensembles d'états uniques spécifiques, et la quatrième est la probabilité totale de ces branches, car leurs probabilités sont égales.

Un critère vraiment clair pour valider le calcul de ces tuples consiste à vérifier le groupe complet d'événements et le nombre total de toutes les branches uniques. Pour ce faire, nous pouvons créer une fonction générale qui résumera tous les éléments de leurs tuples complexes, quelle que soit la complexité de leur structure interne. Un exemple est présenté dans la capture d'écran ci-dessus. Une telle fonction doit être récurrente ; elle doit s'appeler elle-même. Il s'agira dans ce cas d'une fonction universelle quelque soit le nombre d'états et le nombre d'étapes. En ce qui concerne le nombre de branches uniques, la valeur réelle est calculée comme suit :

• Pow(N, n)

En d'autres termes, le nombre d'états du système doit être élevé à la puissance du nombre d'étapes. De cette manière, nous obtiendrons toutes les combinaisons possibles de chaînes uniques composées de nos états. Dans la figure, ce nombre est représenté par la variable "CombTotal". La somme obtenue sera comparée à cette variable.

Pour compter les tuples, nous devons utiliser des fonctions similaires avec la même structure récurrente :

Comme vous pouvez le constater, ils sont très similaires. Il n'y a que quelques différences. A chaque niveau, il faut en plus multiplier le résultat par le nombre de combinaisons sur les étapes libres restantes. Lors du calcul des probabilités, le résultat doit être multiplié par la probabilité de l'état en cours d'examen. N'oubliez pas non plus de multiplier par la probabilité déjà accumulée de la chaîne. Tous les états sont accumulés un par un jusqu'à ce qu'il n'y ait plus de cellules libres, les cellules représentant le nombre d'étapes.

Nous pouvons également considérer un exemple d'extraction d'états à partir des données que nous connaissons. Par exemple, nous disposons de statistiques de trading, dans lesquelles les informations suivantes sont stockées pour chaque ordre : durée de vie, volume, perte ou profit, etc. L'échantillon étant fini, le nombre d'états est également fini. Par exemple, nous pouvons déterminer le nombre d'options de profit dans l'échantillon. Chaque valeur de profit unique peut être considérée comme un état unique. Comptez le nombre d'occurrences de tous ces bénéfices dans l'échantillon, divisez-le par le nombre total de toutes les positions et vous obtiendrez la probabilité d'un état particulier. Répétez cette opération pour tous les états. Si l'on fait la somme de toutes ces probabilités, on obtient 1. Dans ce cas, tout est fait correctement. De la même manière, nous pouvons classer les transactions en fonction de la durée de vie de l'ordre. En d'autres termes, un état peut être toute caractéristique unique d'un événement. Dans ce cas, une transaction est considérée comme un événement, et les paramètres de la transaction sont les caractéristiques d'un événement particulier. Dans notre cas, les exemples d'état peuvent être les suivants :

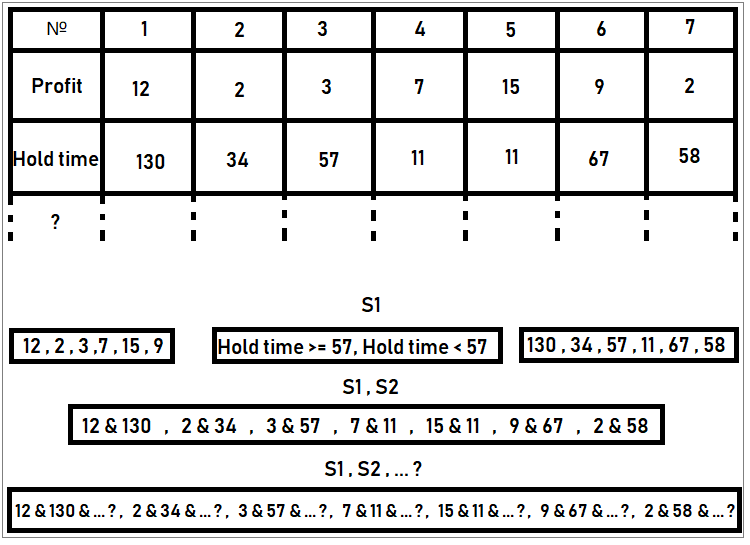
La figure montre un exemple de compilation d'ensembles d'états. Selon les règles, les états doivent former un groupe complet d'événements, c'est-à-dire qu'il ne doit pas y avoir d'états conjoints. La probabilité de ces événements peut être calculée en divisant le nombre d'ordres dans le tableau avec des états spécifiques par le nombre de tous les ordres (qui est de 7 dans notre cas). Il s'agit de l'exemple des ordres, mais nous pouvons travailler avec n'importe quel autre état.

Conclusion

Dans cet article, j'ai essayé de montrer comment évaluer des échantillons de données, comment en créer de nouveaux à partir de ces échantillons en classant les données et en les combinant en ensembles d'états dont les probabilités peuvent être calculées. C'est à vous de décider ce que vous voulez faire de ces données. Je pense que la meilleure façon de procéder consiste à créer plusieurs échantillons et à les évaluer - c'est ce qu'on appelle aussi le regroupement d'échantillons. Le regroupement d'échantillons peut servir de bon filtre pour améliorer les performances de trading des systèmes existants. Elle peut également être utilisée pour tirer profit d'une stratégie apparemment non rentable : il suffit de regrouper les données et de trouver les échantillons rentables souhaités. Et surtout, ces mécanismes peuvent être utilisés comme étapes de traitement des données dans des systèmes de trading évolutifs. Nous mettrons ces mécanismes en pratique plus tard, lorsque nous passerons à l'assemblage d'un système de trading auto-adaptatif. Pour l'instant, ce n'est qu'une brique de plus.

Références

• Combinatoire et théorie des probabilités pour le trading (Partie I) : L'essentiel
  
• Combinatoire et théorie des probabilités pour le trading (Partie II) : Fractale universelle
  
• Combinatoire et théorie des probabilités pour le trading (Partie III) : Le premier modèle mathématique