Yeniden alma algoritması: Çok dövizli alım-satım simülasyonu

İçindekiler

• Giriş
• Alım-satım simülasyonu ihtiyacının açıklanması
• Ayrıklaştırma mantığı kullanılarak fiyat simülasyonunun matematiksel modeli
• Model testi
• Uzman Danışman testi
• Sonuç

Giriş

Önceki makalede size muhtemelen bilmediğiniz birçok yararlı özellik gösterdim, ancak en ilginç şey burada - araştırma veya alım-satım simülasyonu. Bazen strateji sınayıcı yeterli değildir. Bu, piyasayı tanımak için çok uygun bir araç olsa da, sadece ilk adımdır. Bir önceki makaleyi dikkatlice okuduysanız, büyük olasılıkla nedenini zaten biliyorsunuzdur.

Alım-satım simülasyonu ihtiyacının açıklanması

Alım-satım simülasyonunun nedeni, doğrudan herhangi bir alım-satım enstrümanının geçmiş veri miktarının sınırlı olması gerçeğinde yatmaktadır. Bu konu ancak bir önceki makalede verdiğim materyali anladığınızda veya başka bir alternatif yolla görülebilir.  

Problemin özü, basit bir fiyat geçmişinin her zaman yeterli olmamasıdır, çünkü bu geçmiş rastgele ve rastgele olmayan birçok küresel olayın kesişiminde oluşur ve bir olayın ortaya çıkması için sayısız senaryo vardır. Şu anda her şeyi olabildiğince basit bir şekilde anlatmaya çalışıyorum, ancak olasılık teorisinin diline geçersek ve aynı zamanda bir önceki makalenin kazanımlarını kullanırsak, bildiğimiz tüm enstrümanların fiyatlarının geçmişinin farklı gelişebileceğini fark ederiz.

"Geleceğe Dönüş" filmini izlediyseniz bu gerçek çok açıktır. Bilimsel açıdan pek çok hata ve komik tutarsızlıklar içeriyor, ancak yine de bu film burada verilen mesajın ana fikrini aktarıyor. Mesajın özü, gelişen olayların tek bir versiyonunun bizim için yeterli olmadığı ve bunların maksimum sayısını dikkate almamız gerektiğidir. Geçmiş bize sadece bir versiyon sunar ve bu versiyonun büyüklüğü bazen objektif bir değerlendirme için yetersiz kalabilir. Örneğin, yakın zaman önce birçok aracı kurum en popüler kripto sembollerinden bazılarını listeledi. Bu, bu sembolleri test etme ve alım-satım yapma olasılığı açısından çok iyidir. Ancak dezavantajı, çubuklar üzerinde çalışan Uzman Danışmanlar için sürdürülebilir alım-satım sistemleri geliştirmek için yeterli geçmiş veri olmamasıdır.

Simülasyon, yapay enstrümanlar yaratmaya ve bunların fiyatlarını her seferinde tamamen farklı bir şekilde oluşturmaya izin verecektir. Bu bize matematiksel yeniden alma modelini ve bir önceki makalede bahsettiğim diğer önemli matematiksel ilkeleri incelemek için mümkün olan en geniş çerçeveyi sağlayacaktır. Bir diğer önemli avantaj ise paralel alım-satım için sınırsız sayıda bağımsız enstrümanı simüle edebilecek olmamızdır. Sonuç olarak, artık test süresi ve bağımsız olarak işlem gören enstrümanların sayısı konusunda bir sınırlamamız bulunmamaktadır. Elbette bunlar gerçek fiyatlar olmayacaktır, ancak fiyatlandırma yasaları açısından gerçek fiyatlardan hiçbir şekilde farklı olmayacaklardır.

Ayrıklaştırma mantığı kullanılarak fiyat simülasyonunun matematiksel modeli

Görevimiz bağlamında, "keyfi ayrıklaştırma" yaklaşımının kullanılması fazlasıyla yeterlidir, çünkü güçlü bir ayrıklaştırma, yalnızca bu tür sistemlerin makasa otomatik olarak daha etkili bir şekilde direnmesi nedeniyle algoritmamızın verimliliğini artıracaktır. Bununla birlikte, tiklerin simülasyonuna da izin veren bir algoritma oluşturdum. Bir tik pratikte en küçük zaman dilimidir. Tik gelişleri arasındaki süre çok farklıdır, ancak tikler arasındaki ortalama süreyi hesaplarsanız, ilk yaklaşım olarak tikleri taklit edebilirsiniz.

Burada bir çubuktan kastımız, görsel açıdan algılamamız için uygun olan sabit bir zaman aralığıdır. Ancak bu sadece size uygun olduğu söylendiği için uygundur ve bundan kaçamazsınız, çünkü tüm işlem terminalleri özellikle bu paradigma için uyarlanmıştır. Ancak bu, fiyatlandırmayı ayrıklaştırmanın en iyi yolu olmaktan uzaktır. Sanırım birçoğunuz "renko" kavramını biliyorsunuz. Fiyat ayrıklaştırmasına yönelik bu yaklaşımın tek bir amacı vardır - zamandan uzaklaşmak. Bu yaklaşımın değeri, farklı yaklaşımlar ve yatırımcılar için tamamen farklı olabilir. Ancak, bu örneği sadece fiyat serilerini ayrıklaştırmanın alternatif yollarından birini göstermek için kullanıyorum. Anladığım kadarıyla bu örnek, görevimiz bağlamında tamamen farklı ve alışılmadık bir ayrıklaştırma mantığı kullanacağımızı, ancak fiyatlandırmayı aşırı hesaplama maliyetleri olmadan çok basit ve verimli bir şekilde modellememize izin vereceğini söylemelidir.

Hesaplama gücü açısından verimli ve ekonomik bir paradigmanın doğru inşası için aşağıdaki şekle bir göz atın:

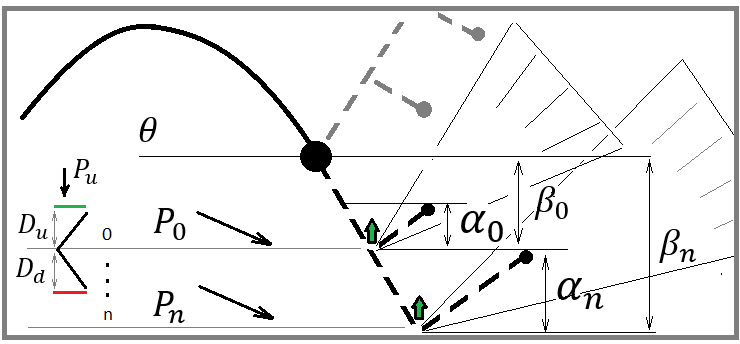
Görsel, fiyat geri dönüşleri için birkaç olası senaryoyu göstermektedir. Görseldeki iki geri dönüş benim için kesinlikle herhangi bir şekilde seçilebilecek keyfi iki noktayı ifade ediyor ve seçim yönteminin hiçbir önemi yok. Önemli olan, olası bir geri dönüş noktası olarak kabul edilebilecek herhangi bir noktayı keyfi olarak seçebilmemizdir.

"Olası" kelimesi her matematikçiye, belirli bir noktada istenen bir olayın gerçekleşme olasılığının bulunduğunu hemen söylemelidir. Bizim durumumuzda, belirli bir olayın keyfi olabileceğini söyleyebiliriz. Geri dönüş olayı, fiyat artışının üst ve alt sınırları ile karakterize edilir. Bu olayın olasılığı aşağıdaki şekilde hesaplanabilir:

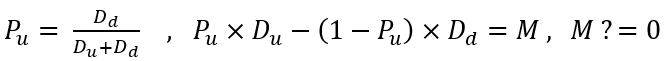
Burada üst sınıra ulaşma olasılığı ve bu formülün türetildiği denklem yer almaktadır. Denklem, öngörücü bir anın olmaması durumunda fiyat artışının matematiksel beklentisini karakterize eder. Öngörücü anın eksikliği sıfır beklentiye dönüşür, ancak simülasyonumuzda öngörücü an parametrelerini ayarlayabilmek istiyorum, böylece simüle edilmiş fiyatlandırmamızın yataylık özelliklerini uygun şekilde güçlendirebilir veya zayıflatabiliriz. Nihayetinde, bunun yeniden alma algoritmasını nasıl etkilediğini görecek ve yeniden alma algoritmasını kullanarak çeşitlendirilmiş alım-satım için çalışan bir matematiksel model elde edeceksiniz. Ama önce size tüm bunların arkasındaki matematiği sunmak istiyorum.

Şu anda, tüm bu denklemlerin güzel ve görünüşte yararlı olduğunu görebiliriz, ancak şu ana kadar enstrümanın yataylığını (geri dönüş) ayarlamak için uygun bir algoritma yoktur. Böyle bir algoritma geliştirmek için aşağıdaki değerleri girmemiz gerekir:

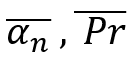
İlk değer aslında ortalama "alfa" değeridir. Buna, keyfi bir aşağı yönlü hareketten sonra fiyat geri dönüş değerinin matematiksel beklentisi de diyebiliriz. İkinci değer, önceki hareketine göre göreceli bir değer olarak ifade edilen geri dönüş yüzdesinin matematiksel beklentisidir. Bu miktarların temeli, tek istisna dışında aynıdır:

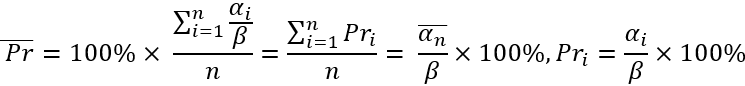
Burada size sadece bu büyüklüklerin nasıl ilişkili olduğunu ve nasıl hesaplandığını gösteriyorum. Modelimizde, ortalama geri dönüşü ortalama yüzdesini belirleyerek düzenleyeceğiz ve ortalama fiyat geri dönüşünü belirlemek için bunu kullanarak mantığı tersine çevireceğiz. Ortalama geri dönüş yüzdesinin piyasa yataylığı parametresi için düzenleyici bir değer olarak çok uygun olduğunu kabul etmelisiniz. Bu yüzde sıfır olarak ayarlanırsa, aslında rastgele fiyatlandırmaya ihtiyaç duyarız (bu sadece bir örnektir). Dikkat çekmek istediğim tek şey, tüm fiyat düşüşlerinin "teta" noktasına göre değerlendirildiğidir. Umarım tanımlamalarımdaki serbestliği bağışlarsınız, çünkü bu materyal tamamen bana aittir ve burada başka birinin çalışmasının bir damlası bile yoktur. Bu denklemler bir sonraki adımda ne yapacağımı anlamak için gereklidir.

Herhangi bir fiyatlandırmanın bir diğer önemli özelliği de volatilitedir (fiyat değişim hızı). Bu parametre zamanla ilişkilidir ve bu değeri ayarlamak için son derece uygun bir yol bulmalıyız. Bu, fiyatlandırma hızını kolay ve etkili bir şekilde kontrol etmemize ve alım-satım döngülerinin zamanlamasını doğru bir şekilde hesaplamamıza olanak sağlamalıdır. Şu anda tüm bunlar çok karmaşık görünebilir, ancak uygulamaya geçtiğimde ve size nasıl çalıştığını göstermeye başladığımda çok daha net olacaktır. Önce volatiliteyi ele alalım.

Klasik yorumda volatilite biraz daha farklıdır, daha ziyade minimumdan maksimuma ve tam tersi, maksimumdan minimuma olası göreceli fiyat hareketinin derecesidir. Bu, fiyat hareket hızını ayarlamak için çok uygunsuz bir yoldur. Sabit bir süre boyunca ortalama fiyat hareketini ölçmeyi içeren çok daha uygun bir yol vardır. Böyle segmentlere sahibiz. Bunlara çubuk denir. Aslında, çubuk başına fiyat değişimi değerinin rastgele bir değişkeninin dağılım yasasına sahibiz. Bu değer ne kadar büyük olursa, fiyat volatilitesi (değişim hızı) da o kadar büyük olur. Aşağıdaki ayarları giriyoruz:

"S" değerinin rastgele dağılımının simüle edilmesi gerekip gerekmediğine gelince, bunun gerekli olmadığını söyleyebilirim. Bilmeniz gereken tek şey, gerçek fiyatlandırmanın matematiksel modelde kullanacağımız yöntemden farklı olacağıdır. "S" değerini ortalama değerinde sabitlemeyi öneriyorum. Her adımın zamanı zaten sabit olduğundan, hem adımın büyüklüğünü hem de zaman içindeki süresini elde ederiz. Bu, daha sonra alım-satım sisteminin yıllık kârlılığını değerlendirmemize ve alım-satım döngüsünün ortalama süresini ölçmemize olanak tanıyacaktır. Şimdi ilerlemek için aşağıdaki resme bir göz atalım:

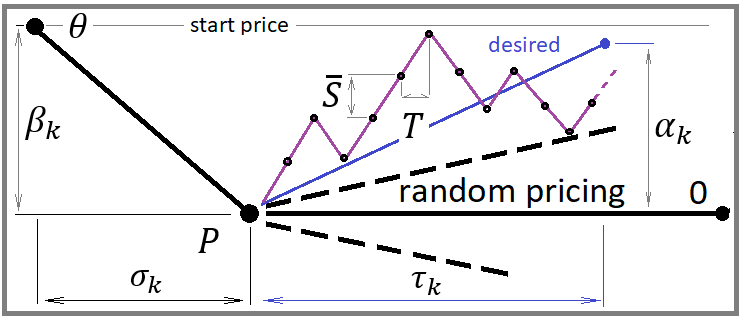
Her adım için fiyatlandırma simülasyonu yapmamız gerekeceğinden, adımın aşağı ya da yukarı olabileceği açıktır. Eğer her iki yönde de eşit olasılıklı bir adım belirlersek, o zaman rastgele fiyatlandırma elde ederiz. Bu, yataylığı düzenlemek için bu adım olasılıklarını değiştirmemiz gerektiği anlamına gelir. Bu, fiyatın yukarı veya aşağı hareket etmeye başladığı fiyatın başlangıç noktasına bir tür "yerçekimi" sağlanması olacaktır. Bizim durumumuzda, aşağıdakileri gerçekleştirmemiz gerekecektir:  

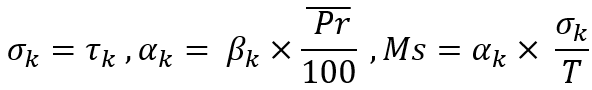
Bu durumda, modeli basitleştirmek için, seçilen ortalama fiyat geri dönüşünün, önceki fiyat artışı veya düşüşü için harcanan zamanın aynısını gerektirdiğini varsaydım. Bu hesaplamaların amacı, tek bir adım için anlık beklentiyi belirlemek ve böylece adımın yukarı doğru gerçekleşme olasılığını hesaplamaktır. Bu olasılıkla, yeni adımın simülasyonu ayarlanır. Bu değer, her bir alım-satım enstrümasyonu için her adımdan sonra yeniden hesaplanır.

Burada çok önemli bir nokta var: her bir enstrümanı ayrı ayrı tanımlarsak, her biri için ortalama fiyat değişikliği verilerini içeren bir dizi oluşturmamız gerekecektir. Ancak benim görevim çerçevesinde tüm enstrümanlar eşittir ve bu nedenle bir adımı ortalama fiyat değişim yüzdesi şeklinde tanımlamak için genel ve daha uygun bir özellik sunabiliriz:

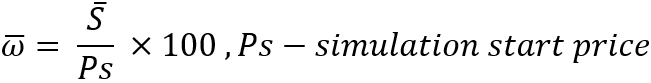
Bu özelliğin avantajı, herhangi bir mevcut fiyata göre değişmez olmasıdır. Dahası, ideal enstrümanları ele alırsak, simülasyonun hangi fiyattan başladığı önemli değildir, çünkü bu test sırasında kâr veya zararı etkilemeyecektir. Bunu anladıktan sonra, yeniden alma algoritmamız için paralel alım-satıma, örneğin 1'e eşit fiyattan güvenle başlayabiliriz. Bu değeri belirledikten sonra, adım değerinin kendisini hesaplamak zaten mümkündür:

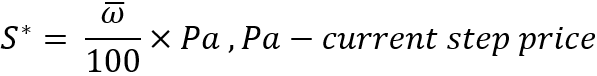
Artık adımı bildiğimize göre, yukarı doğru bir adım olma olasılığını hesaplamak için gerekli tüm verileri topladığımızı söyleyebiliriz. Bunu yapmak için, bazı değişikliklerle birlikte bir adımın matematiksel beklentisi için orijinal formülümüzü kullanıyoruz:

Bu yerine koyma işleminden sonra, yukarı doğru bir adım olasılığı için bu denklemi çözebilir ve son olarak kayıp olasılığı elde edebiliriz:

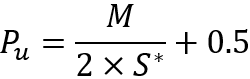
Dikkat edilmesi gereken tek husus, bu denklemlerin simülasyon fiyatının başlangıç noktasının altına düştüğü durumlar için geçerli olduğudur. Ama fiyat yükseldiğinde ne yapmalı? Her şey çok basit. Sadece grafiğin aynasını dikkate almamız gerekiyor. Bu yapılabilir çünkü mükemmel enstrümanlar düşünüyoruz. Fiyat grafiğinin belirli bir "P = P(t)" ifadesiyle tanımlanabileceğini hayal edersek, enstrümanın tersine çevrilmesi şöyle görünecektir:

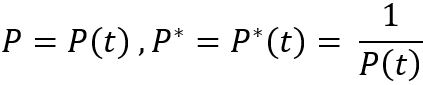
Bu ters çevirme, fiyatın başlangıç noktasının üzerine çıktığı durum için de denklemlerin çalışmasını sağlayacaktır. Anlamamız gereken tek şey, fiyatlar kullanılarak hesaplanan ifadelerimizdeki tüm miktarların (örneğin, deltalar) eksi birinci kuvvete yükseltilmiş halihazırda dönüştürülmüş fiyatı kullanması gerektiğidir.

Şimdi bir alım-satım modeli oluşturalım. Başlangıçta kripto para birimlerinin spot alım-satımı amacıyla tasarlandığı için tek yönlü yaptım. Bununla birlikte, bu alım-satım modeli forex döviz çiftleri için de uygundur. Mesele şu ki, model örneğin yalnızca yeniden alma durumunda çalışıyorsa, o zaman yeniden satma için de eşit derecede iyi çalışacaktır. Tek şey, test sırasında üst yarı dalgaları atlayacağız ve sadece alt dalgalar üzerinde çalışacağız. Alım-satım modelini yönetmek için aşağıdaki özellikleri girdim:

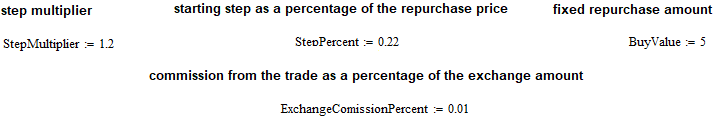
Başlangıç alışı "1-Step Percent/100" fiyatından başlar ve yeniden alma adımı "1-Step Percent/100"e eşit olacaktır. Aslında, başlangıç fiyatıyla hala bir çarpma işlemi yapılmalıdır, ancak bu fiyatı bire eşit aldığımız için, adımın hesaplanması büyük ölçüde basitleştirilmiştir. Buna ek olarak, tekrarlayan adım artışı imkanı getirilmiştir. Örneğin, her bir sonraki yeniden alma adımını bir öncekine göre N kat artırabilir veya aynı şekilde azaltabiliriz. Tüm bunlar ilgili katsayının değerine bağlıdır. Yeniden alma adımı, enstrümanın karşıt para biriminde ölçülür (baz para biriminde değil). Bu kural kripto para birimleri için de geçerlidir.

Modeli basitleştirmek için, bu durumda uygulanan alım-satım enstrümanlarının yaklaşık olarak şu şekilde olduğu varsayılmıştır: EURUSD, GBPUSD, NZDUSD ve benzeri, yani işlem gören tüm enstrümanlar için işlem gören enstrümanın karşıt para birimi aynı olmalıdır. Bu, zaten çok karmaşık olan bir modeli basitleştirir, ancak hem son makaledeki matematiksel ilkeleri test etmek hem de yeniden alma algoritmalarını optimize etmek için oldukça yeterlidir. Bizim durumumuzda makas, aynı şey olan bir komisyon şeklinde dikkate alınır. Genel olarak, parametreler matematiksel model prototipi için yeterlidir. Yeniden alma sürecine bir göz atalım:

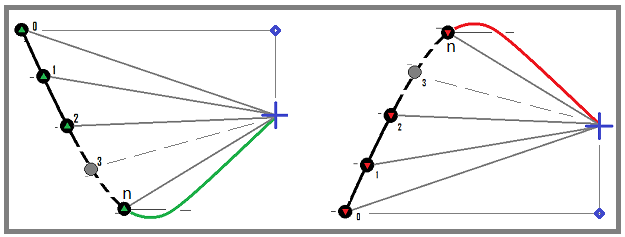
İlk seçeneği kullanacağız (yeşil dönüş hareketli). Bu aslında baz para birimini satın almak ve daha sonra mavi noktada satmaktır. Bu yaklaşımla, tamamlanan her alım-satım döngüsü kârlı olacaktır. Aynı şey kırmızı dönüş hareketi olan satış döngüsü için de geçerlidir, ancak dediğim gibi, modelin mümkün olduğunca çok işlevli olması ve hem forex piyasasında işlem yapmak hem de kripto para borsalarında spot işlem yapmak üzere uygun olması için bunları atlayacağız.

Model, işlem kaldıracının bir rol oynamayacağı şekilde yapılmıştır. Pratik kısmı daha iyi anlayabilmeniz için size yeterince teorik bilgi verdiğimi düşünüyorum ve bu, birisinin benim kazanımlarımı kullanarak kendi modelini oluşturmasına yardımcı olabilir.

Model testi

Testimize farklı fiyat oluşturma varyasyonlarıyla başlayalım. Fiyat oluşturmadaki farkı görsel olarak göstermek için önce modeli aşağıdaki konuma ayarlayalım:

Bu ayar ile rastgele fiyatlandırma elde edeceğiz. Bu bakış açısıyla üretilmiş birkaç fiyata bakalım:

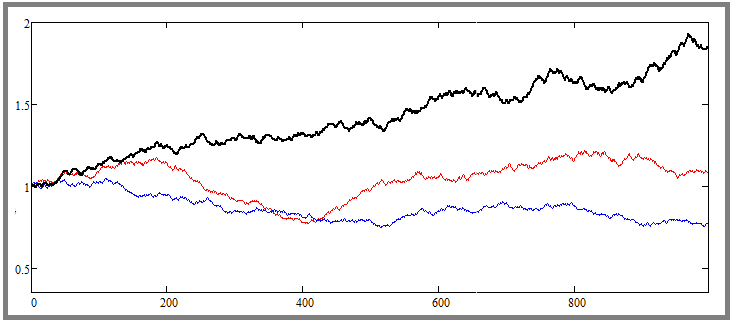
Bu, rastgele seçilen iki fiyatı ve başlangıç fiyatından en büyük sapmaya sahip olan başka bir ek eğriyi gösteren matematiksel modelden alınan bir grafiktir. Matematiksel modelde, paralel olarak simüle edilecek gerekli sayıda enstrüman ayarlamak mümkündür ve bunların çok sayıda olması doğaldır ve her zaman en az simetrik ve en volatil olan bir tane olacaktır. Ancak umarım bunun yalnızca olasılıksal süreçlerin bir sonucu olduğunu anlamışsınızdır. Şimdi parametreyi farklı bir konuma koyalım:

Daha önce anlamış olabileceğiniz gibi, bu adım fiyatın başlangıç noktasına geri dönüş ağırlığını oluşturur. Sonuç aşağıdaki gibidir:

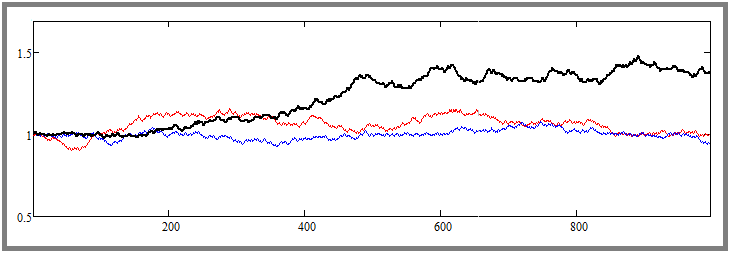
Önceki ve şimdiki görüntü arasındaki farka dikkat edin. Burada yataylık ayarını zaten istenen yöne doğru zorladık. Eğrilerin başlangıç fiyatına doğru güçlü bir şekilde bastırıldığını görebiliriz - aynı şey siyahla renklendirilmiş en volatil fiyatta da oldu. Her iki örnekte de her bir enstrüman için tam bin adım simüle edilmiştir. Daha sonra bu sayıları artıracağım ve her şeyin nasıl çalıştığını ve hangi parametrelerin tam olarak etkilendiğini anlamak için onlarla oynayacağım.

Şimdi yapay alım-satımı test etmek için hangi parametrelerin kullanılacağını ve nasıl test edilmesi gerektiğini belirlemek gerekiyor. Bir önceki makalede yanıtladığım soruları hızlıca hatırlayalım. Daha basit ve anlaşılır bir şekilde şunlardı:

1. Yeniden alma ile alım-satım sistemlerinin kârlılık durumu.
2. İdeal alım-satım enstrümanları için sonsuz alım-satımda kâr çizgisi mükemmel bir düz çizgiye eğilim gösterir mi?
3. Sabit bir alım-satım süresinde enstrüman sayısı sonsuza doğru arttıkça kâr çizgisi mükemmel bir düz çizgiye doğru eğilim gösterir mi?

Kârlılık durumunu öğrenelim. Bunu yapmak için, önce rastgele fiyatlandırma kullanarak paralel alım-satım yapalım ve sonuca bakalım. Yaklaşık olarak aşağıdaki gibi görünecektir:

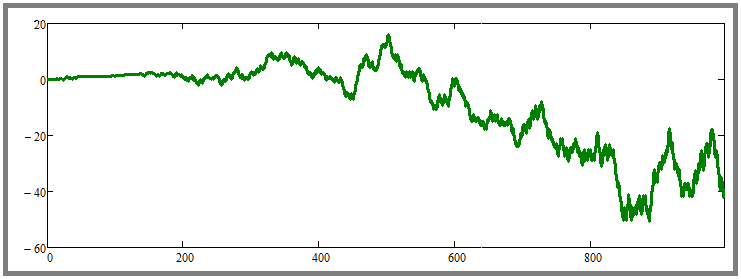
Farklı denemelerde ya kârlı ya da kârsız eğriler elde edilmiştir. Henüz net olmamakla birlikte, rastgele fiyatlama durumunda yeniden alımların yararsızlığının teyidi için paralel olarak işlem gören enstrüman sayısındaki aşırı bir artış kullanılabilir. Bunların sayısını örneğin yüze çıkarırsak ve aynı zamanda her bir enstrüman için simülasyon adımı sayısını 10,000'e çıkarırsak ne olacağını görelim:

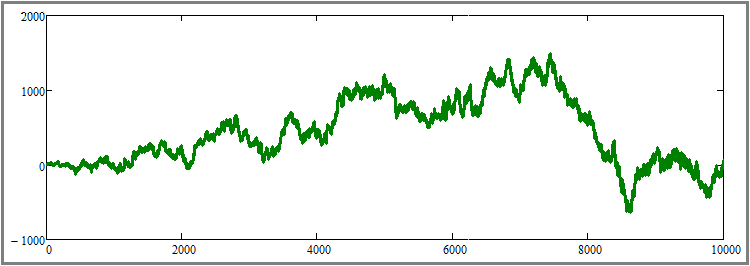
Gördüğünüz gibi, ne paralel olarak işlem gören enstrüman sayısındaki artışın ne de test süresindeki artışın gözle görülür bir etkisi olmuştur. Büyük olasılıkla bu, önceki makalede matematiksel olarak kanıtlanan, yeniden alma algoritması da dahil olmak üzere herhangi bir alım-satım sisteminin, tamamen rastgele fiyatlandırma durumunda ve öngörücü bir an olmadan hesabı boşalttığı gerçeğini doğrulamaktadır. Bu aşamada, 1. maddenin teorik ve pratik olarak kanıtlandığını düşünüyorum. Şimdi ikinci maddeye geçelim ve aşağıdaki ayarı yapalım:

Testlerime göre, bu geri dönüş ağırlığı herhangi bir okuyucunun etkiyi görsel olarak değerlendirmesi için oldukça yeterli oldu. Elbette daha düşük bir yüzde ayarlayabiliriz, ancak etki bu kadar belirgin olmayacaktır. Simülasyon adımı sayısını orijinal değer olan bin adıma sıfırladım. Şimdi sonuca bakalım:

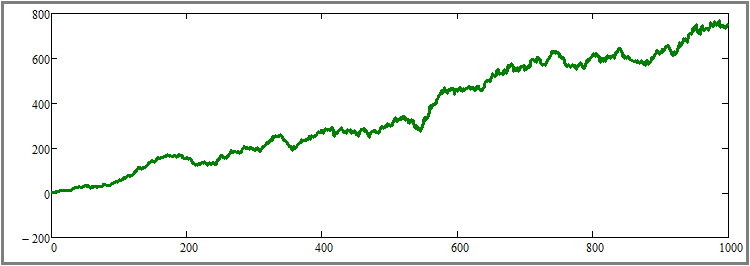
Bu grafiğin, diğer şeylerin yanı sıra, bir önceki maddenin ispatına bir ek olduğunu, ancak aynı zamanda bir sonraki maddenin ispatı için de bir başlangıç noktası olduğunu anlamak zor olmayacaktır. Planımdaki bir sonraki şey, başka hiçbir parametreyi değiştirmeden tüm test segmentlerinin süresini artırmaktır. Anlaşılır olması için, her bir enstrüman için simülasyon adımı sayısını elli kat artırdım - 1000'den 50,000'e. Bu oldukça büyük bir artış, ancak birden fazla test yapmadan ve sonuçların ortalamasını almadan bu etkiyi görsel olarak hissetmenin tek yolu bu. Sonuca bakalım:

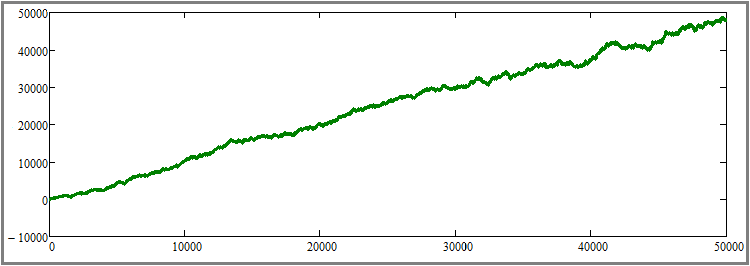
Gördüğümüz gibi, eğri çok daha yumuşak hale gelmiş ve düz bir çizgiye yaklaşmıştır; bu da test süresi arttıkça doğrusallık faktörünün (grafik güzelliği) artmasına ilişkin ikinci ilkenin tam olarak tahmin edildiği gibi çalıştığı anlamına gelmektedir. Elbette bu, yalnızca seçilen stratejinin kârlı olduğunun bilindiği varsayımıyla doğrudur. Bu aşamada, ikinci maddenin teorik ve pratik olarak kanıtlanmış olduğunu düşünüyorum.

Şimdi simülasyon adımı sayısını başlangıç seviyesi olan bin adıma geri döndürelim ve paralel olarak işlem gören enstrüman sayısını on kat artırarak 1000 değerine çıkaralım. Maddeye göre, grafik güzelliğinde gözle görülür bir artış elde etmeliyiz. Bakalım bu doğru mu?

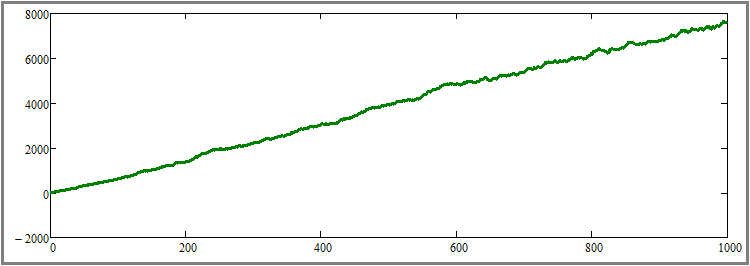
Gördüğümüz gibi, bu hipotez doğrulanmıştır ve etki son derece belirgindir. Bu aşamada, her üç hipotezin de teorik ve pratik olarak kanıtlandığına inanıyorum. Sonuçlar aşağıdaki gibidir:

1. Herhangi bir alım-satım sisteminin kârlılığının koşulu, öngörücü bir anın varlığıdır.
2. Alım-satım veya geriye dönük test süresinin artmasıyla, kârlı bir alım-satım sisteminin herhangi bir eğrisi daha güzel ve düz hale gelir (otomatik lot olmadan) + [1. maddenin yerine gelmesi şartıyla].
3. Bir çok dövizli alım-satım sistemi için işlem gören döviz çiftlerinin sayısındaki artışla veya aynı anda işlem gören sistemlerin sayısındaki artışla, alım-satım sisteminin kârlılık eğrisi daha güzel ve düz hale gelir + [bu sistemlerin her biri için 1. maddenin yerine gelmesi şartıyla].

Uzman Danışman testi

Hem otomatik hem de manuel alım-satımla mümkün olduğunca verimli ve güvenli bir şekilde para kazanmak için yeniden alma algoritması da dahil olmak üzere alım-satım sistemlerini nasıl doğru kullanacağımızı bulduk. Para yönetiminin hesaplanması ve alım-satım sistemlerinin doğru kombinasyonu için diğer çeşitli durumlar, daha sonra yazacağım ayrı bir makaleyi hak ediyor.

Bu bölümü, yeniden alma algoritmasının çalışan bir strateji olduğu gerçeğini açıkça görebilmeniz için ekledim. Bunu yapmak için, matematiksel modelimizi tekrarlayan bir test Uzman Danışmanı oluşturdum, tek fark üst yarım dalgaları da (satış alım-satım döngüleri) işlemesidir. MetaTrader 5 için benzer bir alım-satım sistemi oluşturma olasılığını kanıtlayan bazı ayarlar buldum. İşte onlardan biri:

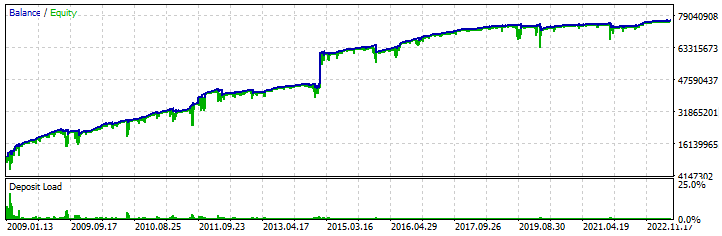
Test, matematiksel modelimize benzer şekilde tüm "28" döviz çiftinin paralel testi kullanılarak 2009'dan 2023'e kadar olan dönemde gerçekleştirilmiştir. Test algoritmasını oluşturmak için önceki makalelerimden birinde anlattığım çoklu robot şablonunu kullandım. Elbette, kâr eğrisi ideal olmaktan uzaktır ve bu tür bir alım-satım için başlangıç bakiyesi çok büyük olmalıdır, ancak yine de bu makaledeki görevim size hazır bir robot vermek değil, matematiksel modele yakınlığı göstermektir. Anlamanız gereken en önemli şey, belirli değişikliklerle bu algoritmanın çok daha güvenli, daha verimli ve daha uygulanabilir olacağıdır. İyileştirmelerin özünü kendiniz keşfetmenizi öneririm. Genellikle gizli olan şeyleri gösterdiğim için bunun adil olacağını düşünüyorum.

Uzman Danışman, ayar dosyasının yanı sıra matematiksel modelin kendisi ile birlikte makaleye bir dosya olarak eklenmiştir ve dilerseniz yapılarını daha ayrıntılı olarak inceleyebilir ve belki de fikri daha da geliştirebilirsiniz. Aslında matematiksel modelimde burada anlattığımdan çok daha fazla kullanım alanı var. Geriye dönük testten sonra kendi çıktı parametreleri seti sayesinde birçok önemli alım-satım özelliğini hesaplamaktadır. Elbette, işlevselliği çok sınırlıdır, ancak kanıt ve yaklaşık tahminler için yeterlidir.

Sonuç

Bu makalede, çeşitlendirme ilkesinin işe yaradığını ve kullanılması gerektiğini kanıtlamanın pratik kısmını tamamladım. En önemlisi, önceki makale ile birlikte, en azından alım-satımınızın verimliliğini artırmanıza olanak tanıyan birçok önemli şeyi hem teorik hem de pratik olarak kanıtladım. Buna ek olarak, yeniden alma algoritmasının on yıldan uzun bir süre boyunca hayatta kalması, oluşturulan Uzman Danışmanın yardımıyla kanıtlanmıştır.

Bunu göz önünde bulundurduğumuzda, fiyatlandırmanın dalga teorisini ya da piyasanın yataylığını teyit etmiş oluyoruz. Ek bir teyit olarak bu makaleye de göz atmanızı tavsiye ederim. Yazar, makalemde anlattığım algoritmanın tamamen aynısını önemli ölçüde kullanıyor. Buradan, test Uzman Danışmanımı geliştirmek veya kendi Uzman Danışmanınızı oluşturmak için bu etkileri nasıl kullanacağınıza dair ek bilgi edinebilirsiniz.