差分微積分とは?
そうなんです。
Δf(xk) = f (xk+1) - f (xk)
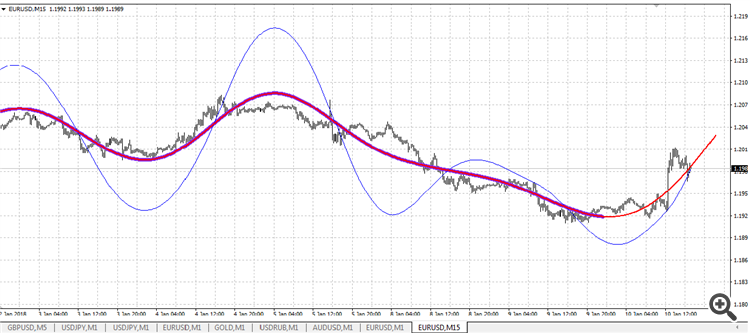
チャート上ではこのように表示されます。
青-赤の線は、てこ比72の4次多項式による補間(区間内の点を見つけること)です。
a1_Buffer[i]=((open[i] - Znach) +5061600*a1_Buffer[i+1 ]-7489800 *a1_Buffer[i+2 ]+4926624*a1_Buffer[i+3 ]-1215450*a1_Buffer[i+4 ])/1282975;
細い青線は、レバレッジ78の次数2の多項式による外挿(区間外の点を見つけること)である。
a2_Buffer[i]= 3160*a1_Buffer[i] -6240 *a1_Buffer[i+1 ] + 3081*a1_Buffer[i+2 ];
赤線は4乗の多項式を構成する線です。再描画され、最後のバーの始点が基準となります。
a4_Buffer[i+92]=a1_Buffer[i]; if(i<=10) { for(z=92-1;z>=0;z--){ a4_Buffer[i+0+z]= 5*a4_Buffer[i+1+z] - 10*a4_Buffer[i+2+z] + 10*a4_Buffer[i+3+z] - 5*a4_Buffer[i+4+z] + 1*a4_Buffer[i+5+z]; }}
差分微積分とは?
そうなんです。
Δf(xk) = f (xk+1) - f (xk)
はい。
ニュートンの二項式に直接関係するものである。
等距離の点については、その通りです。
1*Y1-2*Y2+1*Y3=0は 直線の差分方程式である。
1*Y1-3*Y2+3*Y3-1*Y4=0 - 2次放物線の差分方程式。
1*Y1-4*Y2+6*Y3-4*Y4+1*Y5=0 - 3次の放物線の差分方程式です。
トピックスとも重なります。
https://www.mql5.com/ru/forum/61389/page48#comment_5633264
https://www.mql5.com/ru/forum/211220/page2#comment_5632736 .

- 2017.07.20
- www.mql5.com
はい。
みんなそうしてきたのに...。執筆
未来は過去に依存するのか?
みんなそうしてきたのに...。執筆
未来は過去に依存するのか?
すべての行動には、現在の痕跡があり、それは当然ながら未来に影響します。:))))
このスレッドでは哲学は抜きにして、数学、プログラミング、テスト、最適化だけを議論することを提案します。
はい。
ニュートンの二項式に直接関係する。
等距離の点ではその通りです。
Y1-2*Y2+Y3=0 - 直線の差分方程式。
Y1-3*Y2+3*Y3-Y4 =0 - 2次放物線の差分方程式。
Y1-4*Y2+6*Y3-4*Y4 + Y5 =0 - は3次放物線の差分方程式である。
この処方を試されましたか?
Y = a0 + a1X + a2X^2 + a3X^3 + a4X^4
のところです。
Xは直前のバーの価格です。
Y - 現在のバーの価格です。
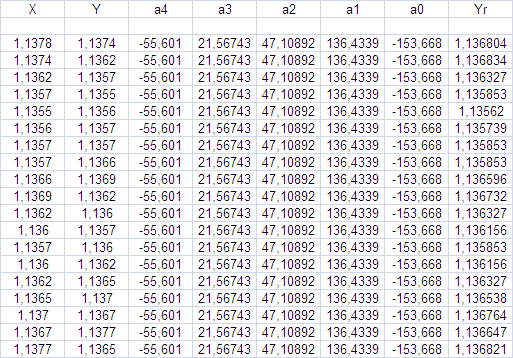
そうして、次のような絵が出来上がるのです。
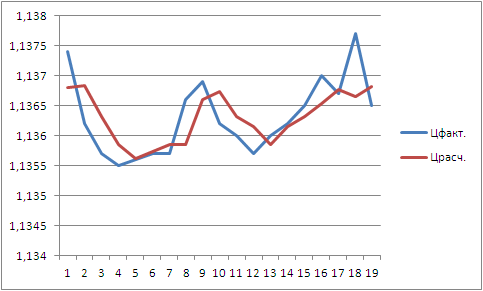
この処方を試されましたか?
Y = a + bX + cX^2 + dX^3 + eX^4
もちろんこの形式ではXとYがあるが、漸化式ではYとすべての係数(a+bX+cX^2+dX^3+ eX^4)のみを減らしてY自身の5つの値に置き換えている。
コードを見てみると、フィードバックフィルタの一種であることは間違いないでしょうか?5061600、4926624などの係数はどこから来ているのでしょうか?
実は、インディーはどこから来たかというと、インターネットです。))
1.コードを見てみると、これはフィードバック付きのフィルタの一種であることがわかりました。
2.また、5061600、4926624などの係数はどこから来たのでしょうか?
3.一般的に、インダクターはどこから来たのか、ネットから?))
1.デカルト、ニュートン、パスカル、テイラー、ラグランジュと、400年前に書かれた歴史しかないフィルターなんです。
2.係数が算出されます。2年目にはラグランジュやテイラーの手法を知ることができたようです。係数の計算には多くのバリエーションがあるようです。
3.特にこの作品は、今日描いたものです。:)))))
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
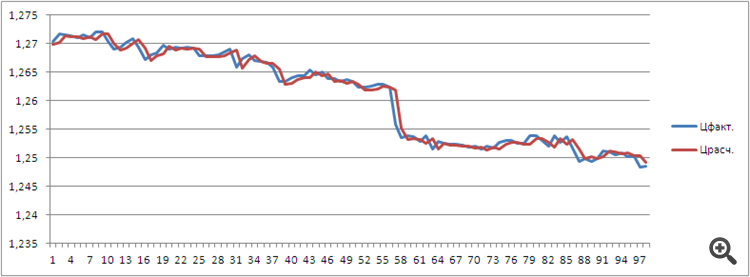
このスレッドで、差分計算に関する指標や専門家をオープンソースコードで集めることを提案します。
興味をもってもらえれば、いずれは役に立つものを作ったり、描いたりすることになるでしょう。:)
例としてインジケータを 分かりやすく書き直しました。