
모집단 최적화 알고리즘: 원숭이 알고리즘(MA)
콘텐츠:
1. 소개
원숭이 알고리즘(MA)은 메타 휴리스틱 검색 알고리즘입니다. 이 글에서는 알고리즘의 주요 구성 요소를 설명하고 상승(상향 이동), 로컬 점프 및 글로벌 점프와 관련한 솔루션을 제시합니다. 이 알고리즘은 2007년에 R. Zhao와 W. Tang이 제안했습니다. 이 알고리즘은 원숭이가 먹이를 찾아 산을 넘고 이동하는 원숭이의 행동을 시뮬레이션합니다. 원숭이는 산이 높을수록 정상에 더 많은 먹이가 있다고 생각한다는 사실을 가정합니다.
원숭이가 탐험하는 영역은 피트니스 함수 함수이므로 가장 높은 산이 문제의 해에 해당합니다(전역 최대화 문제를 고려합니다). 각 원숭이는 현재 위치에서 산의 정상에 도달할 때까지 위로 이동합니다. 정상에 가는 프로세스는 목표 함수의 값을 점진적으로 개선하도록 설계되었습니다. 그런 다음 원숭이는 더 높은 산을 찾기 위해 무작위의 방향으로 로컬에서 점프를 하고 위로 올라가는 동작을 반복합니다. 일정 횟수의 등반과 로컬 점프를 수행한 원숭이는 초기의 위치 근처의 주변을 충분히 탐험했다고 생각합니다.
검색 공간의 새로운 영역을 탐색하기 위해 원숭이는 긴 글로벌 점프를 수행합니다. 위의 단계는 알고리즘의 매개변수에서 지정된 횟수만큼 반복됩니다. 문제의 해는 주어진 원숭이 모집단에서 찾은 정점 중 가장 높은 정점으로 선언됩니다. 그러나 MA는 등반 과정에서 로컬 최적화 솔루션을 찾는 데 상당한 계산 시간을 소비합니다. 글로벌 점프 프로세스는 알고리즘의 수렴 속도를 높일 수 있습니다. 이 과정의 목적은 원숭이가 로컬 검색에 빠지지 않고 새로운 검색 기회를 찾게 하는 것입니다. 이 알고리즘은 간단한 구조, 상대적으로 높은 신뢰성, 로컬 최적 솔루션 검색 등의 장점이 있습니다.
MA는 비선형성, 비분산성, 고차원성을 특징으로 하는 여러 복잡한 최적화 문제를 해결할 수 있는 새로운 유형의 진화 알고리즘입니다. 다른 알고리즘과의 차이점은 MA가 로컬화 최적 솔루션을 찾기 위해 주로 등반 프로세스를 사용하기 때문에 소요되는 시간이 길다는 점입니다. 다음 섹션에서는 알고리즘의 주요 구성 요소, 제시된 솔루션, 초기화, 등반, 관찰 및 점프에 대해 설명합니다.
2. 알고리즘
원숭이 알고리즘을 쉽게 이해하려면 의사 코드로 시작하는 것이 좋습니다.
MA 알고리즘 의사 코드:
1. 검색 공간에 원숭이를 무작위로 배포합니다.
2. 원숭이 위치의 높이를 측정합니다.
3. 로컬 점프를 정해진 횟수만큼 수행합니다.
4. 3단계에서 얻은 새로운 정점이 더 높으면 이 위치에서 로컬 점프를 수행해야 합니다.
5. 로컬 점프 횟수 제한을 모두 소진하고 새로운 정점을 찾지 못하면 글로벌 점프를 수행합니다.
6. 5단계가 끝나면 3단계를 반복합니다.
7. 정지 기준이 충족될 때까지 2단계부터 반복합니다.
의사 코드의 각 지점을 더 자세히 분석해 보겠습니다.
1. 최적화를 시작할 때 원숭이에게 검색 공간은 알려지지 않습니다. 동물은 미지의 지형에 무작위로 배치됩니다. 먹이의 위치는 어느 곳에서나 같은 확률이기 때문입니다.
2. 원숭이 위치의 높이를 측정하는 과정은 피트니스 함수 작업을 수행하는 것입니다.
3. 로컬 점프를 만들 때는 알고리즘 매개변수에 지정된 개수에 제한이 있습니다. 이것은 원숭이는 먹이 영역에서 작은 로컬 점프를 통해 현재 위치를 개선하려고 한다는 것을 의미합니다. 새로 찾은 음식 소스가 더 좋으면 4단계로 이동합니다.
4. 새로운 식량 공급원이 발견되면 로컬 점프 횟수가 초기화됩니다. 그러면 이제 이곳에서 새로운 식량 공급원을 찾을 수 있습니다.
5. 로컬 점프가 더 나은 먹이를 발견하지 못하면 원숭이는 현재 지역을 충분히 탐험했고 더 멀리 떨어진 새로운 장소를 찾아야 할 때라고 결론을 내립니다. 이 시점에서 추가 상승의 방향에 대한 의문이 생깁니다. 알고리즘의 아이디어는 모든 원숭이의 좌표 중심을 사용하여 무리에 있는 원숭이 간의 의사소통을 하도록 하는 것입니다: 원숭이는 큰 소리를 지를 수 있고 공간 청각이 좋기 때문에 무리의 정확한 위치를 파악할 수 있습니다. 동시에 무리의 위치를 알면 (무리는 음식이 없는 곳에 있지 않을 것입니다) 음식의 최적의 새로운 위치를 대략적으로 계산할 수 있고 원숭이는 이 방향으로 점프를 해야 합니다.
원래 알고리즘에서는 원숭이는 모든 원숭이의 좌표 중심과 동물의 현재 위치를 통과하는 선을 따라 글로벌 점프를 합니다. 점프의 방향은 좌표의 중심을 향하거나 중심과 반대 방향으로 설정할 수 있습니다. 중심에서 반대 방향으로 점프하는 것은 원숭이들이 근사 좌표로 먹이를 찾는 논리와 모순됩니다. 실제로 알고리즘 실험을 통해 확인 된 바는 글로벌 최적값에서 거리가있을 확률이 50 %입니다.
연습에 따르면 좌표 중심을 넘어 점프하는 것이 점프하지 않거나 반대 방향으로 점프하는 것보다 더 유리한 것으로 나타났습니다. 언뜻 보기에는 모든 원숭이가 한 지점에 집중되는 일은 발생하지 않습니다. 비록 언뜻 보기에는 로직에 따라 그럴것 같지만 말입니다. 실제로 로컬 점프의 한계를 다 쓴 원숭이들은 중앙보다 더 멀리 점프하여 모집단의 모든 원숭이들의 위치를 회전시킵니다. 이 알고리즘을 따르는 고등 유인원 무리를 상상해 보면 동물 무리가 때때로 무리의 기하학적 중심을 뛰어넘어 더 풍부한 먹이를 향해 이동하는 모습을 볼 수 있습니다. 이러한 '팩 이동'의 효과는 알고리즘의 애니메이션에서 시각적으로 명확하게 확인할 수 있습니다(원래 알고리즘에는 이러한 효과가 없으며 결과가 더 나쁩니다).
6. 글로벌 점프를 한 원숭이는 새로운 장소에서 먹이의 위치를 지정하기 시작하고 이 프로세스는 중지 기준이 충족될 때까지 계속됩니다.
알고리즘의 전체 아이디어는 하나의 다이어그램에 쉽게 담을 수 있습니다. 원숭이의 움직임은 그림 1에서 숫자가 있는 원으로 표시되어 있습니다. 각 숫자는 원숭이의 새로운 위치입니다. 작은 노란색 원은 실패한 로컬 점프 시도를 나타냅니다. 숫자 6은 로컬 점프 한도가 모두 소진되어 새로운 최고의 위치를 찾지 못한 위치를 나타냅니다. 숫자가 없는 원은 나머지 팩의 위치를 나타냅니다. 팩의 기하학적 중심은 좌표(x,y)가 있는 작은 원으로 표시됩니다.
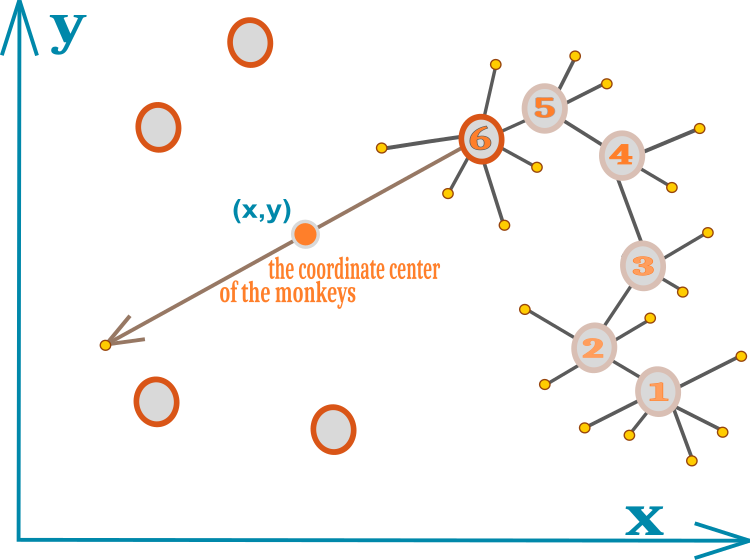
그림 1. 원숭이 무리의 움직임을 도식적으로 표현한 도표
MA 코드를 살펴보겠습니다.
팩에 있는 원숭이는 S_Monkey 구조로 설명하는 것이 편리합니다. 구조에는 현재 좌표가 있는 c [] 배열, 가장 좋은 음식 좌표가 있는 cB [] 배열(이 좌표가 있는 위치에서 로컬 점프가 발생함), 각각 현재 지점의 높이 값과 가장 높은 지점의 값인 h 및 hB가 포함됩니다. lCNT - 위치를 개선하려는 시도의 횟수를 제한하는 로컬 점프 카운터입니다.
//—————————————————————————————————————————————————————————————————————————————— struct S_Monkey { double c []; //coordinates double cB []; //best coordinates double h; //height of the mountain double hB; //best height of the mountain int lCNT; //local search counter }; //——————————————————————————————————————————————————————————————————————————————
C_AO_MA 원숭이 알고리즘 클래스는 앞서 설명한 알고리즘과 다르지 않습니다. 원숭이 무리는 클래스에서 m[] 구조체의 배열로 표현됩니다. 메서드 및 멤버 클래스의 선언은 코드 양이 많지 않습니다. 알고리즘이 간결하기 때문에 다른 많은 최적화 알고리즘과 달리 여기에는 정렬이 없습니다. 우리에게는 최적화된 매개변수의 최대, 최소, 단계를 설정하기 위한 배열과 알고리즘의 외부 매개변수를 전달하기 위한 상수 변수가 필요합니다. 이제 MA의 주요 로직이 포함된 메서드에 대한 설명으로 넘어가겠습니다.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_MA { //---------------------------------------------------------------------------- public: S_Monkey m []; //monkeys public: double rangeMax []; //maximum search range public: double rangeMin []; //minimum search range public: double rangeStep []; //step search public: double cB []; //best coordinates public: double hB; //best height of the mountain public: void Init (const int coordNumberP, //coordinates number const int monkeysNumberP, //monkeys number const double bCoefficientP, //local search coefficient const double vCoefficientP, //jump coefficient const int jumpsNumberP); //jumps number public: void Moving (); public: void Revision (); //---------------------------------------------------------------------------- private: int coordNumber; //coordinates number private: int monkeysNumber; //monkeys number private: double b []; //local search coefficient private: double v []; //jump coefficient private: double bCoefficient; //local search coefficient private: double vCoefficient; //jump coefficient private: double jumpsNumber; //jumps number private: double cc []; //coordinate center private: bool revision; private: double SeInDiSp (double In, double InMin, double InMax, double Step); private: double RNDfromCI (double min, double max); private: double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool revers); }; //——————————————————————————————————————————————————————————————————————————————
공용 Init() 메서드는 알고리즘을 초기화하는 데 사용됩니다. 여기서 우리는 배열의 크기를 설정합니다. 원숭이가 찾은 최적의 영역의 품질을 가능한 최소 '두 배' 값으로 초기화하고 MA 구조 배열의 해당 변수에 대해서도 동일한 작업을 수행합니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_MA::Init (const int coordNumberP, //coordinates number const int monkeysNumberP, //monkeys number const double bCoefficientP, //local search coefficient const double vCoefficientP, //jump coefficient const int jumpsNumberP) //jumps number { MathSrand ((int)GetMicrosecondCount ()); // reset of the generator hB = -DBL_MAX; revision = false; coordNumber = coordNumberP; monkeysNumber = monkeysNumberP; bCoefficient = bCoefficientP; vCoefficient = vCoefficientP; jumpsNumber = jumpsNumberP; ArrayResize (rangeMax, coordNumber); ArrayResize (rangeMin, coordNumber); ArrayResize (rangeStep, coordNumber); ArrayResize (b, coordNumber); ArrayResize (v, coordNumber); ArrayResize (cc, coordNumber); ArrayResize (m, monkeysNumber); for (int i = 0; i < monkeysNumber; i++) { ArrayResize (m [i].c, coordNumber); ArrayResize (m [i].cB, coordNumber); m [i].h = -DBL_MAX; m [i].hB = -DBL_MAX; m [i].lCNT = 0; } ArrayResize (cB, coordNumber); } //——————————————————————————————————————————————————————————————————————————————
각 반복마다 실행해야 하는 첫 번째 공용 메서드 Moving()은 원숭이 점프 로직을 구현합니다. 첫 번째 반복에서 '개정' 플래그가 '거짓'인 경우 연구 공간의 좌표 범위에서 무작위 값으로 에이전트를 초기화해야 하며 이는 무리 서식지 내 원숭이의 무작위적인 위치와 동일합니다. 글로벌 및 로컬 점프 계수 계산과 같이 반복되는 연산을 줄이기 위해 해당 좌표(각 좌표는 고유한 차원을 가질 수 있음)에 대한 값을 v [] 및 b [] 배열에 저장합니다. 각 원숭이의 로컬 점프 카운터를 0으로 초기화해 보겠습니다.
//---------------------------------------------------------------------------- if (!revision) { hB = -DBL_MAX; for (int monk = 0; monk < monkeysNumber; monk++) { for (int c = 0; c < coordNumber; c++) { m [monk].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]); m [monk].c [c] = SeInDiSp (m [monk].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); m [monk].h = -DBL_MAX; m [monk].hB = -DBL_MAX; m [monk].lCNT = 0; } } for (int c = 0; c < coordNumber; c++) { v [c] = (rangeMax [c] - rangeMin [c]) * vCoefficient; b [c] = (rangeMax [c] - rangeMin [c]) * bCoefficient; } revision = true; }
모든 원숭이의 좌표 중심을 계산하려면 좌표 수에 해당하는 차원을 가진 cc [] 배열을 사용합니다. 여기서 아이디어는 원숭이의 좌표를 더하고 결과 합계를 모집단의 크기로 나누는 것입니다. 따라서 좌표의 중심은 좌표의 산술 평균입니다.
//calculate the coordinate center of the monkeys---------------------------- for (int c = 0; c < coordNumber; c++) { cc [c] = 0.0; for (int monk = 0; monk < monkeysNumber; monk++) { cc [c] += m [monk].cB [c]; } cc [c] /= monkeysNumber; }
의사 코드에 따르면 로컬 점프의 한계에 도달하지 않으면 원숭이는 해당 위치에서 동일한 확률로 모든 방향으로 점프합니다. 로컬 점프 원의 반경은 b[] 배열의 좌표 치수에 따라 다시 계산되는 로컬 점프 계수에 의해 조절됩니다.
//local jump-------------------------------------------------------------- if (m [monk].lCNT < jumpsNumber) //local jump { for (int c = 0; c < coordNumber; c++) { m [monk].c [c] = RNDfromCI (m [monk].cB [c] - b [c], m [monk].cB [c] + b [c]); m [monk].c [c] = SeInDiSp (m [monk].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } }
이제 MA 로직의 매우 중요한 부분으로 넘어가 보겠습니다. 이 부분은 알고리즘의 성능은 글로벌 점프의 구현에 따라 크게 좌우된다는 점에서 매우 중요한 부분입니다. 여러 저자가 다양한 각도에서 이 문제에 접근하여 다양한 해결책을 제시합니다. 연구에 따르면 로컬 점프는 알고리즘의 수렴에 거의 영향을 미치지 않는 것으로 나타났습니다. 알고리즘이 로컬 극한에서 "점프"하는 것을 결정하는 것은 글로벌 점프입니다. 글로벌 점프를 실험한 결과 이 알고리즘의 결과를 개선하는 실행 가능한 접근 방식은 단 한 가지 뿐이었습니다.
위에서 좌표의 중심을 향해 점프하는 것이 좋으며 끝점이 중심과 현재 좌표 사이가 아닌 중심 뒤에 있는 것이 더 좋습니다. 이 접근 방식은 뻐꾸기 최적화 알고리즘(COA)에 대한 문서에서 자세히 설명한 레비 비행 방정식을 적용합니다.
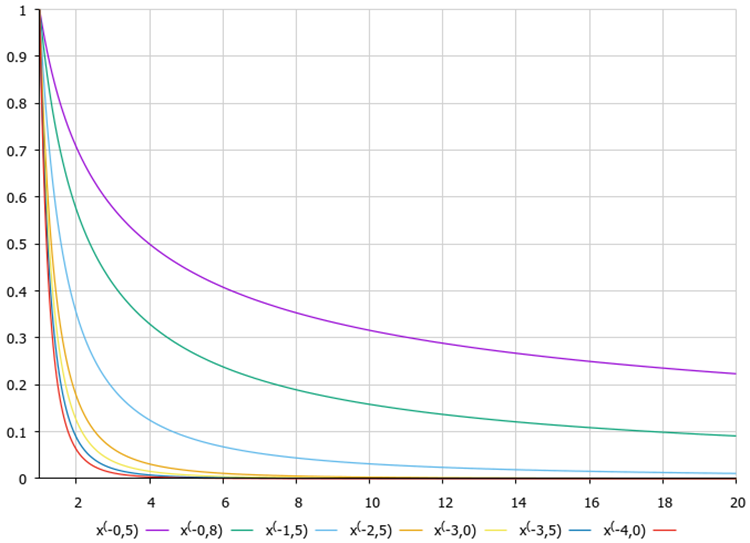
그림 2. 방정식 차수에 따른 레비 비행 함수 그래프
원숭이 좌표는 다음 공식을 사용하여 계산합니다:
m [monk].c [c] = cc [c] + v [c] * pow (r2, -2.0);
설명:
cc [c] - 좌표의 중심 좌표입니다,
v [c] - 검색 공간의 크기로 다시 계산된 점프 반경 계수입니다,
r2 - 1~20 범위의 숫자입니다.
이 연산에 레비 비행을 적용하면 원숭이가 좌표 중심 부근에 닿을 확률은 높아지고 중심을 벗어날 확률은 낮아집니다. 이를 통해 새로운 먹거리를 발굴하는 동시에 검색의 연구와 채집 사이의 균형을 유지하도록 합니다. 수신된 좌표가 허용 범위의 하한을 초과하는 경우 해당 좌표는 범위의 상한까지 해당 거리로 전송됩니다. 상한선을 초과하는 경우에도 마찬가지입니다. 좌표 계산이 끝나면 얻은 값이 경계와 연구 단계를 준수하는지 확인합니다.
//global jump------------------------------------------------------------- for (int c = 0; c < coordNumber; c++) { r1 = RNDfromCI (0.0, 1.0); r1 = r1 > 0.5 ? 1.0 : -1.0; r2 = RNDfromCI (1.0, 20.0); m [monk].c [c] = cc [c] + v [c] * pow (r2, -2.0); if (m [monk].c [c] < rangeMin [c]) m [monk].c [c] = rangeMax [c] - (rangeMin [c] - m [monk].c [c]); if (m [monk].c [c] > rangeMax [c]) m [monk].c [c] = rangeMin [c] + (m [monk].c [c] - rangeMax [c]); m [monk].c [c] = SeInDiSp (m [monk].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); }
로컬/글로벌 점프를 한 후 점프 카운터를 1씩 늘립니다.
m [monk].lCNT++;
Revision()은 적합도 함수가 계산된 후 각 반복마다 호출되는 두 번째 공용 메서드입니다. 이 방법은 더 나은 솔루션이 발견되면 글로벌 솔루션을 업데이트합니다. 로컬 및 전역 점프 후 결과를 처리하는 로직은 서로 다릅니다. 로컬 점프의 경우 현재 위치에 대해 개선되었는지 확인하고 업데이트해야 하지만(다음 반복에서는 이 새로운 위치에서 점프가 이루어짐) 글로벌 점프의 경우 개선 여부를 확인할 필요가 없으며 어떤 경우에도 이 위치에서 새로운 점프가 이루어집니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_MA::Revision () { for (int monk = 0; monk < monkeysNumber; monk++) { if (m [monk].h > hB) { hB = m [monk].h; ArrayCopy (cB, m [monk].c, 0, 0, WHOLE_ARRAY); } if (m [monk].lCNT <= jumpsNumber) //local jump { if (m [monk].h > m [monk].hB) { m [monk].hB = m [monk].h; ArrayCopy (m [monk].cB, m [monk].c, 0, 0, WHOLE_ARRAY); m [monk].lCNT = 0; } } else //global jump { m [monk].hB = m [monk].h; ArrayCopy (m [monk].cB, m [monk].c, 0, 0, WHOLE_ARRAY); m [monk].lCNT = 0; } } } //——————————————————————————————————————————————————————————————————————————————
이 알고리즘의 접근 방식이 파티클 군집(PSO)및 유사한 검색 전략 로직을 가진 다른 군집 지능 알고리즘 그룹과 유사하다는 것을 알 수 있습니다.
3. 테스트 결과
MA 테스트 스탠드 결과:
2023.02.22 19:36:21.841 Test_AO_MA (EURUSD,M1) C_AO_MA:50;0.01;0.9;50
2023.02.22 19:36:21.841 Test_AO_MA (EURUSD,M1) =============================
2023.02.22 19:36:26.877 Test_AO_MA (EURUSD,M1) 5 Rastrigin's; Func 10000 실행 결과: 64.89788419898215
2023.02.22 19:36:26.878 Test_AO_MA (EURUSD,M1) 점수: 0.80412
2023.02.22 19:36:36.734 Test_AO_MA (EURUSD,M1) 25 Rastrigin's; Func 10000 실행 결과: 55.57339368461394
2023.02.22 19:36:36.734 Test_AO_MA (EURUSD,M1) 점수: 0.68859
2023.02.22 19:37:34.865 Test_AO_MA (EURUSD,M1) 500 Rastrigin's; Func 10000 실행 결과: 41.41612351844293
2023.02.22 19:37:34.865 Test_AO_MA (EURUSD,M1) 점수: 0.51317
2023.02.22 19:37:34.865 Test_AO_MA (EURUSD,M1) =============================
2023.02.22 19:37:39.165 Test_AO_MA (EURUSD,M1) 5 Forest's; Func 10000 실행 결과: 0.4307085210424681
2023.02.22 19:37:39.165 Test_AO_MA (EURUSD,M1) 점수: 0.24363
2023.02.22 19:37:49.599 Test_AO_MA (EURUSD,M1) 25 Forest's; Func 10000 실행 결과: 0.19875891413613866
2023.02.22 19:37:49.599 Test_AO_MA (EURUSD,M1) 점수: 0.11243
2023.02.22 19:38:47.793 Test_AO_MA (EURUSD,M1) 500 Forest's; Func 10000 실행 결과: 0.06286212143582881
2023.02.22 19:38:47.793 Test_AO_MA (EURUSD,M1) 점수: 0.03556
2023.02.22 19:38:47.793 Test_AO_MA (EURUSD,M1) =============================
2023.02.22 19:38:53.947 Test_AO_MA (EURUSD,M1) 5 Megacity's; Func 10000 실행 결과: 2.8
2023.02.22 19:38:53.947 Test_AO_MA (EURUSD,M1) 점수: 0.23333
2023.02.22 19:39:03.336 Test_AO_MA (EURUSD,M1) 25 Megacity's; Func 10000 실행 결과: 0.96
2023.02.22 19:39:03.336 Test_AO_MA (EURUSD,M1) 점수: 0.08000
2023.02.22 19:40:02.068 Test_AO_MA (EURUSD,M1) 500 Megacity's; Func 10000 실행 결과: 0.34120000000000006
2023.02.22 19:40:02.068 Test_AO_MA (EURUSD,M1) 점수: 0.02843
테스트 함수에 대한 알고리즘의 시각화에 주의를 기울이면 동작에 패턴이 없습니다. 우리는 이점이 RND 알고리즘과 매우 유사하다는 점에 유의해야 합니다. 로컬 극단에 약간의 에이전트가 응집되어 있어 알고리즘에 의해 솔루션을 개선하려는 시도가 있다는 것을 나타내지만 명백한 잼은 없습니다.

Rastrigin 테스트 함수에서 MA
포레스트 테스트 함수 MA
메가시티 테스트 함수 MA.
테스트 결과 분석으로 넘어가겠습니다. 채점 결과에 따르면 MA 알고리즘은 GSA와 FSS 사이의 최하위 순위를 차지합니다. 알고리즘 테스트는 결과의 점수가 최고와 최악 사이의 상대적인 값인 비교 분석의 원칙에 기반하기 때문에 한 테스트에서 뛰어난 결과를 얻은 알고리즘이 등장하고 다른 테스트에서 결과가 좋지 않으면 다른 테스트 알고리즘의 매개 변수가 변경되는 경우가 있습니다.
그러나 MA의 결과로 인해 표에 있는 다른 테스트 알고리즘의 결과가 다시 계산되지는 않았습니다. 상대적 결과가 0이면서 등급이 더 높은 알고리즘(예: GSA)이 있지만 MA는 최악의 테스트 결과는 하나도 없습니다. 따라서 알고리즘이 다소 소극적으로 동작하고 검색 능력이 충분히 표현되지는 않지만 안정적인 결과를 보여주기 때문에 최적화 알고리즘으로서는 긍정적인 품질인 것입니다.
| AO | 설명 | Rastrigin | Rastrigin final | 숲 | 숲 최종 | 메가시티(이산) | 메가시티 최종 | 최종 결과 | ||||||
| 10 params (5 F) | 50 params (25 F) | 1000 params(500 F) | 10 params (5 F) | 50 params (25 F) | 1000 params(500 F) | 10 params (5 F) | 50 params (25 F) | 1000 params(500 F) | ||||||
| HS | 하모니 검색 | 1.00000 | 1.00000 | 0.57048 | 2.57048 | 1.00000 | 0.98931 | 0.57917 | 2.56848 | 1.00000 | 1.00000 | 1.00000 | 3.00000 | 100.000 |
| ACOm | 개미 식민지 최적화 M | 0.34724 | 0.18876 | 0.20182 | 0.73782 | 0.85966 | 1.00000 | 1.00000 | 2.85966 | 1.00000 | 0.88484 | 0.13497 | 2.01981 | 68.094 |
| IWO | 침입성 잡초 최적화 | 0.96140 | 0.70405 | 0.35295 | 2.01840 | 0.68718 | 0.46349 | 0.41071 | 1.56138 | 0.75912 | 0.39732 | 0.80145 | 1.95789 | 67.087 |
| COAm | 뻐꾸기 최적화 알고리즘 M | 0.92701 | 0.49111 | 0.30792 | 1.72604 | 0.55451 | 0.34034 | 0.21362 | 1.10847 | 0.67153 | 0.30326 | 0.41127 | 1.38606 | 50.422 |
| FAm | 반딧불이 알고리즘 M | 0.60020 | 0.35662 | 0.20290 | 1.15972 | 0.47632 | 0.42299 | 0.64360 | 1.54291 | 0.21167 | 0.25143 | 0.84884 | 1.31194 | 47.816 |
| BA | 박쥐 알고리즘 | 0.40658 | 0.66918 | 1.00000 | 2.07576 | 0.15275 | 0.17477 | 0.33595 | 0.66347 | 0.15329 | 0.06334 | 0.41821 | 0.63484 | 39.711 |
| ABC | 인공 꿀벌 군집 | 0.78424 | 0.34335 | 0.24656 | 1.37415 | 0.50591 | 0.21455 | 0.17249 | 0.89295 | 0.47444 | 0.23609 | 0.33526 | 1.04579 | 38.937 |
| BFO | 박테리아 먹이 채집 최적화 | 0.67422 | 0.32496 | 0.13988 | 1.13906 | 0.35462 | 0.26623 | 0.26695 | 0.88780 | 0.42336 | 0.30519 | 0.45578 | 1.18433 | 37.651 |
| GSA | 중력 검색 알고리즘 | 0.70396 | 0.47456 | 0.00000 | 1.17852 | 0.26854 | 0.36416 | 0.42921 | 1.06191 | 0.51095 | 0.32436 | 0.00000 | 0.83531 | 35.937 |
| MA | 원숭이 알고리즘 | 0.33300 | 0.35107 | 0.17340 | 0.85747 | 0.03684 | 0.07891 | 0.11546 | 0.23121 | 0.05838 | 0.00383 | 0.25809 | 0.32030 | 14.848 |
| FSS | 물고기 떼 검색 | 0.46965 | 0.26591 | 0.13383 | 0.86939 | 0.06711 | 0.05013 | 0.08423 | 0.20147 | 0.00000 | 0.00959 | 0.19942 | 0.20901 | 13.215 |
| PSO | 파티클 스웜 최적화 | 0.20515 | 0.08606 | 0.08448 | 0.37569 | 0.13192 | 0.10486 | 0.28099 | 0.51777 | 0.08028 | 0.21100 | 0.04711 | 0.33839 | 10.208 |
| RND | 랜덤 | 0.16881 | 0.10226 | 0.09495 | 0.36602 | 0.07413 | 0.04810 | 0.06094 | 0.18317 | 0.00000 | 0.00000 | 0.11850 | 0.11850 | 5.469 |
| GWO | 회색 늑대 최적화 | 0.00000 | 0.00000 | 0.02672 | 0.02672 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.18977 | 0.03645 | 0.06156 | 0.28778 | 1.000 |
요약
고전적인 MA 알고리즘은 기본적으로 등반 프로세스를 사용하여 로컬 최적 솔루션을 찾는 것으로 구성됩니다. 상승 단계는 로컬 솔루션의 근사치의 정확도에 결정적인 역할을 합니다. 로컬 점프의 상승 단계가 작을수록 솔루션의 정확도는 높아지지만, 글로벌 최적값을 찾는 데 더 많은 반복이 필요하게 됩니다. 반복 횟수를 줄여 계산 시간을 줄이기 위해 많은 연구자들은 최적화 초기 단계에서 ABC, COA, IWO와 같은 다른 최적화 방법을 사용하고 MA를 사용하여 글로벌 솔루션을 구체화할 것을 권장합니다. 저는 이 접근 방식에 동의하지 않습니다. 저는 MA 대신 설명한 알고리즘을 즉시 사용하는 것이 더 편리하다고 생각하지만 MA는 발전 가능성이 있어 추가 실험과 연구를 위한 좋은 대상입니다.
원숭이 알고리즘은 자연에 뿌리를 둔 모집단 기반의 알고리즘입니다. 다른 많은 메타 휴리스틱 알고리즘과 마찬가지로 이 알고리즘은 진화적이며 비선형성, 비차별성, 검색 공간의 고차원성 등 여러 최적화 문제를 높은 수렴률로 해결할 수 있습니다. 원숭이 알고리즘의 또 다른 장점은 이 알고리즘이 적은 수의 매개변수로 제어되므로 구현하기가 매우 쉽다는 것입니다. 결과의 안정성에도 불구하고 수렴률이 낮기 때문에 계산 복잡도가 높은 문제를 푸는 데 원숭이 알고리즘을 추천할 수 없는데 이는 상당한 수의 반복이 필요하기 때문입니다. 동일한 작업을 더 짧은 시간(반복 횟수)에 수행하는 다른 알고리즘도 많이 있습니다.
수많은 실험에도 불구하고 고전적인 버전의 알고리즘은 평가표의 하단에서 세 번째 라인보다 높아질 수 없었고 국부적인 극단에 갇혀 있었으며 이산 함수에서 극도로 열악하게 작동했습니다. 저는 이에 대한 기사를 쓰고 싶은 마음이 특별히 없었습니다. 저는 이를 개선하려는 시도를 해보았습니다. 이러한 시도 중 하나는 글로벌 점프에 확률 편향을 사용하고 글로벌 점프 자체의 원리를 수정하여 수렴 지표를 일부 개선하고 결과의 안정성을 높이는 것이었습니다. 많은 MA 연구자들은 알고리즘을 현대화 할 필요성이 있다고 생각합니다. 그래서 원숭이 알고리즘에 많은 수정이 이루어지고 있습니다. 저는 MA의 모든 종류의 수정을 고려할 의도는 아니었습니다. 알고리즘 자체가 뛰어난 것이 아니라 파티클 스웜(PSO)의 변형이기 때문이었습니다. 실험 결과는 이 글에 제시된 알고리즘의 최종 버전으로 추가 'm'(수정됨) 표시가 없는 상태입니다.
알고리즘 테스트 결과의 히스토그램은 아래에 나와 있습니다.
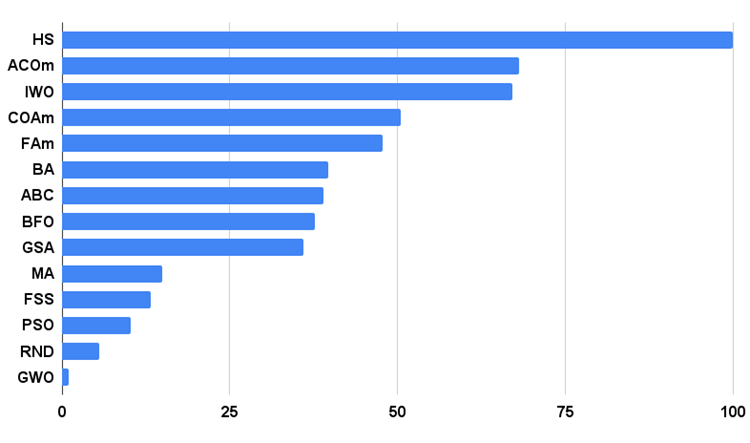
그림 3. 알고리즘 테스트 결과 히스토그램
MA 장단점:
1. 간편한 구현.
2. 낮은 수렴률에도 불구하고 확장성이 우수.
3. 개별 함수에서 우수한 성능.
4. 적은 수의 외부 매개변수.
단점:
1. 낮은 수렴률.
2. 검색에 많은 수의 반복이 필요.
3. 전반적인 효율성이 낮음.
각각의 기사에는 이전의 모든 기사에서 다룬 알고리즘 코드의 최신 버전이 업데이트된 아카이브가 포함되어 있습니다. 이 기사는 저자의 축적된 경험을 바탕으로 작성되었으며 개인적인 의견을 나타냅니다. 결론과 판단은 실험을 기반으로 합니다.
MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/12212
경고: 이 자료들에 대한 모든 권한은 MetaQuotes(MetaQuotes Ltd.)에 있습니다. 이 자료들의 전부 또는 일부에 대한 복제 및 재출력은 금지됩니다.
이 글은 사이트 사용자가 작성했으며 개인의 견해를 반영합니다. Metaquotes Ltd는 제시된 정보의 정확성 또는 설명 된 솔루션, 전략 또는 권장 사항의 사용으로 인한 결과에 대해 책임을 지지 않습니다.
 데이터 과학 및 머신 러닝 - 신경망(1부): 피드 포워드 신경망에 대한 이해
데이터 과학 및 머신 러닝 - 신경망(1부): 피드 포워드 신경망에 대한 이해