Algorithmes d'optimisation de la population : Monkey Algorithm, Algorithme du Singe (MA)

Sommaire :

1. Introduction
2. Algorithme
3. Résultats des tests

1. Introduction

L'Algorithme des Singes (MA) est un algorithme de recherche métaheuristique. Cet article décrit les principaux composants de l'algorithme et présente des solutions pour l'ascension (mouvement vers le haut), le saut local et le saut global. L'algorithme a été proposé par R. Zhao et W. Tang en 2007. L'algorithme simule le comportement des singes qui se déplacent et sautent par-dessus les montagnes à la recherche de nourriture. On suppose que les singes viennent du fait que plus la montagne est haute, plus il y a de nourriture à son sommet.

La zone explorée par les singes est un paysage de fonction d'aptitude, de sorte que la montagne la plus haute correspond à la solution du problème (nous considérons le problème de la maximisation globale). À partir de sa position actuelle, chaque singe monte jusqu'à ce qu'il atteigne le sommet de la montagne. Le processus de montée est conçu pour améliorer progressivement la valeur de la fonction cible. Ensuite, le singe effectue une série de sauts locaux dans une direction aléatoire dans l'espoir de trouver une montagne plus haute, et le mouvement ascendant est répété. Après avoir effectué un certain nombre de montées et de sauts locaux, le singe estime qu'il a suffisamment exploré le paysage à proximité de sa position initiale.

Pour explorer une nouvelle zone de l'espace de recherche, le singe effectue un long saut global. Les étapes ci-dessus sont répétées un nombre déterminé de fois dans les paramètres de l'algorithme. La solution du problème est déclarée être le plus grand des sommets trouvés par la population de singes donnée. Cependant, le MA consacre un temps de calcul important à la recherche de solutions optimales locales au cours du processus d'ascension. Le processus de saut global peut accélérer le taux de convergence de l'algorithme. L'objectif de ce processus est de forcer les singes à trouver de nouvelles opportunités de recherche afin de ne pas tomber dans la recherche locale. L'algorithme présente des avantages tels qu'une structure simple, une fiabilité relativement élevée et une bonne recherche de solutions optimales locales.

Le MA est un nouveau type d'algorithme évolutionnaire qui peut résoudre de nombreux problèmes d'optimisation complexes caractérisés par la non-linéarité, la non-différentiabilité et la haute dimensionnalité. La différence avec les autres algorithmes est que le temps passé par le MA est principalement dû à l'utilisation du processus de montée pour trouver des solutions optimales locales. Dans la section suivante, je décrirai les principaux composants de l'algorithme, les solutions présentées, l'initialisation, la montée, l'observation et le saut.

2. Algorithme

Pour faciliter la compréhension de l'algorithme du singe, il est raisonnable de commencer par un pseudo-code.

Pseudo-code de l'algorithme MA :

1. Répartir les singes de manière aléatoire dans l'espace de recherche.
2. Mesurer la hauteur de la position du singe.
3. Effectuer des sauts locaux un nombre fixe de fois.
4. Si le nouveau sommet obtenu à l'étape 3 est plus élevé, des sauts locaux doivent être effectués à partir de cet endroit.
5. Si la limite du nombre de sauts locaux est épuisée et qu'aucun nouveau sommet n'est trouvé, effectuer un saut global.
6. Après l'étape 5, répéter l'étape 3
7. Répéter l'opération à partir de l'étape 2 jusqu'à ce que le critère d'arrêt soit rempli.

Analysons plus en détail chaque point du pseudo-code.

1. Au tout début de l'optimisation, l'espace de recherche est inconnu des singes. Les animaux sont localisés de manière aléatoire sur des terrains non cartographiés, puisque la position de la nourriture est également probable à n'importe quel endroit.

2. Le processus de mesure de la hauteur de la position du singe est l'accomplissement de la tâche de la fonction d'aptitude.

3. Lors des sauts locaux, leur nombre est limité par les paramètres de l'algorithme. Cela signifie que le singe essaie d'améliorer sa position actuelle en faisant de petits sauts locaux dans le domaine alimentaire. Si la source de nourriture nouvellement trouvée est meilleure, passer à l'étape 4.

4. Une nouvelle source de nourriture a été trouvée, le nombre de sauts locaux est réinitialisé. La recherche d'une nouvelle source de nourriture se fera désormais à partir de cet endroit.

5. Si les sauts locaux ne conduisent pas à la découverte d'une meilleure source de nourriture, le singe en conclut que la zone actuelle est entièrement explorée et qu'il est temps de chercher un nouvel endroit plus éloigné. À ce stade, la question se pose de savoir dans quelle direction les sauts vont se poursuivre. L'idée de l'algorithme est d'utiliser le centre des coordonnées de tous les singes, ce qui permet une certaine communication - communication entre les singes d'un groupe : les singes peuvent crier fort et, ayant une bonne audition spatiale, ils sont capables de déterminer la position exacte de leurs proches. En même temps, connaissant la position de leurs proches (les proches ne seront pas dans les endroits où il n'y a pas de nourriture), il est possible de calculer approximativement la nouvelle position optimale de la nourriture, il est donc nécessaire de faire un saut dans cette direction.

Dans l'algorithme original, le singe effectue un saut global le long d'une ligne passant par le centre de coordonnées de tous les singes et la position actuelle de l'animal. La direction du saut peut être soit vers le centre des coordonnées, soit dans la direction opposée au centre. Un saut dans la direction opposée au centre contredit la logique même de la recherche de nourriture avec des coordonnées approximatives pour tous les singes, ce qui a été confirmé par mes expériences avec l'algorithme - en fait, il s'agit d'une probabilité de 50% qu'il y ait une distance par rapport à l'optimum global.

La pratique a montré qu'il est plus rentable de sauter au-delà du centre de coordonnées que de ne pas sauter ou de sauter dans la direction opposée. La concentration de tous les singes en un seul point ne se produit pas, bien qu'à première vue une telle logique la rende inévitable. En effet, les singes, ayant épuisé la limite des sauts locaux, sautent plus loin que le centre, faisant ainsi pivoter la position de tous les singes de la population. Si nous imaginons mentalement les grands singes obéissant à cet algorithme, nous verrons une meute d'animaux sautant de temps en temps par-dessus le centre géométrique du groupe, alors que la meute elle-même se déplace vers une source de nourriture plus riche. Cet effet de "déplacement du paquet" est clairement visible sur l'animation de l'algorithme (l'algorithme original n'a pas cet effet et les résultats sont moins bons).

6. Après avoir effectué un saut global, le singe commence à spécifier la position de la source de nourriture dans le nouvel endroit. Le processus se poursuit jusqu'à ce que le critère d'arrêt soit rempli.

L'ensemble de l'algorithme peut facilement tenir sur un seul diagramme. Le mouvement du singe est indiqué par des cercles numérotés dans la figure 1. Chaque numéro est une nouvelle position pour le singe. Les petits cercles jaunes représentent les tentatives de saut local qui ont échoué. Le chiffre 6 indique la position dans laquelle la limite des sauts locaux a été épuisée et où aucune nouvelle meilleure position n'a été trouvée. Les cercles sans numéro représentent les emplacements du reste du groupe. Le centre géométrique du paquet est indiqué par un petit cercle de coordonnées (x, y).

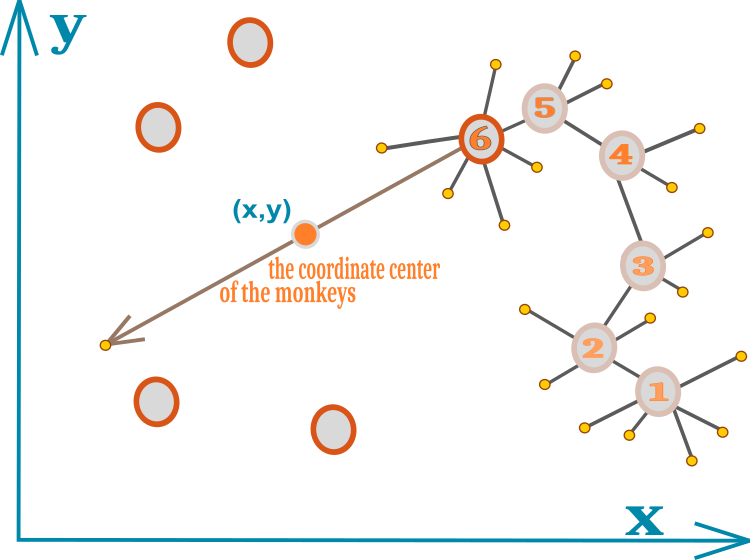
Figure 1. Représentation schématique du mouvement d'un singe dans un groupe

Jetons un coup d'œil au code du MA.

Il est pratique de décrire un singe dans le groupe avec la structure S_Monkey. La structure contient le tableau c[] avec les coordonnées actuelles, le tableau cB[] avec les meilleures coordonnées alimentaires (c'est à partir de la position avec ces coordonnées que les sauts locaux se produisent), h et hB - la valeur de la hauteur du point actuel et la valeur du point le plus élevé, respectivement et lCNT - le compteur de sauts locaux qui limite le nombre de tentatives d'amélioration d'une position.

//——————————————————————————————————————————————————————————————————————————————
struct S_Monkey
{
  double c  []; //coordinates
  double cB []; //best coordinates
  double h;     //height of the mountain
  double hB;    //best height of the mountain
  int    lCNT;  //local search counter
};
//——————————————————————————————————————————————————————————————————————————————

La classe d'algorithmes du singe C_AO_MA n'est pas différente des algorithmes examinés précédemment. Une meute de singes est représentée dans la classe par un tableau de structures m[]. Les déclarations de méthodes et de membres dans la classe sont faibles en termes de volume de code. L'algorithme étant concis, il n'y a pas de tri, contrairement à de nombreux autres algorithmes d'optimisation. Nous aurons besoin de tableaux pour définir le maximum, le minimum et le pas des paramètres optimisés, ainsi que de variables constantes pour leur transmettre les paramètres externes de l'algorithme. Passons maintenant à la description des méthodes qui contiennent la logique principale de MA.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_MA
{
  //----------------------------------------------------------------------------
  public: S_Monkey m       []; //monkeys
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //minimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double hB;           //best height of the mountain

  public: void Init (const int    coordNumberP,     //coordinates number
                     const int    monkeysNumberP,   //monkeys number
                     const double bCoefficientP,    //local search coefficient
                     const double vCoefficientP,    //jump coefficient
                     const int    jumpsNumberP);    //jumps number

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordNumber;       //coordinates number
  private: int    monkeysNumber;     //monkeys number

  private: double b [];              //local search coefficient
  private: double v [];              //jump coefficient
  private: double bCoefficient;      //local search coefficient
  private: double vCoefficient;      //jump coefficient
  private: double jumpsNumber;       //jumps number
  private: double cc [];             //coordinate center

  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

La méthode publique Init() sert à initialiser l'algorithme. Nous définissons ici la taille des tableaux. Nous initialisons la qualité du meilleur territoire trouvé par le singe avec la valeur de type double minimale possible, et nous ferons de même avec les variables correspondantes des tableaux de la structure MA.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_MA::Init (const int    coordNumberP,    //coordinates number
                    const int    monkeysNumberP,  //monkeys number
                    const double bCoefficientP,   //local search coefficient
                    const double vCoefficientP,   //jump coefficient
                    const int    jumpsNumberP)    //jumps number
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  hB       = -DBL_MAX;
  revision = false;

  coordNumber   = coordNumberP;
  monkeysNumber = monkeysNumberP;
  bCoefficient  = bCoefficientP;
  vCoefficient  = vCoefficientP;
  jumpsNumber   = jumpsNumberP;

  ArrayResize (rangeMax,  coordNumber);
  ArrayResize (rangeMin,  coordNumber);
  ArrayResize (rangeStep, coordNumber);
  ArrayResize (b,         coordNumber);
  ArrayResize (v,         coordNumber);
  ArrayResize (cc,        coordNumber);

  ArrayResize (m, monkeysNumber);

  for (int i = 0; i < monkeysNumber; i++)
  {
    ArrayResize (m [i].c,  coordNumber);
    ArrayResize (m [i].cB, coordNumber);
    m [i].h    = -DBL_MAX;
    m [i].hB   = -DBL_MAX;
    m [i].lCNT = 0;
  }

  ArrayResize (cB, coordNumber);
}
//——————————————————————————————————————————————————————————————————————————————

La première méthode publique Moving(), qui doit être exécutée à chaque itération, met en œuvre la logique du saut du singe. À la première itération, lorsque l'indicateur "revision" est "faux", il est nécessaire d'initialiser les agents avec des valeurs aléatoires dans la gamme de coordonnées de l'espace étudié, ce qui équivaut à la localisation aléatoire des singes dans l'habitat de la meute. Afin de réduire le nombre d'opérations répétées, telles que le calcul des coefficients des sauts globaux et locaux, nous stockons les valeurs des coordonnées correspondantes (chacune des coordonnées peut avoir sa propre dimension) dans les tableaux v[] et b[]. Remettons à zéro le compteur des sauts locaux de chaque singe. 

//----------------------------------------------------------------------------
if (!revision)
{
  hB = -DBL_MAX;

  for (int monk = 0; monk < monkeysNumber; monk++)
  {
    for (int c = 0; c < coordNumber; c++)
    {
      m [monk].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      m [monk].c [c] = SeInDiSp  (m [monk].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      m [monk].h     = -DBL_MAX;
      m [monk].hB    = -DBL_MAX;
      m [monk].lCNT  = 0;
    }
  }

  for (int c = 0; c < coordNumber; c++)
  {
    v [c] = (rangeMax [c] - rangeMin [c]) * vCoefficient;
    b [c] = (rangeMax [c] - rangeMin [c]) * bCoefficient;
  }

  revision = true;
}

Pour calculer le centre de coordonnées de tous les singes, utilisez le tableau cc[] dont la dimension correspond au nombre de coordonnées. Il s'agit ici d'additionner les coordonnées des singes et de diviser la somme obtenue par la taille de la population. Ainsi, le centre de coordonnées est la moyenne arithmétique des coordonnées.

//calculate the coordinate center of the monkeys----------------------------
for (int c = 0; c < coordNumber; c++)
{
  cc [c] = 0.0;

  for (int monk = 0; monk < monkeysNumber; monk++)
  {
    cc [c] += m [monk].cB [c];
  }

  cc [c] /= monkeysNumber;
}

Selon le pseudo-code, si la limite des sauts locaux n'est pas atteinte, le singe sautera de son emplacement dans toutes les directions avec la même probabilité. Le rayon du cercle de sauts locaux est régulé par le coefficient de sauts locaux, qui est recalculé en fonction de la dimension des coordonnées du tableau b[].

//local jump--------------------------------------------------------------
if (m [monk].lCNT < jumpsNumber) //local jump
{
  for (int c = 0; c < coordNumber; c++)
  {
    m [monk].c [c] = RNDfromCI (m [monk].cB [c] - b [c], m [monk].cB [c] + b [c]);      
    m [monk].c [c] = SeInDiSp (m [monk].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

Passons maintenant à une partie très importante de la logique du MA : les performances de l'algorithme dépendent largement de la mise en œuvre des sauts globaux. Différents auteurs abordent cette question sous différents angles et proposent toutes sortes de solutions. Selon la recherche, les sauts locaux ont peu d'effet sur la convergence de l'algorithme. Ce sont les sauts globaux qui déterminent la capacité de l'algorithme à "sauter" des extrema locaux. Mes expériences avec les sauts globaux n'ont révélé qu'une seule approche viable pour cet algorithme particulier qui améliore les résultats.

Plus haut, nous avons discuté de l'opportunité de sauter vers le centre des coordonnées. Il est préférable que le point d'arrivée soit derrière le centre, et non entre le centre et les coordonnées actuelles. Cette approche applique les équations de vol de Levy que nous avons décrites en détail dans l'article sur l'algorithme d'optimisation du coucou(COA).

Figure 2. Graphiques de la fonction de vol de Lévy en fonction du degré de l'équation

Les coordonnées du singe sont calculées à l'aide de l'équation suivante :

m[monk].c[c] = cc[c] + v[c] * pow(r2, -2.0);

avec :

cc[c] - les coordonnées du centre des coordonnées,

v[c] - le coefficient du rayon de saut recalculé à la dimension de l'espace de recherche,

r2 - un nombre compris entre 1 et 20.

En appliquant le vol de Levy à cette opération, nous obtenons une probabilité plus élevée que le singe frappe à proximité du centre des coordonnées et une probabilité plus faible qu'il se trouve loin du centre. Nous assurons ainsi un équilibre entre la recherche et l'exploitation de la recherche, tout en découvrant de nouvelles sources de nourriture. Si la coordonnée reçue dépasse la limite inférieure de la plage autorisée, elle est transférée à la distance correspondante à la limite supérieure de la plage. Il en va de même pour le dépassement de la limite supérieure. À la fin du calcul de coordonnées, vérifiez que la valeur obtenue est conforme aux limites et à l'étape de recherche :

//global jump-------------------------------------------------------------
for (int c = 0; c < coordNumber; c++)
{
  r1 = RNDfromCI (0.0, 1.0);
  r1 = r1 > 0.5 ? 1.0 : -1.0;
  r2 = RNDfromCI (1.0, 20.0);

  m [monk].c [c] = cc [c] + v [c] * pow (r2, -2.0);
          
  if (m [monk].c [c] < rangeMin [c]) m [monk].c [c] = rangeMax [c] - (rangeMin [c] - m [monk].c [c]);
  if (m [monk].c [c] > rangeMax [c]) m [monk].c [c] = rangeMin [c] + (m [monk].c [c] - rangeMax [c]);
          
  m [monk].c [c] = SeInDiSp (m [monk].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
}

Après avoir effectué des sauts locaux/globaux, augmentez le compteur de sauts d'une unité :

m [monk].lCNT++;

Revision() est la deuxième méthode publique appelée à chaque itération après le calcul de la fonction d'aptitude. Cette méthode met à jour la solution globale si une meilleure solution est trouvée. Les logiques de traitement des résultats après les sauts locaux et globaux diffèrent l'une de l'autre. Dans le cas d'un saut local, il est nécessaire de vérifier si la position actuelle s'est améliorée et de la mettre à jour (dans les itérations suivantes, des sauts sont effectués à partir de cette nouvelle position). Alors que dans le cas des sauts globaux, il n'y a pas de vérification des améliorations - de nouveaux sauts seront effectués à partir de cette position dans tous les cas.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_MA::Revision ()
{
  for (int monk = 0; monk < monkeysNumber; monk++)
  {
    if (m [monk].h > hB)
    {
      hB = m [monk].h;
      ArrayCopy (cB, m [monk].c, 0, 0, WHOLE_ARRAY);
    }

    if (m [monk].lCNT <= jumpsNumber) //local jump
    {
      if (m [monk].h > m [monk].hB)
      {
        m [monk].hB = m [monk].h;
        ArrayCopy (m [monk].cB, m [monk].c, 0, 0, WHOLE_ARRAY);
        m [monk].lCNT = 0;
      }
    }
    else //global jump
    {
      m [monk].hB = m [monk].h;
      ArrayCopy (m [monk].cB, m [monk].c, 0, 0, WHOLE_ARRAY);
      m [monk].lCNT = 0;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Nous pouvons remarquer la similitude des approches de cet algorithme avec un groupe d'algorithmes d'intelligence en essaim, tels que l'essaim de particules (PSO) et d'autres avec une logique de stratégie de recherche similaire.

3. Résultats des tests

Résultats du banc d'essai MA :

2023.02.22 19:36:21.841    Test_AO_MA (EURUSD,M1)    C_AO_MA:50;0.01;0.9;50
2023.02.22 19:36:21.841    Test_AO_MA (EURUSD,M1) =============================
2023.02.22 19:36:26.877    Test_AO_MA (EURUSD,M1)    5 Rastrigin's ; Func runs 10000 result : 64,89788419898215
2023.02.22 19:36:26.878    Test_AO_MA (EURUSD,M1)    Score : 0,80412
2023.02.22 19:36:36.734    Test_AO_MA (EURUSD,M1)    25 Rastrigin's ; Func runs 10000 result : 55,57339368461394
2023.02.22 19:36:36.734    Test_AO_MA (EURUSD,M1)    Score : 0,68859
2023.02.22 19:37:34.865    Test_AO_MA (EURUSD,M1)    500 Rastrigin's ; Func runs 10000 result : 41,41612351844293
2023.02.22 19:37:34.865    Test_AO_MA (EURUSD,M1)    Score : 0,51317
2023.02.22 19:37:34.865    Test_AO_MA (EURUSD,M1) =============================
2023.02.22 19:37:39.165    Test_AO_MA (EURUSD,M1)    5 Forest's ; Func runs 10000 result : 0,4307085210424681
2023.02.22 19:37:39.165    Test_AO_MA (EURUSD,M1)    Score : 0,24363
2023.02.22 19:37:49.599    Test_AO_MA (EURUSD,M1)    25 Forest's ; Func runs 10000 result : 0,19875891413613866
2023.02.22 19:37:49.599    Test_AO_MA (EURUSD,M1)    Score : 0,11243
2023.02.22 19:38:47.793    Test_AO_MA (EURUSD,M1)    500 Forest's ; Func runs 10000 result : 0,06286212143582881
2023.02.22 19:38:47.793    Test_AO_MA (EURUSD,M1)    Score : 0,03556
2023.02.22 19:38:47.793    Test_AO_MA (EURUSD,M1) =============================
2023.02.22 19:38:53.947    Test_AO_MA (EURUSD,M1)    5 Megacity's ; Func runs 10000 result : 2,8
2023.02.22 19:38:53.947    Test_AO_MA (EURUSD,M1)    Score : 0,23333
2023.02.22 19:39:03.336 Test_AO_MA (EURUSD,M1)    25 Megacity's ; Func runs 10000 result : 0,96
2023.02.22 19:39:03.336    Test_AO_MA (EURUSD,M1)    Score : 0,08000
2023.02.22 19:40:02.068    Test_AO_MA (EURUSD,M1)    500 Megacity's ; Func runs 10000 result : 0,34120000000000006
2023.02.22 19:40:02.068    Test_AO_MA (EURUSD,M1)    Score : 0,02843

En prêtant attention à la visualisation de l'algorithme sur les fonctions de test, il convient de noter qu'il n'y a pas de modèle dans le comportement, qui est très similaire à celui de l'algorithme RND. Il y a une petite concentration d'agents dans les extrêmes locaux, ce qui indique que l'algorithme tente d'affiner la solution, mais il n'y a pas de blocage évident.

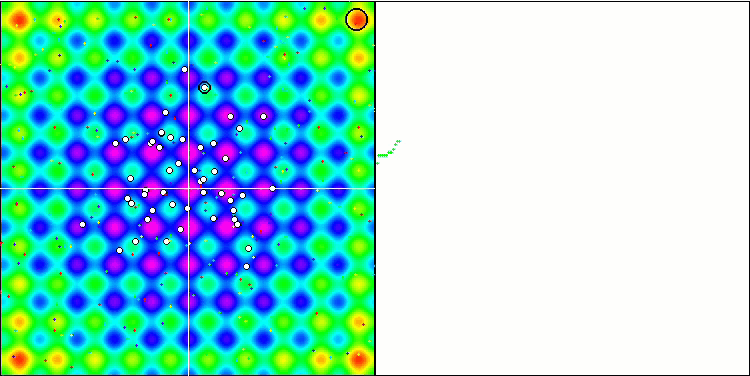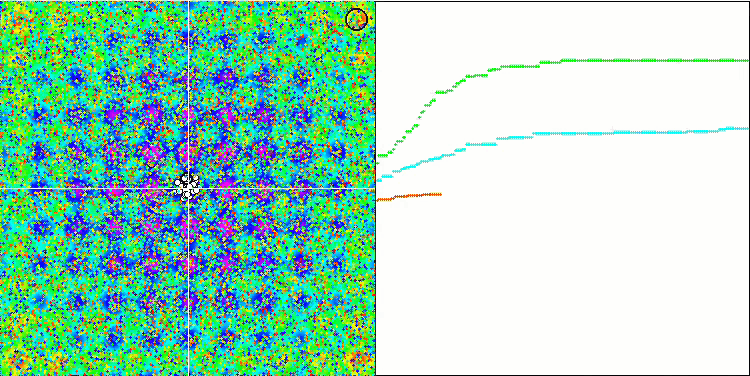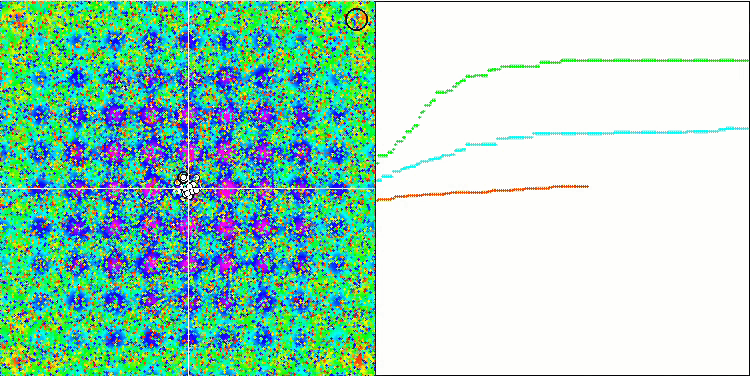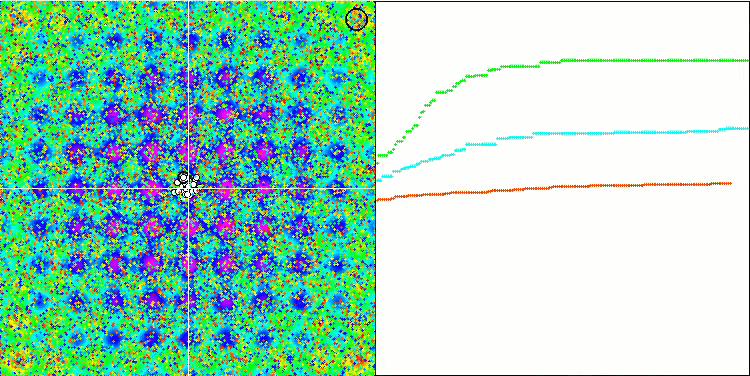
  MA sur la fonction de test de Rastrigin.

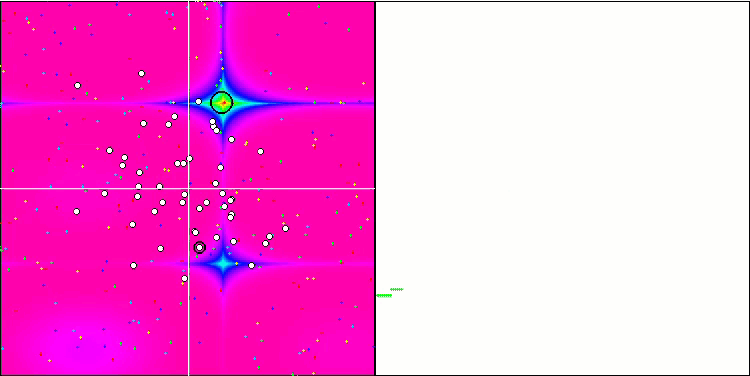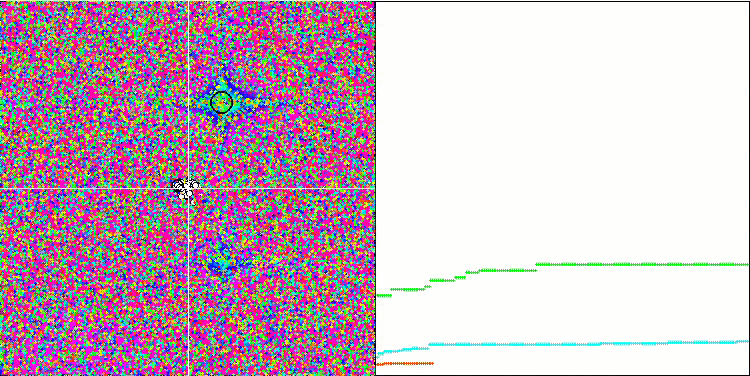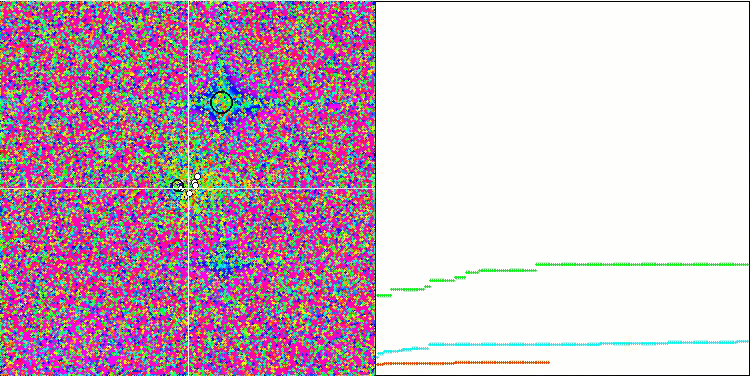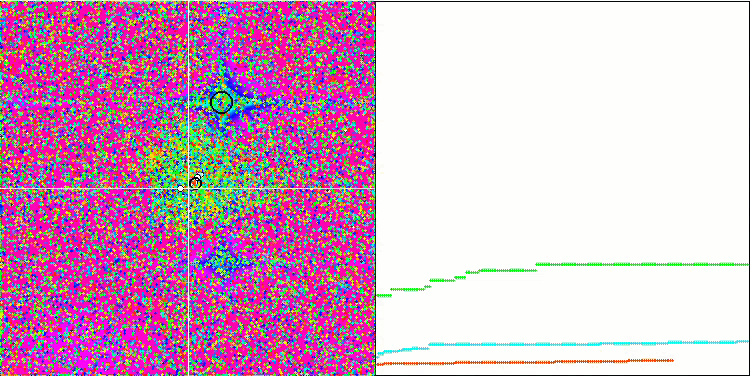
  MA sur la fonction de test Forest.

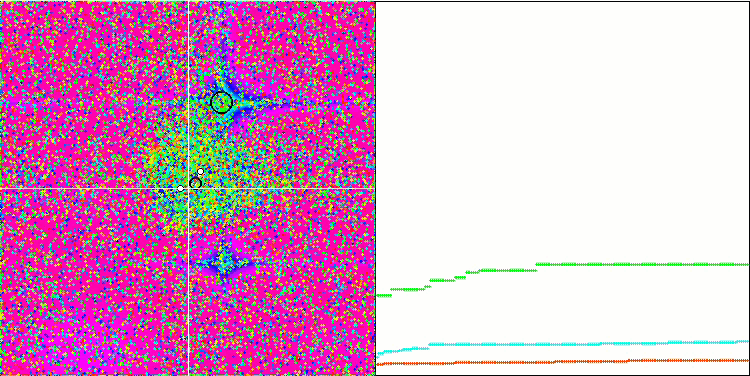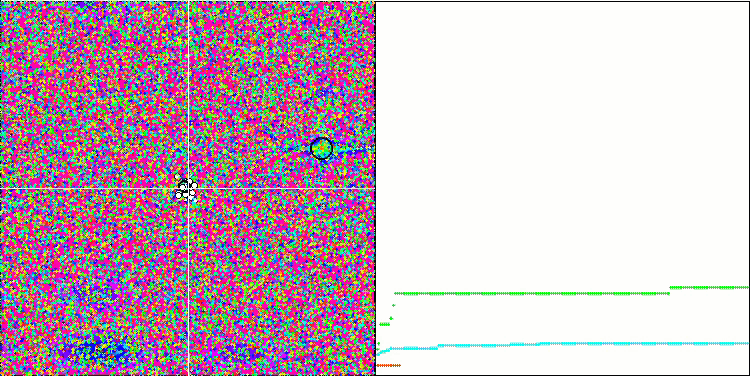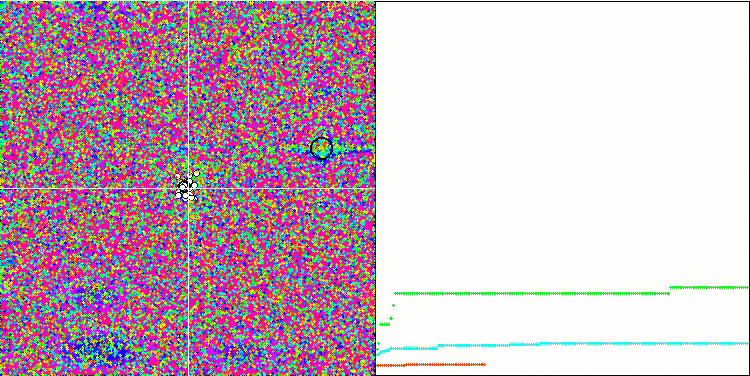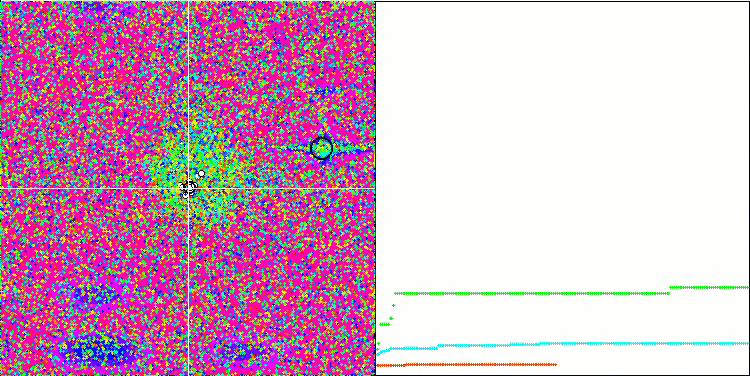
  MA sur la fonction de test Megacity.

Passons maintenant à l'analyse des résultats des tests. Sur la base des résultats, l'algorithme MA se classe en bas du tableau entre GSA et FSS. Étant donné que le test des algorithmes est basé sur le principe de l'analyse comparative, dans lequel les scores des résultats sont des valeurs relatives entre le meilleur et le pire, l'émergence d'un algorithme avec des résultats exceptionnels dans un test et des résultats médiocres dans d'autres entraîne parfois un changement dans les paramètres des autres participants au test.

Mais les résultats de MA n'ont pas entraîné un nouveau calcul des résultats des autres participants au test figurant dans le tableau. MA n'a pas de résultat de test unique qui serait le plus mauvais, bien qu'il y ait des algorithmes avec zéro résultat relatif et une note plus élevée (par exemple, GSA). Par conséquent, bien que l'algorithme se comporte de manière plutôt modeste et que la capacité de recherche ne soit pas suffisamment bien exprimée, l'algorithme présente des résultats stables, ce qui est une qualité positive pour les algorithmes d'optimisation.

AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrète)			Megacity final	Résultat final
		10 paramètres (5 F)	50 paramètres (25 F)	1.000 paramètres (500 F)		10 paramètres (5 F)	50 paramètres (25 F)	1.000 paramètres (500 F)		10 paramètres (5 F)	50 paramètres (25 F)	1.000 paramètres (500 F)
HS	recherche d'harmonie	1,00000	1,00000	0,57048	2,57048	1,00000	0,98931	0,57917	2,56848	1,00000	1,00000	1,00000	3,00000	100,000
ACOm	optimisation par colonies de fourmis M	0,34724	0,18876	0,20182	0,73782	0,85966	1,00000	1,00000	2,85966	1,00000	0,88484	0,13497	2,01981	68,094
IWO	Optimisation des mauvaises herbes envahissantes	0,96140	0,70405	0,35295	2,01840	0,68718	0,46349	0,41071	1,56138	0,75912	0,39732	0,80145	1,95789	67,087
COAm	algorithme d'optimisation coucou M	0,92701	0,49111	0,30792	1,72604	0,55451	0,34034	0,21362	1,10847	0,67153	0,30326	0,41127	1,38606	50,422
FAm	algorithme firefly M	0,60020	0,35662	0,20290	1,15972	0,47632	0,42299	0,64360	1,54291	0,21167	0,25143	0,84884	1,31194	47,816
BA	algorithme des chauves-souris	0,40658	0,66918	1,00000	2,07576	0,15275	0,17477	0,33595	0,66347	0,15329	0,06334	0,41821	0,63484	39,711
ABC	colonie d'abeilles artificielles	0,78424	0,34335	0,24656	1,37415	0,50591	0,21455	0,17249	0,89295	0,47444	0,23609	0,33526	1,04579	38,937
BFO	optimisation du butinage bactérien	0,67422	0,32496	0,13988	1,13906	0,35462	0,26623	0,26695	0,88780	0,42336	0,30519	0,45578	1,18433	37,651
GSA	algorithme de recherche gravitationnelle	0,70396	0,47456	0,00000	1,17852	0,26854	0,36416	0,42921	1,06191	0,51095	0,32436	0,00000	0,83531	35,937
MA	algorithme du singe	0,33300	0,35107	0,17340	0,85747	0,03684	0,07891	0,11546	0,23121	0,05838	0,00383	0,25809	0,32030	14,848
FSS	recherche d'un banc de poissons	0,46965	0,26591	0,13383	0,86939	0,06711	0,05013	0,08423	0,20147	0,00000	0,00959	0,19942	0,20901	13,215
PSO	optimisation par essaims de particules	0,20515	0,08606	0,08448	0,37569	0,13192	0,10486	0,28099	0,51777	0,08028	0,21100	0,04711	0,33839	10,208
RND	aléatoire	0,16881	0,10226	0,09495	0,36602	0,07413	0,04810	0,06094	0,18317	0,00000	0,00000	0,11850	0,11850	5,469
GWO	optimiseur du loup gris	0,00000	0,00000	0,02672	0,02672	0,00000	0,00000	0,00000	0,00000	0,18977	0,03645	0,06156	0,28778	1,000

Résumé

L'algorithme MA classique consiste essentiellement à utiliser le processus de montée pour trouver des solutions optimales locales. L'étape de montée joue un rôle décisif dans la précision de l'approximation de la solution locale. Plus le pas de montée pour les sauts locaux est petit, plus la précision de la solution est élevée, mais plus il faut d'itérations pour trouver l'optimum global. Pour réduire le temps de calcul en diminuant le nombre d'itérations, de nombreux chercheurs recommandent d'utiliser d'autres méthodes d'optimisation aux étapes initiales de l'optimisation, telles que ABC, COA, IWO, et d'utiliser MA pour affiner la solution globale. Je ne suis pas d'accord avec cette approche. Je pense qu'il est plus opportun d'utiliser immédiatement les algorithmes décrits plutôt que MA, bien que MA ait un potentiel de développement qui en fait un bon objet pour d'autres expériences et études. 

L'algorithme du singe est un algorithme basé sur la population qui trouve ses racines dans la nature. Comme beaucoup d'autres algorithmes métaheuristiques, cet algorithme est évolutif et peut résoudre un certain nombre de problèmes d'optimisation, y compris la non-linéarité, la non-différentiabilité et la haute dimensionnalité de l'espace de recherche, avec un taux de convergence élevé. Un autre avantage de l'algorithme du singe est qu'il est contrôlé par un petit nombre de paramètres, ce qui le rend relativement facile à mettre en œuvre. Malgré la stabilité des résultats, le faible taux de convergence ne permet pas de recommander l'algorithme du singe pour la résolution de problèmes à forte complexité de calcul, car il nécessite un nombre important d'itérations. Il existe de nombreux autres algorithmes qui effectuent le même travail en un temps plus court (nombre d'itérations).

Malgré mes nombreuses expériences, la version classique de l'algorithme ne parvenait pas à dépasser la troisième ligne du bas du tableau de classement, restait bloquée dans les extrêmes locaux et fonctionnait très mal sur les fonctions discrètes. Je n'avais pas particulièrement envie d'écrire un article à ce sujet, mais j'ai essayé de l'améliorer. L'une de ces tentatives a permis d'améliorer les indicateurs de convergence et d'accroître la stabilité des résultats en utilisant un biais de probabilité dans les sauts globaux, ainsi qu'en révisant le principe des sauts globaux eux-mêmes. De nombreux chercheurs du MA soulignent la nécessité de moderniser l'algorithme, c'est pourquoi de nombreuses modifications ont été apportées à l'algorithme du singe. Je n'avais pas l'intention d'envisager toutes sortes de modifications du MA, car l'algorithme lui-même n'est pas exceptionnel, il s'agit plutôt d'une variante de l'essaim de particules (PSO). Le résultat de ces expériences est la version finale de l'algorithme présentée dans cet article, sans la mention "m" (modifié).

L'histogramme des résultats du test de l'algorithme est présenté ci-dessous.

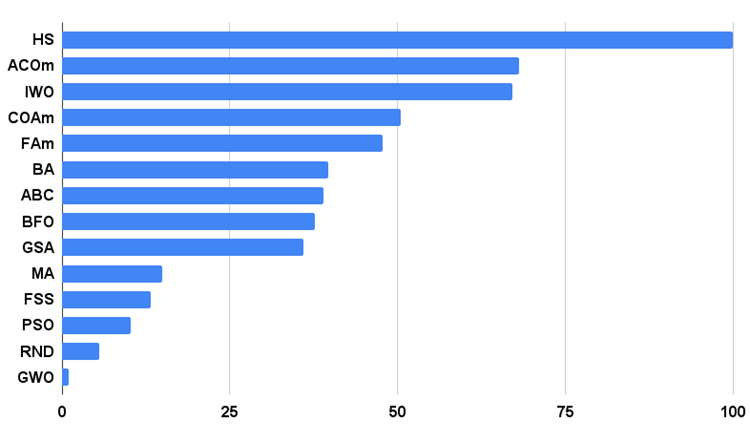
Figure 3. Histogramme des résultats des tests des algorithmes

Avantages et inconvénients du MA :

Avantages :
1. Mise en œuvre facile
2. Bonne évolutivité malgré un faible taux de convergence
3. Bonne performance sur les fonctions discrètes
4. Nombre réduit de paramètres externes

Inconvénients :
1. Faible taux de convergence
2. Nécessite un grand nombre d'itérations pour une recherche
3. Faible efficacité globale

Chaque article présente une archive contenant les versions actuelles mises à jour des codes algorithmiques de tous les articles précédents. L'article est basé sur l'expérience accumulée par l'auteur et représente son opinion personnelle. Les conclusions et les jugements sont basés sur les expériences.