Candlestick Momentum Blau_CMtm - indicator for MetaTrader 5

Author: Andrey N. Bolkonsky

Candlestick Momentum Indicator (q-period Candlestick Momentum) by William Blau is described in the book "Momentum, Direction, and Divergence: Applying the Latest Momentum Indicators for Technical Analysis".

• WilliamBlau.mqh must be placed in terminal_data_folder\MQL5\Include\
• Blau_CMtm.mq5 must be placed in terminal_data_folder\MQL5\Indicators\

Momentum is the difference between the current price (for example, closing price of the bar) and the previous price (several bars ago). Momentum can be applied to any timeframe and period.

According to William Blau, the Candlestick Momentum is defined as a change of the price over the fixed interval:

where:

• close - close price of the bar (candle);
• open - open price of the bar (candle).

Candlestick momentum can be plus or minus in the sense that an up momentum is positive when the close is greater than the open; the reverse is true when the open is greater than the close giving a negative value to the downward momentum.

The definintion of Candlestick Momentum can be extended:

1. Candlestick Momentum can be applied to any timeframe;
   
2. The applied price (closing price, open price) may vary.

The definition of the q-period Candlestick Momentum

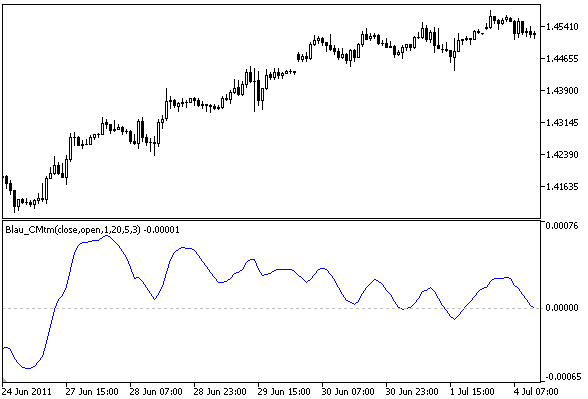
Candlestick Momentum Indicator by William Blau

Calculation:

The formula for calculation of Candlestick Momentum looks as follows:

where:

• q - number of bars, used in calculation of Candlestick Momentum;
• price1 - close price;
• price2[q–1] - open price q bars ago.

The smoothed q-period Candlestick Momentum is calculated as follows:

where:

• q - number of bars, used in calculation of q-period Candlestick Momentum;
• price1 - close price;
• price2 - open price q bars ago;
• cmtm(price1,price2,q)=price1-price2[q-1] - q-period Candlestcik Momentum;
• EMA(cmtm(price1,price2,q),r) - 1st smoothing - EMA (r), applied to q-period Candlestick Momentum;
• EMA(EMA(...,r),s) - 2nd smoothing - EMA(s), applied to result of the 1st smoothing;
• EMA(EMA(EMA(...,r),s),u) - 3rd smoothing - EMA(u), applied to result of the 2nd smoothing.

• q - period of Candlestick Momentum Indicator (by default q=1);
• r - period of the 1st EMA, applied to Candlestick Momentum (by default r=20);
• s - period of the 2nd EMA, applied to result of the 1st smoothing (by default s=5);
• u - period of the 3rd EMA, applied to result of the 2nd smoothing (by default u=3);
• AppliedPrice1 - price type (by default AppliedPrice=PRICE_CLOSE);
• AppliedPrice2 - price type (by default AppliedPrice=PRICE_OPEN).

• q>0;
• r>0, s>0, u>0. If r, s or u are equal to 1, the smoothing is not used;
• Min. rates =(q-1+r+s+u-3+1).