
Applying OLAP in trading (part 1): Online analysis of multidimensional data
Traders often have to analyze huge amounts of data. These often include numbers, quotes, indicator values and trading reports. Due to the large number of parameters and conditions, on which these numbers depend, let us consider them in parts and view the entire process from different angles. The entire amount of information forms kind of a virtual hypercube, in which each parameter defines its own dimension, which is perpendicular to the rest. Such hypercubes can be processed and analyzed using the popular OLAP ( Online Analytical Processing) technology.
The "online" word in the approach name does not refer to the Internet, but means promptness of results. The operation principle implies the preliminary calculation of the hypercube cells, after which you can quickly extract and view any cross section of the cube in a visual form. This can be compared to the optimization process in MetaTrader: the tester first calculates trading variants (which may take quite a long time, i.e. it is not prompt), and then outputs a report, which features the results linked to input parameters. Starting from build 1860, the MetaTrader 5 platform supports dynamic changes of viewed optimization results by switching various optimization criteria. This is close to OLAP idea. But for a complete analysis, we need the possibility to select many other slices of the hypercube.
We will try to apply the OLAP approach in MetaTrader and to implement multidimensional analysis using MQL tools. Before proceeding to implementation, we need to determine the data to analyze. These may include trading reports, optimization results or indicator values. The selection at this stage is not quite important, because we aim to develop a universal object-oriented engine applicable to any data. But we need to apply the engine to specific results. One of the most popular tasks is the analysis of the trading report. We will consider this task.
Within a trading report, a breakdown of profit by symbols, days of the week, buy and sell operations might be useful. Another option is to compare performance results of different trading robots (i.e. separately for each magic number). The next logical question is whether it is possible to combine various dimensions: symbols by days of the week in relation to Expert Advisors, or to add some other grouping. All this can be done using OLAP.
Architecture
According to the object-oriented approach, a large task should be broken down into simple logically related parts, while each part performs its own role based on incoming data, internal state and some sets of rules.
The first class which we will use is a record containing source data — 'Record'. Such a record can store data related to one trading operation or one optimization pass, etc.
A 'Record' is a vector with an arbitrary number of fields. Since this is an abstract entity, the meaning of each field is not important. For each specific application, we will create a derived class which "knows" the purpose of the fields and processes them accordingly.
Another class 'DataAdapter' is needed to read records from some abstract source (such as a trading account history, a CSV file, an HTML report or data obtained on the web using WebRequest). At this stage it only performs one function: it iterates through records one by one and provides access to them. Later, we will be able to create derived classes for each real application. These classes will fill in arrays of records from relevant sources.
All records can be somehow displayed in the hypercube cells. At this stage we do not know how to do this, but this is the idea of the project: to distribute input values from the record fields among the cube cells and to calculate for them the generalized statistics using the selected aggregate functions.
The basic cube level provides only the main properties such as the number of dimensions, their names and the size of each dimension. This data is provided in the MetaCube class.
Derived classes then fill in relevant statistics to these cells. The most common examples of specific aggregators include the sum of all values or the average value of the same field for all records. However there will be much more different types of aggregators.
To enable the aggregation of values in the cells, each record must receive the set of indexes, which uniquely map it into a certain cell of the cube. This task will be performed by the special 'Selector' class. The Selector corresponds to one side (axis, coordinate) of the hypercube.
The abstract Selector base class provides a programming interface for defining a set of valid values and for mapping each entry into one of these values. For example, if the purpose is to divide records by days of the week, then the derived Selector class should return the number of the day of the week, from 0 to 6. The number of allowable values for a particular Selector defines the size of this cube dimension. This is obvious for the day of the week, i.e. 7.
Furthermore, sometimes it is useful to filter some of the records (to exclude them from analysis). Therefore, we need a Filter class. It is similar to the Selector, but it sets additional limitations on the allowable values. For example, we can create a filter based on the selector of the days of the week. In this filter, it is possible to specify the days which need to be excluded from the calculation or to be included therein.
Once the cube has been created (i.e. the aggregate functions for all cells have been calculated), the result can be visualized and analyzed. For this purpose, let us reserve the special 'Display' class.
To combine all the aforementioned classes into a whole unit, let us create a kind of control center, the Analyst class.
This looks as follows in the UML notation (this can be considered as an action plan, which can be checked at any development stage).
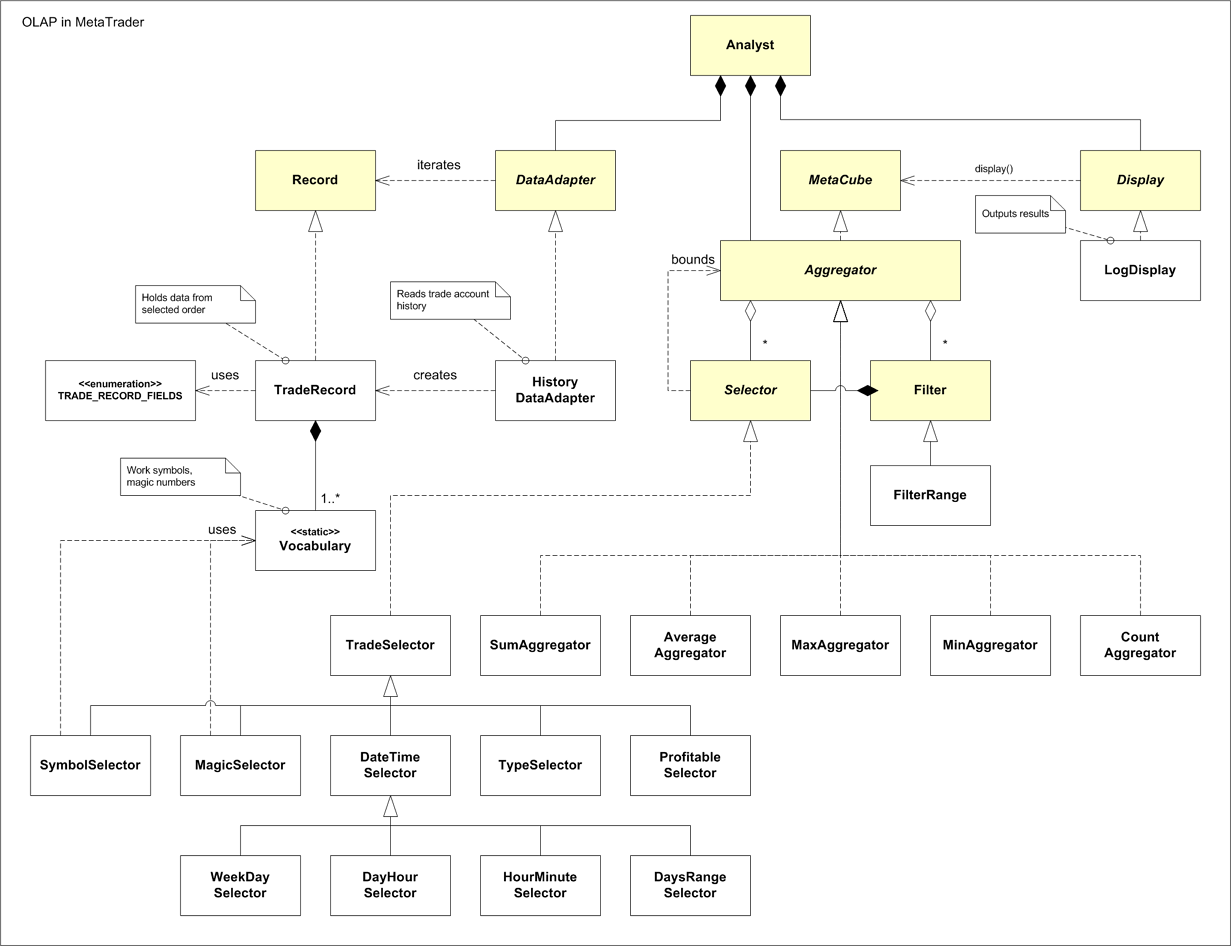
Online Analytical Processing in MetaTrader
Some of the classes are omitted here. However it reflects the general basis of the hypercube construction as well as it shows the aggregate functions which will be available for calculations in the hypercube cells.
Base class implementation
Now we will proceed to the implementation of the classes described above. Let us start with the Record class.
class Record { private: double data[]; public: Record(const int length) { ArrayResize(data, length); ArrayInitialize(data, 0); } void set(const int index, double value) { data[index] = value; } double get(const int index) const { return data[index]; } };
It simply stores arbitrary values in the 'data' array (vector). The vector length is set in the constructor.
Records from different sources will be read using DataAdapter.
class DataAdapter { public: virtual Record *getNext() = 0; virtual int reservedSize() = 0; };
The getNext method must be called in a loop until it returns NULL (which means that there are no more records). All received records should be saved somewhere (this task will be discussed later). The reservedSize method enables optimized memory distribution (if the number of records in the source is known in advance).
Each hypercube dimension is calculated based on one or more record fields. It is convenient to mark each field as an element of an enumeration. For example, for analyzing the account trading history, the following enumeration can be used.
// MT4 and MT5 hedge enum TRADE_RECORD_FIELDS { FIELD_NONE, // none FIELD_NUMBER, // serial number FIELD_TICKET, // ticket FIELD_SYMBOL, // symbol FIELD_TYPE, // type (OP_BUY/OP_SELL) FIELD_DATETIME1, // open datetime FIELD_DATETIME2, // close datetime FIELD_DURATION, // duration FIELD_MAGIC, // magic number FIELD_LOT, // lot FIELD_PROFIT_AMOUNT, // profit amount FIELD_PROFIT_PERCENT,// profit percent FIELD_PROFIT_POINT, // profit points FIELD_COMMISSION, // commission FIELD_SWAP, // swap FIELD_CUSTOM1, // custom 1 FIELD_CUSTOM2 // custom 2 };
The last two fields can be used for calculating non-standard variables.
The below enumeration can be suggested for the analysis of MetaTrader optimization results.
enum OPTIMIZATION_REPORT_FIELDS { OPTIMIZATION_PASS, OPTIMIZATION_PROFIT, OPTIMIZATION_TRADE_COUNT, OPTIMIZATION_PROFIT_FACTOR, OPTIMIZATION_EXPECTED_PAYOFF, OPTIMIZATION_DRAWDOWN_AMOUNT, OPTIMIZATION_DRAWDOWN_PERCENT, OPTIMIZATION_PARAMETER_1, OPTIMIZATION_PARAMETER_2, //... };
An individual enumeration should be prepared for each practical application case. Then it can be used as a parameter of the Selector template class.
template<typename E> class Selector { protected: E selector; string _typename; public: Selector(const E field): selector(field) { _typename = typename(this); } // returns index of cell to store values from the record virtual bool select(const Record *r, int &index) const = 0; virtual int getRange() const = 0; virtual float getMin() const = 0; virtual float getMax() const = 0; virtual E getField() const { return selector; } virtual string getLabel(const int index) const = 0; virtual string getTitle() const { return _typename + "(" + EnumToString(selector) + ")"; } };
The selector field stores only one value, an element of the enumeration. For example, if TRADE_RECORD_FIELDS is used, a selector for buy/sell operation can be created as follows:
new Selector<TRADE_RECORD_FIELDS>(FIELD_TYPE);
The _typename field is auxiliary. It will be overwritten in all derived classes to identify selectors, which is useful when visualizing results. The field is used in the virtual getTitle method.
The major part of operation is performed by a class in the 'select' method. Here, each input record is mapped as a specific index value along the coordinate axis, which is formed by the current selector. The index must be in the range between the values returned by the getMin and getMax methods, while the total number of indexes is equal to the number returned by getRange. If the record cannot be correctly mapped in the sector definition area, for some reason, the 'select' method returns false. If the mapping has been performed correctly, true is returned.
The getLabel method returns a user-friendly description of the specific index. For example, for buy/sell operations, index 0 must generate "buy", while index 1 must generate "sell".
Implementing specific selector and data adapter classes for the trading history
Since we are going to analyze the trading history, let us introduce an intermediary class of selectors based on the TRADE_RECORD_FIELDS enumeration.
class TradeSelector: public Selector<TRADE_RECORD_FIELDS> { public: TradeSelector(const TRADE_RECORD_FIELDS field): Selector(field) { _typename = typename(this); } virtual bool select(const Record *r, int &index) const { index = 0; return true; } virtual int getRange() const { return 1; // this is a scalar by default, returns 1 value } virtual double getMin() const { return 0; } virtual double getMax() const { return (double)(getRange() - 1); } virtual string getLabel(const int index) const { return EnumToString(selector) + "[" + (string)index + "]"; } };
By default, it maps all record into the same cell. For example, using this selector, you can obtain the total profit data.
Now, based on this selector we can easily determine specific derivative types of selectors. This is also used for grouping records by the operation type (buy/sell).
class TypeSelector: public TradeSelector { public: TypeSelector(): TradeSelector(FIELD_TYPE) { _typename = typename(this); } virtual bool select(const Record *r, int &index) const { ... } virtual int getRange() const { return 2; // OP_BUY, OP_SELL } virtual double getMin() const { return OP_BUY; } virtual double getMax() const { return OP_SELL; } virtual string getLabel(const int index) const { const static string types[2] = {"buy", "sell"}; return types[index]; } };
We have defined the class using the FIELD_TYPE element in the constructor. The getRange method returns 2, because here we only have 2 possible types: OP_BUY or OP_SELL. The getMin and getMax methods return correspondent constants. What should the 'select' method contain?
First, we need to decide which information will be stored in each record. This can be done using the TradeRecord class, which is derived from Record and is adapted for working with the trading history.
class TradeRecord: public Record { private: static int counter; protected: void fillByOrder() { set(FIELD_NUMBER, counter++); set(FIELD_TICKET, OrderTicket()); set(FIELD_TYPE, OrderType()); set(FIELD_DATETIME1, OrderOpenTime()); set(FIELD_DATETIME2, OrderCloseTime()); set(FIELD_DURATION, OrderCloseTime() - OrderOpenTime()); set(FIELD_MAGIC, OrderMagicNumber()); set(FIELD_LOT, (float)OrderLots()); set(FIELD_PROFIT_AMOUNT, (float)OrderProfit()); set(FIELD_PROFIT_POINT, (float)((OrderType() == OP_BUY ? +1 : -1) * (OrderClosePrice() - OrderOpenPrice()) / SymbolInfoDouble(OrderSymbol(), SYMBOL_POINT))); set(FIELD_COMMISSION, (float)OrderCommission()); set(FIELD_SWAP, (float)OrderSwap()); } public: TradeRecord(): Record(TRADE_RECORD_FIELDS_NUMBER) { fillByOrder(); } };
The auxiliary fillByOrder method demonstrates how most of the record fields can be filled based on the current order. Of course, the order
must be pre-selected somewhere else in the code. Here we use the notation of the MetaTrader 4 trading functions. MetaTrader 5 support will be
implemented by including the
MT4Orders library (one of the versions is attached below, always check and download the
current version). Thus we can create a cross-platform code.
The number of the TRADE_RECORD_FIELDS_NUMBER fields can be either hard coded as a macro definition or it can be calculated dynamically based on the TRADE_RECORD_FIELDS enumeration. The second approach is implemented in the attached code, for which the special templatized EnumToArray function is used.
As can be seen from the fillByOrder method, the FIELD_TYPE field is filled by the operation type from OrderType. Now we can get back to the TypeSelector class and implement its 'select' method.
virtual bool select(const Record *r, int &index) const { index = (int)r.get(selector); return index >= getMin() && index <= getMax(); }
Here we read the field value (selector) from the input record (r) and assign its value (which can be either OP_BUY or OP_SELL) to the index output parameter. Calculation only includes market orders, therefore false is returned for all other types. Later we will consider other selector types.
Now it is time to develop a data adapter for the trading history. This is the class in which TradeRecord records will be generated based on the account's real trading history.
class HistoryDataAdapter: public DataAdapter { private: int size; int cursor; protected: void reset() { cursor = 0; size = OrdersHistoryTotal(); } public: HistoryDataAdapter() { reset(); } virtual int reservedSize() { return size; } virtual Record *getNext() { if(cursor < size) { while(OrderSelect(cursor++, SELECT_BY_POS, MODE_HISTORY)) { if(OrderType() < 2) { return new TradeRecord(); } } return NULL; } return NULL; } };
The adapter sequentially passes through all orders which are available in history and creates a TradeRecord instance for each market order. The code is presented here in a simplified form. During actual use, we may need to create objects not of the TradeRecord class, but of a derived class: we have reserved two custom fields for the TRADE_RECORD_FIELDS enumeration. Therefore HistoryDataAdapter is a template class, while the template parameter is the actual class of generated record objects. The Record class must contain an empty virtual method for filling custom fields:
virtual void fillCustomFields() {/* does nothing */};
You can analyze the full implementation approach for yourself: the CustomTradeRecord class is used in the core. In fillCustomFields, this class (which is a child of TradeRecord) calculates MFE (Maximum Favorable Excursion) and MAE (Maximum Adverse Excursion) for each position and it records these values to the fields FIELD_CUSTOM1 and FIELD_CUSTOM2.
Implementing aggregators and a control class
We need a place to create the adapter and to call its getNext method. Now we will deal with the "control center", the Analyst class. In addition to the adapter launch, the class must store the received records in an internal array.
template<typename E> class Analyst { private: DataAdapter *adapter; Record *data[]; public: Analyst(DataAdapter &a): adapter(&a) { ArrayResize(data, adapter.reservedSize()); } ~Analyst() { int n = ArraySize(data); for(int i = 0; i < n; i++) { if(CheckPointer(data[i]) == POINTER_DYNAMIC) delete data[i]; } } void acquireData() { Record *record; int i = 0; while((record = adapter.getNext()) != NULL) { data[i++] = record; } ArrayResize(data, i); } };
The class does not create an adapter, but it receives a ready one as a constructor parameter. This is a well-known design principle — dependency injection. It allows the detaching of Analyst from a specific DataAdapter implementation. In other words, we can easily replace various adapter variants without the need for modifications in the Analyst class.
The Analyst class is now able to fill the internal array of records, but it still does not know how to perform the main function, i.e. how to aggregate data. This task will be implemented by the aggregator.
Aggregators are classes which can calculate predefined variables (statistics) for the selected record fields. The base class for aggregators is MetaCube, which is a storage based on a multidimensional array.
class MetaCube { protected: int dimensions[]; int offsets[]; double totals[]; string _typename; public: int getDimension() const { return ArraySize(dimensions); } int getDimensionRange(const int n) const { return dimensions[n]; } int getCubeSize() const { return ArraySize(totals); } virtual double getValue(const int &indices[]) const = 0; };
The 'dimensions' array describes the hypercube structure. Its size is equal to the number of selectors used, that is, dimensions. Each element of the 'dimensions' array contains the cube size in this dimension, which is determined by the range of values of the appropriate selector. For example, in order to view profits by day of the week, we need to create a selector which returns the day number as an index from 0 to 6, according to the order (position) opening or closing time. Since this is the only selector, the 'dimensions' array will have 1 element, and its value will be 7. If we add another selector, for example the earlier described TypeSelector, to view profits in terms of the day of the week and the type of operation, the 'dimensions' array will contain 2 elements with the values of 7 and 2. This also means that the hypercube will contain 14 cells with statistics.
The array with all values (14 in our example) is contained in 'totals'. Since the hypercube is multidimensional, it may seem that the array is declared as having only one dimension. This is because we do not know in advance the hypercube dimensions which the user will need to add. In addition, MQL does not support multidimensional arrays in which absolutely all dimensions would be distributed dynamically. Therefore, the usual "flat" array (vector) is used. A special indexing will be used to store cells in several dimensions in this array. Next, let us consider the calculation of offsets for each dimension.
The base class does not allocate and does not initialize arrays, while this is performed by derived classes.
Since all the aggregators are expected to have many common features, let us pack them all in one intermediate class.
template<typename E> class Aggregator: public MetaCube { protected: const E field;
Each aggregator processes a specific record field. This field is specified in the class, in the 'field' variable, which is filled in the constructor (see below). For example, this can be the profit (FIELD_PROFIT_AMOUNT).
const int selectorCount; const Selector<E> *selectors[];
The calculations are performed in a multi-dimensional space, which is formed of an arbitrary number of selectors (selectorCount). We have previously considered the calculation of profits with a breakdown by day of the week and by operation type, which requires two selectors. They are stored in the 'selectors' array of references. The selector objects are passed as the constructor parameters.
public: Aggregator(const E f, const Selector<E> *&s[]): field(f), selectorCount(ArraySize(s)) { ArrayResize(selectors, selectorCount); for(int i = 0; i < selectorCount; i++) { selectors[i] = s[i]; } _typename = typename(this); }
As you remember, the 'totals' array for storing the calculated values is one-dimensional. The following function is used to convert the indexes of the multidimensional selectors space into an offset in a one-dimensional array.
int mixIndex(const int &k[]) const { int result = 0; for(int i = 0; i < selectorCount; i++) { result += k[i] * offsets[i]; } return result; }
It accepts an array with indexes as an input and returns the sequential number of the element. The 'offsets' array is used here — by this time the array must be already filled. Its initialization is one of the key points and it is performed in the setSelectorBounds method.
virtual void setSelectorBounds() { ArrayResize(dimensions, selectorCount); int total = 1; for(int i = 0; i < selectorCount; i++) { dimensions[i] = selectors[i].getRange(); total *= dimensions[i]; } ArrayResize(totals, total); ArrayInitialize(totals, 0); ArrayResize(offsets, selectorCount); offsets[0] = 1; for(int i = 1; i < selectorCount; i++) { offsets[i] = dimensions[i - 1] * offsets[i - 1]; // 1, X, Y*X } }
Its purpose is to obtain the ranges of all selectors and to sequentially multiply them: thus we can determine the number of elements to "jump" over when increasing the coordinate by one in each hypercube dimension.
The calculation of aggregated variables is performed in the calculate method.
// build an array with number of dimensions equal to number of selectors virtual void calculate(const Record *&data[]) { int k[]; ArrayResize(k, selectorCount); int n = ArraySize(data); for(int i = 0; i < n; i++) { int j = 0; for(j = 0; j < selectorCount; j++) { int d; if(!selectors[j].select(data[i], d)) // does record satisfy selector? { break; // skip it, if not } k[j] = d; } if(j == selectorCount) { update(mixIndex(k), data[i].get(field)); } } }
The method is called for the array of records. Each record in the loop is passed in turn to each selector. If it is successfully mapped in valid indexes in all selectors (each selector has its own index), then the full set of indexes is saved in the k local array. If all the selectors have determined indexes, the 'update' method is called. The following is input into the method: the offset in the 'totals' array (the offset is calculated using the aforementioned mixIndex) and the value of the specified 'field' (it is set in the aggregators) from the current record. In the profit distribution analysis example, the 'field' variable will be equal to FIELD_PROFIT_AMOUNT, while the values for this field will be provided by the OrderProfit() call.
virtual void update(const int index, const float value) = 0;
The update method is abstract in this class and it must be redefined in its heirs.
Also the aggregator must provide at least one method for accessing the calculation results. The simplest one of them is receiving the value of a specific cell based on the entire set of indexes.
double getValue(const int &indices[]) const { return totals[mixIndex(indices)]; } };
The base class Aggregator performs almost all of the rough work. Now we can easily implement a lot of specific aggregators.
But first, let us get back to the Analyst class: we need to add to it a reference to the aggregator, which will also be passed through the constructor parameter.
template<typename E> class Analyst { private: DataAdapter *adapter; Record *data[]; Aggregator<E> *aggregator; public: Analyst(DataAdapter &a, Aggregator<E> &g): adapter(&a), aggregator(&g) { ArrayResize(data, adapter.reservedSize()); }
In the acquireData method, we will configure the hypercube dimensions using the additional call of the aggregator's setSelectorBounds method.
void acquireData() { Record *record; int i = 0; while((record = adapter.getNext()) != NULL) { data[i++] = record; } ArrayResize(data, i); aggregator.setSelectorBounds(i); }
The main task, i.e. the calculation of all values of the hypercube, will be implemented in the aggregator (we have already considered the 'calculate' method before; here the array of records is passed to it).
void build()
{
aggregator.calculate(data);
}
This is not all about the Analyst class. Earlier, we planned to enable it to display the results, by formalizing it as a special Display interface. The interface is connected to Analyst in a similar way (by passing a reference to the constructor):
template<typename E> class Analyst { private: ... Display *output; public: Analyst(DataAdapter &a, Aggregator<E> &g, Display &d): adapter(&a), aggregator(&g), output(&d) { ... } void display() { output.display(aggregator); } };
The 'Display' contents are simple:
class Display { public: virtual void display(MetaCube *metaData) = 0; };
It contains an abstract virtual method to which the hypercube is input as a data source. Some of the parameters which influence the value printing order are omitted here, for brevity. The visualization specifics and the necessary additional settings will appear in the derived classes.
To test the analytical classes, we need to have at least one implementation of the 'Display' interface. Let us create it by writing messages to the Experts journal. It will be called LogDisplay. The interface will loop through all coordinates of the hypercube and will print the aggregated values together with the appropriate coordinates, roughly as follows:
class LogDisplay: public Display { public: virtual void display(MetaCube *metaData) override { int n = metaData.getDimension(); int indices[], cursors[]; ArrayResize(indices, n); ArrayResize(cursors, n); ArrayInitialize(cursors, 0); for(int i = 0; i < n; i++) { indices[i] = metaData.getDimensionRange(i); } bool looping = false; int count = 0; do { ArrayPrint(cursors); Print(metaData.getValue(cursors)); for(int i = 0; i < n; i++) { if(cursors[i] < indices[i] - 1) { looping = true; cursors[i]++; break; } else { cursors[i] = 0; } looping = false; } } while(looping && !IsStopped()); } };
I say 'roughly' because the LogDisplay implementation for a more convenient formating of logs would be a bit more complicated. The full version of the class is available in attached source code.
Of course, this is not as efficient as a chart would be, but the creation of two- or three-dimensional images is another separate subject, which we will not consider (though you can use different technologies for this, such as objects, canvas and external graphical libraries, including those based on web technologies).
Thus, we have the Aggregator base class. On its basis, we can easily obtain several derived classes with specific calculations of aggregated variables in the update method. In particular, the following simple code can be used to calculate the sum of the values which are extracted by a certain selector from all the records:
template<typename E> class SumAggregator: public Aggregator<E> { public: SumAggregator(const E f, const Selector<E> *&s[]): Aggregator(f, s) { _typename = typename(this); } virtual void update(const int index, const float value) override { totals[index] += value; } };
Only a minor complication is needed to calculate the average:
template<typename E> class AverageAggregator: public Aggregator<E> { protected: int counters[]; public: AverageAggregator(const E f, const Selector<E> *&s[]): Aggregator(f, s) { _typename = typename(this); } virtual void setSelectorBounds() override { Aggregator<E>::setSelectorBounds(); ArrayResize(counters, ArraySize(totals)); ArrayInitialize(counters, 0); } virtual void update(const int index, const float value) override { totals[index] = (totals[index] * counters[index] + value) / (counters[index] + 1); counters[index]++; } };
Having considered all the classes involved, let us generalize their interaction algorithm:
- Create the HistoryDataAdapter object;
- Create several specific selectors (each of the selectors is bound to at least one field, such as trading operation type, etc.) and save them to an array;
- Create the specific aggregator object, e.g. SumAggregator. Pass to it the array of selectors and the indication of the field, based on which the aggregation should be performed;
- Create the LogDisplay object;
- Create the Analyst object using the objects of the adapter, the aggregator and the display;
- Call sequentially:
analyst.acquireData();
analyst.build();
analyst.display();
- Do not forget to delete the objects at the end.
Special case: dynamic selectors
Our program is almost ready. Previously we omitted a part of it in order to simplify the description. Now it is time to eliminate it.
All the aforementioned selectors had a constant range of values. For example, there are always 7 days in a week, while the market orders are either Buy or Sell. However, the range may not be known in advance, which happens quite often.
We may need a hypercube reflecting working symbols or EA magic numbers. For the solution of this task, we will first need to collect all the unique instruments or magic numbers in some internal array, and then we will use the array size for the relevant selector range.
Let us create the 'Vocabulary' class for managing these internal arrays. We will analyze its use in conjunction with the SymbolSelector class.
Our implementation of the vocabulary is quite straightforward (you can replace it with any preferred one).
template<typename T> class Vocabulary { protected: T index[];
The 'index' array is reserved for storing unique values.
public: int get(const T &text) const { int n = ArraySize(index); for(int i = 0; i < n; i++) { if(index[i] == text) return i; } return -(n + 1); }
The 'get' method is used to check whether a certain values already exists in the array. If there is such a value, the method returns the found index. If the value does not exist in the array, the method returns the array size increased by 1, with a minus sign. This enables a slight optimization of the next method for adding a new value to the array.
int add(const T text) { int n = get(text); if(n < 0) { n = -n; ArrayResize(index, n); index[n - 1] = text; return n - 1; } return n; }
Also we need to provide methods for receiving the array size and the values stored therein, by index.
int size() const { return ArraySize(index); } T operator[](const int slot) const { return index[slot]; } };
In our case, the working symbols are analyzed in the context of orders (positions), therefore let us embed the vocabulary into the TradeRecord class.
class TradeRecord: public Record { private: ... static Vocabulary<string> symbols; protected: void fillByOrder(const double balance) { ... set(FIELD_SYMBOL, symbols.add(OrderSymbol())); // symbols are stored as indices from vocabulary } public: static int getSymbolCount() { return symbols.size(); } static string getSymbol(const int index) { return symbols[index]; } static int getSymbolIndex(const string s) { return symbols.get(s); }
The vocabulary is described as a static variable, because it is shared for the entire trading history.
Now we can implement SymbolSelector.
class SymbolSelector: public TradeSelector { public: SymbolSelector(): TradeSelector(FIELD_SYMBOL) { _typename = typename(this); } virtual bool select(const Record *r, int &index) const override { index = (int)r.get(selector); return (index >= 0); } virtual int getRange() const override { return TradeRecord::getSymbolCount(); } virtual string getLabel(const int index) const override { return TradeRecord::getSymbol(index); } };
The magic number selector is implemented in a similar way.
The general list of provided selectors includes the following (the necessity of external binding to the field is indicated in parentheses; if it is omitted, this means that binding to a specific field is already provided inside the selector class):
- TradeSelector (any field) — a scalar, one value (a summary of all records for "real" aggregators or the field value of a certain record for IdentityAggregator (see below));
- TypeSelector — Buy or Sell depending on OrderType();
- WeekDaySelector (datetime type field) — the day of the week, e.g. in OrderOpenTime() or OrderCloseTime();
- DayHourSelector (datetime type field) — hour within the day;
- HourMinuteSelector (datetime type field) — minute within the hour;
- SymbolSelector — working symbol, an index in the unique OrderSymbol() vocabulary;
- SerialNumberSelector — the sequence number of the record (order);
- MagicSelector — the magic number, an index in the unique OrderMagicNumber() vocabulary;
- ProfitableSelector — true = profit, false = loss, from the OrderProfit() field;
- QuantizationSelector (double type field) — a vocabulary of random double type values (for example, for the lot size);
- DaysRangeSelector — example of a custom selector with two datetime type fields (OrderCloseTime() and OrderOpenTime()), which is based on the DateTimeSelector class, the common parent of all selectors for datetime type fields; unlike the other selectors which are defined in the core, this selector is implemented in the demo EA (see below).
SerialNumberSelector significantly differs from other selectors. Its range is equal to the total number of records. This enables the generation of a hypercube, in which the records are sequentially counted in one of the dimensions (usually in the first one, X), while the specified fields are copied in the other dimension. The fields are defined by the selectors: specialized selectors already include field binding; if you need a field for which there is no ready selector, such as 'swap', then the universal TradeSelector can be used. In other words, SerialNumberSelector enables the possibility to read the source record data within the aggregating hypercube metaphor. This is done by using the pseudo-aggregator IdentityAggregator (see below).
The following aggregators are available:
- SumAggregator — the sum of the field values;
- AverageAggregator — the average field value;
- MaxAggregator — the maximum field value;
- MinAggregator — the minimum field value;
- CountAggregator — the number of records;
- ProfitFactorAggregator — the ratio of the sum of positive field values to the sum of negative field values;
- IdentityAggregator (SerialNumberSelector along the X axis) — a special selector type for the "transparent" copying of field values to the hypercube, without aggregation;
- ProgressiveTotalAggregator (SerialNumberSelector along the X axis) — a cumulative total for the field;
The last two aggregators differ from the rest. When IdentityAggregator is selected, the hypercube size is always equal to 2. The records are reflected along the X axis using SerialNumberSelector, while each count along the second axis (actually it is vector/column) corresponds to one selector, using which the field to be read from the source records is determined. So if there are three additional selectors (in addition to SerialNumberSelector), there will be three counts along the Y axis. However, the cube still has two dimensions: the X and Y axes. Usually the cube is generated according to a different principle: each selector corresponds to its own dimension, so 3 dimensions mean 3 axes.
ProgressiveTotalAggregator treats the first dimension in a special way. As its name implies, the aggregator enables the calculation of the cumulative total, while this is done along the X axis. For example, if you specify the profit field in the aggregator parameter, you will obtain the general balance curve. If you plot symbols (SymbolSelector) along the Y axis (in the second selector), there will be multiple [N] balance curves for each of the available symbols. If the second selector is MagicSelector, there will be separate [M] balance curve of different Expert Advisors. Moreover, both parameters can be combined: set SymbolSelector along Y and set MagicSelector along the Z axis (or vice versa): you will obtain [N*M] balance curves, each having a different magic number and symbol combination.
Now the OLAP engine is ready. We have omitted some of the description parts to keep the article concise. For example, the article does not provide the description of the filters (Filter, FilterRange classes), which were provided in the architecture. Furthermore, this hypercube can present the aggregated values not only one by one (method getValue(const int &indices[])), but also it can return them as a vector using the following method:
virtual bool getVector(const int dimension, const int &consts[], PairArray *&result, const SORT_BY sortby = SORT_BY_NONE)
The method output is the special PairArray class. It stores an array of structures with the pairs of [value;name]. For example, if we build a cube reflecting profit by symbols, then each sum corresponds to a specific symbol - therefore its name is indicated in a pair next to the value. As can be seen from the method prototype, it is able to sort PairArray in different modes: ascending or descending, by values or by tags:
enum SORT_BY // applicable only for 1-dimensional cubes { SORT_BY_NONE, // none SORT_BY_VALUE_ASCENDING, // value (ascending) SORT_BY_VALUE_DESCENDING, // value (descending) SORT_BY_LABEL_ASCENDING, // label (ascending) SORT_BY_LABEL_DESCENDING // label (descending) };
Sorting is supported only on one-dimensional hypercubes. In theory it could be implemented for the arbitrary number of dimensions, but this is quite a routine work. Those interested can implement such sorting.
Full source codes are attached.
OLAPDEMO Example
Now let us test the hypercube. Let's create a non-trading Expert Advisor which can analyze the account trading history. Let's call it OLAPDEMO. Include the header file in which all the main OLAP classes are contained.
#include <OLAPcube.mqh>
Although the hypercube can process an arbitrary number of dimensions, for simplicity let us limit them to three now. This means that the user can use up to 3 selectors at the same time. Define the supported selector types using the elements of the special enumeration:
enum SELECTORS { SELECTOR_NONE, // none SELECTOR_TYPE, // type SELECTOR_SYMBOL, // symbol SELECTOR_SERIAL, // ordinal SELECTOR_MAGIC, // magic SELECTOR_PROFITABLE, // profitable /* custom selector */ SELECTOR_DURATION, // duration in days /* all the next require a field as parameter */ SELECTOR_WEEKDAY, // day-of-week(datetime field) SELECTOR_DAYHOUR, // hour-of-day(datetime field) SELECTOR_HOURMINUTE, // minute-of-hour(datetime field) SELECTOR_SCALAR, // scalar(field) SELECTOR_QUANTS // quants(field) };
Use the enumeration to describe the input parameters which set the selectors:
sinput string X = "————— X axis —————"; input SELECTORS SelectorX = SELECTOR_SYMBOL; input TRADE_RECORD_FIELDS FieldX = FIELD_NONE /* field does matter only for some selectors */; sinput string Y = "————— Y axis —————"; input SELECTORS SelectorY = SELECTOR_NONE; input TRADE_RECORD_FIELDS FieldY = FIELD_NONE; sinput string Z = "————— Z axis —————"; input SELECTORS SelectorZ = SELECTOR_NONE; input TRADE_RECORD_FIELDS FieldZ = FIELD_NONE;
Each selector group contains an input for setting the optional record field (some of the selectors require the fields, others do not).
Let us specify one filter (although multiple filters can be used). The filter will be disabled by default.
sinput string F = "————— Filter —————"; input SELECTORS Filter1 = SELECTOR_NONE; input TRADE_RECORD_FIELDS Filter1Field = FIELD_NONE; input float Filter1value1 = 0; input float Filter1value2 = 0;
The idea of the filter: take into account only those records in which the specified Filter1Field field has the specific Filter1value1 value (Filter1value2 must be the same, which is required for the creation of the Filter object in this example). Keep in mind that the value for symbol or magic number fields denotes an index in the corresponding vocabulary. The filter can optionally include not one value, but a range of values between Filter1value1 and Filter1value2 (if they are not equal, since the FilterRange object can only be created for two different values). This implementation has been created for the demonstration of the filtering possibility, while it can be greatly expanded for future practical usage.
Let us describe another enumeration for the aggregators:
enum AGGREGATORS { AGGREGATOR_SUM, // SUM AGGREGATOR_AVERAGE, // AVERAGE AGGREGATOR_MAX, // MAX AGGREGATOR_MIN, // MIN AGGREGATOR_COUNT, // COUNT AGGREGATOR_PROFITFACTOR, // PROFIT FACTOR AGGREGATOR_PROGRESSIVE, // PROGRESSIVE TOTAL AGGREGATOR_IDENTITY // IDENTITY };
It will be used in a group of input parameters which describe the working aggregator:
sinput string A = "————— Aggregator —————"; input AGGREGATORS AggregatorType = AGGREGATOR_SUM; input TRADE_RECORD_FIELDS AggregatorField = FIELD_PROFIT_AMOUNT;
All the selectors including those used in the optional filter are initialized in OnInit.
int selectorCount; SELECTORS selectorArray[4]; TRADE_RECORD_FIELDS selectorField[4]; int OnInit() { selectorCount = (SelectorX != SELECTOR_NONE) + (SelectorY != SELECTOR_NONE) + (SelectorZ != SELECTOR_NONE); selectorArray[0] = SelectorX; selectorArray[1] = SelectorY; selectorArray[2] = SelectorZ; selectorArray[3] = Filter1; selectorField[0] = FieldX; selectorField[1] = FieldY; selectorField[2] = FieldZ; selectorField[3] = Filter1Field; EventSetTimer(1); return(INIT_SUCCEEDED); }
OLAP is run only once, by timer.
void OnTimer() { process(); EventKillTimer(); } void process() { HistoryDataAdapter history; Analyst<TRADE_RECORD_FIELDS> *analyst; Selector<TRADE_RECORD_FIELDS> *selectors[]; ArrayResize(selectors, selectorCount); for(int i = 0; i < selectorCount; i++) { selectors[i] = createSelector(i); } Filter<TRADE_RECORD_FIELDS> *filters[]; if(Filter1 != SELECTOR_NONE) { ArrayResize(filters, 1); Selector<TRADE_RECORD_FIELDS> *filterSelector = createSelector(3); if(Filter1value1 != Filter1value2) { filters[0] = new FilterRange<TRADE_RECORD_FIELDS>(filterSelector, Filter1value1, Filter1value2); } else { filters[0] = new Filter<TRADE_RECORD_FIELDS>(filterSelector, Filter1value1); } } Aggregator<TRADE_RECORD_FIELDS> *aggregator; // MQL does not support a 'class info' metaclass. // Otherwise we could use an array of classes instead of the switch switch(AggregatorType) { case AGGREGATOR_SUM: aggregator = new SumAggregator<TRADE_RECORD_FIELDS>(AggregatorField, selectors, filters); break; case AGGREGATOR_AVERAGE: aggregator = new AverageAggregator<TRADE_RECORD_FIELDS>(AggregatorField, selectors, filters); break; case AGGREGATOR_MAX: aggregator = new MaxAggregator<TRADE_RECORD_FIELDS>(AggregatorField, selectors, filters); break; case AGGREGATOR_MIN: aggregator = new MinAggregator<TRADE_RECORD_FIELDS>(AggregatorField, selectors, filters); break; case AGGREGATOR_COUNT: aggregator = new CountAggregator<TRADE_RECORD_FIELDS>(AggregatorField, selectors, filters); break; case AGGREGATOR_PROFITFACTOR: aggregator = new ProfitFactorAggregator<TRADE_RECORD_FIELDS>(AggregatorField, selectors, filters); break; case AGGREGATOR_PROGRESSIVE: aggregator = new ProgressiveTotalAggregator<TRADE_RECORD_FIELDS>(AggregatorField, selectors, filters); break; case AGGREGATOR_IDENTITY: aggregator = new IdentityAggregator<TRADE_RECORD_FIELDS>(AggregatorField, selectors, filters); break; } LogDisplay display; analyst = new Analyst<TRADE_RECORD_FIELDS>(history, aggregator, display); analyst.acquireData(); Print("Symbol number: ", TradeRecord::getSymbolCount()); for(int i = 0; i < TradeRecord::getSymbolCount(); i++) { Print(i, "] ", TradeRecord::getSymbol(i)); } Print("Magic number: ", TradeRecord::getMagicCount()); for(int i = 0; i < TradeRecord::getMagicCount(); i++) { Print(i, "] ", TradeRecord::getMagic(i)); } Print("Filters: ", aggregator.getFilterTitles()); Print("Selectors: ", selectorCount); analyst.build(); analyst.display(); delete analyst; delete aggregator; for(int i = 0; i < selectorCount; i++) { delete selectors[i]; } for(int i = 0; i < ArraySize(filters); i++) { delete filters[i].getSelector(); delete filters[i]; } }
The auxiliary createSelector function is defined as follows:
Selector<TRADE_RECORD_FIELDS> *createSelector(int i) { switch(selectorArray[i]) { case SELECTOR_TYPE: return new TypeSelector(); case SELECTOR_SYMBOL: return new SymbolSelector(); case SELECTOR_SERIAL: return new SerialNumberSelector(); case SELECTOR_MAGIC: return new MagicSelector(); case SELECTOR_PROFITABLE: return new ProfitableSelector(); case SELECTOR_DURATION: return new DaysRangeSelector(15); // up to 14 days case SELECTOR_WEEKDAY: return selectorField[i] != FIELD_NONE ? new WeekDaySelector(selectorField[i]) : NULL; case SELECTOR_DAYHOUR: return selectorField[i] != FIELD_NONE ? new DayHourSelector(selectorField[i]) : NULL; case SELECTOR_HOURMINUTE: return selectorField[i] != FIELD_NONE ? new DayHourSelector(selectorField[i]) : NULL; case SELECTOR_SCALAR: return selectorField[i] != FIELD_NONE ? new TradeSelector(selectorField[i]) : NULL; case SELECTOR_QUANTS: return selectorField[i] != FIELD_NONE ? new QuantizationSelector(selectorField[i]) : NULL; } return NULL; }
All the classes except for DaysRangeSelector are imported from the header file, while DaysRangeSelector is described inside the OLAPDEMO Expert Advisor as follows:
class DaysRangeSelector: public DateTimeSelector<TRADE_RECORD_FIELDS> { public: DaysRangeSelector(const int n): DateTimeSelector<TRADE_RECORD_FIELDS>(FIELD_DURATION, n) { _typename = typename(this); } virtual bool select(const Record *r, int &index) const override { double d = r.get(selector); int days = (int)(d / (60 * 60 * 24)); index = MathMin(days, granularity - 1); return true; } virtual string getLabel(const int index) const override { return index < granularity - 1 ? ((index < 10 ? " ": "") + (string)index + "D") : ((string)index + "D+"); } };
This is the custom selector implementation example. It groups trading positions by their lifetime in the market, in days.
If you run the EA on any online account and select 2 selectors, SymbolSelector and WeekDaySelector, you can receive the following results in logs:
Analyzing account history Symbol number: 5 0] FDAX 1] XAUUSD 2] UKBrent 3] NQ 4] EURUSD Magic number: 1 0] 0 Filters: no Selectors: 2 SumAggregator<TRADE_RECORD_FIELDS> FIELD_PROFIT_AMOUNT [35] X: SymbolSelector(FIELD_SYMBOL) [5] Y: WeekDaySelector(FIELD_DATETIME2) [7] ... 0.000: FDAX Monday 0.000: XAUUSD Monday -20.400: UKBrent Monday 0.000: NQ Monday 0.000: EURUSD Monday 0.000: FDAX Tuesday 0.000: XAUUSD Tuesday 0.000: UKBrent Tuesday 0.000: NQ Tuesday 0.000: EURUSD Tuesday 23.740: FDAX Wednesday 4.240: XAUUSD Wednesday 0.000: UKBrent Wednesday 0.000: NQ Wednesday 0.000: EURUSD Wednesday 0.000: FDAX Thursday 0.000: XAUUSD Thursday 0.000: UKBrent Thursday 0.000: NQ Thursday 0.000: EURUSD Thursday 0.000: FDAX Friday 0.000: XAUUSD Friday 0.000: UKBrent Friday 13.900: NQ Friday 1.140: EURUSD Friday ...
Five symbols were traded on the account. The hypercube size: 35 cells. All the combinations of symbols and days of the week are shown along with the corresponding profit/loss amount. Please note that WeekDaySelector requires an explicit indication of the field, since each position has two dates, open date (FIELD_DATETIME1) and close date (FIELD_DATETIME2). Here we selected FIELD_DATETIME2.
In order to analyze not only the current account history, but also arbitrary trading reports in the HTML format, as well as CSV files with MQL5 Signals history, methods from my previous article ( Extracting structured data from HTML pages using CSS selectors and How to visualize multicurrency trading history based on HTML and CSV reports) were added to the OLAP library. Additional layer classes have been written to integrate them with OLAP. In particular, the header file HTMLcube.mqh contains the trade record class HTMLTradeRecord and the HTMLReportAdapter which is inherited from the DataAdapter. The header file CSVcube.mqh accordingly contains the record class CSVTradeRecord and the CSVReportAdapter. HTML reading is provided by WebDataExtractor.mqh, while CSV is read by CSVReader.mqh. Input parameters for report downloading and general principles of working with the reports (including the selection of suitable symbols in case prefixes and suffixes are used) are described in detail in the second article mentioned above.
Here are the Signal analyzing results (a CSV file). We used an aggregator by the profit factor and a breakdown by symbols. The results are sorted in the descending order:
Reading csv-file ***.history.csv 219 records transferred to 217 trades Symbol number: 8 0] GBPUSD 1] EURUSD 2] NZDUSD 3] USDJPY 4] USDCAD 5] GBPAUD 6] AUDUSD 7] NZDJPY Magic number: 1 0] 0 Filters: no Selectors: 1 ProfitFactorAggregator<TRADE_RECORD_FIELDS> FIELD_PROFIT_AMOUNT [8] X: SymbolSelector(FIELD_SYMBOL) [8] [value] [title] [0] inf "NZDJPY" [1] inf "AUDUSD" [2] inf "GBPAUD" [3] 7.051 "USDCAD" [4] 4.716 "USDJPY" [5] 1.979 "EURUSD" [6] 1.802 "NZDUSD" [7] 1.359 "GBPUSD"
The inf value is generated in the source code, when there are profits and no losses. As you can see, the comparison of real values and their sorting is done in such a way that the "infinity" is greater than any other finite numbers.
Of course, viewing the trading report analysis results in logs is not very convenient. A better solution is to have a Display interface
implementation, which can present the hypercube in a visual graphical form. Despite its apparent simplicity, the task requires
preparatory steps and a large amount of routine coding. Therefore we will consider it in the second part of the article.
Conclusions
The article outlines a well-known approach for the online analysis of big data (OLAP) as applied to the history of trading operations. Using MQL, we implemented the basic classes which enable the generation of a virtual hypercube based on selected variables (selectors), as well as the generation of various aggregated values on their bases. This mechanism can also be applied to process optimization results, to select trading signals according to selected criteria and in other areas where the large data amount requires the utilization of knowledge extraction algorithms for decision making.
Attached files:
- Experts/OLAP/OLAPDEMO.mq5 — a demo Expert Advisor;
- Include/OLAP/OLAPcube.mqh — the main header file with the OLAP classes;
- Include/OLAP/PairArray.mqh — the array of [value;name] pairs with support for all sorting variants;
- Include/OLAP/HTMLcube.mqh — combining OLAP with data loaded from HTML reports;
- Include/OLAP/CSVcube.mqh — combining OLAP with data loaded from CSV files;
- Include/MT4orders.mqh — the MT4orders library for working with orders in a single style both in МТ4 and in МТ5;
- Include/Marketeer/WebDataExtractor.mqh — the HTML parser;
- Include/Marketeer/empty_strings.h — the list of empty HTML tags;
- Include/Marketeer/HTMLcolumns.mqh — definition of column indexes in HTML reports;
- Include/Marketeer/CSVReader.mqh — the CSV parser;
- Include/Marketeer/CSVcolumns.mqh — definition of column indexes in CSV reports;
- Include/Marketeer/IndexMap.mqh — an auxiliary header file which implements an array with a key- and index-based combined access;
- Include/Marketeer/RubbArray.mqh — an auxiliary header file with the "rubber" array;
- Include/Marketeer/TimeMT4.mqh — an auxiliary header file which implements data processing functions in the MetaTrader 4 style;
- Include/Marketeer/Converter.mqh — an auxiliary header file for converting data types;
- Include/Marketeer/GroupSettings.mqh — an auxiliary header file which contains group settings of input parameters.
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/6602
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Applying OLAP in trading (part 2): Visualizing the interactive multidimensional data analysis results
Applying OLAP in trading (part 2): Visualizing the interactive multidimensional data analysis results
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
nothing is missing, i.e. it is not clear at all what the article is about. Here, one should have a certain understanding of the laws of emptiness that, having given up abstract reasoning, would formulate his concrete claims to emptiness.
topics directly related to TC are interesting, research. Personally.
Year 15 and 17. Two articles. And you complain that not enough people write about trading. I say fill the gap, if there is demand and desire.
What's stopping you from doing it? That's the question.
Yes, I have two articles about trading.
By the way, according to English-speaking readers, my article "How to reduce risks..." is among the top ten (at least 60 thousand readers in several languages is not a bad result).
I mean that it is better to write 2 articles that will help many people in developing a trading system, than 100 articles about libraries that give almost nothing for algorithmic trading.
Market dynamics is extremely complex (it is a non-stationary process), that's why I am surprised by programmes, in which 1 line is market analysis and 1000 lines are code of dubious services.
I am sure that the goal of the resource ( www.mql5.com, which is definitely the #1 resource in the industry) is to popularise algorithmic trading, not programming for programming's sake.
I'm attaching an example of simple wrapper for OLAP classes. The wrapper can be embedded into your EA to analyse instantly trading history at the end of a single pass in the tester.
To choose required analytical sections (selectors) and type of aggregation, the wrapper can be used in EA's OnDeinit, something like this:
OLAP is usefull for splitting data by some attributes, which are not provided by standard tester report (for example, profits by symbols, duration, etc).
All dependencies (required header files) can be found in the article. Slightly updated OLAPcube.mqh and Converter.mqh are attached as well.