
What Is a Martingale?
It is difficult to say why the word martingale has so many meanings. But one thing is doubtless: If a trader uses martingale strategy, it is always critical for his or her deposit. What are advantages and disadvantages of martingale betting strategy? How can one catch spliking in one's strategy? Is the market martingale? All these and some other closely related and interrelated questions will be discussed in this present article.
Etymology
Martingale is English for martegal (French dialiect word meaning inhabitant of Martigues; Martigues is - or was - a village in France). The oldest meaning of martingale seems to be is a piece of tack used on horses to control head carriage. This meaning is, at least, the best known one, but another meaning is more important for us: martingale is a betting strategy. The gambler doubles his bet after every loss, so that the first win would recover all previous losses plus win a profit equal to the original stake. Traders give this name to all related strategies, as well. Mathematicians, besides, use the term of martingale to name a stochastic process in which the conditional expectation of the next value, given the current and preceding values, is the current value. It is a kind of "fair game" where nobody wins and nobody loses. As to that French village, Martigues, its inhabitants were considered to be eccentric and probably venturesome. Anyway, this multitude of meanings is sometimes the reason why some people use it in a wrong way. So, what is martingale?
Martingale as a Strategy
on red at table five. … It seems that he is persevering and plays in maximums.”
Ian Fleming, Casino Royale
So what progressive system did Bond use? As mentioned before, martingale means doubling of the initial stake when lost in a gambling game, for example, in roulette. At the first glance, this strategy, if there are no limitations on the stake, seems to be profitable. One must be lucky one day! However, the world is not overcrowded with those who became rich using roulette, though the strategy seems to be elementary. So what is the matter? Eventually, if even we have not an unlimited amount of money, we can hold out rather long having strated with a small stake!
This or similar logic guides unwise people in their urge to try such a strategy on their whole money. But not on roulette, not at all! Some people are educated in such a way that they do not go in for games of chance. They try it on Forex. Those more intelligent and adventurous often try it on somebody else's money, too. So the new-made quack trader starts playing. Profitable trades alternate with losing ones, but the gamer earns money for some time due to doubling of the stake. This makes the trader to believe in his or her choice. However, earlier or later (for the trader's health, it is better if it happens earlier…) the streak of bad luck becomes so long that there is no money for another doulbing of stake. As a result, one more unfortunate appears in the vast expanses of the internet. An unhappy trader who "had come short of money near to the victory" and who "had been beaten by pure mischance". It is good if not "because the broker gave false quotes".
To be serious, there should not be many traders who buy into classical martingale. One should not underestimate stupidity of some knights of fortune, though. More intricate means are used that can be generally called 'spiking'. The following is meant here. Suppose you are proposed to choose: gain 1 dollar with the probability of 99% or lose 99 dollars with the probability of 1%. The mean result of this trade will equal to zero, of course. Generally, it is unprofitable and risky! Insignificant profits will be compensated with disastrous losses and disturbances (this is why the word 'spiking' is used here). It is extremely easy to make such a trade on Forex: You will obtain something like this if you place StopLoss at the level which is 99 times more than TakeProfit. Is it unrealistic? But what can we say about lots of those trading with StopLoss incommensurate to TakeProfit or even (how terrible!) without it at all?
Of course, the main harm is not the above. Imagine: Somebody wants to test or monitor such an "expert". How many profitable trades will be made, in the most cases, before one great losing trade carries the trader off? And how long he will cry then about his "misfortune" and "come short of money at the last moment"!
However, the matter is not only that there are no stop orders. The inseparable companion of spiking and no stops is overstaying the position. Within this time, the price sometimes runs very far away.
But "grail" experts based on martingale appear again and again and many discuss this trading method on forums quite seriously. Why? Strategies playing with incommensurate stops, doubled lots, overstaying, and other tricks of the kind turn to be tested шт an absolutely unreliable way. It is known from practical experience that such a strategy can easily be fabricated for the specific history and then gives charming results. Used on a real account, this strategy can work for a week, a month, a year, make 10, 20 or 50 trades and give good/excellent results with a bit of luck. And then the only wrong trade will carry them off. So what joins these strategies?
Martingale as a Process
the basic definitions are inspired by crude notions of gambling,
but the theory has become a sophisticated tool of modern abstract mathematics..."
J.L. Doob, What Is a Martingale?
Actually, mathematicians have known martingale for not very long time. Its first mathematical descriptions were published towards the middle of the 20th century. The creators were inspired by the wish to generalize the notion of "fair play", like roulette without commissions, or dice, or pitch-farthing, which we will consider later in this article. So many different definitions of the martingale process can be found in the vast expances of the net! The formal definition will not help, though, if one does not master a rather serious theoretical apparatus. Thus, we will try to give a simple but rather rigorous definition here: Martingale is a process that, in the mean, does not do up or down with the time. So, if we want to predict the next value basing on all preceding values, there will no better value than the current one (in terms of mean-square values).
It must be said that the question about whether or not the currency exchange rate fluctuations approach to the martingale is essential. Statistical observations, though, would sooner give a negative answer to this question. For example, currency rate increments are anticorrelated. This presupposition underlies many classical and neoclassic models (Bachelier, Black-Sholes-Merton, …) and allows drawing the far-reaching conclusions about behavior of derivatives (options, forwards, …). Besides, martingale terminology fits well into the concept of effective market that "fairly" defines the price at every instant. So it is economically reasonable.
One of the cornerstones of the martingale theory is the theorem on stopping and further contruction of stochastic integral. The theorem states that no reasonable strategy can help to earn money using martingale. How so? a serious-minded reader will ask. What's the matter with martingale strategy? Why does the theorem discard it as an "unreasonable"? The matter is that the most reasonable strategies are limited either in price (to be clearer, in FX terms, stop orders are placed) or in time, i.e., the horizon is fixed, at reaching of which we surely close the trade. The most important thing is that they all are limited in stake (volumes, amounts of lots per trade, etc.). Any strategy that satisfies one of the two first conditions and the third one is always "reasonable". Many other strategies are "reasonable", too, but we do not want to get into technical details now. Martingale strategy has three disadvantages: first, unlimited stakes; second, unlimited time, and, finally, the "martingaling" player will suffer huge drawdowns. This example shows very well that one cannot earn anything using this method since stakes and playing time are limited. It also helps to understand that a "profitable" strategy can be simulated in even an innocent game!
However, let us come down to earth and illustrate all the above theory with some simple examples.
Example
And green of life the golden tree."
J.W. Goethe, Faust
English translation by B. Taylor
Let us consider a pitch-farthing game with a well-balanced coin, i.e., a coin, for which probability of heads is the same as probability of tails. Let player B pay player A one ruble if it is heads and A pays B one ruble if it is tails. Below are exemplary evolutions of the A's capital depending on the amount of tosses made (Fig.1) – chance paths (blue and red).
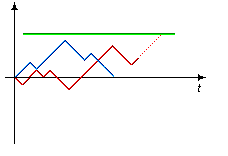
Fig. 1
On average, players do not gain or lose when tossing a coin, in the sense that one of them - we don't know which one - will surely gain a ruble and another one will lose a ruble. Mathematical expectation of changes in their capitals equals to zero. This, together with independent coin tossing, states that player A' capital growth is a martingale. This allows making many conclusions at the same time. For example, a conclusion about that this game is fair, in the sense it is not possible to earn statistically in this game, i.e., average of any stopping strategy will be zero. Let our player to play with a fixed amount of lots bearing in mind the martingale consequences. The theory states that he will not be able to earn money using any reasonable method. How so? you might say. The player can wait until he is "in the black" and just stop playing (green "takeprofit" level in Fig. 1). Yes, but unfortunately, though this event will take place some time, he will have to wait for it very long on average. Strictly speaking, mathematical expectancy of winning time is equal to infinity what does not fit into the "reasonable strategy" concept. Moreover, if he still decides to "sit" losses out, his drawdowns will be disastrous when he finally stops. This situation is often observed at beginning traders.
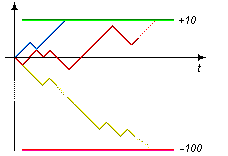
Fig. 2
But our player is not so simple! According to all mentioned above, he placed a "large" stoploss and a "little" takeprofit, as shown in Fig. 2. Now limited in capital, his strategy has become "reasonable". When he tries to experiment, the strategy grows hand over fist within a long time, especially for there are no commissions in pitch-farthing. So what is the matter? Can it be true that the theorem is incorrect? No, it remains valid! Just, if you use the theorem to calculate carefully, for example, takeprofit or stoploss probability, it will turn out that nothing more than spiking is realized since short takeprofit is used in 9 cases of 10 while huge stoploss is in only 1 case of 10. Such "postponing" of risks can be costly for the player - he will lose everything one day.
Primitive as it is, the pitch-farthing example still reveals hidden agendas of a risky money management or of the martingale strayegy. In fact, we just add pure risk to our position, nothing else.Thus, let us summarize all the above.
Conclusions
Everything would be ok, but the market, as was mentioned above, is not a martingale. And eventually, what is the whole point of forex trading but an attempt to earn money? So what boots all those theoretical observations for the real trading? The point is that, even in case of theoretical impossibility to earn something as in our example with the chance path, there are more ways to deceive oneself or an observer by providing a "profitable" (at least, at the first glance) strategy. No wonder that the same strategies are used to hourly create "grails" and ensnare investors. But one can escape many illusions keeping in mind the martingale/spiking theory.
Let us now formulate some rules of rational trading based on this article. So, if you don't want your system to be fudged with history, suffer huge drawdowns and raise doubts of potential investors, follow the rules below:
- place stops (stoplosses/takeprofits);
- try to make your stoploss proportioned to the takeprofit and timeframe;
- do not overstay your position out of proportion to the trading timeframe – it can be "cut" by the time elapsed since the trade began or in another way, there are many methods, in this case;
- do not increase the amount of lots trying to recoup – do not assimilate with those who play an all-or-nothing game in casinos (neither assimilate with that Bond)!
The rules above are not strict. The most of strategies are built in such a way that, for example, positions are not cancelled by stoploss or takeprofit at all. It must be said that here we can go to the average profitable or losing trade, for instance, or relate the amount of lots with the would-be risk level of the trade. However, the above rules should be considered as a kind of ideal for clarity and transparency of the Expert Advisor specifically and of the strategy generally. A trader, especially a beginner, should be aiming at this ideal.
The last thing I would like to put for the interested reader is the problem dating back to Daniel Bernoulli and the 18th century. It is the so-called St. Petersburg paradox. Suppose X is playing such a game: 1 ruble is at stake. A well-balanced coin is tossed. If it is heads, the game will be stopped and X will take the stake. If it is tails, the stake will be doubled, and so on: toss a coin, heads stop the game and take money, tails - double the stake and toss again... Question: How much should X pay to play this game? As it can be seen, X always wins in this game, but different amounts of money depending on what the coin says. In other words, how much would YOU pay to participate in this attraction of generosity without example? If this problem excites the curiosity, its solution will be discussed in comments.
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/1446
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Effective Averaging Algorithms with Minimal Lag: Use in Indicators
Effective Averaging Algorithms with Minimal Lag: Use in Indicators
 Testing Visualization: Manual Trading
Testing Visualization: Manual Trading
 MQL4 as a Trader's Tool, or The Advanced Technical Analysis
MQL4 as a Trader's Tool, or The Advanced Technical Analysis
 Testing Visualization: Functionality Enhancement
Testing Visualization: Functionality Enhancement
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
try to make an indicator use 'your martingale' , so no money needed
Then you can make a moving average on the equity/balance of this 'martingale strategy' .
If this indi, up then your martingale is "in line", you can use this sta
Martingale system is risky but till now its famous strategy to create EA.
Thanks for the article.