PreCogniTrade

PreCogniTrade: Ein fortschrittlicher technischer Indikator zur Vorhersage des Marktes (Beta-Phase)

PreCogniTrade ist ein revolutionärer technischer Indikator, der für Trader entwickelt wurde, die einen Wettbewerbsvorteil auf den Finanzmärkten suchen. Dieser Indikator analysiert nicht nur aktuelle Trends, sondern sagt auch zukünftige Kursbewegungen mit unheimlicher Genauigkeit voraus, was ihn zu einem unschätzbaren Werkzeug für jede Handelsstrategie macht.

Hauptmerkmale:

• 
  
• Vorhersage zukünftiger Bewegungen: Verwendet komplexe Algorithmen und prädiktive Analysen, um Marktbewegungen vorherzusehen, bevor sie eintreten.
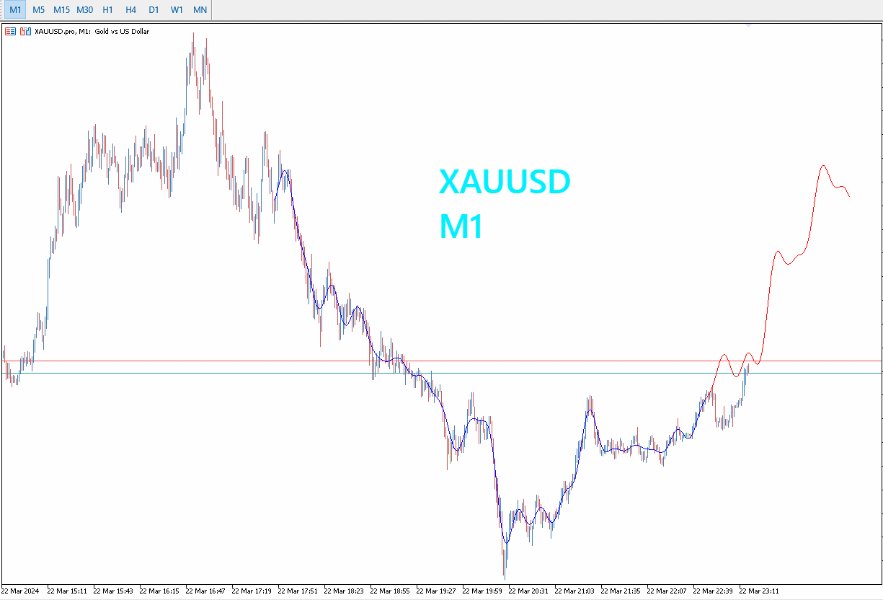
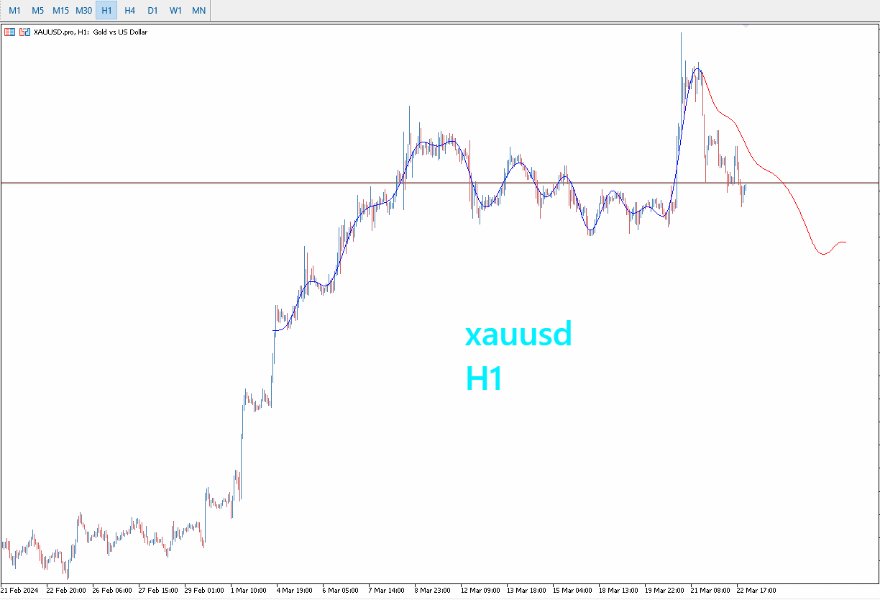
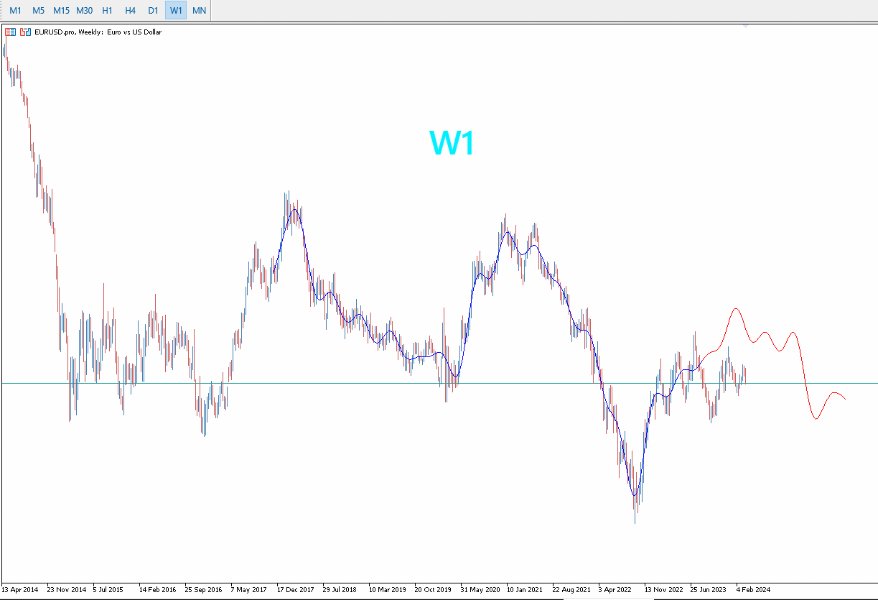
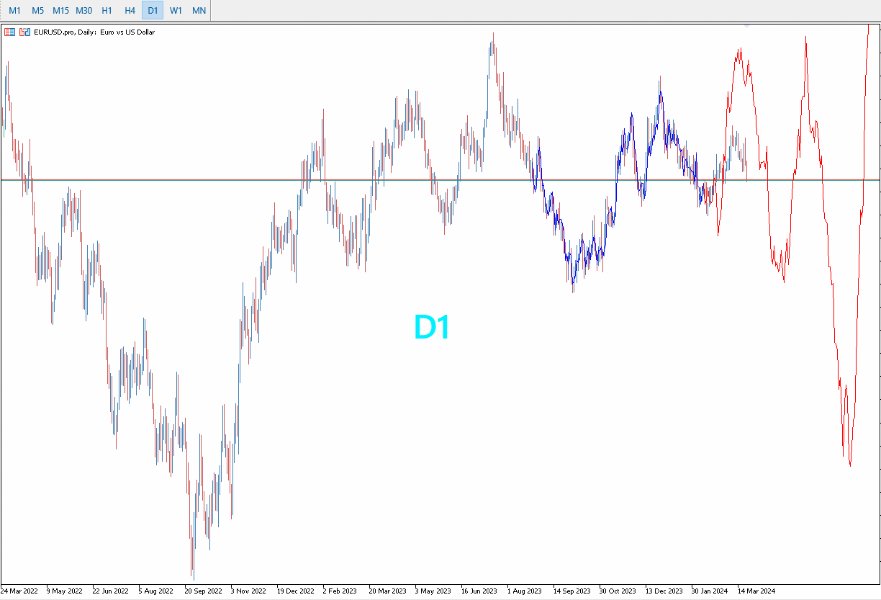
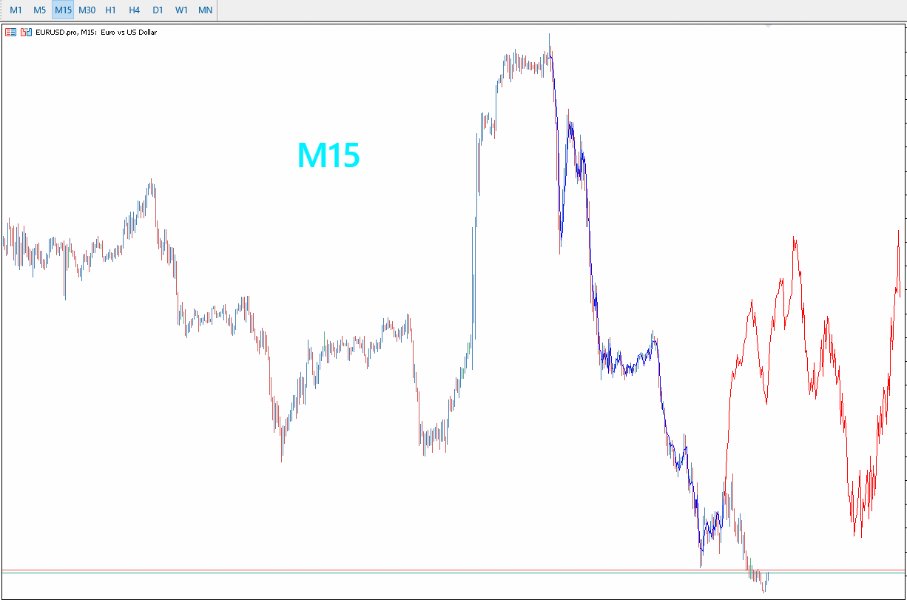
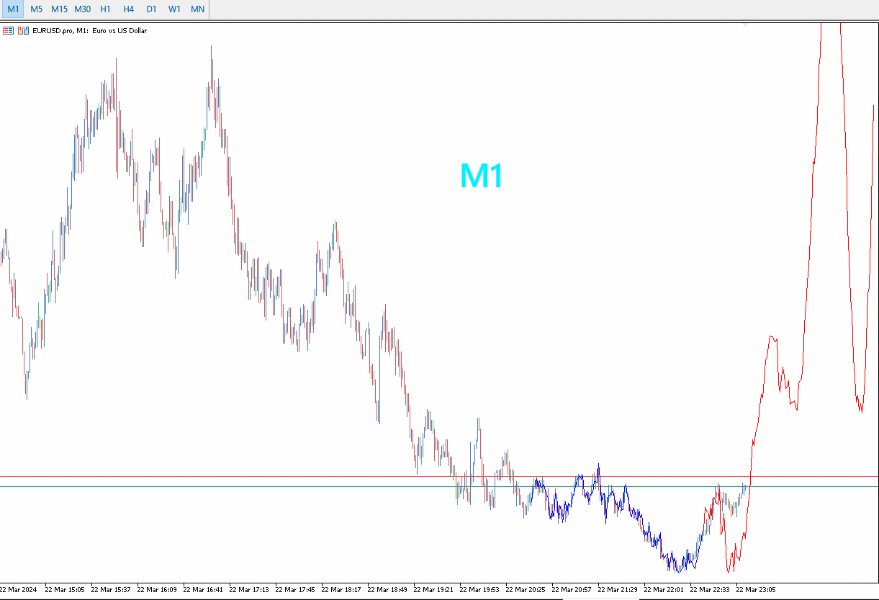
• Optimiert für längere Zeitrahmen: PreCogniTrade glänzt besonders bei längeren Zeitrahmen, wo die Vorhersagen stabiler und zuverlässiger sind.
• Dynamische Visualisierung: Zeichnet die wahrscheinliche Kursbewegung mit ihren Impulsen und Rücksetzern, so dass Händler ihre Trades klarer visualisieren und planen können.
• Komplexe Formeln: Von allen Indikatoren in meinem Arsenal enthält PreCogniTrade die komplexesten Formeln, die eine Vielzahl von technischen und quantitativen Faktoren für eine genaue Vorhersage integrieren.

Die Bedeutung von PreCogniTrade liegt in seiner Fähigkeit, Händlern tiefe Einblicke in das künftige Marktverhalten zu geben und ihnen so zu ermöglichen, fundierte und proaktive Entscheidungen zu treffen. Mit diesem Indikator können Händler ihre Strategien an die erwarteten Marktbewegungen anpassen und so ihre Erfolgschancen maximieren und das Risiko minimieren.

Zusammenfassend lässt sich sagen, dass PreCogniTrade ein unverzichtbares Instrument ist, das die Art und Weise, wie Händler mit den Finanzmärkten interagieren, verändert und eine einzigartige Perspektive bietet, die über die traditionelle technische Analyse hinausgeht. Seine Implementierung über längere Zeiträume stellt sicher, dass Händler sich auf seine Signale verlassen können, um intelligentere und profitablere Handelsentscheidungen zu treffen.

Die Extrapolationsmethode ist ein statistisches Verfahren, das zur Schätzung zukünftiger oder unbekannter Werte auf der Grundlage bekannter Daten verwendet wird. Sie ist besonders nützlich bei der Zeitreihenanalyse und der geografischen Analyse, da sie die Auswirkungen zeitlicher und räumlicher Faktoren auf die Daten berücksichtigen kann.

Wie funktioniert die Extrapolation?

Bei der Extrapolation wird eine bekannte Folge von Werten über den beobachteten Bereich hinaus verlängert. Wenn Sie z. B. Verkaufsdaten für die letzten zwei Jahre haben, können Sie die Extrapolation nutzen, um die Verkäufe des nächsten Jahres vorherzusagen.

Gängige Extrapolationsmethoden:

- Lineare Extrapolation: Verwendet eine lineare Gleichung zur Vorhersage künftiger Ergebnisse. Sie eignet sich für Vorhersagen, die nahe an den bekannten Daten liegen.

- Polynomielle Extrapolation: Verwendet eine polynomielle Gleichung, um Vorhersagen zu treffen. Sie wird verwendet, wenn Datenpunkte einen nicht linearen Trend aufweisen, und kann genauere Vorhersagen liefern.

Es ist zu beachten, dass die Extrapolation mit Unsicherheiten und Risiken behaftet ist, da sie auf der Annahme beruht, dass sich vergangene Trends in der Zukunft fortsetzen werden. Daher sollten die Ergebnisse mit Vorsicht interpretiert werden, und es ist ratsam, die Extrapolation in Verbindung mit anderen Analysetechniken und kontextbezogenen Überlegungen anzuwenden.

Die Autokorrelationsmethode ist eine statistische Technik, die die Korrelation eines Signals mit sich selbst über verschiedene Zeitintervalle hinweg misst. Das heißt, sie bewertet die Ähnlichkeit zwischen den Beobachtungen einer Variablen in Abhängigkeit von der zeitlichen Verzögerung zwischen ihnen.

Wie funktioniert die Autokorrelation? Die Autokorrelation vergleicht ein Signal mit einer verzögerten Kopie seiner selbst, um sich wiederholende Muster oder das Vorhandensein eines periodischen Signals zu erkennen, das möglicherweise durch Rauschen verdeckt wird. Sie wird auch verwendet, um die fehlende Grundfrequenz eines Signals zu ermitteln, die durch seine harmonischen Frequenzen impliziert wird.

Anwendungen der Autokorrelation:

Zeitreihenanalyse: Bei der Zeitreihenanalyse kann die Autokorrelation periodische Muster und Trends in den Daten aufdecken.

Signalverarbeitung: In der Signalverarbeitung wird die Autokorrelation zur Analyse von Funktionen oder Wertereihen verwendet, z. B. von Signalen im Zeitbereich.

ARMA- und ARIMA-Modelle: In der Ökonometrie ist die Autokorrelation eine Schlüsselkomponente der Modelle des autoregressiven gleitenden Durchschnitts (ARMA) und des autoregressiven integrierten gleitenden Durchschnitts (ARIMA), die für die Analyse und Vorhersage von Wirtschaftsdaten verwendet werden.

Die Autokorrelation kann positiv oder negativ sein und ihr Wert schwankt zwischen -1 und 1. Eine positive Autokorrelation zeigt an, dass auf einen beobachteten Anstieg in einem Zeitintervall tendenziell ein Anstieg im verzögerten Zeitintervall folgt. Eine negative Autokorrelation deutet hingegen darauf hin, dass auf einen Anstieg ein Rückgang folgt.

Es ist wichtig, daran zu denken, dass die Autokorrelation nur ein Analyseinstrument ist und in Verbindung mit anderen Methoden verwendet werden sollte, um ein vollständigeres Verständnis der Daten zu erhalten.

Die gewichtete Burg-Methode ist eine fortgeschrittene Technik der Spektralanalyse, die zu den autoregressiven (AR) Schätzmethoden gehört. Diese Technik wird verwendet, um die Schätzung des Spektrums eines Signals zu verbessern, insbesondere bei der Arbeit mit begrenzten oder verrauschten Daten.

Merkmale der gewichteten Burg-Methode:

- Minimierung des Vorhersagefehlers: schätzt AR-Koeffizienten durch Minimierung eines gewichteten Maßes der linearen Vorwärts- und Rückwärtsvorhersagefehler.

- Datenadaptive Gewichtung: Verwendet Gewichte, die proportional zur gemeinsamen Energie der Vorwärts- und Rückwärtsprozessrealisierungen sind, was zu einer stabilen Filterdarstellung führt.

- Verbesserte spektrale Leistung: Im Vergleich zu anderen gewichteten Burg-Verfahren weist die gewichtete Burg-Methode Verbesserungen bei der Frequenzverzerrung und Auflösung auf.

Diese Methode ist besonders nützlich in Bereichen wie der Signalverarbeitung und der Ökonometrie, wo eine genaue Spektralschätzung erforderlich ist, um das zukünftige Verhalten auf der Grundlage historischer Daten zu analysieren und vorherzusagen. Obwohl es sich um ein leistungsfähiges Werkzeug handelt, ist es wichtig, es in Verbindung mit anderen Analysetechniken einzusetzen, um robustere und zuverlässigere Ergebnisse zu erhalten.

Die Burg-Methode mit Helme-Nikkias-Gewichtungsfunktionen ist eine fortgeschrittene Variante der traditionellen Burg-Methode, die zur Schätzung der spektralen Leistung verwendet wird. Dieser Ansatz kombiniert die Burg-Methode, die für ihre hohe Auflösung bei kurzen Datensätzen und für die Erstellung eines stabilen Modells bekannt ist, mit Helme-Nikkias-Gewichtungsfunktionen, um die Genauigkeit der Spektralschätzung zu verbessern.

Die traditionelle Burg-Methode passt ein autoregressives (AR) Modell an das Signal an, indem sie die Vorwärts- und Rückwärtsvorhersagefehler im Sinne der kleinsten Quadrate minimiert. Helme-Nikkias-Gewichtungsfunktionen werden angewandt, um die Daten im AR-Modellanpassungsprozess unterschiedlich zu gewichten, was besonders nützlich sein kann, wenn es sich um Signale mit nicht-stationären Eigenschaften handelt oder wenn bestimmte Teile des Signals gegenüber anderen hervorgehoben werden sollen.

Die Kombination dieser Techniken ermöglicht eine robustere und genauere Spektralschätzung, was bei Anwendungen wie der Signalanalyse und der Echtzeit-Datenverarbeitung von Vorteil ist. Es ist jedoch zu beachten, dass die Ergebnisse, wie bei jeder Schätzungsmethode, mit Vorsicht und im Kontext des in den Daten vorhandenen Signals und Rauschens interpretiert werden müssen.

Die Itakura-Saito-Methode, auch bekannt als Itakura-Saito-Abstand, ist eine Technik zur Messung der Differenz zwischen einem Originalspektrum und einer Annäherung an dieses Spektrum. Obwohl es sich nicht um ein Wahrnehmungsmaß handelt, ist es so konzipiert, dass es die Wahrnehmungs(un)ähnlichkeit widerspiegelt. Sie wurde von Fumitada Itakura und Shuzo Saito in den 1960er Jahren vorgeschlagen.

Die Itakura-Saito-Distanz ist als Bregman-Divergenz definiert, die durch die negative logarithmische Funktion erzeugt wird, aber sie ist keine echte Metrik, da sie nicht symmetrisch ist und die Dreiecksungleichung nicht erfüllt. Im Zusammenhang mit der Faktorisierung nichtnegativer Matrizen kann die Itakura-Saito-Divergenz als Maß für die Faktorisierungsqualität verwendet werden, die ein aussagekräftiges statistisches Modell der Komponenten voraussetzt und durch ein iteratives Verfahren gelöst werden kann.

Diese Methode ist besonders nützlich bei der Spektralanalyse und wird häufig in Anwendungen wie der Signalverarbeitung und der Echtzeitdatenanalyse eingesetzt. Die Entscheidung, den Itakura-Saito-Abstand anstelle anderer Maße zu verwenden, beruht auf seiner Fähigkeit, eine genauere Schätzung des Spektrums zu liefern, insbesondere in Situationen, in denen die Daten begrenzt oder mit Rauschen verunreinigt sein können.

Die modifizierte Kovarianzmethode ist ein Verfahren zur Spektralschätzung, das zur Analyse der Leistungsspektraldichte (PSD) eines Signals verwendet wird. Diese Methode passt ein autoregressives (AR) Modell an das Signal an, indem die Vorwärts- und Rückwärtsvorhersagefehler im Sinne der kleinsten Quadrate minimiert werden.

Hauptmerkmale der modifizierten Kovarianzmethode:

- AR-Schätzung: Passt ein autoregressives Modell durch Minimierung der Vorhersagefehler an.

- Fehlerminimierung: Minimiert die Vorwärts- und Rückwärtsprognosefehler.

- Modellstabilität: Erzeugt immer ein stabiles Modell, was für die Zuverlässigkeit der Spektralschätzung entscheidend ist.

- Hohe Auflösung: Bietet eine hohe Auflösung für kurze Datensätze, was in Situationen, in denen die Datenmenge begrenzt ist, von Vorteil ist.

Diese Methode ist in der Signalverarbeitung und Echtzeitdatenanalyse weit verbreitet und bietet ein robustes Werkzeug für die Schätzung des Leistungsspektrums in verschiedenen Anwendungen.