
Leistungsfähige adaptive Indikatoren - Theorie und Umsetzung in MQL5
Einleitung
Dieser Beitrag stützt sich auf zwei hervorragende Werke von John F. Ehlers: „Raketenwissenschaft für Börsenhändler“ (Rocket Science for Traders) und „Kybernetische Analyse für Wertpapiere und Terminkontrakte“ (Сybernetic Analysis for Stock and Futures). Der ungewöhnliche Marktanalyseansatz mithilfe von Verfahren der digitalen Signalverarbeitung und der Anwendung komplexer Zahlen zur Ermittlung von Marktabläufen hat mich genötigt, mich in dieses Thema einzuarbeiten und in der Folge drei von John F. Ehlers eingeführte adaptive Indikatoren in MQL5 umzusetzen.
In diesem Beitrag werden die theoretischen Grundlagen adaptiver Indikatoren und ihrer Umsetzung in der Programmiersprache MQL5 behandelt. Außerdem werden die adaptiven Indikatoren ihren nicht anpassungsfähigen Entsprechungen gegenübergestellt.
Die Verwendung von komplexen Zahlen und Phasenvektoren zur Messung von Marktzyklen
Einige Begriffe aus der Theorie der komplexen Zahlen mögen für Leser ohne technischen Hintergrund verblüffend erscheinen, deshalb empfehle ich diesen, sich vor der Lektüre dieses Beitrages auf Wikipedia mit der Theorie vertraut zu machen und sich eine Einführung in den Umgang mit komplexen Zahlen anzusehen.
Der Phasenvektor
Bei dem auch als Phasor bezeichneten Phasenvektor handelt es sich um einen Vektor, der die Amplitude und die Phase eines periodischen Ablaufs (Zyklus) angibt. Gemäß der Eulerschen Formel kann eine komplexe Zahl (bestehend aus einem Real- und einem Imaginärteil) in einer Form abgebildet werden, in der ein Winkel als Argument in der Phase erscheint. Das ermöglicht die anschauliche Darstellung periodischer Abläufe (Zyklen). Die Abbildung unten beinhaltet eine Animation, die die Rotation des Phasenvektors der Sinuskurve abbildet.
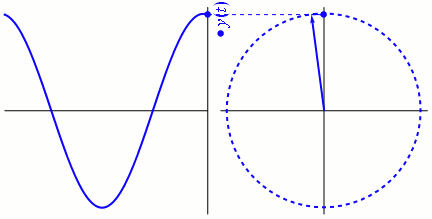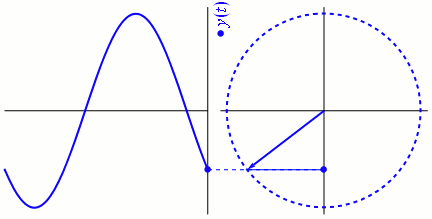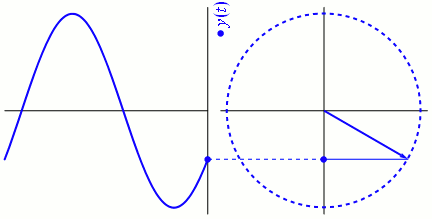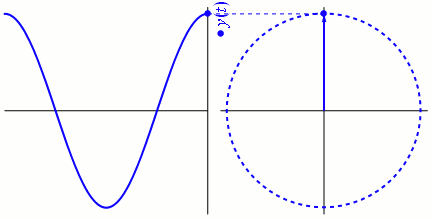
Mag sein, dass sich beim ersten Anblick dieser Animation die Frage aufdrängt, in welcher Beziehung der Phasenvektor zum Ablauf steht. Zum Verständnis ist es besser, den periodischen Ablauf als den rechts abgebildeten rotierenden Phasenvektor zu betrachten und nicht in Form der üblichen Sinuskurve links.
Ich stelle mir das folgendermaßen vor: die volle Umdrehung des Phasenvektors um 360° (oder einen ![]() -Radian) ist über den gesamten Zyklus identisch. Der jeweils aktuelle Winkel des Phasenvektors zeigt an, in welchem Teil des Zyklus (welcher Phase) wir uns befinden. Die y-Achse bildet die Amplitude des periodischen Ablaufs ab.
-Radian) ist über den gesamten Zyklus identisch. Der jeweils aktuelle Winkel des Phasenvektors zeigt an, in welchem Teil des Zyklus (welcher Phase) wir uns befinden. Die y-Achse bildet die Amplitude des periodischen Ablaufs ab.
Der Phasenvektor kann in zwei Bestandteile aufgegliedert werden: InPhase (Kosinus) und Quadratur (Sinus). Eine ausführliche Darstellung der Ermittlung dieser Bestandteile liefert Kapitel 6 „Die Hilbert-Transformationen“ in „Raketenwissenschaft für Börsenhändler“ (Rocket Science for Traders). Dieses Kapitel lege ich allen ans Herz, die sich eingehender damit befassen möchten.
Momentan kommt es für uns lediglich darauf an, dass wir zur Berechnung der adaptiven Indikatoren ein Signal (in Wellenform) in ein aus zwei Bestandteilen zusammengesetztes komplexes Signal umwandeln müssen. Wie erreichen wir das? Habe ich die Hilbert-Transformation bereits erwähnt? Ja tatsächlich. Genau das vermag die Hilbert-Transformation zu tun.
Die Messung der Laufzeit des Zyklus
Zur praktischen Anwendung der Hilbert-Transformation hat John Ehlers sie in seinem Buch in eine Reihe aus vier Einzelbestandteilen zerlegt.
Der Ausdruck für den „Quadratur“-Bestandteil lautet wie folgt:
![]()
und der Bestandteil InPhase ist der um drei Balken verzögerte Kurs:
![]()
Nach der Berechnung der Bestandteile InPhase und Quadratur (wie wir wissen, sind das eigentlich der Real- und der Imaginärteil einer komplexen Zahl) können wir die Phasenverschiebung zwischen dem aktuellen und dem vorherigen Balken berechnen. Bei dem aktuellen Balken ist die Phase gleich ![]() , für den vorhergehenden ist sie gleich
, für den vorhergehenden ist sie gleich ![]() . Unter Verwendung der trigonometrischen Gleichung:
. Unter Verwendung der trigonometrischen Gleichung:
![]()
erhalten wir den Ausdruck für die als DeltaPhase bezeichnete differenzielle Phase.
Dem Wert der Variablen DeltaPhase hat Ehlers zusätzliche Beschränkungen auferlegt: sie darf nicht negativ sein und ist auf das Intervall 0,1; 1,1 beschränkt (das entspricht einer Zykluslänge von 6 bis 63 Balken). Es hat sich gezeigt, dass DeltaPhase für reale Daten nicht glatt aussieht, was eine Glättung erforderlich macht.
Das beste Verfahren für die Glättung von Daten mit Ausreißern (spiky data) ist ein Medianfilter, weshalb eine Median-Glättung über fünf DeltaPhase-Daten angewendet wird, deren Ergebnis in die Variable MedianDelta eingeht. Der durch ![]() dividierte MedianDelta-Wert wird im Weiteren zur Berechnung der Laufzeit des Hauptzyklus (Dominant Cycle), nach dem wir gesucht haben, verwendet.
dividierte MedianDelta-Wert wird im Weiteren zur Berechnung der Laufzeit des Hauptzyklus (Dominant Cycle), nach dem wir gesucht haben, verwendet.
Während der Berechnung hat sich gezeigt, dass bei der Messung eine Verschiebung um etwa 0,5 vorliegt, die beseitigt werden muss, weshalb die Rechenformel um ein entsprechendes Glied erweitert wurde. Zu guter Letzt wird der berechnete Wert für den Dominant Cycle mithilfe des EMA mit den Werten Alpha = 0,33 bzw. = 0,1 zwei Mal geglättet. Ich empfehle dringend die Lektüre des Buches „Raketenwissenschaft für Börsenhändler“ (s. A. o.), das eine Veranschaulichung der Belastbarkeit des Algorithmus am Beispiel eines sinusartigen Signals bietet, dessen Laufzeit schrittweise von 6 auf 40 heraufgesetzt wird.
Ausgestattet mit dem theoretischen Rüstzeug sind wir jetzt bereit für die Umsetzung des Laufzeitindikators CyclePeriod in MQL5.
Indikator der Laufzeit des Zyklus (CyclePeriod Indicator)
Der Indikator besteht aus zwei Linien: der „cycle“-Linie, die die Laufzeit des Zyklus anzeigt, sowie der Signallinie („trigger“), bei der es sich üblicherweise um die um einen Balken verzögerte „cycle“-Linie handelt. Angesichts der im vorhergehenden Abschnitt gelieferten Beschreibung und des Quellcodes in der Funktion OnCalculate() ist leicht zu verstehen, welchen Linien die Messung der Laufzeit des Zyklus obliegt.
//+------------------------------------------------------------------+ //| CyclePeriod.mq5 | //| Copyright 2011, Investeo.pl | //| http://Investeo.pl | //+------------------------------------------------------------------+ #property copyright "Copyright 2011, Investeo.pl" #property link "http://Investeo.pl" #property version "1.00" #property indicator_separate_window #property description "CyclePeriod indicator - described by John F. Ehlers" #property description "in \"Cybernetic Analysis for Stocks and Futures\"" #property indicator_buffers 2 #property indicator_plots 2 #property indicator_width1 1 #property indicator_width2 1 #property indicator_type1 DRAW_LINE #property indicator_type2 DRAW_LINE #property indicator_color1 Green #property indicator_color2 Red #property indicator_label1 "Cycle" #property indicator_label2 "Trigger Line" #define Price(i) ((high[i]+low[i])/2.0) double Smooth[]; double Cycle[]; double Trigger[]; //double Price[]; double Q1[]; // Quadrature component double I1[]; // InPhase component double DeltaPhase[]; double InstPeriod[]; double CyclePeriod[]; input double InpAlpha=0.07; // alpha //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping ArraySetAsSeries(Cycle,true); ArraySetAsSeries(CyclePeriod,true); ArraySetAsSeries(Trigger,true); ArraySetAsSeries(Smooth,true); //ArraySetAsSeries(Price,true); SetIndexBuffer(0,CyclePeriod,INDICATOR_DATA); SetIndexBuffer(1,Trigger,INDICATOR_DATA); PlotIndexSetDouble(0,PLOT_EMPTY_VALUE,0.0); PlotIndexSetDouble(1,PLOT_EMPTY_VALUE,0.0); return(0); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { //--- long tickCnt[1]; int i; int ticks=CopyTickVolume(Symbol(), 0, 0, 1, tickCnt); if(ticks!=1) return(rates_total); double DC, MedianDelta; Comment(tickCnt[0]); if(prev_calculated==0 || tickCnt[0]==1) { //--- last counted bar will be recounted int nLimit=rates_total-prev_calculated-1; // start index for calculations ArraySetAsSeries(high,true); ArraySetAsSeries(low,true); ArrayResize(Smooth,Bars(_Symbol,_Period)); ArrayResize(Cycle,Bars(_Symbol,_Period)); //ArrayResize(Price,Bars(_Symbol,_Period)); ArrayResize(CyclePeriod,Bars(_Symbol,_Period)); ArrayResize(InstPeriod,Bars(_Symbol,_Period)); ArrayResize(Q1,Bars(_Symbol,_Period)); ArrayResize(I1,Bars(_Symbol,_Period)); ArrayResize(DeltaPhase,Bars(_Symbol,_Period)); if (nLimit>rates_total-7) // adjust for last bars nLimit=rates_total-7; for(i=nLimit;i>=0 && !IsStopped();i--) { Smooth[i] = (Price(i)+2*Price(i+1)+2*Price(i+2)+Price(i+3))/6.0; if (i<rates_total-7) { Cycle[i] = (1.0-0.5*InpAlpha) * (1.0-0.5*InpAlpha) * (Smooth[i]-2.0*Smooth[i+1]+Smooth[i+2]) +2.0*(1.0-InpAlpha)*Cycle[i+1]-(1.0-InpAlpha)*(1.0-InpAlpha)*Cycle[i+2]; } else { Cycle[i]=(Price(i)-2.0*Price(i+1)+Price(i+2))/4.0; } Q1[i] = (0.0962*Cycle[i]+0.5769*Cycle[i+2]-0.5769*Cycle[i+4]-0.0962*Cycle[i+6])*(0.5+0.08*InstPeriod[i+1]); I1[i] = Cycle[i+3]; if (Q1[i]!=0.0 && Q1[i+1]!=0.0) DeltaPhase[i] = (I1[i]/Q1[i]-I1[i+1]/Q1[i+1])/(1.0+I1[i]*I1[i+1]/(Q1[i]*Q1[i+1])); if (DeltaPhase[i] < 0.1) DeltaPhase[i] = 0.1; if (DeltaPhase[i] > 0.9) DeltaPhase[i] = 0.9; MedianDelta = Median(DeltaPhase, i, 5); if (MedianDelta == 0.0) DC = 15.0; else DC = (6.28318/MedianDelta) + 0.5; InstPeriod[i] = 0.33 * DC + 0.67 * InstPeriod[i+1]; CyclePeriod[i] = 0.15 * InstPeriod[i] + 0.85 * CyclePeriod[i+1]; Trigger[i] = CyclePeriod[i+1]; } } //--- return value of prev_calculated for next call return(rates_total); } //+------------------------------------------------------------------+ double Median(double& arr[], int idx, int m_len) { double MedianArr[]; int copied; double result = 0.0; ArraySetAsSeries(MedianArr, true); ArrayResize(MedianArr, m_len); copied = ArrayCopy(MedianArr, arr, 0, idx, m_len); if (copied == m_len) { ArraySort(MedianArr); if (m_len %2 == 0) result = (MedianArr[m_len/2] + MedianArr[(m_len/2)+1])/2.0; else result = MedianArr[m_len / 2]; } else Print(__FILE__+__FUNCTION__+"median error - wrong number of elements copied."); return result; }
Wir können ihn überprüfen, indem wir ihn mit einem beliebigen Diagramm verknüpfen, er funktioniert mit jedem Kürzel und in jedem Zeitraum
(s. Abb.).
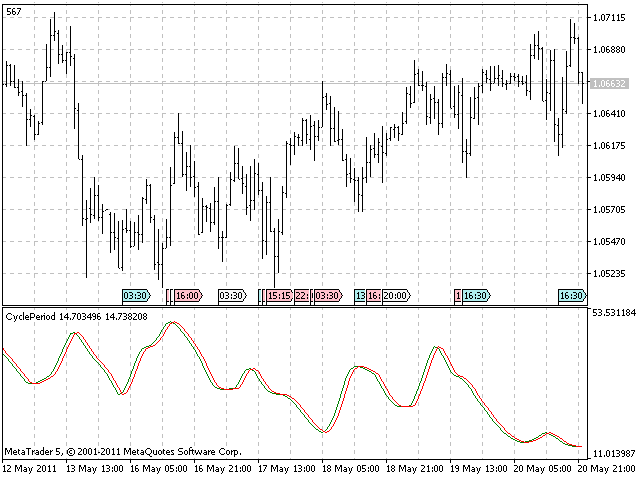
Mithilfe dieses Indikators kann eine neue Generation adaptiver Indikatoren umgesetzt werden, Indikatoren, die sich auf den jeweils aktuellen Zeitraum der Marktentwicklung einstellen.
Der Indikator CyberCycle
Bei dem Indikator CyberCycle handelt es sich um einen Hochfrequenzfilter aus dem Buch „Kybernetische Analyse für Wertpapiere und Terminkontrakte“ (Сybernetic analysis for stocks and futures). Dieser Filter lässt lediglich einen Bestandteil eines Zeitreihendurchlaufs übrig.
Darüber hinaus werden die zwei- bzw. dreibalkigen Bestandteile des Zyklus durch Glättung des Ergebnisses mittels eines Niederfrequenzfilters mit begrenztem Ansprechen auf einen Impuls aus diesem entfernt.
Der Programmcode für diesen und weitere Indikatoren des hier vorliegenden Beitrags wurde auf der Grundlage der in dem Buch vorgestellten Indikatoren aus der Programmiersprache EFL (Tradestation) in MQL5 übersetzt.
//+------------------------------------------------------------------+ //| CyberCycle.mq5 | //| Copyright 2011, Investeo.pl | //| http://Investeo.pl | //+------------------------------------------------------------------+ #property copyright "Copyright 2011, Investeo.pl" #property link "http://Investeo.pl" #property version "1.00" #property indicator_separate_window #property description "CyberCycle indicator - described by John F. Ehlers" #property description "in \"Cybernetic Analysis for Stocks and Futures\"" #property description "This indicator is available for free download." #property indicator_buffers 2 #property indicator_plots 2 #property indicator_width1 1 #property indicator_width2 1 #property indicator_type1 DRAW_LINE #property indicator_type2 DRAW_LINE #property indicator_color1 Green #property indicator_color2 Red #property indicator_label1 "Cycle" #property indicator_label2 "Trigger Line" #define Price(i) ((high[i]+low[i])/2.0) double Smooth[]; double Cycle[]; double Trigger[]; input double InpAlpha=0.07; // alpha //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping ArraySetAsSeries(Cycle,true); ArraySetAsSeries(Trigger,true); ArraySetAsSeries(Smooth,true); SetIndexBuffer(0,Cycle,INDICATOR_DATA); SetIndexBuffer(1,Trigger,INDICATOR_DATA); PlotIndexSetDouble(0,PLOT_EMPTY_VALUE,0.0); PlotIndexSetDouble(1,PLOT_EMPTY_VALUE,0.0); return(0); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { //--- long tickCnt[1]; int i; int ticks=CopyTickVolume(Symbol(), 0, 0, 1, tickCnt); if(ticks!=1) return(rates_total); Comment(tickCnt[0]); if(prev_calculated==0 || tickCnt[0]==1) { //--- last counted bar will be recounted int nLimit=rates_total-prev_calculated-1; // start index for calculations ArraySetAsSeries(high,true); ArraySetAsSeries(low,true); ArrayResize(Smooth,Bars(_Symbol,_Period)); ArrayResize(Cycle,Bars(_Symbol,_Period)); if(nLimit>rates_total-4) // adjust for last bars nLimit=rates_total-4; for(i=nLimit;i>=0 && !IsStopped();i--) { Smooth[i]=(Price(i)+2*Price(i+1)+2*Price(i+2)+Price(i+3))/6.0; if(i<rates_total-5) { Cycle[i]=(1.0-0.5*InpAlpha) *(1.0-0.5*InpAlpha) *(Smooth[i]-2.0*Smooth[i+1]+Smooth[i+2]) +2.0*(1.0-InpAlpha)*Cycle[i+1]-(1.0-InpAlpha)*(1.0-InpAlpha)*Cycle[i+2]; } else { Cycle[i]=(Price(i)-2.0*Price(i+1)+Price(i+2))/4.0; } //Print(__FILE__+__FUNCTION__+" received values: ",rCnt); Trigger[i]=Cycle[i+1]; } } //--- return value of prev_calculated for next call return(rates_total); } //+------------------------------------------------------------------+
Eine Bildschirmaufnahme von dem Indikator folgt unten.
Sie haben womöglich bemerkt, dass alle Indikatoren dieses Beitrags ähnlich aussehen, dennoch unterscheiden sich die Algorithmen ihrer Umsetzung.
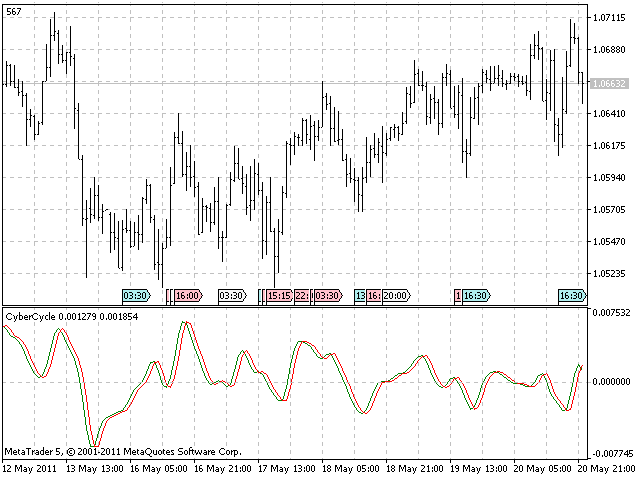
Der Handelsalgorithmus gemäß diesem Indikator ist simple: Kaufen, wenn die „cycle“-Linie die Signallinie von unten nach oben schneidet. Und folglich Verkaufen, wenn sie sie von oben nach unten schneidet. Ich schlage vor, dass Sie selbst eine Handelsstrategie auf der Grundlage dieses Indikators in einem Expert-System oder einem Handelssignalmodul umsetzen.
Der adaptive Indikator CyberCycle
Im Wesentlichen geht es in diesem Beitrag darum, zu verdeutlichen, wie wir Indikatoren anpassungsfähig (adaptiv) machen können, das heißt, wie wir sie mit einer dynamischen Zykluslaufzeit anstelle einer statischen berechnen können. Dazu müssen wir zum Auslesen der aktuellen Laufzeit des Zyklus eine Verknüpfung zu dem Indikator CyclePeriod herstellen und den ermittelten Wert im weiteren Verlauf in der Funktion OnCalculate() verwenden.
Zunächst benötigen wir die Bezeichnung (das Handle) für den Indikator:
hCyclePeriod=iCustom(NULL,0,"CyclePeriod",InpAlpha); if(hCyclePeriod==INVALID_HANDLE) { Print("CyclePeriod indicator not available!"); return(-1); }
und müssen anschließend in der Funktion OnCalculate() die Daten des Indikatorzwischenspeichers anfordern:
int copied=CopyBuffer(hCyclePeriod,0,i,1,CyclePeriod); if(copied<=0) { Print("FAILURE: Could not get values from CyclePeriod indicator."); return -1; } alpha1 = 2.0/(CyclePeriod[0]+1.0);
Der Wert „Alpha“ in der exponentiellen Glättung ist verbunden mit dem Zeitraum des einfachen gleitenden Durchschnittswertes „Length“ und zwar in dem Verhältnis ![]() . Zur Berechnung von „Alpha“ in dem adaptiven Indikator CyberCycle verwendet Ehlers den Zeitraum des „Dominant Cycle“ als Wert für „Length“.
. Zur Berechnung von „Alpha“ in dem adaptiven Indikator CyberCycle verwendet Ehlers den Zeitraum des „Dominant Cycle“ als Wert für „Length“.
Hier folgt der vollständige Programmcode für den Indikator:
//+------------------------------------------------------------------+ //| AdaptiveCyberCycle.mq5 | //| Copyright 2011, Investeo.pl | //| http://Investeo.pl | //+------------------------------------------------------------------+ #property copyright "Copyright 2011, Investeo.pl" #property link "http://Investeo.pl" #property version "1.00" #property indicator_separate_window #property description "Adaptive CyberCycle indicator - described by John F. Ehlers" #property description "in \"Cybernetic Analysis for Stocks and Futures\"" #property description "This indicator is available for free download." #property indicator_buffers 2 #property indicator_plots 2 #property indicator_width1 1 #property indicator_width2 1 #property indicator_type1 DRAW_LINE #property indicator_type2 DRAW_LINE #property indicator_color1 Green #property indicator_color2 Red #property indicator_label1 "Cycle" #property indicator_label2 "Trigger Line" #define Price(i) ((high[i]+low[i])/2.0) double Smooth[]; double Cycle[]; double Trigger[]; int hCyclePeriod; input double InpAlpha=0.07; // alpha for Cycle Period //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping ArraySetAsSeries(Cycle,true); ArraySetAsSeries(Trigger,true); ArraySetAsSeries(Smooth,true); SetIndexBuffer(0,Cycle,INDICATOR_DATA); SetIndexBuffer(1,Trigger,INDICATOR_DATA); PlotIndexSetDouble(0,PLOT_EMPTY_VALUE,0.0); PlotIndexSetDouble(1,PLOT_EMPTY_VALUE,0.0); hCyclePeriod=iCustom(NULL,0,"CyclePeriod",InpAlpha); if(hCyclePeriod==INVALID_HANDLE) { Print("CyclePeriod indicator not available!"); return(-1); } return(0); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { //--- long tickCnt[1]; int i; int ticks=CopyTickVolume(Symbol(), 0, 0, 1, tickCnt); if(ticks!=1) return(rates_total); double CyclePeriod[1],alpha1; Comment(tickCnt[0]); if(prev_calculated==0 || tickCnt[0]==1) { //--- last counted bar will be recounted int nLimit=rates_total-prev_calculated-1; // start index for calculations ArraySetAsSeries(high,true); ArraySetAsSeries(low,true); ArrayResize(Smooth,Bars(_Symbol,_Period)); ArrayResize(Cycle,Bars(_Symbol,_Period)); if(nLimit>rates_total-4) // adjust for last bars nLimit=rates_total-4; for(i=nLimit;i>=0 && !IsStopped();i--) { Smooth[i]=(Price(i)+2*Price(i+1)+2*Price(i+2)+Price(i+3))/6.0; int copied=CopyBuffer(hCyclePeriod,0,i,1,CyclePeriod); if(copied<=0) { Print("FAILURE: Could not get values from CyclePeriod indicator."); return -1; } alpha1 = 2.0/(CyclePeriod[0]+1.0); //Print(alpha1); //Print(CyclePeriod[0]); if(i>=0) { Cycle[i]=(1.0-0.5*alpha1) *(1.0-0.5*alpha1) *(Smooth[i]-2.0*Smooth[i+1]+Smooth[i+2]) +2.0*(1.0-alpha1)*Cycle[i+1]-(1.0-alpha1)*(1.0-alpha1)*Cycle[i+2]; //Print("Smooth["+IntegerToString(i)+"]="+DoubleToString(Smooth[i])+" Cycle["+IntegerToString(i)+"]="+DoubleToString(Cycle[i])); } else { Cycle[i]=(Price(i)-2.0*Price(i+1)+Price(i+2))/4.0; } //Print(__FILE__+__FUNCTION__+" received values: ",rCnt); Trigger[i]=Cycle[i+1]; } } //--- return value of prev_calculated for next call return(rates_total); } //+------------------------------------------------------------------+
So sieht eine Abbildung des Indikators aus:
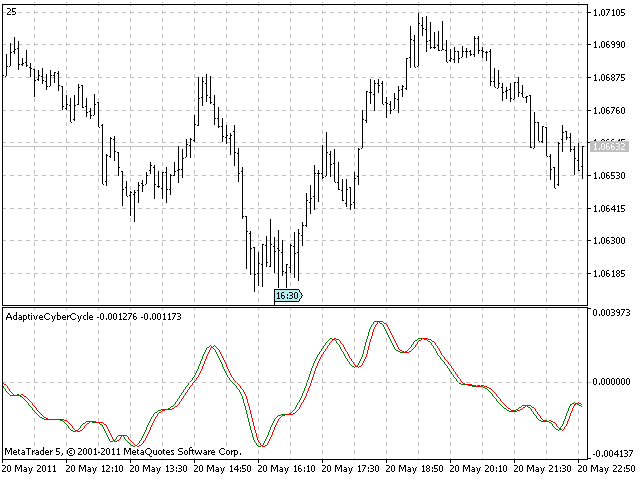
Damit ist unser erster adaptiver Indikator fertig! Laut Buch soll er empfindlicher sein als sein nicht anpassungsfähiges Pendant.
Häufig treten Kauf- und Verkaufssignale in einem Balken eher auf als bei der nicht adaptiven Variante.
Dasselbe können wir bei zwei weiteren Indikatoren wiederholen, was ausreichen sollte, um das allgemeine Muster zur Erstellung adaptiver Indikatoren zu veranschaulichen.
Der Schwerpunktindikator Center of Gravity
Unter dem Schwerpunkt (center of gravity) eines körperlichen Gegenstands versteht man dessen Gleichgewichtspunkt. Der Grundgedanke hier besteht darin, diesen Begriff auf der Grundlage des Verhältnisses der Größe der Verzögerung (lag) verschiedener Filter zu ihren jeweiligen Koeffizienten in den Börsenhandel einzuführen.
Bei dem einfachen gleitenden Durchschnittswert (SMA, Simple Moving Average) sind alle Koeffizienten gleich, der Schwerpunkt liegt in der Mitte.
Bei einem gewichteten gleitenden Durchschnittswert (WMA, Weighted Moving Average) haben die jüngsten Kurse mehr Gewicht als die älteren. Um genau zu sein: die WMA-Koeffizienten bezeichnen die Umrisse eines Dreiecks. Der Dreiecksschwerpunkt liegt bei einem Drittel der Länge der Basis des Dreiecks. Der allgemeine Ausdruck für die Schwerpunktberechnung bei dem vorliegenden Beobachtungsfenster sieht folgendermaßen aus:
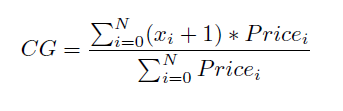
Die Lage des Gleichgewichtspunktes ergibt sich aus der Summe des Produkts der Verhältnisse der Kurse in dem Fenster zu dem jeweils entsprechenden Kurs (+1 wurde eingeführt da die Nummerierung von 0 bis N erfolgt und nicht von 1 bis N).
Das Hauptmerkmal des Indikators Center of Gravity (CG) besteht darin, dass er entlang der Schwingungen an- bzw. absteigt und im Grunde ein verzögerungsfreier Oszillator ist.
Der Programmcode und eine Bildschirmaufnahme
//+------------------------------------------------------------------+ //| CenterOfGravity.mq5 | //| Copyright 2011, Investeo.pl | //| http://Investeo.pl | //+------------------------------------------------------------------+ #property copyright "Copyright 2011, Investeo.pl" #property link "http://Investeo.pl" #property version "1.00" #property indicator_separate_window #property description "CG indicator - described by John F. Ehlers" #property description "in \"Cybernetic Analysis for Stocks and Futures\"" #property description "This indicator is available for free download." #property indicator_buffers 2 #property indicator_plots 2 #property indicator_width1 1 #property indicator_width2 1 #property indicator_type1 DRAW_LINE #property indicator_type2 DRAW_LINE #property indicator_color1 Green #property indicator_color2 Red #property indicator_label1 "Cycle" #property indicator_label2 "Trigger Line" #define Price(i) ((high[i]+low[i])/2.0) double Smooth[]; double Cycle[]; double Trigger[]; input double InpAlpha=0.07; // alpha input int InpCGLength=10; //CG window size //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping ArraySetAsSeries(Cycle,true); ArraySetAsSeries(Trigger,true); ArraySetAsSeries(Smooth,true); SetIndexBuffer(0,Cycle,INDICATOR_DATA); SetIndexBuffer(1,Trigger,INDICATOR_DATA); PlotIndexSetDouble(0,PLOT_EMPTY_VALUE,0.0); PlotIndexSetDouble(1,PLOT_EMPTY_VALUE,0.0); return(0); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { //--- long tickCnt[1]; int i; double Num, Denom; // Numerator and Denominator for CG int ticks=CopyTickVolume(Symbol(), 0, 0, 1, tickCnt); if(ticks!=1) return(rates_total); Comment(tickCnt[0]); if(prev_calculated==0 || tickCnt[0]==1) { //--- last counted bar will be recounted int nLimit=rates_total-prev_calculated-1; // start index for calculations ArraySetAsSeries(high,true); ArraySetAsSeries(low,true); ArrayResize(Smooth,Bars(_Symbol,_Period)); ArrayResize(Cycle,Bars(_Symbol,_Period)); if(nLimit>rates_total-InpCGLength) // adjust for last bars nLimit=rates_total-InpCGLength; for(i=nLimit;i>=0 && !IsStopped();i--) { Num = 0.0; Denom = 0.0; for (int count=0; count<InpCGLength; count++) { Num += (1.0+count)*Price(i+count); Denom += Price(i+count); } if (Denom != 0.0) Cycle[i] = -Num/Denom+(InpCGLength+1.0)/2.0; else Cycle[i] = 0.0; //Print(__FILE__+__FUNCTION__+" received values: ",rCnt); Trigger[i]=Cycle[i+1]; } } //--- return value of prev_calculated for next call return(rates_total); } //+------------------------------------------------------------------+
folgen unten: Bitte beachten Sie die geringfügige Verzögerung (lag).
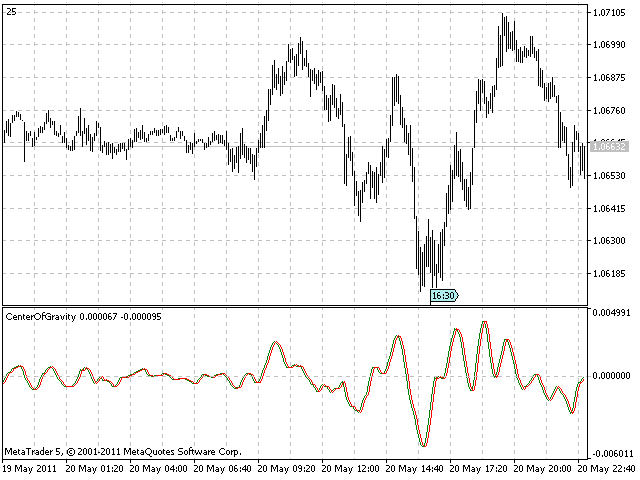
Adaptive Fassung des Schwerpunktindikators Center of Gravity
Der Oszillator Center of Gravity (CG) ermittelt den „Schwerpunkt“ der Daten eines Fensters von fest vorgegebener Breite. Der adaptive CG-Oszillator nutzt den Zeitraum des vorherrschenden Zyklus (Dominant Cycle) als Breite des dynamischen Fensters. Zur Ermittlung des Zeitraums des vorherrschenden Zyklus kommt folgender Code zum Einsatz:
copied=CopyBuffer(hCyclePeriod,0,i,1,CyclePeriod); if(copied<=0) { Print("FAILURE: Could not get values from CyclePeriod indicator."); return -1; } CG_len = floor(CyclePeriod[0]/2.0);
Der vollständige Quellcode des Indikators folgt unten; vergleichen Sie ihn bitte mit der nicht anpassungsfähigen Fassung sowie mit dem adaptiven Indikator CyberCycle.
//+------------------------------------------------------------------+ //| AdaptiveCenterOfGravity.mq5 | //| Copyright 2011, Investeo.pl | //| http://Investeo.pl | //+------------------------------------------------------------------+ #property copyright "Copyright 2011, Investeo.pl" #property link "http://Investeo.pl" #property version "1.00" #property indicator_separate_window #property description "Adaptive CG indicator - described by John F. Ehlers" #property description "in \"Cybernetic Analysis for Stocks and Futures\"" #property description "This indicator is available for free download." #property indicator_buffers 2 #property indicator_plots 2 #property indicator_width1 1 #property indicator_width2 1 #property indicator_type1 DRAW_LINE #property indicator_type2 DRAW_LINE #property indicator_color1 Green #property indicator_color2 Red #property indicator_label1 "Cycle" #property indicator_label2 "Trigger Line" #define Price(i) ((high[i]+low[i])/2.0) double Smooth[]; double Cycle[]; double Trigger[]; int hCyclePeriod; input double InpAlpha=0.07; // alpha //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping ArraySetAsSeries(Cycle,true); ArraySetAsSeries(Trigger,true); ArraySetAsSeries(Smooth,true); SetIndexBuffer(0,Cycle,INDICATOR_DATA); SetIndexBuffer(1,Trigger,INDICATOR_DATA); PlotIndexSetDouble(0,PLOT_EMPTY_VALUE,0.0); PlotIndexSetDouble(1,PLOT_EMPTY_VALUE,0.0); hCyclePeriod=iCustom(NULL,0,"CyclePeriod",InpAlpha); if(hCyclePeriod==INVALID_HANDLE) { Print("CyclePeriod indicator not available!"); return(-1); } return(0); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { //--- long tickCnt[1]; int i, copied; double Num,Denom; // Numerator and Denominator for CG double CG_len; int ticks=CopyTickVolume(Symbol(), 0, 0, 1, tickCnt); if(ticks!=1) return(rates_total); double CyclePeriod[1]; Comment(tickCnt[0]); if(prev_calculated==0 || tickCnt[0]==1) { //--- last counted bar will be recounted int nLimit=rates_total-prev_calculated-1; // start index for calculations ArraySetAsSeries(high,true); ArraySetAsSeries(low,true); ArrayResize(Smooth,Bars(_Symbol,_Period)); ArrayResize(Cycle,Bars(_Symbol,_Period)); copied=CopyBuffer(hCyclePeriod,0,0,1,CyclePeriod); if(copied<=0) { Print("FAILURE: Could not get values from CyclePeriod indicator."); return -1; } if(nLimit>rates_total-int(CyclePeriod[0])-2) // adjust for last bars nLimit=rates_total-int(CyclePeriod[0])-2; for(i=nLimit;i>=0 && !IsStopped();i--) { copied=CopyBuffer(hCyclePeriod,0,i,1,CyclePeriod); if(copied<=0) { Print("FAILURE: Could not get values from CyclePeriod indicator."); return -1; } CG_len = floor(CyclePeriod[0]/2.0); //Print("CG_len="+DoubleToString(CG_len)); Num=0.0; Denom=0.0; for(int count=0; count<int(CG_len); count++) { Num+=(1.0+count)*Price(i+count); Denom+=Price(i+count); } if(Denom!=0.0) Cycle[i]=-Num/Denom+(CG_len+1.0)/2.0; else Cycle[i]=0.0; //Print(__FILE__+__FUNCTION__+" received values: ",rCnt); Trigger[i]=Cycle[i+1]; } } //--- return value of prev_calculated for next call return(rates_total); } //+------------------------------------------------------------------+
Die folgende Abbildung zeigt eine Bildschirmaufnahme des Indikators AdaptiveCG:
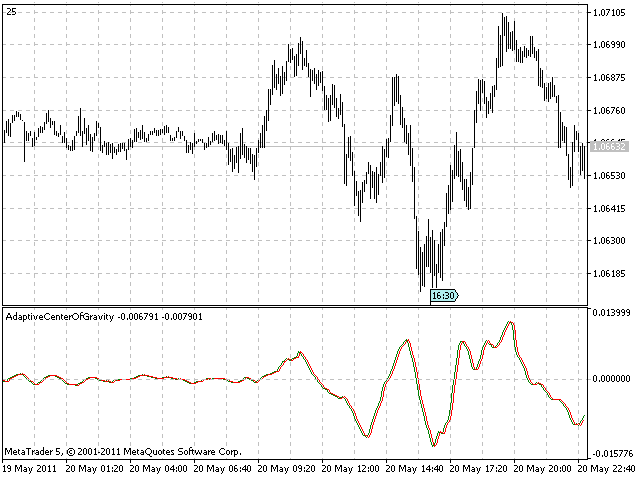
Der Indikator RVI
RVI steht für Relative Vigor Index (Index der relativen Kraft [der Dynamik]). Er beruht auf dem Umstand, dass bei einer Hausse der Schlusskurs gewöhnlich über dem Eröffnungskurs liegt, während sich dies bei einer Baisse umgekehrt verhält.
Die Kraft (Vigor) der Bewegung wird als das Verhältnis der Differenz aus Schluss- und Eröffnungskurs zur Kursspanne gemessen:
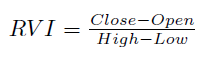
Dieser Indikator ist für zahlreiche Nutzer der MetaTrader-Instanz für Ausgabegeräte (Terminal) ein alter Bekannter, der jetzt zum Lieferumfang gehört.
Dennoch sei hier sein Code angeführt:
//+------------------------------------------------------------------+ //| RVI.mq5 | //| Copyright 2009, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2009, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property description "Relative Vigor Index" //--- indicator settings #property indicator_separate_window #property indicator_buffers 2 #property indicator_plots 2 #property indicator_type1 DRAW_LINE #property indicator_type2 DRAW_LINE #property indicator_color1 Green #property indicator_color2 Red #property indicator_label1 "RVI" #property indicator_label2 "Signal" //--- input parameters input int InpRVIPeriod=10; // Period //--- indicator buffers double ExtRVIBuffer[]; double ExtSignalBuffer[]; //--- #define TRIANGLE_PERIOD 3 #define AVERAGE_PERIOD (TRIANGLE_PERIOD*2) //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ void OnInit() { //--- indicator buffers mapping SetIndexBuffer(0,ExtRVIBuffer,INDICATOR_DATA); SetIndexBuffer(1,ExtSignalBuffer,INDICATOR_DATA); IndicatorSetInteger(INDICATOR_DIGITS,3); //--- sets first bar from what index will be drawn PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,(InpRVIPeriod-1)+TRIANGLE_PERIOD); PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,(InpRVIPeriod-1)+AVERAGE_PERIOD); //--- name for DataWindow and indicator subwindow label IndicatorSetString(INDICATOR_SHORTNAME,"RVI("+string(InpRVIPeriod)+")"); PlotIndexSetString(0,PLOT_LABEL,"RVI("+string(InpRVIPeriod)+")"); PlotIndexSetString(1,PLOT_LABEL,"Signal("+string(InpRVIPeriod)+")"); //--- initialization done } //+------------------------------------------------------------------+ //| Relative Vigor Index | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total,const int prev_calculated, const datetime &Time[], const double &Open[], const double &High[], const double &Low[], const double &Close[], const long &TickVolume[], const long &Volume[], const int &Spread[]) { int i,j,nLimit; double dValueUp,dValueDown,dNum,dDeNum; //--- check for bars count if(rates_total<=InpRVIPeriod+AVERAGE_PERIOD+2) return(0); // exit with zero result //--- check for possible errors if(prev_calculated<0) return(0); // exit with zero result //--- last counted bar will be recounted nLimit=InpRVIPeriod+2; if(prev_calculated>InpRVIPeriod+TRIANGLE_PERIOD+2) nLimit=prev_calculated-1; //--- set empty value for uncalculated bars if(prev_calculated==0) { for(i=0;i<InpRVIPeriod+TRIANGLE_PERIOD;i++) ExtRVIBuffer[i]=0.0; for(i=0;i<InpRVIPeriod+AVERAGE_PERIOD;i++) ExtSignalBuffer[i]=0.0; } //--- RVI counted in the 1-st buffer for(i=nLimit;i<rates_total && !IsStopped();i++) { dNum=0.0; dDeNum=0.0; for(j=i;j>i-InpRVIPeriod;j--) { dValueUp=Close[j]-Open[j]+2*(Close[j-1]-Open[j-1])+2*(Close[j-2]-Open[j-2])+Close[j-3]-Open[j-3]; dValueDown=High[j]-Low[j]+2*(High[j-1]-Low[j-1])+2*(High[j-2]-Low[j-2])+High[j-3]-Low[j-3]; dNum+=dValueUp; dDeNum+=dValueDown; } if(dDeNum!=0.0) ExtRVIBuffer[i]=dNum/dDeNum; else ExtRVIBuffer[i]=dNum; } //--- signal line counted in the 2-nd buffer nLimit=InpRVIPeriod+TRIANGLE_PERIOD+2; if(prev_calculated>InpRVIPeriod+AVERAGE_PERIOD+2) nLimit=prev_calculated-1; for(i=nLimit;i<rates_total && !IsStopped();i++) ExtSignalBuffer[i]=(ExtRVIBuffer[i]+2*ExtRVIBuffer[i-1]+2*ExtRVIBuffer[i-2]+ExtRVIBuffer[i-3])/AVERAGE_PERIOD; //--- OnCalculate done. Return new prev_calculated. return(rates_total); } //+------------------------------------------------------------------+
Die folgende Abbildung zeigt eine Bildschirmaufnahme des gewöhnlichen Indikators RVI mit einem voreingestellten Zeitraum von 10:
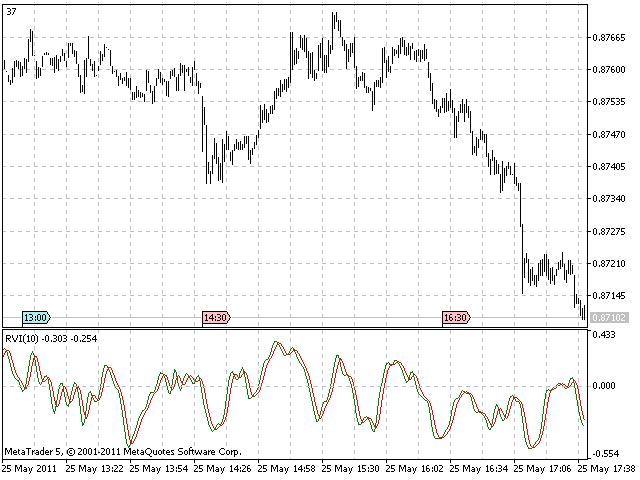
Der adaptive Indikator RVI
Wie bei den vorgenannten Indikatoren (oder genauer, bei deren anpassungsfähigen Varianten) müssen wir den Wert für den Dominant Cycle aus dem Indikator CyclePeriod beziehen und auf den Zeitraum des Indikators RVI anwenden. Die Variable „Length“ wird als gewichteter und über die letzten 4 Balken gemittelter gleitender Durchschnittswert des Zeitraums CyclePeriod berechnet:
copied=CopyBuffer(hCyclePeriod,0,0,4,CyclePeriod); if(copied<=0) { Print("FAILURE: Could not get values from CyclePeriod indicator."); return -1; } AdaptiveRVIPeriod = int(floor((4*CyclePeriod[0]+3*CyclePeriod[1]+2*CyclePeriod[2]+CyclePeriod[3])/20.0));
Unten folgt der vollständige Programmcode der anpassungsfähigen Ausführung des Indikators RVI:
//+------------------------------------------------------------------+ //| Adaptive RVI.mq5 | //| Based on RVI by MetaQuotes Software Corp. | //| Copyright 2009, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2009, MetaQuotes Software Corp." #property copyright "2011, Adaptive version Investeo.pl" #property link "https://www.mql5.com" #property description "Adaptive Relative Vigor Index" //--- indicator settings #property indicator_separate_window #property indicator_buffers 2 #property indicator_plots 2 #property indicator_type1 DRAW_LINE #property indicator_type2 DRAW_LINE #property indicator_color1 Green #property indicator_color2 Red #property indicator_label1 "AdaptiveRVI" #property indicator_label2 "Signal" #define Price(i) ((high[i]+low[i])/2.0) //--- input parameters input int InpRVIPeriod=10; // Initial RVI Period //--- indicator buffers double ExtRVIBuffer[]; double ExtSignalBuffer[]; //--- int hCyclePeriod; input double InpAlpha=0.07; // alpha for Cycle Period int AdaptiveRVIPeriod; #define TRIANGLE_PERIOD 3 #define AVERAGE_PERIOD (TRIANGLE_PERIOD*2) //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0,ExtRVIBuffer,INDICATOR_DATA); SetIndexBuffer(1,ExtSignalBuffer,INDICATOR_DATA); IndicatorSetInteger(INDICATOR_DIGITS,3); hCyclePeriod=iCustom(NULL,0,"CyclePeriod",InpAlpha); if(hCyclePeriod==INVALID_HANDLE) { Print("CyclePeriod indicator not available!"); return(-1); } //--- sets first bar from what index will be drawn PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,(InpRVIPeriod-1)+TRIANGLE_PERIOD); PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,(InpRVIPeriod-1)+AVERAGE_PERIOD); //--- name for DataWindow and indicator subwindow label IndicatorSetString(INDICATOR_SHORTNAME,"AdaptiveRVI"); PlotIndexSetString(0,PLOT_LABEL,"AdaptiveRVI"); PlotIndexSetString(1,PLOT_LABEL,"Signal"); //--- initialization done return 0; } //+------------------------------------------------------------------+ //| Relative Vigor Index | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total,const int prev_calculated, const datetime &Time[], const double &Open[], const double &High[], const double &Low[], const double &Close[], const long &TickVolume[], const long &Volume[], const int &Spread[]) { int i,j,nLimit; double dValueUp,dValueDown,dNum,dDeNum; double CyclePeriod[4]; int copied; copied=CopyBuffer(hCyclePeriod,0,0,4,CyclePeriod); if(copied<=0) { Print("FAILURE: Could not get values from CyclePeriod indicator."); return -1; } AdaptiveRVIPeriod = int(floor((4*CyclePeriod[0]+3*CyclePeriod[1]+2*CyclePeriod[2]+CyclePeriod[3])/20.0)); //--- check for bars count if(rates_total<=AdaptiveRVIPeriod+AVERAGE_PERIOD+2) return(0); // exit with zero result //--- check for possible errors if(prev_calculated<0) return(0); // exit with zero result //--- last counted bar will be recounted nLimit=AdaptiveRVIPeriod+2; if(prev_calculated>AdaptiveRVIPeriod+TRIANGLE_PERIOD+2) nLimit=prev_calculated-1; //--- set empty value for uncalculated bars if(prev_calculated==0) { for(i=0;i<AdaptiveRVIPeriod+TRIANGLE_PERIOD;i++) ExtRVIBuffer[i]=0.0; for(i=0;i<AdaptiveRVIPeriod+AVERAGE_PERIOD;i++) ExtSignalBuffer[i]=0.0; } //--- RVI counted in the 1-st buffer for(i=nLimit;i<rates_total && !IsStopped();i++) { copied=CopyBuffer(hCyclePeriod,0,rates_total-i-1,4,CyclePeriod); if(copied<=0) { Print("FAILURE: Could not get values from CyclePeriod indicator."); return -1; } AdaptiveRVIPeriod = int(floor((4*CyclePeriod[0]+3*CyclePeriod[1]+2*CyclePeriod[2]+CyclePeriod[3])/20.0)); dNum=0.0; dDeNum=0.0; for(j=i;j>MathMax(i-AdaptiveRVIPeriod, 3);j--) { //Print("rates_total="+IntegerToString(rates_total)+" nLimit="+IntegerToString(nLimit)+ // " AdaptiveRVIPeriod="+IntegerToString(AdaptiveRVIPeriod)+" j="+IntegerToString(j)); dValueUp=Close[j]-Open[j]+2*(Close[j-1]-Open[j-1])+2*(Close[j-2]-Open[j-2])+Close[j-3]-Open[j-3]; dValueDown=High[j]-Low[j]+2*(High[j-1]-Low[j-1])+2*(High[j-2]-Low[j-2])+High[j-3]-Low[j-3]; dNum+=dValueUp; dDeNum+=dValueDown; } if(dDeNum!=0.0) ExtRVIBuffer[i]=dNum/dDeNum; else ExtRVIBuffer[i]=dNum; } //--- signal line counted in the 2-nd buffer nLimit=AdaptiveRVIPeriod+TRIANGLE_PERIOD+2; if(prev_calculated>AdaptiveRVIPeriod+AVERAGE_PERIOD+2) nLimit=prev_calculated-1; for(i=nLimit;i<rates_total && !IsStopped();i++) ExtSignalBuffer[i]=(ExtRVIBuffer[i]+2*ExtRVIBuffer[i-1]+2*ExtRVIBuffer[i-2]+ExtRVIBuffer[i-3])/AVERAGE_PERIOD; //--- OnCalculate done. Return new prev_calculated. return(rates_total); } //+------------------------------------------------------------------+
Eine Bildschirmaufnahme von dem adaptiven Indikator RVI mit dynamischer Fensterbreite:
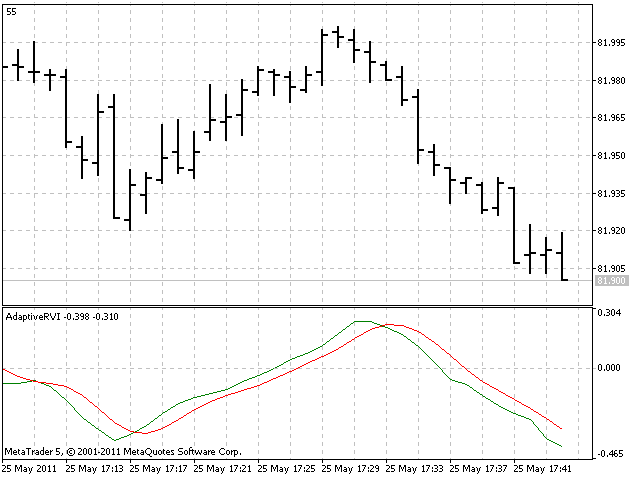
Fazit
In dem Beitrag wurden die anpassungsfähigen Ausführungen dreier technischer Indikatoren betrachtet sowie deren Umsetzung in MQL5 vorgestellt.
Ich hoffe, dass Ihnen die Lektüre dieses Artikels den Mechanismus zur Programmierung adaptiver Indikatoren hat näher bringen können. Alle vorgestellten Indikatoren sind im Anhang beigefügt.
Fühlen Sie sich ermutigt, zu experimentieren und auch aus anderen Indikatoren anpassungsfähige Varianten zu entwickeln.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/288
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Analyse der wesentlichen Merkmale von Zeitreihen
Analyse der wesentlichen Merkmale von Zeitreihen
 Der MQL5-Assistent für Neueinsteiger
Der MQL5-Assistent für Neueinsteiger
 Zeitreihenvorhersage mittels exponentieller Glättung
Zeitreihenvorhersage mittels exponentieller Glättung
 Implementierung der Automatischen Analyse der Elliott-Wellen in MQL5
Implementierung der Automatischen Analyse der Elliott-Wellen in MQL5
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Weiß jemand, wie man den Intervallzeitraum von 6 auf 63 ändert, wie es im Artikel steht?
Danke, im Voraus.
Ich habe herausgefunden, wie man die variable Periode für eine andere ändern kann, indem man den Costant 6.28318 und vielleicht die Kompensationszahl 0.5 bei dieser Gleichung"DC =(6.28318/MedianDelta)+0.5;" im Code der Zyklusperiode ändert, falls jemand den gleichen Zweifel hat.
Ich habe festgestellt, dass es vielleicht einen Fehler im Artikel gibt oder es ist nicht ganz klar, warum dieDeltaPhase zwischen <0.1, 1.1> und im Code zwischen <0.1, 0.9> liegt.
Ich möchte sagen, dass dies nur meine Zweifel und meine Überlegungen sind, aber es ist ein großartiger Artikel.
Vielen Dank!
Veröffentlichter Artikel Advanced Adaptive Indicator Theory and Implementation in MQL5:
Autor: investeo
Gute Arbeit, investeo,
Könnten Sie mir einen Tipp geben, wie ich mathematisch zu den InPhase- und Quadratur-Formeln aus der Hilbert-Transformation komme?
Ich arbeite daran, aber es widerstrebt mir.
Danke
Kann ich diese MQL5-Indikatoren in MQL4 verwenden?
Nein! Sie müssen den Code konvertieren und anpassen, damit er mit MQL4 funktioniert.