Diskussion zum Artikel "Zeitreihenvorhersage mittels exponentieller Glättung"

Neuer Kommentar
 

Neuer Artikel Zeitreihenvorhersage mittels exponentieller Glättung :

Dieser Beitrag möchte dem Leser einige Modelle zur exponentiellen Glättung für kurzfristige Vorhersagen von Zeitreihen näher bringen. Darüber hinaus werden Fragen der Optimierung und Berechnung der Vorhersageergebnisse berührt sowie Beispiele für Programmskripte und Indikatoren vorgestellt. Dieser Artikel soll als erster Einstieg in die Grundsätze von Vorhersagen auf der Grundlage exponentieller Glättungsmodelle dienen.

3. Exponentielle Glättung

Sehen wir uns zunächst das Elementarmodell an:

mit:

  • X(t) für den untersuchten (modellierten) Vorgang
  • L(t) für den veränderlichen Grad des Vorgangs und
  • r(t) für eine Zufallsgröße mit dem Zentralwert Null.

Wie zu sehen beinhaltet das Modell die Summe zweier Bestandteile, von denen uns der Grad des Vorgangs L(t) interessiert, und genau diesen versuchen wir hier herauszuarbeiten.

Bekanntermaßen kann man bei der Mittelung einer Zufallssequenz versuchen, ihre Streuung einzudämmen, das heißt, das Ausmaß ihrer Abweichung vom Durchschnittswert zu verringern. Deshalb ist davon auszugehen, dass wir, wenn der mithilfe unseres elementaren Modells beschriebene Vorgang gemittelt (geglättet) wird, die Zufallskomponente r(t), wenn wir ihr schon nicht ganz entgehen können, merklich abschwächen und dadurch den für uns interessanten Grad L(t) aussondern können.

Dazu greifen wir zur einfachen exponentiellen Glättung (Simple Exponential Smoothing, kurz: SES).

Autor: Victor

 
Ich gratuliere dem Autor zu einem Artikel mit einer gewissen theoretischen Grundlage.
 

Ich komme nicht durch das Labyrinth des Codes, aber ich würde es gerne vergleichen.

Ursprüngliches Angebot

Wir haben die folgenden Glättungsvarianten:

Ergebnis der Glättung

Regressionsgleichung:

eurusd = c(1)*eurusdsm(-1) + c(2)*trend + c(3)

Schätzung der Regressionsgleichung

Variable Koeffizient Stand.osh. t-Statistik Wahrscheinlichkeit

EURUSDSM(-1) 0.759607 0.049127 15.46225 0.0000
REND 0.000207 5.79E-05 3.577804 0.0005
C 0.314884 0.065276 4.823886 0.0000


R-Quadrat = 0,788273

Standardfehler der Regression = 0,015172

Aus den erhaltenen Zahlen geht hervor, dass:

alle Regressionskoeffizienten sind signifikant (die Wahrscheinlichkeit, dass sie gleich Null sind, ist gleich Null)

ein ziemlich hohes (aber nicht sehr hohes) R-Quadrat, das besagt, dass die Regression 78 % der Varianz erklärt

der Standardfehler beträgt 151 Pips. Das ist eine enorme Zahl.

Können wir den daraus resultierenden Zahlen trauen?

Ich würde das nicht, denn laut Jarque-Bera beträgt die Wahrscheinlichkeit, dass die geglättete Reihe eine Normalverteilung aufweist, 31 %.

Lassen Sie uns eine Vorhersage machen:

Der Prognosefehler liegt nicht weit hinter dem Regressionsfehler und übersteigt 100 Pips

Schauen wir uns die Grafik des Prognosefehlers an:

Der Fehler ist variabel, was bedeutet, dass das zukünftige Verhalten der Prognose unbekannt ist!

Um den Grund dafür herauszufinden, schauen wir uns die Korrelation der Koeffizienten der Regressionsgleichung an:

Wir können feststellen, dass die Koeffizienten c(1) und c(3) zu fast 100% korreliert sind.

Daraus schließe ich, dass wir die exponentielle Glättung nicht für die Vorhersage verwenden können.

Warum erhalten wir unterschiedliche Ergebnisse?

Mir ist klar, dass die optimalen Parameter, die Sie gefunden haben, nichts weiter als eine triviale Anpassung sind. Die Regression selbst ist hoffnungslos, ihre Koeffizienten sind korreliert.

 
Warum haben wir разные результаты?

Mir ist klar, dass die optimalen Parameter, die Sie gefunden haben, nichts weiter als eine triviale Anpassung sind. Die Regression selbst ist hoffnungslos, die Koeffizienten sind korreliert.

Ich danke Ihnen für Ihr Interesse an dem Artikel.

Bitte klären Sie, was Sie meinen? Welche Ergebnisse konvergieren nicht und was sind die optimalen Parameter?

 
victorg:

Bitte klären Sie, was Sie damit meinen?


Verzeihung, Sie sagen, Sie können es verwenden, aber meine Schlussfolgerung ist, dass Sie es nicht können.
 
faa1947:
Verzeihung, Sie sagen, Sie können es verwenden, aber meine Schlussfolgerung ist, dass Sie es nicht können.
Wofür und zu welchem Zweck?
 
victorg:
Was ist zu verwenden und warum?

Abschließend ist festzustellen, dass die Modelle der exponentiellen Glättung in bestimmten Fällen in der Lage sind, Prognosen zu erstellen, die genauso genau sind wie die Prognosen, die mit komplexeren Modellen erstellt wurden, was einmal mehr bestätigt, dass das komplexeste Modell nicht immer das beste ist.


Meine Schlussfolgerung ist, dass die exponentielle Glättung nicht für Prognosen verwendet werden sollte.

Was sind Ihre Fragen und warum stellen Sie sie?

 
faa1947:

Meine Schlussfolgerung ist, dass man die exponentielle Glättung nicht für Prognosen verwenden kann.

Worum geht es bei Ihren Fragen und warum stellen Sie sie?

Ich würde gerne versuchen, etwas zu beantworten, aber dazu muss ich zumindest die Frage kennen. Sonst muss ich raten und phantasieren.

Ich werde versuchen, es noch einmal zu verdeutlichen.

Exponentielle Glättungsmodelle können nicht zur Vorhersage des Eurusd-Paares verwendet werden, irgendwelche Zitate oder überhaupt nicht?

P.S..

Sie haben in Ihrem Text: "Regressionsgleichung:eurusd = c(1)*eurusdsm(-1) + c(2)*trend + c(3)". Warum Regression, der Artikel handelt von exponentiellen Glättungsmodellen, und es gibt ein anderes Modell, anstelle von c(3) gibt es eine Zufallsvariable mit einer gewissen Verteilung und Streuung?

 
victorg:

In Ihrem Text: "Regressionsgleichung:eurusd = c(1)*eurusdsm(-1) + c(2)*trend + c(3)". Warum Regression, der Artikel handelt von exponentiellen Glättungsmodellen, und es gibt ein anderes Modell, dort ist statt c(3) eine Zufallsvariable mit irgendeiner Verteilung und Varianz?

Es funktioniert nicht, wenn ein Blinder mit einem Tauben spricht. Schieben wir es auf.

Nochmals Glückwunsch zu einem guten Artikel.

 
faa1947:

Es funktioniert nicht, von einem Blinden zu einem Tauben zu sprechen. Das sollten wir verschieben.

Nochmals herzlichen Glückwunsch zu einem guten Artikel.

Ich bin wirklich sehr neugierig auf Ihren Standpunkt zur Vorhersage mittels exponentieller Glättung. Es gibt viele Dinge, die ich einfach nicht weiß, und ich versuche immer gerne, bei jeder Gelegenheit etwas Neues zu entdecken, deshalb stelle ich Fragen.

Wenn es nicht zu viel Mühe macht, erklären Sie mir bitte, warum man der Prognose nicht trauen kann, wenn die Verteilung der ursprünglichen Sequenz (oder der geglätteten ursprünglichen Sequenz) nicht normal ist? Oder habe ich Sie missverstanden?

Vielen Dank für die Glückwünsche.

 

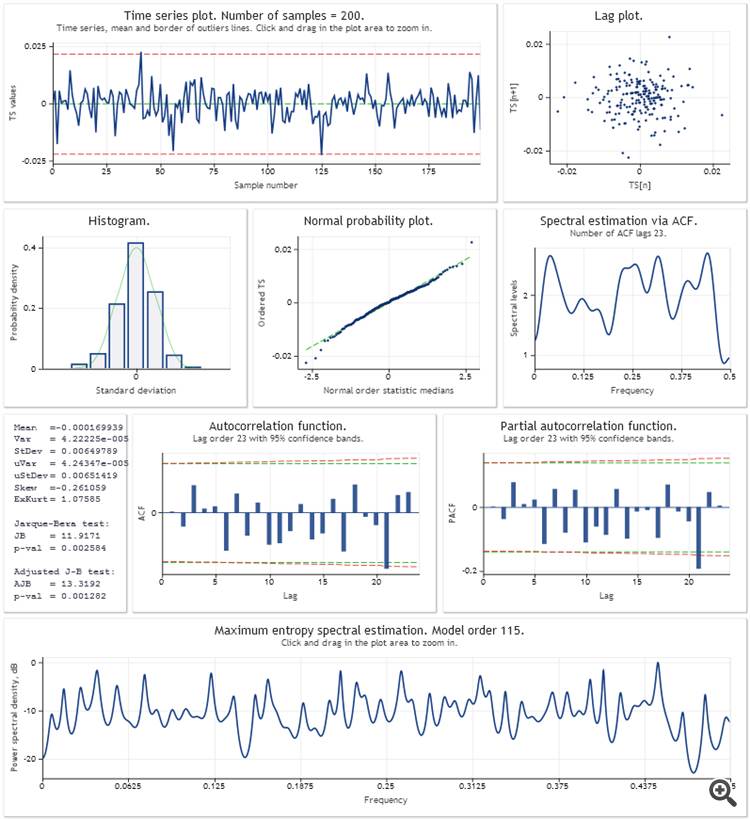
Es folgt eine Analyse des Vorhersagefehlers in einem Schritt für das additive lineare Wachstumsmodell mit Dämpfung. Die Modellparameter wurden anhand einer Stichprobe der letzten 200 Werte von USDJPY,M1 optimiert. Auf die gleiche Weise wie im Skript Optimisation_Test.mq5 aus dem Artikel.


https:// www.mql5.com/ru/articles/292

12
Neuer Kommentar