Vom Neuling zum Experten: Entmystifizierung versteckter Fibonacci-Retracement-Levels

Inhalt:

1. Einführung
2. Strategie zur Umsetzung
3. Tests und Ergebnisse
4. Schlussfolgerung
5. Anlagen

Einführung

Fibonacci-Retracement-Levels sind weit verbreitet, aber manchmal reagiert der Preis auf zwischenzeitliche oder wiederholte Nicht-Standard-Verhältnisse. Unsere Frage lautet: Können wir systematische, datengestützte Methoden verwenden, um solche Niveaus zu entdecken, um zu testen, ob sie häufiger als einmal auftreten, und um sie, falls sie robust sind, als erstklassige Niveaus in unsere Handelsinstrumente und -strategien aufzunehmen?

 Warum traditionelle Fibonacci-Levels unvollständig sein können

Die klassische Fibonacci-Verhältnisse wie 23,6 %, 38,2 %, 50 %, 61,8 % und 78,6 % sind von der Fibonacci-Folge und dem Goldenen Schnitt abgeleitet. Obwohl dies weithin akzeptiert wird, stellen Händler oft fest, dass die Märkte manchmal Zwischen- oder alternative Retracement-Levels respektieren, die nicht in dieser traditionellen Reihe enthalten sind. Dies deutet darauf hin, dass der Standardrahmen das Marktverhalten möglicherweise nicht vollständig erfasst.

Beobachtungen von versteckten Marktreaktionen

Erfahrungsgemäß stockt der Kurs oft, kehrt um oder beschleunigt sich in der Nähe von Niveaus zwischen 50 % und 61,8 % oder um andere nicht standardisierte Punkte. Wir sollten diese „versteckten“ Fibonacci-Niveaus als solche bezeichnen. Die Schwierigkeit besteht darin, dass solche Beobachtungen subjektiv sind, auf der visuellen Inspektion von Charts beruhen und möglicherweise nicht für alle Instrumente oder Zeitrahmen gelten.

Die Herausforderung der anekdotischen Evidenz gegenüber dem statistischen Beweis

Die visuelle Mustererkennung ist anfällig für Bestätigungsfehler: Wir erinnern uns an die Zeiten, in denen der Preis auf ein vermutetes Niveau reagierte, vergessen aber die Fehlschläge. Ohne systematische Tests bleiben diese versteckten Werte spekulativ. Dennoch bieten uns anekdotische Belege einen Ausgangspunkt, um diese Ideen auf strukturierte Weise zu testen und die Theorie, auf die sich Händler verlassen, genauer zu machen. Die Herausforderung besteht darin, echte strukturelle Tendenzen von Zufälligkeiten und Rauschen zu unterscheiden.

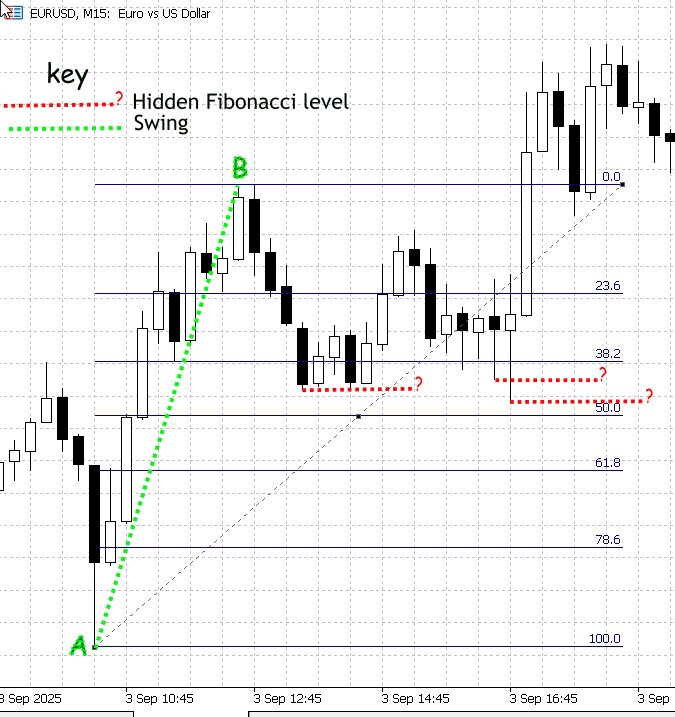
Abbildung 1.  Demonstration von Nicht-Standard-Fibonacci-Retracement-Levels

Abbildung 1 (oben) ist ein Screenshot von MetaTrader 5, der EURUSD auf dem Zeitrahmen M15 zeigt. Der „Swing“ A-B wurde mit dem Fibonacci-Tool gemessen; die Standard-Retracement-Levels sind blau eingezeichnet und beschriftet. Der Kurs hat nicht genau auf diesen klassischen Quoten gestoppt, sondern es ist eine deutliche Kursaktivität an den Zwischenpunkten zwischen den markierten Niveaus (38,2 und 50) zu erkennen. Ich habe diese Zwischenreaktionen mit roten gestrichelten Linien hervorgehoben und mit „?“ gekennzeichnet, um darauf hinzuweisen, dass es sich um unbekannte, potenziell bedeutsame Werte handelt.

Diese Zwischenreaktionen sind genau das, was unsere Forschung lösen soll. Obwohl wir die genauen Retracement-Werte programmatisch berechnen und einzeichnen könnten, ist eine manuelle Überprüfung unzuverlässig, da das integrierte Fibonacci-Tool nur die Lehrbuchverhältnisse darstellt. Dazu ist ein zweistufiger Prozess erforderlich: Erstens muss eine große Menge normalisierter Retracement-Beobachtungen gesammelt und statistisch gefiltert werden, um festzustellen, welche Zwischenbänder wiederholt eingehalten werden; zweitens muss ein Algorithmus implementiert werden, der diese validierten Niveaus kalibriert und auf dem MetaTrader 5 Fibonacci-Tool darstellt (mit Konfidenzwerten versehen).

Strategie zur Umsetzung

Methoden zur Erkennung von Balkengröße und Schwankungen

Für dieses Projekt werden die Höchst- und Tiefstwerte eines jeden Balkens als einfacher Schwankungsbereich behandelt. Wir wenden einen Minimum-Range-Filter an (z. B. einen ATR-Multiplikator), um Rauschen zu unterdrücken und uns auf sinnvolle Bewegungen zu konzentrieren. Dieser Balkenbereichs-Proxy ist absichtlich leichtgewichtig: Er ist einfach zu implementieren, kann schnell über große Historien laufen und liefert einen deterministischen Datensatz mit einer Beobachtung pro geschlossenem Balken, der ideal für statistische Entdeckungen ist.

In zukünftigen Phasen werden wir eine verfeinerte Erkennung von „Swings“ über mehrere Balken einsetzen, um längere oder strukturell signifikante Schwankungen zu erfassen. Wir haben uns bewusst dafür entschieden, mit Balkenbereichen zu beginnen, um den technischen Aufwand so gering wie möglich zu halten, damit wir schnell große Stichproben erheben, unsere statistischen Methoden validieren und dann iterieren können. Die Durchführbarkeit des Ansatzes beruht auf einer praktischen Marktbeobachtung: Kerzen bilden häufig einen Teil der vorherigen Bewegung zurück und erzeugen messbare Spitzen in einer normalisierten Retracement-Verteilung. Siehe Abbildung 2 für eine Illustration des Intrabalken-Retracement-Verhaltens, das als Motivation für diese Methode dient.

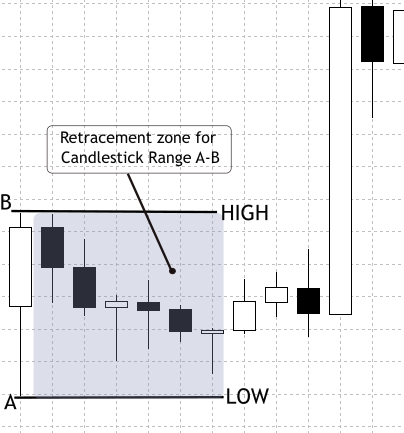
Abbildung 2. Retracement des Kerzenbereichs

 Datenerhebung und -aufbereitung

Der erste Schritt besteht darin, historische OHLCV-Daten für mehrere Instrumente (z. B. EURUSD, GBPUSD, S&P500, XAUUSD) und Zeitrahmen (M15, H1, H4, D1) zu sammeln. Eine hinreichend große Stichprobe – im Idealfall drei bis fünf Jahre – stellt sicher, dass verschiedene Marktregimes vertreten sind, von Trendphasen bis hin zu Konsolidierungen. Außerdem müssen die Daten vor der Verwendung bereinigt werden, indem fehlende Balken, anormale Spitzen und Lücken herausgefiltert werden, die die Analyse verfälschen könnten. Diese Grundlage garantiert, dass der Retracement-Datensatz eine echte Marktstruktur und keine zufälligen Anomalien widerspiegelt.

Auf dieser sauberen Basis aufbauend, wird jede geschlossene Stange wie ein in sich geschlossener Schwenkbereich behandelt. Das Hoch und das Tief definieren die Referenzgrenzen, und der nächste Balken wird auf seine Retracement-Tiefe untersucht. Um Rauschen zu unterdrücken, werden Bereiche, die kleiner als ein ATR-basierter Schwellenwert sind, ausgeschlossen. Der Retracement-Prozentsatz wird dann auf eine 0-100-Skala normalisiert und zusammen mit Metadaten wie Symbol, Zeitrahmen, Richtung, Zeitstempel und Volumen aufgezeichnet. Entscheidend ist, dass nicht alle Sequenzen akzeptiert werden: Der „collector“ lehnt ungültige Fälle ab, in denen der Testbalken außerhalb des vorherigen Bereichs öffnet oder entgegen der Richtung des Referenzbalkens schließt. Die Logik des erweiterten Fensters blendet aufeinanderfolgende innere Balken oder Flags, Engulfing-Muster und Lücken aus, um sicherzustellen, dass sie nicht mit gewöhnlichen Retracements verwechselt werden. Durch die Anwendung dieser Validierungen und die Erfassung von Metadaten ist der resultierende Datensatz sowohl sauber als auch reproduzierbar – bereit für die statistische Untersuchung der klassischen Fibonacci-Verhältnisse.

Entwicklung eines Datenerfassungsskripts

In den nächsten Schritten werden wir unser Datenerfassungsskript in MQL5 vorbereiten und es verwenden, um eine CSV-Datei mit Rückverfolgungsdaten zu erstellen. Diese Datei wird dann in Jupyter Notebook analysiert, um Muster zu erkennen und Erkenntnisse zu gewinnen.

Initialisierung – wir legen die Steuerelemente und Hilfsfunktionen fest

Oben werden alle Parameter deklariert, die das Verhalten steuern: die Anzahl der zu untersuchenden Balken, die ATR-Einstellungen, die Lookahead-Limits und die Ausgabe-Flags. Wenn das Skript startet, liest es diese Eingaben und bereitet zwei kleine Hilfsprogramme vor (einen Formatierer und einen Zeitrahmen-Zeichenfolgen-Mapper), damit der übrige Code ordentlich bleibt. Das Skript erstellt dann einen Ausgabedateinamen, der Symbol und Zeitrahmen enthält, und öffnet eine CSV-Datei zum Schreiben. Wenn die Datei nicht geöffnet werden kann, wird das Programm angehalten und ein Fehler gemeldet, sodass wir immer wissen, ob der Lauf tatsächlich gestartet wurde.

//--- input parameters
input int      BarsToProcess     = 20000;   // how many candidate reference bars to process
input int      StartShift        = 1;       // skip most recent N bars
input int      ATR_Period        = 14;      // ATR period
input double   ATR_Multiplier    = 0.3;     // min ATR filter
input int      MaxLookahead      = 3;       // extended-window lookahead
input bool     UsePerfectSetup   = true;    // require perfect setups
input bool     OutputOnlySameDir = false;   // require same-dir support
input bool     IncludeInvalidRows= false;   // output invalids
input string   OutFilePrefix     = "CandleRangeData"; // file prefix

//--- output file
string OutFileName = StringFormat("%s_%s_%s.csv", OutFilePrefix, _Symbol, PeriodToString(_Period));
int fh = FileOpen(OutFileName, FILE_WRITE|FILE_CSV|FILE_ANSI);
if(fh == INVALID_HANDLE) {
   PrintFormat("Error opening file %s", OutFileName);
   return;
}

Volatilitäts-Basislinie – wir erstellen einen ATR-Handle, damit das Skript Störungen herausfiltern kann

Vor dem Scannen der Balken wird ein ATR-Indikator-Handle erstellt. Für jeden in Frage kommenden Referenzbalken liest das Skript die ATR für diesen Balken aus; der ATR-Wert dient als Volatilitätsmaßstab. Wenn der Bereich eines Balkens kleiner als ATR * ATR_Multiplier ist, behandelt das Skript den Balken als Rauschen und überspringt ihn. Das Entfernen von winzigen Bereichen verhindert, dass kleine, zufällige Balken zu falschen Retracement-Einträgen führen. Das erhöht die Signalqualität.

//--- prepare ATR handle
int atr_handle = iATR(_Symbol, _Period, ATR_Period);
if(atr_handle == INVALID_HANDLE) {
   Print("ATR handle invalid");
   FileClose(fh);
   return;
}

Hauptscanschleife – das Skript durchläuft die Historie

Das Skript iteriert die geschlossenen Balken rückwärts von StartShift bis zum verfügbaren Verlauf oder bis BarsToProcess. Für jede Iteration (jeden potenziellen Referenzbalken) liest das Skript das High, Low, Open und Close des Referenzbalkens, berechnet die Range und wendet sofort das ATR-Gate an. Wenn der Balken gültig ist, analysiert das Skript den oder die Testbalken, die auf die Referenz folgen. Diese Schleife ist der Motor, der die rohe Geschichte in potenzielle Retracement-Ereignisse umwandelt. Auf diese Weise reduzieren wir die Zahl der schlechten Fälle frühzeitig, um die nachgelagerten Statistiken zu verbessern.

int bars = iBars(_Symbol,_Period);
double atr_buf[];

for(int r = StartShift; r <= bars - 1; r++) {
   double RefTop   = iHigh(_Symbol,_Period,r);
   double RefBot   = iLow(_Symbol,_Period,r);
   double RefOpen  = iOpen(_Symbol,_Period,r);
   double RefClose = iClose(_Symbol,_Period,r);
   double Range    = RefTop - RefBot;
   
   // ATR filter
   if(CopyBuffer(atr_handle,0,r,1,atr_buf) <= 0) continue;
   if(Range < atr_buf[0] * ATR_Multiplier) continue;
   
   // process this reference...
}

Bestimmen Sie die Referenzrichtung – wir bezeichnen den „Swing“ als auf-, abwärts oder neutral

Für den Referenzbalken wird geprüft, ob er über (aufwärts), unter (abwärts) oder gleich dem Eröffnungskurs (neutral) geschlossen hat. Diese Richtung entscheidet darüber, welches Extrem des Testbalkens ein Retracement darstellt (eine Aufwärtsbewegung sucht nach Tiefs, eine Abwärtsbewegung nach Hochs). Die Normalisierung des Retrace-Prozentsatzes hängt davon ab, ob die Referenz nach oben oder nach unten gerichtet war.

string RefDir;
if(RefClose > RefOpen)      RefDir = "Bull";
else if(RefClose < RefOpen) RefDir = "Bear";
else                        RefDir = "Neutral";

Anfängliche Prüfleiste und Validierung des perfekten Setups – wir überprüfen zuerst die einfachen, sauberen Fälle

Das Skript liest den unmittelbar folgenden Balken (Testbalken) nach der Referenz; dieser Balken ist der Ort, an dem das Retracement normalerweise stattfindet. Wenn wir den Filter „Perfektes Setup“ aktiviert haben, prüft das Skript zwei Bedingungen: Der Testbalken muss innerhalb des Referenzbereichs öffnen und darf nicht entgegen der Referenzrichtung schließen (z. B. darf der Schlusskurs des Testbalken bei einer Aufwärts-Referenz nicht gefallen sein). Wenn der Testbalken fehlschlägt und wir keine Diagnosezeilen wünschen, überspringt das Skript das Schreiben von Daten für diese Referenz.

int testIndex   = r - 1;
double testOpen = iOpen(_Symbol,_Period,testIndex);
double testClose= iClose(_Symbol,_Period,testIndex);

bool ValidSetup = true;
if(UsePerfectSetup) {
   if(testOpen < RefBot || testOpen > RefTop) ValidSetup = false;
   if(RefDir=="Bull" && testClose < testOpen) ValidSetup = false;
   if(RefDir=="Bear" && testClose > testOpen) ValidSetup = false;
}

if(!ValidSetup && !IncludeInvalidRows) continue;

Erweitertes Fenster-Handling – das Skript kann realistische Retracements mehrerer Balken erfassen

Wenn diese Funktion aktiviert ist, schaut das Skript weiter zurück (eine konfigurierbare Anzahl von Bars), um kurze Sequenzen zusammenzufassen, die zusammen das wahre Retracement-Extrem ergeben. Beim Scannen der Vorschaubalken werden drei Dinge getan:

1. Erkennen von Lücken: Wenn sich ein Balken außerhalb des Referenzbereichs öffnet, kennzeichnet das Skript eine Lücke und zeichnet deren Größe auf.
2. Wenn mehrere kleine aufeinanderfolgende Balken vollständig innerhalb des Referenzbereichs liegen, aktualisiert das Skript den Extremwert (Ext) auf das niedrigste Tief (im Aufwärtsfall) oder das höchste Hoch (im Abwärtsfall) über diese Balken und erhöht InsideCount.
3. Erkennen von Engulfing-Kerzen – wenn ein späterer Balken die Referenz vollständig verschlingt, klassifiziert das Skript ihn als Engulf und setzt das Flag HighMomentum.

Dieser Zusammenbruch stellt sicher, dass die Beobachtung die abgeschlossene Retracement-Episode und nicht eine verfrühte Teilberührung darstellt.

double Ext = (RefDir=="Bull") ? testLow : testHigh;
string SeqType = "Single";
bool HighMomentum = false;
int InsideCount = 0;

for(int k=1; k<=MaxLookahead; k++) {
   int idx = r - k;
   if(idx < 0) break;
   double kOpen = iOpen(_Symbol,_Period,idx);
   double kHigh = iHigh(_Symbol,_Period,idx);
   double kLow  = iLow(_Symbol,_Period,idx);
   
   if(kOpen > RefTop || kOpen < RefBot) { SeqType="Gap"; break; }
   if(kHigh <= RefTop && kLow >= RefBot) {
      if(RefDir=="Bull") Ext = MathMin(Ext,kLow);
      if(RefDir=="Bear") Ext = MathMax(Ext,kHigh);
      InsideCount++;
      continue;
   }
   if(kHigh >= RefTop && kLow <= RefBot) {
      SeqType="Engulf";
      HighMomentum=true;
      break;
   }
   // if retrace detected, stop
   break;
}

Berechnung des Retracement-Prozentsatzes – das Skript normalisiert das Ergebnis für die Analyse

Anhand des letzten aufgezeichneten Extremwertes (Ext) berechnet das Skript RetracePct auf einer Skala von 0-100:

• Im Aufwärtsfall: RetracePct = (RefTop - Ext) / Range * 100
• Im Abwärtsfall: RetracePct = (Ext - RefBot) / Range * 100

Dann kennzeichnet es das Ereignis:

• NoRetrace wenn negativ (Preis hat sich entfernt),
• Retracement wenn zwischen 0 und 100,
• Erweiterung, wenn über 100 (Preis hat sich über die Referenz hinaus bewegt).

double Rpct = EMPTY_VALUE;
string Type = "Undefined";

if(RefDir=="Bull") Rpct = (RefTop - Ext) / Range * 100.0;
if(RefDir=="Bear") Rpct = (Ext - RefBot) / Range * 100.0;

if(Rpct < 0)       Type="NoRetrace";
else if(Rpct<=100) Type="Retracement";
else               Type="Extension";

Praktische Diagnostik – Berechnung des handelbaren Abstands und der Nähe zu den klassischen Fibonacci-Levels

Wir berechnen RetracePips, die absolute Anzahl von Pips, die der Retrace repräsentiert, sodass wir triviale, nicht handelbare Berührungen (z. B. kleiner als der Spread) ausschließen können. Wir berechnen auch, welche klassische Fibonacci-Stufe am nächsten liegt und wie nahe (NearestFibPct, NearestFibDistPct). Schließlich wird SameDirSupport festgelegt, indem geprüft wird, ob der repräsentative Balken (der letzte Balken in der zusammengeklappten Sequenz) in der gleichen Richtung wie die Referenz geschlossen hat.

double RetracePips = (RefDir=="Bull") ? (RefTop-Ext)/_Point : (Ext-RefBot)/_Point;

// Same-dir support
bool SameDirSupport = (RefDir=="Bull") ? (testClose >= testOpen) : (testClose <= testOpen);

// Nearest Fibonacci comparison
double fibLevels[] = {0,23.6,38.2,50.0,61.8,78.6,100.0};
double nearest = fibLevels[0];
double minDist = fabs(Rpct - fibLevels[0]);
for(int i=1;i<ArraySize(fibLevels);i++) {
   double d = fabs(Rpct - fibLevels[i]);
   if(d < minDist) { minDist = d; nearest = fibLevels[i]; }
}

Regeln für die Ausgabe

Anhand von Flags (OutputOnlySameDir, IncludeInvalidRows) überspringt oder schreibt das Skript die Zeile. Wenn es schreibt, enthält die Zeile alle Metadaten (Zeit, Symbol, RefTop/RefBot, Ext, RetracePips, RetracePct, SeqType, SameDirSupport, nächste Fib-Übereinstimmung, Volumen und Spread). Die Datei ist deterministisch: Dasselbe Symbol, derselbe Zeitrahmen und dieselben Parameter ergeben immer dieselbe CSV-Datei.

if(OutputOnlySameDir && !SameDirSupport) continue;

FileWrite(fh,
   _Symbol,
   PeriodToString(_Period),
   TimeToString(iTime(_Symbol,_Period,r),TIME_DATE|TIME_SECONDS),
   RefTop, RefBot, Range, RefDir,
   Ext, RetracePips, Rpct, Type,
   SeqType, HighMomentum, InsideCount,
   SameDirSupport, nearest, minDist
);

Aufräumen und Berichterstattung – wir beenden den Lauf und berichten dem Team, was passiert ist.

Nach der Schleife gibt das Skript den ATR-Handle frei, schließt die Datei und gibt eine kurze Zusammenfassung aus, die angibt, wie viele Zeilen geschrieben und wie viele ungültige Kandidaten übersprungen wurden. Dieses unmittelbare Feedback leitet unsere nächste Aktion (z. B. Erhöhung der Balken, Lockerung der Filter oder Änderung des ATR-Multiplikators).

IndicatorRelease(atr_handle);
FileClose(fh);
PrintFormat("CandleRangeData_v2: finished. Wrote %d rows to %s", written, OutFileName);

Statistische Analyse und Visualisierung von Fibonacci-Retracement-Daten mit Python in Jupyter Notebook

Um unsere Forschung voranzutreiben, werden wir Python verwenden, um die Daten zu verfeinern und statistische Berichte zu erstellen. Zu diesem Zweck habe ich das Jupyter Notebook gewählt, da es einen verbesserten Arbeitsablauf für Python bietet und die Art von Ergebnissen unterstützt, die wir erreichen wollen.

Das Jupyter Notebook ist eine interaktive Webumgebung, die für wissenschaftliche Berechnungen, Datenanalysen und Visualisierungen entwickelt wurde. Es ermöglicht die Koexistenz von Code, visuellen Ausgaben und Dokumentation im selben Arbeitsbereich, was es besonders effektiv für forschungsorientierte Aufgaben macht. In unserem Fall bietet diese Umgebung die Flexibilität, mit Retracement-Daten zu experimentieren, statistische Methoden zu testen und Ergebnisse wie Histogramme und Dichteplots sofort zu visualisieren. Im Gegensatz zu einem statischen Skript, das von Anfang bis Ende ausgeführt werden muss, können wir mit Jupyter kleine Zellen unabhängig voneinander ausführen – ein wertvoller Vorteil, wenn wir Berechnungen anpassen oder bestimmte Schritte erneut ausführen müssen, ohne den gesamten Prozess neu zu starten. Dieser interaktive Arbeitsablauf passt gut zu dem iterativen und explorativen Charakter der Mustererkennung in Finanzdaten.

Im Folgenden finden Sie eine Übersicht über die Schritte zur Einrichtung von Jupyter Notebook unter Windows.

Um die unten stehenden Zellen auszuführen, verwenden Sie Jupyter (Notebook oder Lab) unter Windows. Die Schritte sind:

1. Installieren Sie Python 3.10+ von python.org (wählen Sie „Add Python to PATH“).
2. Öffnen Sie eine Eingabeaufforderung (PowerShell oder CMD) und erstellen Sie eine virtuelle Umgebung (optional, aber empfohlen):

python -m venv venv
venv\Scripts\activate

3. Installieren Sie Jupyter und die erforderlichen Bibliotheken:

pip install jupyter pandas numpy matplotlib scipy scikit-learn

4. Starten Sie Jupyter:

Wenn Sie in einem bestimmten Ordner arbeiten möchten, verwenden Sie den Befehl cd, um das Verzeichnis zu wechseln. Um zum Beispiel zu einem Ordner zu navigieren, in den die CSV-Datei exportiert wird, in der Regel C:\user\IhrComputername\MQL5\Dateien, würden Sie Folgendes eingeben:

cd C:\Users\YourComputerName\TerminalDataFolder\MQL5\Files

Danach starten Sie es mit

jupyter notebook

Bibliotheken und ihre Verwendungszwecke

• pandas – laden und manipulieren von CSV-Tabellen (Zeilen/Spalten).
• numpy – numerische Arrays und mathematische Hilfsmittel.
• matplotlib – Zeichnen von Histogrammen und KDEs.
• scipy – Statistikfunktionen und KDE.
• scikit-learn (sklearn) – Gaußsche Mischungsmodelle für 1-D-Clustering. 

Zelle 1 – Einrichten der Python-Umgebung

Zu Beginn unseres Notizbuchs bereiten wir die Umgebung vor, indem wir die Python-Bibliotheken importieren, die unsere Analyse unterstützen werden. Jede Bibliothek spielt eine spezielle Rolle bei der Verarbeitung der aus dem MQL5-Skript exportierten Daten.

• Pandas (pd) wird für die Verarbeitung strukturierter Daten verwendet. Es ermöglicht uns, die CSV-Datei mit den Retracement-Datensätzen zu laden, Zeilen und Spalten zu manipulieren und auf einfache Weise Statistiken zu berechnen.
• Numpy (np) bietet mathematische Werkzeuge und numerische Operationen, wie Arrays und lineare Algebra, die vielen unserer statistischen Berechnungen zugrunde liegen.
• Matplotlib.pyplot (plt) ist die Grundlage für die Erstellung von Diagrammen wie Histogrammen und Dichteplots, die uns helfen, das Retracement-Verhalten zu visualisieren.
• Seaborn (sns) baut auf matplotlib auf, um elegantere und einfacher zu erstellende Diagramme zu liefern, die statistische Muster deutlicher machen.
• Scipy.stats (stats) bringt fortgeschrittene statistische Methoden wie die Kerndichteschätzung (KDE), Hypothesentests und Wahrscheinlichkeitsverteilungen ein.
• Sklearn.mixture.GaussianMixture stammt aus der Bibliothek scikit-learn für maschinelles Lernen und ermöglicht die Anpassung von Gaußschen Mischmodellen. Dies ist nützlich, wenn man Retracement-Levels clustert, um zu erkennen, wo sich verborgene Fibonacci-ähnliche Levels konzentrieren könnten.

Indem wir diese Zelle betreiben, laden wir effektiv alle für unsere Arbeit benötigten Werkzeuge.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
from sklearn.mixture import GaussianMixture

Zelle 2 – CSV laden und eine boolesche Spalte ValidSetup_bool erstellen

An diesem Punkt des Notizbuchs beginnt das Skript mit dem Laden des aus MQL5 exportierten Retracement-Datensatzes. Die CSV-Datei wird in einen Pandas DataFrame eingelesen, und das Programm gibt sofort aus, wie viele Zeilen geladen wurden und welche Spalten verfügbar sind. Dies ist ein wichtiger Prüfpunkt, da er bestätigt, dass der Dateipfad korrekt ist und die erwarteten Felder, wie RetracementPct, Type oder ValidSetup, vorhanden sind. Zur Veranschaulichung der Struktur zeigt das Skript auch die ersten Zeilen an, damit wir schnell überprüfen können, ob die Daten mit dem übereinstimmen, was wir von unserem MetaTrader-Export erwarten.

Sobald der Datensatz im Speicher ist, besteht die nächste Aufgabe darin, zu entscheiden, welche Zeilen für die weitere Analyse gültig sind. Das Problem ist, dass nicht allen Retracement-Berechnungen des MQL5-Skripts vertraut werden sollte: Einige können unvollständig sein oder als ungültige Setups gekennzeichnet werden. Da Datensätze leicht unterschiedliche Spaltennamen für die Gültigkeit verwenden können (z. B. ValidSetup, Valid oder validsetup), sucht das Skript in mehreren gängigen Varianten. Wird eine gefunden, werden die Ergebnisse in einer neuen booleschen Spalte mit der Bezeichnung ValidSetup_bool zusammengefasst. Werte wie „True“, „1“ oder „Yes“ werden als gültig interpretiert. Wenn überhaupt keine Gültigkeitsspalte gefunden wird, behandelt das Skript standardmäßig alle Zeilen als gültig, um sicherzustellen, dass wir noch mit Daten arbeiten können. Schließlich wird ein gefilterter Datensatz mit der Bezeichnung df_valid erstellt, der nur gültige Zeilen enthält, und es wird eine Schnellstatistik gedruckt, die zeigt, wie viele Zeilen insgesamt geladen wurden und wie viele den Gültigkeitsfilter passiert haben.

# Robust Cell 2: load CSV and create a boolean ValidSetup_bool column
import pandas as pd
from IPython.display import display

csv_file = "CandleRangeData_NZDUSD_H4.csv"   # <- set your filename here
df = pd.read_csv(csv_file, sep=None, engine="python")
print("Loaded rows:", len(df))
print("Columns found:", list(df.columns))

# Show first 5 rows
display(df.head())

# Try to detect a 'valid setup' column (several common name variants)
candidates = ["ValidSetup", "validsetup", "Valid_Setup", "Valid", "valid", 
              "ValidSetup_bool", "Valid_Setup_bool"]
found = None
for c in candidates:
    if c in df.columns:
        found = c
        break

# Case-insensitive detection if exact not found
if found is None:
    lower_map = {col.lower(): col for col in df.columns}
    for c in candidates:
        if c.lower() in lower_map:
            found = lower_map[c.lower()]
            break

# Create boolean column 'ValidSetup_bool' using detected column or fallback
if found is not None:
    print("Using column for validity:", found)
    series = df[found].astype(str).str.strip().str.lower()
    df["ValidSetup_bool"] = series.isin(["true", "1", "yes", "y", "t"])
else:
    print("No ValidSetup-like column found. Creating ValidSetup_bool=True for all rows (no filtering).")
    df["ValidSetup_bool"] = True

# Quick stats
total = len(df)
valid_count = df["ValidSetup_bool"].sum()
print(f"Total rows = {total}, ValidSetup_bool True = {valid_count}")

# Create df_valid for downstream cells (the rest of notebook expects df_valid)
df_valid = df[df["ValidSetup_bool"] == True].copy()
print("df_valid rows:", len(df_valid))

# Display preview
display(df_valid.head())

Zelle 3 – Berechnung der Retracement-Werte auf der Grundlage des Schemas des „collectors“

Mit einem gültigen Datensatz, der in Zelle 2 vorbereitet wurde, konzentriert sich das Notizbuch nun darauf, sicherzustellen, dass die Retracement-Werte durchgängig für die Analyse zur Verfügung stehen. Im exportierten MetaTrader-Datensatz können einige dieser Felder bereits berechnet sein, während andere aus den Rohpreisen abgeleitet werden müssen. Mit diesem Schritt wird der Prozess der Retracement-Berechnung harmonisiert.

Als Erstes müssen Sie sicherstellen, dass die Spalte Bereich numerisch ist. Diese Spalte, die aus dem MQL5-Kollektor exportiert wird, stellt die Gesamtgröße des Bezugsbalkens dar (die Differenz zwischen seinem oberen und unteren Ende). Die Umwandlung in eine Fließkommazahl garantiert, dass sich die nachfolgenden mathematischen Operationen wie erwartet verhalten.

Als Nächstes prüft das Skript, ob der MetaTrader-Export bereits die Spalte RetracementPct enthält. Falls vorhanden, wird dieser Wert als prozentuales Retracement interpretiert (z.B. 50 bedeutet 50%) und durch Division durch 100 in einen normierten Bruchteil zwischen 0 und 1 umgewandelt. Dieser Ansatz gewährleistet die Konsistenz der Berechnungen und die Wiederverwendung vorberechneter Werte, sofern vorhanden. Wenn keine solche Spalte gefunden wird, greift das Skript auf die manuelle Berechnung des Retracements mit Hilfe der Formel zurück:

Hier steht Ext für das extreme Retracement-Niveau, das erreicht wurde, bevor der Balken geschlossen wurde, und RefBot für den Tiefpunkt des Referenzbalkens. Dividiert man den Abstand zwischen Ext und RefBot durch die gesamte Range, erhält man das proportionale Retracement.

Da Retracements immer zwischen 0 % und 100 % liegen sollten, wendet das Skript eine Clip-Operation an, um alle Werte in das Intervall [0,1] zu zwingen. Dies schützt vor Anomalien, die durch Unregelmäßigkeiten bei den Daten oder Überschreitungen bei den Berechnungen verursacht werden.

Schließlich druckt das Notizbuch zur Überprüfung die ersten Zeilen der Schlüsselspalten RefTop, RefBot, Ext, Range und Retracement aus, um zu bestätigen, dass die berechneten oder importierten Retracement-Werte vernünftig aussehen. Diese Vorschau gibt uns die Gewissheit, dass die Pipeline konsistente normalisierte Retracement-Maße erzeugt, die für die anschließende statistische Analyse bereit sind.

# Cell 3: Compute retracement values based on the collector's schema

# In our MT5 output:
# - RefTop = top of the reference bar
# - RefBot = bottom of the reference bar
# - Ext    = the extreme retracement reached before close
# - RetracementPct = retracement % already computed in MT5

# 1. Use the collector's "Range" directly
df_valid["Range"] = df_valid["Range"].astype(float)

# 2. Use the already provided retracement percentage (if available)
if "RetracementPct" in df_valid.columns:
    df_valid["Retracement"] = df_valid["RetracementPct"].astype(float) / 100.0
    print("Using MT5-calculated RetracementPct column.")
else:
    # fallback: compute from RefTop/RefBot and Ext
    df_valid["Retracement"] = (df_valid["Ext"].astype(float) - df_valid["RefBot"].astype(float)) / df_valid["Range"]
    print("No RetracementPct column found — computed from RefTop/RefBot/Ext.")

# 3. Clip between 0 and 1 (0%–100%)
df_valid["Retracement"] = df_valid["Retracement"].clip(0, 1)

# Quick check
print("Preview of retracement values:")
display(df_valid[["RefTop","RefBot","Ext","Range","Retracement"]].head())

Abbildung 3. Tabelle der berechneten Werte

Zelle 4 – Visuelle Verteilung der Retracement-Werte

Nachdem die Retracement-Werte nun validiert und standardisiert wurden, übernimmt diese Zelle die Aufgabe, ihre Verteilung zu visualisieren. Vor dem Plotten fügt das Skript jedoch eine zusätzliche Sicherung hinzu: Es stellt sicher, dass eine brauchbare Retracement-Spalte vorhanden ist, unabhängig davon, welche Spalten im MetaTrader-Export enthalten waren.

Die Logik beginnt mit der Prüfung, ob Retracement bereits vorhanden ist. Wenn nicht, wird versucht, sie zu konstruieren. Zunächst sucht es nach RetracementPct, dem prozentualen Retracement, das von MetaTrader 5 exportiert wird, und wandelt es in eine normalisierte 0-1-Skala um. Wenn diese Spalte nicht verfügbar ist, greift das Skript auf eine nutzerdefinierte Berechnung mit RefTop, RefBot, Ext und RefDir zurück. Die Einbeziehung von RefDir (Richtung des Referenzbalkens) macht diese Berechnung robust, da Retracements für steigende und fallende Referenzbalken unterschiedlich interpretiert werden müssen:

• Bei einem Aufwärtsbalken wird das Retracement vom RefTop bis zum Extremwert gemessen.
• Bei einem Abwärtsbalken wird er vom RefBot bis zum Extremwert gemessen.

Wenn keine der erforderlichen Spalten vorhanden ist, gibt der Code eine klare Fehlermeldung aus, in der die fehlenden Felder beschrieben werden.

Sobald die Retracement-Werte zusammengestellt sind, werden sie abgeschnitten, um innerhalb des gültigen Intervalls [0,1] zu bleiben, und NaN-Einträge werden gelöscht. Wenn nach der Bereinigung keine gültigen Werte mehr vorhanden sind, bricht das Skript mit einer Fehlermeldung ab, um irreführende Darstellungen zu vermeiden. Andernfalls wird die Anzahl der verwertbaren Beobachtungen zur Transparenz ausgedruckt.

 Wenn die Seaborn-Bibliothek verfügbar ist, verwendet das Skript sns.histplot, um ein Histogramm zu erstellen, das zur besseren Übersichtlichkeit mit einer glatten KDE-Kurve überlagert wird. Wenn es nicht installiert ist, wird ein Ersatz mit reiner Matplotlib ausgelöst: ein Histogramm plus eine manuell berechnete Kerneldichteschätzung (über scipy.stats.gaussian_kde). Dadurch wird sichergestellt, dass die Handlung auch in minimalen Umgebungen gut aussieht.

Das endgültige Diagramm ist eindeutig mit Achsentiteln beschriftet und auf den Bereich 0-1 auf der X-Achse beschränkt. Sie zeigt die Gesamtverteilung der Retracement-Verhältnisse über alle gültigen Setups an und gibt einen unmittelbaren Eindruck davon, wie häufig flache, mittlere oder tiefe Retracements auftreten. Optional kann die Abbildung in einer PNG-Datei mit exakter Größe für Dokumentations- oder Präsentationszwecke gespeichert werden.

# Plotting cell 4 (robust): ensures 'Retracement' exists and draws a 750px-wide plot
import numpy as np
import matplotlib.pyplot as plt

# --- Build 'Retracement' column if needed ---
if "Retracement" not in df_valid.columns:
    if "RetracementPct" in df_valid.columns:
        # MT5 already computed it as percent (0-100)
        df_valid["Retracement"] = pd.to_numeric(df_valid["RetracementPct"], errors="coerce") / 100.0
        print("Using existing RetracementPct -> created Retracement (0-1).")
    else:
        # try to compute from RefTop/RefBot/Ext with direction awareness
        required = {"RefTop","RefBot","Ext","RefDir"}
        if required.issubset(set(df_valid.columns)):
            def compute_r(row):
                try:
                    rng = float(row["RefTop"]) - float(row["RefBot"])
                    if rng == 0: 
                        return np.nan
                    if str(row["RefDir"]).strip().lower().startswith("b") :  # Bull
                        return (float(row["RefTop"]) - float(row["Ext"])) / rng
                    elif str(row["RefDir"]).strip().lower().startswith("be"): # Bear
                        return (float(row["Ext"]) - float(row["RefBot"])) / rng
                    else:
                        return np.nan
                except Exception:
                    return np.nan
            df_valid["Retracement"] = df_valid.apply(compute_r, axis=1).astype(float)
            print("Computed Retracement from RefTop/RefBot/Ext/RefDir.")
        else:
            raise KeyError("No 'Retracement' or 'RetracementPct' column, and required columns for computation are missing. "
                           "Found columns: " + ", ".join(df_valid.columns))

# Clip to 0..1
df_valid["Retracement"] = df_valid["Retracement"].clip(lower=0.0, upper=1.0)

# Drop NaNs
vals = df_valid["Retracement"].dropna().values
if len(vals) == 0:
    raise ValueError("No valid retracement values to plot after preprocessing.")

print(f"Plotting {len(vals)} retracement observations (0..1 scale).")

# --- Plot size: target ~750 px width ---
# Use figsize such that width_inches * dpi = 750. We'll choose dpi=100, width=7.5in.
fig_w, fig_h = 7.5, 4.0
fig, ax = plt.subplots(figsize=(fig_w, fig_h), dpi=100)

# Prefer seaborn if available for nice KDE overlay, otherwise fallback
try:
    import seaborn as sns
    sns.histplot(vals, bins=50, stat="density", kde=True, ax=ax)
except Exception:
    # fallback to matplotlib
    ax.hist(vals, bins=50, density=True, alpha=0.6)
    # manual KDE overlay
    from scipy.stats import gaussian_kde
    kde = gaussian_kde(vals)
    xgrid = np.linspace(0,1,500)
    ax.plot(xgrid, kde(xgrid), linewidth=2)

ax.set_title("Retracement Ratio Distribution")
ax.set_xlabel("Retracement (0 = 0%, 1 = 100%)")
ax.set_ylabel("Density")
ax.set_xlim(0,1)
plt.tight_layout()

# Optionally save a sized PNG (uncomment to save)
# plt.savefig("retracement_distribution_750px.png", dpi=100)

plt.show()

Abbildung 4. Retracement-Ratio-Verteilung

Zelle 5 – Kerndichteschätzung (KDE)

In diesem Schritt gehen wir über die grundlegende Visualisierung hinaus und führen eine fortgeschrittene statistische Analyse durch: Kerndichteschätzung (KDE) kombiniert mit Peak-Erkennung. Dieser Ansatz hilft dabei, häufige Retracement-Levels – die „ausgeblendeten“ Zonen, in denen der Kurs oft zum Stillstand oder zur Umkehr neigt – zu erkennen, indem die Form der Verteilung und nicht nur die rohen Zählwerte in einem Histogramm analysiert werden.

Das Skript stellt zunächst sicher, dass die Spalte Retracement in normalisierter Form (0-1) verfügbar ist. Fehlt er, wird er entweder aus dem Feld RetracementPct oder, falls erforderlich, aus RefTop, RefBot, Ext und RefDir unter Anwendung derselben Auf- und Abwärtslogik wie oben beschrieben wiederhergestellt. Nach dem Beschneiden der Werte auf den gültigen [0,1]-Bereich und dem Streichen von NaNs wird geprüft, ob es mindestens 10 gültige Retracement-Punkte gibt. Dies verhindert verrauschte oder bedeutungslose KDE-Schätzungen, wenn der Datensatz zu klein ist.

Anschließend wird die KDE über ein feines Raster von 1001 Punkten berechnet, das sich von 0 bis 1 erstreckt. Diese hohe Auflösung ermöglicht es der Dichtekurve, subtile Strukturen in den Daten zu erfassen, wie z. B. mehrere lokale Maxima. Um diese Maxima zu identifizieren, normalisiert das Skript die Dichtekurve und wendet scipy.signal.find_peaks an, das so konfiguriert ist, dass es winzige Fluktuationen ignoriert, indem es eine minimale Prominenz und einen minimalen Abstand vorschreibt. Die sich daraus ergebenden Spitzenindizes entsprechen den Retracement-Niveaus, bei denen die Dichtefunktion lokal am stärksten ist, d. h. den in den Daten verborgenen „bevorzugten“ Retracement-Niveaus.

Zur Veranschaulichung wird die KDE-Kurve schraffiert dargestellt, und jeder erkannte Peak wird mit einem roten Punkt hervorgehoben und mit seinem Retracement-Prozentsatz (z. B. 38,20 %) kommentiert. Im Gegensatz zur vorherigen Plot-Zelle ist hier keine feste Pixelbreite vorgeschrieben, sodass sich die Größe der Abbildung flexibel an verschiedene Umgebungen anpassen lässt. Beschriftungen, Achsenbereiche und ein Raster sorgen für eine saubere und interpretierbare Darstellung.

Abschließend gibt das Skript eine Liste der entdeckten Retracement-Levels als Prozentsätze zusammen mit ihren relativen Prominenzwerten aus, was sowohl eine visuelle als auch numerische Zusammenfassung darüber liefert, wo die stärksten versteckten Retracement-Levels liegen könnten. Diese Kombination aus KDE und Spitzenerkennung verwandelt rohe Retracement-Beobachtungen in verwertbare statistische Erkenntnisse.

# Cell 5: KDE + peak detection (robust, flexible sizing)
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
from scipy.signal import find_peaks

# --- ensure Retracement column exists (0..1 scale) ---
if "Retracement" not in df_valid.columns:
    if "RetracementPct" in df_valid.columns:
        df_valid["Retracement"] = pd.to_numeric(df_valid["RetracementPct"], errors="coerce") / 100.0
    else:
        required = {"RefTop","RefBot","Ext","RefDir"}
        if required.issubset(set(df_valid.columns)):
            def compute_r(row):
                try:
                    rng = float(row["RefTop"]) - float(row["RefBot"])
                    if rng == 0:
                        return np.nan
                    rd = str(row["RefDir"]).strip().lower()
                    if rd.startswith("b"):  # Bull
                        return (float(row["RefTop"]) - float(row["Ext"])) / rng
                    elif rd.startswith("be") or rd.startswith("bear"):  # Bear
                        return (float(row["Ext"]) - float(row["RefBot"])) / rng
                    else:
                        return np.nan
                except Exception:
                    return np.nan
            df_valid["Retracement"] = df_valid.apply(compute_r, axis=1).astype(float)
        else:
            raise KeyError("Cannot build 'Retracement' — missing required columns. Found: " + ", ".join(df_valid.columns))

# Clip and drop NaNs
df_valid["Retracement"] = df_valid["Retracement"].clip(0,1)
vals = df_valid["Retracement"].dropna().values
n = len(vals)
if n < 10:
    raise ValueError(f"Too few retracement observations to compute KDE/peaks reliably (n={n}).")

# --- KDE on a fine grid ---
grid = np.linspace(0, 1, 1001)   # 0.001 (0.1%) resolution
kde = stats.gaussian_kde(vals)
dens = kde(grid)

# --- peak detection on normalized density ---
dens_norm = dens / dens.max()
peaks_idx, props = find_peaks(dens_norm, prominence=0.02, distance=8)  # tweak params as needed
peak_levels = grid[peaks_idx]
peak_heights = dens[peaks_idx]

# --- Plot (flexible sizing, no fixed pixel restriction) ---
fig, ax = plt.subplots(figsize=(8, 4))  # default flexible size
ax.plot(grid, dens, label="KDE", linewidth=2)
ax.fill_between(grid, dens, alpha=0.2)

# annotate peaks
for lvl, h in zip(peak_levels, peak_heights):
    ax.plot(lvl, h, "o", color="red")
    ax.text(lvl, h, f" {lvl*100:.2f}%", va="bottom", ha="left", fontsize=9)

ax.set_title("Kernel Density of Retracement Ratios")
ax.set_xlabel("Retracement (0 = 0%, 1 = 100%)")
ax.set_ylabel("Density")
ax.set_xlim(0,1)
ax.grid(True, linestyle="--", alpha=0.5)
plt.tight_layout()
plt.show()

# --- print candidate levels ---
print("Candidate Hidden Retracement Levels (%):")
print(np.round(peak_levels*100, 2))
print("Peak prominences (relative):", np.round(props["prominences"], 4) if "prominences" in props else "n/a")

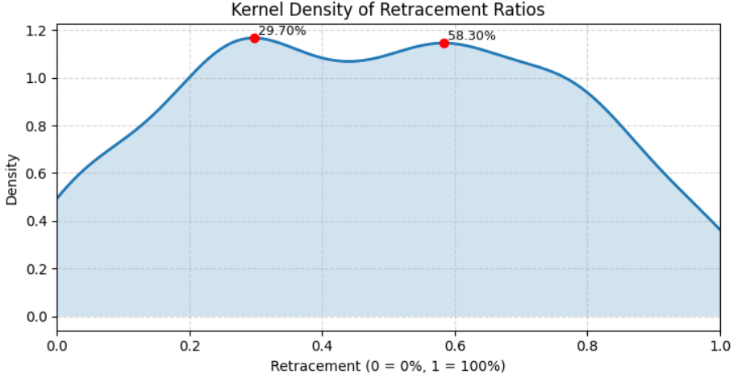
Abbildung 5. Kerneldichte der Retracement-Ratios

Tests und Ergebnisse

Alle Zellen im Jupyter-Notebook lieferten visuelle Ergebnisse, die statistisch ausgewertet werden konnten. Unter jeder Zelle haben wir sowohl den Code als auch die entsprechende Ausgabe dargestellt, was einen der Hauptvorteile der Arbeit in Jupyter veranschaulicht: die Möglichkeit, Berechnung und Visualisierung nahtlos zu kombinieren.

Nach der Ausführung der endgültigen Ausgabezelle, die dazu dient, die aufgelösten versteckten Werte zu speichern, haben wir festgestellt, dass nur zwei signifikante Niveaus für den H4-Zeitrahmen des NZDUSD-Paares erkannt wurden. Obwohl dies nützliche Einblicke in die Datenstruktur lieferte, hat der Hypothesentest unsere Erwartungen nicht bestätigt.

Detected peaks at (pct): [29.7 58.3]
Bootstrap 200/1000...
Bootstrap 400/1000...
Bootstrap 600/1000...
Bootstrap 800/1000...
Bootstrap 1000/1000...
Bootstrap done in 4.5s

Peak testing results (window ±0.40%):
Level 29.700%  mass=9.909890e-03  p=0.4960   significant=False
Level 58.300%  mass=9.729858e-03  p=0.4960   significant=False

Accepted (FDR<0.05) candidate levels (pct): []

Der Algorithmus entdeckte zwei mögliche Spitzenwerte in der Datenverteilung, die bei 29,7 % und 58,3 % lagen. Diese Spitzen stellen Punkte dar, an denen der Algorithmus anfänglich lokale Datenkonzentrationen beobachtete, die auf eine mögliche verborgene Struktur oder wiederholte Muster hindeuten.

Um festzustellen, ob diese Spitzenwerte statistisch aussagekräftig sind oder nur zufällige Schwankungen darstellen, führte das Modell einen Bootstrap-Test mit 1000 Wiederholungsstichproben durch. Das Bootstrap-Verfahren schätzte, wie oft ähnliche Spitzenwerte in zufällig gemischten Versionen der Daten auftauchen würden, was ein Maß für die statistische Signifikanz darstellt.

Für beide Erkennungsstufen:

• Niveau 29,7% → Masse = 0,0099, p = 0,4960 → Nicht signifikant
• Niveau 58,3% → Masse = 0,0097, p = 0,4960 → Nicht signifikant

Die p-Werte (≈0,50) deuten darauf hin, dass diese Spitzenwerte in den randomisierten Bootstrap-Stichproben genauso häufig auftraten wie in den realen Daten, d. h. sie waren statistisch nicht vom Rauschen zu unterscheiden. Da kein Peak den Schwellenwert für die Falschentdeckungsrate (FDR) von 0,05 überschritt, kam der Algorithmus zu dem Schluss, dass es im Datensatz für den gewählten Zeitrahmen (H4 auf NZDUSD) keine signifikanten versteckten Pegel gab.

 Backtesting-Strategien mit ermittelten Niveaus

In MetaTrader 5 habe ich experimentiert, indem ich zwei nutzerdefinierte Retracement-Levels zum Standard-Fibonacci-Set hinzugefügt habe: 29,7% und 58,3%. Unsere Jupyter-Analyse ergab für beide Ebenen die Ergebnisse Masse = 0,0099, p = 0,4960 bzw. Masse = 0,0097, p = 0,4960, die statistisch nicht signifikant waren. Auf den Charts zeigte sich jedoch, dass eines dieser Niveaus in der Vergangenheit von den Kursen respektiert wurde. Dies deutet darauf hin, dass der statistische Test zwar keine Signifikanz bestätigte, aber dennoch von praktischer Relevanz sein könnte, die es zu erforschen gilt.

Derzeit wurden diese Werte manuell hinzugefügt, aber zukünftige Arbeiten könnten die programmatische Integration solcher Werte in MetaTrader 5 für automatisierte Tests über mehrere Paare und Zeitrahmen beinhalten. Siehe Abbildung 6 unten zur Veranschaulichung.

Abbildung 6. Neue Levels aufgelöst

Schlussfolgerung

Dieses Projekt wurde von Ehrgeiz und Neugier getrieben – von chartbasierten Beobachtungen der Kursentwicklung innerhalb des Fibonacci-Retracement-Rahmens über das Erkennen von Unregelmäßigkeiten in der Interaktion des Kurses mit bekannten Niveaus bis hin zur Frage, ob zwischen den traditionellen Retracement-Punkten versteckte Niveaus existieren könnten. Um diese Ideen zu erforschen, kombinierten wir MQL5 für die automatische Datenerfassung mit Python in der interaktiven Webumgebung Jupyter, die leistungsstarke Werkzeuge für die Datenanalyse, Visualisierung und mehrsprachige Integration bietet.

Obwohl wir erfolgreich erste Ergebnisse erzielt haben, traten einige Herausforderungen auf. Unser Datensatz war begrenzt, und die manuelle Anwendung von berechneten Retracement-Werten auf Charts war vielversprechend, entsprach aber nicht unseren ursprünglichen Hypothesen. Dies deutet darauf hin, dass sowohl unser Datenerfassungsprozess als auch unsere Methoden zur Erkennung von Schwankungen und Rückschritten möglicherweise noch verfeinert werden müssen. Eine Ausweitung der Analyse auf mehrere Währungspaare und Zeitrahmen sowie eine Überarbeitung der Erkennungsalgorithmen würde die Genauigkeit und Zuverlässigkeit wahrscheinlich verbessern.

Trotz dieser Rückschläge ist das Fundament, das wir gelegt haben, wertvoll. Es zeigt, wie MQL5 und Python für die quantitative Handelsforschung kombiniert werden können und dient als praktischer Ausgangspunkt für Anfänger, die die Automatisierung von Handelsplattformen mit Data Science verbinden wollen. Obwohl die anfänglichen Ergebnisse unsere Erwartungen nicht vollständig erfüllten, zeigen die Charts weiterhin interessante Möglichkeiten auf, die eine weitere Untersuchung wert sind. Mit robusteren Tests und verfeinerten Methoden könnte diese Forschungsrichtung immer noch Einblicke in verborgene Retracement-Dynamiken gewähren.

Anders als bei der Hinzufügung nutzerdefinierter Retracement-Levels, die auf Vermutungen beruhen, nutzt dieser Ansatz die Datenwissenschaft zusammen mit den verfügbaren MQL5-Tools, um Effizienz und Struktur in den Prozess zu bringen. Nachstehend finden Sie eine Tabelle mit den beigefügten Ressourcen. Sie sind herzlich eingeladen, die Quellen und Experimente durchzugehen und Ihre Gedanken zur weiteren Diskussion mitzuteilen. Bis zur nächsten Veröffentlichung, bleiben Sie dran.

Anlagen

Dateiname	Version	Beschreibung
CandleRangeData.mq5	1.0	MQL5-Skript, das Kerzenbereichs- und Retracement-Daten aus MetaTrader 5-Charts sammelt und in das CSV-Format zur Analyse exportiert.
HiddenFiboLevels.ipynb	K.A.	Jupyter Notebook mit Python-Code zum Laden der exportierten CSV-Datei, Bereinigen der Daten, Testen potenzieller versteckter Fibonacci-Retracement-Levels und Visualisieren der Ergebnisse.
CandleRangeData_NZDUSD_H4.csv	K.A.	Vom MQL5-Skript erzeugter Beispieldatensatz für das Währungspaar NZDUSD auf dem H4-Zeitrahmen, der als Input für die Python-Analyse verwendet wird.