Statistische Verifizierung des Labouchere-Geldverwaltungssystems

Es gibt drei verschiedene Arten von Lügen: Lügen, verdammte Lügen, und Statistiken.

Einführung

Während ich am Wochenende in den Tiefen des Internets umhersurfte, stieß ich auf ein Geldverwaltungssystem, von dem ich zuvor niemals gehört hatte. Es trägt den Namen Labouchere, und es ist auch als „Abbruchsystem“ bekannt ( Ein Devisenhandels-„Staubsaugersystem“ unter Benutzung von Labouchere, auf Russisch). Die englische Beschreibung des Systems finden Sie hier: here. Das System stellt eine Variante von Martingale dar, weil Sie Ihre Einsätze erhöhen müssen, wenn Sie zuvor verloren haben – und umgekehrt verringern Sie Ihre Einsätze, nachdem Sie gewonnen haben. Allerdings stellt dieses System eine weniger aggressive Version dar, weil die Einsätze hierbei nicht verdoppelt werden, sondern stattdessen um einen bestimmten Betrag erhöht werden.

Untenstehend finden Sie einige der Passagen, welche die Funktion des Systems beschreiben, und die mich besonders beeindruckt haben:

• „Also: Bitte beachten Sie, dass die Anzahl der profitablen Trades mindestens bei 33 - 40 % liegen sollte, damit das System korrekt arbeiten kann und Sie gewinnen können!!!“  – Dies ist ein äußerst starkes Statement. Allerdings geht daraus nicht eindeutig hervor, weshalb der anfängliche Prozentbereich so breit gewählt ist – von 33 % bis hin zu 40 %.

• „Behalten Sie bitte stets im Hinterkopf, dass diese Methode von Spielcasinos als ein betrügerisches Vorgehen beim Spielen betrachtet werden kann.“  –  Wirklich? Kann dieses Schema also tatsächlich funktionieren?!

• „Aber das Prinzip bleibt dasselbe – 33 % an Gewinnen kompensieren 66 % an Verlusten. Wenn Sie also dieses Geldverwaltungsschema im echten Devisenhandel einsetzen möchten, dann benötigen Sie ein Handelssystem, bei dem Sie eine Gewinnchance von 50 % und einen Gewinnfaktor von >=1 besitzen.“

In der Tat heißt es im erwähnten Artikel, dass Sie ein Handelssystem benötigen, wo die Anzahl der gewinnbringenden Handelsgeschäfte genau der Anzahl der verlustbringenden Handelsgeschäfte entspricht, und die Gewinnwahrscheinlichkeit also bei 50 % (oder zumindest „mehr als 33 %“) liegt. Falls Sie über ein solches System verfügen, dann kann die Labouchere-Methode es für Sie ganz einfach profitabel machen! Müssen wir aber überhaupt nach einem mathematischen System suchen, das uns eine solche Gewinnswahrscheinlichkeit verspricht, weil es eine Möglichkeit gibt, es in den positiven Bereich hineinzubringen? Es ist schließlich nicht allzu schwierig, ein Handelssystem zu konzipieren, das in 47 % der Fälle zu gewinnbringenden Handelsgeschäften führt...

Lassen Sie uns einmal sehen, inwiefern das Labouchere-System unsere Gewinne beeinflusst.

Der Mindesteinsatz wird im Allgemeinen als eins angenommen. Wenn wir gewinnen, dann bleibt die Größe des Einsatzes gleich, während unsere Handelsbilanz sich leicht erhöht.

Wenn wir verlieren, dann wird die Größe unseres Einsatzes um eins erhöht – bis hin zu 2, und wir addieren die Größe des verlustbringenden Einsatzes zum nächsten Einsatz dazu :

-1

Falls wir an dieser Stelle gewinnen, dann sollten wir 2 zu unserem nächsten Einsatz addieren :

-1 2

Dann streichen wir diese beiden Nummern durch, weil wir es geschafft haben, unseren Verlust wieder zurückzugewinnen (in anderen Worten: Wir haben unseren Kontostand im Zuge einer Serie aus zwei Spieleinsätzen um eins erhöht).

Jetzt möchten wir uns einmal den Fall einer längeren Serie von verlustbringenden Handelsgeschäften ansehen.

-1

Unser Einsatz beträgt 2. Der Verlust:

-1 -2

Unser Einsatz beträgt 3. Der Verlust:

-1 -2 -3

Unser Einsatz beträgt 4. Der Verlust:

-1 -2 -3 -4

Unser Einsatz beträgt 5. Der Verlust:

-1 -2 -3 -4 -5

Unser Einsatz beträgt 6. Wieder einmal der Verlust:

-1 -2 -3 -4 -5 -6

Unser Einsatz beträgt 7. Jetzt endlich gewinnen wir :

-1 -2 -3 -4 -5 -6 +7

Daher streichen wir also "-1", "-6" und "+7" durch, weil unser erfolgreicher Einsatz die beiden verlustbringenden Spielrunden wieder ausgeglichen hat. Der nächste Einsatz besteht aus der Summe des ersten und des letzten der Werte, die noch in der Zeile verbleiben, d.h. er ist wieder einmal 7. Falls wir gewinnen:

-2 -3 -4 -5 +7

Wir streichen "-2", "-5" und "+7". Unser nächster Einsatz ist wieder einmal die Summe des ersten und des letzten der Werte, die noch in der Zeile verbleiben. Ja, es ist wieder einmal 7 (einige Anwender der Methode empfehlen, zu solch einem Einsatz 1 hinzu zu addieren, sodass Sie den Minimalgewinn anstelle von 0 erhalten, wenn Sie Glück haben sollten). Falls wir gewinnen:

-3 -4 +7

Wir streichen sämtliche Zahlen, die in der Zeile verbleiben, weil wir all unsere Verluste zurückgewonnen haben.

Falls wir bei einem der Zwischenschritte einen Verlust einfahren sollten, dann wird die Größe dieses Verlustes ebenfalls in die Zeile eingetragen, und der nächste Spieleinsatz entspricht dann der Summe des ersten und des letzten Wertes in der Zeile.

Was sind also unsere ersten Schlussfolgerungen?

1. Eine Serie von sechs Verlusten wird in der Tat durch eine Serie von nur drei Gewinnen kompensiert (allerdings sollte es tatsächlich eine Serie sein; wir werden später darüber sprechen). Auf den ersten Blick scheint es uns dieses System wirklich sehr einfach zu machen, den Markt ohne jegliche Verluste zu verlassen.

2. Die Höhe des Einsatzes wird hierbei viel langsamer erhöht als beim System von Martingale. Falls wir eine solche Serie mit dem ursprünglichen Martingale-System durchgespielt hätten, dann hätte unser letzter Spieleinsatz den ersten Einsatz um das 64-fache übersteigen müssen.

3. Der gesamte Absenkungsbetrag der Einzahlungen (d.h. die Summe der verlorengegangenen Einsätze) im obigen Beispiel beträgt lediglich 21, während sie beim ursprünglichen System von Martingale bei 63 gelegen hätte.

4. Einfache Berechnungen zeigen uns, dass wir 13 Verluste in Folge erleiden müssten, um all unsere Gelder zu verlieren, falls der ursprüngliche Einsatz ein Prozent des Einzahlungsbetrages betragen würde, und es wären 44 Verluste infolge erforderlich, falls der ursprüngliche Einsatz bei 0,1 % liegen sollte. Sie denken sich jetzt vielleicht Folgendes: „44 Verluste in Folge bei einem Gewinn-Verlust-Verhältnis von 50/50!? Die Wahrscheinlichkeit für den Eintritt dieses Falls ist unglaublich klein! Es ist viel wahrscheinlicher, dass ich von einem Meteoriten erschlagen werde! Mit einer solchen Wahrscheinlichkeit kann ich sehr gut leben!“, etc.).

5. Sie können ganz leicht eine Vielzahl von Studien finden, welche die Nachteile und Gefahren des Systems von Martingale beschreiben. In der Tat können Sie diese Nachteile selbst überprüfen, indem Sie ganz einfache Berechnungen mithilfe eines Bleistiftes und einem Stück Papier anstellen. Allerdings war ich nicht in der Lage, ähnliche Studien in Bezug auf das Labouchere-System zu finden.

6. Das Spielsystem schaut äußerst kompliziert aus, und daher fällt die Berechnung der mathematischen Eintrittswahrscheinlichkeit auch recht schwer.

Aber lassen Sie uns zu unserer verlustbringenden Serie von Spielen zurückkehren. Nehmen wir einmal an, dass auf unsere sechs Verluste in Folge nur zwei Gewinne gefolgt wären: 3. Dann würde unsere Zeile von Zahlen wie folgt aussehen:

-3 -4

Wir setzen 7 aufs Spiel und verlieren:

-3 -4 -7

Wir setzen 10 aufs Spiel (beachten Sie, dass wenn wir verlieren, der Spieleinsatz um 3 anstelle von 1 ansteigt, wodurch die Serie für unsere ursprüngliche Einzahlung viel gefährlicher wird). Wir verlieren abermals:

-3 -4 -7 -10

Wir müssen jetzt einen Einsatz von 13 tätigen.

Das System erfordert also, dass wir unsere Einsätze um mehr als 1 erhöhen, falls es zu wiederholten Verlusten kommt. Dies scheint der einzige Weg zu sein, um die erlittenen Verluste vollständig wieder auszugleichen. Und an dieser Stelle kann unser ursprünglicher Einzahlungsbetrag wirklich in Gefahr kommen, weil wir nämlich eine Serie von Gewinnen benötigen, um den erlittenen Verlust wieder auszugleichen. Die Kalkulation auf Papier erscheint uns als zu kompliziert und langweilig...

Sind Sie daran interessiert, was dieses System leisten kann? Falls ja, dann lassen Sie uns noch tiefer in die Materie eintauchen.

Bestimmung der Aufgabe: Thema und Methoden

Die wichtigste Frage ist diejenige, ob das Geldverwaltungssystem von Labouchere wirklich in der Lage ist, eine mathematische Wahrscheinlichkeit zu unseren Gunsten zu verschieben (d.h. in den positiven Bereich). Die zitierte Passage, welche eine Bedingung von 33 % an gewinnbringenden Spielrunden nennt, erscheint uns als recht unrealistisch, wie wir gar nicht weiter betonen müssen. Aber wäre ein Anteil an gewinnbringenden Runden in Höhe von 49 % oder 50 % genug? Und falls nicht, hat das System von Labouchere dann vielleicht irgendwelche anderen Vorteile zu bieten?

Wir werden Statistiken verwenden, was bedeutet, dass wir hierzu ein MQL-Programm entwickeln müssen (in diesem Fall handelt es sich um MQL4, weil ich MQL5 noch nicht vollständig beherrsche). Wir werden unser Programm Millionen von Spielrunden durchlaufen lassen und dabei tausende von Einzahlungsbeträgen „vernichten“ lassen – und dann werden wir uns die Resultate davon ansehen, ohne dass wir unser echtes Kapital aufs Spiel gesetzt hätten. Falls das Programm sich als profitabel erweisen sollte, dann wird es auch möglich sein, diesen Algorithmus im echten Trading einzusetzen.

Das System von Labouchere wurde auf der Gewinn-Verlust-Annahme aufgebaut. Es kann ebenfalls für andere Verhältnisse adaptiert werden, allerdings scheint mir dies nicht praktikabel. Falls das System die mathematische Wahrscheinlichkeit mit Gewinn = Verlust beeinflussen kann, dann kann es ebenfalls andere Verhältnisse beeinflussen – und falls es dazu nicht in der Lage sein sollte, dann würden wir ganz einfach unsere Zeit damit verschwenden, uns mögliche Adaptierungen zu überlegen.

Darüber hinaus können wir uns das System mit Gewinn = Verlust und einem Gleichgewichtswert von 50 % an gewinnbringenden Werten sehr viel leichter vorstellen, weil wir alle mit dem Werfen einer Münze vertraut sind. Wir möchten unserem Programm daher den Namen Münzentest geben.

Zunächst sollten wir die Hauptfunktionen unseres künftigen Programms beschreiben:

1. Wir sollten die Möglichkeit dazu haben, die Gewinnwahrscheinlichkeit zu verändern. Ein Verhältnis von 50/50 ist lediglich ein Spezialfall eines Gleichgewichtswertes.

2. Wir sollten auch die Möglichkeit haben, ein Risikoniveau festzulegen. Das Labouchere-System arbeitet mit einer festen Einsatzgröße. Falls wir die Größe unseres anfänglichen Einsatzes allerdings der Größe unserer Einzahlung anpassen, dann wird das System überhaupt nicht mehr funktionieren, weil unser Einzahlungsbetrag nie wieder zu seiner ursprünglichen Größe zurückkehren wird, nachdem sämtliche Werte aus der Zeile gestrichen wurden. Wir können allerdings die Größe des Wetteinsatzes, nachdem wir einen Verlust erlitten haben, neu kalkulieren – allerdings wird dies zu Bruchzahlen führen, mit denen man nur schwer arbeiten kann. Daher werden wir zwei Variablen verwenden, um das Risikoniveau einzustellen – die Größe der ursprünglichen Einzahlung und die Höhe des anfänglichen Spieleinsatzes.

3. Es ist notwendig, eine maximale Anzahl der Spielrunden pro Einzahlung zu definieren. Diese Anzahl sollte groß genug sein, sodass wir herausfinden können, ob wir den Einzahlungsbetrag verlieren werden – auch dann, wenn wir mit einem äußerst niedrigen anfänglichen Risiko beginnen. Schließlich könnte sich der Prozess endlos hinziehen, wenn der ursprüngliche Einzahlungsbetrag durch Gewinne immer weiter ansteigt, und auf diese Weise würden wir vielleicht nie das Ergebnis erfahren.

4. Wir sollten ebenfalls über eine Möglichkeit verfügen, um die Ergebnisse von Handelsserien mit einem einzigen Einzahlungsbetrag zu analysieren, sowohl um das Programm zu debuggen, als auch, um unsere Handelslogik zu überdenken. Ein Ausdruck der entsprechenden Daten in eine Datei wird für unsere Zwecke genügen.

5. Nachdem wir damit fertig sind, einen Code für einen einzelnen Einzahlungsdurchgang zu schreiben, sollten wir damit fortfahren, die Statistiken von einer Serie von Durchgängen mit separaten Einzahlungen und (idealerweise) mit verschiedenen Parametern zu sammeln. Wie Sie sich vorstellen können, bedeutet das Ergebnis eines einzigen Experimentes in diesem Zusammenhang nur sehr wenig. Die statistischen Ergebnisse werden ebenfalls in der vorgenannten Datei dokumentiert werden. Wir werden nicht mehr länger eine Chronik der individuellen Einzahlungen analysieren müssen.

Unser automatisiertes System zur Wahl der Größe des Einsatzes kann möglicherweise im echten Trading eingesetzt werden, und daher sollten wir es wirklich perfekt machen.

Die tatsächliche Eröffnung von Handelsgeschäften in MetaTrader ist für uns zu diesem Zeitpunkt vollkommen nutzlos, und darüber hinaus wäre sie extrem rechenintensiv und würde zu viele Computerressourcen in Anspruch nehmen. Wir müssen lediglich die Resultate von zufälligen Handelsgeschäften festhalten, bei denen wir eine erforderliche Losgröße und eine vorgegebene Gewinnwahrscheinlichkeit verwenden. Mit diesem Gedanken im Hinterkopf werden wir ein Skript entwickeln, weil diese Art von MQL-Programmen sich perfekt für einen einzelnen Durchgang eignet, verglichen mit Expert Advisors oder Indikatoren.

Die statistische Verifizierung der Qualität des Pseudozufallszahlengenerators

Die Qualität des Pseudozufallszahlengenerators (PRNG) ist für uns von größter Wichtigkeit, weil dieser nämlich dazu benutzt werden wird, um das Ergebnis jedes einzelnen Handelsgeschäftes zu bestimmen (d.h. Gewinn oder Verlust). Die Akkuratheit einer langen Serie von Gewinnen und Verlusten und deren Verteilung ist von entscheidender Bedeutung. Wir werden versuchen, Letzteres zu evaluieren, ohne dabei auf komplizierte mathematische Theorien über die Statistik zurückzugreifen.

Dieser Artikel hat es sich nicht zum Ziel gesetzt, eine ernsthafte Studie über die Qualität des PRNG durchzuführen (wenn wir dies tun wollten, dann müssten wir 15 verschiedene Testreihen durchführen). Wir sind vorrangig an den Qualitäten des PRNG interessiert, welche das System von Labouchere und dessen Testergebnisse beeinflussen – und daher benötigen wir keine allzu komplexen Überprüfungsprozeduren.

MetaTrader beinhaltet die standardisierte MathRand()-PRNG-Funktion. Die PRNG-Sequenz wird dabei durch die iMathSrand()-Funktion initialisiert.

Lassen Sie uns ein kleines Skript (RandFile) schreiben, um die Qualität des standardmäßig bereitgestellten PRNG zu überprüfen. Diese Skript wird über zwei Parameter verfügen:

• Die Anzahl (in Millionen) der zufälligen 32-bit-Wörter, welche generiert werden sollen (ein 32-bit-Wort je drei Aufrufen der MathRand()-Funktion; dies liefert 15 signifikante Bits). Die Maßeinheit ist die übliche Dezimalmillion, anstelle von 2 erhöht zur 20. Potenz, weil wir nämlich die Resultate auch visuell analysieren möchten.

• Der logische Parameter ist CalcSeries (falls die Distribution von ähnlichen Bitserienlängen kalkuliert werden soll).

Die Kalkulation der Verteilung von Bitserienlängen ist äußerst ressourcenintensiv (und dadurch erhöht sich die Ausführungszeit des Skriptes um das Zehnfache). Daher wurde es als eine separate Option arrangiert.

Das Skript produziert die folgenden Resultate:

• Die Berechnung time (angezeigt im Journal);
• Die Anzahl von 1 bits, die unter allen anderen generierten Bits festgestellt wurden (angezeigt im Journal);
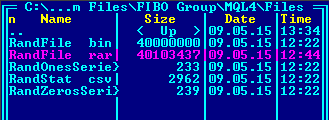
• RandFile.bin-Datei — eine Binärdatei mit dem Operationsergebnis des PRNG;
• RandStat.csv-Datei — eine Log-Datei mit den Häufigkeitsraten bestimmter Bytes ;
• RandOnesSeries.csv-Datei — eine Log-Datei mit den "1"-Bit-Serienlängen;
• RandZerosSeries.csv-Datei — eine Log-Datei mit den"0"-Bit-Serienlängen.

Lassen Sie uns drei Testreihen von verschiedener Länge generieren:

• 10 Millionen Testwörter von jeweils 4 Bytes (40 Millionen Bytes insgesamt);
  
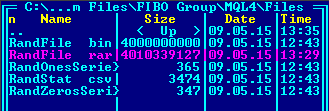
• 100 Millionen Testwörter von jeweils 4 Bytes (400 Millionen Bytes insgesamt);
• 1000 Millionen Testwörter von jeweils 4 Bytes (4000 Millionen Bytes insgesamt).

Jetzt wollen wir die folgenden Parameter überprüfen :

1. Komprimierbarkeit der Dateien mit Zufallsdaten durch WinRAR mit den maximalen Kompressionseinstellungen. Hochqualitative Zufallsdaten lassen sich nicht komprimieren. Natürlich ist die mangelnde Komprimierbarkeit bestimmter Dateien keine Garantie dafür, dass es sich bei ihrem Inhalt tatsächlich um hochqualitative Zufallsdaten handelt. Aber wenn sich diese Dateien komprimieren lassen, dann bedeutet dies, dass die Daten über statistische Regelmäßigkeiten verfügen.

   

   

   

2. Anzahl von "1" -Bits :
   

   	Gleichgewichtswert	tatsächlicher Wert	Absolute Abweichung	Abweichung, %
   10 Millionen	160 000 000	160 004 431	4 431	0,0027694
   100 Millionen	1 600 000 000	1 599 978 338	21 662	0,0013539
   1000 Millionen	16 000 000 000	15 999 996 180	3 820	0,0000239

3. Häufigkeitsrate von bestimmten Bytes' und deren Werten in zufälligen Dateien:

   
   

   
   

   
   

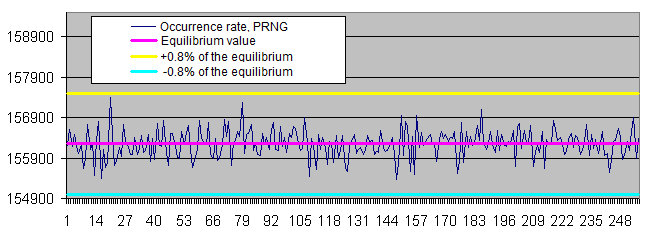
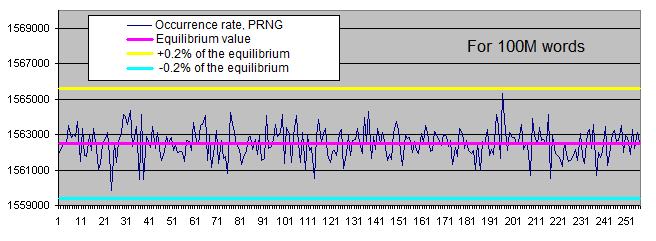
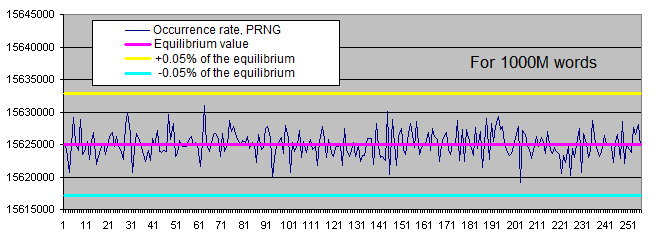
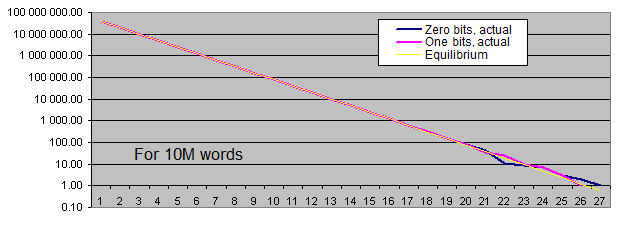
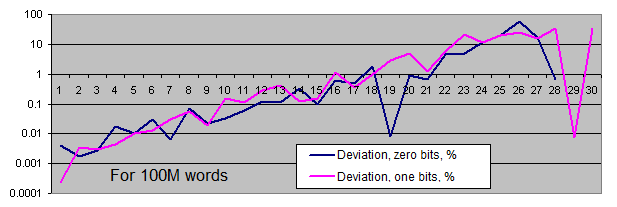
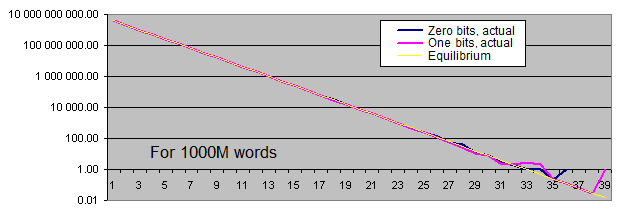
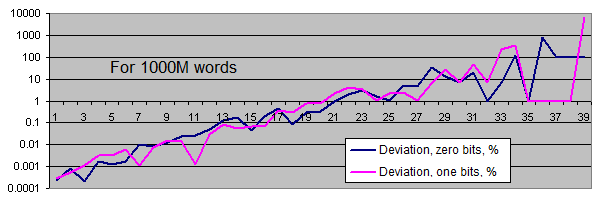
4. Längen von identischen Bit-Serien . Wir werden zwei Charts für jede Probengröße generieren :

   • Der erste Chart zeigt die tatsächliche Anzahl von festgestellten identischen Bit-Serien einer bestimmten Länge an, sowie den Gleichgewichtswert der Anzahl der Serien dieser Länge (in logarithmischer Darstellung);
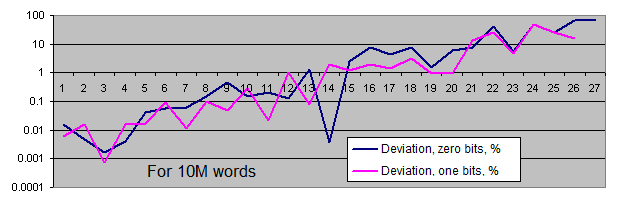
   • Der zweite Chart zeigt die prozentuale Abweichung des tatsächlichen Betrages der festgestellten identischen Bit-Serien vom Gleichgewichtswert an (in logarithmischer Darstellung).

   Das lineare Chartschema ist nicht für uns geeignet, weil unsere Werte extrem breit gestreut sind (die Werte rangieren von 1 bis 4.000.000.000, oder von 0,00001 bis 6000 – und sie müssen alle auf einem einzigen Chart dargestellt werden). Darüber hinaus wird der Chart, der den Gleichgewichtswert der Anzahl der langen Serien in einem logarithmischen Schema darstellt, als eine durchgehende Linie gezeichnet – d.h. während die Länge der Serie sich um 1 erhöht, halbiert sich die Wahrscheinlichkeit ihres Auftretens.

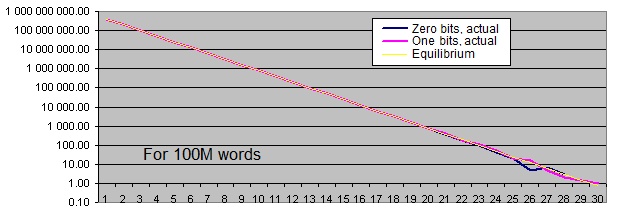
Was sind also nun unsere Schlussfolgerungen?

• Die Standard-Effizienz des PRNG ist für unsere Aufgabe akzeptabel.

• Die Archivierung der Dateien, welche das Ergebnis der Arbeit des PRNG enthalten, erlaubt nicht deren Kompression.

• Die Anzahl der Bits von null und eins korrespondiert mit dem Äquidistanzwert. Die Abweichung vom Gleichgewichtswert (als Prozentsatz) nimmt ab, während die Probengröße zunimmt.

• Die Verteilung der Häufigkeitsrate bestimmter Bytes in den Arbeitsresultaten des PRNG fluktuiert innerhalb eines engen Bandes rund um den Gleichgewichtswert. Die Streuung der Häufigkeitsrate reduziert sich, während die Probengröße erhöht wird.

• Die Häufigkeitsrate von identischen Bit-Serien weicht vom Gleichgewichtswert lediglich dann ab, wenn die Serie ziemlich lang ist (was recht selten der Fall ist). Mit der Erhöhung der Länge der Testreihe bewegt sich die tatsächliche Häufigkeitsrate des „Abweichungspunktes“ mit dem Anstieg der Serienlänge weg vom Gleichgewichtswert, und sie bewegt sich rund um den Wert von 100 Inklusionen für die gesamte Sequenz.

Daher haben wir keinerlei größeren statistischen Fehler in dem standardmäßigen PRNG entdeckt, welche dazu geeignet wären, unsere Testergebnisse zu verfälschen – selbst bei Sequenzen von ungefähr 3 Milliarden Generierungen (3 Generierungen werden pro 32-bit-Wort benutzt).

Das Schreiben der CLabouchere-Klasse für die Verwaltung der Positionsgrößen

Die CLabouchere-Klasse hat sich als klein genug herausgestellt. Ihr Interface besteht lediglich aus zwei Wrapper -Funktionen für die Einstellung/den Empfang der anfänglich gewählten Los-Größe sowie zwei tatsächlichen Arbeitsfunktionen – für die Einstellung eines Handelsergebnisses und den Empfang der aktuellen Positionsgröße, sowie für die Rückstellung auf den ursprünglichen Zustand :

// Labouchere money management.
// Take/stop is assumed = 1/1.
class CLabouchere
{
        private:
        protected:
                // Initial lot. By default - 0.1.
                double p_dStartLot;

                // The string where numbers are stored according to Labouchere
                double p_dLotsString[];
        public:
                void CLabouchere();
                void ~CLabouchere();

                double GetStartLot() {return p_dStartLot;};
                void SetStartLot(double a_dStartLot) {p_dStartLot = a_dStartLot;};

                // Return a lot that is to be used during the next market entry
                double GetCurrentLot();

                // Write the current trade result - take (true) or stop (false)
                void SetResult(bool a_bResult);

                // Reset to the initial state except for the initial lot
                void Init() {ArrayResize(p_dLotsString, 0);};
};

Das Schreiben des Skriptes. Vorläufige Evaluierung

Jetzt es ist an der Zeit, ein einfaches Skript zu schreiben, das über ungefähr 100 Strings verfügen wird. Die Eingabeparameter sind wie folgt :

//--- input parameters
input int RepeatsCount=100000;
input int StartBalance = 10000;
input int Take = 50;
input double SuccessPercent = 50.0;
// If true, SuccessPercent is ignored
input bool FiftyFifty = true;

Das Skript nimmt eine Reihe von Handelsvorgängen vor – so lange, bis der ursprüngliche Einzahlungsbetrag verloren ist, oder bis der RepeatsCount erreicht wurde.

Der Fall eines Gewinn-/Verlust-Verhältnisses = 50/50 wird als separater Parameter eingestellt. In diesem letzteren Fall wird ein Bild einer Pseudo-Zufallszahl dazu benutzt, einen Münzwurf zu simulieren. Andernfalls wird ein Gewinn-/Verlust-Grenzwert kalkuliert und mit einer Zufallszahl verglichen. Der separate Parameter für das Verhältnis von 50/50 wurde implementiert, weil der Arbeitszyklus des PRNG bezüglich einzelner Bits für uns ziemlich gut passt, obwohl wir keine Evaluation der Auftrittszyklen der Werte jenseits eines Grenzwertes vorgenommen haben.

Die Voreinstellungen :

• Einzahlungsgröße – 10.000;
• Anfänglicher Einsatz – 50 (0,5 % der ursprünglichen Einzahlung).

Ungefähr nach dem zehnten Durchlauf des Skriptes erhalten wir ein spektakuläres Resultat – der Einzahlungsbetrag beträgt nachdem 2335. Schritt 46.300. Allerdings kommt es bereits nach dem 2372. Schritt zu herben Verlusten:

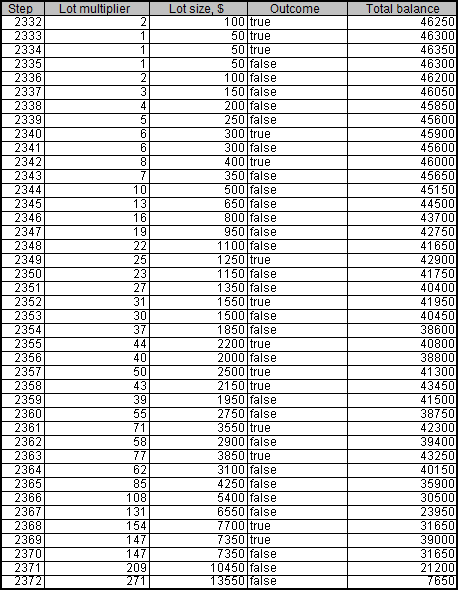
So sieht das Ganze dann auf dem Chart aus :

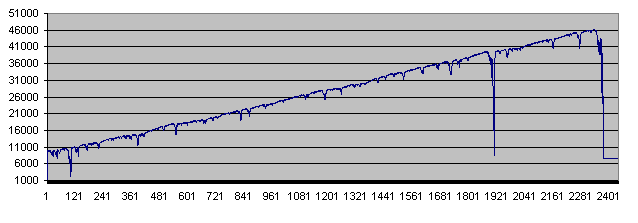
Wie wir sehen können, ist der Kontostand zweimal auf kritische Werte gefallen, bevor das Guthaben schließlich vollkommen verbraucht war.

In einigen Fällen wurde der ursprüngliche Einzahlungsbetrag innerhalb der ersten paar Dutzend Handelsvorgänge ausgelöscht – und es gab keinen einzigen Fall, wo der ursprüngliche Einzahlungsbetrag eine Lebenszeit von mehr als 100.000 Handelsvorgängen hatte.

Während ich verschiedene Parameter ausprobierte, kamen mir folgende Änderungen in den Sinn :

• Es erscheint mir als vernünftig, einen weiteren Parameter hinzuzufügen, welcher den Betrag der Gelder definiert, dievom Handelskonto abgebucht werden sollen. Falls wir es schaffen könnten, die Gelder vom Handelskonto abzuziehen, welche den ursprünglichen Einzahlungsbetrag übersteigen, bevor dieser schließlich ausgelöscht wird, dann wird unser ursprünglicher Einzahlungsbetrag ganz einfach zu einem vorhersehbaren Verlust. Daher habe ich einen neuen Parameter namens PocketPercent implementiert. Diese definiert den Prozentsatz erfolgreicher Handelsvorgänge, den wir vom Handelskonto abbuchen und dessen Gelder wir somit „in unsere Tasche stecken“. Der Zugriff auf dieses „Taschengeld“ ist anschließend verboten, und lediglich die Gelder, welche sich noch auf dem Handelskonto befinden, werden somit dem Risiko des Verlustes ausgesetzt. Und das ist auch gut so, denn auf diese Art und Weise läuft es üblicherweise im echten Leben ab.

• Natürlich sollte der ursprüngliche Einzahlungsbetrag viele Male hintereinander in einer Schleife gestartet werden (es wäre eine ziemlich eintönige Aufgabe, den Start hunderte von Malen manuell vornehmen zu müssen). Wir sollten also einige der Parameter variieren – PocketPercent und Take (die anfängliche Größe des Einsatzes), und darüber hinaus die durchschnittlichen Ergebnisse kalkulieren (d.h. die „Taschengelder“ und die Einzahlungsgelder, weil der ursprüngliche Einzahlungsbetrag niemals ganz auf Null reduziert werden wird, sondern lediglich bis zu dem Betrag, ab dem es nicht mehr möglich ist, den nächsten Trade einzugehen).

• Wir sollten über zwei Versionen des Skriptes verfügen: Die erste Version soll wiederholte Handelsvorgänge durchführen, ohne dabei die Details darüber in eine Datei zu schreiben, während die zweite Version in einer umgekehrten Art und Weise funktionieren soll. Wiederholte Durchgänge bedeuten, dass wir den Objekt-Code benutzen sollten. Daher entwickeln wir den „Arbeitscode“ als die CCoinTest-Klasse, während wir die Skripte so einfach wie möglich ausgestalten.

Der Code für das Skript für den einfachen Durchgang ist so einfach, dass ich ihn hier in Gänze zeigen kann (die ganze Arbeit, inklusive des Schreibens der Handelsdokumentation in eine Datei, wird durch die CCoinTest-Klasse erledigt):

#include <CCoinTest.mqh>

//--- input parameters
input int RepeatsCount=100000;
input int StartBalance = 10000;
input int Take = 50;
input int PocketPercent = 10;
input double SuccessPercent = 50.0;
input string S2 = "If true, SuccessPercent is ignored";
input bool FiftyFifty = true;
input string S3 = "If true, use a fixed lot instead of Labouchere";
input bool FixedLot = false;

void OnStart()
{
        MathSrand(GetTickCount());

        CCoinTest Coin;

        Coin.SetRepeatsCount(RepeatsCount);
        Coin.SetStartBalance(StartBalance);
        Coin.SetTake(Take);
        Coin.SetPocketPercent(PocketPercent);
        Coin.SetSuccessPercent(SuccessPercent);
        Coin.SetFiftyFifty(FiftyFifty);
        Coin.SetFileName("Coin.csv");
        Coin.SetFixedLot(FixedLot);

        Coin.Go();
}

Nachdem wir das Taschengeld hinzugefügt haben, stellt sich der Chart der Arbeit des Systems ein wenig anders dar (40% des Gewinns werden im folgenden Beispiel abgebucht):

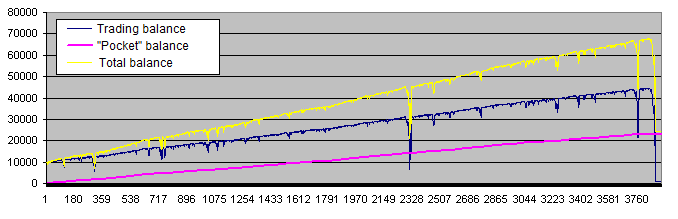
Die lilafarbene Linie (der Kontostand für das „Taschengeld“) gleicht dem perfekten Chart eines Handelskontos, von dem jeder Trader träumt. Aber in der Tat sollten wir der gelben Linie größere Beachtung schenken (dem Gesamtkontostand des Handelskontos und des „Taschengeldes“), und diese Linie sieht nicht so gut aus. Darüber hinaus sind die folgenden Charts viel weiter verbreitet :

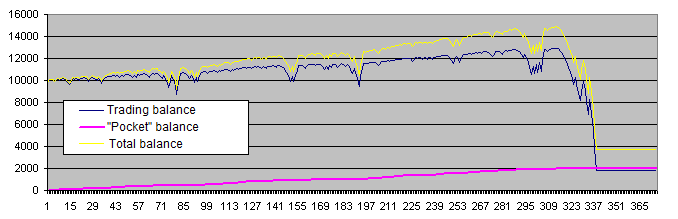
Untenstehend sind unsere Schlussfolgerungen zum gegenwärtigen Zeitpunkt :

• Das System demonstriert tatsächlich das Verhalten, welches vom Autor beabsichtigt war: Die Verluste im Handel werden oftmals wieder ausgeglichen, und der ursprüngliche Einzahlungsbetrag steigt weiter an.

• Manchmal enden solche Versuche allerdings auch in vollständigen Fehlschlägen. Tatsächlich hat das System lediglich zwei Optionen zur Verfügung, nachdem ein Verlust aufgetreten ist – es kann den Verlust entweder wieder ausgleichen, oder aber den gesamten ursprünglichen Einzahlungsbetrag verlieren.

• Je länger der ursprüngliche Einzahlungsbetrag überlebt, umso größere Kontostände werden erreicht.

• Der anfängliche Einsatz bei diesen Beispielen beträgt 0,5 % des ursprünglichen Einzahlungsbetrages (50 von 10.000). Im ersten Beispiel wurde das zugrundeliegende Risikoniveau auf ungefähr 0,1 % reduziert (der ursprüngliche Einzahlungsbetrag wurde auf das 4,5 fache vermehrt, wobei der anfängliche Einsatz stets gleich blieb). Allerdings konnten auch diese Maßnahmen den ursprünglichen Einzahlungsbetrag nicht vor dem letztendlichen Verlust bewahren.

Abschließende Evaluierung für verschiedene Wahrscheinlichkeitswerte. Vergleich der Resultate des Labouchere-Systems mit Systemen, die auf festen Einsätzen basieren

Jetzt kommen wir zum aufregendsten Teil der Veranstaltung – wir sammeln die Ergebnisse von vielen verschiedenen Experimenten. Wir stehen kurz davor, herauszufinden, ob die Gewinne von erfolgreichen Handelsgeschäften in der Lage sind, die Verluste der fehlgeschlagenen Handelsgeschäfte auszugleichen. Vielleicht stellt sich der Algorithmus als effizient heraus, falls die anfängliche Größe des Einsatzes niedriger gewählt wird (dadurch erhalten wir einen besseren Schutz für den Einzahlungsbetrag) – oder vielleicht sollte die anfängliche Größe des Einsatzes sogar höher gewählt werden? Welchen Prozentsatz der erzielten Gewinne sollten wir von einem Handelskonto abbuchen? Wird sich das System von Labouchere überhaupt im Vergleich mit einem System, das mit einer festen Rate arbeitet, unterscheiden? Und was wird passieren, falls das ursprünglich gewählte System eine positive mathematische Wahrscheinlichkeit hat (die „Münze“ gewinnt öfter)? Wie Sie bereits sehen können, gibt es jede Menge Fragen, die wir in einer geeigneten Art und Weise beantworten sollten.

Das Skript, mit dem die ursprünglichen Einzahlungsbeträge in eine Schleife mit verschiedenen Parametern eingebracht werden, besteht aus ungefähr 100 Strings. Ich werde Ihnen hier lediglich ein paar Fragmente zeigen.

Die Eingabeparameter :

//--- input parameters
input int RepeatsCount=100000;
input int StartBalance = 10000;
input string S1 = "Amount of deposits lost";
input int Deposits = 100;
input double SuccessPercent = 50.0;
input string S2 = "If true, SuccessPercent is ignored";
input bool FiftyFifty = true;
input string S3 = "If true, use a fixed lot instead of Labouchere";
input bool FixedLot = false;

Die Arrays, welche die anfängliche Größe des Einsatzes enthalten, und der Gewinnanteil in Prozent, den wir uns „in die Tasche stecken“:

// PocketPercent array
int iPocketPercents[24] = {1, 2, 3, 5, 7, 10, 15, 20, 25, 30, 35, 40, 45, 50, 60, 70, 75, 80, 85, 90, 95, 97, 98, 99};

// Initial bet array
int iTakes[15] = {5, 10, 15, 20, 50, 75, 100, 150, 200, 300, 400, 500, 1000, 2000, 3000};

Wie wir sehen können variiert der anfängliche Größe des Einsatzes zwischen 5 (0,05 % der ursprünglichen Einzahlung) bis hin zu 3000 (30 % der ursprünglichen Einzahlung). Die Gelder, welche wir in unsere Tasche stecken, variieren von 1 % bis 99 %. Diese Parameter wurden mit Sicherheitsmargen gewählt, die sich in vernünftigen Grenzen in beiden Richtungen überlappen.

Daher gestaltet sich der Suchraum zweidimensional. 360 diskrete Punkte (24 * 15) befinden sich innerhalb dieses Raums. Die durchschnittlichen Gesamt-Kontostände (die Summe aus „Taschengeldern“ und den Handelsgeldern des Handelskontos) und die durchschnittliche Anzahl von Handelsvorgängen, bevor der Einzahlungsbetrag verlorengegangen ist (Lebenszeit des Einzahlungsbetrages) werden basierend auf den Ergebnissen der Testreihe für jeden einzelnen der Punkte kalkuliert. Die Anzahl der Einzahlungsvorgänge pro Testreihe wird durch den Parameter Einzahlungen festgesetzt.

Die Resultate der Berechnung des zweidimensionalen Raums sind dreidimensional, was bedeutet, dass man diese Ergebnisse nur schwer mit zweidimensionalen Hilfsmitteln abbilden kann. Um dieses Problem zu lösen, möchten wir ganz einfach zweidimensionale Charts zeichnen, wobei die X-Achse für die Seriennummern der Punkte stehen soll, die sich im Suchraum befinden (von 0-359). Falls nötig werden wir bestimmte Werte für Takes und PocketPercent separat eingeben.

Nach dem Durchlauf durch 100 Einzahlungsbeträge stellt sich der durchschnittliche Kontostand wie folgt dar :

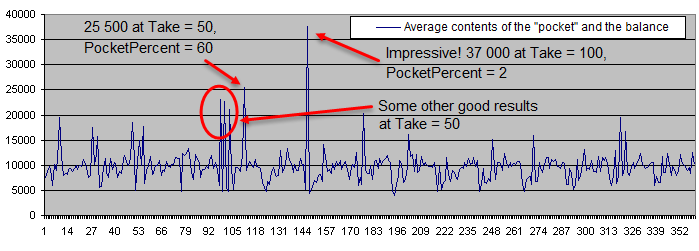
Untenstehend sehen Sie den Lebenszeit-Chart der Einzahlungen (in logarithmischer Darstellung):

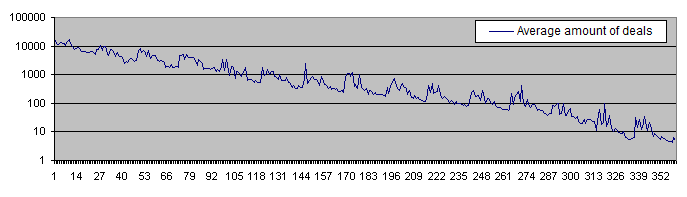
Die Lebenszeit des Einzahlungsbetrages übersteigt 10.000 Handelsvorgänge bei einem anfänglichen Risiko von 0,05 % – und sie verringert sich daraufhin stetig bis auf weniger als zehn Handelsvorgänge, bei einem anfänglichen Risiko von 30 %. Der hohe PocketPercent-Wert reduziert ebenfalls die durchschnittliche Anzahl von Handelsvorgängen, bevor ein Einzahlungsbetrag verlorengeht. Dieses Resultat war zu erwarten.

Wir können ein paar vielversprechende Punkte auf dem Chart auswählen, welche den durchschnittlichen Betrag unseres „Taschengeldes“ sowie den durchschnittlichen Handelskontostand darstellen. Diese Punkte befinden sich ganz nahe beieinander, also werden wir hoffentlich den optimalen Bereich finden. Jetzt möchten wir die Resultate für den Wert der Einzahlungen von Deposits = 1 000 kalkulieren und ihn auf demselben Chart überlagern:

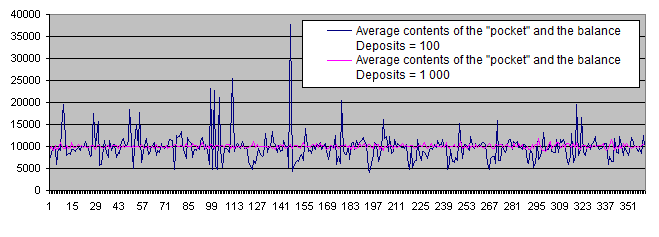
Wie wir sehen können ist der vermutete Optimalbereich ganz einfach unter dem Druck einer ausreichend großen Zahl von statistischen Daten verschwunden. Unabhängig von irgendwelchen Parametern fluktuiert der Chart nahe des ursprünglichen Kontostandes von 10.000.

Daher ist Deposits = 100 noch nicht ausreichend. Alle weiteren Experimente werden wir mit Deposits = 10000 durchführen.

Lassen Sie uns einmal die Ergebnisse des Systems von Labouchere und der Systeme mit einem fixen Einsatz auf einem einzigen Chart darstellen:

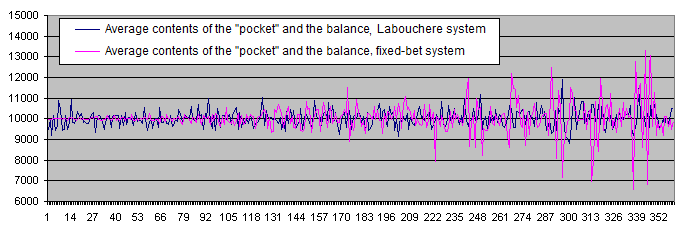
Der Lebenszeit-Chart für Einzahlungen beim System von Labouchere und System mit festen Einsätzen:

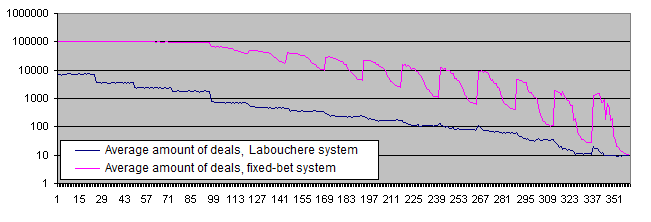
Schlussfolgerungen :

• Das Endergebnis des Systems von Labouchere stimmt überhaupt nicht mit dem System mit festen Einsätzen überein.

• Im Gegensatz zum System von Labouchere zeigt das System mit festen Einsätzen eine erhöhte Streuung der Daten rund um den Durchschnittswert. Es scheint so, als ob die festen Einzahlungs-Werte nicht mit dem statistischen Verhalten des Systems mit festen Einsätzen harmonieren würden.

• Die Lebensdauer der Einzahlung ist deutlich niedriger, wenn man das System von Labouchere verwendet (10 und mehr Male mit den meisten Parametern, und sogar noch mehr als 100 Male mit bestimmten Parametern). Im Falle eines niedrigen Risikoniveaus können wir sehen, dass der Chart die Begrenzung, welche durch den Parameter RepeatsCount gesetzt wurde, erreicht (der voreingestellte Wert beträgt 100.000). Diese Resultate bestätigen teilweise die verbreitete Meinung, dass die Systeme, welche in der Lage sind, das Risikoniveau zu erhöhen, für den getätigten Einzahlungsbetrag gefährlich sind. Solche Systeme führen zu einer reduzierten Lebensdauer der getätigten Einzahlung, obwohl wir noch keine Gefahren für die finanziellen Ergebnisse festgestellt haben (zumindest im Durchschnitt und unter der Voraussetzung, dass ein bestimmter Gewinn-Prozentsatz abgehoben wird).

Wir wollen nun einen neuen Skript-Parameter einführen, welcher es uns gestatten wird, ausreichende statistische Daten zur Evaluierung des Verhaltens von hochriskanten Bereichen zu sammeln:

input string S2 = "Minimum amount of deals per each pair of parameters";
input int MinDeals = 10000000;

Falls wir dabei weniger als 10 Millionen Trades pro 1000 verlorenen Einzahlungen erhalten sollten, dann sollten wir fortfahren.

Infolgedessen werden die Daten auf dem Chart weniger breit gestreut :

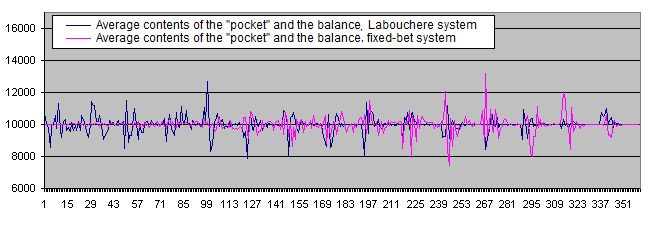
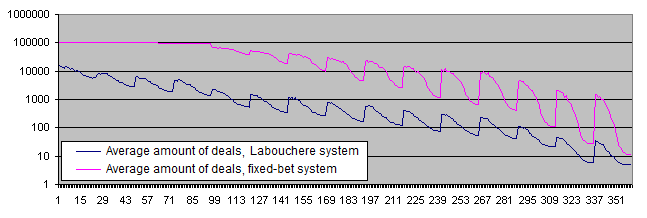
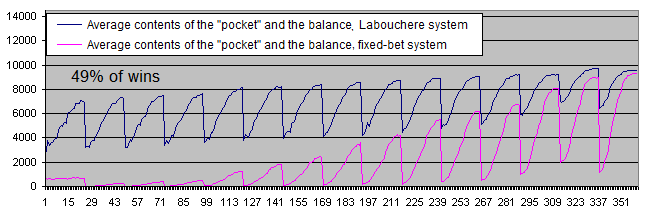
Und jetzt möchten wir die Arbeitsweise der Systeme überprüfen, indem wir die ursprünglichen Systemwahrscheinlichkeiten benutzen, die nicht gleich dem Verhältnis von 50/50 sind.

Die Lebensdauer der Einzahlung:

Was können wir auf diesen Charts erkennen?

• Im Falle von 49 % an gewinnbringenden Handelsvorgängen werden beide Systeme ganz klar unprofitabel.

• Die finanziellen Ergebnisse des Systems mit festen Einsätzen sind sehr niedrig, wodurch sich zeigt, dass die Abbuchung der erzielten Gewinne in das Konto für unser „Taschengeld“ in Verbindung mit dem System von Labouchere deutlich praktikabler ist als bei dem System mit festen Einsätzen, falls wir von einem Gewinnverhältnis von weniger als 50 % ausgehen. Die Gelder werden nur dann auf das Konto für die „Taschengelder“ transferiert, nachdem wir aus einem verlustbringenden Handelsgeschäft herausgekommen sind.

  Im Gegensatz zum System mit festen Einsätzen ist das System von Labouchere in der Lage, immer und immer wieder neue Rekordwerte zu erzielen (solange noch genügend Geld zur Verfügung steht, um einen weiteren Handelsvorgang zu tätigen) – und dies gilt sogar für eine Gewinnrate von 49 %. Im Falle, dass der Einzahlungsbetrag rapide dahin schmilzt, werden menschliche Trader vermutlich nicht mehr 100.000, ja noch nicht einmal 10.000 weitere Handelsvorgänge starten, bis ihr Einzahlungsbetrag endgültig verlorengegangen ist. Sie werden stattdessen schon viel früher mit dem Handel aufhören. Der Algorithmus des Systems mit festgelegten Einsätzen kann das nicht tun. Der Algorithmus des Systems von Labouchere ist in dieser Hinsicht allerdings viel menschlicher, weil er sich genauso verhält, wie es ein menschlicher Trader, der durch immer neue Rekorde ermutigt wurde, tun würde – und er handelt so immer weiter, bis der ursprünglich getätigte Einzahlungsbetrag schließlich vollkommen vernichtet wurde.

Erinnern Sie sich noch an den schönfärberischen Artikel, den ich in der Einführung zitiert habe? In diesem Artikel heißt es, dass das System sogar mit einem Gewinnanteil von"33-40 %" funktionieren soll. Lassen Sie uns die obere Grenze (40 %) des genannten Bereiches einmal durchspielen, einfach aus purem Jux:

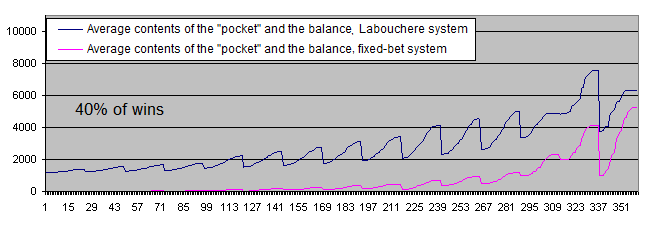
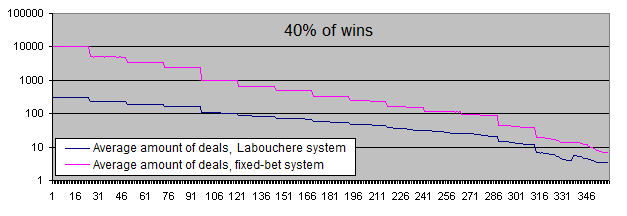
Jetzt möchten wir auch noch die positive mathematische Wahrscheinlichkeit des ursprünglichen Systems berücksichtigen (mehr als 50 % gewinnbringende Handelsvorgänge ).

Wir müssen die Charts für den Handelskontostand im logarithmischen Schema darstellen, selbst mit einem Gewinnanteil von 51 %.

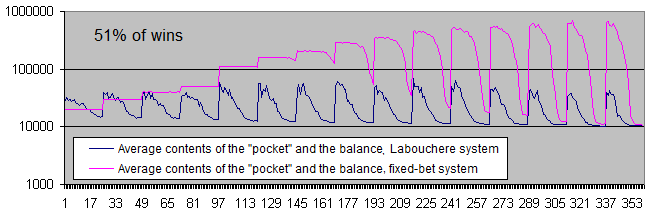
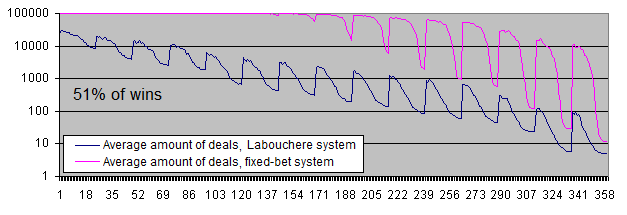
Schlussfolgerungen :

• Beide Systeme haben sich hin zu positiven Wahrscheinlichkeiten verlagert.

• Im Falle eines niedrigen Risikoniveaus zeigt das System mit festen Einsätzen eine unbegrenzte „Vitalität.“ In anderen Worten: Es ist fast unmöglich, einen ursprünglich getätigten Einzahlungsbetrag zu verlieren.

• Allerdings ist das System von Labouchere immer noch in der Lage, den ursprünglich getätigten Einzahlungsbetrag zu vernichten (allerdings müssen Sie dabei unser „Taschengeld“ berücksichtigen).

• Das System mit festen Einsätzen erzielt unter Verwendung der meisten Parameter mehr als zehnmal so viel Profit als das System von Labouchere (und manchmal sogar 17 mal mehr Profit mit bestimmten Parametern).

Die meisten Leser werden nun vielleicht denken, dass das System mit festen Einsätzen rundum dem System von Labouchere überlegen ist. Es schützt nicht nur einen ursprünglich getätigten Einzahlungsbetrag viel effektiver, sondern es erzielt auch noch einen Gewinn, der zehnmal so hoch ist! Unglücklicherweise lassen sie sich dabei von den Statistiken täuschen.

Das System mit festen Einsätzen findet seine Beschränkung nach 100.000 Handelsvorgängen pro getätigter Einzahlung. Falls der Parameter RepeatsCount auf den Wert von 200.000 eingestellt worden wäre, dann hätte das System zweimal mehr Profit erzielt. „Aber es ist doch wunderbar!“, werden die Leser, welche sich durch die Statistiken täuschen lassen, nun sagen. Und wieder einmal werden sie falsch liegen.

Werfen Sie einmal einen Blick auf den Chart mit dem durchschnittlich von den Systemen pro Handelsvorgang (Trade) erzielten Gewinnen (in der logarithmischen Darstellung):

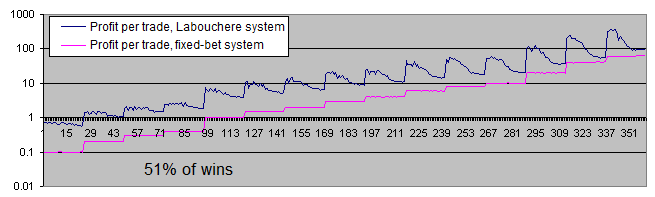
Der Chart für den Gewinn pro Trade, ausgedrückt als Prozentsatz der ursprünglichen Einsätze, macht das Gesamtbild sogar noch klarer:

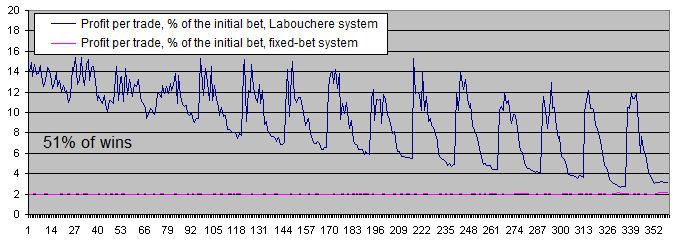
Schlussfolgerungen :

• Das System mit festen Einsätzen erzielt 2 % des anfänglichen Einsatzes pro Trade. Dies ist auch vollkommen konsistent mit der dahinterstehenden Theorie, weil das Gewinn-Verlust-Verhältnis hierbei 51/49 beträgt. In anderen Worten, die Gewinne übersteigen die Verluste um 2.

• Das System von Labouchere erzielt einen höheren Gewinn – selbst mit den unpassendsten Parametern. Und falls die Parameter korrekt gewählt werden, dann kann es einen Gewinn erzielen, der 6-7 Mal so hoch ist.

Es hat also den Anschein, dass Sie, falls Sie unendlich viel Zeit zur Verfügung hätten, mit dem System von Labouchere ziemlich große Erfolge erzielen könnten.

Sie könnten vielleicht argumentieren, dass das System mit den festen Einsätzen mit einem System mit festen Risiko-Prozentsätzen ersetzt werden könnte, sodass der Gewinn pro Trade gesteigert werden könnte (tatsächlich wird der erzielte Gewinn kontinuierlich ansteigen, allerdings sollten wir ähnliche Distanzen zu Vergleichszwecken benutzen). Allerdings sollte in diesem Fall das Volumen einer Position auch dann verändert werden, wenn wir das System von Labouchere verwenden.

Das System von Labouchere scheint also profitabler zu sein, oder etwa nicht?

Falls Sie jetzt mit „Ja“ antworten, dann haben Sie sich wieder einmal von den Statistiken täuschen lassen.

Werfen Sie einmal einen Blick auf diese Übersicht :

Einsatzgröße	Prozentsatz der Gelder , die auf das „Taschengeldkonto“ übertragen wurden	Durchschnittliche Höhe von „Taschengeld“ und Kontostand System von Labouchere	Durchschnittliche Anzahl von Handelsvorgängen, System von Labouchere	Durchschnittliche Höhe von „Taschengeld“ und Kontostand System mit festen Einsätzen	Durchschnittliche Anzahl von Handelsvorgängen System mit festen Einsätzen	Gewinn pro Trade, System von Labouchere	Gewinn pro Trade, System mit festen Einsätzen	Gewinn pro Trade, % des ursprünglichen Einsatzes, System von Labouchere	Gewinn pro Trade, % des ursprünglichen Einsatzes System mit festen Einsätzen
75	10	51 177.34	3 728.62	160 489.6	99 530.41	11.04	1.51	14.72	2.02
500	45	14 016.36	127.27	349 479	33 771.46	31.56	10.05	6.31	2.01

In der Tat können wir ganz einfach den gleichen Gewinnbetrag erzielen, indem wir das System mit festen Einsätzen verwenden. Wir müssen hierzu lediglich unseren Einsatz um das Siebenfache erhöhen (von 0,75 % auf 5 % in diesem Fall). Natürlich stellen 5 % ein hochriskantes Niveau dar. Aber das System mit festen Einsätzen verfügt in diesem Fall immer noch über eine „Vitalität,“ die zehnmal höher liegt.

Es hat also den Anschein, als ob das System mit festen Einsätzen für den Trader vorteilhafter wäre, oder etwa nicht?

Wieder einmal haben Sie die Statistiken getäuscht.

In der Tat spielt es überhaupt keine Rolle, wie viele Handelsvorgänge Ihre ursprüngliche Einzahlung überlebt (im Durchschnitt gesprochen, natürlich), weil wir nämlich einen Teil der Profite auf unser „Taschengeldkonto“ überweisen. Die Summe der „Taschengelder“ übersteigt die Ersteinzahlung um ein Vielfaches, und insofern ist der Verlust der Ersteinzahlung letztendlich überhaupt nicht von Bedeutung.

Vielleicht ist die eindeutigste Schlussfolgerung, welche wir aus diesen Berechnungen ziehen können, die Folgende: „Falls der Anteil an gewinnbringenden Handelsvorgängen bei 51 % liegt, so sind die Gewinne, welche sich mit dem System von Labouchere und dem System mit festen Einsätzen erzählen lassen, in etwa gleich – unter der Voraussetzung, dass das vorgenannte System über einen anfänglichen Einsatz von 0,75 % des ursprünglich getätigten Einzahlungsbetrages verfügt, und dass 10 % der erzielten Gewinne vom Handelskonto abgebucht werden. Das letztgenannte System muss hierbei über einen festen Einsatz von 5 % der ursprünglich getätigten Einzahlung verfügen, und 45 % der erzielten Gewinne müssen vom Handelskonto abgebucht werden. Das System von Labouchere erreicht dasselbe Profitabilitätsniveau, indem die Positionsgröße während seines Betriebes erhöht wird.“

Außerdem sollten Sie stets bedenken, dass alle statistischen Schlussfolgerungen lediglich dann als gültig angesehen werden, nachdem eine unglaublich große Anzahl von Experimenten durchgeführt wurde. Ein einziges virtuelles Handelskonto kann man auf virtuelle Art und Weise in mehrere Unterkonten mit virtuellen Einzahlungsbeträgen aufteilen. Der Verlust eines virtuellen Einzahlungsbetrages bedeutet, dass man einen Teil seines Handelskontos verloren hat, und dass man dann zu der ursprünglichen Einsatzgröße zurückkehrt, wenn ein bestimmtes Risikoniveau erreicht wurde. Allerdings zeigt der Artikel, dass eine Simulation mit 100 Einzahlungsbeträgen immer noch zu weit verstreuten Daten führt. Falls wir aber den Einzahlungsbetrag eines Traders in 100 Teile aufteilen, wird ein normaler Handel unmöglich sein.

Welches System ist denn nun besser? Dies ist schwer zu sagen. Die Wahl des Systems hängt von den Präferenzen des Traders ab, und die mathematische Wahrscheinlichkeit des ursprünglichen Systems ist hierbei von entscheidender Bedeutung. Der Code, welcher im Artikel gezeigt wurde, gestattet es jedermann, das System von Labouchere auf seinem eigenen Handelssystem zum Laufen zu bringen.

Lassen Sie uns einmal die Charts beider Systeme mit einem Anteil von 55 % an gewinnbringenden Handelsgeschäften analysieren :

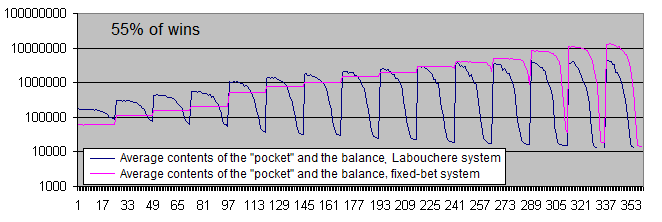
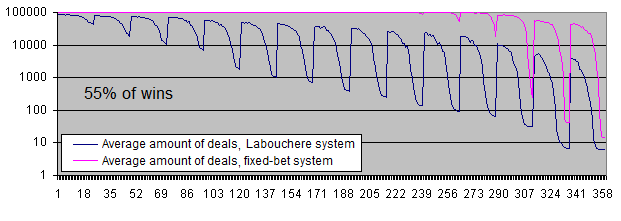
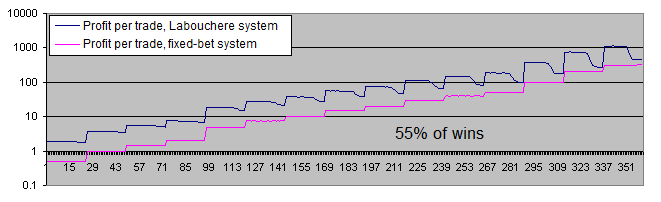
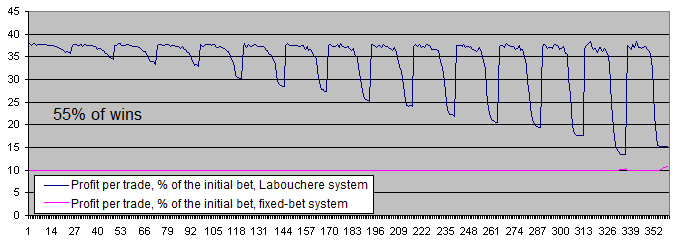
Bei einem Anteil von 55 % an gewinnbringenden Handelsvorgängen werden beide Systeme profitabel.

Die große Differenz zwischen den durchschnittlichen Gewinnen pro Trade hat sich vom 6-7-fachen (bei 51 % an gewinnbringenden Handelsvorgängen) auf ungefähr das 3,7-fache verringert (bei 55 % an gewinnbringenden Handelsvorgängen). Dies erklärt sich durch die Tatsache, dass bei einer höheren Wahrscheinlichkeit des ursprünglichen Systems das System von Labouchere weniger Zeit im verlustbringenden Terra verbringt – und daher muss es auch nicht allzu oft mit einer erhöhten Losgröße handeln.

Fazit

Es ist kein Wunder geschehen. Das Geldverwaltungssystem von Labouchere ist nicht in der Lage, ein verlustmachendes oder sogar ein neutrales System in ein profitables System zu verwandeln.

Außerdem lassen sich die Quellen einiger Mythen und Missverständnisse bezüglich des Systems von Labouchere nun ganz klar erkennen :

• Das System verfügt über eine hohe Komplexität, welche die genaue Berechnung der Ergebnisse des Systems verhindert.
• Bei manuellen Testläufen des Systems mangelt es einfach an ausreichend statistischen Daten.
  
• Die Fähigkeit des Systems, immer und immer wieder neue Rekordgewinne zu erzielen – sogar dann, wenn das ursprüngliche System über eine negative Wahrscheinlichkeit verfügt – führt dazu, dass die Trader an seine Effizienz glauben.
  

Ist das System von Labouchere einen Versuch wert, wenn man es im Zusammenhang mit einem System, das über eine positive Wahrscheinlichkeit verfügt, anwenden möchte? Die Wahl liegt ganz bei Ihnen. Das System von Labouchere ist ziemlich kompliziert, und seine Effizienz kann man kaum als besonders herausragend bezeichnen. In jedem Fall kann ich Ihnen zwei Ratschläge an die Hand geben: Überschreiten Sie niemals das akzeptable Risikoniveau, falls Ihnen Ihre Ersteinzahlung lieb und teuer ist, und versuchen Sie, die mathematische Wahrscheinlichkeit Ihres Handelssystems zu verbessern.