
Bildung von Kursreihenmittelwerten für Zwischenberechnungen ohne zusätzliche Puffer
Einleitung
In meinem Artikel Grundsätze der rationalen Neuberechnung von Indikatoren habe ich hinreichend überzeugende Versuche durchgeführt, die belegen, dass bei Weitem nicht jeder Aufruf eines benutzerdefinierten oder gar eines technischen Indikators im Programmcode die optimale Lösung zur Ausführung von Zwischenberechnungen in dem gerade entwickelten Indikator ist.
Das Endergebnis hinsichtlich der Geschwindigkeit seiner Ausführung kann sich als erheblich schlechter erweisen, als es wäre, wenn wir den für die Zwischenberechnungen erforderlichen Programmcode unmittelbar in unserem Indikator platziert hätten.
Diese Herangehensweise an das Schreiben des Codes könnte sich als sehr verlockend erweisen, wenn sie sich einfach genug umsetzen ließe. In Wirklichkeit ergibt sich jedoch eine recht ernsthafte Verkomplizierung des Codes durch die Einführung zusätzlicher Indikatorpuffer zur Speicherung der Ergebnisse der Zwischenberechnungen.
Bei der ganzen Mannigfaltigkeit der der Zwischenberechnungen erweisen sich häufig alle möglichen Algorithmen zur Bildung von Mittelwerten als die notwendigsten. In den meisten Fällen können für sie recht allgemein gültige einfache benutzerdefinierte Funktionen verwendet werden, die die Erstellung dieses Codes erheblich erleichtern. Um eben die Arbeit mit diesen Funktionen und ihre Erstellung geht es in diesem Beitrag.
1. Der Grundgedanke hinter den Funktionen zur Mittelwertbildung, die mit nur einem Balken arbeiten
Der klassische Ansatz zur Bildung des Mittelwertes an dem aktuellen Balken besteht darin, dass aus dem Zwischenspeicher des Indikators, in den vorher alle erforderlichen Daten geladen wurden, eine beliebige Anzahl älterer Werte, die dem Zeitraum der Mittelwertbildung entspricht, ausgewählt und ihr Mittelwert gebildet wird.
Die Verarbeitung dieser Auswahl sieht aus wie folgt:
SmoothVar(bar) = Function(Var(bar - (n-1)), Var(bar - (n-2)), ......... Var(bar))
mit:
- SmoothVar(bar) — gemittelter Parameter;
- bar — Nummer des Balkens, für den die Berechnung erfolgt;
- Var(bar - (n-1)) — zu mittelnder um (n-1) versetzter Balken;
- n — Anzahl der Balken für die Mittelwertbildung.
Ein ähnliches Herangehen an die Mittelwertbildung führt dazu, dass in unserem Fall zwei Berechnungsdurchgänge vorliegen. In Ersterem werden die Daten berechnet und in einem Zwischenspeicher (Indikatorpuffer) abgelegt. Im zweiten Durchgang erfolgt auf der Grundlage dieser Daten mithilfe der von mir oben vorgeschlagenen Formel die Mittelwertbildung unter Einschaltung eines weiteren Durchgangs zur gründlichen Durchsuchung der Zellen des Indikatorpuffers. Diese Berechnung würde bedeutend einfacher aussehen, wenn die Auswahl der zwischengespeicherten Daten in der Funktion selbst gespeichert würde. In diesem Fall sähe die Funktion zur Bildung des Mittelwerts etwa so aus:
SmoothVar(bar) = Function(Var(bar),bar)
Der neue Wert Var(bar) wird in die Werteauswahl innerhalb der Funktion auf dem aktuellen Balken eingeschrieben, der überflüssig werdende Wert der Variablen Var(bar - n) dagegen wird aus der Auswahl entfernt. Bei diesem Vorgehen sieht der Code für die Bildung des Mittelwerts aus den zwischengespeicherten Daten recht trivial aus und erfordert keine zusätzlichen Indikatorpuffer. Innerhalb der Funktion wird exakt die zur Berechnung eines Balkens erforderliche Anzahl Daten in einem Datenfeld (Array) gespeichert, nicht jedoch alle historischen Kursverlaufsdaten.
In diesem Fall liegt auch insgesamt nur ein Durchgang zur Berechnung der Daten vor. Es ist hinzuzufügen, dass diese Funktion zur Mittelwertbildung erst dann für den aktuellen Balken aufgerufen werden kann, wenn sie zuvor bereits für alle vorhergehenden Balken aufgerufen worden ist.
2. Die klassische Mittelwertbildung als Beispiel für die Umsetzung einer Funktion, die mit einem Balken arbeitet
Derartige Funktionen zur Mittelwertbildung müssen Variablen enthalten, die ihren Wert zwischen den Aufrufen der jeweiligen Funktion nicht verlieren dürfen. Dabei können gleichmäßige Mittelwertbildungen mit mehreren Parametern im Code mehrfach verwendet werden, weshalb es zur Vermeidung von Konflikten bei der Nutzung gemeinsamer Speicherbestände am besten ist, diese Funktionen in Form von Klassen anzulegen; was hier auch getan wurde.
Die Algorithmen der klassischen Mittelwertbildung werden in der Klasse CMoving_Average bereitgestellt:
class CMoving_Average : public CMovSeriesTools { public: double MASeries (uint begin, // Index of start of reliable bars uint prev_calculated, // Amount of history in bars at a previous tick uint rates_total, // Amount of history in bars at a current tick int Length, // Period of averaging ENUM_MA_METHOD MA_Method, // Method of averaging (MODE_SMA, MODE_EMA, MODE_SMMA, MODE_LWMA) double series, // Value of price series calculated for the bar with the 'bar' number uint bar, // Bar index bool set // Direction of indexing of arrays. ); double SMASeries (uint begin, // Index of start of reliable bars uint prev_calculated,// Amount of history in bars at a previous tick uint rates_total, // Amount of history in bars at a current tick int Length, // Period of averaging double series, // Value of price series calculated for the bar with the 'bar' number uint bar, // Bar index bool set // Direction of indexing of arrays. ); double EMASeries (uint begin, // Index of start of reliable bars uint prev_calculated, // Amount of history in bars at a previous tick uint rates_total, // Amount of history in bars at a current tick double Length, // Period of averaging double series, // Value of price series calculated for the bar with the 'bar' number uint bar, // Bar index bool set // Direction of indexing of arrays. ); double SMMASeries(uint begin, // Index of start of reliable bars uint prev_calculated, // Amount of history in bars at a previous tick uint rates_total, // Amount of history in bars at a current tick int Length, // Period of averaging double series, // Value of price series calculated for the bar with the 'bar' number uint bar, // Bar index bool set // Direction of indexing of arrays. ); double LWMASeries(uint begin, // Index of start of reliable bars uint prev_calculated, // Amount of history in bars at a previous tick uint rates_total, // Amount of history in bars at a current tick int Length, // Period of averaging double series, // Value of price series calculated the bar with the 'bar' number uint bar, // Bar index bool set // Direction of indexing of arrays. ); protected: double m_SeriesArray[]; int m_Size_, m_count, m_weight; double m_Moving, m_MOVING, m_Pr; double m_sum, m_SUM, m_lsum, m_LSUM; };
Diese Klasse ist aus der Basisklasse CMovSeriesToolsabgeleitet, die weitere geschützte Funktionen-Methoden sowie eine Korrektheitsprüfung für den Zeitraum der gleitenden Durchschnittswerte enthält.
In der Basisklasse ist ein allgemeingültiger zusätzlicher Programmcode angelegt, der in allen von mir vorgestellten Klassen verwendet wird, und den immer wieder in alle abgeleiteten Klassen zu kopieren, unzweckmäßig wäre. In den anwendungsorientierten Aufgaben zur Verwendung der Mittelwertbildung werden die geschützten Elemente der Klassen nicht ausdrücklich verwendet, sodass ihre Vorstellung auf später verschoben werden kann.
Im den Bestand der Klasse CMoving_Average befinden sich fünf gleichmäßige Funktionen zur Mittelwertbildung, deren Bezeichnungen für sich sprechen und keiner ausführlichen Kommentare bedürfen.
Bei der ersten Funktion MASeries() handelt es sich um eine integrale Sammlung der übrigen vier Funktionen, was die Auswahl des Algorithmus zur Mittelwertbildung mithilfe des Parameters MA_Method ermöglicht. Die Codes für die Algorithmen zur Mittelwertbildung sind geschwindigkeitsoptimiert und aus eben diesem Grund tauchen in der Funktion neben den Hauptparametern (Length, series, bar) noch die zusätzlichen Parameter begin, prev_calculated, rates_total und set auf, deren Zweck sich vollkommen mit dem der gleichnamigen Indikatorvariablen deckt.
Der Parameter set markiert die Kennziffern der Elemente einer Kursreihe series in den Funktionen zur Mittelwertbildung ähnlich wie bei den Datenfeldern für die Variablen.
Es ist zu berücksichtigen, dass bei allen Mittelwertbildungsfunktionen dieser Klasse der Parameter Length festgelegt ist und nicht geändert werden darf, während der Programmcode ausgeführt wird! Für die Funktion EMASeries() der Klasse CMoving_Average nimmt dieser Parameter die Art double an!
Jetzt, da wir uns mit der Klasse CMoving_Average vertraut gemacht haben, wenden wir uns der praktischen Verwendung der Indikatoren zu. Dazu müssen wir zunächst mithilfe der Anweisung #include den Inhalt der Datei MASeries_Cls.mqh auf globaler Ebene in den Code des geplanten Indikators einfügen:
#include <MASeries_Cls.mqh>
Anschließend legen wir die erforderliche Anzahl der Mittelwertbildungen im Indikatorcode sowie in dem Codeblock OnCalculate() (vor den Verarbeitungsroutinen der Zyklen und den geschweiften Klammern) fest und nehmen die der Anzahl der erforderlichen Mittelwertbildungen entsprechende Deklarierung der statischen Variablen der Klasse CMoving_Average vor. Für jede Mittelwertbildung muss eine eigene Klassenvariable oder eine Zelle in dem Datenfeld der Klasse vorhanden sein.
//---- declaration of variables of the class CMoving_Average из файла MASeries_Cls.mqh static CMoving_Average MA1, MA2, MA3, MA4;
Die Klassenvariablen in der Funktion OnCalculate() werden als statisch deklariert, weil ihr Inhalt zwischen den Aufrufen der Funktion erhalten bleiben muss. Hier können wir mit der eigentlichen Mittelwertbildung beginnen. Als Beispiel präsentiere ich vier aufeinander folgende Verfahren zur Bildung des Mittelwertes einer Kursreihe - SMA/EMA/SMMA/LWMA (der Indikator MAx4.mq5):
//---- The main cycle of indicator calculation for(bar = first; bar < rates_total; bar++) { //----+ Four calls of the function MASeries. ma1_ = MA1.MASeries(start1, prev_calculated, rates_total, Length1, MODE_SMA, price[bar], bar, false); ma2_ = MA2.MASeries(start2, prev_calculated, rates_total, Length2, MODE_EMA, ma1_, bar, false); ma3_ = MA3.MASeries(start3, prev_calculated, rates_total, Length3, MODE_SMMA, ma2_, bar, false); ma4_ = MA4.MASeries(start4, prev_calculated, rates_total, Length4, MODE_LWMA, ma3_, bar, false); //---- MAx4[bar] = ma4_ + dPriceShift; }
Nach jeder Mittelwertbildung (mit Ausnahme der jeweils letzten) wird das Ergebnis dem folgenden Algorithmus zur Mittelwertbildung unterzogen und das Endergebnis in dem Indikatorpuffer zwischengespeichert.
In diesem Code besteht die verantwortungsvollste Aufgabe in der äußerst aufmerksamen vorherigen Bereitstellung der Variablen für die Kennziffern für den Anfang der zuverlässigen Erfassung der Balken. In unserem Fall dürfte das etwa folgendermaßen aussehen:
//---- Initialization of variables of start of reliable information start1 = 0 + begin; start2 = Length1 + begin; start3 = Length1 + begin; // the previous EMA averaging doesn't change the start of reliable information start4 = Length1 + Length3 + begin;
Es ist zu beachten, dass in dem hier vorliegenden Fall der LWMA-Algorithmus zur Bildung des Mittelwerts der letzte ist und nichts bestimmt, dass jedoch, wenn er nicht der letzte wäre, die Verschiebung des Anfangs der Datenberechnung nicht gleich Length4 sondern gleich Length4+1 wäre!
Ich möchte hinzufügen, dass, wenn aus dem der Mittelwertbildung vorausgehenden Code nicht ganz klar wird, welches die Kennziffer des Anfangs der zuverlässigen Berechnung der Balken ist, es besser ist, diesen Wert etwas höher anzusetzen und ihn später auf experimentellem Weg herunterzusetzen, wenn es soweit ist.
3. Vergleich des mithilfe der Klassen angelegten Indikators mit seinen Entsprechungen, die sich technischer und benutzerdefinierter Indikatoren bedienen
Es wäre äußerst interessant, Tests zum Vergleich der Geschwindigkeit der Arbeit des geschaffenen Indikators MAx4.mq5 mit seinem identischen Pendant (iMAx4.mq5), das den technischen Indikator iMA() verwendet, anzustellen.
Gut, sobald wir uns also entschieden haben, den Test durchzuführen, wäre es vollkommen vernünftig auch den Indikator (MAx3x1.mq5) genauso zu prüfen wie MAx4.mq5, wobei bei Ersterem die erste Mittelwertbildung durch Aufruf des technischen Indikators iMA() erfolgt und die übrigen drei mithilfe der Klasse CMoving_Average. Und weil zum Lieferumfang für die Anwendungsinstanz auf dem Ausgabegerät (Terminal) auch noch der Indikator Custom Moving Average.mq5 gehört, wurde auch auf der Grundlage dieses Indikators zu Testzwecken ein entsprechendes Gegenstück (cMAx4.mq5) angelegt.
Für die bevorstehende Untersuchung wurden vier Expert-Systeme programmiert: MAx4_Test.mq5, iMAx4_Test.mq5, MAx3x1_Test.mq5 und cMAx4_Test.mq5. Die Testbedingungen sind in dem Beitrag Grundsätze der rationalen Neuberechnung von Indikatoren hinlänglich dargestellt worden. In dem hier vorliegenden Artikel halte ich mich nicht mit allen Einzelheiten der Tests auf, sondern beschränke mich auf die Endergebnisse der Testläufe aller vier Expert-Systeme in dem Strategieprüfprogramm für die zurückliegenden 12 Monate bezüglich des Währungspaares EURUSD Н4 mit Abbildung jeder Kursänderung und mit dem Wert 500 für den Eingangsparameter „period“ bei allen getesteten Expert-Systemen.
Am schlechtesten von allen hat in unseren Tests der Indikator mit den Aufrufen der benutzerdefinierten Indikatoren abgeschnitten, diese Spielart der Codeprogrammierung ist niemanden zu empfehlen, der nicht hoffnungslos faul ist. Natürlich sind die Ergebnisse eines weiteren „Führenden“ in den Tests, der sich auf Platz 2 von hinten eingefunden hat und vollständig auf den Aufruf technischer Indikatoren aufgebaut ist, erheblich besser, gleichwohl jedoch immer noch sehr weit vom Optimum entfernt.
Der wahre Testsieger ist der mithilfe der Klassen entwickelte Indikator!
Das hybride System, das sowohl Klassen als auch den Aufruf technischer Indikatoren nutzt, belegt Platz zwei, obwohl es bei Weitem nicht immer richtig funktioniert, und wenn die zur Überprüfung eines Indikators benötigte Zeit ausschlaggebend ist, ist es allemal besser diese Varianten in jedem Einzelfall selbst zu prüfen.
Übersicht über die umgesetzten Klassen zur Bildung von Mittelwerten
| Nr. | Algorithmus | Bezeichnung der Klasse | Dateiname | Verschiebung des Anfangs der zuverlässigen Berechnung der Balken nach Anwendung des Algorithmus |
Möglichkeit der dynamischen Änderung des Parameters Length |
|---|---|---|---|---|---|
| 1 | Klassische Mittelwertbildung | CMoving_Average | MASeries_Cls.mqh | Length/0/Length/Length + 1 (SMA/EMA/SMMA/LWMA) | Nein |
| 2 | Standardabweichung | CStdDeviation | StdDevSeries_Cls.mqh | Länge (Length) | Nein |
| 3 | JMA-Glättung | CJJMA | JJMASeries_Cls.mqh | 30 | Ja |
| 4 | T3-Glättung | CT3 | T3Series_Cls.mqh | 0 | Ja |
| 5 | Ultralineare Mittelwertbildung | CJurX | JurXSeries_Cls.mqh | 0 | Ja |
| 6 | Mittelwertbildung nach Tushar Chande | CCMO | CMOSeries_Cls.mqh | Länge + 1 (Length + 1) | Nein |
| 7 | Mittelwertbildung nach Kaufman | KAMA | AMASeries_Cls.mqh | Länge + 3 (Length + 3) | Nein |
| 8 | Parabolische Mittelwertbildung | CParMA | ParMASeries_Cls.mqh | Länge (Length) | Nein |
| 9 | Änderungsgeschwindigkeit | CMomentum | MomSeries_Cls.mqh | Länge + 1 (Length + 1) | Nein |
| 10 | Normalisierte Änderungsgeschwindigkeit | CnMomentum | nMomSeries_Cls.mqh | Länge + 1 (Length + 1) | Nein |
| 11 | Änderungsrate | CROC | ROCSeries_Cls.mqh | Länge + 1 (Length + 1) | Nein |
Die gerade betrachtete Klasse CMoving_Average beinhaltet fünf Algorithmen zur Mittelwertbildung.
In der Klasse CCMO ist es außer den Mittelwertbildungsalgorithmen ein Oszillator vorhanden.
In den übrigen Klassen liegt jeweils nur ein Algorithmus zur Mittelwertbildung vor. Die Ideologie der Verwendung einer jeden der vorgestellten Klassen stimmt vollkommen mit dem Vorgehen bei der Verwendung der Klasse CMoving_Average überein. Der Code aller Mittelwertbildungsalgorithmen (mit Ausnahme des parabolischen) wurde zur Erzielung der maximalen Ausführungsgeschwindigkeit optimiert. Der Code des Algorithmus der parabolischen Mittelwertbildung wurde aufgrund der Aufwendigkeit dieses Vorgangs nicht optimiert. Bei den letzten drei Algorithmen handelt es sich nicht um Mittelwertbildungen. Ich habe sie lediglich wegen ihrer großen Beliebtheit und Vereinbarkeit mit der Arbeit der bekannten technischen Analysten hinzugefügt.
Zur Vereinfachung des Verständnisses des Materials wäre es besser, die Mittelwertbildungsalgorithmen in Form separater Dateien im Format .mqh aufzuführen, aber für die praktische Verwendung ist es wesentlich geeigneter, all diese Klassen in einer einzigen Datei abzulegen, und genau das wurde hier getan.
Für den Einsatz in Indikatoren wurden alle vorgestellten Klassen in der Datei SmoothAlgorithms.mqh abgelegt. Darüber hinaus wurde der Inhalt dieser Datei um die Funktionen der Datei iPriceSeries.mqh erweitert. In den Beispielen in diesem Beitrag findet nur die Funktion PriceSeries() Verwendung:
double PriceSeries ( uint applied_price, // Price constant uint bar, // Index of shift for a specified number of periods back or forward // relatively to a current bar. const double& Open [], const double& Low [], const double& High [], const double& Close[] )
Diese Funktion ist für den Einsatz in Indikatoren gedacht, die mithilfe der zweiten Form des Aufrufs der Funktion OnCalculate() angelegt wurden.
Der Grundgedanke bei der Erstellung dieser Funktion besteht darin, den Umfang der Kurszeitreihen in der Aufzählung ENUM_APPLIED_PRICE um eigene Varianten zu erweitern. Die Funktion gibt den Wert der Kurszeitreihe anhand ihrer Kennziffer aus, diese kann zwischen 1 und 11 variieren.
4. Praktische Beispiele für die Umsetzung des Programmcodes unter Verwendung von Klassen zur Mittelwertbildung
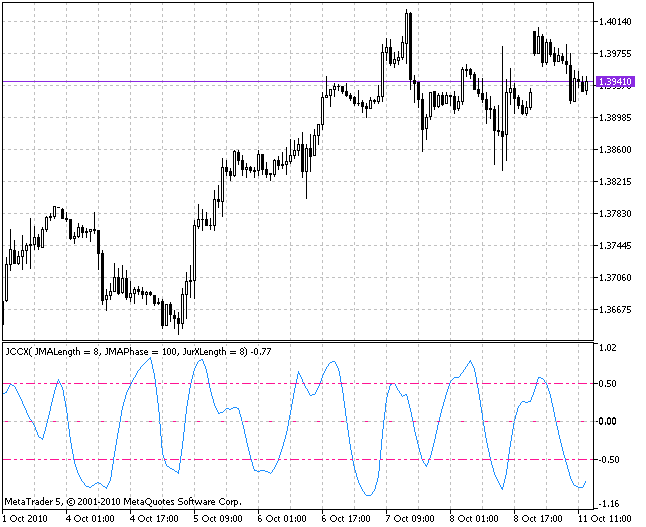
Es reicht, noch ein weiteres Beispiel unter Verwendung der übrigen Klassen vorzustellen, um sich davon zu überzeugen, dass sich alles genauso wie in dem ersten Beispiel mit der vierfachen Mittelwertbildung abspielt. Ich stelle hier eine Umsetzungsvariante für die Funktion OnCalculate() in Form einer Entsprechung zu dem Indikator CCI unter Verwendung der Klassen CJJMA und CJurX (JCCX.mq5) vor:
int OnCalculate(const int rates_total, // amount of history in bars on a current tick const int prev_calculated, // amount of history in bars on a previous tick const datetime& time[], const double& open[], const double& high[], const double& low[], const double& close[], const long& tick_volume[], const long& volume[], const int& spread[] ) { //----+ //---- Checking whether there are enough bars for calculation if (rates_total < 0) return(0); //---- Declaration of variables with floating point double price_, jma, up_cci, dn_cci, up_jccx, dn_jccx, jccx; //----+ Declaration of integer variables int first, bar; //---- calculation of start number 'first' for the cycle of recalculation of bars if (prev_calculated == 0) // checking for the first start of calculation of indicator first = 0; // starting number for calculation of all bars else first = prev_calculated - 1; // starting number for calculation of new bars //---- declaration of variables of the class CJurX from the file SmoothAlgorithms.mqh static CJurX Jur1, Jur2; //---- declaration of variables of the class CJMA from the file SmoothAlgorithms.mqh static CJJMA JMA; //---- Main cycle of calculation of the indicator for(bar = first; bar < rates_total; bar++) { //----+ Calling the PriceSeries function to get the input price price_ price_ = PriceSeries(IPC, bar, open, low, high, close); //----+ One call of the JJMASeries function to get JMA jma = JMA.JJMASeries(0, prev_calculated, rates_total, 0, JMAPhase, JMALength, price_, bar, false); //----+ Determine the deviation of price from the value of JMA up_cci = price_ - jma; dn_cci = MathAbs(up_cci); //----+ Two calls of the JurXSeries function. up_jccx = Jur1.JurXSeries(30, prev_calculated, rates_total, 0, JurXLength, up_cci, bar, false); dn_jccx = Jur2.JurXSeries(30, prev_calculated, rates_total, 0, JurXLength, dn_cci, bar, false); //---- Preventing zero divide in empty values if (dn_jccx == 0) jccx = EMPTY_VALUE; else { jccx = up_jccx / dn_jccx; //---- Limitation of the indicator from the top and from the bottom if (jccx > +1)jccx = +1; if (jccx < -1)jccx = -1; } //---- Loading the obtained value to the indicator buffer JCCX[bar] = jccx; } //----+ return(rates_total); }
Nur habe ich dieses Mal den Code des Indikators auf globaler Ebene um die entsprechenden Klassen aus einer anderen Datei erweitert:
#include <SmoothAlgorithms.mqh>
Jetzt möchte ich Ihre Aufmerksamkeit auf ein weiteres Moment richten. Es geht darum, dass die riesige Anzahl der Indikatoren auch als Funktionen eines Balkens dargestellt werden kann, mit denen zu arbeiten, sich bei der Verwendung von Klassen als ausgesprochen einfach erweist.
Es wäre zum Beispiel interessant, ein Bollinger-Band auf der Grundlage des gleitenden Durchschnitts Vidya von Tushar Chande anzulegen. Dabei kommen zwei Klassen, CCMO und CStdDeviation, zum Einsatz. Dank der ersten Klasse erhalten wir den Wert des gleitenden Durchschnitts VIDYA, während wir mithilfe der zweiten den Wert der Standardabweichung der Kursreihe von dem gleitenden Durchschnitt bestimmen.
Anschließend nutzen wir diese Abweichung zur Berechnung der Ober- und der Untergrenze des Bandes:
//+------------------------------------------------------------------+ // Description of the classes CStdDeviation{}; and CCMO{}; | //+------------------------------------------------------------------+ #include <SmoothAlgorithms.mqh> //+==================================================================+ //| The algorithm of getting the Bollinger channel from | //| the moving average VIDYA | //+==================================================================+ class CVidyaBands { public: double VidyaBandsSeries(uint begin, // number of the start of reliable calculation of bars uint prev_calculated, // amount of history on a previous tick in bars uint rates_total, // amount of history on a current tick in bars int CMO_period, // the period of averaging of the oscillator CMO double EMA_period, // the period of averaging of EMA ENUM_MA_METHOD MA_Method, // the type of averaging int BBLength, // the period of averaging of the Bollinger channel double deviation, // Deviation double series, // Value of the price series calculated for a bar with the number 'bar' uint bar, // Bar index bool set, // Direction of indexing of arrays double& DnMovSeries, // Value of the lower border of the channel for a current bar double& MovSeries, // Value of the middle line of the channel for a current bar double& UpMovSeries // Value of the upper border of the channel for a current bar ) { //----+ //----+ Calculation of the middle line MovSeries = m_VIDYA.VIDYASeries(begin, prev_calculated, rates_total, CMO_period, EMA_period, series, bar, set); //----+ Calculation of the Bollinger channel double StdDev = m_STD.StdDevSeries(begin+CMO_period+1, prev_calculated, rates_total, BBLength, deviation, series, MovSeries, bar, set); DnMovSeries = MovSeries - StdDev; UpMovSeries = MovSeries + StdDev; //----+ return(StdDev); } protected: //---- declaration of variables of the classes CCMO and CStdDeviation CCMO m_VIDYA; CStdDeviation m_STD; };
Damit haben wir eine ganz kleine und sehr schlichte Klasse!
Die letzten drei Eingangsparameter der Funktion VidyaBandsSeries() geben jeweils über eine Verknüpfung die erforderlichen Werte des betreffenden Bandes aus.
Es sei darauf hingewiesen, dass die Klassenvariablen in diesem Fall nicht in der Funktion VidyaBandsSeries() deklariert und auch nicht statisch gemacht werden dürfen, weil statische Variablen in Klassen eine vollkommen andere Bedeutung haben. Deshalb muss die Deklarierung auf der globalen Ebene der Klasse erfolgen:
protected: //---- declaration of variables of the classes CCMO and CStdDeviation CCMO m_VIDYA; CStdDeviation m_STD;
In einem gewöhnlichen Bollinger-Band weisen der Zeitraum der Mittelwertbildung des gleitenden Durchschnitts und der Zeitraum der Bildung des Mittelwerts für das Band selbst stets denselben Wert auf.
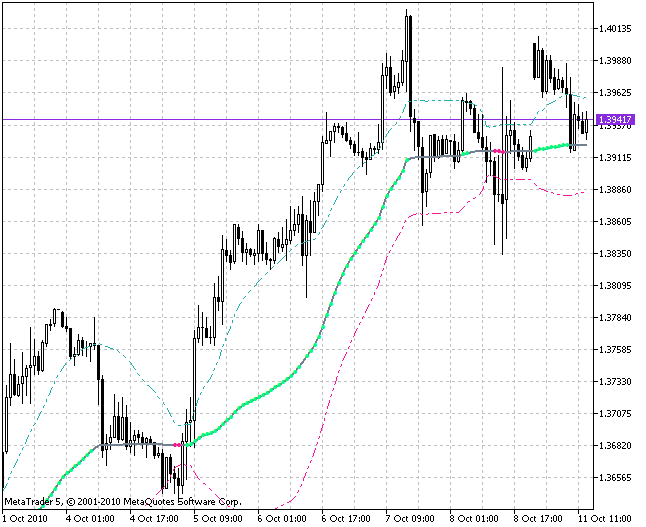
In der hier vorliegenden Klasse habe ich diese Parameter zur Gewährleistung der größtmöglichen Freiheit unterschiedlich gestaltet (EMA_period bzw. BBLength). Der auf der Grundlage dieser Klasse angelegte Indikator (VidyaBBands.mq5) selbst ist hinsichtlich der Verwendung der Klasse CVidyaBands derart schlicht, dass die Analyse seines Codes in diesem Beitrag unterbleiben kann.
Diese Klassen mit Indikatorfunktionen werden am besten ebenfalls in einer eigenen MQH-Datei untergebracht. Bei mir heißt sie IndicatorsAlgorithms.mqh.
5. Vergleich der Arbeitsgeschwindigkeit des Indikators, der Klassen verwendet, mit seinem Gegenstück, das dies nicht tut
Es sollte gleich zu Beginn geklärt werden, wie sehr die Verwendung von Klassen beim Schreiben des Indikatorcodes dessen Arbeit verlangsamt.
Deshalb wurde der Code des Indikators JJMA.mq5 ohne Verwendung von Klassen geschrieben (JMA.mq5) und anschließend unter genau denselben Bedingungen getestet, die auch bei unseren vorhergehenden Prüfungen gegolten haben. Die Endergebnisse der Tests weichen nicht sehr stark voneinander ab:

Natürlich kostet der Inhalt der Klassen etwas, aber das sind Kinkerlitzchen im Vergleich zu den Vorteilen, die sie bieten.
6. Die Vorteile der Verwendung von Klassen zur Mittelwertbildung
Ein, bereits hinreichend überzeugender Vorteil der Verwendung dieser Algorithmen besteht darin, dass sie den Aufruf benutzerdefinierter und technischer Indikatoren ersetzen, was häufig zu einer erheblichen Steigerung der Arbeitsgeschwindigkeit des entwickelten, weiter oben vorgestellten Programmcodes führt.
Ein weiterer praktischer Vorteil dieser Klassen ist die erstaunliche Einfachheit ihrer Verwendung. Zum Beispiel stellt alles, was William Blau in seinem recht bekannten Buch Momentum, Direction, and Divergence ausführt, ein echtes Testgelände für diesen Ansatz zur Programmierung von Indikatoren dar. Der Indikatorcode ist äußerst komprimiert und verständlich, und besteht häufig nur aus einem einzigen Zyklus zur Neuberechnung der Balken.
Man kann leicht einen beliebigen klassischen oder technischen Indikator anlegen und dazu alternative Algorithmen zur Bildung von Mittelwerten verwenden. Eine recht breite Auswahl an Algorithmen zur Mittelwertbildung bietet mehr Möglichkeiten zur Erstellung nicht ganz traditioneller Handelssysteme in aller Regel mit einer früheren Ermittlung des Trends und einer geringeren Anzahl falscher Ausschläge.
7. Einige Empfehlungen zur Anwendung von Mittelwertbildungsalgorithmen in dem Code eines konkreten Indikators
Eine flüchtige Durchsicht beliebiger, mithilfe verschiedener Algorithmen umgesetzter Indikatoren aus dem Anhang zu diesem Beitrag genügt, um zu verstehen, dass diese Algorithmen sich stark voneinander unterscheiden.
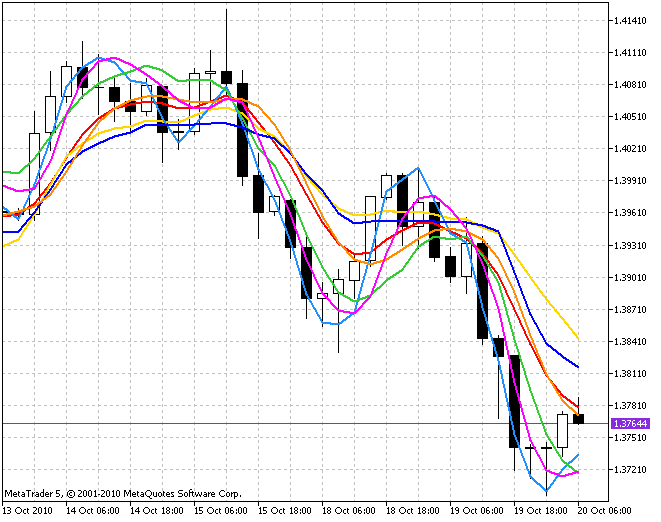
Und deshalb wäre es nicht unvernünftig anzunehmen, dass bei Weitem nicht jeder der vorhandenen Algorithmen für jede Verwendung gleich gut geeignet ist. Auch wenn es recht mühselig wäre, eine ausreichend strenge Grenzlinie um den Anwendungsbereich des einen oder anderen Indikators zu ziehen, ist es dennoch möglich, allgemeine Empfehlungen zu ihrer Verwendung zu geben.
Die Algorithmen von Tushar Chande und Kaufman beispielsweise sind zur Ermittlung von Trendsituationen gedacht, aber für eine weitere Glättung zum Herausfiltern des Kursrauschens völlig ungeeignet. Somit wäre es vorzuziehen, in Indikatoren, die diese Algorithmen verwenden, entweder unverarbeitete Kursreihen oder die Werte von Indikatoren einzugeben, in denen von vornherein keine Mittelwertbildung vorgesehen ist. Es folgt das Ergebnis der Verarbeitung der Werte des Momentum-Indikators unter Verwendung des Algorithmus von Kaufman (der Indikator 4c_Momentum_AMA.mq5):
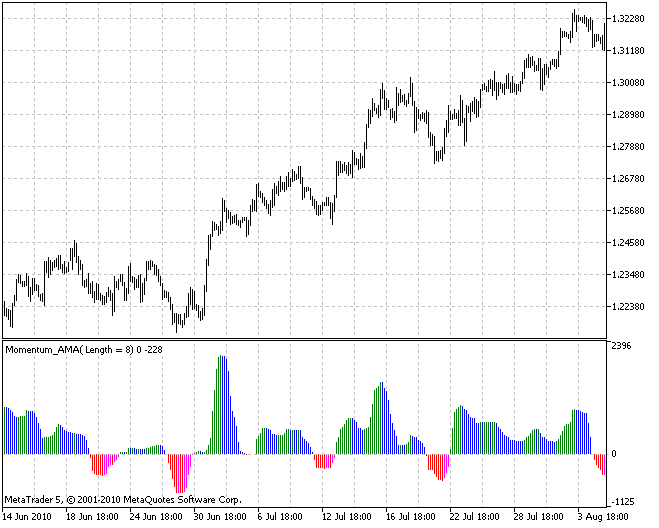
Meiner Meinung nach bedürfen die klassischen Mittelwertbildungsalgorithmen keiner besonderen Empfehlung. Ihr Anwendungsgebiet ist recht groß. Überall, wo der Einsatz dieser Algorithmen möglich ist, können die verbleibenden vier Mittelwertbildungen (JMA, T3, die ultralineare und die parabolische) mit Erfolg verwendet werden. Hier haben wir zum Beispiel den Indikator MACD, bei dem die Mittelwertbildungen EMA und SMA durch JMA ersetzt worden sind (der Indikator JMACD.mq5):
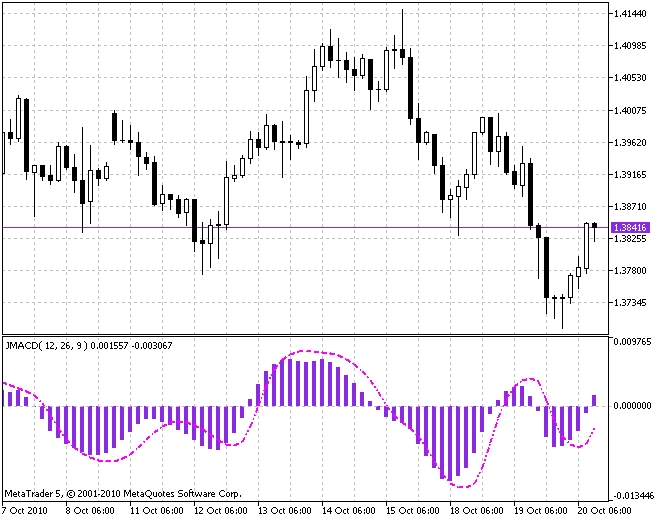
Und hier ist das Ergebnis ohne Austausch des Mittelwertbildungsalgorithmus in dem Indikator, dafür aber mit einer Glättung des bereits berechneten Indikators für eine bessere Qualität bei der Ermittlung des aktuellen Trends (der Indikator JMomentum.mq5):
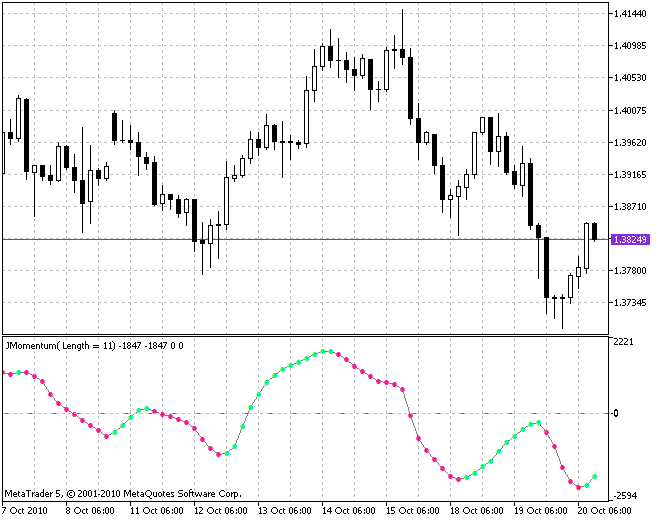
Selbstverständlich ändert sich das Verhalten der Finanzmärkte ständig, weswegen es naiv wäre anzunehmen, dass man diesen einen, für ein bestimmtes Segment der Finanzmärkte jetzt und für alle Zeit absolut idealen Algorithmus finden könnte. Aber nein! Nichts ist für die Ewigkeit! Nichtsdestotrotz verwende ich zum Beispiel für diesen sich ständig wandelnden Markt in meinen Handelssystemen häufig solche Indikatoren für den schnellen und den mittelfristigen Trend wie JFATL.mq5 und J2JMA.mq5. Ich bin vollkommen zufrieden mit den Prognosen auf ihrer Grundlage.
Da wäre noch etwas zu ergänzen. Die Mittelwertbildungsalgorithmen als solche sind mehrfach verwendbar. Recht ordentliche Ergebnisse erhält man, wenn man bereits gemittelte Werte einer erneuten Mittelwertbildung unterzieht. Ehrlich gesagt habe ich die Untersuchung des Vorgehens zum Anlegen von Indikatoren in diesem Beitrag genau mit diesem Indikator begonnen (der Indikator MAx4.mq5).
8. Allgemeine Vorstellung von der Erstellung des Codes für die Algorithmen zur Mittelwertbildung
Und jetzt, zum Abschluss dieses Beitrags, möchte ich in aller Kürze auf die Einrichtung der Mittelwertbildungsfunktionen selbst eingehen.
Zunächst einmal beinhalten die meisten Algorithmen zur Bildung von Mittelwerten dynamische Variablendatenfelder der Art m_SeriesArray[] zur Speicherung der Werte des Eingangsparameters series.
Beim Auftreten von für die Berechnung aussagekräftigen Daten muss diesen einmal Speicherplatz in dem entsprechenden Datenfeld zugewiesen werden. Das erledigt die Funktion SeriesArrayResize() der Klasse CMovSeriesTools.
//----+ Changing the size of the array of variables if(bar==begin && !SeriesArrayResize(__FUNCTION__, Length, m_SeriesArray, m_Size_)) return(EMPTY_VALUE);
Danach muss für jeden Balken an die Stelle des jeweils ältesten Werts der aktuelle Wert der Kursreihe series in dieses Datenfeld eingetragen und die Kennziffer dieser Position in der Variablen m_count festgeschrieben werden. Das geschieht mithilfe der Funktion Recount_ArrayZeroPos() der Klasse CMovSeriesTools.
//----+ transposition and initialization of cells of the array m_SeriesArray
Recount_ArrayZeroPos(m_count, Length_, prev_calculated, series, bar, m_SeriesArray);
Und jetzt müssen wir, um das benötigte Element mit der entsprechenden Verschiebung in Bezug auf das aktuelle zu finden, die Funktion Recount_ArrayNumber() der Klasse CMovSeriesTools verwenden:
for(iii=1; iii<=Length; iii++, rrr--) { kkk = Recount_ArrayNumber(m_count, Length_, iii); m_sum += m_SeriesArray[kkk] * rrr; m_lsum += m_SeriesArray[kkk]; m_weight += iii; }
Üblicherweise wird in solchen Fällen das jüngste Element an die Nullposition gesetzt, und alle übrigen (mit Ausnahme des allerältesten) werden provisorisch nacheinander auf die jeweils folgenden Positionen umgeschrieben, aber das ist hinsichtlich der Ressourcen des Computers nicht ökonomisch, dagegen erscheint der oben dargestellte, nur geringfügig kompliziertere Ansatz zweckmäßiger.
Neben den unmittelbaren Mittelwertbildungsalgorithmen sind im Hauptteil dieser Funktionen auch die Aufrufe der Funktionen zur Bestimmung der Position des Balkens relativ zum Beginn der Balkenzählung enthalten:
//----+ Checking the start of reliable calculation of bars if(BarCheck1(begin, bar, set)) return(EMPTY_VALUE);
des Zeitpunktes, zu dem genügend Daten zur anfänglichen Bereitstellung der Variablen vorhanden sind:
//----+ Initialization of zero if(BarCheck2(begin, bar, set, Length))
sowie der Situationen, in denen der letzte Balken geschlossen wird:
//----+ Saving values of the variables if(BarCheck4(rates_total, bar, set))
oder eben nicht geschlossen wird:
//----+ Restoring values of the variables if(BarCheck5(rates_total, bar, set))
Die erste Überprüfung legt die Situation fest, in der nicht genügend Balken für die Arbeit der Mittelwertbildungsfunktion vorhanden sind, sie gibt ein leeres Ergebnis aus. Nach erfolgreichem Durchlaufen der zweiten Prüfung, wenn die Daten für die erste Berechnung ausreichen, erfolgt die einmalige Bereitstellung der Variablen. Die beiden letzten Prüfungen werden für die korrekte mehrmalige Verarbeitung der Werte auf dem aktuellen noch nicht geschlossenen Balken benötigt. Darüber habe ich bereits in meinem der Optimierung des Programmcodes gewidmeten Beitrag geschrieben.
Jetzt noch einige Worte zur Optimierung des Programmcodes dieser Funktionen, damit sie mit maximaler Geschwindigkeit arbeiten. Der Algorithmus SMA geht zum Beispiel davon aus, dass in jedem Balken der Mittelwert aus einer Auswahl von Werten der Kursreihe für den betreffenden Zeitraum gebildet wird. Diese Werte werden buchstäblich summiert und durch den Zeitraum auf jedem Balken dividiert.
Aber es geht darum, dass die Summe auf dem vorhergehenden Balken sich von der des aktuellen dadurch unterscheidet, dass bei Ersterer der Wert der Kursreihe mit einer Verschiebung gegenüber dem aktuellen Zeitraum hinzugefügt wird, bei der zweiten dagegen der aktuelle Wert. Somit wäre es erheblich sinnvoller, diese Summe ein einziges Mal bei der Bereitstellung der Funktion zu berechnen und danach bei jedem Balken zu dieser Summe den jeweils neuen Wert der Kursreihe hinzu zu addieren und den ältesten des Abrufs des vorhergehenden Balkens abzuziehen. Genau das erfolgt in dieser Funktion.
Fazit
Die unterschiedlichen in dem Beitrag mithilfe von Klassen umgesetzten Mittelwertbildungsalgorithmen sind so einfach, gleichmäßig und allgemeingültig, dass bei ihrer Aneignung keine nennenswerten Schwierigkeiten auftreten sollten.
Die angehängten Dateien enthalten eine mehr als umfassende Anzahl von Beispielen, um das Verständnis dieses Ansatzes zur Erstellung des Programmcodes für Indikatoren noch weiter zu erleichtern. In der gepackten Datei Include__.zip sind alle Klassen auf Dateien verteilt. Include.zip enthält zwei zur Zusammenstellung aller in Indicators__2.zip abgelegten Indikatoren erforderliche Dateien. Die zu testenden Expert-Systeme befinden sich in der gepackten Datei Experts.zip.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/180
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Anlegen eines Spektrumanalysators
Anlegen eines Spektrumanalysators
 Marktbeobachtung mithilfe vorgefertigter Klassen
Marktbeobachtung mithilfe vorgefertigter Klassen
 Ein einfaches Beispiel zur Erstellung eins Indikators mittels Qualitativaussagenlogik (unscharfer oder fuzzy Logik)
Ein einfaches Beispiel zur Erstellung eins Indikators mittels Qualitativaussagenlogik (unscharfer oder fuzzy Logik)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.

Das Problem ist gelöst, Sie müssen nur noch die Aufzählung aus.... nehmen.
Das Problem ist gelöst, Sie müssen nur noch die Aufzählung aus.... nehmen.
Das Problem ist gelöst, Sie müssen nur noch die Aufzählung aus.... nehmen.
JA, GUT! Ich hab's!
Wie?