追加バッファなしの中間計算用物価系列の平均化
945
0
はじめに
私の記事『インディケータの経済的計算原理』で、コード内でカスタムインディケータおよびテクニカルインディケータを毎回呼び出さないことが、作成中のインディケータの中間計算においてもっとも最適な方法であると証明する合理的で説得力のある検証を行いました。
実行の最終スピードは、インディケータの中に中間計算用コードを入れると、予想と比べるとかなり遅いものとなりました。
それが十分シンプルであれば、コードを書くこのような方法はたいへん魅力的なものです。事実、中間計算結果を格納する追加バッファの記述を入れると、コードはかなり複雑になります。
中間計算の多様性にもかかわらず、そこで必要とされるものの多くは平均化の異なるアルゴリズムです。ほとんどの場合、それらのために、そういったコードを書く手間をかなり省くシンプルで汎用的なカスタム関数を使います。本稿では、そのような関数を作成し、連携するプロセスについて述べていきます。
1. 一つのバーと連携する平均化関数の一般的考え方
現在バーを平均化する一般的方法は中間インディケータバッファにあります。そのバッファは必要な情報を書き込み、以前の値範囲、それは平均化期間に等しい値です、を選択し、平均値を計算します。
この選択処理手順は以下です。
SmoothVar(bar) = Function(Var(bar - (n-1)), Var(bar - (n-2)), ......... Var(bar))
ここで
- SmoothVar(bar) — 平均化されたパラメータ
- bar — バー数、それに対し計算が行われます。
- Var(bar - (n-1)) — バー上での移動 (n-1) を伴う平均化パラメータ
- n — 平均化するバー数
今回の場合、平均化方法は2サイクルの計算を招きます。最初のサイクルでは、データが計算され中間バッファに入れられます。二番目のサイクルで、インディケータバッファの追加セル検索を行う別のサイクルを使って、上述の式を基に平均化が行われます。関数自体に中間データの選択を集積すると、この計算はずっと簡単に見えます。この場合、平均化関数は以下のようなものです。
SmoothVar(bar) = Function(Var(bar), bar)
新しい値Var(bar) が現在バーの関数内の値選択に書き込まれます。そして不要となったVar(bar - n) の値が選択から削除されます。この方法で、平均化コードはささいなものに見え、それ以上のインディケータバッファは要求しません。関数内部では、配列がバー一つの計算に要求される正確に必要なデータ量だけを格納します。
この場合、データ計算サイクルも一つだけです。現在バーでこの平均化関数を呼ぶだめにはまず、それ以前のバーすべてでその関数を呼ぶ必要があることに注意が必要です！
2. 一つのバーを連携する従来型平均化関数の実装例
平均化関数はその関数呼び出し中に値を失わない変数を含む必要があります。また、異なるパラメータを有するシングルタイプの平均化は複数回一つのコードで使用されます。そのため、今日数メモリリソースの衝突を避けるため、classes関数を実装する必要があります。以下は私の例です
従来型の平均化アルゴリズムは CMoving_Averageクラスに記述されます。
class CMoving_Average : public CMovSeriesTools { public: double MASeries (uint begin, // Index of start of reliable bars uint prev_calculated, // Amount of history in bars at a previous tick uint rates_total, // Amount of history in bars at a current tick int Length, // Period of averaging ENUM_MA_METHOD MA_Method, // Method of averaging (MODE_SMA, MODE_EMA, MODE_SMMA, MODE_LWMA) double series, // Value of price series calculated for the bar with the 'bar' number uint bar, // Bar index bool set // Direction of indexing of arrays. ); double SMASeries (uint begin, // Index of start of reliable bars uint prev_calculated,// Amount of history in bars at a previous tick uint rates_total, // Amount of history in bars at a current tick int Length, // Period of averaging double series, // Value of price series calculated for the bar with the 'bar' number uint bar, // Bar index bool set // Direction of indexing of arrays. ); double EMASeries (uint begin, // Index of start of reliable bars uint prev_calculated, // Amount of history in bars at a previous tick uint rates_total, // Amount of history in bars at a current tick double Length, // Period of averaging double series, // Value of price series calculated for the bar with the 'bar' number uint bar, // Bar index bool set // Direction of indexing of arrays. ); double SMMASeries(uint begin, // Index of start of reliable bars uint prev_calculated, // Amount of history in bars at a previous tick uint rates_total, // Amount of history in bars at a current tick int Length, // Period of averaging double series, // Value of price series calculated for the bar with the 'bar' number uint bar, // Bar index bool set // Direction of indexing of arrays. ); double LWMASeries(uint begin, // Index of start of reliable bars uint prev_calculated, // Amount of history in bars at a previous tick uint rates_total, // Amount of history in bars at a current tick int Length, // Period of averaging double series, // Value of price series calculated the bar with the 'bar' number uint bar, // Bar index bool set // Direction of indexing of arrays. ); protected: double m_SeriesArray[]; int m_Size_, m_count, m_weight; double m_Moving, m_MOVING, m_Pr; double m_sum, m_SUM, m_lsum, m_LSUM; };
このクラスは、他に保護関数メソッドと移動平均期間の正確性のチェックを含む基本クラス CMovSeriesToolsから派生します。
基本クラスにはその他私が提案する全クラスで使用される汎用コードが含まれます。そのため、それを派生クラスに何度もコピーするのは意味のないことです。平均化を使っての適用されたタスクでは、保護されたクラスメンバはな形式では使われません。そのため、今はそれを見ていくことはしません。
CMoving_Averageクラスは5個のシングルタイプ関数で交際されています。その名前からそれらの機能がわかりやすいので詳細を語る必要はないと思います。
最初のMASeries() 関数は、他の4つの関数の集合体integral collectionで、それによってパラメータ MA_Methodを使って平均化のアルゴリズムを選択することができます。平均化アルゴリズムのコードは、最高のパフォーマンスのために最適化され、これは関数の主要なパラメータ（長さ、シリーズ、バー）に 追加のパラメータが補われている理由です。追加パラメータは次のようなものです。まず、 prev_calculated, rates_total とセットその目的は同じ名前のベクトル関数を全く同じです。
パラメータ 'set' は、平均化関数内で変数配列と同じになるように価格系列エレメント 'series' のインデックスフラグを設定します。
このクラスのすべての平均化関数は固定されたパラメータを持ち、それはプログラムコードが実行されるとき変更することができないことに配慮が必要です。CMoving_AverageクラスのEMASeries()関数はこのタイプのパラメータを二重に持ちます！
そして、CMoving_Averageクラスです。インディケータで使い始めることができます。そのために、 #include 指令を使いグローバルスコープで作成するインディケータコードにMASeries_Cls.mqhファイルのコンテンツを追加します。
#include <MASeries_Cls.mqh>
それから、インディケータコードの中で平均化に必要な手順の数を決め、OnCalculate()部分（ループ処理前の中括弧）で要求される平均化手順数に応じてCMoving_Average クラスを宣言します。 クラスの配列には平均化の各手順のための個別クラス変数やセルがあるはずです。
//---- declaration of variables of the class CMoving_Average из файла MASeries_Cls.mqh static CMoving_Average MA1, MA2, MA3, MA4;
OnCalculate()関数内のクラス変数は静的に宣言されます。理由はそれらの値がこの関数の呼び出しのと呼び出しの間で保持される必要があるからです。 これで平均化自体を始めることができます。例として、価格系列の連続した4つの平均化手順を示します。 - SMA/EMA/SMMA/LWMA (インディケータ MAx4.mq5):
//---- The main cycle of indicator calculation for(bar = first; bar < rates_total; bar++) { //----+ Four calls of the function MASeries. ma1_ = MA1.MASeries(start1, prev_calculated, rates_total, Length1, MODE_SMA, price[bar], bar, false); ma2_ = MA2.MASeries(start2, prev_calculated, rates_total, Length2, MODE_EMA, ma1_, bar, false); ma3_ = MA3.MASeries(start3, prev_calculated, rates_total, Length3, MODE_SMMA, ma2_, bar, false); ma4_ = MA4.MASeries(start4, prev_calculated, rates_total, Length4, MODE_LWMA, ma3_, bar, false); //---- MAx4[bar] = ma4_ + dPriceShift; }
それぞれ前の平均化（最後のものは含まない）結果は平均化の次のアルゴリズムで使用され、最終結果がインディケータバッファに渡されます。
このコードのもっとも重要な部分は信頼性のあるバーの開始を示すインデックス値の細心の注意を払った予備初期化だと思います。ここの場合は以下です。
//---- Initialization of variables of start of reliable information start1 = 0 + begin; start2 = Length1 + begin; start3 = Length1 + begin; // the previous EMA averaging doesn't change the start of reliable information start4 = Length1 + Length3 + begin;
この場合、平均化のLWMAアルゴリズムが最後のもので、それは何にも影響を与えませんが、もしそれが最後でなければ、信頼のおける情報のスタートの移動はLength4+1、長さ4ではないとなることには注意が必要です！
信頼できる情報のスタートがどのナンバーからかということが前のコードからはっきりしていないなら、大きい方の数字を取って必要ならば試しにその数字を減らしていきます。
3. テクニカルインディケータおよびカスタムインディケータおよびを使用する類似を伴なくクラス使用により作成されたインディケータ比較
作成されたインディケータMAx4.mq5のパフォーマンスを、テクニカルインディケータiMA()を使うそっくりな類似インディケータ (iMAx4.mq5) と比較するのはたいへん面白いと思います。
検証を行うことをきめたらすぐに、MAx4.mq5に似た別のインディケータ(MAx3x1.mq5)の検証を行うことは合理的ですが、最初の平均化はテクニカルインディケータiMA()を呼んで、他の3つはCMoving_Averageクラスを使って行います。私は、クライアント端末のインディケータの標準セットがCustom Moving Average.mq5 インディケータをインクルードするとすぐに、検証するため、そのベースに別の類似インディケータ(cMAx4.mq5)を作成しました。
のちの分析に備え、Expert Advisorsの検証準備をしたのです。：それぞれ、MAx4_Test.mq5、 iMAx4_Test.mq5、 MAx3x1_Test.mq5、 cMAx4_Test.mq5。その検証条件詳細は『インディケータの経済的計算原理』稿に述べられています。ですから、ここでは検証について詳しく述べませんが、4件のExpert Advisorすべてを、EURUSD Н4に関し、毎ティックをモデル化し、全EA「期間」入力パラメータの値を500として 過去12か月間についてストラテジーテスタで実行した結果をお見せします。
カスタムインディケータを呼ぶインディケータが最悪の結果を示しています。このコード記述のバリアントは怠け者にだけ推奨されるものですＡ！!別の「リーダー」も遅れてやってきていますが、テクニカルインディケータを呼ぶことを基にしたものは、もっとましな結果です。ただし、まだ理想からは程遠いものです。
検証の真のリーダーはクラスを使って作成されたインディケータです！
クラスとテクニカルインディケータの混合は二番目の成績でした。が、子の結果もいつもそのように出るとは限りません。インディケータ検証時間が決定的であれば、毎回そのような状況になるたびに個人的にそのようなバリアントを確認するのがよいでしょう。
平均化クラス実装の概観
| № | アルゴリズム | クラス名 | ファイル名 | アルゴリズム適用後の 信頼性の高いバーの始発点変化 |
パラメータ長の動的変化の可能性 |
|---|---|---|---|---|---|
| 1 | 従来の平均化 | CMoving_Average | MASeries_Cls.mqh | 長さ/0/長さ/長さ + 1 (SMA/EMA/SMMA/LWMA) | no |
| 2 | 標準偏差 | CStdDeviation | StdDevSeries_Cls.mqh | 長さ | no |
| 3 | JMA 平滑化 | CJJMA | JJMASeries_Cls.mqh | 30 | yes |
| 4 | T3 平滑化 | CT3 | T3Series_Cls.mqh | 0 | yes |
| 5 | ウルトラリネアの平滑化 | CJurX | JurXSeries_Cls.mqh | 0 | yes |
| 6 | Tushar Chandeの平滑化 | CCMO | CMOSeries_Cls.mqh | 長さ + 1 | no |
| 7 | Kaufman's 平滑化 | CAMA | AMASeries_Cls.mqh | 長さ + 3 | no |
| 8 | パラボリック平均化 | CParMA | ParMASeries_Cls.mqh | 長さ | no |
| 9 | 変化速度 | CMomentum | MomSeries_Cls.mqh | 長さ + 1 | no |
| 10 | 変化速度の標準化 | CnMomentum | nMomSeries_Cls.mqh | 長さ + 1 | no |
| 11 | 変化率 | CROC | ROCSeries_Cls.mqh | 長さ + 1 | no |
前に述べたCMoving_Averageクラスは平均化のアルゴリズムを5つインクルードします。
CCMOクラスは平均化アルゴリズムをとオシレータを含みます。
その他のクラスは単一の平均化アルゴリズムをインクルードします。提案のクラスのどれを使うのも、そのイデオロギーは、上記で述べたCMoving_Averageクラスの使用手順とまったく同じです。すべての平均化アルゴリズムのコード（パラボリックは除き）は実行の最高速度に最適化されています。パラボリック平均化コードは手順が複雑なため、最適化されていません。最後の3個のアルゴリズムのは平均化しません。それを加えたのは、人気の技術分析家の著書があり、よく使われるのと互換性のためです。
情報が理解しやすいように、平均化アルゴリズムのは.mqhファイルに個別に入れるとよいでしょう。また、実用のために最良バリアントは独立したファイルに持つのがよいでしょう。
インディケータで使用するには、提案のクラスはすべてSmoothAlgorithms.mqhファイル一つに入れています。また、このファイルにはiPriceSeries.mqhファイルの関数が追加されています。PriceSeries() 関数だけが本稿の例で使用されています。
double PriceSeries ( uint applied_price, // Price constant uint bar, // Index of shift for a specified number of periods back or forward // relatively to a current bar. const double& Open [], const double& Low [], const double& High [], const double& Close[] )
この関数は、OnCalculate()関数を呼ぶ二番目のタイプとして使用されるためインディケータと連携しています。
この関数作成の主な発想は、列挙ENUM_APPLIED_PRICE の価格時系列セットを拡張するためです。この関数は価格時系列の値1 ～ 11の数字で返します。
4. 平均化クラスを使用したプログラムコード実装実用例
その他クラスを使用した別の例をお見せすることで十分だと思います。それで、すべては四重平均化と同じ方法で行われることを確認してください。CJJMAクラスおよびCJurX(JCCX.mq5)クラスを用い、CCIインディケータの類似で OnCalculate()関数を実装するバリアントをお見せしようと思います。
int OnCalculate(const int rates_total, // amount of history in bars on a current tick const int prev_calculated, // amount of history in bars on a previous tick const datetime& time[], const double& open[], const double& high[], const double& low[], const double& close[], const long& tick_volume[], const long& volume[], const int& spread[] ) { //----+ //---- Checking whether there are enough bars for calculation if (rates_total < 0) return(0); //---- Declaration of variables with floating point double price_, jma, up_cci, dn_cci, up_jccx, dn_jccx, jccx; //----+ Declaration of integer variables int first, bar; //---- calculation of start number 'first' for the cycle of recalculation of bars if (prev_calculated == 0) // checking for the first start of calculation of indicator first = 0; // starting number for calculation of all bars else first = prev_calculated - 1; // starting number for calculation of new bars //---- declaration of variables of the class CJurX from the file SmoothAlgorithms.mqh static CJurX Jur1, Jur2; //---- declaration of variables of the class CJMA from the file SmoothAlgorithms.mqh static CJJMA JMA; //---- Main cycle of calculation of the indicator for(bar = first; bar < rates_total; bar++) { //----+ Calling the PriceSeries function to get the input price price_ price_ = PriceSeries(IPC, bar, open, low, high, close); //----+ One call of the JJMASeries function to get JMA jma = JMA.JJMASeries(0, prev_calculated, rates_total, 0, JMAPhase, JMALength, price_, bar, false); //----+ Determine the deviation of price from the value of JMA up_cci = price_ - jma; dn_cci = MathAbs(up_cci); //----+ Two calls of the JurXSeries function. up_jccx = Jur1.JurXSeries(30, prev_calculated, rates_total, 0, JurXLength, up_cci, bar, false); dn_jccx = Jur2.JurXSeries(30, prev_calculated, rates_total, 0, JurXLength, dn_cci, bar, false); //---- Preventing zero divide in empty values if (dn_jccx == 0) jccx = EMPTY_VALUE; else { jccx = up_jccx / dn_jccx; //---- Limitation of the indicator from the top and from the bottom if (jccx > +1)jccx = +1; if (jccx < -1)jccx = -1; } //---- Loading the obtained value to the indicator buffer JCCX[bar] = jccx; } //----+ return(rates_total); }
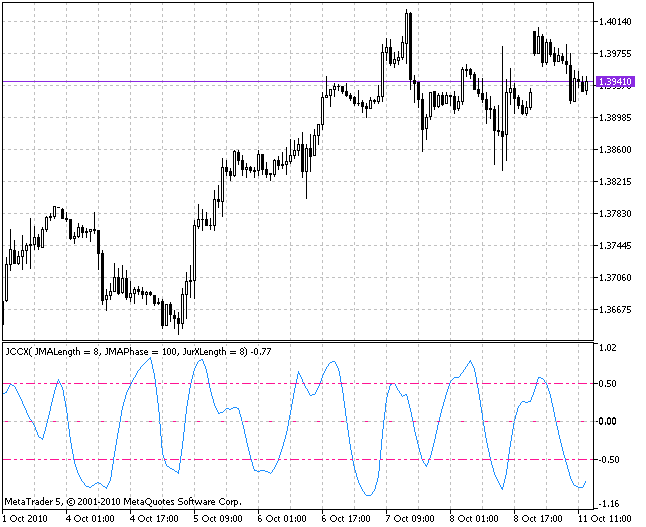
ただし、今回はインディケータコードにグローバルスコープからの別ファイルから適切なクラスを追加しました。
#include <SmoothAlgorithms.mqh>
では、みなさんの注意を別のものに向けたいと思います。事は、膨大な数のインディケータが一つのバーの関数として表されるということです。これはクラスを使って連携するのはひじょうに都合のよいものです。
たとえば、Tushar ChandeのVidya移動平均に基づきボリンジャーチャネルを描くのは面白いことです。 ここでは、2つのクラスCCMOおよび CStdDeviationが使われます。最初のクラスを使って、移動平均VIDYAの値を取得します。また、二番目のクラスを使って、移動平均の価格系列の標準偏差値を計算します。
その後、チャネルの上下境界の計算にこの偏差を使います。
//+------------------------------------------------------------------+ // Description of the classes CStdDeviation{}; and CCMO{}; | //+------------------------------------------------------------------+ #include <SmoothAlgorithms.mqh> //+==================================================================+ //| The algorithm of getting the Bollinger channel from | //| the moving average VIDYA | //+==================================================================+ class CVidyaBands { public: double VidyaBandsSeries(uint begin, // number of the start of reliable calculation of bars uint prev_calculated, // amount of history on a previous tick in bars uint rates_total, // amount of history on a current tick in bars int CMO_period, // the period of averaging of the oscillator CMO double EMA_period, // the period of averaging of EMA ENUM_MA_METHOD MA_Method, // the type of averaging int BBLength, // the period of averaging of the Bollinger channel double deviation, // Deviation double series, // Value of the price series calculated for a bar with the number 'bar' uint bar, // Bar index bool set, // Direction of indexing of arrays double& DnMovSeries, // Value of the lower border of the channel for a current bar double& MovSeries, // Value of the middle line of the channel for a current bar double& UpMovSeries // Value of the upper border of the channel for a current bar ) { //----+ //----+ Calculation of the middle line MovSeries = m_VIDYA.VIDYASeries(begin, prev_calculated, rates_total, CMO_period, EMA_period, series, bar, set); //----+ Calculation of the Bollinger channel double StdDev = m_STD.StdDevSeries(begin+CMO_period+1, prev_calculated, rates_total, BBLength, deviation, series, MovSeries, bar, set); DnMovSeries = MovSeries - StdDev; UpMovSeries = MovSeries + StdDev; //----+ return(StdDev); } protected: //---- declaration of variables of the classes CCMO and CStdDeviation CCMO m_VIDYA; CStdDeviation m_STD; };
シンプルで小さなクラス取得です！
関数VidyaBandsSeries() の最後の3つの入力パラメータはチャンネルが必要とする値をリンクを通じて渡します。
この場合、関数VidyaBandsSeries()内ではクラスの変数は宣言したりそれらを静的にすることはできません。というのも、クラス内の静的変数はまったく異なる意味を持つからです。それがクラスのグローバルスコープで宣言を行う理由です。
protected: //---- declaration of variables of the classes CCMO and CStdDeviation CCMO m_VIDYA; CStdDeviation m_STD;
一般的なボリンジャーチャネルでは、移動平均の平均期間とチャネル自体の平均化期間はつねに等しくなっています。
このクラスでは、自由度が高まるようにパラメータを別に作成しました。(EMA_period と BBLength). このクラスを基に作成されたインディケータ自体 (VidyaBBands.mq5)は、CVidyaBandsクラスを使うのにとてもシンプルなので、本稿でその分析をするに及びません。
インディケータ関数のそのようなクラスは個別の mqhファイルに収めることた必要です。私はその関数をIndicatorsAlgorithms.mqhファイルに収めました。
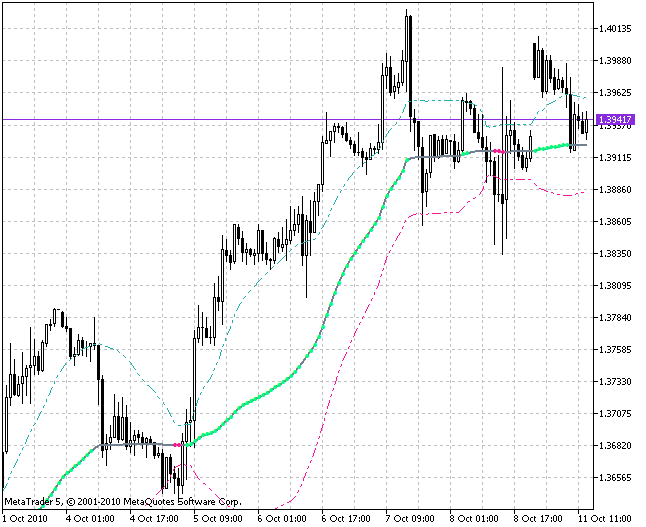
5. クラスを使う インディケータとクラスを使わないインディケータのパフォーマンス比較
まず、見つけたいのは、インディケータのコードを書いているとき、クラスの使用はどのようにパフォーマンス低下を招くのか？ということです。
このために、インディケータJJMA.mq5 のコードがクラス (JMA.mq5)を使わずに書かれ、そしてそれが前と同じ条件で検証されました。検証の最終結果に大きな差は見られません。
クラスを使うのにいくつか追加で変更がありますが、それは示すメリットに比べると大したものではありません。
6. 平均化クラス使用のメリット
これらアルゴリズムを使うメリットのひとつは、とても説得力のあるものですが、呼び出しの置き換えにより、上で作成されたコードのパフォーマンスを著しく高めるということです。
別のそのようなクラスの実用的メリットは、それらを使う上での利便ン性です。たとえば、William Blau氏著の人気の一冊 "Momentum, Direction and Divergence " で述べられているすべてが、インディケータを書くこの種の方法にまさにうってつけだと思えるのです。インディケータコードは最大限圧縮されており、わかりやすく、バー再計算に一度のサイクルですむことが多いのです。
どんなインディケータでも簡単に作成することができます。 - 平均化の別の手法を使えば、一般的なものでも技術的なものでも。平均化アルゴリズムの広い多様性が、従来のトレードシステムでないものを作成する大きな可能性を与えてくれます。それに伴うのはトレンドを早く見つけ出せること、そして失敗がおこりにくくなることです。
7. 特定のインディケータコードで平均化アルゴリズム使用における提案
ここで述べている、異なる平均化アルゴリズムを使って作成されたインディケータをちょっと見ると、それぞれいかに違っているかがわかります。
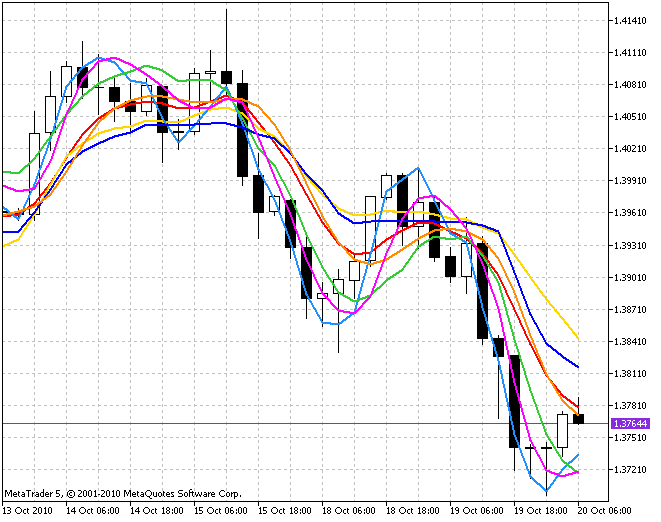
提案されるアルゴリズムがすべて等しくそれぞれの状況に適してはいない、と推測するのは妥当でしょう。どのアルゴリズムを使うかはっきりとした境界線を引くのはむつかしいですが、一般的な提案はできると思います。
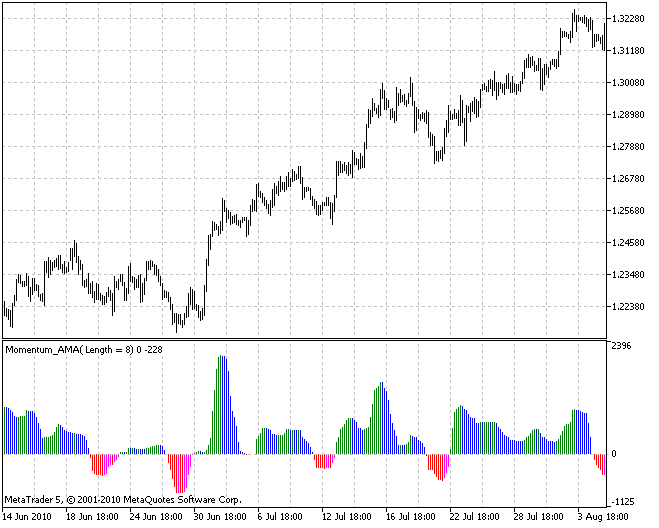
たとえば、Tushar ChandeとKaufmanのアルゴリズムはトレンド状況の判断を目的としており、 それ以外のノイズ除去目的の平滑化には適していません。そのため、これらアルゴリズムには未処理の価格系列や平均化しないインディケータ値を入力するのが適しています。Kaufmanのアルゴリズムを用いたインディケータMomentumの値の処理結果があります。 (インディケータ 4c_Momentum_AMA.mq5)
一般的な平均化アルゴリズムには特別な提案は必要ないと思います。それらの適用範囲はきわめて広いものです。これらアルゴリズムが使われるところはどこでも、左の4つのアルゴリズムを問題なく使うことができます。 (JMA、T3、 ウルトラリネア、パラボリック)ここに EMA と SMA がJMA平均化と置き換えられたMACDインディケータがあります。 (インディケータ JMACD.mq5):
そしてここに、現在の傾向をよりよく判断するために平均化のアルゴリズムを変える代わりに計算されたインディケータを平滑化した結果があります。 (インディケータJMomentum.mq5):
マーケットの相場はつねに変動し、そのため永遠にファイナンシャルマーケットの特定の部分のためのただ一つの理想的アルゴリズムを見つけようと思うのは世間知らずというものです。悲しいかな！この世で永遠に変わらないものなどありませんよ！わたしにしたところで、たとえばですが、常に変動するこのマーケットで高速＆中期トレンドのインディケータをよく使います。JFATL.mq5 and J2JMA.mq5などです。私はそれらを基にした予測にかなり満足しています。
他につけ加えたいことは、平均化アルゴリズムは再利用可能だということです。すでに平均化した値を繰り返し平均化すると良い結果が出やすくなります。事実、本稿でもインディケータをそこからドローする処理の分析を始めました。 (インディケータ MAx4.mq5)
8. 平均化アルゴリズムのコード構成の一般的発想
本稿も終わりがけですが、注目いただきたいのは平均化そのもののメカニズムについてです。
まず、平均化アルゴリズムは、入力パラメータ'series'の値を格納するためにほとんどがm_SeriesArray[]タイプの変数の動的配列をインクルードします。
計算に重要な情報が出現するやいなや、そのようは配列に一度にメモリを割り当てる必要があります。それはクラスCMovSeriesToolsの関数SeriesArrayResize()を使って行います。
//----+ Changing the size of the array of variables if(bar==begin && !SeriesArrayResize(__FUNCTION__, Length, m_SeriesArray, m_Size_)) return(EMPTY_VALUE);
それからそれぞれのバーで配列のもっとも古い値に価格系列'series'の現在の値を書き、変数m_count内にその位置の番号を記憶する必要があります。それはクラスCMovSeriesToolsの関数Recount_ArrayZeroPos() を用いて行われます。
//----+ transposition and initialization of cells of the array m_SeriesArray
Recount_ArrayZeroPos(m_count, Length_, prev_calculated, series, bar, m_SeriesArray);
現在エレメントに対して相対的に移動したエレメントを見つける必要がある場合、クラスCMovSeriesToolsの関数Recount_ArrayNumber() を使う必要があります。
for(iii=1; iii<=Length; iii++, rrr--) { kkk = Recount_ArrayNumber(m_count, Length_, iii); m_sum += m_SeriesArray[kkk] * rrr; m_lsum += m_SeriesArray[kkk]; m_weight += iii; }
通常、このような状況では、最も新しいエレメントがゼロポジションに書かれ、その他はまえもって返し値で次のポジションに上書きされます。ただし、それはコンピュータリソースの節約にはなりません。上で述べられているより複雑な方法はより合理的なように思えます！
また、平均化アルゴリズムのコードには、関数の本体にバー計算の始点に対し相対的ポジションのバーを判断するのに使用される関数呼び出しを含みます。
//----+ Checking the start of reliable calculation of bars if(BarCheck1(begin, bar, set)) return(EMPTY_VALUE);
変数初期化開始のための十分な情報があるとき
//----+ Initialization of zero if(BarCheck2(begin, bar, set, Length))
また、最後のバーがクローズされている状況
//----+ Saving values of the variables if(BarCheck4(rates_total, bar, set))
または、クローズされていない状況
//----+ Restoring values of the variables if(BarCheck5(rates_total, bar, set))
最初のチェックは関数が動作するに十分なバーがない状況を判断し、空の結果を返します。二番目のチェックが問題なく行われると、最初の計算に十分なデータがあり、変数の初期化が一度行われます。最後の2件のチェックは、現在クローズされていないバーの値を正しい複数回処理するのに必要です。それについてはプログラムコードの最適化を扱った記事ですでに述べています。
ここから、そのような関数が最大のパフォーマンスを行うためのプログラムコードの最適化について少しお話します。たとえば、SMAアルゴリズムは各バーにおいて価格系列の選択された期間の値を平均化します。こういった値は文字通りバーの期間によって足され、割らます。
ただ、前のバーの合計と現在バーの合計の違いは、最初のバーは現在バーから相対的に1期間移動した価格系列の値に加算され、二番目のバーは現在バーに加算されている点です。そのため、そのような合計を出すのは関数の初期化中一度だけであるまた、それからそれぞれのバーで価格系列の新規の値だけがこの合計に追加され、古い値はそこから引かれる、というのはきわめて妥当です。まさにこれが関数で行われているのです。
おわりに
本稿で提案しているクラスを使用した平均化アルゴリズムの実装はシンプルで、シングルタイプで、汎用的です。そのため学習に何も困難はないと思います。
本稿に添付されているアーカイブは、インディケータコードを書くこの方法のやさしい理解のため、数々の例を提供しています。アーカイブInclude__en.zip のすべてのクラスはファイルで配布されています。アーカイブ Include_en.zip にはアーカイブ Indicators.zipのインディケータをすべてコンパイルするのに十分なファイルが2つだけあります。検証用有理数はアーカイブExperts.zipで参照いただけます。
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/180
スペクトラム分析の構築
新しいMQL4のオフラインチャート
William Blauの指数MQL5におけるトレーディングシステムパート 1：インディケータ
標準ライブラリクラスを使ってオリジナルのMarket Watchを作成します。
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索