Averaging Price Series for Intermediate Calculations Without Using Additional Buffers

Introduction

In my article "The Principles of Economic Calculation of Indicators" I made reasonably convincing tests that prove the fact that not every single call of a custom or technical indicator in a code is the most optimal way of performing intermediate calculations in a developed indicator.

The final speed of execution may appear to be much lower, comparing to what we would have if we placed the code for intermediate calculations right in our indicator.

This kind of approach to writing a code would be very attractive, if it were simple enough. In fact, it appears to be a serious complication of a code with describing additional buffers used for storing intermediate results of calculation.

Despite the variety of intermediate calculations, most needed in them are different algorithms of averaging. In most cases, for them we can use simple and universe custom functions that significantly simplify the task of writing such a code. The process of creating these functions and working with them will be described in this article.

1. The General Idea of Functions of Averaging that Work with One Bar

The classic approach to averaging on a current bar consists in an intermediate indicator buffer, which we fill with required information, and then select a range of previous values, which is equal to the averaging period, and calculate the average value.

The procedure of processing this selection looks as following:

SmoothVar(bar) = Function(Var(bar - (n-1)), Var(bar - (n-2)), ......... Var(bar)) 

where:

• SmoothVar(bar) — averaged parameter;
• bar — number of a bar, for which the the calculation is performed;
• Var(bar - (n-1)) — average parameters with a shift on (n-1) bars;
• n — number of bars for averaging.
  

Such approach to averaging, in our case, leads to appearing of two cycles of calculation. In the first cycle, the data is calculated and put in an intermediate buffer. In the second cycle, the averaging using another cycle of additional search of cells of the indicator buffer is performed on the basis of the formula suggested above. This calculation will look much easier, if we accumulate the selection of intermediate data within the function itself. In this case, the function of averaging will look as following:

SmoothVar(bar) = Function(Var(bar), bar)

A new value Var(bar) is written to the selection of values inside the function on a current bar, and the values of Var(bar - n) that become unnecessary are deleted from the selection. With this approach, a code of averaging looks pretty trivial and doesn't require additional indicator buffers. Inside the function, the array stores the exact necessary amount of data required for calculation of one bar, not the entire history data.

In this case, there is also only one cycle of data calculation. It should be noted that in order to call this function of averaging on a current bar, you should call it on all previous bars first!

2. The Classic Averaging as an Example of Implementing a Function that Works with One Bar

Such functions of averaging should contain variables that mustn't lose their values between the calls of those functions. In addition, the single-type averaging with different parameters may be used in a code for many times; therefore, to avoid a conflict of using shared memory resources, we should implement those functions as classes; and that's what I've done.

The algorithms of classic averaging are described in the class CMoving_Average:

class CMoving_Average : public CMovSeriesTools
  {
public:  
   double    MASeries  (uint begin,               // Index of start of reliable bars
                       uint prev_calculated,      // Amount of history in bars at a previous tick
                       uint rates_total,          // Amount of history in bars at a current tick
                       int Length,               // Period of averaging
                       ENUM_MA_METHOD MA_Method, // Method of averaging (MODE_SMA, MODE_EMA, MODE_SMMA, MODE_LWMA)
                       double series,              // Value of price series calculated for the bar with the 'bar' number
                       uint bar,                   // Bar index
                       bool set                  // Direction of indexing of arrays.
                      );

   double    SMASeries (uint begin,          // Index of start of reliable bars
                       uint prev_calculated,// Amount of history in bars at a previous tick
                       uint rates_total,     // Amount of history in bars at a current tick
                       int Length,            // Period of averaging
                       double series,         // Value of price series calculated for the bar with the 'bar' number
                       uint bar,              // Bar index
                       bool set              // Direction of indexing of arrays.
                      );
                        
   double    EMASeries (uint begin,            // Index of start of reliable bars
                       uint prev_calculated, // Amount of history in bars at a previous tick
                       uint rates_total,     // Amount of history in bars at a current tick
                       double Length,         // Period of averaging
                       double series,        // Value of price series calculated for the bar with the 'bar' number
                       uint bar,              // Bar index
                       bool set              // Direction of indexing of arrays.
                      );
                        
   double    SMMASeries(uint begin,              // Index of start of reliable bars
                         uint prev_calculated, // Amount of history in bars at a previous tick
                         uint rates_total,     // Amount of history in bars at a current tick
                         int Length,            // Period of averaging
                         double series,         // Value of price series calculated for the bar with the 'bar' number
                         uint bar,              // Bar index
                         bool set              // Direction of indexing of arrays.
                      );

   double    LWMASeries(uint begin,               // Index of start of reliable bars
                         uint prev_calculated, // Amount of history in bars at a previous tick
                         uint rates_total,      // Amount of history in bars at a current tick
                         int Length,             // Period of averaging
                         double series,          // Value of price series calculated the bar with the 'bar' number
                         uint bar,               // Bar index
                         bool set               // Direction of indexing of arrays.
                        );

protected:
   double            m_SeriesArray[];
   int               m_Size_, m_count, m_weight;
   double            m_Moving, m_MOVING, m_Pr;
   double            m_sum, m_SUM, m_lsum, m_LSUM;
  };

This class is derived from the base class CMovSeriesTools that contains additional protected functions-methods and a check of correctness of period of moving averages.

The base class contains an additional universal code that is used in all classes I suggest, and there is no point in copying it for many times to the derived classes. In applied tasks of using the averaging, the protected class members are not used in explicit form, so let's suspend their overview for the time being.

The class CMoving_Average consists of five single-type functions of averaging, whose names speak for themselves, and they don't need to be described in details.

The first function MASeries() is an integral collection of four other functions that allow selecting an algorithm of averaging using the parameter MA_Method. The code of the algorithms of averaging are optimized for maximum performance, and this is the reason why the main parameters of functions (Length, series, bar) are supplemented with additional parameters begin, prev_calculated, rates_total and set, whose purpose is absolutely identical to the indicator variables with the same names.

The parameter 'set' sets the flag of indexing of elements of a price series 'series' in the functions of averaging to be the same as the arrays of variables.

We should consider that all the averaging functions of this class have the parameter Length fixed and it cannot be changed when the program code is being executed! The function EMASeries() of the class CMoving_Average has this parameter of the type double!

Now, as we got acquainted with the class CMoving_Average, we can start using it in indicators. To do it, using the #include directive add the contents of the MASeries_Cls.mqh file on the global scope to the code of indicator that you develop:

#include <MASeries_Cls.mqh> 

Then you should determine the necessary number of averaging procedures in the indicator code, and then in the OnCalculate() part (before the loop operators and curly brackets) declare the static variables of the CMoving_Average class according to the required number of procedures of averaging. There must be a separate variable of the class and a separate cell in the array of the class for each procedure of averaging.

//---- declaration of variables of the class CMoving_Average из файла MASeries_Cls.mqh
static CMoving_Average MA1, MA2, MA3, MA4;

The variables of the class in the OnCalculate() function are declared as static ones, because their values must be kept between the calls of this function. Now we can start working with averaging itself. As an example, I'm going to show four consecutive procedures of averaging of price series - SMA/EMA/SMMA/LWMA (the indicator MAx4.mq5):

//---- The main cycle of indicator calculation 
for(bar = first; bar < rates_total; bar++) 
 {
  //----+ Four calls of the function MASeries.  
  ma1_ = MA1.MASeries(start1, prev_calculated, rates_total, Length1, MODE_SMA,  price[bar], bar, false);
  ma2_ = MA2.MASeries(start2, prev_calculated, rates_total, Length2, MODE_EMA,  ma1_,       bar, false);
  ma3_ = MA3.MASeries(start3, prev_calculated, rates_total, Length3, MODE_SMMA, ma2_,       bar, false);
  ma4_ = MA4.MASeries(start4, prev_calculated, rates_total, Length4, MODE_LWMA, ma3_,       bar, false);
  //----       
  MAx4[bar] = ma4_ + dPriceShift;
 }

The result of each previous averaging (excluding the last one) is used in the next algorithm of averaging, and the final result is passed to the indicator buffer.

I think, the most crucial part of this code is very careful preliminary initialization of variables of indexes that show the start of reliable bars. In this situation, it will look as following:

//---- Initialization of variables of start of reliable information
start1 = 0 + begin;
start2 = Length1 + begin;
start3 = Length1 + begin; // the previous EMA averaging doesn't change the start of reliable information
start4 = Length1 + Length3 + begin;

Note, that in this situation, the LWMA algorithm of averaging is the last one and it doesn't affect anything; but if it weren't the last one, then the shift of start of reliable information would be equal to Length4+1, not Length4!

I want to add, if it's not clear from the previous code, which number the reliable information starts from, take a bigger number and then decrease it experimentally if needed.

3. Comparing the Indicator Created using Classes with its Analogs That Use Technical and Custom Indicators

It would be very interesting to compare the performance of the created indicator MAx4.mq5 with its identical analog (iMAx4.mq5) that uses the technical indicator iMA().

Well, as soon as we have decided to perform the test, it will be reasonable to test another indicator (MAx3x1.mq5) similar to MAx4.mq5, but having the first averaging made using the call of the technical indicator iMA() and the other three using the class CMoving_Average. And as soon as the standard set of indicators of the client terminal includes the Custom Moving Average.mq5 indicator, I have made another analogous indicator on its bases for testing purposes (cMAx4.mq5).

For the forthcoming analysis I prepared for test Expert Advisors: MAx4_Test.mq5, iMAx4_Test.mq5, MAx3x1_Test.mq5 and cMAx4_Test.mq5 respectively. The conditions of conducting such tests were described in details in the "The Principles of Economic Calculation of Indicators" article. In this article, I'm not going to describe the details of the test, but I'm going to show the final results of running of all four Expert Advisor in the strategy tester for the last 12 months on EURUSD Н4 with modelling of every tick and the value of the 'period' input parameters of all EA's equal to 500.

 

The worst results in our tests are shown by the indicator that calls custom indicators; therefore, this variant of writing a code can be recommended only to the lazy ones! Of course, another "leader" coming last but one that is based on calls of technical indicators has much better results, however, they're too far from an ideal.

The real leader of the tests is the indicator that is developed using classes!

The hybrid that uses classes and technical indicators took the second place, but it doesn't happen always; if the time of testing of an indicator is crucial, then it's better to check such variants personally for each situation.

Overview of Implemented Classes of Averaging

№	Algorithm	Class Name	File Name	Shift of Start of Reliable Bars After Applying an Algorithm	Possibility of Dynamic Change of the Parameter Length
1	Classic Averaging	CMoving_Average	MASeries_Cls.mqh	Length/0/Length/Length + 1 (SMA/EMA/SMMA/LWMA)	no
2	Standard Deviation	CStdDeviation	StdDevSeries_Cls.mqh	Length	no
3	JMA Smoothing	CJJMA	JJMASeries_Cls.mqh	30	yes
4	T3 Smoothing	CT3	T3Series_Cls.mqh	0	yes
5	Ultralinear Smoothing	CJurX	JurXSeries_Cls.mqh	0	yes
6	Tushar Chande's Smoothing	CCMO	CMOSeries_Cls.mqh	Length + 1	no
7	Kaufman's Smoothing	CAMA	AMASeries_Cls.mqh	Length + 3	no
8	Parabolic Averaging	CParMA	ParMASeries_Cls.mqh	Length	no
9	Speed of Change	CMomentum	MomSeries_Cls.mqh	Length + 1	no
10	Normalized Speed of Change	CnMomentum	nMomSeries_Cls.mqh	Length + 1	no
11	Rate of Change	CROC	ROCSeries_Cls.mqh	Length + 1	no

The previously described class CMoving_Average includes five algorithms of averaging.

The class CCMO contains algorithms of averaging and oscillator.

The other classes include single algorithms of averaging. The ideology of using any of the suggested classes is absolutely the same to the procedure of using the class CMoving_Average described above. The code of all the averaging algorithms (except for the parabolic one) is optimized for maximum speed of execution. The code of parabolic averaging was not optimized, due to the complexity of this process. The last three algorithms do not represent an averaging. I've added them because of their high popularity and compatibility with the works of popular technical analysts.

For easier understanding of information, it's better to represent the averaging algorithms in separate .mqh files; and for practical use, the best variant is to have them in a single file.

For using in indicators, all the suggested classes are packed to the single file SmoothAlgorithms.mqh. In addition to it, the file is supplemented with the functions of the iPriceSeries.mqh file. Only the PriceSeries() function is used in examples of this article:

double PriceSeries
 (
  uint applied_price,  // Price constant
  uint   bar,          // Index of shift for a specified number of periods back or forward
                          // relatively to a current bar.
  const double& Open [],
  const double& Low  [],
  const double& High [],
  const double& Close[]
 )

This function is intended for working with indicators bases on using of the second type of calling of the OnCalculate() function.

The main idea of creating this function is to extend the set of price timeseries of the enumeration ENUM_APPLIED_PRICE with custom variants. The function returns the value of a price timeseries by its number that varies from 1 to 11.

4. Practical Examples of Implementation of a Program Code using the Averaging Classes

If it's enough to show another example of using the other classes, to be sure that everything is done in the same way as with the fourfold averaging. I'm going to show a variant of implementation of the function OnCalculate() in an analog of the CCI indicator using the classes CJJMA and CJurX (JCCX.mq5)

int OnCalculate(const int rates_total,       // amount of history in bars on a current tick
              const int prev_calculated,   // amount of history in bars on a previous tick
              const datetime& time[],
              const double& open[],
              const double& high[],
              const double& low[],
              const double& close[],
              const long& tick_volume[],
              const long& volume[],
              const int& spread[]
             )
  {
//----+   
   //---- Checking whether there are enough bars for calculation
   if (rates_total < 0) return(0);
    
   //---- Declaration of variables  with floating point  
   double price_, jma, up_cci, dn_cci, up_jccx, dn_jccx, jccx;
   //----+ Declaration of integer variables
   int first, bar;
   
   //---- calculation of start number 'first' for the cycle of recalculation of bars
   if (prev_calculated == 0) // checking for the first start of calculation of indicator
        first = 0;           // starting number for calculation of all bars
   else first = prev_calculated - 1; // starting number for calculation of new bars
   
   //---- declaration of variables of the class CJurX from the file SmoothAlgorithms.mqh
   static CJurX Jur1, Jur2;
   //---- declaration of variables of the class CJMA from the file SmoothAlgorithms.mqh
   static CJJMA JMA;
   
   //---- Main cycle of calculation of the indicator
   for(bar = first; bar < rates_total; bar++)
    {
     //----+ Calling the PriceSeries function to get the input price price_
     price_ = PriceSeries(IPC, bar, open, low, high, close); 

     //----+ One call of the JJMASeries function to get JMA
     jma = JMA.JJMASeries(0, prev_calculated, rates_total, 0, JMAPhase, JMALength, price_, bar, false); 

     //----+ Determine the deviation of price from the value of JMA
     up_cci = price_ - jma;         
     dn_cci = MathAbs(up_cci);

     //----+ Two calls of the JurXSeries function.  
     up_jccx = Jur1.JurXSeries(30, prev_calculated, rates_total, 0, JurXLength, up_cci, bar, false);
     dn_jccx = Jur2.JurXSeries(30, prev_calculated, rates_total, 0, JurXLength, dn_cci, bar, false); 

     //---- Preventing zero divide in empty values
     if (dn_jccx == 0) jccx = EMPTY_VALUE;
     else
      {
       jccx = up_jccx / dn_jccx;
       
       //---- Limitation of the indicator from the top and from the bottom
       if (jccx > +1)jccx = +1;
       if (jccx < -1)jccx = -1;
      }

     //---- Loading the obtained value to the indicator buffer
     JCCX[bar] = jccx;
    }
//----+     
   return(rates_total);
  }

 

But this time I added the appropriate classes from another file on the global scope in the code of the indicator:

#include <SmoothAlgorithms.mqh>

Now, I want to hold your attention on another thing. The matter is a huge number of indicators can be represented as functions of one bar, which are really comfortable to work with by using classes.

For example, it would be interesting to draw the Bollinger channel on the basis of the moving average Vidya of Tushar Chande. In this case, two classes CCMO and CStdDeviation are used. Using the first class, we get the value of the moving average VIDYA; and using the second one, we calculate the value of standard deviation of the price series for the moving average.

After that, we use this deviation for the calculation of the upper and lower border of the channel:

//+------------------------------------------------------------------+
// Description of the classes CStdDeviation{}; and CCMO{};           | 
//+------------------------------------------------------------------+ 
#include <SmoothAlgorithms.mqh> 
//+==================================================================+
//|  The algorithm of getting the Bollinger channel from             |
//|  the moving average VIDYA                                        |
//+==================================================================+
class CVidyaBands
{
public:
  double VidyaBandsSeries(uint begin,                // number of the start of reliable calculation of bars
                         uint prev_calculated,      // amount of history on a previous tick in bars
                         uint rates_total,          // amount of history on a current tick in bars
                         int CMO_period,            // the period of averaging of the oscillator CMO
                         double EMA_period,         // the period of averaging of EMA
                         ENUM_MA_METHOD MA_Method, // the type of averaging
                         int BBLength,             // the period of averaging of the Bollinger channel
                         double deviation,          // Deviation
                         double series,             // Value of the price series calculated for a bar with the number 'bar'
                         uint bar,                  // Bar index
                         bool set,                  // Direction of indexing of arrays
                         double& DnMovSeries,       // Value of the lower border of the channel for a current bar
                         double& MovSeries,         // Value of the middle line of the channel for a current bar
                         double& UpMovSeries        // Value of the upper border of the channel for a current bar 
                        ) 
   {
//----+
    //----+ Calculation of the middle line    
    MovSeries = m_VIDYA.VIDYASeries(begin, prev_calculated, rates_total, 
                                    CMO_period, EMA_period, series, bar, set); 
    //----+ Calculation of the Bollinger channel
    double StdDev = m_STD.StdDevSeries(begin+CMO_period+1, prev_calculated, rates_total, 
                                      BBLength, deviation, series, MovSeries, bar, set);
    DnMovSeries = MovSeries - StdDev;
    UpMovSeries = MovSeries + StdDev;
//----+
    return(StdDev); 
   }

  protected:
    //---- declaration of variables of the classes CCMO and CStdDeviation
    CCMO           m_VIDYA;
    CStdDeviation  m_STD;
};

So, we got a simple and small class!

The last three input parameters of the function VidyaBandsSeries() pass the necessary values of the channel through a link.

I would like to note that in this case, you cannot declare the variables of classes within the function VidyaBandsSeries() and make them static, because static variables in classes have a very different meaning. That's why this declaration must be made on the global scope of the class:

protected: 
  //---- declaration of variables of the classes CCMO and CStdDeviation 
  CCMO           m_VIDYA; 
  CStdDeviation  m_STD;

In a normal Bollinger channel, the period of averaging of the moving average and the period of averaging of the channel itself are always equal.

In this class, I've made those parameters separate to give you more freedom (EMA_period and BBLength). The indicator itself (VidyaBBands.mq5) made on the basis of this class is so simple in using of the class CVidyaBands that we don't need to analyze its code in the article.

Such classes of indicator functions should be placed in a separate mqh file. I have placed such functions in the file IndicatorsAlgorithms.mqh.

 

5. Comparing Performance of an Indicator that Uses Classes with a One that Doesn't 

First of all, I want to find out, how the use of classes when writing a code of an indicator decreases its performance?

For this purpose, the code of the indicator JJMA.mq5 was written without using the classes (JMA.mq5), then it was tested in the same conditions as during the previous test. The final results of the tests don't have a big difference:

 

Of course, there are some additional charges for using the classes, but they are not significant comparing to the advantages they provide. 

6. Advantages of Using the Classes of Averaging

One advantage of using these algorithms, which is really convincing, is that the replacement of calls of technical and custom indicators leads to a great increase of performance of the developed code described above.

Another practical advantage of such classes is a great convenience of using them. For example, everything that is described in the popular book by William Blau "Momentum, Direction and Divergence " appears to be a real testing ground for this kind of approach to writing indicators. The code of indicators comes out as maximally compressed, understandable and often consisting of a single cycle of recalculation of bars.

You can easily develop any indicator - a classic or technical one, using the alternative methods of averaging. A pretty wide variety of the algorithms of averaging provides wide possibilities for creating non-traditional trade systems, often with an early detection of trends and smaller number of false triggering.

7. Some Recommendations on Using the Averaging Algorithms in a Specific Indicator Code

A quick single look at any indicator developed using different averaging algorithms described here is enough to understand how different those algorithms are.

 

 

Therefore, it would be reasonable to suppose that not all of the suggested algorithms are equally good in every situation. Though it would be hard to determine a strict limit of using of one or another algorithm, it is possible to provide you with some general recommendations on using them.

For example, the algorithms of Tushar Chande and Kaufman are intended for determining trend situations and are not suitable for additional smoothing for the purpose of noise filtering. Therefore, it's better to input either unprocessed price series or indicator values without averaging to these algorithms. Here is the result of processing of values of the indicator Momentum using the Kaufman's algorithm (the indicator 4c_Momentum_AMA.mq5)

 

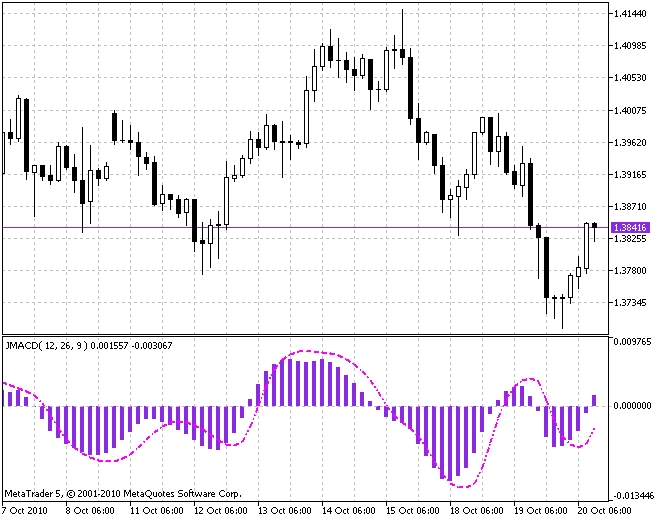
I think that the algorithms of classic averaging don't need any special recommendations. Their application area is pretty wide. Everywhere, where these algorithms are used, you can successfully use the four left algorithms (JMA, T3, ultralinear and parabolic). Here is an example of the MACD indicator where EMA and SMA are replaced with the JMA averaging (the indicator JMACD.mq5):

 

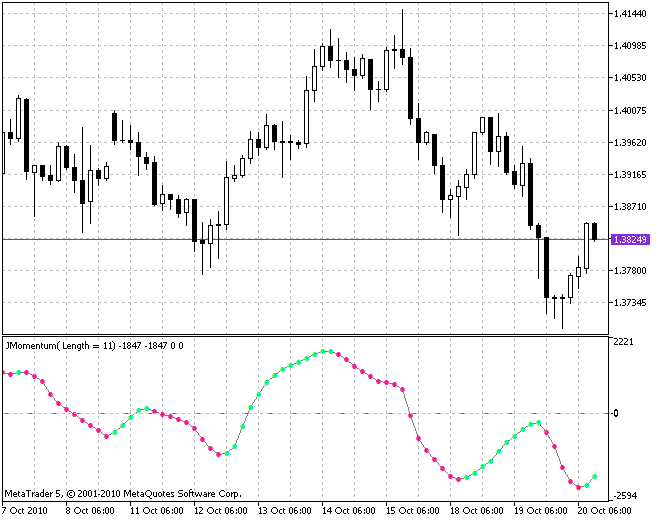
And here is the result of smoothing of the calculated indicator instead of changing its algorithm of averaging for a better quality of determining the current tendency (the indicator JMomentum.mq5):

It's not a surprise that the behavior of markets changes constantly; therefore, it would be naive to think that you can find the one and the only ideal algorithm for a certain part of financial market now and forever! Alas! Nothing in this world lasts forever! Nevertheless, as for me for example, at this eternally changing market I often use the indicators of fast and medium-term trends like JFATL.mq5 and J2JMA.mq5. I'm quite satisfied with predictions on their basis.

Another thing I want to add. The averaging algorithms are reusable. Good results can be obtained when applying repeated averaging to already averaged values. As a matter of fact, in this article I began analyzing the process of drawing of indicator from it (the indicator MAx4.mq5).

8. The General Idea of Composing Code of the Algorithms of Averaging

And now, at the end of the article, I would like to pay your attention to the mechanism of the functions of averaging themselves.

First of all, most of the algorithms of averaging include dynamic arrays of variables of the type m_SeriesArray[] for storing the values of the input parameter 'series'.

As soon as the information significant for calculation appears, you should allocate the memory for such array for one time. It is done using the function SeriesArrayResize() of the class CMovSeriesTools.

//----+ Changing the size of the array of variables
if(bar==begin && !SeriesArrayResize(__FUNCTION__, Length, m_SeriesArray, m_Size_))
   return(EMPTY_VALUE);

Then on every bar you should write the current value of the price series 'series' to the oldest value of the array and memorize the number of its position in the variable m_count. It is done using the function Recount_ArrayZeroPos() of the class CMovSeriesTools.

//----+ transposition and initialization of cells of the array m_SeriesArray 
Recount_ArrayZeroPos(m_count, Length_, prev_calculated, series, bar, m_SeriesArray);

And now, if we need to find an element with a relative shift to the current element, we should use the function Recount_ArrayNumber() of the class CMovSeriesTools:

for(iii=1; iii<=Length; iii++, rrr--)
   {
    kkk = Recount_ArrayNumber(m_count, Length_, iii);
    m_sum += m_SeriesArray[kkk] * rrr;
    m_lsum += m_SeriesArray[kkk];
    m_weight += iii;
   }

Usually in such situations, the newest element is written to a zero position and the others (except the oldest one) are preliminary overwritten to the next positions by turn; however, it is not saving the computer resources, and the more complex approach described above appears to be more rational!

In addition to the algorithms of averaging, the bodies of those functions contain the calls of functions used for determination of bar positions relatively to the start of calculation of bars:

//----+ Checking the start of reliable calculation of bars
if(BarCheck1(begin, bar, set)) return(EMPTY_VALUE);

the moment when there is enough information for the start initialization of variables:

//----+ Initialization of zero
if(BarCheck2(begin, bar, set, Length))

and situations when the last bar is closed:

//----+ Saving values of the variables 
if(BarCheck4(rates_total, bar, set))

or not closed:

//----+ Restoring values of the variables
if(BarCheck5(rates_total, bar, set))

The first check determines a situation when there are not enough bars for the averaging function to work, and it returns an empty result. Once the second check is successfully passed and there is enough data for the first calculation, the initialization of variables is performed for one time. Two last checks are necessary for the correct multiple processing of values on the current unclosed bar. I already described it in my article devoted to the optimization of a program code.

And now a few words about the optimization of the program code of such functions for the maximum performance. For example, the SMA algorithm implies averaging the selected values of a period of a price series on every bar. Those values are literally summed and divided by the period on each bar.

But the difference between the sum on the previous bar and the sum on the current bar is the first one is summed with the value of the price series with a shift on one period relatively to the current period and the second one - with the current value. Therefore, it would be much rational to calculate such sum only once during the initialization of functions, and then on each bar add only new values of the price series to this sum and subtract the oldest values from it. This exactly is done in such a function.

Conclusion

Suggested in the article implementations of the algorithms of averaging using the classes are simple, single-type and universal, so you won't have any troubles studying them.

The archives attached to the article contain a lot of examples for easier understanding of this approach to writing code of indicators. In the archive Include__en.zip all the classes are distributed in files. The archive Include_en.zip contains only two files that are sufficient to compile all the indicators in the archive Indicators.zip. The Expert Advisors for testing are in the archive Experts.zip.