MetaTrader 5 / 예
English Русский 中文 Español Deutsch 日本語 Português Français Italiano Türkçe
preview
모집단 최적화 알고리즘: 묘목 파종 및 성장(SSG)

모집단 최적화 알고리즘: 묘목 파종 및 성장(SSG)

MetaTrader 5 — 예 |
188 127
Andrey Dik
Andrey Dik

콘텐츠:

1. 소개
2. 알고리즘
3. 테스트 결과


1. 소개

자연의 모든 생명체는 특정한 법칙의 지배를 받습니다. 이는 변화하는 환경 조건에서 생존하는 데 도움이 됩니다. 식물이 환경에 적응할 수 있는 다양한 옵션이 있습니다. 그들 중 일부는 계절적 변화를 견딜 수 있고 다른 일부는 수분 부족, 고온 또는 저온, 수분 매개체가 없는 경우에도 적응할 수 있습니다. 식물 중 가장 안정적인 유기체 중 하나는 나무이며 그중 일부는 5만 년 이상 살면서 군락을 형성할 수 있습니다.

자연은 컴퓨터 계산의 개발과 발명에 있어 많은 효과적인 아이디어를 얻을 수 있는 무궁무진한 영감의 원천입니다. 사실 진화 컴퓨팅은 진화를 컴퓨터 시뮬레이션에 투영한 것으로 진화 계산, 인공 면역학, 집단 방법 등 자연에서 일어나는 프로세스에서 영감을 얻은 최적화 방법이 많이 있습니다. SSG는 기본적으로 묘목이라 불리우는 잠재적 솔루션의 정원을 사용하여 반복적인 생성과 조합의 프로세스로 정의됩니다. 묘목 파종 및 성장(SSG) 알고리즘은 2002년에 A. Karci가 공동 저자와 함께 제안한 것으로 이 알고리즘은 성장하는 나무의 진화에서 영감을 받아 나무의 성장과 가지가 나는 것을 모델링합니다.


2. 알고리즘

이 알고리즘은 작성자가 명확하게 설명하지 않은 몇 안 되는 알고리즘 중 하나입니다(기본 조항과 아이디어만 제공됨). 저자가 제시한 알고리즘 연산자 또한 프로그램의 알고리즘 구현을 위한 이미 준비된 지침이 아니며 자식 트리와 부모 트리의 상호 작용에 대한 명확한 지침도 없습니다. 연산자가 실행되는 어떠한 주문이던 실행되며 모든 사용자는 더 나은 묘목을 얻기 위해 주문을 변경할 수 있습니다.

넓은 의미에서 SSG는 최적화 알고리즘이 아니라 최적화 품질을 개선하기 위해 다른 알고리즘을 보완하도록 설계된 일반적인 규칙의 집합입니다. 즉 SSG는 모든 진화적 모집단 알고리즘을 위한 부가 기능으로 상상력의 여지가 있고 최적화 알고리즘의 특정한 구현을 실험해 볼 수 있는 기회가 됩니다. 저는 이전의 알고리즘을 작성하면서 제 생각과 경험을 적용하여 이들이 SSG와 함께 작동하도록 했습니다. 실험 결과는 독자의 판단을 돕기 위해 아래에 제시되어 있습니다.

알고리즘을 이해하려면 우리는 나무를 최적화 에이전트라고 생각해야 합니다. 나무는 최적화 문제에 대한 해결책이고 각각의 가지는 문제의 최적화 매개변수입니다. 그림 1에는 자식 나무와 부모 나무의 추상적이고 예술적인 그림이 나와 있습니다. 나무 기둥은 최적화할 매개변수의 집합입니다. 각각의 가지는 별도의 최적화된 파라미터로 가지의 길이는 해당 파라미터의 허용 가능한 값 범위에 의해 제한됩니다. 가지의 방향은 중요하지 않으며 그림에서 차이를 강조하기 위해 표시된 것일 뿐입니다.

나무

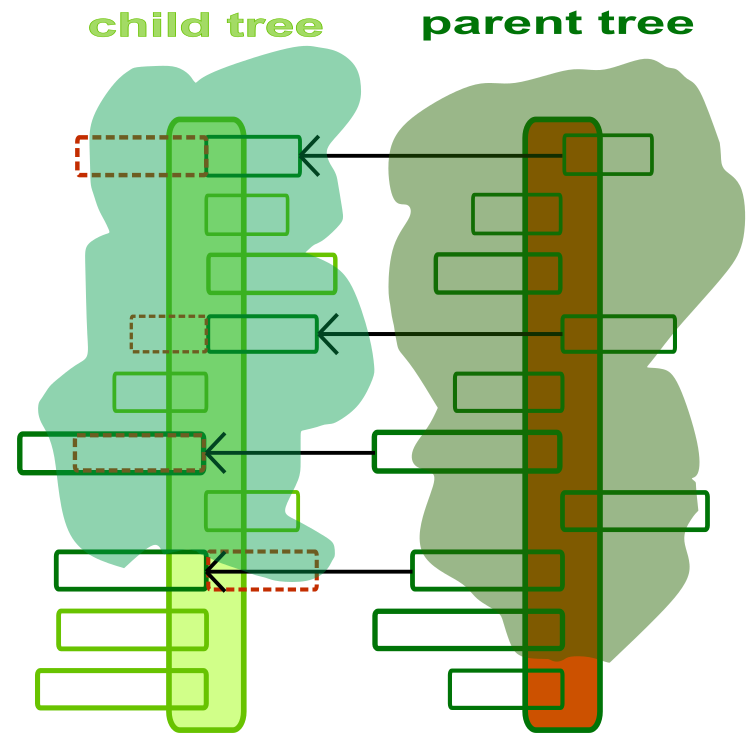
그림 1. 자식 및 부모 나무. 점선은 부모 가지로 대체된 자식 가지를 나타냅니다.

따라서 나뭇가지는 검색 공간에서 나무의 좌표입니다.

SSG 알고리즘은 공통 솔루션 집단의 후보인 새로운 솔루션을 생성하는 변형 연산자로 구성됩니다. 주요 변형 연산자는 교차, 가지 및 백신 접종입니다. 묘목을 심는 것은 서로 같은 방향 (서쪽, 동쪽, 북쪽, 남쪽)으로 등거리에서 수행해야 하며 이것이 메서드의 초기 단계입니다. 좌표(최적화된 매개변수)가 3개 이상인 경우 '균일' 심기는 검색 공간에 묘목을 단순히 무작위로 배포하는 것입니다. 그런 다음 묘목이 자라고, 교배하고, 가지를 치고, 백신 접종 과정이 진행됩니다.

SSG 알고리즘의 단계와 연산자를 살펴 보겠습니다:

1) 묘목 심기.

검색 공간은 묘목의 정원으로 볼 수 있습니다. 그러므로 모든 묘목이 정원 전체에 고르게 분포되어 있어야 합니다. 농부는 모종을 파종할 때 서로 간섭하지 않고 모종이 더 빨리 자라도록 서로 같은 거리에 파종하기만 하면 됩니다. 묘목 기르기를 시뮬레이션 하여 문제를 해결하려면 처음에 생성되는 임의의 해가 유효한 검색 공간에 고르게 분포되어야 합니다.

좌표가 두세 개 있으면 묘목을 균등하게 분배하는 데 문제가 없지만 좌표가 세 개 이상일 경우에는 무작위 분포를 사용하는 것이 더 쉽습니다. 실제로는 적은 수의 좌표인 경우 묘목의 균일 한 분포에 대해 신경 쓸 필요가 없습니다. 작업은 큰 문제가 아니며 솔루션이 높은 정확도로 얻어지는 것으로 알려져 있습니다. 따라서 우리는 알고리즘의 좌표 수에 관계없이 정원에서 묘목의 무작위 분포를 사용할 것입니다.

2) 묘목(나무) 키우기, 세 명의 연산자가 순차적으로 실행됩니다.

2.1) 교차.

"교차" 연산자의 목적은 현재 존재하는 묘목에서 묘목 간의 정보를 교환하여 새로운 묘목을 만드는 것입니다. 교차는 기본적으로는 부모 트리에서 자식 트리로 가지의 복사본을 이식하는 작업입니다(그림 1). 각 묘목 쌍마다 다른 크로스오버 계수가 사용되며, 이는 곧 크로스오버 확률입니다. 교차 확률은 한 쌍의 묘목에서 묘목간의 거리에 따라 달라지며 거리가 멀수록 교차 확률이 낮아집니다. 교차 연산자는 조합 메커니즘을 제공하는 알고리즘의 매우 중요한 메서드입니다. 에이전트 간의 정보를 결합하면 최적화 알고리즘의 전반적인 품질을 크게 향상시킬 수 있습니다.

2.2) 가지치기.

연산자는 가지의 성장을 모델링합니다. 성장은 양수(신장) 또는 음수(건조)일 수 있습니다. "묘목의 어느 지점에서든 가지를 키우려면 근처에 이전에 싹을 틔운 가지가 없어야 합니다." 이것은 알고리즘 작성자가 연산자에 대해 대략적으로 설명한 것입니다. 사실 이 프로세스는 보기보다 간단하고 명확하며 자식 트리의 기존 가지를 수정하는 것입니다(구체적인 수정 방법은 명시되어 있지 않습니다).

각 개별 가지의 수정 가능성은 현재 반복과 가지의 마지막 수정이 이루어진 반복 사이에 더 많은 반복이 경과할수록 높아집니다. 저는 제 실험을 통해 이 연산자의 비효율성을 확인할 수 있었습니다. 또한 수정 메서드의 사용과 관련한 직접적인 설명이 없었습니다. 저는 이 문제를 해결하는 방법으로 레비 비행 분배 법에 따라 가지 길이의 변경을 적용했습니다. 수정은 알고리즘의 외부 매개변수로 지정된 확률과 강도로 수행됩니다.

2.3) 백신 접종.

백신 접종 과정은 묘목의 유사성이 있는 경우 두 개의 서로 다른 묘목 사이에서 이루어집니다. 묘목의 유사성은 백신 접종의 성공 여부에 영향을 미치며 가중 거리의 산술 평균에 비례합니다. 이 연산자는 교차 연산자와 유사하며 가지 교환으로 구성되며 알고리즘에 에이전트 간의 정보를 결합하는 추가적인 방법을 제공합니다. 이 연산자는 기사에서 강조 표시되지만 소스 코드에 주석 처리되어 있으며 테스트 결과는 참여하지 않고 표시됩니다. 왜냐하면 백신 접종은 결과를 악화시키기 때문입니다.

3) 나무의 적합성 계산.

4) 정원에 새 묘목 심기.

교차, 분기 및 예방 접종 연산자의 도움으로 얻은 묘목은 임시 솔루션 (딸 정원)입니다. 이 단계에서 n 개의 가장 좋은 묘목 (알고리즘의 외부 매개 변수)을 선택하고 정원에서 n 개의 최악의 나무를 대체하여 정원에 배치해야 합니다. 정원에서 최악의 나무보다 더 나쁘더라도 묘목으로 대체하는 것은 어떤 경우에도 발생할 수 있다는 점에 유의해야 합니다.

이제 성장하는 나무 알고리즘의 코드를 살펴보면서 이 연구의 흥미진진한 절정인 테스트 결과의 검토에 점점 더 가까워질 수 있습니다.

각각의 나무를 정원 구조로 표현하는 것이 편리하며 이는 꽃이 만발한 정원을 만들기 위한 기초가 될 것입니다. 이 알고리즘에서 '나무' 엔티티는 [] 좌표와 적합도 값 f라는 두 가지 구성 요소만 필요하며 이보다 더 간단한 것은 없습니다.

//——————————————————————————————————————————————————————————————————————————————
struct S_Garden
{
  double c []; //coordinates
  double f;    //fitness
};
//——————————————————————————————————————————————————————————————————————————————

SG 알고리즘의 C_AO_SSG 클래스는 특별한 것이 아닙니다. 여기에 있는 모든 내용은 앞서 살펴본 알고리즘에서 볼수 있는 매우 친숙한 내용입니다. 우리는 클래스에서 부모 정원과 자식 정원을 운영하기 위한 멤버와 메서드를 선언합니다. 임시 정원은 정렬 방법이 작동하도록 하기 위한 것입니다. 우리는 자식 정원과 부모 정원을 모두 정렬해야 합니다. 솔루션 전체의 최적 좌표 배열과 최적의 적합도 값, 알고리즘의 외부 파라미터를 저장하기 위한 상수 변수를 선언해 보겠습니다.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_SSG
{
  //============================================================================
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: S_Garden pGarden []; //parent's garden
  public: S_Garden cGarden []; //child's garden
  public: S_Garden gardenT []; //temp garden
  public: double cB        []; //best coordinates
  public: double fB;           //fitness of the best coordinates

  public: void Init (const int    coordinatesP,          //Number of coordinates
                     const int    numberTreesP,          //Number of trees
                     const double seedlingsReplacementP, //Seedlings replacement
                     const double probabMatingOperatorP, //Probability mating operator
                     const double probabBranchOperatorP, //Probability branching operator
                     const double powerBranchOperatorP); //Power branching operator

  public: void Sowing      (int iter);
  public: void Germination ();


  //============================================================================
  private: void   Sorting        (S_Garden &garden []);
  private: double SeInDiSp       (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI      (double Min, double Max);
  private: double Scale          (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool Revers);

  private: double vec [];               //Vector
  private: int    ind [];
  private: double val [];
  private: double r;

  private: bool   sowing;               //Sowing
  private: int    coordinates;          //Coordinates number
  private: int    numberTrees;          //Number of trees
  private: int    seedlingsReplacement; //Seedlings replacement
  private: double probabMatingOperator; //Probability mating operator
  private: double probabBranchOperator; //Probability branching operator
  private: double powerBranchOperator;  //Power branching operator
};
//——————————————————————————————————————————————————————————————————————————————

Init () 초기화 메서드에서 배열에 메모리를 할당하고 상수 매개변수에 값을 할당합니다. seedlingsReplacementP 매개변수는 부모 정원에 심을 자식 묘목의 수를 담당하는 정원 크기의 소수점(0.0~1.0)으로 설정되므로 정원 크기의 정수 표현으로 변환해야 합니다. 초기 정원 묘목 플래그를 재설정하고 가능한 가장 작은 두 배 값으로 전역 결정 변수를 초기화해 보겠습니다.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SSG::Init (const int    coordinatesP,          //Number of coordinates
                     const int    numberTreesP,          //Number of trees
                     const double seedlingsReplacementP, //Seedlings replacement
                     const double probabMatingOperatorP, //Probability mating operator
                     const double probabBranchOperatorP, //Probability branching operator
                     const double powerBranchOperatorP)  //Power branching operator
{
  MathSrand (GetTickCount ());
  sowing = false;
  fB     = -DBL_MAX;

  coordinates    = coordinatesP;
  numberTrees    = numberTreesP;

  if (seedlingsReplacementP >= 1.0)
  {
    seedlingsReplacement = numberTreesP;
  }
  else
  {
    if (seedlingsReplacementP <= 0.0)
    {
      seedlingsReplacement = 1;
    }
    else seedlingsReplacement = int(numberTreesP * seedlingsReplacementP);
  }

  probabMatingOperator = probabMatingOperatorP;
  probabBranchOperator = probabBranchOperatorP;
  powerBranchOperator  = powerBranchOperatorP;

  ArrayResize (rangeMax,  coordinates);
  ArrayResize (rangeMin,  coordinates);
  ArrayResize (rangeStep, coordinates);
  ArrayResize (vec,       coordinates);
  ArrayResize (cB,        coordinates);


  ArrayResize (pGarden,  numberTrees);
  ArrayResize (cGarden,  numberTrees);
  ArrayResize (gardenT,  numberTrees);
  ArrayResize (ind,      numberTrees);
  ArrayResize (val,      numberTrees);

  for (int i = 0; i < numberTrees; i++)
  {
    ArrayResize (pGarden  [i].c, coordinates);
    ArrayResize (cGarden  [i].c, coordinates);
    ArrayResize (gardenT  [i].c, coordinates);
    cGarden [i].f = -DBL_MAX;
  }
}
//——————————————————————————————————————————————————————————————————————————————

모든 반복에서 호출되는 첫 번째 공개 메서드인 Sowing()은 묘목 씨 뿌리기입니다. 첫 번째 반복에서는 알고리즘이 막 실행 중일 때 묘목을 균일한 분포로 정원(검색 공간) 주변에 무작위로 흩뿌립니다. 여기서 우리가 볼수 있는 것은 다음과 같습니다; 좌표가 최적화 매개변수의 최소값과 최대값 사이의 허용 범위에서 무작위로 생성되고 우리는 허용 범위를 벗어나는지를 확인한 다음 최적화 단계에 따라 좌표 값을 가져옵니다.

이 단계에서는 묘목의 적응력이 최소화되고 우리는 vec[] 벡터를 설정합니다. 이를 활용해 우리는 분기 연산자에서 가지의 증분 크기를 조정하고 검색 공간에서 가능한 최대 유클리드 거리 r을 계산합니다. 이를 통해 교차 연산자가 나무 쌍 사이의 거리에 따라 확률을 결정하도록 합니다.

//the first planting of trees-------------------------------------------------
if (!sowing)
{
  fB = -DBL_MAX;
  r = 0.0;

  for (int t = 0; t < numberTrees; t++)
  {
    for (int c = 0; c < coordinates; c++)
    {
      cGarden [t].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      cGarden [t].c [c] = SeInDiSp (cGarden [t].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }

    cGarden [t].f = -DBL_MAX;
  }

  for (int c = 0; c < coordinates; c++)
  {
    vec [c] = rangeMax [c] - rangeMin [c];
    r += vec [c] * vec [c];
  }

  r = sqrt (r);

  return;
}

다음으로 Sowing() 메서드에서 교차, 분기 및 백신 접종 연산자는 두 번째 및 후속 반복에서 실행됩니다. 연산자들은 메인 루프에서 순차적으로 실행됩니다:

//tree growth-----------------------------------------------------------------
int child, parent;
double rnd;
double ed; //euclidean distance
double eM;
double u;
double temp;

for (int t = 0; t < numberTrees; t++)

연산자를 실행할 때 '자식'과 '부모'의 개념은 매우 임의적입니다. 이들은 실제로는 새로운 묘목을 만들기 위한 기본 정보의 출처일 뿐입니다. 새 묘목은 자식 트리에서 모든 가지(기억하시겠지만 분기는 최적화할 매개변수입니다)를 복사하고 부모 트리에서 새 가지를 받습니다.

각각의 새로운 묘목에 대해서 정원의 모든 나무에서 동일한 확률로 자식과 부모 나무 두 그루가 무작위로 개별적으로 선택됩니다. 즉 모든 나무는 자신의 적합성에 관계없이 동일한 확률로 새로운 묘목의 생성에 참여할 수 있는 것입니다. 따라서 '자식'과 '부모'는 단순히 부모 정원 배열에 있는 원래 두 트리의 인덱스입니다. 

ed = 0.0;

rnd = RNDfromCI (0.0, numberTrees - 1);
child = (int)MathRound (rnd);
if (child < 0) child = 0;
if (child > numberTrees - 1) child = numberTrees - 1;

rnd = RNDfromCI (0.0, numberTrees - 1);
parent = (int)MathRound (rnd);
if (parent < 0) parent = 0;
if (parent > numberTrees - 1) parent = numberTrees - 1;

if (child == parent) parent++;
if (parent > numberTrees - 1) parent = 0;

ArrayCopy (cGarden [t].c, pGarden [child].c, 0, 0, WHOLE_ARRAY);

첫 번째 연산자는 교차 또는 활용(짝짓기)입니다. 인덱스 t를 가진 묘목에서 교차 연산자를 실행하려면 '자식' 및 '부모' 인덱스를 사용하여 자식과 부모 트리 사이의 유클리드 공간을 계산해야 합니다:

//mating operator-----------------------------------------------------------
for (int c = 0; c < coordinates; c++)
{
  temp = pGarden [child].c [c] - pGarden [parent].c [c];
  ed += temp * temp;
}

ed = sqrt (ed);

유클리드 거리는 검색 공간에서 가능한 최대 유클리드 거리 r로 정규화를 통해 교차 확률을 계산하는 방정식에 관여합니다:

eM = 1.0 - (ed / r);

[0.0;1.0] 범위의 난수를 생성합니다. 결과 수가 계산된 확률 eM에 해당하면 각 가지에 대해 probabMatingOperator 확률로 부모 트리에서 가지를 복사하는 교차 작업을 수행합니다. 만약 eM 확률이 충족되지 않으면 자식 트리의 모든 원래 가지를 사용하여 다음 명령문을 실행합니다.

rnd = RNDfromCI (0.0, 1.0);

if (rnd <= eM)
{
  for (int c = 0; c < coordinates; c++)
  {
    rnd = RNDfromCI (0.0, 1.0);

    if (rnd <= probabMatingOperator) cGarden [t].c [c] = pGarden [parent].c [c];
  }
}

다음으로 가지 연산자가 실행됩니다. 이 연산자는 길이를 늘리거나 줄이는 등 다양한 가지를 제공하며. 새로운 길이의 가지를 생성하는 주요 연산자입니다. 나머지 연산자는 결합의 역할만 수행하며 새로운 고유 가지를 생성하지 않습니다. 각 가지에 대해 [0.0;1.0] 범위의 난수를 생성하고 probabBranchOperator의 확률이 충족되면 Levy 비행 분포 법칙에 따라 가지의 길이를 변경하여 분기를 수행합니다.

보시다시피 묘목의 모든 가지가 변경되는 것은 아닙니다. 가지들은 이전 문의 부모 트리에서 가지를 복사했는지 아니면 원래 자식 가지인지에 관계없이 변경됩니다. 가지를 수정한 후 범위를 벗어난 값이 있는지 확인하고 최적화 단계와 일치하도록 가져옵니다.

//branching operator--------------------------------------------------------
for (int c = 0; c < coordinates; c++)
{
  rnd = RNDfromCI (0.0, 1.0);

  if (rnd < probabBranchOperator)
  {
    double r1 = RNDfromCI (0.0, 1.0);
    r1 = r1 > 0.5 ? 1.0 : -1.0;
    double r2 = RNDfromCI (1.0, 20.0);

    cGarden [t].c [c] = cGarden [t].c [c] + r1 * vec [c] * powerBranchOperator * pow (r2, -2.0);
    cGarden [t].c [c] = SeInDiSp (cGarden [t].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

세 번째 연산자는 백신 접종입니다. 저자는 백신 접종 연산자를 조합 연산자로 간주했으며 자식과 부모 트리의 가지가 쌍의 모든 가지의 평균 차이보다 더 큰 경우 부모 트리에서 가지를 복사하기 위해 수행되어야 합니다. 매우 복잡하게 들리지만 이 연산자는 거의 사용되지 않으므로 소스 파일에서 이 연산자는 주석 처리되어 있습니다. 이 경우 저는 전문가로서의 역할을 할 수는 없습니다. 그러므로 이 연산자에 대해 정확하게 이해하지 못했을 수 있습니다.

//vaccinating operator------------------------------------------------------
u = 0.0;
    
for (int c = 0; c < coordinates; c++)
{
  u += fabs (cGarden [t].c [c] - pGarden [parent].c [c]) / vec [c];
}

u /= coordinates;

for (int c = 0; c < coordinates; c++)
{
  if (fabs (cGarden [t].c [c] - pGarden [parent].c [c]) / vec [c] >= u)
  {
    cGarden [t].c [c] = pGarden [parent].c [c];
  }
}

알고리즘의 마지막, 그러나 가장 중요한 작동인 발아를 위한 시간이 왔습니다. 각 반복마다 실행에 필수인 두 번째 공용 메서드 Germination()을 실행합니다.

첫 번째 반복이 끝나가고 있다면 ('파종' 플래그로 확실히 알 수 있습니다) 이는 부모 정원이 비어 있음을 의미합니다. 우리는 모든 어린 나무를 하나씩 복사하여 부모 정원에 자식 정원의 모든 묘목을 심습니다. 그런 다음 Sorting() 메서드를 사용하여 적합성 값별로 부모 정원을 정렬합니다. 나무가 정렬되면 인덱스 0의 나무리가 가장 적합도가 높으며 이 나무가 아직 최적이 아닌 경우에 우리는 최적의 글로벌 솔루션을 업데이트할 수 있습니다.

if (!sowing)
{
  for (int t = 0; t < numberTrees; t++) pGarden [t] = cGarden [t];

  Sorting (pGarden);

  if (pGarden [0].f > fB)
  {
    fB = pGarden [0].f;

    ArrayCopy (cB, pGarden [0].c, 0, 0, WHOLE_ARRAY);
  }
  
  sowing = true;
  return;
}

코드에서는 '파종' 플래그가 신중하게 'true'로 설정되었으므로 우리는 알고리즘의 두 번째 및 후속 반복에만 도달하게 됩니다. 두 번째와 이후의 반복에서는 묘목을 부모 정원으로 옮기기 전에 자식 정원을 분류하고 가장 상태가 나쁜 나무는 교체되어야 합니다. 이제 글로벌 솔루션이 개선되었는지 확인한 다음 가장 좋은 묘목을 부모 정원의 끝에 복사해 보겠습니다.

결론적으로 부모 정원을 정렬하는 일만 남아 있습니다. 정원 사회의 새로운 구성원은 오래된 세대의 나무를 대체할 수 있는, 최적화 문제를 해결할수 있을 것입니다.

//planting some part from all child trees-------------------------------------
Sorting (cGarden);

if (cGarden [0].f > fB)
{
  fB = cGarden [0].f;

  ArrayCopy (cB, cGarden [0].c, 0, 0, WHOLE_ARRAY);
}

for (int t = 0; t < seedlingsReplacement; t++) pGarden [numberTrees - seedlingsReplacement + t] = cGarden [t];

Sorting (pGarden);


3. 테스트 결과

SSG 테스트 스탠드 결과:

2023.03.09 12:50:37.207 Test_AO_SSG (GBPUSD,M1) C_AO_SSG:50;0.3;0.5;0.4;0.1
2023.03.09 12:50:37.207 Test_AO_SSG (GBPUSD,M1) =============================
2023.03.09 12:50:45.954 Test_AO_SSG (GBPUSD,M1) 5 Rastrigin's; Func 10000 실행 결과: 80.7052793572295
2023.03.09 12:50:45.954 Test_AO_SSG (GBPUSD,M1) 점수: 0.99998
2023.03.09 12:50:59.290 Test_AO_SSG (GBPUSD,M1) 25 Rastrigin's; 10000 Func 실행 결과: 77.3972262608643
2023.03.09 12:50:59.290 Test_AO_SSG (GBPUSD,M1) 점수: 0.95900
2023.03.09 12:52:25.368 Test_AO_SSG (GBPUSD,M1) 500 Rastrigin's; 10000 Func 실행 결과: 52.24518909141432
2023.03.09 12:52:25.368 Test_AO_SSG (GBPUSD,M1) 점수: 0.64735
2023.03.09 12:52:25.368 Test_AO_SSG (GBPUSD,M1) =============================
2023.03.09 12:52:31.419 Test_AO_SSG (GBPUSD,M1) 5 Forest's; Func 10000 실행 결과: 1.331178589711503
2023.03.09 12:52:31.419 Test_AO_SSG (GBPUSD,M1) 점수: 0.75298
2023.03.09 12:52:42.575 Test_AO_SSG (GBPUSD,M1) 25 Forest's; Func 10000 실행 결과: 1.019329018074209
2023.03.09 12:52:42.575 Test_AO_SSG (GBPUSD,M1) 점수: 0.57658
2023.03.09 12:53:48.922 Test_AO_SSG (GBPUSD,M1) 500 Forest's; Func 10000 실행 결과: 0.25410121872226443
2023.03.09 12:53:48.922 Test_AO_SSG (GBPUSD,M1) 점수: 0.14373
2023.03.09 12:53:48.922 Test_AO_SSG (GBPUSD,M1) =============================
2023.03.09 12:53:57.201 Test_AO_SSG (GBPUSD,M1) 5 Megacity's; Func 10000 실행 결과: 6.4
2023.03.09 12:53:57.201 Test_AO_SSG (GBPUSD,M1) 점수: 0.53333
2023.03.09 12:54:08.004 Test_AO_SSG (GBPUSD,M1) 25 Megacity's; Func 10000 실행 결과: 4.504
2023.03.09 12:54:08.004 Test_AO_SSG (GBPUSD,M1) 점수: 0.37533
2023.03.09 12:56:07.061 Test_AO_SSG (GBPUSD,M1) 500 Megacity's; Func 10000 실행 결과: 1.2336
2023.03.09 12:56:07.061 Test_AO_SSG (GBPUSD,M1) 점수: 0.10280
2023.03.09 12:56:07.061 Test_AO_SSG (GBPUSD,M1) =============================
2023.03.09 12:56:07.061 Test_AO_SSG (GBPUSD,M1) 전체 점수: 5.09109

SSG에는 매개변수가 많지 않습니다. 그러나 이는 알고리즘을 조정한 결과입니다(원래 SSG에는 매개변수가 훨씬 더 적습니다). 그러나 모든 매개변수는 각별한 주의가 필요합니다. 테스트에는 다음과 같은 매개변수가 사용되었습니다. 기억하시겠지만 모든 기사에서는 테스트에서 가능한 최고의 결과를 얻을 수 있는 최상의 알고리즘 매개변수를 제공합니다.

C_AO_SSG:50;0.3;0.5;0.4;0.1

input int NumberTrees_P = 50; - 정원에 있는 나무의 수입니다. 저는 이 매개 변수를 기본값(제 실험에서는 기본값)으로 두고 실험하지 않았습니다. 값이 100인 경우 알고리즘은 더 나은 총합 결과를 산출하지만 정원의 크기를 고려할 때 정원별로 허용되는 반복 횟수가 감소하기 때문에 확장성이 떨어집니다. 가지가 많은 정원에는 진화할 시간이 없습니다.

input double SeedlingsReplacement_P = 0.3; - 딸 정원에서 부모 정원으로 옮길 묘목의 비율.
input double ProbabMatingOperator_P = 0.5; - 한 쌍의 나무 사이의 거리를 고려한 확률이 충족되면 교차(부모 나무에서 가지를 복사)할 확률.
input double ProbabBranchOperator_P = 0.4; - 분기 확률(가지의 성장/축소). 이는 알고리즘의 성능에 큰 영향을 미치는 중요한 매개변수입니다(일반적으로 모든 매개변수가 중요함).
input double PowerBranchOperator_P = 0.1; - 분기 강도. 이것은 최적화되는 매개변수 차원의 스케일링 계수이며 1.0 이상이면 정원의 경계까지 가지가 성장하고 0.0이면 가지가 성장하지 않으며 이는 다시말해 새로운 가지 크기가 발생하지 않고 알고리즘이 단순한 조합 도구로 변질됩니다(SSG를 사용하는 데는 좋은 아이디어이지만 여기에는 더 많은 연구가 필요함).

테스트 함수에서 SSE 알고리즘의 애니메이션을 보면 정원에서 나무의 움직임 패턴이 없으며 국부적 극한에서 일부 "뭉침"만 눈에 띄는 것을 알 수 있습니다. 그러나 이전에 고려했던 알고리즘과 비교했을 때 높은 품질의 융합이 눈에 띕니다. 결과의 안정적인 재현성도 주목할 만합니다.


라스트리진

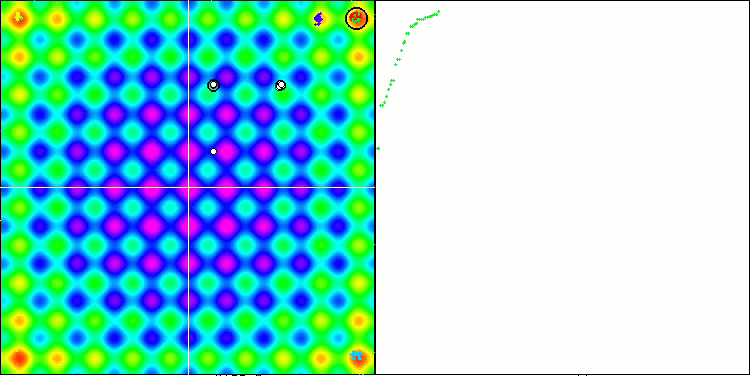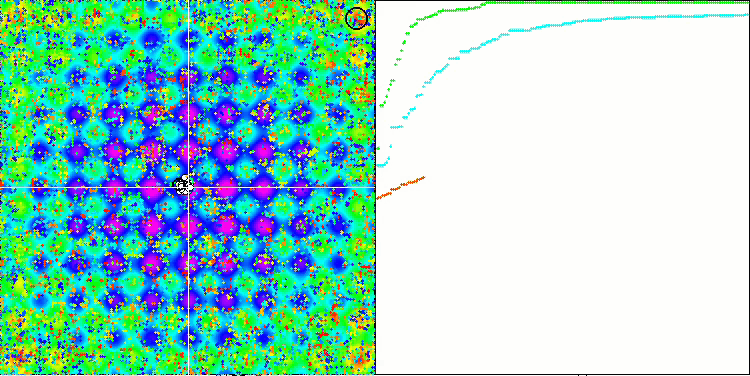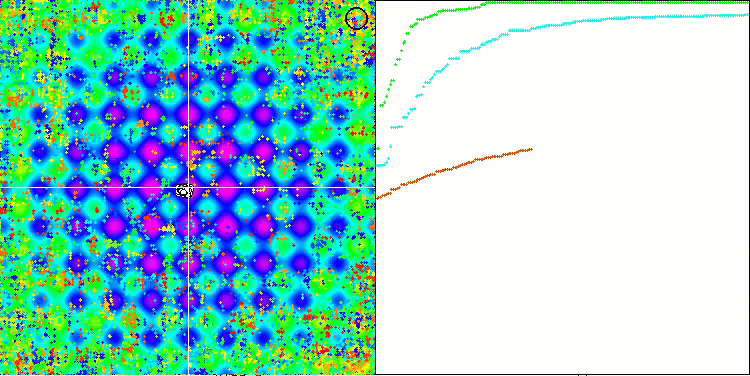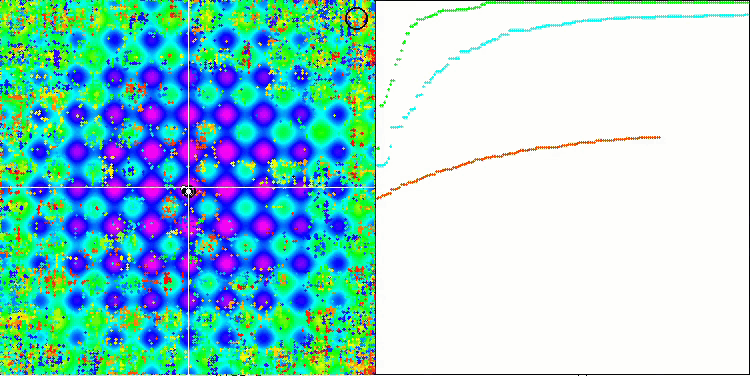
  라스트리진 테스트 함수의 SSG.

숲

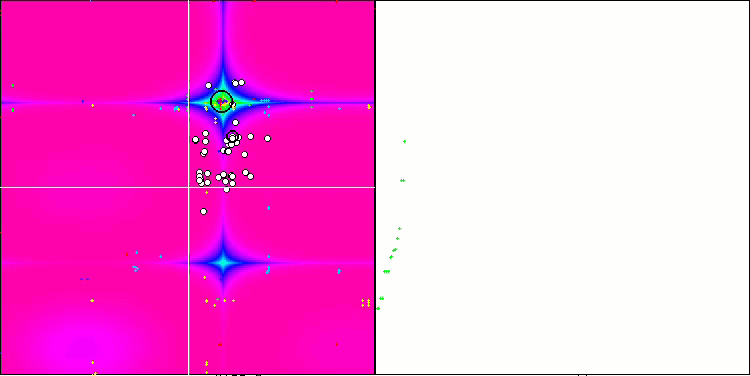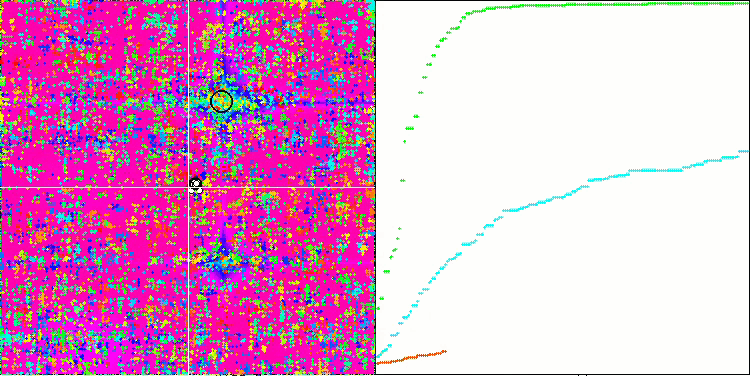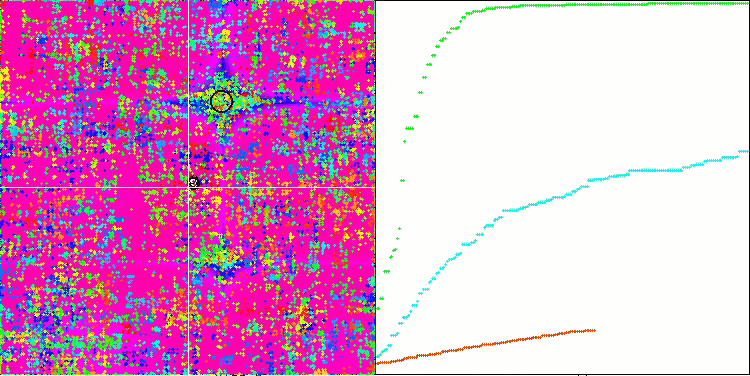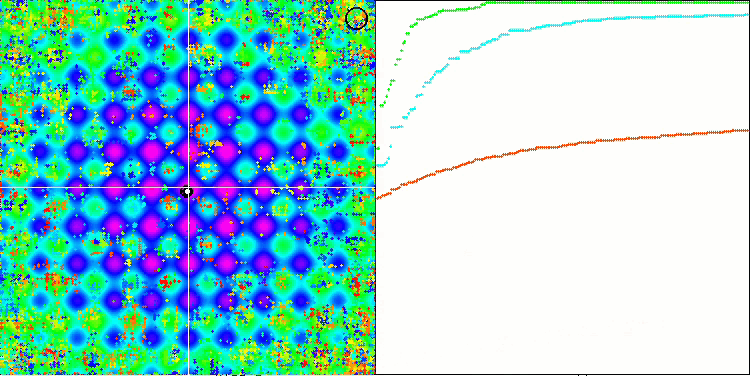
  숲 테스트 함수의 SSG.

메가시티

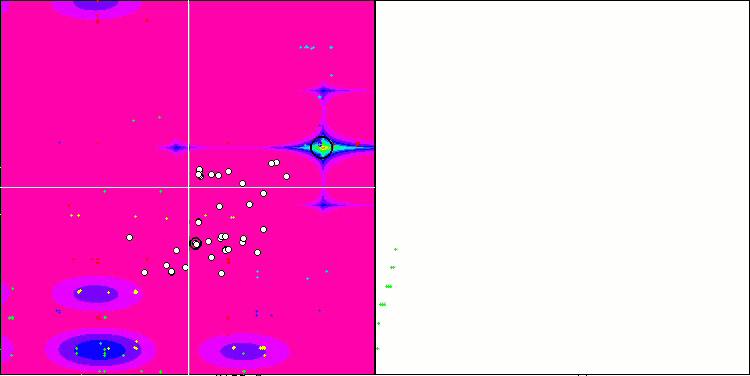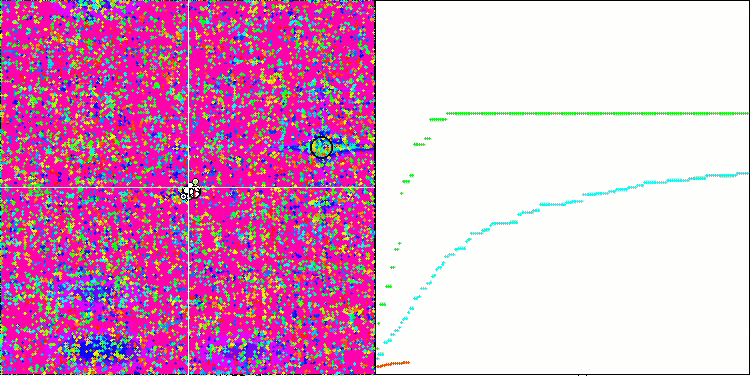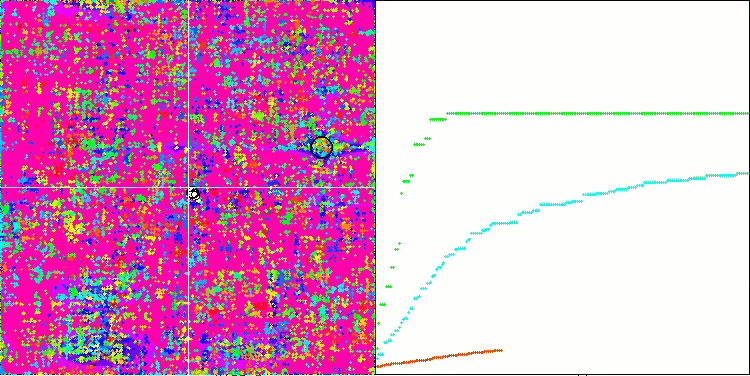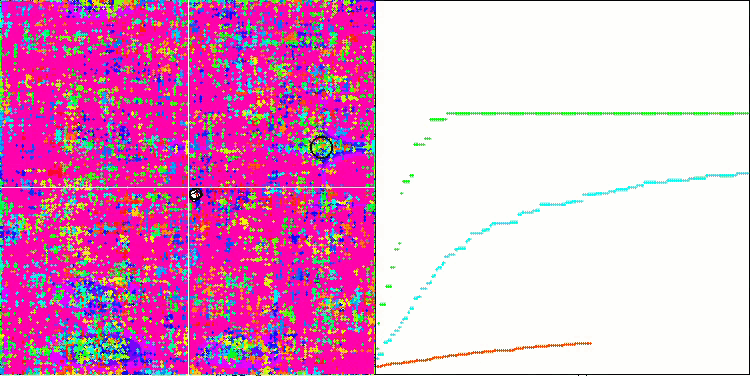
  메가시티 테스트 함수의 SSG.


이제 SSG 알고리즘의 결과에 대해 살펴 보겠습니다. 분명히 이야기할 것이 있습니다. 이 알고리즘이 경쟁자들을 제치고 당당히 평점 1위에 등극했습니다! 이 알고리즘은 의사 결정 트리를 수정하기 위해 적합성 지식을 직접 사용하지 않습니다. 적합성은 자식 정원과 부모 정원을 정렬하는 데만 필요하기 때문에 알고리즘이 테스트에서 이처럼 놀라운 결과를 보여줄 수 있었다는 것이 더욱 놀랍습니다.

오리엔티어링에서 시각장애인 팀이 비장애인 팀을 이긴 것과 같은 이치입니다. 이 알고리즘은 6번의 테스트 중 4번의 테스트에서 다른 참가자들보다 앞섰으며 선두를 차지하지 않은 테스트에서도 크게 뒤처지지 않았습니다. SSG는 메가시티 개별 함수에서 가장 근접한 경쟁자인 HS를 60% 가까이 앞지르며 HS보다 가장 인상적인 우위를 보였습니다! 이는 알고리즘의 뛰어난 확장성을 보여줍니다. "샤프" 숲 테스트 함수에서도 최고의 확장성 결과가 관찰되었습니다. SSG는 이 테스트에서 최고 경쟁자(ACOm)를 30% 가까이 앞섰습니다.

AO

설명

라스트진

라스트진 최종

숲

숲 최종

메가시티(이산)

메가시티 최종

최종 결과

10 params (5 F)

50 params (25 F)

1000 params(500 F)

10 params (5 F)

50 params (25 F)

1000 params(500 F)

10 params (5 F)

50 params (25 F)

1000 params(500 F)

SSG

묘목 파종 및 성장

1.00000

1.00000

0.65914

2.65914

0.70823

0.94522

1.00000

2.65345

0.71532

0.85412

1.00000

2.56944

100.000

HS

하모니 검색

0.99676

0.95282

0.57048

2.52006

1.00000

0.98931

0.44806

2.43736

1.00000

1.00000

0.41537

2.41537

93.370

ACOm

개미 식민지 최적화 M

0.34611

0.17985

0.20182

0.72778

0.85966

1.00000

0.77362

2.63327

1.00000

0.88484

0.05606

1.94090

66.407

IWO

침입성 잡초 최적화

0.95828

0.67083

0.35295

1.98207

0.68718

0.46349

0.31773

1.46840

0.75912

0.39732

0.33289

1.48933

61.691

COAm

뻐꾸기 최적화 알고리즘 M

0.92400

0.46794

0.30792

1.69987

0.55451

0.34034

0.16526

1.06012

0.67153

0.30326

0.17083

1.14561

48.226

FAm

반딧불이 알고리즘 M

0.59825

0.33980

0.20290

1.14095

0.47632

0.42299

0.49790

1.39721

0.21167

0.25143

0.35258

0.81568

41.042

ABC

인공 꿀벌 군집

0.78170

0.32715

0.24656

1.35541

0.50591

0.21455

0.13344

0.85390

0.47444

0.23609

0.13926

0.84979

37.204

BA

박쥐 알고리즘

0.40526

0.63761

1.00000

2.04287

0.15275

0.17477

0.25989

0.58741

0.15329

0.06334

0.17371

0.39034

36.703

GSA

중력 검색 알고리즘

0.70167

0.45217

0.00000

1.15384

0.26854

0.36416

0.33204

0.96475

0.51095

0.32436

0.00000

0.83531

35.834

BFO

박테리아 먹이 채집 최적화

0.67203

0.30963

0.13988

1.12154

0.35462

0.26623

0.20652

0.82736

0.42336

0.30519

0.18932

0.91786

34.700

MA

원숭이 알고리즘

0.33192

0.33451

0.17340

0.83983

0.03684

0.07891

0.08932

0.20508

0.05838

0.00383

0.10720

0.16941

13.185

FSS

물고기 떼 검색

0.46812

0.25337

0.13383

0.85532

0.06711

0.05013

0.06516

0.18240

0.00000

0.00959

0.08283

0.09242

12.089

PSO

파티클 스웜 최적화

0.20449

0.08200

0.08478

0.37127

0.13192

0.10486

0.21738

0.45415

0.08028

0.02110

0.01957

0.12095

9.696

RND

랜덤

0.16826

0.09743

0.09495

0.36065

0.07413

0.04810

0.04715

0.16938

0.00000

0.00000

0.04922

0.04922

4.916

GWO

회색 늑대 최적화

0.00000

0.00000

0.02672

0.02672

0.00000

0.00000

0.00000

0.00000

0.18977

0.03645

0.02557

0.25179

1.000



요약

SSG 특징: 최적화된 함수의 차별성 및 연속성에 대한 요구 사항이 없으며 적용되는 표현 및 인코딩 유형에 대한 제한이 없습니다. 이 알고리즘은 개별 에이전트의 적합성 정보와 전체적으로 최적의 솔루션을 사용하지 않습니다. 이러한 기능 덕분에 SSG는 매우 복잡한 문제를 포함한 다양한 최적화 문제에 쉽게 적용될 수 있습니다. SSG는 트레이더들이 직면하는 문제와 머신 러닝에 사용되기로 적극 권장됩니다. 이 글을 쓰는 시점에서 묘목 파종 및 성장 알고리즘은 융합의 품질, 결과의 안정성 및 확장성 측면에서 확실한 선두주자입니다.

그림 2는 알고리즘의 테스트 결과를 보여줍니다.

차트

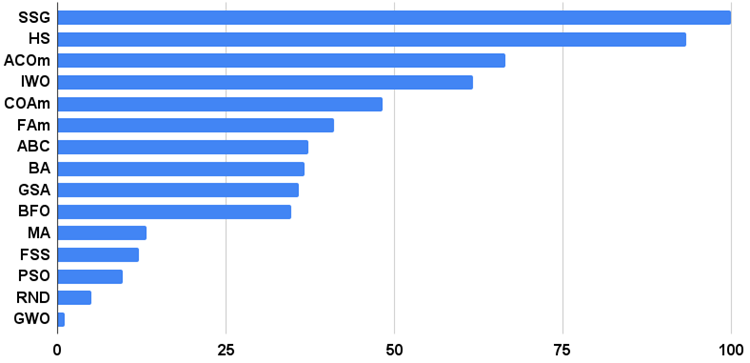
그림 2. 알고리즘 테스트 결과 히스토그램

SSG 알고리즘의 장단점:

장점:
1. 간편한 구현.
2. 모든 유형의 함수에서 예외 없이 뛰어난 융합성을 발휘.
3. 인상적인 확장성.

단점:
1. 직관적으로 명확하기는 하지만 많은 사용자 지정 옵션이 있습니다.

각각의 기사에는 이전의 모든 기사에서 다룬 알고리즘 코드의 최신 버전이 업데이트된 아카이브가 포함되어 있습니다. 이 기사는 저자의 축적된 경험을 바탕으로 작성되었으며 저자의 개인적인 의견을 나타냅니다. 결론과 판단은 실험을 기반으로 합니다.


MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/12268

경고: 이 자료들에 대한 모든 권한은 MetaQuotes(MetaQuotes Ltd.)에 있습니다. 이 자료들의 전부 또는 일부에 대한 복제 및 재출력은 금지됩니다.

이 작가의 다른 글

최근 코멘트 | 토론으로 가기 (127)
Aleksey Nikolayev
Aleksey Nikolayev | 2 4월 2023 에서 09:08
fxsaber #:

자가 교육의 경우, 측정에 대한 복잡성의 의존성은 어떻게 되나요?

안드레이 딕 #:

나는 고백합니다-모르겠습니다. 나는 그것이 비선형 적으로 빠르게 성장한다는 것만 알고 있습니다.

알레세이 니콜라 베프가 여기에 나타났습니다. 아마도 그는이 질문에 대한 정확한 답을 알고있을 것입니다. 포럼 사용자에게 전화하는 방법을 잊었습니다.

여기서는 정확한 지식이 거의 불가능하며 일부 추정치 만 가능합니다.

1) 극한 수와 관련된 좌석 수의 증가. 매끄러운 경우를 가정해 보겠습니다(불연속적인 변형은 항상 어느 정도 정확도로 매끄러운 변형으로 근사화할 수 있습니다). 극값은 기울기의 퇴화가 있는 지점에 있으며, 헤시안의 서수의 부호에 의해 결정됩니다. 차원 N과 (단순화를 위해) 헤시안 고유값의 각 부호가 동일한 확률 0.5의 무작위 선택에 의해 결정된다고 가정하면 모든 부호가 동일할 확률(따라서 극한값)은 2/(2^N)=2^(1-N) 입니다. 2차원의 경우 0.5(50%)와 같으며, 이는 그림에서 잘 보이고 안장의 수가 극단의 수와 거의 같습니다. 10차원의 경우, 극값은 이미 0.2% 미만이 될 것입니다.

2) 실제로 극값을 찾는 모든 알고리즘은 동적 시스템을 생성하며, 이는 차원이 증가함에 따라 점점 더 혼란스러워지는 경향이 있습니다. 만델브로 집합은 2차원의 경우 이차함수의 근을 반복적으로 찾을 때 발생하는 동적 시스템에서 발생한다는 것을 기억할 수 있습니다.) 많은 수의 좌석은 시스템을 더욱 혼돈스럽게 만들 뿐입니다.

fxsaber
fxsaber | 2 4월 2023 에서 09:52
Aleksey Nikolayev #:

여기서는 정확한 지식은 거의 불가능하며 일종의 추정치만 가능합니다.

1) 극한값 수에 대한 안장 수의 증가. 매끄러운 경우를 가정해 보겠습니다(불연속적인 변형은 항상 어느 정도 정확도로 매끄러운 변형으로 근사화할 수 있습니다). 극값은 기울기의 퇴화가 있는 지점에 있으며 헤시안의 서수의 부호에 의해 결정됩니다. 차원 N과 (단순화를 위해) 헤시안 고유값의 각 부호가 동일한 확률 0.5의 무작위 선택에 의해 결정된다고 가정하면 모든 부호가 동일할 확률(따라서 극한값)은 2/(2^N)=2^(1-N) 입니다. 2차원의 경우 0.5(50%)와 같으며, 이는 그림에서 잘 보이고 안장의 수가 극단의 수와 거의 같습니다. 10차원의 경우 극값은 이미 0.2% 미만이 될 것입니다.

2) 실제로 극값을 찾는 알고리즘은 차원이 커질수록 점점 더 혼란스러워지는 동적 시스템을 생성합니다. 만델브로 집합은 2차원의 경우 이차함수의 근을 반복적으로 찾을 때 발생하는 동적 시스템에서 발생한다는 것을 기억할 수 있습니다.) 많은 수의 좌석은 시스템을 더욱 혼란스럽게 만들 뿐입니다.

다차원 변형에 대한 상당히 비관적인 계산이 얻어집니다.

Aleksey Nikolayev
Aleksey Nikolayev | 2 4월 2023 에서 10:21
fxsaber #:

다변량 변수에 대한 계산은 다소 비관적입니다.

일반적으로 그렇습니다. 그렇기 때문에 일반적으로 다차원의 경우 손실 함수의 표면 장치에 대한 완전한 연구 작업이 설정되지 않습니다. 글로벌 극값을 찾는 작업도 마찬가지입니다. 사실, 충분히 좋은 점을 찾는 것으로 제한됩니다. 예를 들어 MO에서처럼 좋은 특성을 가진 손실 함수를 구성할 수 있는 경우는 예외일 수 있습니다.

hoang dung
hoang dung | 1 5월 2023 에서 08:18
큰 가치
Andrey Dik
Andrey Dik | 1 5월 2023 에서 08:32
감사합니다!
모집단 최적화 알고리즘: 전자기 유사 알고리즘(ЕМ) 모집단 최적화 알고리즘: 전자기 유사 알고리즘(ЕМ)
이 문서에서는 다양한 최적화 문제에서 전자기 알고리즘을 사용하는 원리, 방법 및 그 가능성에 대해 알아봅니다. EM 알고리즘은 대량의 데이터와 다차원 함수를 다룰 수 있는 효율적인 최적화 도구입니다.
MQL5 전략 테스터를 이해하고 효과적으로 사용하기 MQL5 전략 테스터를 이해하고 효과적으로 사용하기
MQL5 프로그래머나 개발자는 중요하고 가치 있는 도구를 마스터해야 합니다. 이러한 도구 중 하나가 전략 테스터입니다. 이 글은 MQL5의 전략 테스터를 이해하고 효과적으로 사용하기 위한 실용적인 가이드입니다.
Expert Advisor에 지표를 포함시키기 위한 기성 템플릿(1부): 오실레이터 Expert Advisor에 지표를 포함시키기 위한 기성 템플릿(1부): 오실레이터
이 기사에서는 오실레이터 카테고리에 있는 표준 지표를 살펴봅니다. 우리는 매개변수 선언 및 설정, 지표 초기화 및 초기화 해제, 지표 버퍼에서 데이터 및 신호를 수신하는 등의 EA에서 바로 사용할 수 있는 템플릿을 만들 것입니다.
MQL5를 사용하여 맞춤형 실제 강도 지수 지표를 만드는 방법 MQL5를 사용하여 맞춤형 실제 강도 지수 지표를 만드는 방법
이글은 맞춤형 지표를 만드는 방법에 대한 새로운 글입니다. 이글에서 우리는 실제 강도 지수(TSI)를 기반으로 Expert Advisor를 만들 것입니다.