
MQL5 中的范畴论 (第 15 部分):函子与图论
概述
在上一篇文章中,我们目睹了前期文章中涵盖的概念(如线性序)如何视作范畴,以及为什么它们的“态射”在与其它范畴相关时即构成函子。在本文中,我们将阐述来自前期文章中的概括,即通过查看图论如何具有与上一篇文章中查看的线性序类似的用途。为了使用图论,我们将 MQL5 日历数据重构为图形,由此作为一个范畴。这将是一个关键焦点。本文的目的仍然会像我们之前的一篇,寻求明示在两个范畴之间函子的波动性预测潜力。不过,在这种情况下,我们的域范畴是一个图形,而协域将在预排序时间序列中显示标准普尔 500 指数波动率值(并非 VIX)。
MQL5 日历灌注数据重构为图形
当我们把范畴论与数据库制程联系起来时,MQL5 财经日历已被涵盖,故此在此重新涉及它与交易者的相关性并不适宜。为了将其表示为图形,即一连串的边线和节点,首先需要预先选择我们将包含在范畴中的新闻项目的子集。从财经日历网站上可以明显看出,有很多项目可供选择,不过,如果我们决定基于一个松散的假设只选择四个项目,并将它们连接起来,如下图所示:
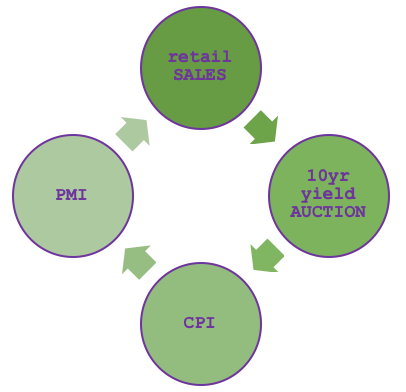
那么我们的假设会颇具争议,零售销售数字是制造业采购经理人指数(PMI)数据的函数,其派生自 CPI,而 CPI 又是由国债竞售业绩的结果而来,而国债竞售业绩也基于零售销售数字。因此,这是一个简单的循环,其准确性不是本文的主题,而更多意味着从财经日历数据勾勒可能的图形构图。
图论通过创建两个直截了当的表格,一个是顶点的配对表,另一个用作顶点的索引,来简化复杂的互连系统。图形可以被视为一个范畴,因为顶点可以被视为对象(域),这意味着边线当作态射。作为旁注,这与上一篇文章中看到的线性序有何不同,顾名思义,是线性。图论倾向于容纳更复杂的连接,其中对象/域可以连接到多个对象。
故此,我们不会像上一篇文章中关于线性序那样,将该范畴中的单个对象与标普波动率范畴中的对象配对,而是将顶点对的行数与标普范畴配对。这意味着它不能同构,由于鉴于标普是基于时间的,故多行被捆绑,并与标普中的单个对象(数据点)配对。这也意味着我们的域对象将构成四个元素(循环中四个项目的各自最后数值)。
范畴论和函子回顾
正如本文中已经提到的,范畴论已有许多应用,但大多数公开参考文献在代数拓扑方面倾向于零,这可能是因为该主题的原始作者,这就是为什么将 MQL5 应用于交易看似很新颖的原因。事实上,大多数熟悉 MQL5 的交易者倾向于使用神经网络来开发他们的前沿系统,或许是因为与范相比,它们经历的研究更久,这不应该阻止探索范畴,因为底线是大多数交易者都在寻求前沿,如果一个系统或方法太常见,那么能找到一个的几率就会降低。
函子,正如我们在上一篇文章中曾提过的,实际上是范畴之间的态射。这些“态射”不仅将两个范畴中的对象连接起来,而且还将范畴之间的同态连接起来。
在上一篇文章中,我们测试了两个场景,一个是使用两个范畴之间的对象连接,另一个是考虑相同范畴之间的态射连接。函子是两者的对数,出于我们的意图,尽管我们一次取一个来探索两者之间的差异,并为每个提供策略测试报告,这些突显出预测纳斯达克波动率的相对重要性。鉴于 2020年 1 月 1 日至 2020年 3 月 15 日的测试窗口较短,无法得出哪种映射更佳的结论,但结果当中的差异表明具有高度敏感性,因此需要强调一个盖过其它。
创建标准普尔 500 指数波动率范畴
SP500 波动率数据的收集和处理很简单,类似于我们在上一篇文章中衡量纳斯达克波动率的方式。VIX 是我们将在这里研究的单独指标,读者注意这一点很重要。故此,当前的波动率读数将在以下清单之后在每根新柱线上重新计算:
double _float_value=0.0; //where R is an instance of MqlRates... _float_value=(R.high-R.low)/Point();
如前所述,标普将形成我们的协域,对象捕获的波动率值作为一个对象的集合,以及它们之间的态射捕获波动率读数之间的相对变化。此范畴的初始化可以按如下方式处理:
//+------------------------------------------------------------------+ //| Get SP500-100 data from symbol (NDX100 for this broker). | //| Load it into SP500 category. | //+------------------------------------------------------------------+ void SetSP500(MqlRates &R) { _hmorph_sp500.Let(); double _float_value=0.0; _float_value=(R.high-R.low)/Point(); _element_value.Let();_element_value.Cardinality(1);_element_value.Set(0,DoubleToString(_float_value)); _domain_sp500.Cardinality(1);_domain_sp500.Set(0,_element_value); //_category_sp500.Domains(_category_sp500.Domains()+1); _category_sp500.SetDomain(_category_sp500.Domains(),_domain_sp500); }
正如我们在上一篇文章中所见,如果我们能将一个带有滞后的域映射到这个协域,我们就具备对标普 500 指数的波动性进行一些预测的能力。与上一篇文章一样,我们将在相同的信号和资金管理设置上分别测试对象和态射函子,从而衡量灵敏度。
从财经日历到标普 500 指数的函子
我们将使用以下清单构建财经日历数据的范畴:
//+------------------------------------------------------------------+ //| Get Ocean data from file defined in input. | //| Load it into Ocean category. | //+------------------------------------------------------------------+ void SetEconomic(MqlRates &R) { datetime _time=R.time; int _elements=1; _e_retail.Let(); SampleEvents(_time,_e_retail,IntToCountry(__country),__currency,TYPE_RETAIL_SALES);//printf(__FUNCSIG__+"...retail. "); _e_cpi.Let(); string _cpi_time="";_e_retail.Get(0,_cpi_time); SampleEvents(StringToTime(_cpi_time),_e_cpi,IntToCountry(__country),__currency,TYPE_CPI);//printf(__FUNCSIG__+"...cpi. "); _e_auction.Let(); string _auction_time="";_e_cpi.Get(0,_auction_time); SampleEvents(StringToTime(_auction_time),_e_auction,IntToCountry(__country),__currency,TYPE_AUCTION_10YR);//printf(__FUNCSIG__+"...auction. "); _e_pmi.Let(); string _pmi_time="";_e_auction.Get(0,_pmi_time); SampleEvents(StringToTime(_pmi_time),_e_pmi,IntToCountry(__country),__currency,TYPE_PMI);//printf(__FUNCSIG__+"...pmi. "); _domain_economic.Cardinality(__ECON); _domain_economic.Set(0,_e_retail); _domain_economic.Set(1,_e_cpi); _domain_economic.Set(2,_e_auction); _domain_economic.Set(3,_e_pmi); _category_economic.SetDomain(_category_economic.Domains(),_domain_economic); }
该域中的每个对象都有两个顶点,它们是成对的日历值,其中至少有一个顶点位于协域中波动率值的时间范围内。由于这些财经数据大约每隔一个月发布一次,我们将在月度时间帧内进行测试。与上一篇文章一样,我们的函子映射将含有对象中每个数据点的系数。此处的区别在于,我们面临着多个对象映射到协域中同一波动性的可能性。理想情况下,我们需要分别从每个对象获取系数(对于线性映射),并在预测中使用它们。这意味着它们捆绑后必然会在态射映射提供的预测之上造成相互冲突的预测。这就是为什么出于本文目的,我们可以权衡从日历数据到标普范畴的每个函子映射,并将所有值的点积总和映射到波动率值。
与上一篇文章一样,函子的实际应用将轮流遵循两种方案,我们将在第一次迭代中映射对象,然后在下一次迭代中映射态射。来自 'Output()' 函数的对象映射将是:
//+------------------------------------------------------------------+ //| Get Forecast value, forecast for next change in price bar range. | //+------------------------------------------------------------------+ double GetObjectsForecast(MqlRates &R) { double _output=0.0; //econ init SetEconomic(R); //sp500 init SetSP500(R); matrix _domain; vector _codomain,_inputs; _domain.Init(__ECON+1,__ECON); for(int r=0;r<__ECON+1;r++) { CDomain<string> _d;_d.Let(); _category_economic.GetDomain(_category_economic.Domains()-r-1,_d); for(int c=0;c<__ECON;c++) { CElement<string> _e; _d.Get(c,_e); string _s; _e.Get(1,_s); _domain[r][c]=StringToDouble(_s); } } _codomain.Init(__ECON); for(int r=0;r<__ECON;r++) { CDomain<string> _d;_d.Let(); _category_sp500.GetDomain(_category_sp500.Domains()-r-1,_d); CElement<string> _e; _d.Get(0,_e); string _s; _e.Get(0,_s); _codomain[r]=StringToDouble(_s); } _inputs.Init(__ECON);_inputs.Fill(__constant_morph); M(_domain,_codomain,_inputs,_output,1); return(_output); }
我们的态射到态射的映射也将以不同的方式处理,即把由变化增量定义的顶点态射,映射到标普波动率数据点态射(亦由变化值定义)。这将遵循如下过程:
//+------------------------------------------------------------------+ //| Get Forecast value, forecast for next change in price bar range. | //+------------------------------------------------------------------+ double GetMorphsForecast(MqlRates &R) { ... for(int r=0;r<__ECON+1;r++) { ... for(int c=0;c<__ECON;c++) { CElement<string> _e_new; _d_new.Get(c,_e_new); string _s_new; _e_new.Get(1,_s_new); CElement<string> _e_old; _d_old.Get(c,_e_old); string _s_old; _e_old.Get(1,_s_old); _domain[r][c]=StringToDouble(_s_new)-StringToDouble(_s_old); } } _codomain.Init(__ECON); for(int r=0;r<__ECON;r++) { ... CElement<string> _e_new; _d_new.Get(0,_e_new); string _s_new; _e_new.Get(0,_s_new); CElement<string> _e_old; _d_old.Get(0,_e_old); string _s_old; _e_old.Get(0,_s_old); _codomain[r]=StringToDouble(_s_new)-StringToDouble(_s_old); } _inputs.Init(__ECON);_inputs.Fill(__constant_morph); M(_domain,_codomain,_inputs,_output,1); return(_output); }
函子的这两个部分的示意图表示也与我们上一篇文章中涵盖内容略有不同,因为我们的关系将不再是那种同构情况。我们可按如下方式概括对象到对象的映射:
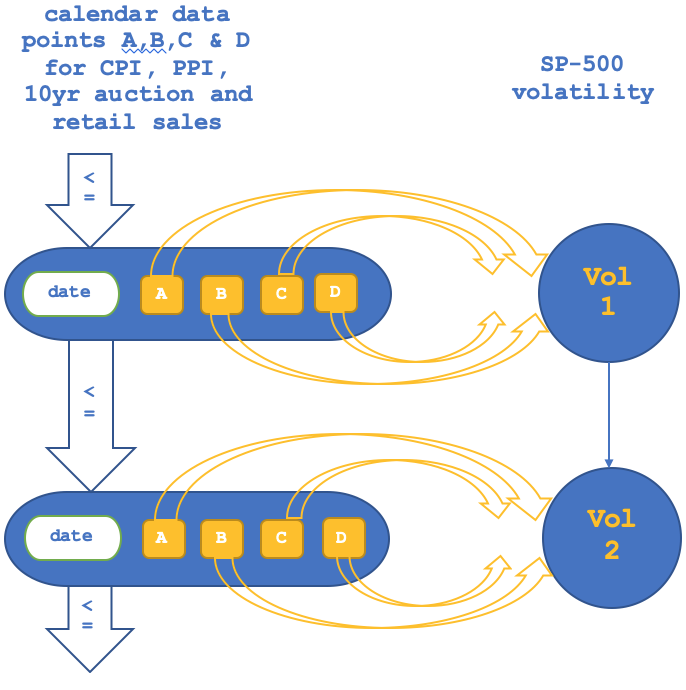
对于态射到态射,观感如下:

不幸的是,MQL5 的策略测试器在测试当中不允许访问财经日历事件。开发更强大的交易系统会带来更多性能提升。故此,由于我们已为其编写了脚本,因此我们能做的最好的事情就是基于我们的预测打印出波动率的预测变化,如果您遍历一些历史记录,您能感觉到我们的预测有多准确。
尽管如此,如果我们基于经纪商提供的价格数据运行脚本,我们可以依据日历数据图形和 SP500 波动率及其连接函子来构造我们的两个范畴,我们能够获得以下日志,对波动率进行预测。对象到对象的函子映射打印的日志:
2023.07.30 13:45:47.035 ct_15_w (SPX500,MN1) void OnStart() Objects forecast is: 0.00000000, on: 2020.01.01 00:00, with actual being: 54260.00000000 2023.07.30 13:45:47.134 ct_15_w (SPX500,MN1) void OnStart() Objects forecast is: 0.00000000, on: 2020.02.01 00:00, with actual being: 95438.00000000 2023.07.30 13:45:47.265 ct_15_w (SPX500,MN1) void OnStart() Objects forecast is: 0.00000000, on: 2020.03.01 00:00, with actual being: 53588.00000000 2023.07.30 13:45:47.392 ct_15_w (SPX500,MN1) void OnStart() Objects forecast is: 0.00000000, on: 2020.04.01 00:00, with actual being: 30352.00000000 2023.07.30 13:45:47.512 ct_15_w (SPX500,MN1) void OnStart() Objects forecast is: 0.00000000, on: 2020.05.01 00:00, with actual being: 29694.00000000 2023.07.30 13:45:47.644 ct_15_w (SPX500,MN1) void OnStart() Objects forecast is: -716790.11376869, on: 2020.06.01 00:00, with actual being: 21905.00000000 2023.07.30 13:45:47.740 ct_15_w (SPX500,MN1) void OnStart() Objects forecast is: -12424.22112077, on: 2020.07.01 00:00, with actual being: 26509.00000000 2023.07.30 13:45:47.852 ct_15_w (SPX500,MN1) void OnStart() Objects forecast is: 53612.17123096, on: 2020.08.01 00:00, with actual being: 37890.00000000 ... 2023.07.30 13:45:50.294 ct_15_w (SPX500,MN1) void OnStart() Objects forecast is: -27774.72154618, on: 2022.09.01 00:00, with actual being: 42426.00000000 2023.07.30 13:45:50.377 ct_15_w (SPX500,MN1) void OnStart() Objects forecast is: 46751.59791572, on: 2022.10.01 00:00, with actual being: 39338.00000000 2023.07.30 13:45:50.487 ct_15_w (SPX500,MN1) void OnStart() Objects forecast is: -19820.29385469, on: 2022.11.01 00:00, with actual being: 37305.00000000 2023.07.30 13:45:50.593 ct_15_w (SPX500,MN1) void OnStart() Objects forecast is: -5370.60103622, on: 2022.12.01 00:00, with actual being: 30192.00000000 2023.07.30 13:45:50.700 ct_15_w (SPX500,MN1) void OnStart() Objects forecast is: -4662833.98425755, on: 2023.01.01 00:00, with actual being: 25359.00000000 2023.07.30 13:45:50.795 ct_15_w (SPX500,MN1) void OnStart() Objects forecast is: 33455.47933459, on: 2023.02.01 00:00, with actual being: 30681.00000000 2023.07.30 13:45:50.905 ct_15_w (SPX500,MN1) void OnStart() Objects forecast is: -40357.22273603, on: 2023.03.01 00:00, with actual being: 12502.00000000 2023.07.30 13:45:51.001 ct_15_w (SPX500,MN1) void OnStart() Objects forecast is: -37676.03496283, on: 2023.04.01 00:00, with actual being: 18835.00000000 2023.07.30 13:45:51.094 ct_15_w (SPX500,MN1) void OnStart() Objects forecast is: -54634.02723538, on: 2023.05.01 00:00, with actual being: 28877.00000000 2023.07.30 13:45:51.178 ct_15_w (SPX500,MN1) void OnStart() Objects forecast is: -35897.40757724, on: 2023.06.01 00:00, with actual being: 23306.00000000 2023.07.30 13:45:51.178 ct_15_w (SPX500,MN1) void OnStart() corr is: 0.36053106 with morph constant as: 50000.00000000
态射到态射打印的日志:
2023.07.30 13:47:38.737 ct_15_w (SPX500,MN1) void OnStart() Morphs forecast is: 0.00000000, on: 2020.01.01 00:00, with actual being: 54260.00000000 2023.07.30 13:47:38.797 ct_15_w (SPX500,MN1) void OnStart() Morphs forecast is: 0.00000000, on: 2020.02.01 00:00, with actual being: 95438.00000000 2023.07.30 13:47:38.852 ct_15_w (SPX500,MN1) void OnStart() Morphs forecast is: 0.00000000, on: 2020.03.01 00:00, with actual being: 53588.00000000 2023.07.30 13:47:38.906 ct_15_w (SPX500,MN1) void OnStart() Morphs forecast is: 0.00000000, on: 2020.04.01 00:00, with actual being: 30352.00000000 2023.07.30 13:47:39.010 ct_15_w (SPX500,MN1) void OnStart() Morphs forecast is: 0.00000000, on: 2020.05.01 00:00, with actual being: 29694.00000000 2023.07.30 13:47:39.087 ct_15_w (SPX500,MN1) void OnStart() Morphs forecast is: -2482719.31391738, on: 2020.06.01 00:00, with actual being: 21905.00000000 ... 2023.07.30 13:47:41.541 ct_15_w (SPX500,MN1) void OnStart() Morphs forecast is: -86724.54189079, on: 2022.11.01 00:00, with actual being: 37305.00000000 2023.07.30 13:47:41.661 ct_15_w (SPX500,MN1) void OnStart() Morphs forecast is: -126817.99564744, on: 2022.12.01 00:00, with actual being: 30192.00000000 2023.07.30 13:47:41.793 ct_15_w (SPX500,MN1) void OnStart() Morphs forecast is: -198737.93199622, on: 2023.01.01 00:00, with actual being: 25359.00000000 2023.07.30 13:47:41.917 ct_15_w (SPX500,MN1) void OnStart() Morphs forecast is: -280104.88246660, on: 2023.02.01 00:00, with actual being: 30681.00000000 2023.07.30 13:47:42.037 ct_15_w (SPX500,MN1) void OnStart() Morphs forecast is: 24129.34336223, on: 2023.03.01 00:00, with actual being: 12502.00000000 2023.07.30 13:47:42.157 ct_15_w (SPX500,MN1) void OnStart() Morphs forecast is: 4293.73674465, on: 2023.04.01 00:00, with actual being: 18835.00000000 2023.07.30 13:47:42.280 ct_15_w (SPX500,MN1) void OnStart() Morphs forecast is: 763492.31964126, on: 2023.05.01 00:00, with actual being: 28877.00000000 2023.07.30 13:47:42.401 ct_15_w (SPX500,MN1) void OnStart() Morphs forecast is: -30298.30836734, on: 2023.06.01 00:00, with actual being: 23306.00000000 2023.07.30 13:47:42.401 ct_15_w (SPX500,MN1) void OnStart() corr is: 0.03400012 with morph constant as: 50000.00000000
从上面打印出的日志可以看出几点。首先,前五个月的预测值均为零。我认为这是由于没有足够的价格数据来进行完整的计算,就像许多指标的偶尔情况。其次,负值是预测的一部分,但我们只是在寻找一个严格的正值,为我们指示下一根柱线上的波动率。这可能归因于未能调整低波动率值的大小,因为我们使用的是 MQL5 标准库回归工具,其使用恒等矩阵来求解我们的多系数(4)。绕过这个问题的方法是通过下面建议的函数对负值进行归一化。
//+------------------------------------------------------------------+ //| Normalizes negative projections to positive number. | //+------------------------------------------------------------------+ double NormalizeForecast(double NegativeValue,double CurrentActual,double PreviousActual,double PreviousForecast) { return(CurrentActual+(((CurrentActual-NegativeValue)/CurrentActual)*fabs(PreviousActual-PreviousForecast))); }
如果我们现在运行脚本,并检查我们的预测与实际值之间的相关性,我们肯定会得到不同的结果,特别是因为方程常数是一个非常敏感的值,它在很大程度上决定了我们最终得到的输出和预测。我们将其设置为零,得到下面生成的日志。首先,我们运行对象到对象的函子:
2023.07.30 14:43:42.224 ct_15_w_n (SPX500,MN1) void OnStart() Objects forecast is: 15650.00000000, on: 2020.01.01 00:00, with actual being: 54260.00000000 ... 2023.07.30 14:43:45.895 ct_15_w_n (SPX500,MN1) void OnStart() Objects forecast is: 15718.63125861, on: 2023.03.01 00:00, with actual being: 12502.00000000 2023.07.30 14:43:45.957 ct_15_w_n (SPX500,MN1) void OnStart() Objects forecast is: 12187.53007421, on: 2023.04.01 00:00, with actual being: 18835.00000000 2023.07.30 14:43:46.026 ct_15_w_n (SPX500,MN1) void OnStart() Objects forecast is: 19185.80075759, on: 2023.05.01 00:00, with actual being: 28877.00000000 2023.07.30 14:43:46.129 ct_15_w_n (SPX500,MN1) void OnStart() Objects forecast is: 11544.54076238, on: 2023.06.01 00:00, with actual being: 23306.00000000 2023.07.30 14:43:46.129 ct_15_w_n (SPX500,MN1) void OnStart() correlation is: 0.46195608 with morph constant as: 0.00000000
然后我们运行我们的脚本,同时基于态射到态射函子进行预测,再次采用相同的方程常数为零。
2023.07.30 14:45:54.257 ct_15_w_n (SPX500,MN1) void OnStart() Morphs forecast is: 54260.00000000, on: 2020.02.01 00:00, with actual being: 95438.00000000 ... 2023.07.30 14:45:57.449 ct_15_w_n (SPX500,MN1) void OnStart() Morphs forecast is: 257937.92970615, on: 2023.05.01 00:00, with actual being: 28877.00000000 2023.07.30 14:45:57.527 ct_15_w_n (SPX500,MN1) void OnStart() Morphs forecast is: 679078.55629755, on: 2023.06.01 00:00, with actual being: 23306.00000000 2023.07.30 14:45:57.527 ct_15_w_n (SPX500,MN1) void OnStart() correlation is: -0.03589660 with morph constant as: 0.00000000
我们得到略高的相关性 0.46,对比没有常规化时得到的相关性为 0.3。这可能表明常规化有一些好处,但在我们的例子中,输入常数从 50000 变化,如前所述,预测和相关性对它非常敏感。故此,由于我们只有一个输入,因此适当的策略测试器运行,可以优化该值,并得到更有意义的结果。
对交易者的影响
在我看来,范畴论对金融分析的一个被忽视的价值是转移学习。刚刚分享的链接将您带到维基百科进行介绍,但无法轻易推断出我们将从此处的应用程序中获得什么样的益处。从上面的测试中,我们得出了对象函子映射和态射映射之间的系数。若优化完成,得出这些系数的过程必然是计算密集型的,特别是如理想预期,在 MQL5 的策略测试器中涵盖了很长区间的历史数据。
也因之函子系数是集合假设的一部分,上面已经推进作为一个循环,可以说,这些系数以特定的方式作用于财经日历中的美元货币值,可能同样适用于欧元区财经日历值对 EURO-STOXX 波动率的影响,或 FTSE 波动率对英镑值。这确实提供了可能的组合列表,我们的函子变得无价的地方在于从一次冗长的计算密集型优化中获得的系数,并将它们应用于这些替代方案中的任何一个,在纸面上基于我们的假设可以产生比平均结果更好的结果。
为了概括这一点,使用如下所示的输入:
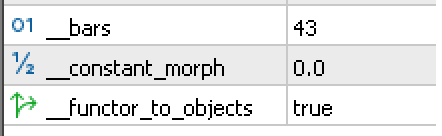
我们对替代货币及其各自的净值指数进行一些测试。如果我们从欧元区财经日历值开始,挑选德国作为一个范畴,在由函子配对的范畴中与 DAX30 波动率范畴配对,那么通过我们上面的设置,我们得到下面的测试报告:
2023.07.30 15:12:25.655 ct_15_w_n (GER30,MN1) void OnStart() Objects forecast is: 75550.00000000, on: 2020.01.01 00:00, with actual being: 210640.00000000 2023.07.30 15:12:25.727 ct_15_w_n (GER30,MN1) void OnStart() Objects forecast is: 210640.00000000, on: 2020.02.01 00:00, with actual being: 431320.00000000 ... 2023.07.30 15:12:28.445 ct_15_w_n (GER30,MN1) void OnStart() Objects forecast is: 144734.23693128, on: 2022.09.01 00:00, with actual being: 154697.00000000 2023.07.30 15:12:28.539 ct_15_w_n (GER30,MN1) void OnStart() Objects forecast is: 171908.69769099, on: 2022.10.01 00:00, with actual being: 156643.00000000 2023.07.30 15:12:28.648 ct_15_w_n (GER30,MN1) void OnStart() Objects forecast is: 298789.42486333, on: 2022.11.01 00:00, with actual being: 99044.00000000 2023.07.30 15:12:28.753 ct_15_w_n (GER30,MN1) void OnStart() Objects forecast is: 178962.89317906, on: 2022.12.01 00:00, with actual being: 137604.00000000 2023.07.30 15:12:28.901 ct_15_w_n (GER30,MN1) void OnStart() Objects forecast is: 440957.33259197, on: 2023.01.01 00:00, with actual being: 55544.00000000 2023.07.30 15:12:29.032 ct_15_w_n (GER30,MN1) void OnStart() Objects forecast is: 143198.91357580, on: 2023.02.01 00:00, with actual being: 124659.00000000 2023.07.30 15:12:29.151 ct_15_w_n (GER30,MN1) void OnStart() Objects forecast is: 24327.24201304, on: 2023.03.01 00:00, with actual being: 48737.00000000 2023.07.30 15:12:29.267 ct_15_w_n (GER30,MN1) void OnStart() Objects forecast is: 167059.32862279, on: 2023.04.01 00:00, with actual being: 69888.00000000 2023.07.30 15:12:29.357 ct_15_w_n (GER30,MN1) void OnStart() Objects forecast is: 67301.73632062, on: 2023.05.01 00:00, with actual being: 74073.00000000 2023.07.30 15:12:29.470 ct_15_w_n (GER30,MN1) void OnStart() Objects forecast is: 87406.10063493, on: 2023.06.01 00:00, with actual being: 104992.00000000 2023.07.30 15:12:29.470 ct_15_w_n (GER30,MN1) void OnStart() correlation is: 0.02260757 with morph constant as: 0.00000000
对于英镑和 FTSE-100 指数,我们得到:
2023.07.30 15:12:45.341 ct_15_w_n (UK100,MN1) void OnStart() Objects forecast is: 45860.00000000, on: 2020.01.01 00:00, with actual being: 109780.00000000 2023.07.30 15:12:45.381 ct_15_w_n (UK100,MN1) void OnStart() Objects forecast is: 109780.00000000, on: 2020.02.01 00:00, with actual being: 210420.00000000 2023.07.30 15:12:45.420 ct_15_w_n (UK100,MN1) void OnStart() Objects forecast is: 210420.00000000, on: 2020.03.01 00:00, with actual being: 87250.00000000 2023.07.30 15:12:45.466 ct_15_w_n (UK100,MN1) void OnStart() Objects forecast is: 87250.00000000, on: 2020.04.01 00:00, with actual being: 58380.00000000 2023.07.30 15:12:45.508 ct_15_w_n (UK100,MN1) void OnStart() Objects forecast is: 1581489.63705309, on: 2020.05.01 00:00, with actual being: 58370.00000000 ... 2023.07.30 15:12:46.685 ct_15_w_n (UK100,MN1) void OnStart() Objects forecast is: 153576.16806574, on: 2023.01.01 00:00, with actual being: 30453.00000000 2023.07.30 15:12:46.710 ct_15_w_n (UK100,MN1) void OnStart() Objects forecast is: 222058.94934174, on: 2023.02.01 00:00, with actual being: 77051.00000000 2023.07.30 15:12:46.739 ct_15_w_n (UK100,MN1) void OnStart() Objects forecast is: 50993.02046828, on: 2023.03.01 00:00, with actual being: 30780.00000000 2023.07.30 15:12:46.784 ct_15_w_n (UK100,MN1) void OnStart() Objects forecast is: 66795.26430874, on: 2023.04.01 00:00, with actual being: 45453.00000000 2023.07.30 15:12:46.832 ct_15_w_n (UK100,MN1) void OnStart() Objects forecast is: 75492.86146563, on: 2023.05.01 00:00, with actual being: 28845.00000000 2023.07.30 15:12:46.876 ct_15_w_n (UK100,MN1) void OnStart() Objects forecast is: 92298.50964858, on: 2023.06.01 00:00, with actual being: 49472.00000000 2023.07.30 15:12:46.876 ct_15_w_n (UK100,MN1) void OnStart() correlation is: 0.14415363 with morph constant as: 0.00000000
从我们的初始日志中可以清楚地看出,即使我们能够进行预测,但由于策略测试器中使用日历数据受限,我们无法可靠地验证它们。显然,我们的假设并不成立,坦率地说,上面得到的美元和 SP500 的 0.46 相关性很难确定。
事实上,相关性值是一个临时的“解决方案”,因为它只是一个非常早期的指标,表明预测的可靠性,或取决于输入的选择,在我们的例子中,主要的一个是域范畴与其协域之间的线性关系系数。从长远来看,更可靠的选择是手动将这些财经日历数据导出到 CSV 文件,以供智能系统读取,甚至可以导出到数据库中,从而更安全地保存。无论哪种选项,都可以在理想的很长区间内进行适当的测试。
除了预测波动率作为判定理想止损的一种手段外,您还希望有一种系统级的方式进行持仓规模调整。为了达成这一点,依据我们的方法论,假设您有一个不受约束的时间序列数据范畴,即特定证券的交易历史,其中范畴内的每个对象代表特定的交易结果,对象之间的箭头(态射)表示这些结果随时间的变化。
为了使用该范畴来设置或预测交易系统的理想持仓规模,我们将通过函子将其映射到另一个基于实际交易结果的理想持仓规模时间序列的范畴,也许还有随之而来的波动性。由此,举例,如果交易是亏损的,那么当时的对象,在范畴中将记录较小的持仓规模,而如果它是盈利的,则将记录较大的持仓规模。波动性可以作为持仓更小或更大的额外因素,具体取决于交易期间记录的波动性。故此,缩放尺度可能是这样的,当交易亏损时,理想的持仓规模会根据波动率读数成比例地缩小。同样,如果交易结果是赚了,那么理想的持仓规模也会与波动率成比例地再次放大。正如预期的那样,映射函子将具有滞后性,例如现在的交易结果与下一个周期的持仓规模相关联。
函子不仅将交易结果与预期的理想持仓规模连接起来,而且还将交易结果之间的态射与理想持仓规模之间的态射连接起来。正如我们在上一篇文章和上面所见,一个可以检查另一个,但一个更有见地的问题可能是映射函数如何将域连接到协域。
到目前为止,我们已经使用了基于过去结果回归的非常基本的系数。从本文末尾和上一篇文章的附件中您可以看出,我们假设将一个简单的常数加上一个系数添加到域值中,从而获得可以解释为简单线性关系的协域值。但除了线性关系之外,域值还可以通过二次关系映射到协域,其中,如果我们的最高指数是 2,那么我们有一个额外的系数,该系数乘以域值的平方,得出连接的协域对应物。当然,一个人使用的指数越多,他在定义函子映射时需要的系数就越多。
不过,除了这种简单且容易出错的方法之外,另一种替代方法是让人工神经网络定义两个域之间的同态映射。这必须同时针对对象和态射进行,并且在大多数情况下,通过对大量数据进行训练必然会产生更准确的结果;但撇开准确性问题不谈,从直觉上讲,这是正确的方法,因为神经网络擅长接受多个输入,并产生单个输出,这适用于这种情况。
结束语
总而言之,这里涵盖的要点是依据财经日历数据构图,将该图形视为一个范畴,并且像我们之前的文章一样,使用滞后于标普 500 指数波动率的函子关系来预测标普 500 指数的波动率。我们使用这些预测来移动持仓的尾随停止,就像这些系列中的情况一样。除了调整持仓的止损外,我们还可以使用函子关系来设置新订单的持仓规模,甚至定义任何可交易证券的入场信号。就使用 IDE 向导装配智能系统而言,这些系列摒弃了最后两个示例,因为我觉得读者可以更好地根据自己的策略优调这些概念。到目前为止,我们还收集了变形和现在的函子关系的定义。我们一直在使用粗略的增量值,这些值可能具有从域到协域的线性或二次关系,但人工神经网络也可以用于定义此映射。我们可以在下一篇文章中对此进行研究。
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/13033
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 时间序列挖掘的数据标签(第4部分):使用标签数据的可解释性分解
时间序列挖掘的数据标签(第4部分):使用标签数据的可解释性分解
