デイトレーディングの時間変換の原則

はじめに

過去の価格の動きを分析する上で監視の統計的同質性は重要な役割を果たしています。そのような同質性が発生した際、トレーディングシステムを構築する規則性を明らかにするためのプロセスのプロパティを深く学ぶことができます。しかし、それはよく知られた事実であり、最初のアプローチにて交換レートのプロセスは、非同質的であり、すなわち、異なるトレーディングセッションの活動と関連する同質性があります：欧米、アジアなどのセッションです。

システム開発者や熟練した人は、移動平均の最もシンプルなインジケーターは、実際異なるユニットであると考えることはないでしょう。間違いなく、時間ではなく、価格の観点でまとめられたシステムです。典型的な例は、マイナーですがレンコ・カギメソッドに基づくシステムです。しかし、それらの大半はインジケーターを通して間接的に時間に縛られています。

上記は、ディトレードシステムのみを言及しています。より大きなタイムフレームにおいて、もし季節性があったとしても、そこまで明白でありません。そして、ディトレーディングにおいて、それは本質的で、そのシステムが異なる時間で異なる利益生を示すことがあるという事実に導かれます。そのような効果をもたらす要因と、それらを防ぐ方法に注目しましょう。

理論

偶然的なプロセスの統計の観点では、価格の変化のプロセスは特定の異なる種類であると見なされ、集中度の高いエリアから低いエリアへのエネルギーや物質の移動です。時間変化は、比較的簡単に調整されたブラウニアンモーションへマルチンゲールを移行することはよく知られています。

価格の変化のプロセスが、拡散やマルチンゲールか否かの質問にとらわれず、時間の変換プロセスから時間において統計的に同質なプロセスのよりシンプルな方法で調整されたものに移行する上で何も妨害するものがないということに注目しましょう。このため、時間の分離なしでバーを使用することが妥当ですが、固定の数のティックを用います。つまり、バーは60分間ではなく、1000ティックを含んでいます。

そのような時間は理論上、オペレーショナルと呼ばれ、時間変換のプロセスにおいて自然です。このような場合、そのプロセスは統計的に一定の平均偏差を持ち、より明確に形成するマーケットの雰囲気を理解し、効果的に偶発的な変動から分けることができます。そして、共通のインジケーターを用いることは可能なだけではなく、より同質的になります。」しかし、不幸にもMetaTrader4はそのようなオプションは含まれません。なので、時間を考慮してシステムを再調整するという別のメソッドを用います。以下は、改良を加えられたインジケーターの例です。しかし、まず不均質性について分析しましょう。

統計データ

通貨ペアチャートはマーケットのアクティビティが１日の特定の時期に減少することを示しています。例:

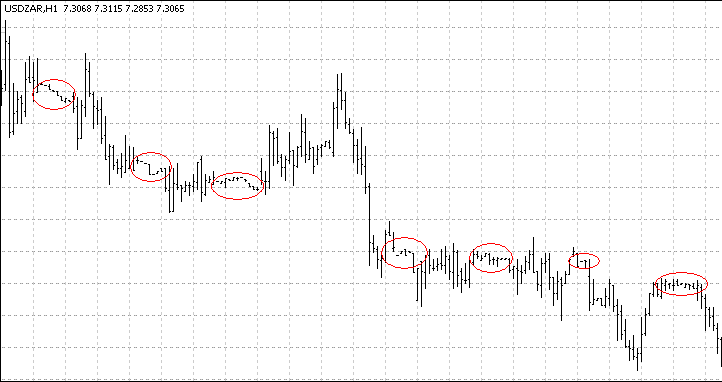
さらに、同じ効果が人気の通貨ペアで観測されています。これは、量やボラテイリティのより詳しい調査への興味をかきたてます。１日のボラティリティの変動へのより良い理解のために、一つのバーのティックなどの量が重要であることは明白です。しかし、その量自体は偶然的な値であり、過去の平均を参照する必要があります。もし統計的な「生の材料」が「間違った」方向に動作すれば、そのような参照はあまり法律に沿いません。

これらの仮説をチェックするために、簡単なインジケーター ExpectedVolumeを記述しましょう、１時間ごとに過去のティックの平均量を計算し、histSteps は、各ステップのスパンは１日ですが、より少し早く進みます。これらのパラメーターの典型的な値は、100と1です。そのテストは、タイムフレームH1にて実行され、その他のタイムフレームのパラメーターは変更される必要があります。こちらがそのインジケーターのコードです：

//+------------------------------------------------------------------+
//|                                             Expected Volumes.mq4 |
//|                                     Copyright © 2007, Amir Aliev |
//|                                      http://finmat.blogspot.com/ |
//+------------------------------------------------------------------+
#property  copyright "Copyright © 2007, Amir Aliev"
#property  link      "http://finmat.blogspot.com/"
//---- 
#property indicator_separate_window
#property indicator_buffers 1
#property indicator_color1 Blue
//---- input parameters
extern int hist_steps = 100;      // Number of observations
extern int span = 1;              // Days to step back each time 
//---- buffers
double ExtMapBuffer1[];
int sum;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int init()
  {
   string short_name;
//---- indicators
   SetIndexStyle(0, DRAW_HISTOGRAM);
   SetIndexBuffer(0,ExtMapBuffer1);
//----
   short_name = "Expected volumes(" + hist_steps + ")";
   IndicatorShortName(short_name);
   SetIndexLabel(0, short_name);
   return(0);
  }
//+------------------------------------------------------------------+
//| Custom indicator deinitialization function                       |
//+------------------------------------------------------------------+
int deinit()
  {
//----
   return(0);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int start()
  {
   int counted_bars = IndicatorCounted();
   int rest = Bars - counted_bars;
   int j, k, u;
//----     
   while(rest >= 0)
     {
      if(Bars - rest < span * 23 * hist_steps) 
        {
         ExtMapBuffer1[rest] = 0;     
         rest--; 
         continue;                                   
        }
      sum = 0;
      j = 0;
      k = 0;
      u = 0;
      while(j < hist_steps && k < Bars) 
        {
         if(TimeHour(Time[rest+k]) == TimeHour(Time[rest]))
           {
            u++;
            if(u == span)
              {
               u = 0;
               j++;
               sum += Volume[rest + k]; 
              }
            k += 23;
           }
         k++;
        }
      ExtMapBuffer1[rest] = sum / hist_steps;     
      rest--;                                    
     }
//----
   return(0);
  }
//+------------------------------------------------------------------+

統計的な同質性をチェックするために、その観測は独立し、平日で分割されている必要があります。このために、 span=5を割り当てます。以下を取得しましょう：

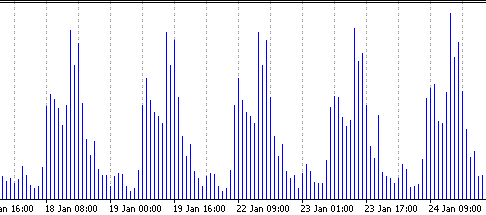
隣接しているこぶは、ほとんど同一です。１時間ごとのティックにつけられたボラティリティは、統計的に同質ということです。このボラティリティの構造は、以下の写真から明確です（左は、EURUSD、右はUSDJPY）：

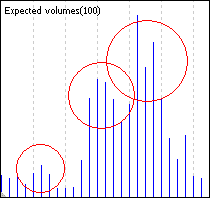
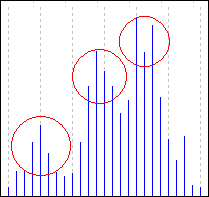
アジア、ヨーロッパ、アメリカの三つのトレーディングセッションのピーク時のアクティビティを示しています。これらのトレーディングセッションへの分割は、あまりありません - 時折、そのほかのセッションが除外されます。いくつかの特異性、例えば、アメリカセッション中のアクティビティの特色などに気づくことができます。

インジケーターの変更

インジケーターを変更する際、それらにどれほど時間が正確にふくまれているのか理解することがとても重要です。Moving Averageのようなシンプルなインジケーターにおいて、これは容易ですが、Alligatorなどは変更が難しいです。

最終的に「オペレーショナル」なタイムフレームを導入することがより合理的です。しかし、いくつかのシンプルなインジケーターを変更してみましょう。最も原始的なものは、訂正された量です - 実際の量は期待される額で分割されます。このインジケーター1からの逸脱は、マーケットでのアクティビティの増加/減少を反映します。コードは、とてもシンプルです。この記事に添付されているファイルに含まれています。

次の例は、Averageです。実際、バーの特性に重みをつける必要があり、その平均はバーの中のティックの量によって構成されます。最終的な数字は、すべてのティックの価格値の合計に完全に等しくはありません。より正確な評価のため、「オープン」ではなく、バーの重み付けされた平均を取得する必要があります。そのインジケーターは、力ずくで構築され、その計算はたくさんの不必要なCPUコストを必要とします。そのため、一つパラメーターが追加され、過去のバーの量は標準で500に等しくなります。さらに、平均の期間は、バーではなく、ティックの量にセットされます。こちらがコードです:

//+------------------------------------------------------------------+
//|                                                Corrected SMA.mq4 |
//|                                     Copyright © 2007, Amir Aliev |
//|                                    http://finmat.blogspot.com/   |
//+------------------------------------------------------------------+
#property copyright "Copyright © 2007, Amir Aliev"
#property link      "http://finmat.blogspot.com/"
//----
#property indicator_chart_window
#property indicator_color1 Red
//---- input parameters
extern int MA_Ticks = 10000;
extern int MA_Shift = 0;
extern int MA_Start = 500;
//---- indicator buffers
double ExtMapBuffer[];
double ExpVolBuffer[];
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int init()
  {
//----
   SetIndexStyle(0, DRAW_LINE);
   SetIndexShift(0, MA_Shift);
   IndicatorBuffers(2);
//---- indicator buffers mapping
   SetIndexBuffer(0, ExtMapBuffer);
   SetIndexBuffer(1, ExpVolBuffer);
   SetIndexDrawBegin(0, 0);  
//---- initialization done
   return(0);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int start()
  {
   int counted_bars = IndicatorCounted();
   int rest  = Bars - counted_bars;
   int restt = Bars - counted_bars;
   double sum;                               
   int ts;                                   
   int evol;                                 
   int volsum;
   int j;
//----
   while(restt >= 0)
     {
       volsum = 0;
       for(int k = 0; k < 30; k++) 
           volsum += iVolume(NULL, 0, restt + k*24); 
       ExpVolBuffer[restt] = volsum / 30;
       restt--;
     }
//----
   while(ExpVolBuffer[rest] == 0 && rest >= 0) 
       rest--;
   rest -= MA_Ticks / 200;
   if(rest > MA_Start) 
       rest = MA_Start;  
//----
   while(rest >= 0)
     {
       sum = 0;
       ts = 0;
       j = rest;
       while(ts < MA_Ticks)
         {
           evol = ExpVolBuffer[j];
           Print("Evol = ", evol);
           if(ts + evol < MA_Ticks)
             {
               sum += evol * Open[j];
               ts += evol;
             }
           else
             {
               sum += (MA_Ticks - ts) * Open[j];
               ts = MA_Ticks;
             }
           j++;
         }
       ExtMapBuffer[rest] = sum / MA_Ticks;
       rest--;
     }   
//----
   return(0);
  }
//+------------------------------------------------------------------+

シンプルなインジケーターが記述された後、より複雑なものを変更するためには問題になりません従って、MACDコードにて、調整された移動平均はシンプルなものの代わりに使用される必要があります。その一致するコードは添付ファイルにて提供されています。

調整された平均の計算のために、１時間ごとのティックの平均は一旦再計算を避けるため計算される必要があります。こちらでは省略されましたが、もし履歴にて完全なテスト/最適化を行う場合、生産性が第一に来ます。加えて、個別に議論される必要のある調整された平均量の計算のための他のアプローチを賞賛する人もいます。

過去の期間の量を平均することは無駄に見えます：係数として用いられる量は、平均の計算にて十分です。そのコードの例はこちらです。技術的な理由で、そのような平均はM1-M5などの小さいタイムフレームにて使用されることが最も好ましいです。

//+------------------------------------------------------------------+
//|                                             Corrected SMA II.mq4 |
//|                                     Copyright © 2007, Amir Aliev |
//|                                      http://finmat.blogspot.com/ |
//+------------------------------------------------------------------+
#property copyright "Copyright © 2007, Amir Aliev"
#property link      "http://finmat.blogspot.com/"
 
#property indicator_chart_window
#property indicator_color1 Red
//---- input parameters
extern int MA_Ticks = 1000;
//---- indicator buffers
double sum = 0;                               
int ticks = 0;
bool collected = false;
bool started = false;
int fbar = 0;
double ExtMapBuffer[];
int oldRange = 0;
int lbarVol = 0;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int init()
  {
//----
   SetIndexStyle(0, DRAW_LINE);
//---- indicator buffers mapping
   SetIndexBuffer(0, ExtMapBuffer);
//---- initialization done
   return(0);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int start()
  {
   int rest = Bars - IndicatorCounted();
   if(!rest)
       return (0);
   Print("Ticks = ", ticks);
   Print("Rest = ", rest);
   Print("fbar = ", fbar);
   rest--;
   fbar += rest;
   while(!collected && (rest >= 0))
     {
      if(ticks + Volume[rest] < MA_Ticks)
        {
         ticks += Volume[rest];
         sum += Volume[rest] * Open[rest];
         if(!started)
           {
            fbar = rest;
            started = true;
           }
         rest--;
         continue;
        }
      collected = true;
     }
   if(!collected)
       return (0);
 
   ticks += (Volume[rest] - lbarVol);
   sum += (Volume[rest] - lbarVol) * Open[rest];
   lbarVol = Volume[rest];
   while(ticks > MA_Ticks)
     {
       Print("fbar-- because bar ticks reaches 1000");
       ticks -= Volume[fbar];
       sum -= Volume[fbar] * Open[fbar];
       fbar--;
     }
   ExtMapBuffer[rest] = sum / ticks;
   rest--;
   while(rest >= 0)
     {
      ticks += Volume[rest];
      sum += Volume[rest] * Open[rest];
      lbarVol = Volume[rest];
      while(ticks > MA_Ticks)
        {
         Print("fbar-- because of new bar ");
         ticks -= Volume[fbar];
         sum -= Volume[fbar] * Open[fbar];
         fbar--;
        }
      ExtMapBuffer[rest] = sum / ticks;
      rest--;
     } 
//----
   return(0);
  }
//+------------------------------------------------------------------+

しかし、著者はこのインジケーターを用いることはいくつかのケースで役にたつが、一般的にこの記事に記載されているものとは異った意味を持つとかんがえています。「苦闘」のあったマーケットにて、価格値を考慮に入れる考えは、小さい値の逸脱はマーケットではなく技術的な理由で引き起こされるためかなり人口的です。加えて、ボラティリティの変化を考慮に入れるのは合理的ではありません。

それぞれ示されているインジケーターは、特別なタスクを考慮に改善されており、例えば、バーの中の値の合計の計算のための平均値を変更したり、平均の計算のパラメーターを変更するなどがあります。遅延感を促す"open"を計算しました。時間変換の概念の脱揮発性は季節的揮発性などこの記事で紹介されていないより広い解釈を許容します。

まとめ

価格平均はかなり不安定で、予測しにくい値であり、統計的観点から、そのボラティリティ、２番目の増加はかなり「愉快」なもので、クラスター属性や株式市場のレベル効果などよく知られた特徴をたくさん持ちます。

そのため、オペレーショナルな時間の概念は、テクニカル分析の観点でとても役に立ち、自然なものです。もちろん、経済の状態に関するいくつかの重要なニュースが特定の時間に発表されるという事実は、その同質性を壊します。しかし、多くの場合、時間変換を用いると、より安定した結果を取得でき、トレーディング戦略の利益性を増加します。