取引のための組合せ論と確率論(第III部): 初めての数学モデル

内容

• はじめに
• 新しい概念
• 平均ステップ数の一般式
• べき関数のプロトタイプの作成
• プロトタイプ限定ファミリーから最高の機能を受け取る一般的なスキーム
• 詳細分析
• データ収集と結論
• 数学モデル全体を計算するためのアルゴリズム
• 最後の方程式を取得するためのプロトタイプ
• 数学的モデルの実装とテスト
• 終わりに
• 参照文献

はじめに

前回の記事で、フラクタルの最初の式を取得しました。これにより、すべての重要なフラクタル関連の値が数学モデルを使用して記述できるという仮定が成り立ちました。このシミュレーションは、そのような値を説明することを目的としておらず、最初のデータの収集に役立ち、そのような構造のより深い分析を可能にするだけです。本稿では、さまざまなエキスパートアドバイザーに適用できる数学的モデルができるまで、最初の数学的モデルを開発するプロセス全体を説明することに特に注意を払うことにしました。

新しい概念

前回の記事で対称的なフラクタルを検討したところ、特定のチャネル内の移動の結果として価格がとる平均ステップ数を計算するための一般式が得られました。これは、同じ対称的でより小さいチャネルの数によって決定されます。 この式は次のとおりです。

1. S = K^2 - ステップが別のチャネルであるという事実に基づく、新しいチャネルの平均ステップ数
2. P = K * P0  --> K = P/P0 - 既知のチャネルが未知のチャネルの何倍か
3. P - 平均ステップ数が不明なチャネルの幅(ステップは元のチャネルの半分のサイズ)
4. P0 - 既知のチャネルの幅

非対称的なチャネルを記述できるようにするには、前述の概念のいくつかを再定義して、理解しやすくする必要があります。それらの中で最も重要なのはKです。この値は、実際には、新しいチャネルで価格がとる必要のあるステップ数を反映しています。ただし、ステップは上向きだけまたは下向きだけだとします。対称的なチャネルの場合、ステップ数は、検討している境界が上か下かに関係なく、上下で等しくなります。これは、問題が上下の境界の両方にミラーされているためです。非対称的なチャネルの場合、前の記事のコードを実験した結果、平均ステップ数は次のように決定されることがわかりました。

• S = n * m - チャネルの非対称的な半分での平均ステップ数
• n - チャネルの上半分に収まるステップ数
• m - チャネルの下半分に収まるステップ数

対称的なチャネルの場合、「m = n」になります。次に、上記に基づいて

• S = n * n = m * m = m * n = n^2 = m^2 = K^2
• K = n = m

これは、最初に導出された式が前の式の特殊なケースにすぎないため、Kが不要であることを意味します。

この関数の興味深い特徴は、S(a*k, b*k) = S(a,b) * S(k,k)ということです。これは非常に簡単に証明できます。

• S(n*k ,m*b) = m*k*n*b = n*m * k*b
• S(n ,m) * S(k ,b) = n*m * k*b

この特性は非常に興味深いものです。追加の反射により、フラクタル全体を記述するために必要なすべての式の導出を提供できます。この特性は、フラクタルの非常に重要な特性であるネスト機能を反映しています。言い換えると、非常に複雑な有限フラクタルは、互いにステップとして機能する2つ以上のより単純なフラクタルとして表すことができます。この特性は、より複雑なケースの式を一般化するために使用されます。

フラクタルに進む前に、上記で定義された式はp=0.5の場合にのみ機能することを思い出してください。市場またはフラクタルパラメータがランダムウォークから逸脱し始めるとすぐに、この式は非常に興味深い変化を始めます。

• Ss[n,m,p] – (任意の方向の)平均ステップ数のより一般的な式
• S(n ,m) = Ss[n,m,0,5] – ランダムウォークの式は一般式の特殊なケースです

平均ステップ数の一般式

より一般的な式の形式を決定するために、フラクタルの入れ子原理の不変性を使用しました。前のレベルと比較して個々のフラクタルの入れ子レベルを考慮する場合、特定のステップでどのステップが発生したかを考える必要はありません。したがって、主要な上向きステップと下向きステップは、前のレベルの状況に対応する頻度と正確に同じ比率で発生します。言い換えると、対応するの入れ子レベルの境界を越えることは、次のの入れ子レベルへの上向きステップまたは下向きステップのいずれかです。しかし、現在のの入れ子レベルのステップの発生頻度の比率は、現在のレベルの構成に依存しないことも知られています。これは、フラクタルの入れ子の原理が任意の確率「p」で観察されることを意味します。これは、「p」値が変更されると、式も変更される必要があるが、何らかの形でそのネスト特性を保持する必要があることを意味します。1つの簡単な経験は、一般式を決定するのに役立ちます。確率pには、ランダムウォーク点と、0と1の2つの極値点があることがわかっています。これらの3つの点で関数が取る値を見てみましょう。次のようになります。

1.  Ss[n,m,1] = Sn[n] = n
2. Ss[n,m,0] = Sm[m] = m
3.  Ss[n,m,0.5] = Sn[n] * Sm[m] = m*n
4.  Sn[n,p] – 上の境界までの一方向のステップ数
5. Sn[m,p] – 下の境界までの一方向のステップ数

最初の場合、下向きステップはありません。すべての鎖が同じルートをたどります。2番目は反対で、すべてのステップは下向きになり、上向きステップはありません。極値では、因数の1つが式から完全に消えます。0乗すると可能です。任意の数の0乗は1に等しくなります。さらに、次数には次の形式の不変性があります。

• A^X * B^X = (A*B)^X

数値の代わりに平均ステップを使用しても、フラクタルの入れ子の原則は維持されます。また、これは、累乗がnとmに依存しないことを示しています。結果として得られる平均ステップ数の一般式は次のとおりです。

• Ss[m,n,p] = ( Sn[n] ^ Pn[p] ) * ( S[m] ^ Pm[p] ) = (n ^ Pn[p] ) * ( m ^ Pm[p] )

フラクタルの入れ子の原理は、次のように図で示すことができます。

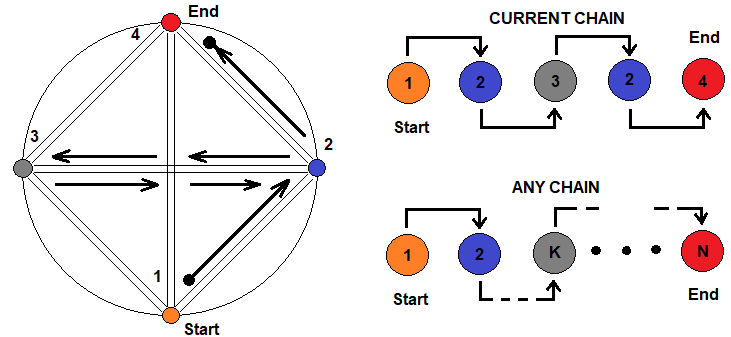
この図は、互いによって表現できるさまざまなフラクタルを象徴する4つの状態を示しています。状態間の移行は、任意の鎖を通じて可能です。右側には任意に選択した鎖が表示されています。その少し下には、この鎖は任意の長さと複雑さである可能性があり、同じ状態を無制限に繰り返すことができることが示されています。これは、フラクタルの平均ステップ数の式を、フラクタルの入れ子レベルを表す一連の積として表すことができることを意味します。

べき関数のプロトタイプの作成

さらなるアイデアは、フラクタルの入れ子の特性と、基数に対する指数の等しいべき関数の不変性から得られます。これらすべての数学的原理は、フラクタルをより深く説明するためのさらなる数式を導き出すのに役立ちます。したがって、さらに2つの関数が得られますが、その形式はわかりません。

• Pn[p] – 上の境界の乗数の累乗
• Pm[p] – 下の境界の乗数の累乗

次のことがわかっています。

• Pn[0.5] = 1 , Pn[1] = 1 , Pn[0] = 0
• Pm[0.5] = 1 , Pm[1] = 1 , Pm[0] = 0

べき関数を分析することにより、適切な関数プロトタイプを作成することができます。次のプロトタイプを選択しました。

1. Pn[p] = 1 , if p >= 0.5
2. Pn[p] = ( (1 – p)/0.5 ) ^ K
3. Pm[p] = 1 , if p <= 0.5
4. Pm[p] = ( p/0.5 ) ^ K
5. Kは指数で関数の平坦性を既成します

「2」と「4」を、与えられた累乗での滑らかな遷移を正確に表すことができる多項式の形で表す方が正確でしょうが、これはここでは冗長だと思います。より正確な多項式を定義したい方は、以下のプロトタイプを使用してください。

• Pn[p] = C1 * ( (1 – p)/0.5 ) ^ K1 + C2 * ( (1 – p)/0.5 ) ^ K2 … + … + CN * ( (1 – p)/0.5 ) *KN
• Pm[p] = C1 * ( p/0.5 ) ^ K1 + C2 * ( p/0.5 ) ^ K2 … + … + CN * ( p/0.5 ) ^ KN
• С1 + С2 + … + … СN = 1は、関連する累乗の重みです
• KNは対応する項の累乗です

私が選択した多項式は、1つの項しかない一般的な多項式の最も単純なバージョンです。宣言されたすべての原則は、小数部の「n、m」について確認できます。

上記の仮定を確認するために、次のプログラムを作成しました。

プログラムの結果からわかるように、すべては正常に機能します。確認するには、2つの数値を比較するだけです。それらが等しい場合、入れ子の原則と、小数のnおよびmを使用する機能が確認されます。

プロトタイプ限定ファミリーから最高の機能を受け取る一般的なスキーム

次に、プロトタイプに必要な係数を検索する方法を特定する必要があります。最も単純な検索タイプを選択しました、目的の範囲で乱数を生成します。メソッドスキームは次のとおりです。

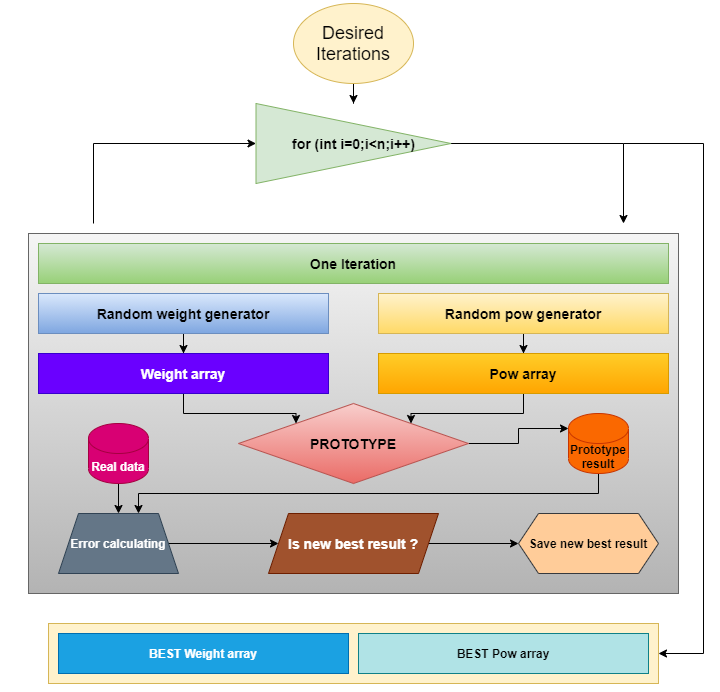
最高なことは、このスキームはあらゆる関数プロトタイプに適していることです。実際のデータと数学モデルをよりよく一致させるためには係数を選択する必要があります。記事の最後では同じ方法を適用して別のプロトタイプを処理するため、同じスキームがさらに有効になります。

詳細分析

次に、この数式の構造をさらに詳しく分析してみましょう。数式の結果は、価格が境界の1つを通過する前にとるステップの平均数です。上下のステップは等しいと見なされますが、この等しいことは実際にはランダムウォークの場合にのみ可能です。非対称的なフラクタルを完全に説明するには、与えられた値が実際に何で構成されているかをさらに特定する必要があります。論理的には、任意のタイプのステップの平均数は、上の境界を越えるときの平均ステップ数と下の境界を越えるときの平均ステップ数の両方に依存します。上の境界を超えることに関連する値を見つけましょう。

• SP[U,ud] = S[U,u] * P[U] + S[U,d] * P[U] = (S[U,u] + S[U,d]) * P[U] = S[U] * P[U]
• S[U] –一連のステップが最初に上の境界に到達した場合のステップの平均数
• S[U,u] – 一連のステップが最初に上の境界に到達した場合の上向きステップの平均数
• S[U,d] – 一連のステップが最初に上の境界に到達した場合の下向きステップの平均数
• P[U] – 価格が最初に上の境界を超える確率
• SP[U,ud] – 上の境界を越えるための平均推定ステップ数

数式は下の境界でも同様です。

• SP[D,ud] = S[D,u] * P[D] + S[D,d] * P[D] = (S[D,u] + S[D,d]) * P[D] = S[D] * P[D]
• S[D] – 一連のステップが最初に下の境界に到達した場合のステップの平均数
• S[D,u] – 一連のステップが最初に下の境界に到達した場合の上向きステップの平均数
• S[D,d] – 一連のステップが最初に下の境界に到達した場合の下向きステップの平均数
• P[D] – 価格が最初に下の境界を超える確率
• SP[D,ud] – 下の境界を越えるための平均推定ステップ数

次のことが明らかになります。

• S = SP[U,ud] + SP[D,ud]

結局のところ、最終的に取得して使用できるすべての値は、5つの基本的な値に依存します。

• S[U,u] = SP[U,u]/P[U] – 一連のステップが最初に上の境界に到達した場合の上向きステップの平均数
• S[U,d] = SP[U,d]/P[U] – 一連のステップが最初に上の境界に到達した場合の下向きステップの平均数
• S[D,u] = SP[D,u]/P[D] – 一連のステップが最初に下の境界に到達した場合の上向きステップの平均数
• S[D,d] = SP[D,d]/P[D] – 一連のステップが最初に下側の境界に到達した場合の下向きステップの平均数
• P[U] – 価格が最初に上の境界を超える確率

さまざまな入力パラメータを使用したフラクタル演算の結果に基づいて、これらの値の式を検索します。前回の記事では、フラクタル出力に次の値を選択しました。

• SP[U,u] –一連のステップが最初に上の境界に到達した場合の上向きステップの平均数
• S[U,d] – 一連のステップが最初に上の境界に到達した場合の下向きステップの平均数
• SP[D,u] – 一連のステップが最初に下の境界に到達した場合の上向きステップの平均数
• SP[D,u] – 一連のステップが最初に下の境界に到達した場合の下向きステップの平均数
• P[U] – 価格が最初に上の境界を超える確率
• P[D] – 価格が最初に下の境界を超える確率
• S = SP - 平均ステップ数

基本値で表すことができる要素の個別のグループを次に示します。

• SP[U]
• S[U,ud] = S[U,u] + S[U,d]
• S[D,ud] = S[D,u] + S[D,d]
• P[D] = 1 – P[U]
• S = SP[U,ud] + SP[D,ud]

フラクタルの数学を扱っている間に広範囲の分析を行いました。それはコンパクトな図で簡単に示すことができます。この図は、数学モデルを検索する結果のプロセスを示しています。

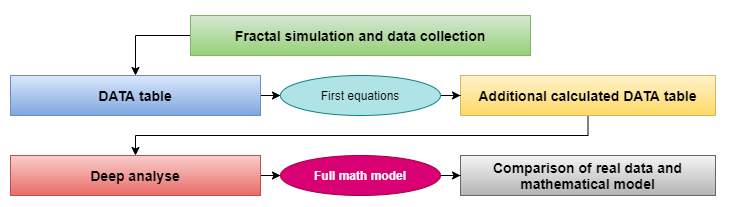
データ収集と結論

フラクタルの計算結果をより詳細に検討した結果、ユニバーサルフラクタルの概念を構築する際に当初決定された6つの値が数学的に関連していることに気付きました。まず対称的な境界のテストを実施し、これらの値の間の依存関係を特定しようとしたところ、何らかの結果が得られました。10の異なるケースについて計算を行いましたが、それで十分でした。

テストインデックス	チャネルの上半分でのステップ数(n)	チャネルの下半分でのステップ数 ( m )	最初のステップの確率   ( p )	上の境界までに可能な上向きステップの平均数 ( SP[U,u]  )	上の境界までに可能な下向きステップの平均数 ( SP[U,d]  )	下の境界までに可能な上向きステップの平均数 ( SP[D,u]  )	下の境界までに可能な下向きステップの平均数 ( SP[D,d]  )	上の境界までに可能なステップの平均数 ( SP[U,ud]  )	下の境界までに可能なステップの平均数 ( SP[D,ud]  )
1	1	1	0.5	0.5	0	0.0	0.5	0.5	0.5
2	2	2	0.5	1.5	0.5	0.5	1.5	2.0	2.0
3	3	3	0.5	3.0	1.5	3.0	1.5	4.5	4.5
4	1	2	0.5	0.888888	0.2222222	0.111111	0.777777	1.11111111	0.8888888
5	2	3	0.5	2.2	1.0	0.8	2.0	3.2	2.8
6	1	2	0.6	1.038781	0.249307	0.066481	0.487534	1.288088	0.554016
7	2	3	0.6	2.811405	1.191072	0.338217	0.906713	4.0024777	1.244931
8	2	3	1.0	2.0	0.0	0.0	0.0	2.0	0.0
9	1	3	0.5	1.25	0.5	0.25	1	1.75	1.25
10	1	4	0.5	1.6	0.8	0.4	1.2	2.4	1.6

 

以下に、フラクタルログに表示されていない計算値の表を示します。これらは、値間の依存関係を評価するために必要になります。

テストインデックス	チャネルの上半分でのステップ数(n)	チャネルの下半分でのステップ数 ( m )	上の境界を越える確率 ( P(U) )	下の境界を越える確率 ( P(D) )	上の境界を越える場合のステップの平均数 (S[U,ud]) = SP[U,ud]/P[U]	下の境界を越える場合のステップの平均数 (S[D,ud]) = SP[D,ud]/P[D]	上の境界の上向きステップの平均数 ( S[U,u]  ) = SP[U,u]/P[U]	上の境界の下向きステップの平均数 ( S[U,d]  ) = SP[U,d]/P[U]	下の境界の上向きステップの平均数 ( S[D,u]  ) = SP[D,u]/(P[D])	下の境界の下向きステップの平均数  ( S[D,d]  ) = SP[D,d]/(P[D])	平均ステップ数   ( S )
1	1	1	0.5	0.5	1.0	1.0	1.0	0.0	0.0	1.0	1
2	2	2	0.5	0.5	4.0	4.0	3.0	1	1	3	4
3	3	3	0.5	0.5	9.0	9.0	6	3	3	6	9
4	1	2	0.66666	0.3333333	1.6666666	2.6666666	1.3333333	0.33333333	0.33333333	2.33333333	2
5	2	3	0.6	0.4	5.3333333	7	3.6666666	1.66666666	2	5	6
6	1	2	0.789473	0.210526	1.631579	2.631579	1.315790	0.315789	0.315789	2.315789	1.842104
7	2	3	0.810166	0.189498	4.940318	6.569626	3.470159	1.470157	1.784805	4.784	5.2474087
8	2	3	1.0	0.0	2.0	0.0	2.0	0.0	0.0	0.0	2.0
9	1	3	0.75	0.25	2.3333333	5	1.6666666	0.6666666	1	4	3
10	1	4	0.8	0.2	3.0	8.0	2	1	2	6	4

 

この表から、4つの未知の値(他のすべての値が構成されています)すべてを計算するために必要な最初の2つの方程式を見つけることができます。式を取得するには、列S[U,u]、S[U,d]、S[D,u]、S[D,d]に注意してください。この列の数値が、列S[U,u]、S[U,d]およびS[D,u]、S[D,d]]でペアごとに同じ小数部分を持っていることは非常に興味深いことです。また、S[U,u] > S[U,d]およびS[D,d] > S[D,u]であることがわかります。これらの値をペアで減算し、m、nと比較すると、この差は、上限または下限の対応するステップ数に正確に等しいことがわかります。

• S[U,u] – S[U,d] = n
• S[D,d] – S[D,u] = m

したがって、基本的な値を決定するのに役立つ2つの非常に重要な値が得られます。2つの方程式では不十分です。しかし、さらに2つの方程式を取得できます。これにより、わずかに異なる論理に基づいて同じ値を決定できます。フラクタルを無限に長く実験すると、上向きステップと下向きステップの発生頻度の比率は、対応する確率に比例します。

これらの比率は、次のことを前提として取得できます。

1. Lim[N0 -- > +無限大] (N0[U]/N0) = p
2. Lim[N0 -- > +無限大] (N0[D]/N0) = 1-p
3. Lim[N0 -- > +無限大] (N0[U]/N) = S[UD,u]
4. Lim[N0 -- > +無限大] (N0[D]/N) = S[UD,d]
5. Lim[N0 -- > +無限大] (N0/N) = S
6. N0 –初期ステップに関連して実行された基本実験の数(複雑な実験を構成します)。
7. N –単純な実験で構成される複雑な実験の数

乗数N0 / N0 = 1を「3」と「4」に導入し、その中の分数を適切に配置すると、次のようになります。

• Lim[N0 -- > +無限大] (N0[U]/N) = Lim[N0 -- > +無限大] (N0[U]/N0 * N0/N) = Lim[N0 -- > +無限大] (N0[U]/N0)  * Lim[N0 -- > +無限大] (N0/N) =  p*S  = S[UD,u]
• Lim[N0 -- > +無限大] (N0[D]/N) = Lim[N0 -- > +無限大] (N0[D]/N0 * N0/N) = Lim[N0 -- > +無限大] (N0[D]/N0)  * Lim[N0 -- > +無限大] (N0/N) = (p-1)*S  = S[UD,d]

これらの極限のそれぞれが有限数である場合、積極限は極限の積として表すことができます。ここでの極限はこの条件に準拠しています。これがこれらの数式の導出方法です。数式は次のとおりです。

• S[UD,u] = S*p
• S[UD,d] = S*(1-p)

これらの値を基本値で表すことをお勧めします。これにより、必要なすべてを決定するためのあと2つの方程式が提供されます。

• S[U,u] * P[U] + S[D,u] * ( 1 – P[U] ) = S*p
• S[U,d] * P[U] + S[D,d] * ( 1 – P[U] ) = S*(1-p)

その結果、4つの方程式に5つの未知数があります。5番目の未知数は、完全なグループを形成する確率の1つです(境界の1つに到達する確率)。5つの未知数すべてを見つけることができるようにするには、5番目の方程式が必要です。連立方程式は、方程式の数が未知数の数と等しい場合にのみ一意の解を持つことができるためです。5番目の式は、上向きステップと下向きステップの違いであることがわかっているため、直感的に取得できます。理想的には、これは次の極限です。

• Lim[Nt[U] -- > +無限大] ((N0[U] - N0[D])/(Nt[U] - Nt[D]) = 1
• Nt[U] - 基本的な上向きステップの確率を使用して計算された基本的な上向きステップの理想的な数
• Nt[D] –基本的な下向きステップの確率を使用して計算された基本的な下向きステップの理想的な数
• N0[U] –基本的な上向きステップの実際の数
• N0[D] –基本的な下向きステップの実際の数

境界を超える確率を使用して、同様の極限を見つけることができます。

• Lim[Nb[U] -- > +無限大] ((N0[U] - N0[D])/(Nb[U] - Nb[D]) = 1
• Nb[U] – 上の境界を越える確率を使用して計算された基本的な上向きステップの理想的な数
• Nb[D] –下の境界を越える確率を使用して計算された基本的な下向きステップのの理想的な数
• N0[U] –基本的な上向きステップの実際の数
• N0[D] –基本的な下向きステップの実際の数

これらの2つの極限を使用すると、和、差、商など、より複雑な制限を作成できます。次の式を減らし、limit N0[U] - N0[D]を完全に排除する商を選択します。これらの2つの極限を徐算し、方程式を変換すると、次のようになります。

• P[U] * n – (1 - P[U]) * m = p * S - (1 - p) *S

これは5番目の方程式であり、そこから境界を越える確率を見つけることができます。その結果、5つの連立方程式が得られます。次のようになります。

1. S[U,u] – S[U,d] = n
2. S[D,d] – S[D,u] = m
3. S[U,u] * P[U] + S[D,u] * ( 1 – P[U] ) = S*p
4. S[U,d] * P[U] + S[D,d] * ( 1 – P[U] ) = S*(1-p)
5. P[U] * n – (1 - P[U]) * m = p * S - (1 - p) *S = 2*p*S - S

4つの未知数を持つ最初の連立方程式でも、同じ結果の方程式が得られます。この連立方程式は、古典的な、変数を連続して除外する方法で解くことができます。

• -->  S[U,u] = n + S[U,d] –  S[U,u]を除外
• -->  S[D,d] = m + S[D,u] –  S[D,d] を除外
• (n + S[U,d]) * P[U] + S[D,u] * ( 1 – P[U] ) = S*p – すべてを式3に代入
• S[U,d] * P[U] + (m + S[D,u]) * ( 1 – P[U] ) = S*(1-p) – すべてを式4に代入

これらの変換の後、式4から式3を減算するので済みます。その後、直感的に得たのと同じ式が得られます。残念ながら、この連立方程式では、残りの4つの値を見つけることができません。うまくいくと思っていたのですが、駄目でした。その理由を理解するために、フラクタルデータの表を分析する必要がありました。これにより、これら4つの量のいずれかの式を作成することができました。この追加の式を使用すると、残りのすべての値を見つけることができます。そのため、この連立方程式は便利であることがわかりました。

数学モデル全体を計算するためのアルゴリズム

まず、S[U,u]がわかるため、他のすべてを見つけるために、逆方程式とその使用順序を定義しましょう。この値を使用するのは、その計算に関連する式を見つけることができたからです。この値を使用すると、最初の式を使用してS[U,d]をすぐに見つけることができます。

• S[U,d] = S[U,u] – n

次に、これら2つの値を式3と4に代入し、残りの値S[D,u]とS[D,d]を見つけます。S[D,u]は、3番目の式からすぐに計算できます。

• S[D,u] = ( S*p – S[U,u] * P[U] ) / ( 1 – P[U] )

ここで、最後の未知数の式を見つけるだけで済みます。得られたS[U,d]の式を4番目の式に代入します。

• S[D,d] = ( S*(1-p) - S[U,d] * P[U]) / ( 1 – P[U] ) =  ( S*(1-p) - ( S[U,u] – n ) * P[U] ) / ( 1 – P[U] )

欠落している要素は、5番目の方程式を解くことで簡単に取得できるP[U]値だけです。これをおこないます。

• P[U] * n – (1 - P[U]) * m = 2*p*S – S
• --> P[U] * (n + m)  =   2 * p * S – S + m
• --> P[U] = ( 2 * p * S – S + m ) / (n + m)

ここでの既知数は次のとおりです。

• n –上の境界までのステップ数
• m –下の境界までのステップ数
• p –最初の上向きステップの確率
• S[U,u] – 上の境界を越えた場合の上向きステップの平均数
• P[U] –上の境界を越える確率

値4は次のように計算できます。

• S[U,u] = Ss[m,n,p] = (n ^ Pn[p] ) * ( m ^ Pm[p] )
• Pn[p] = 1 , if p >= 0.5
• Pn[p] = ( (1 – p)/0.5 ) ^ K
• Pm[p] = 1 , if p <= 0.5
• Pm[p] = ( p/0.5 ) ^ K
• Kは指数で関数の平坦性を既成します

平坦度係数は、少し後で別のプログラムで計算します。次に、最も重要な値を決定する必要があります。表から値S[U,u]を分析することにより、対称境界の2つの値の式を導き出すことができました。

1. S[U,u] = Summ[ i = 0, n] ( i ) (n == mの場合)
2. S[U,d] = Summ[ i = 0, n] ( i-1 ) (n == mの場合)

問題は、これらの式がp = 0.5および対称境界に対してのみ機能することです。数式の概念は、非対称の境界をカバーするように拡張する必要があります。その後、さまざまなp値に対して一般化できます。一般化に進む前に、表のテスト結果は「m > n」にのみ適用されることに注意してください。「m < n」の場合、式は「S[D,d]、S[D,u]」に対して機能します。この場合、他のすべての未知数を見つけるためにアルゴリズムのミラーアナログを作成する必要があります。

同様に、S[D,d]の場合に使用する逆方程式とその順序を定義しましょう。ここでも、2番目の式を使用して値S[D,u]を見つけます。

• S[D,u] = S[D,d] – m

その後、S[U,u]と S[U,d]を見つけるために、両方の値を式3と4に代入できます。S[D,u]は、4番目の式からすぐに計算できます。

• S[U,d] = ( S*(1-p) - S[D,d] * ( 1 – P[U] ) ) / P[U]

ここで、最後の未知数の式を見つけるだけで済みます。得られたS[U,d]の式を、次の3番目の式に代入します。

• S[U,u] = ( S*p – ( S[D,d] – m ) * ( 1 – P[U] ) ) / P[U]

その結果、「n != m」の場合の式S[U,u]、S[D,d]を一般化するために必要なすべてのデータを取得しました。次のデータは、表データの分析から取得されました。

1. m > n, p = 0,5
2. S[U,u] = Summ[ i = 0 … n] ( i ) + (m-1)/3

反対の場合:

1. m < n, p = 0,5
2. S[D,d] = Summ[ i = 0 … m] ( i ) + (n-1)/3

対称的な境界を持つ標準的なケースでは、計算が簡単になります。

1. m = n, p = 0,5
2. S[U,u] = Summ[ i = 0 … n] ( i )
3. S[D,d] = Summ[ i = 0 … m] ( i )

最後の方程式を取得するためのプロトタイプ

次に、考えられるすべてのp値に対してS[U,u]、S[D,d]を記述する変更された関数のプロトタイプを定義しましょう。基本的な実用的なプロトタイプを作成するには、p軸に3点があることと全体的な構造に関するいくつかの仮定が必要です。次の2種類の汎用関数を検討するだけで十分だと思います。

1. Sp[U,u] = S[U,u] ^ K(p)
2. Sp[D,d] = S[D,d] ^ K(q)
3. q = 1-p

最初のタイプは、実際に機能するプロトタイプ、または構造が異なり、別の論理が必要であることを示す特定のマーカーにすることができます。べき関数はすべてのデータをまとめることができることが判明しました。もちろん、もっと複雑でおそらくもっと正確なプロトタイプもあり得ますが、ここでの解決法で十分だと思います。最も重要なことは、論理を理解することです。ただし、モデルを微調整する場合は、記事に示されているデータに基づいて微調整することができます。テストプログラムを作成しました。

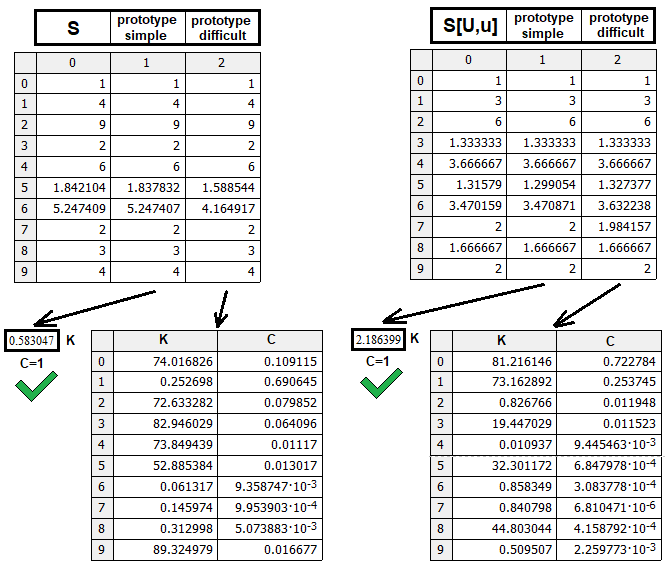
プログラムでS(n,m,p)とS[U,u](n,m,p)の両方のプロトタイプを確認します。関数S[D,d](n,m,p)はS[U,u](n,m,p)にミラーリングされるため、S[D,d](n,m,p) = S[U,u](m,n,p-1)です。この図は、見つかったプロトタイプの効率の比較を示しています。各プロトタイプは、数式内の重みと電力係数の同じ数のランダムな組み合わせでテストされました。単純なプロトタイプは、同じ検索サイクル数でより美しい結果を示します。必要に応じて、追加の計算を実行して、より複雑なプロトタイプで何ができるかを確認することができます。

確認した後、入れ子関数K(p)、K(q)の内部構造を定義する必要があります。その内部構造は、点p = 0、p = 0.5、p = 1、q = 0、q = 0.5、q = 1で必須の一致を提供する必要があります。これらの点での関数値がわかっているため、必要なプロトタイプを簡単に選択できます。

1. p = 0.5 ; Sp[U,u] = S[U,u] --> K(0.5) = 1 ,
2. p = 1.0 ; Sp[U,u] = n = S[U,u]^(Log[S[U,u]-->n]) --> K(1.0) = Log[S[U,u]-->n]
3. p = 0.0 ; Sp[U,u] = 0 = S[U,u]^(-infinity) --> K(0.0) = -infinity
4. q = 0.5 ; Sp[D,d] = S[D,d] --> K(0.5) = 1 ,
5. q = 1.0 ; Sp[D,d]  = n = S[D,d]^(Log[S[U,u]-->m]) --> K(1.0) = Log[S[D,d]-->m]
6. q = 0.0 ; Sp[D,d] = 0 = S[D,d]^(-infinity) --> K(0.0) = -infinity

1番目と4番目の式は、累乗がランダムウォークポイントで1に等しくなければならないことを示しています。2番目と5番目の式は、値を累乗すると、上記の結果表に示されているように、「n」または「m」のいずれかが得られるような累乗である必要があることを示しています。3番目と6番目の式は、0を提供するために、累乗がマイナス無限大に限りなく近づくことを示しています。この事実はさらに、0による除算は無限大などの値につながるため、値pとqがプロトタイプの分母にある必要があることを意味します。関数のべき乗則のプロトタイプを作成した経験はすでにあります。それを基礎として使用し、修正します。問題を詳細に分析すると、このプロトタイプにたどり着きました。

• K(p) = 1 + D * Summ(N) (Kn[0] *  | (( p – 0.5 )/(0.5*p)) | ^ A[0]  + Kn[1] * | (( p – 0.5 )/(0.5*p)) | ^ A[1] + …. + Kn[N] * | (( p – 0.5 )/(0.5*p)) | ^ A[N])
• Kn[0] + Kn[1] + …. Kn[N] = Log[S[U,u]-->n] – 1
• D = (( p – 0.5 )/(0.5*p)) / | (( p – 0.5 )/(0.5*p)) |
• K(q) = 1 + C * Summ(N) (Km[0] * (( q – 0.5 )/(0.5*q)) ^ B[0]  + Km[1] * (( q – 0.5 )/(0.5*q)) ^ B[1] + …. + Km[N] * (( q – 0.5 )/(0.5*q)) ^ B[N])
• Km[0] + Km[1] + …. Km[N] = Log[S[D,d]-->m] – 1
• C = (( q – 0.5 )/(0.5*q)) / | (( q – 0.5 )/(0.5*q)) |
• Kn、Km – 適切な項の重み
• A、B - 項の感度

関数は複雑に見えますが、単純な論理に基づいています。p=0.5、q=0.5の場合、総和記号の下のすべてがゼロになり、1つだけが残るため、条件「1」、「4」が提供されます。p=1、q=1の場合、和の内の関連する分数は累乗され、1になります。|(( p – 0.5 )/(0.5*p)) |。これらの項は、累乗するときに関数の複素数値を除外するために、モジュラス記号で記述されています。代わりに、関連する記号が追加の要素として提供されます。累乗はこれらの項に影響を与えなくなり、合計はLog[S[U,u]-->n] – 1, Log[S[D,D]-->m] - 1になります。この数値を1に加算すると、関数に必要な値Log[S[U,u]-->n], Log[S[D,d]-->m]が得られます。

補間多項式は、同様の論理に従って構築されます。その一例は、よく知られているラグランジュ多項式です。ここでの多項式は、それを適用できる特定のタスク用に設計されています。その利点は、タスクへの完全な適応性です。この曲線のセットから目的の関数を見つけるには、2つの数値配列を見つけるだけで済みます。

数学的モデルの実装とテスト

見つかった式を使用すると、フラクタルを計算するために必要な機能を簡単に実装できます。main関数が返すすべてのデータのコンテナとなる構造体が1つだけ必要になります。その他の機能は補助的なものになります。最後の関数だけが必要です。

struct MathModel1//structure for the first mathematical model
   {
   double S;//the average number of any steps
   double pU;//the probability that the price will first reach the upper border
   double pD;//the probability that the price will first reach the lower border
   double SUu;//the average number of steps up if the price first reaches the upper border
   double SUd;//the average number of steps down if the price first reaches the upper border
   double SDu;//the average number of steps up if the price first reaches the lower border
   double SDd;//the average number of steps down if the price first reaches the lower border
   
   double SPUu;//the average probable number of steps up if the price first reaches the upper border
   double SPUd;//the average probable number of steps down if the price first reaches the upper border
   double SPDu;//the average probable number of steps up if the price first reaches the lower border
   double SPDd;//the average probable number of steps down if the price first reaches the lower border
   
   double SPUud;//the average probable number of steps in any direction if the price first reaches the upper border
   double SPDud;//the average probable number of steps in any direction if the price first reaches the lower border
   
   double SUDu;//the average number of steps up when reaching any of the borders
   double SUDd;//the average number of steps down when reaching any of the borders
   };

double Ss(int n, int m,double p, double K)//prototype of the function of the average number of steps in any direction when reaching any border
   {
   if (p>=0.5) return n*MathPow(m,MathPow((1-p)/0.5,K));
   else return MathPow(n,MathPow(p/0.5,K))*m;
   }

double Log(double a, double b)//logarithm function for any base
   {
   if (MathLog(a) != 0) return MathLog(b)/MathLog(a);
   else return 0.0;
   }

double SUu(int n,int m)//average number of steps up to the upper border if p=0.5
   {
   double rez=0.0;
   if (m>n)
      { 
      for (int i=0;i<=n;i++) rez+=double(i);
      rez+=(m-1)/3.0;
      }
   if (m==n) for (int i=0;i<=n;i++) rez+=double(i);
   return rez;
   }
   
double SDd(int n,int m)//average number of steps down to the lower border if p=0.5
   {
   double rez=0.0;
   if (n>m)
      { 
      for (int i=0;i<=m;i++) rez+=double(i);
      rez+=(n-1)/3.0;
      }   
   if (m==n) for (int i=0;i<=m;i++) rez+=double(i);
   return rez;
   }   

double KpnEasy(int n,int m, double p,double A)//power prototype for steps up m>=n
   {
   double D;
   if ( p-0.5 != 0 ) D=(p-0.5)/MathAbs(p-0.5);
   else D=1.0;
   return 1.0 + D*(Log(SUu(n,m),n) - 1)*MathPow(((p-0.5)/(0.5*p)),A);
   }

double KpmEasy(int n,int m,double p,double A)//power prototype for steps down m<n
   {
   double D;
   if ( 0.5-p != 0 ) D=(0.5-p)/MathAbs(0.5-p);
   else D=1.0;
   return 1.0 + D*(Log(SDd(n,m),m) - 1)*MathPow(((0.5-p)/(0.5*(1.0-p))),A);
   }
   
double SUuS(int n,int m,double p, double A)//full prototype for average steps up m>=n
   {
   return MathPow(SUu(n,m),KpnEasy(n,m,p,A));
   }
   
double SDdS(int n,int m,double p, double A)//full prototype for average steps down  n>m
   {
   return MathPow(SDd(n,m),KpmEasy(n,m,p,A));
   }      
   
MathModel1 CalculateMathModel(int n, int m, double p,double K=0.582897,double A=2.189246)//calculating the entire mathematical model
   {
   MathModel1 Mt;
   if ( m >= n )
      {
      Mt.S=Ss(n,m,p,K);
      Mt.pU=(2*p*Mt.S-Mt.S+m)/(n+m);
      Mt.pD=1.0-Mt.pU;
      Mt.SUu=SUuS(n,m,p,A);
      Mt.SUd=Mt.SUu-n;
      if (1.0-Mt.pU != 0.0) Mt.SDu=(Mt.S*p-Mt.SUu*Mt.pU)/(1.0-Mt.pU);
      else Mt.SDu=0.0;
      if (1.0-Mt.pU != 0.0) Mt.SDd=(Mt.S*(1.0-p)-Mt.SUd*Mt.pU)/(1.0-Mt.pU);
      else Mt.SDd=0.0;
      }
   else
      {
      Mt.S=Ss(n,m,p,K);
      Mt.pU=(2*p*Mt.S-Mt.S+m)/(n+m);
      Mt.pD=1.0-Mt.pU;
      Mt.SDd=SDdS(n,m,p,A);
      Mt.SDu=Mt.SDd-m;
      if (Mt.pU != 0.0) Mt.SUd=(Mt.S*(1.0-p)-Mt.SDd*(1.0-Mt.pU))/Mt.pU;
      else Mt.SUd=0.0;
      if (Mt.pU != 0.0) Mt.SUu=(Mt.S*p-Mt.SDu*(1.0-Mt.pU))/Mt.pU;
      else Mt.SUu=0.0;      
      }
   
   Mt.SPUu=Mt.SUu*Mt.pU;
   Mt.SPUd=Mt.SUd*Mt.pU;
   Mt.SPDu=Mt.SDu*Mt.pD;
   Mt.SPDd=Mt.SDd*Mt.pD;
   
   Mt.SPUud=Mt.SPUu+Mt.SPUd;
   Mt.SPDud=Mt.SPDu+Mt.SPDd;
   
   Mt.SUDu=Mt.SPUu+Mt.SPDu;
   Mt.SUDd=Mt.SPUd+Mt.SPDd;
   
   return Mt;
   }

数学モデルを確認するために、このコードの類似物をMathCad15に実装しました。モデルが正しく構成されていれば、表からの結果は、数学モデルによって返される結果と一致するはずです。プログラムは記事に添付されているので、ご自身で確認してください。記事内でスペースを取りすぎるため直接コードを追加しないことにしましたが、間違いなく結果がわかるはずです。行列を比較して、数学モデルが機能することを確認しましょう。

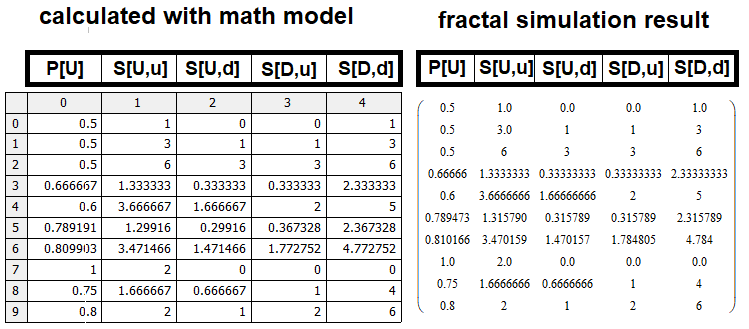
もちろん、いくつかの不正確さがありますが、それは見つかったプロトタイプの値S、S[U,u]、S[D,d]の効率によるものです。わずかな差があるその他の要因は、シミュレーションの不正確さに関連している可能性があります。これは、計算能力の限界によってシミュレーションの深さを制限する必要があるため、シミュレートされたn、mの値が大きいほど大きくなります。

終わりに

数学をすべての最初から考え出す必要があったため、この数学モデルの開発に多くの時間を費やしました。何にしても、結果には満足しています。次の記事では、より普遍的な数学的モデルの開発を試みます。これらのモデルを組み合わせると、主な特性の観点から任意の取引構成を計算できるようになります。さらに、数学モデルは、価格設定プロセスを説明するだけでなく、取引シグナルを説明したり、複雑なストラテジーを単純化したりするためにも使用できます。これには少し時間がかかります。 

参照文献

• 取引のための組合せ論と確率論(第I部):基本

• 取引のための組合せ論と確率論(第II部): ユニバーサルフラクタル