取引のための組合せ論と確率論(第II部): ユニバーサルフラクタル

MetaTrader 5 — トレーディング | 5 10月 2021, 15:53

483

Evgeniy Ilin

内容

はじめに

前回の記事では、取引タスクにフラクタル関数を使用する特定の機能を理解するのに役立つよう、確率論の基本について説明しました。このトピックの続きとして、必要なすべての価格設定プロセスを説明できる、いくつかの「自給自足」のフラクタル関数を示します。それらを一般化して単純化するとともに、明確な定量的推定と明確な回答が不足しているさまざまな質問に答えるための式を作成します。

取引でフラクタルを使用する可能性の評価

前の記事の結果を要約してよりコンパクトで普遍的な形式で提示し、トピックを続けましょう。前の記事でフラクタルを作成した例を覚えていらっしゃいますか。このようなフラクタルはほとんど実用的ではありませんが、この場合、主に感心があるのは決定した構造構築ルールです。結局のところ、これらのルールは3種類のフラクタルに適用できます。

対称的な境界を持つフラクタル
非対称の境界を持つフラクタル
上または下の境界を持つフラクタル

このようなフラクタルは、次のプロセスを説明するために適用できます。

預金制限を考慮に入れて、さまざまなシナリオの確率を評価する機能を備えた取引の模倣の加速(下の境界線は、それ以上の取引が不可能になる預金レベルを象徴する可能性があるため)
フラクタル内の平均ステップ数の推定(たとえば、目的の利益または損失を得るまでに平均していくつの注文があるかを推定)
各ステップの合計平均値の推定(たとえば、より小さなポジション(ポイントまたは価格差のストップレベルがより小さなポジション)の統計に基づいた平均ポジション保持時間を計算)
単一の境界フラクタルに基づくオプションの収益性の評価
その他の機能

ユニバーサルフラクタルを構築するための理論的根拠

前回の記事で導出した構築ルールを使用して、フラクタルがどのように構築されるかを理解するために補足してみましょう。さらに、数式に小さな間違いがあり、境界線を下向きまたは上向きに非対称化することができませんでした。導出された式は正しいことが判明したため、どのフラクタルでも機能します。実際、これはまさにあらゆるフラクタルを実装するための関数です。考えられるすべてのフラクタルは、一般的なフラクタルの特殊なケースです。上で定義した3種類のフラクタルを使用すると、これら3つの特殊なケースを実装するための一般的なフラクタルの条件は次のようになります。

m = n & [ m > s & n > s ]
( m > n || n > m ) & [ m > s & n > s ]
( m > S && n <= S ) || ( n > S && m <= S )

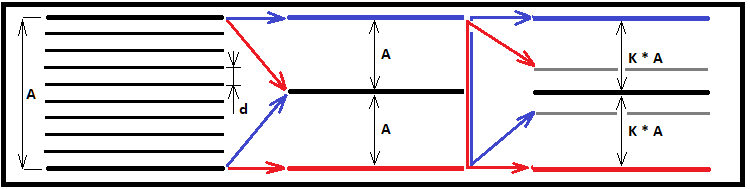
これらの3種類のフラクタルは図式的には次のようになります。

3つのフラクタル

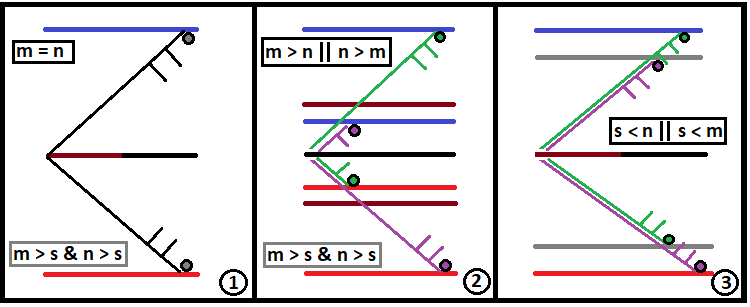
理想的には、「S」は無限大になります。次の変数は、私の以前の記事では説明されていませんでした。ここでは、一般式を使用して特殊なケースを取得する方法の全体像を把握するために、関連する説明を提示します。フラクタルは、原子爆弾のように連鎖反応の原理で機能する関数です。集合連鎖反応が深すぎると、コンピュータがそのような大規模な計算に対処できない可能性があります。ケースが特に重大でない場合は、数分、数時間、さらには数日という非常に長い時間カウントされます。フラクタルで連鎖反応を正しく開始するには、2つの基本的な値を見つける必要があります。

Half - チャネル幅の半分
Middle - 中央線に対応する「U」値

Halfの値は、前の記事で決定した3つのケースすべてについて簡単に計算できます。これは、mとnの算術平均です。

Half = ( n + m ) / 2

2番目の値を実装するには、3つのロジックバリアントを使用する必要がありますが、1番目と2番目のバリアントを1つに組み合わせることができるので、バリアントは2つです。

n >= m
n < m

次に、「U」軸が上を向き、n値がチャネルの上部でmが下部であるとすると、mとnの可能性がある2つのケースに対して2つの比率が得られます。

Middle = Half - m
Middle = - ( Half - n )

前の記事で説明した内部分岐ロジックはこれらの値なしでは実装できないため、これらの値は内部使用のためにフラクタル関数に渡されます。関数プロトタイプは次のとおりです。

double Fractal(double Half, double Middle, int m, int n, int s,double p,int S, int U, double P)

したがって、正しいフラクタル開始のために3つの必須値を渡す必要があります。

Half - チャネル幅の半分
Middle - 中央線に対応する「U」値
m - 下の境界までのステップ数
n - 上の境界までのステップ数
s - 単一チェーンの任意の方向の最大許容ステップ数

他の値は大文字で示され、これらの値が動的であって異なるフラクタルレベルについて異なることを示します。それらの定義は次のとおりです。

S - 現在の確率の連鎖に蓄積されたステップ数(次のフラクタルレベルに渡される)
U - チェーンの始点と終点の間の現在の距離(次のフラクタルレベルに渡される)
P - ベルヌーイスキームに基づくチェーン全体の確率の累積積(次のフラクタルレベルに渡される)

したがって、フラクタルを正しく開始するには、次の値を関数に入力する必要があります。

S = 0(始まりなのでまだ手順がない)
U = 0(同上)
P = 1(これはゼロチェーンであり、次のすべてのステップで完全なグループを構成する必要があるため)

価格設定や取引をシミュレートするフラクタルの一般的なルールの開発を完了するために、前の記事で取得したルールを簡単に書き直してみましょう。これらのルールはフラクタル内で使用され、同じステップのいくつかの式に基づいています。

f = u + d — 将来の組み合わせツリーのステップ数(距離はフラクタル範囲の最も近い境界までの距離によって決定)
s = u - d — 下降セグメントと上昇セグメントで表される最終ステップの数

「u」をループすることを決定しました。さらに、「s」値を新しい「U」として使用します。これは、残りのステップ数でサポートされている場合、次のフラクタルレベルに渡されます。この目的のために、「d」を含まない「u」の式を定義する必要があるので、最初の式を「d」について表現し、それを2番目の式に代入します。

s = 2*u - f

この値は、現在の値がゼロに等しい場合にさらに渡すための「U」の新しい値として使用することもできます。したがって、この「s」を「U」に追加して、さらに渡す必要のある値を取得します。

NewU = s + U - 次のフラクタルレベルに渡す新しい「U」

前の記事ですでに定義したように、この式は、数値「f」の3つの可能な値に基づいて、3つの可能な値を取ります。このアイデアを説明するために、前の記事の図を改訂しました。

「f」の3つのシナリオ

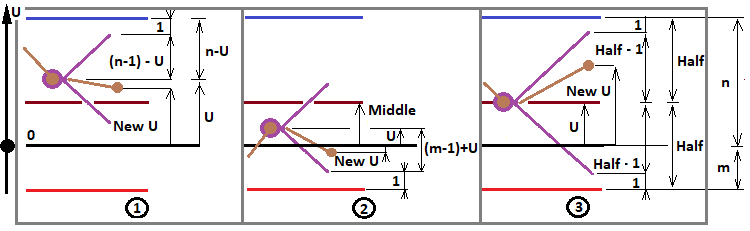
ここではほとんどの問題を解決するのに役立つ可能性のあるすべての可能なフラクタル構成を決定しているため、この図はここでは非常に適切です。この図に従って、「f」の3つのケースを定義します。

f = ( n - 1 ) - U
f = ( m - 1 ) + U
f = Half - 1

これらの3つのケースは、次の条件が満たされた場合に発生します。

U > Middle
U < Middle
U = Middle

次に、次のフラクタルレベルに渡される最後の2つの値を記述し、フラクタルで数値がどのように収集されるかを検討する必要があります。最後の2つの値は、次のように計算されます。

NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i) — 次のフラクタルレベルに渡される新しいチェーン確率「P」
NewS = S + f = S + (floor(Mid) - 1) — 次のフラクタルレベルに渡される新しい「S」

共通変数への数値の収集を開始する前に、同様のブロックで数値を収集する必要があることに注意してください。ただし、この場合は1つの手順しか実行しないため、ベルヌーイスキームは必要ありません。ステートメントの順序は重要ではありません。それらは同じブロックにある必要があります。番号は、「1」と「2」の場合にのみ収集できますが、いくつかの説明があります。

U = n - 1
U = - ( m - 1 )

最初のケースでは、ステップが1つしかないため、前の3つの値の計算が簡単です。

NewU = U - 1
NewP = P * p
NewS = S + 1

2番目のケースでは、わずかな違いがあります。

NewU = U + 1
NewP = P * ( 1 - p )
NewS = S + 1

すべてのフラクタルの一般化に基づいて、これらのフラクタルはそれぞれ2種類に分けられます。

チャネルの上の境界を越える確率の合計を計算するフラクタル
チャネルの下の境界を越える確率の合計を計算するフラクタル

それぞれの種類は、元のフラクタルと組み合わせて、もう1種類のフラクタルに対応します。

上の境界を越えるための平均ステップ数を計算するフラクタル
下の境界を越えるための平均ステップ数を計算するフラクタル

これらの4種類では、合計数の形式が異なります。確率を収集する場合、追加できるのは「P*p」と「P*(1-p)」のみです。他の2つのフラクタルについては、次のフラクタルレベルに渡すために追加の変数が必要です。これらのフラクタルでは、方向が反対の同じサイズのステップを使用するため、それらの確率は「p」または「1-p」のいずれかになります。ただし、「p」が0.5に等しくない場合、この事実は、これらが2つの異なるイベントであり、異なる特性を持つ可能性があることを意味します。特性とは、特定のイベントに対応するいくつかの確率変数のセットを意味します。そのような値の1つはポジションの有効期間です。このような値は必要な数だけ存在する可能性があり、必要に応じて時間と見なすことができます。この部分は、いくつかの簡単な手順で簡略化できます。合計する数値は次の形式になります。

P * p * NewS
P * ( 1 - p ) * NewS

ご覧のとおり、確率は、この完了した一連のステップのステップ数で乗算されます。ただし、この式は、上向きのステップと下向きのステップの可能性が同じである場合にのみ適用されます。別のケースでは、2つの異なる構造体を使用して上下のステップを記述したり、両方の数値を格納する構造体を提供したりする必要があります。2番目のケースでは、フラクタル関数は数値ではなくデータコンテナを返します。コンテナを拡張する必要はありません。さらに、必要なすべてのパラメータを格納できるコンテナを提供しているため、同様のコードで複数の関数を記述する必要はありません。代わりに、すべての関数を1つにまとめま、必要なすべてのパラメータを記述します。フラクタルの種類とそれによって解決されるタスクは、関数の入力パラメータに直接依存します。概念を拡張するには、最初の「S」とそれに相当する「NewS」を次の値に置き換える必要があります。

SU - 選択した確率連鎖からの最後のステップ
SD - 選択した確率連鎖からの最後のステップ
NewSUおよびNewSD - 次のフラクタルレベルに渡される値
SU + SD = S

これらの値は、「S」の定義と同様に定義する必要があります。U > Middleの場合

NewSU = SU
NewSD = SD + 1

U < Middleの場合

NewSU = SU + 1
NewSD = SD

フラクタルの最終アップグレードには、さらに6つの値が必要です。

UpperMidSDown - 上の境界に到達するまでに発生する可能性のある下向きステップ数の合計の平均
UpperMidSUp　- 上の境界に到達するまでに発生する可能性のある上向きステップ数の合計の平均
UpperSummProbability - 上の境界を越える確率
LowerMidSDown - 下の境界に到達するまでに発生する可能性のある下向きステップ数の合計の平均
LowerMidSUp - 下の境界に到達するまでに発生する可能性のある上向きステップ数の合計の平均
LowerSummProbability -下の境界を越える確率

値「1」、「2」、「4」、「5」は、対応するステップ数とそれらの確率の積の合計を示します。これらの値はそのままでは意味がありませんが、後で説明する有用な値の式のコンポーネントです。値「3」と「6」は、完全なグループを形成する2つの境界を越えるという仮説の確率です。これらの値を使用して、他の多くのものを判別できます。

ユニバーサルフラクタルを実装するためのコードの記述

フラクタルを正しく起動するには、フラクタルを起動する前にすべての準備操作を実行し、その後、事前定義されたルールに基づいてフラクタルを正しく起動する関数が必要です。このアルゴリズムのMQL5スタイルの実装を準備しました。

Container StartFractal(int m, int n, int s,double p)//preparing all variables and starting the fractal
   {
   int Minimum;
   if ( m <= n ) Minimum=m;
   else Minimum=n;
   double Middle;
   if ( n >= m ) Middle = (m+n)/2.0 - Minimum;
   else Middle = -((m+n)/2.0 - Minimum);   
   double Half = (m+n)/2.0;
   return Fractal(Half,Middle,m,n,s,p,0,0,0,1.0);
   }

フラクタル計算の後、関数は必要なすべてのデータを含むコンテナを返します。

struct Container//a container for collecting all the necessary data about the fractal
   {
   //values to be summed, for the upper bound
   double UpperMidSUp;//the sum of probabilities multiplied by the number of steps up of a specific chain (to cross the upper bound)
   double UpperMidSDown;//the sum of probabilities multiplied by the number of steps down of a specific chain (to cross the upper bound
   double UpperSummProbability;//the sum of the probabilities (to cross the upper border)
   //values to be summed, for the lower border
   double LowerMidSUp;//the sum of probabilities multiplied by the number of steps up of a specific chain (to cross the lower border)
   double LowerMidSDown;//the sum of probabilities multiplied by the number of steps down of a specific chain (to cross the lower border)
   double LowerSummProbability;//the sum of the probabilities (to cross the lower border)
   
   Container()//default constructor
      {
      UpperMidSUp=0.0;
      UpperMidSDown=0.0;
      UpperSummProbability=0.0;     
      LowerMidSUp=0.0;
      LowerMidSDown=0.0;
      LowerSummProbability=0.0;
      }
   
   //
   void Summ(Container &c0,const Container &c1) const//full sum for operator overloading
      {
      c0.UpperMidSUp=c0.UpperMidSUp+c1.UpperMidSUp;
      c0.UpperMidSDown=c0.UpperMidSDown+c1.UpperMidSDown;
      c0.UpperSummProbability=c0.UpperSummProbability+c1.UpperSummProbability;      
      c0.LowerMidSUp=c0.LowerMidSUp+c1.LowerMidSUp;
      c0.LowerMidSDown=c0.LowerMidSDown+c1.LowerMidSDown;
      c0.LowerSummProbability=c0.LowerSummProbability+c1.LowerSummProbability;
      }            
   void operator+=(Container &c) { Summ(this,c); }//operator += overload
   };

2つの同一の構造体を組み合わせるために、このコンテナには「+=」演算子のオーバーロードが含まれています。この部分は主な機能に使用されます。フラクタル関数は次のとおりです。

Container Fractal(double Half, double Middle, int m, int n, int s,double p,int SU,int SD, int U, double P)//Fractal
   {
   Container C;
   ///to pass to the next fractal level
   int NewU;
   int NewSU;
   int NewSD;
   double NewP;
   ///
   
   if ( U > Middle && SU + SD < s )//case 1
      {
      if ( (n-1) - U > 0 )
         {
         for ( int u=0 ; u <= (n-1) - U; u++ )
            {
            NewU = -(n-1) + 2*u + 2*U;
            NewP = P * (Factorial((n-1) - U)/(Factorial(u)*Factorial((n-1) - U - u))) * pow(p,u)*pow(1.0-p,(n-1) - U - u);
            NewSU = SU + u;
            NewSD = SD + ((n-1) - U - u);
            C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
            }         
         }
      if ( (n-1) - U == 0 )
         {
         NewU = U - 1;
         NewP = P * (1.0 - p);
         NewSU = SU;
         NewSD = SD + 1;
         Container ct;

         ct.UpperMidSDown=P*p*SD;
         ct.UpperMidSUp=P*p*(SU+1);
         ct.UpperSummProbability=P*p;
         
         C+=ct;
         C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
         }         
      }   
   
   if ( U < Middle && SU + SD < s )//case 2
      {
      if ( (m-1) + U > 0 )
         {
         for ( int u=0 ; u <= (m-1) + U; u++ )
            {
            NewU = -(m-1) + 2*u;
            NewP = P * (Factorial((m-1) + U)/(Factorial(u)*Factorial((m-1) + U - u))) * pow(p,u)*pow(1.0-p,(m-1) + U - u);
            NewSU = SU + u;
            NewSD = SD + ((m-1) + U - u);
            C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
            }         
         }
      if ( (m-1) + U == 0 )
         {
         NewU = U + 1;
         NewP = P * p;
         NewSU = SU + 1;
         NewSD = SD;  
         Container ct;

         ct.LowerMidSDown=P*(1.0 - p)*(SD+1);
         ct.LowerMidSUp=P*(1.0 - p)*SU;
         ct.LowerSummProbability=P*(1.0 - p);
         
         C+=ct;
         C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
         }         
      }
  
   if ( U == Middle && SU + SD < s )//case 3
      {
      if ( int(MathFloor(Half))-1 > 0 )
         {
         for ( int u=0 ; u <= int(MathFloor(Half))-1; u++ )
            {
            NewU = -(int(MathFloor(Half))-1) + 2*u + U;
            NewP = P * (Factorial(int(MathFloor(Half))-1)/(Factorial(u)*Factorial(int(MathFloor(Half))-1 - u))) * pow(p,u)*pow(1.0-p,int(MathFloor(Half))-1 - u);
            NewSU = SU + u;
            NewSD = SD + (int(MathFloor(Half))-1 - u);
            C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
            }         
         }
      }
   
   return C;
   }

コードはMetaTrader 5で確認されており、かなりうまく機能します。このロジックは、必要に応じてさらに拡張できますが、高度な可能性はまだたくさんあります。ただし、実装された機能はここでの目的には十分であるため、今のところHA関数入力パラメータのリストを短くすることにしました。コードを注意深く調べると、上記の数学的原理の概要に完全に準拠していることがわかります。このコードは短いですが驚異的に機能します。コードにはできるだけ多くの論理と数学を含める必要があると思います。これが私たちが最終的に必要とするものです。コードは美しくても本来の目的に使用できなければ役に立ちません。私たちの場合、意図された目的は取引への適用性です。確認としてのログは次のとおりです。

すべてのコンテナデータを含むログ

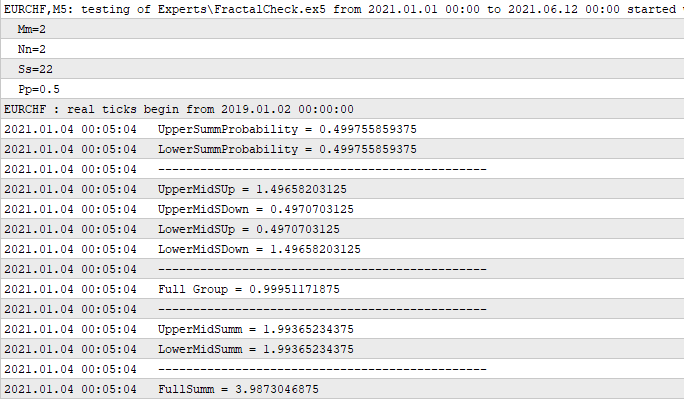
この場合、最初に受け取ったティックでフラクタル全体を計算する単純なエクスパートアドバイザーを作成しました。この計算は1回行われ、それ以上の再計算は必要ありません。最初の6つの数字はコンテナの一部であり、残りはそれらから派生しています。ここでは、最も重要な派生物のみを示します。これらの6つの変数によって、必要になる可能性のある他のすべての変数を受け取ることができることが分かると思います。たとえば、「フルグループ」をご覧ください。前の計算による境界の1つの交差の2つの重複しない仮説の確率の合計は1に等しくなければならないため、この名前が付けられています。それは私たちのコードによって確認されています。この後に、「1」、「2」と「3」、「4」の合計である2つの同じ番号が続きます。後者の数値は最後から2番目の数値の合計です。これは連鎖が通過する平均ステップ数です。「m」と「n」が等しく対称である集合関数のこれらの入力パラメータを設定する理由は後で説明します。

対称フラクタルに基づいた初期式の導出

ログの結果によると、連鎖が通過する平均ステップ数は「4」になります。チャネルは単位ステップの2倍になります。単位ステップとは、「n」と「m」が1に設定されている場合です。言い換えると、小さいチャネルで構成されるチャネルの平均ステップ数を計算する場合(この場合、小さいチャネルの整数が大きいチャネルに適合し、新しいチャネルも対称である)、次を仮定できます。

P [n] = P [n-1] * 2 - 新しいチャネルを構成する前の小さいチャネルの幅に基づいた、新しいチャネル幅の再帰式
S [n] = S [n-1] * 4 - 小さいチャネルの平均値で表された、新しいチャネルの平均ステップ数を計算するための再帰式

「P [0] = 1」と「S [0] = 1」を受け入れ、インデックス「0」から再帰の番号付けを開始すると、この再帰は2つの非常に類似した系列として表すことができます。

P[n] = 2^n , n = 0 ... +無限大
S[n] = 4^n = (2^2)^n = (2^n)^2 = P[n]^2

最初のシリーズをよく見て、2番目のシリーズを正しく変換すると、2番目のシリーズは最初のシリーズの要素を使用して表現できることがわかります。つまり、依存関係「S = S(P) = P^2」が得られます。現在、この依存関係は、チャネル幅の再帰的な倍増にのみ当てはまります。この式を見たとき、任意の大きな数「n」と「m」の適用性を確認することにしました。論理的には、2番目のステップで「n=3」、「m=3」として、同じ変数を計算します。これらの入力パラメータを使用すると、平均ステップ数は「9」になります。上記のコードを使用するか、以下に添付されているMathCad 15プログラムを使用して、この部分をご自分でご確認ください。これらのパラメータにも同じシリーズを提供できます。

P[n] = 3^n , n = 0 ... +無限大
S[n] = 9^n = (3^2)^n = (3^n)^2 = P[n]^2

ご覧のとおり、「S=S(P)=P^2」という同じ関係が得られました。間隔の分割に関連する他のすべての可能なシナリオについて同じことを繰り返すことができますが、これは必須ではありません。この事実は、たとえば、対称チャネル内での価格の平均期間がわかっている場合、他のチャネルで内の価格の平均期間を計算できることを意味します。次のように計算できます。

S = S0 * K^2 - 新しいチャネルの平均ステップ数
T = S * T0 - 新しいチャネルの平均期間
T = T0 * K^2 - 別のチャネルの平均期間で表された新しいチャネルの平均期間は、(S0 = 1の場合)
S0 - 古いチャネルの平均ステップ数
T0 - 古いチャネルの1ステップの平均期間
P = K * P0 -> K = P/P0 - 新しいチャネルが古いチャネルの何倍か
P - 新しいチャネルの幅
P0 - 古いチャネルの幅

次に、MathCad15を使用して仮説をテストできます。まず、2次関係に関する仮定をテストしましょう。

二次関係の確認

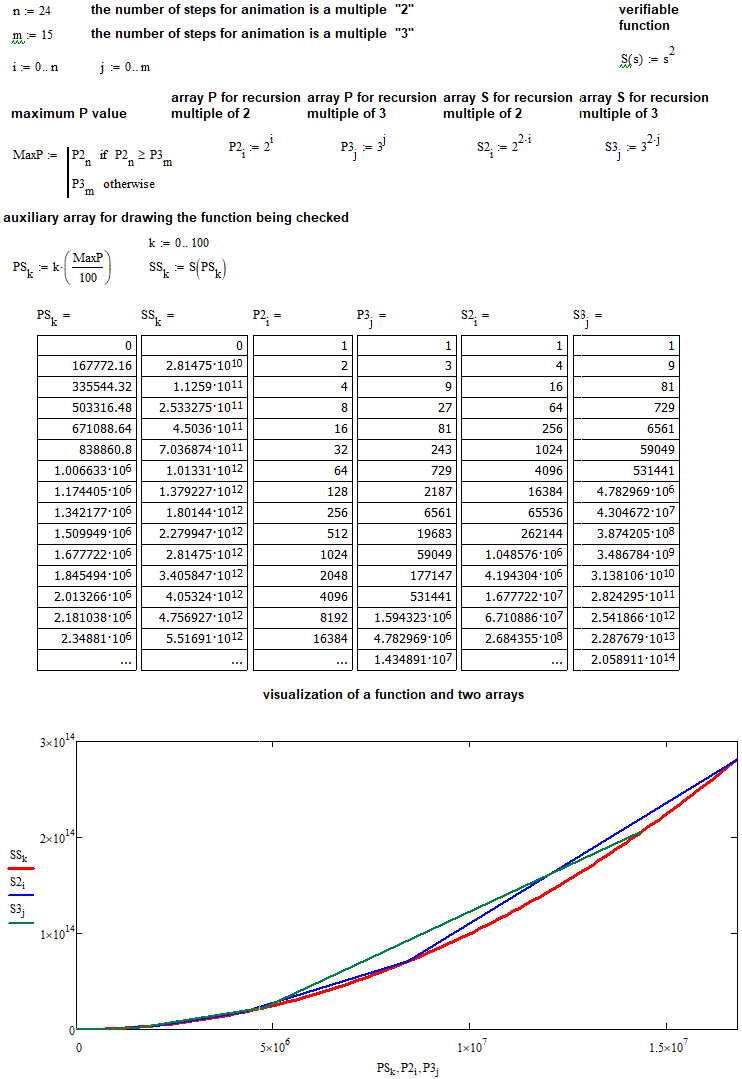
非常に明確なはずです。

すべての正の引数と実際の引数についての、導出された式のパフォーマンスの評価

この式は、すべての整数「P」に対して機能します。しかし、浮動小数点数「K」に使用できるでしょうか。浮動小数点数「K」を提供するためにはトリックを実装する必要があります。平均期間がわかっている価格チャネルがあり、チャネルの内側に「N」回収まるチャネルがあるが、その平均期間はまだわかりらないとします。さらに、同じ式を使用してそれを見つけます。この論理によると

T = T0 * N^2 ---> T0 = T / N^2
T - 平均期間がわかるチャネルの期間
T0 - チャネルを構成している小さいチャネルの平均期間

これは、小さいチャネルの期間を見つけることができることを意味します。これは、分数の増加係数を使用して3番目のチャネルの期間を計算するために必要です。最小のチャネルの期間がわかったので、その幅をポイントで見つけることができます。

d = P / N

次に、次の比率を使用して、このようなチャネルが拡張されたチャネルにいくつ収まるかを計算できます。

Smin = MathFloor( K * P / d ) = MathFloor( K * N )
Lim( N --> +無限大) [ K * N/MathFloor( K * N ) ] = 1

ご覧のとおり、チャネルの幅は狭くなっており、結果には影響しません。2行目は、次に何をすべきかを理解するのに役立つ非常に重要な比率を示しています。これは、ソースチャネルをできるだけ多くのセグメントに分割すると、MathFloor関数の結果として破棄される小数部分を無視できることを示しています。これは、1になりがちな限界によって示されます。この不正確さが紛らわしい場合は、別の値を見つけることができます。

Smax = MathFloor( K * P / d ) + 1 = MathFloor( K * N ) + 1 = Smin + 1

「K * N」の真の値が「Smin」と「Smax」の間にあることがわかります。「N」が無限大になる場合、2つの非常に類似したチャネルが得られ、サイズが1つのセグメントだけ異なるため、平均期間は等しくなります。したがって、必要なチャネルの平均期間は、これらのチャネルの平均期間の算術平均によってより正確に決定されます。

T1 =( T0 * Smin^2 + T0 * Smax^2 ) / 2 = T0 *( Smin^2 + Smax^2 ) / 2
T1 - 決定する必要のあるチャネルの平均期間

次の図は私のアイディアを示しています。

浮動小数点数のアイデアを証明するためのスキーム

チャネルの期間を計算するための代替式が見つかったので、その結果を整数「K」の関数の値と比較して、代わりに浮動小数点数「K」に置き換えることができます。2つの式の結果の値が同一である場合、整数「K」値に対して見つかった関数は、すべての整数に絶対に適用可能であり、「0 ... +無限大」の範囲にあると結論付けることができます。「N = 1000」の最初のチェックを実行してみましょう。次のような場合は、この分割で2つの数字の同一性を確認するのに十分だと思います。

浮動小数点の簡単なチェック

ご覧のとおり、2つの数字は実質的に同じです。論理的には、「N」の値が大きいほど、それらはより同一である必要があります。これは、次のことを前提としても証明できます。

Lim( N --> +無限大) [ (T0 *( Smin^2 + Smax^2 ) / 2) / ( T * K^2 ) ] = 1

この極限の分子は、新しいチャネルの平均期間を計算するための近似式であり、分母は、おそらく同じ値を正確に表す式です。前のスクリーンショットと同じ計算を実行する単純な関数を作成しました。ただし、今回は「1」から始まる「N」の全範囲に適用されます。次に、プログラムの実行結果を見てみましょう。

極限の確認

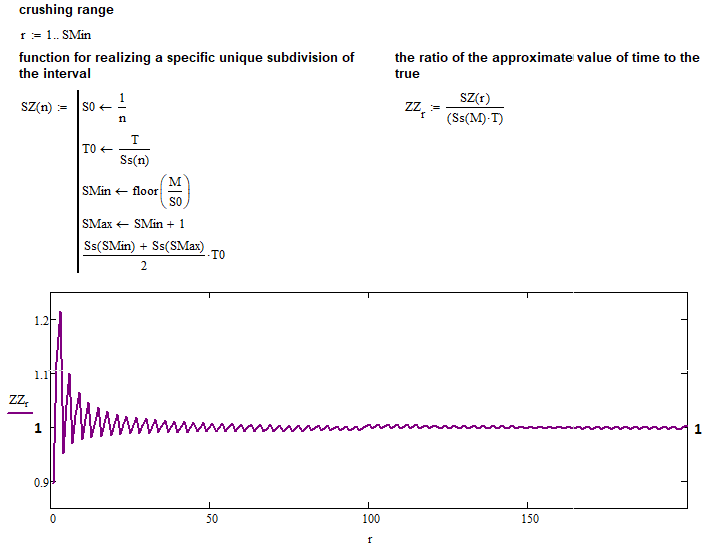
すべての仮定が完全に確認されています。整数「K」に対して見つかった関数は、正の「K」に絶対的に適用できます。これで、たとえば、ユニバーサルフラクタル全体を記述するためのさらなる数学の基礎として、さらなるアクションの基礎として使用できる、単一の非常に便利な関数ができました。

ユニバーサルフラクタルから開発された高度なフラクタル

ユニバーサルフラクタルのさらなる適用の有用で追加の例として、たとえば「n=1」、「m ---> +無限大」、「s=m+1」「p=0.5」の1境界フラクタルをとることができます。これまでのところ、ランダムウォークにのみ適用できる、両方向に等しい確率のステップを持つフラクタルを検討しています。しかし、このフラクタルはすべての可能性を提供します。このような複雑な構造のより深い分析に移るには、まず基本を考慮する必要があります。さらに、この最初のステップで、有用な公式を取得し、これらのフラクタルプロセスに関する基本的な結論を出すことができます。さまざまな「s」値でフラクタルをテストし、次のデータを取得しました。

s = 22 , FullSumm = 2.868 , UpperSummProbability = 0.831
s = 32 , FullSumm = 3.618 , UpperSummProbability = 0.860
s = 42 , FullSumm = 4.262 , UpperSummProbability = 0.877
s = 45 , FullSumm = 4.499 , UpperSummProbability = 0.882

許容ステップ数をさらに増やすと、計算時間の特異点が発生します。つまり、計算時間が大幅に増加するため、数時間または数日かかる場合があります。しかし、平均確率の合計が増加する速度を見ると、このタイプのフラクタルを使用してこの級数の収束を評価することは不可能であることがわかります。しかし、以前に導出された式に基づいて、異なるが非常に有用なフラクタルタイプを使用して収束を評価できます。このフラクタルは、「キャリートレード」と題された非常に人気があり収益性の高いストラテジーの時間を計算するのにも役立ちます。最初に図を示し、次にそれを説明します。

高度なフラクタル

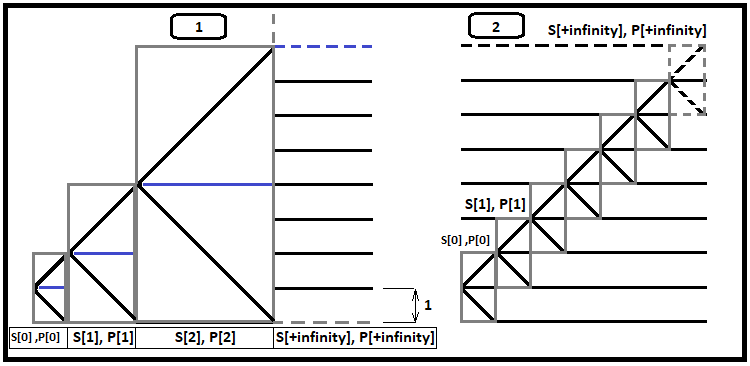
価格設定プロセスが、境界線がどこにあっても、上または下に関係なく、境界線から1ステップ開始することを想像してみてください。上の図は、見やすいように境界を低くした例を示しています。最初のフラクタルを詳しく見てみましょう。各灰色のボックスには、以降のイベントの2つのシナリオが含まれています。

価格がボックスの上端に達する
価格がボックスの下端に達する

価格がチャネルの上限に達すると、この時点で新しい大きなフラクタルが自動的に開始されます。このプロセスをユニバーサルフラクタルと同じように考えると、確率の連鎖が再びわかります。ただし、ここでの式は、チャネルに収まるステップの数に基づいて、対称チャネルで行われるステップの数を示しています(これで、ステップは元のチャネルに収まる小さなチャネルであることがわかります)。

平均ステップ数を計算するためにフラクタル全体を考慮する必要はありません。代わりに、導出された式を各フラクタルに適用します。ここでのステップは同じ値ではありませんが、次のネストされたフラクタルの上限または下限に達したときに行われます。これに基づいて、非常に単純な確率連鎖を作成できます。最初のフラクタルP[0]で境界に到達する確率は0.5に等しくなります。これは、価格が境界に達することを期待して次のフラクタルを作成する必要がある場合に、2番目の可能なケースがあることを意味します。これらのイベントはすべてネストされており、そのような連鎖はすべて完全なグループを形成します。

2番目のフラクタルP[1]で限界に達する確率は、前の確率に0.5を乗算したものに等しくなります。このプロセスは無限に続行できます。平均ステップ数は、導出された式とチェーン確率を使用して決定できます。これを行うには、最初に、上限を超えて下限を超えた平均ステップ数が等しいことを考慮して、個々の連鎖の確率の式を定義します。次がわかりました。

PUp = PDown = P - フラクタルの上限と下限に触れる確率が、ネストされたすべてのフラクタルのすべての境界で等しくなる可能性があることを示す比率
P[j] = 0.5^(j+1) , j = 0 ... +無限大 - 連鎖jが発生する確率
S[i] = S[i-1] + P[i] * ( S[i-1]/P[i-1] + F(D[i]) )、i = 1... +無限大 - すべてのフラクタルの平均推定ステップ数の合計を計算するための繰り返し式レベル(S[0] = 1*0.5 = 0.5の間)
F(K) = K^2 - 平均ステップ数を計算するための導出式
D(i) = 2^i - 次のフラクタルレベルに収まるステップ数
S[i-1]/P[i-1] - 現在の分岐が発生した場合の、残りの説明されていない分岐の平均ステップ数(現在のネストされたフラクタルに加えて、すべてを考慮する必要があるため) 以前に起こったステップ)

2番目のフラクタルは実際には最初のフラクタルと同じです。つまり、それらの連鎖(P[]配列)の確率は同じです。なぜそれが必要なのでしょうか。「キャリートレード」ストラテジーがあるとします。正のスワップでポジションをロックするために、スワップ口座とスワップフリー口座の2つの口座があります。また、平均収益性の高いポジション保持時間を計算する式も必要です。この平均保持時間は、平均ステップ数の式に直接由来します。この記事では、この問題については詳しく説明しません。数学の重要性を示したいだけです。このトピックについては、後で詳しく説明します。次に、2番目のフラクタルの平均確率ステップの式を定義しましょう。

S[j] = S[j-1] + P[j] * ( S[i-1]/P[i-1] + F(1) ) - すべてのフラクタルレベルの平均推定ステップ数の合計を計算するための繰り返し式(S[0] = 1*0.5 = 0.5の間)

この場合、この式は貴重な式の特殊なケースにすぎません。これは、2番目のフラクタルでは常にすべてのフラクタルレベルでK=1であるためです。これらの量の合計の極限が両方のフラクタルで何に等しいかを調べてみましょう。

高度なフラクタル

最初のシリーズは分岐します。つまり、上限がなく、取引が無限である場合、平均時間は無限大に等しくなります。2番目のケースでは、2に等しい明確な極限があります。つまり、正のスワップでポジションを開く場合、平均して2ステップ後にこのポジションを決済する必要があります(したがって、平均ポジション保持時間は2*Tに等しくなります。ここで、Tは、境界の1つに達したときにポジションを決済した場合に提供される平均ポジション保持時間です)。2番目の最も単純なケースでは、スワップ口座が正の数を示している場合でも、両方の口座の両方のポジションを単純に決済します。明らかに、最初の選択肢の方がはるかに魅力的ですが、その実装には、両方の口座での迅速かつスムーズな引き出しと入金が必要になります。この選択肢が不可能な場合は、利益は少ないが安定性が高い従来の選択肢を使用する必要があります。

結果の要約

連載の第2部では、取引での実用化の結果など、非常に興味深い結果を達成しました。さらに重要なのは、フラクタルの可能な適用範囲が巨大であることは今や明らかだということです。本稿では次を行いました。

ユニバーサルフラクタルを構築するための明確な数学的ルールを定義した
記載されている数学的原理に基づいて、実用的なMQL5スタイルのコードを作成した
MetaTrader 5とMathCad15の2つのプラットフォームを使用して原則を確認した
アルゴリズムを使用して、任意のチャネルの期間を計算するための最初の式を取得した
考えられるすべてのケースでプログラミングを使用して数式をテストおよび検証した
得られた式に基づいて、新しいタイプのより速いフラクタルを取得した
その結果、計算を高速化し、ユニバーサルフラクタルでは特定できなかったものを特定した
スワップ取引の問題に高度なフラクタルを使用する特殊なケースに触れた
理論をさらに発展させるためのツールを入手した

また、私のツールボックスが大幅に拡張されたことにも注意してください。これで、確率の異なるステップ(トレンド状況および取引統計分析に関連する状況)でフラクタルを分析できます。繰り返しになりますが、本稿では「p = 1 - p = q = 0.5」の場合のみを考慮していることに注意してください。これは、すべての計算がランダムウォークを説明する状況にのみ適用できることを意味します。したがって、はるかに多くの潜在的な可能性があります。

以下は、フラクタルを研究した後に得られた式です。もう一度、簡単に説明します。

S = K^2 - ステップが別のチャネルと等しいという事実に基づく新しいチャネルの平均ステップ数
T = S * T0 = T0 * K^2 - 未知のチャネルの平均期間
T0 - 既知のチャネルの平均期間
P = K * P0 --> K = P/P0 - 既知のチャネルが未知のチャネルの何倍か
P - 期間が不明なチャネルの幅
P0 - 既知のチャネルの幅

4を1に代入することで、未知のチャネルに入る平均ステップ数を既知の値で表すことができます。1を2に代入すると、このチャネルの平均期間が得られます。これは、既知の値に基づいて計算されます。

T0、P0、P

また、本稿の冒頭で読者が抱くかもしれない質問への回答を追加します。

MetaTrader 5ストラテジーテスターから取引統計を収集できるのに、なぜ数式が必要なのですか。

応答:

すべての金融銘柄がそのような評価に必要な十分な取引履歴を持っているわけではないので、統計を収集することが常に可能であるとは限りません。境界を越えたことのないチャネルを選択できるため、これは大きなチャネルでは不可能です。幅の狭いチャネルと式を使用して、統計では得られないデータを得ることができます。さらに、この種の計算は、比類のない精度と柔軟性を提供します。他にもはるかに多くの利点があります。

終わりに

本稿では、価格設定プロセスに関するさらなる調査を行うために使用できる計算ロジックについての説明を試みました。これまでのところ、実用化できるものはあまりありません。しかし、普遍的なフラクタルのすべての種類を研究し、非対称で単一の境界を持つ価格チャネルを記述するための可能な公式を得ることができると確信しています。次の記事では、ユニバーサルフラクタルの研究を続け、すべての結果を簡単な式として提示することを試みます。また、得られた数式を価格設定プロセスだけでなく、バックテストや取引シグナルの記述にも使用できる、非常に興味深い新しい数学を紹介します。これにより、ストラテジーを時間と確率の観点から完全に正確に分析できるようになります。これは、最終的には取引の最も重要な側面です。