Combinatoire et théorie des probabilités pour le trading (Partie III) : Le premier modèle mathématique

Sommaire

• Introduction
• Nouvelles idées
• Formule générale pour le nombre moyen d'étapes
• Construction d'un prototype de fonction puissance
• Schéma général de réception de la meilleure fonction de la famille limitée par le prototype
• Analyse approfondie
• Collecte des données et conclusions
• Algorithme de calcul du modèle mathématique complet
• Prototypes pour obtenir la dernière équation
• Mise en œuvre et test du modèle mathématique
• Conclusion
• Références

Introduction

Dans l'article précédent, j'ai obtenu la première formule pour les fractales. Cela a permis de supposer que toutes les valeurs importantes liées aux fractales peuvent être décrites à l'aide d'un modèle mathématique. La simulation n'a pas pour but de décrire ces valeurs. Elle a seulement contribué à la collecte des premières données permettant une analyse plus approfondie de ces structures. Dans cet article, j'ai décidé d'accorder une attention particulière à la description de l'ensemble du processus de développement du premier modèle mathématique, jusqu'à la réception du modèle mathématique qui peut être appliqué dans différents Expert Advisors.

Nouvelles idées

En examinant une fractale symétrique dans l'article précédent, nous avons obtenu une formule générale pour calculer le nombre moyen de pas effectués par le prix à la suite d'un mouvement dans un certain couloir, qui est déterminé par le nombre de couloirs symétriques identiques, plus petits. Cette formule est la suivante :

1. S = K^2 – le nombre moyen de pas du nouveau couloir, basé sur le fait qu'un pas est un autre couloir
2. P = K * P0 --> K = P/P0 – combien de fois le couloir connu est plus grand que le couloir inconnu
3. P – la largeur du couloir dont le nombre moyen de pas n'est pas connu (les pas sont égaux à la moitié de la taille du couloir d'origine)
4. P0 – la largeur du couloir connu

Pour pouvoir décrire un couloir asymétrique, nous devons redéfinir certains des concepts mentionnés précédemment pour les rendre plus compréhensibles. Le plus important d'entre eux est K. Cette valeur reflète en fait le nombre de pas que le prix devrait faire dans le nouveau couloir, à condition que les pas ne soient faits que vers le haut ou vers le bas. Dans le cas d'un couloir symétrique, le nombre d'étapes est identique, quelle que soit la limite considérée (franchie), supérieure ou inférieure. Le problème se pose en effet aussi bien pour la limite supérieure que pour la limite inférieure. En ce qui concerne l'asymétrie, suite à l'expérimentation du code dans l'article précédent, nous avons obtenu que le nombre moyen de pas pour ce cas est déterminé comme suit :

• S = n * m – le nombre moyen de pas pour les moitiés asymétriques du couloir
• n – le nombre de marches qui tiennent dans la moitié supérieure du couloir
• m – le nombre de marches qui tiennent dans la moitié inférieure du couloir

Par conséquent, pour le couloir symétrique, nous avons "m = n". Sur la base de ce qui précède :

• S = n * n = m * m = m * n = n^2 = m^2 = K^2
• K = n = m

Cela signifie que la première formule dérivée n'est qu'un cas particulier de la précédente et que K n'est donc plus nécessaire.

Une caractéristique intéressante de cette fonction est que S(a*k, b*k) = S(a, b) * S(k, k), ce qui est très facile à prouver :

• S(n*k ,m*b) = m*k*n*b = n*m * k*b
• S(n ,m) * S(k ,b) = n*m * k*b

Cette propriété est très intéressante. Avec des réflexions supplémentaires, elle peut fournir la dérivation de toutes les formules nécessaires pour décrire l'ensemble de la fractale. Cette propriété reflète une propriété très importante de toute fractale : la capacité d'imbrication. Autrement dit : toute fractale finie d'une grande complexité peut être représentée par deux ou plusieurs fractales plus simples qui servent d'étapes l'une dans l'autre. Cette propriété sera utilisée pour généraliser la formule dans des cas plus complexes.

Avant de passer aux fractales, permettez-moi de vous rappeler que les formules définies ci-dessus ne fonctionnent que si p=0,5. Dès que le marché ou que les paramètres des fractales commencent à s'écarter d'une marche aléatoire, cette formule commence à changer de manière très intéressante, à savoir :

• Ss[n, m, p] – une formule plus générale pour le nombre moyen de pas (dans n'importe quelle direction)
• S(n, m) = Ss[n, m, 0,5] – la formule pour une marche aléatoire est un cas particulier de la formule générale

Formule générale pour le nombre moyen d'étapes

Afin de déterminer la forme d'une formule plus générale, j'ai utilisé l'invariance du principe d'imbrication fractale. Si l'on considère chaque niveau d'imbrication fractale par rapport au précédent, il n'est pas nécessaire de réfléchir aux étapes qui se sont produites à un moment donné. Les étapes primaires de montée et de descente se produisent donc précisément avec les mêmes rapports de fréquences qui correspondaient à la situation du niveau précédent. En d'autres termes, le franchissement d'une limite du niveau d'imbrication correspondant est soit un pas en avant, soit un pas en arrière pour le niveau d'imbrication suivant. Mais il est également connu que le rapport de la fréquence d'occurrence des étapes pour le niveau d'imbrication actuel ne dépend pas de la configuration du niveau actuel. Cela signifie que le principe d'imbrication fractale est observé pour toute probabilité "p". Cela signifie que lorsque la valeur "p" change, la formule doit également changer, mais elle doit en quelque sorte préserver sa propriété d'imbrication. Une simple expérience peut nous aider à déterminer la formule générale. Nous savons que la probabilité p a un point de marche aléatoire et 2 points extrêmes 0 et 1. Voyons quelles valeurs prendra la fonction en ces 3 points. Nous obtenons donc ce qui suit :

1.  Ss[n, m, 1] = Sn[n] = n
2. Ss[n, m, 0] = Sm[m] = m
3.  Ss[n, m, 0.5] = Sn[n] * Sm[m] = m*n
4.  Sn[n, p] – le nombre de pas dans une direction jusqu'à la limite supérieure
5. Sn[m, p] – le nombre de pas dans une direction jusqu'à la limite inférieure

Dans le premier cas, il n'y a pas de descente – toutes les chaînes suivent le même chemin. Le deuxième cas est opposé, et toutes les étapes seront descendantes, sans aucune étape ascendante. Aux valeurs extrêmes, l'un des facteurs disparaît complètement de la formule. C'est possible si vous l'augmentez à 0. Tout nombre à la puissance 0 est égal à 1. Le degré a également une invariance de la forme suivante :

• A^X * B^X = (A*B)^X

Si nous remplaçons les nombres par des pas moyens, le principe d'imbrication fractale sera toujours préservé. Cela montrera également que la puissance ne dépend pas de n et m. La formule générale qui en résulte pour le nombre moyen d'étapes est la suivante :

• Ss[m,n,p] = ( Sn[n] ^ Pn[p] ) * ( S[m] ^ Pm[p] ) = (n ^ Pn[p] ) * ( m ^ Pm[p] )

Le principe de l'imbrication fractale peut être schématisé comme suit :

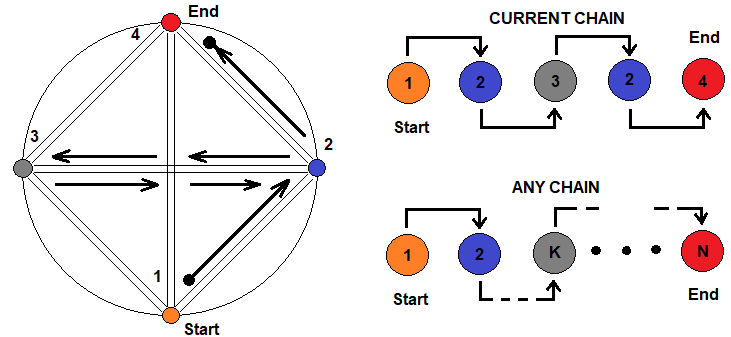
La figure montre 4 états qui symbolisent différentes fractales pouvant être exprimées l'une par l'autre. Le passage d'un état à un autre est possible par n'importe quelle chaîne. Une chaîne choisie arbitrairement est représentée à droite. Un peu plus bas, il est montré que cette chaîne peut être de n'importe quelle longueur et complexité, et que l'on peut itérer à travers le même état un nombre illimité de fois. Cela signifie que la formule du nombre moyen de pas dans une fractale peut être présentée comme une chaîne de produits, qui représentent les niveaux d'imbrication de la fractale.

Construction d'un prototype de fonction puissance

D'autres idées viennent de la propriété d'imbrication fractale et de l'invariance des fonctions de puissance égale par rapport à la base. Tous ces principes mathématiques permettront de dériver d'autres formules pour une description plus approfondie des fractales. Nous obtenons ainsi en plus 2 fonctions dont nous ne connaissons pas la forme :

• Pn[p] – la puissance du multiplicateur de la limite supérieure
• Pm[p] – la puissance du multiplicateur de la limite inférieure

Nous savons ce qui suit :

• Pn[0.5] = 1 , Pn[1] = 1 , Pn[0] = 0
• Pm[0.5] = 1 , Pm[1] = 1 , Pm[0] = 0

En analysant les fonctions de puissance, il est possible de construire un prototype de fonction correspondant. J'ai sélectionné le prototype suivant :

1. Pn[p] = 1 si p >= 0.5
2. Pn[p] = ( (1 - p)/0,5 ) ^ K
3. Pm[p] = 1 si p <= 0.5
4. Pm[p] = ( p/0,5 ) ^ K
5. K est la puissance qui régule la planéité de la fonction

Il serait plus exact de représenter "2" et "4" sous la forme de polynômes qui peuvent décrire avec précision la transition en douceur d'une puissance donnée, mais je pense que cela est redondant ici. Si vous souhaitez définir des polynômes plus précis, voici les prototypes :

• Pn[p] = C1 * ( (1 - p)/0,5 ) ^ K1 + C2 * ( (1 - p)/0,5 ) ^ K2 ... + ... + CN * ( (1 - p)/0.5 ) *KN
• Pm[p] = C1 * ( p/0.5 ) ^ K1 + C2 * ( p/0.5 ) ^ K2 ... + ... + CN * ( p/0.5 ) ^ KN
• С1 + С2 + ... + ... СN = 1 sont les poids pour la puissance concernée.
• KN est la puissance du terme correspondant

Le polynôme que j'ai choisi est la version la plus simple du polynôme général avec un seul terme. Tous les principes déclarés peuvent être vérifiés pour toute fraction "n, m".

J'ai créé le programme suivant pour vérifier les hypothèses ci-dessus :

Comme le montrent les résultats du programme, tout fonctionne comme il se doit. Pour s'en assurer, il suffit de comparer 2 nombres. S'ils sont égaux, le principe d'imbrication et la possibilité d'utiliser des n et m fractionnaires sont confirmés.

Schéma général de réception de la meilleure fonction de la famille limitée par le prototype

Nous devons maintenant déterminer comment nous allons rechercher les coefficients nécessaires pour le prototype. J'ai choisi le type de recherche le plus simple : générer des nombres aléatoires dans l’intervalle souhaité. Le schéma de la méthode est le suivant :

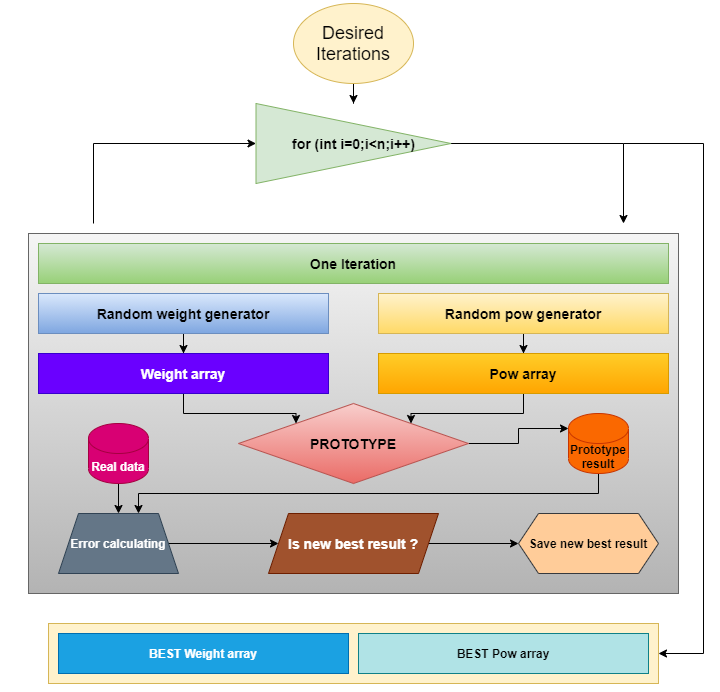
Il convient à tout prototype de fonction si l'on doit trouver des coefficients pour que les données réelles correspondent le mieux possible au modèle mathématique. Le même schéma sera valable plus loin, puisqu'à la fin de l'article, nous appliquerons la même méthode pour traiter un autre prototype.

Analyse approfondie

Analysons maintenant plus en détail la structure de cette formule. Le résultat de la formule est le nombre moyen de pas que le prix fait avant de franchir l'une des frontières. Les pas vers le haut et vers le bas sont considérés comme égaux, mais cette égalité n'est en fait possible que dans le cas d'une marche aléatoire. Pour la description complète d'une fractale asymétrique, il est nécessaire de déterminer également en quoi consiste réellement la valeur donnée. Logiquement, le nombre moyen de pas, quel que soit le type de pas, dépend à la fois du nombre moyen de pas lors du franchissement de la limite supérieure et du nombre moyen de pas lors du franchissement de la limite inférieure. Trouvons des valeurs pertinentes pour le point de passage supérieur de la frontière :

• SP[U, ud] = S[U, u] * P[U] + S[U, d] * P[U] = (S[U, u] + S[U, d]) * P[U] = S[U] * P[U]
• S[U] – le nombre moyen d'étapes à condition que la chaîne d'étapes atteigne d'abord la limite supérieure.
• S[U, u] – le nombre moyen de pas vers le haut, à condition que la chaîne de pas atteigne d'abord la limite supérieure.
• S[U, d] – le nombre moyen de pas vers le bas à condition que la chaîne de pas atteigne d'abord la limite supérieure.
• P[U] – la probabilité que le prix franchisse d'abord la limite supérieure
• SP[U, ud] – le nombre moyen probable d'étapes pour franchir la limite supérieure

Les formules sont similaires pour la limite inférieure :

• SP[D, ud] = S[D, u] * P[D] + S[D, d] * P[D] = (S[D, u] + S[D, d]) * P[D] = S[D] * P[D]
• S[D] – le nombre moyen d'étapes à condition que la chaîne d'étapes atteigne d'abord la limite inférieure.
• S[D, u] – le nombre moyen de pas vers le haut à condition que la chaîne de pas atteigne d'abord la limite inférieure.
• S[D, d] – le nombre moyen de pas vers le bas, à condition que la chaîne de pas atteigne d'abord la limite inférieure.
• P[D] – la probabilité que le prix franchisse d'abord la limite inférieure
• SP[D, ud] – le nombre moyen probable d'étapes pour franchir la limite inférieure

Il apparaît clairement que :

• S = SP[U, ud] + SP[D, ud]

En définitive, toutes les valeurs que nous pouvons obtenir et utiliser dépendent de 5 valeurs fondamentales :

• S[U,u] = SP[U, u]/P[U] – le nombre moyen de pas vers le haut à condition que la chaîne de pas atteigne d'abord la limite supérieure.
• S[U, d] = SP[U, d]/P[U] – le nombre moyen de pas vers le bas à condition que la chaîne de pas atteigne d'abord la limite supérieure.
• S[D, u] = SP[D, u]/P[D] – le nombre moyen de pas vers le haut à condition que la chaîne de pas atteigne d'abord la limite inférieure.
• S[D, d] = SP[D, d]/P[D] – le nombre moyen de pas vers le bas à condition que la chaîne de pas atteigne d'abord la limite inférieure.
• P[U] – la probabilité que le prix franchisse d'abord la limite supérieure

Nous chercherons les formules pour ces valeurs en nous basant sur les résultats de l'opération fractale avec différents paramètres d'entrée. Dans l'article précédent, j'ai sélectionné les valeurs suivantes pour la sortie fractale :

• SP[U, u] – le nombre moyen de pas vers le haut à condition que la chaîne de pas atteigne d'abord la limite supérieure.
• SP[U, d] – le nombre moyen de pas vers le bas à condition que la chaîne de pas atteigne d'abord la limite supérieure.
• SP[D, u] – le nombre moyen de pas vers le haut à condition que la chaîne de pas atteigne d'abord la limite inférieure.
• SP[D, d] – le nombre moyen de pas vers le bas, à condition que la chaîne de pas atteigne d'abord la limite inférieure.
• P[U] – la probabilité que le prix franchisse d'abord la limite supérieure
• P[D] – la probabilité que le prix franchisse d'abord la limite inférieure
• S = SP – le nombre moyen de pas éventuels

Il s'agit d'un groupe distinct d'éléments qui peuvent être exprimés en termes de valeurs fondamentales :

• SP[U]
• S[U, ud] = S[U, u] + S[U, d]
• S[D, ud] = S[D, u] + S[D, d]
• P[D] = 1 - P[U]
• S = SP[U, ud] + SP[D, ud]

Lorsque j'ai abordé les mathématiques des fractales, j'ai effectué une analyse approfondie, qui peut être brièvement illustrée par un diagramme compact. Le diagramme montre le processus de recherche d'un modèle mathématique qui en résulte :

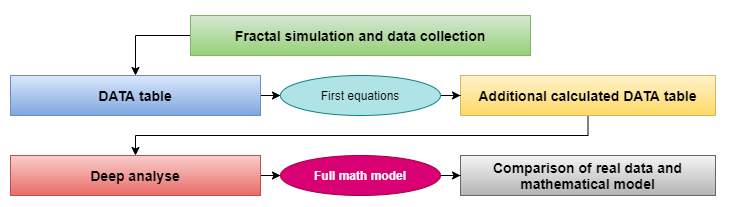
Collecte des données et conclusions

En examinant plus en détail les résultats des calculs fractals, j'ai remarqué que les 6 valeurs initialement déterminées lors de la construction du concept de fractale universelle sont mathématiquement liées. J'ai effectué des tests dans un premier temps pour des limites symétriques et j'ai essayé d'identifier des dépendances entre ces valeurs. J'ai obtenu quelques résultats. J'ai fait les calculs pour 10 cas différents, et cela s'est avéré suffisant :

Indice de test	Pas dans la moitié supérieure du couloir (n)	Pas dans la moitié inférieure du couloir ( m )	Probabilité du pas initial   ( p )	Nombre moyen probable de pas ascendants pour la limite supérieure ( SP[U, u] )	Nombre moyen probable de pas descendants pour la limite supérieure ( SP[U, d] )	Nombre moyen probable de pas ascendants pour la limite inférieure ( SP[D, u] )	Nombre moyen probable de pas descendants pour la limite inférieure ( SP[D, d] )	Nombre moyen probable de pas pour la limite supérieure ( SP[U, ud] )	Nombre moyen probable de pas pour la limite inférieure ( SP[D, ud] )
1	1	1	0,5	0,5	0	0,0	0,5	0,5	0,5
2	2	2	0,5	1,5	0,5	0,5	1,5	2,0	2,0
3	3	3	0,5	3,0	1,5	3,0	1,5	4,5	4,5
4	1	2	0,5	0,888888	0,2222222	0,111111	0,777777	1,11111111	0,8888888
5	2	3	0,5	2,2	1,0	0,8	2,0	3,2	2,8
6	1	2	0,6	1,038781	0,249307	0,066481	0,487534	1,288088	0,554016
7	2	3	0,6	2,811405	1,191072	0,338217	0,906713	4,0024777	1,244931
8	2	3	1,0	2,0	0,0	0,0	0,0	2,0	0,0
9	1	3	0,5	1,25	0,5	0,25	1	1,75	1,25
10	1	4	0,5	1,6	0,8	0,4	1,2	2,4	1,6

 

Je présente ci-dessous un tableau avec les valeurs calculées qui ne sont pas affichées dans le journal des fractales. Nous en aurons besoin pour évaluer les dépendances entre les valeurs :

Indice de test	Pas dans la moitié supérieure du couloir (n)	Pas dans la moitié inférieure du couloir ( m )	Probabilité de franchissement de la limite supérieure ( P(U) )	Probabilité de franchissement de la limite inférieure ( P(D) )	Nombre moyen de pas lors du franchissement de la limite supérieure (S[U, ud]) = SP[U, ud]/P[U]	Nombre moyen de pas lors du franchissement de la limite inférieure (S[D, ud]) = SP[D, ud]/P[D]	Nombre moyen de pas ascendants pour la limite supérieure ( S[U, u] ) = SP[U, u]/P[U]	Nombre moyen de pas descendants pour la limite supérieure ( S[U, d] ) = SP[U, d]/P[U]	Nombre moyen de pas ascendants pour la limite inférieure ( S[D, u] ) = SP[D, u]/(P[D])	Nombre moyen  de pas descendants pour la limite inférieure ( S[D, d] ) = SP[D, d]/(P[D])	Nombre moyen de pas   ( S )
1	1	1	0,5	0,5	1,0	1,0	1,0	0,0	0,0	1,0	1
2	2	2	0,5	0,5	4,0	4,0	3,0	1	1	3	4
3	3	3	0,5	0,5	9,0	9,0	6	3	3	6	9
4	1	2	0,66666	0,3333333	1,6666666	2,6666666	1,3333333	0,33333333	0,33333333	2,33333333	2
5	2	3	0,6	0,4	5,3333333	7	3,6666666	1,66666666	2	5	6
6	1	2	0,789473	0,210526	1,631579	2,631579	1,315790	0,315789	0,315789	2,315789	1,842104
7	2	3	0,810166	0,189498	4,940318	6,569626	3,470159	1,470157	1,784805	4,784	5,2474087
8	2	3	1,0	0,0	2,0	0,0	2,0	0,0	0,0	0,0	2,0
9	1	3	0,75	0,25	2,3333333	5	1,6666666	0,6666666	1	4	3
10	1	4	0,8	0,2	3,0	8,0	2	1	2	6	4

 

À partir de ce tableau, vous pouvez trouver les deux premières équations nécessaires pour calculer les 4 valeurs inconnues (dont toutes les autres valeurs sont composées). Pour obtenir les formules, faites attention aux colonnes S[U, u], S[U, d], S[D, u], S[D, d]. Il est très intéressant de constater que les nombres de cette colonne ont la même partie fractionnaire par paire dans les colonnes S[U, u], S[U, d] et dans S[D, u], S[D, d]. Vous pouvez également constater que S[U, u] > S[U, d] et S[D, d] > S[D, u]. Si l'on soustrait ces valeurs deux à deux et que l'on compare avec m, n, il s'avère que cette différence est exactement égale au nombre correspondant de pas vers la limite supérieure ou inférieure :

• S[U, u] - S[U, d] = n
• S[D, d] - S[D, u] = m

Nous obtenons ainsi 2 valeurs très importantes qui nous aideront à déterminer les valeurs fondamentales. Deux équations ne suffisent pas. Mais nous pouvons obtenir deux autres équations, qui permettront de déterminer les mêmes valeurs sur la base d'une logique légèrement différente. Si nous expérimentons la fractale pendant un temps infiniment long, le rapport entre la fréquence d'apparition des pas vers le haut et vers le bas sera proportionnel aux probabilités correspondantes.

Ces ratios peuvent être obtenus en supposant que :

1. Lim[N0 -- > +infini] (N0[U]/N0) = p
2. Lim[N0 -- > +infini] (N0[D]/N0) = 1-p
3. Lim[N0 -- > +infini] (N0[U]/N) = S[UD, u]
4. Lim[N0 -- > +infini] (N0[D]/N) = S[UD, d]
5. Lim[N0 -- > +infini] (N0/N) = S
6. N0 – le nombre d'expériences élémentaires réalisées par rapport aux étapes initiales (qui constituent une expérience complexe)
7. N – le nombre d'expériences complexes composées d'expériences simples

Si nous introduisons le multiplicateur N0/N0 = 1 dans "3" et "4" et que nous arrangeons correctement les fractions à l'intérieur, nous obtenons ce qui suit :

• Lim[N0 -- > +infini] (N0[U]/N) = Lim[N0 -- > +infini] (N0[U]/N0 * N0/N) = Lim[N0 -- > +infini] (N0[U]/N0) * Lim[N0 -- > +infini] (N0/N) = p*S = S[UD, u]
• Lim[N0 -- > +infini] (N0[D]/N) = Lim[N0 -- > +infini] (N0[D]/N0 * N0/N) = Lim[N0 -- > +infini] (N0[D]/N0) * Lim[N0 -- > +infini] (N0/N) = (p-1)*S = S[UD, d]

La limite du produit peut être représentée comme le produit des limites, si chacune de ces limites est un nombre fini. Nos limites sont conformes à cette condition. C'est ainsi que ces formules sont dérivées. Les formules sont les suivantes :

• S[UD, u] = S*p
• S[UD, d] = S*(1-p)

Il est préférable d'exprimer ces valeurs en termes de valeurs fondamentales, ce qui permet d'obtenir les deux équations manquantes pour déterminer tout ce dont nous avons besoin :

• S[U, u] * P[U] + S[D, u] * ( 1 - P[U] ) = S*p
• S[U, d] * P[U] + S[D, d] * ( 1 - P[U] ) = S*(1-p)

Par conséquent, 4 équations ont 5 valeurs inconnues. La cinquième inconnue est l'une des probabilités qui forment le groupe complet (probabilité d'atteindre l'une des limites). Pour pouvoir trouver les 5 inconnues, nous avons besoin de la cinquième équation, car un système d'équations ne peut avoir une solution unique que si le nombre d'équations est égal au nombre d'inconnues. La cinquième équation peut être obtenue intuitivement, car nous savons qu'il s'agit de la différence entre les pas de montée et de descente. Idéalement, c'est la limite :

• Lim[Nt[U] -- > +infini] ((N0[U] - N0[D])/(Nt[U] - Nt[D]) = 1
• Nt[U] = – le nombre idéal de pas de base vers le haut, calculé à l'aide d'une probabilité de pas de base vers le haut
• Nt[D] – le nombre idéal de pas de base vers le bas, calculé en utilisant la probabilité d'un pas de base vers le bas
• N0[U] – le nombre réel de pas de base vers le haut
• N0[D] – le nombre réel de pas de base vers le bas

Nous pouvons trouver une limite similaire en utilisant les probabilités de franchissement des limites :

• Lim[Nb[U] -- > +infini] ((N0[U] - N0[D])/(Nb[U] - Nb[D]) = 1
• Nb[U] – le nombre idéal de pas de base vers le haut, calculé à partir d'une probabilité de franchissement de la limite supérieure.
• Nb[D] – le nombre idéal de pas de base vers le bas, calculé à partir d'une probabilité de franchissement de la limite inférieure.
• N0[U] – le nombre réel de pas de base vers le haut
• N0[D] – le nombre réel de pas de base vers le bas

À partir de ces deux limites, on peut en composer une plus complexe, comme leur somme, leur différence ou leur quotient. Je choisirai le quotient, qui réduira l'expression suivante et éliminera complètement la limite N0 [U] - N0 [D]. En divisant ces deux limites et en transformant l'équation, nous obtenons ce qui suit :

• P[U] * n - (1 - P[U]) * m = p * S - (1 - p) *S

Il s'agit de la cinquième équation, à partir de laquelle nous pouvons trouver les probabilités de franchissement des limites. Nous obtenons ainsi un système à 5 équations. Il se présentera comme suit :

1. S[U, u] - S[U, d] = n
2. S[D, d] - S[D, u] = m
3. S[U, u] * P[U] + S[D, u] * ( 1 - P[U] ) = S*p
4. S[U, d] * P[U] + S[D, d] * ( 1 - P[U] ) = S*(1-p)
5. P[U] * n - (1 - P[U]) * m = p * S - (1 - p) *S = 2*p*S - S

Le système d'équations initial à 4 inconnues fournit également la même équation résultante.  Le système peut être résolu de manière classique, en excluant successivement les variables :

• --> S[U, u] = n + S[U, d] – exclure "S[U, u]"
• --> S[D, d] = m + S[D, u] – exclure "S[D, d]"
• (n + S[U, d]) * P[U] + S[D, u] * ( 1 - P[U] ) = S*p – substituer tout à l'équation 3
• S[U, d] * P[U] + (m + S[D, u]) * ( 1 - P[U] ) = S*(1-p) – substituer tout à l'équation 4

Après ces transformations, il suffit de soustraire l'équation 3 de l'équation 4 pour obtenir la même équation que celle obtenue intuitivement. Malheureusement, ce système d'équations ne permet pas de trouver les 4 valeurs restantes. J'espérais que ce système fonctionnerait, mais ce n'est pas le cas. Pour en comprendre la raison, j'ai dû analyser le tableau avec des données fractales. Cela m'a permis de créer une formule pour l'une de ces quatre quantités. Avec cette formule supplémentaire, nous pouvons trouver toutes les autres valeurs. Le système s'est donc avéré utile.

Algorithme de calcul du modèle mathématique complet

Définissons d'abord les équations inverses et la séquence de leur utilisation pour trouver toutes les autres, connaissant S[U, u]. J'utilise cette valeur parce que j'ai réussi à trouver les formules nécessaires à son calcul. Avec cette valeur, nous pouvons immédiatement trouver S[U, d] en utilisant la première équation :

• S[U, d] = S[U, u] - n

Substituez ensuite ces deux valeurs dans les équations 3 et 4 et trouvez les valeurs restantes S[D, u] et S[D, d]. S[D, u] peut être calculé immédiatement à partir de la troisième équation :

• S[D, u] = ( S*p - S[U, u] * P[U] ) / ( 1 - P[U] )

Il ne nous reste plus qu'à trouver une formule pour la dernière valeur inconnue. Substituer l'expression obtenue pour S[U, d] dans la quatrième équation :

• S[D, d] = ( S*(1-p) - S[U, d] * P[U]) / ( 1 - P[U] ) = ( S*(1-p) - ( S[U, u] - n ) * P[U] ) / ( 1 - P[U] )

Le seul élément manquant est la valeur P[U] qui peut être facilement obtenue en résolvant la cinquième équation. C'est ce que nous allons faire :

• P[U] * n - (1 - P[U]) * m = 2*p*S - S
• --> P[U] * (n + m) = 2 * p * S - S + m
• --> P[U] = ( 2 * p * S - S + m ) / (n + m)

Les valeurs connues sont les suivantes :

• n – le nombre de pas jusqu'à la limite supérieure
• m – le nombre de pas vers le bas jusqu'à la limite inférieure
• p – la probabilité de l'étape initiale vers le haut
• S[U, u] – le nombre moyen de pas vers le haut à condition que la limite supérieure soit franchie
• P[U] – la probabilité de franchir la limite supérieure

La valeur 4 peut être calculée :

• S[U, u] = Ss[m, n, p] = (n ^ Pn[p] ) * ( m ^ Pm[p] )
• Pn[p] = 1 si p >= 0.5
• Pn[p] = ( (1 - p)/0,5 ) ^ K
• Pm[p] = 1 si p <= 0.5
• Pm[p] = ( p/0,5 ) ^ K
• K est la puissance qui régule la planéité de la fonction

Nous calculerons le coefficient de planéité dans un programme séparé un peu plus tard. Nous devons maintenant déterminer la valeur la plus importante. En analysant la valeur S[U, u] du tableau, j'ai réussi à dériver des formules pour 2 valeurs de limites symétriques :

1. S[U, u] = Somme[ i = 0, n] ( i ) si n == m
2. S[U, d] = Somme[ i = 0, n] ( i-1 ) si n == m

Le problème est que ces formules ne fonctionnent que pour p = 0,5 et pour des limites symétriques. Le concept des formules devrait être élargi pour couvrir les limites asymétriques. Ensuite, nous pouvons la généraliser pour différentes valeurs de p. Avant de procéder à la généralisation, il convient de noter que les résultats des tests figurant dans le tableau ne sont applicables que pour "m > n". Si "m < n", les formules fonctionneront pour "S[D, d], S[D, u]". Dans ce cas, il est nécessaire de créer un miroir analogue de l'algorithme pour trouver toutes les autres valeurs inconnues.

Définissons également les équations inverses et l'ordre dans lequel elles doivent être utilisées dans le cas de S[D, d]. Trouvons à nouveau la valeur S[D, u] à l'aide de la deuxième équation :

• S[D, u] = S[D, d] - m

Les deux valeurs peuvent ensuite être substituées dans les équations 3 et 4 afin de trouver S[U, u] et S[U, d]. S[D, u] peut être calculé immédiatement à partir de la quatrième équation :

• S[U, d] = ( S*(1-p) - S[D, d] * ( 1 - P[U] ) ) / P[U]

Il ne nous reste plus qu'à trouver une formule pour la dernière valeur inconnue. Substituons l'expression obtenue pour S[U, d] dans la troisième équation :

• S[U, u] = ( S*p - ( S[D, d] - m ) * ( 1 - P[U] ) ) / P[U]

Nous avons ainsi obtenu toutes les données nécessaires pour généraliser les formules S[U, u], S[D, d] pour les cas où "n != m". Les données suivantes ont été obtenues à partir de l'analyse des données du tableau :

1. m > n, p = 0,5
2. S[U, u] = Somme[ i = 0 ... n] ( i ) + (m-1)/3

Dans le cas contraire :

1. m < n, p = 0,5
2. S[D, d] = Somme[ i = 0 ... m] ( i ) + (n-1)/3

Les calculs seront plus simples pour le cas standard avec des limites symétriques :

1. m = n, p = 0,5
2. S[U, u] = Somme[ i = 0 ... n] ( i )
3. S[D, d] = Somme[ i = 0 ... m] ( i )

Prototypes pour obtenir la dernière équation

Définissons maintenant un prototype de la fonction modifiée qui décrira S[U, u], S[D, d] pour toutes les valeurs possibles de p. Pour construire un prototype fonctionnel de base, nous avons besoin de 3 points sur l'axe p et de quelques hypothèses concernant la structure globale. Je pense qu'il suffit de considérer deux types de fonctions génériques :

1. Sp[U, u] = S[U, u] ^ K(p)
2. Sp[D, d] = S[D, d] ^ K(q)
3. q = 1-p

Le premier type peut être un prototype fonctionnel réel ou un certain marqueur indiquant que la structure est différente et nécessite une autre logique. Il s'est avéré que la fonction de puissance est capable de rassembler toutes les données. Bien sûr, il peut y avoir des prototypes plus complexes, peut-être plus précis, mais je pense que notre solution est tout à fait suffisante. Le plus important est de comprendre la logique. Si toutefois vous souhaitez affiner le modèle, vous pourrez le faire sur la base des données présentées dans l'article. J'ai créé un programme de test :

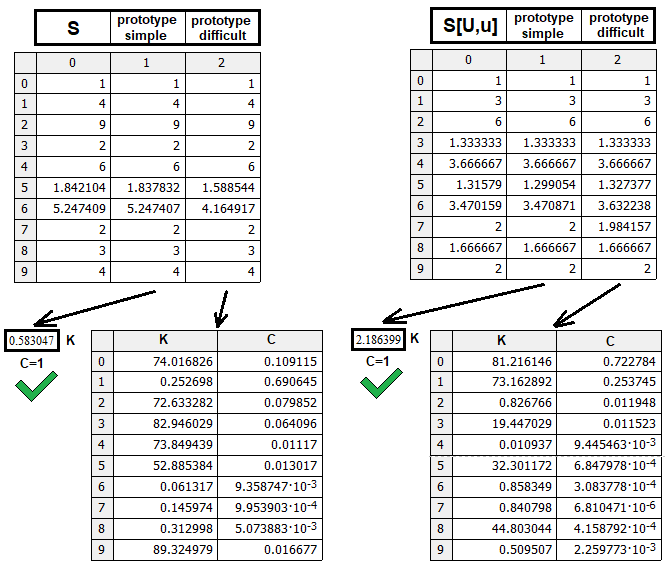
Le programme vérifie les deux prototypes, S(n, m, p) et S[U, u](n, m, p). Aucune vérification n'est nécessaire pour S[D, d](n, m, p), car cette fonction est reflétée dans S[U, u](n, m, p), et donc S[D, d](n, m, p) = S[U, u](m, n, p-1). La figure montre la comparaison des prototypes trouvés en termes d'efficacité. Chaque prototype a été testé avec le même nombre de combinaisons aléatoires de poids et de coefficients de puissance dans les formules. Le prototype plus simple donne de meilleurs résultats avec le même nombre de cycles de recherche. Si nécessaire, il est possible d'effectuer des calculs supplémentaires pour voir ce que des prototypes plus complexes sont capables de faire.

Après vérification, nous devons définir la structure interne des fonctions imbriquées "K(p)", "K(q)". Sa structure interne doit assurer la coïncidence obligatoire aux points p=0, p=0,5, p=1, q=0, q=0,5, q=1. Nous connaissons les valeurs de la fonction en ces points, ce qui facilite la sélection du prototype requis :

1. p = 0,5 ; Sp[U, u] = S[U,u] --> K(0,5) = 1 ,
2. p = 1.0 ; Sp[U, u] = n = S[U, u]^(Log[S[U, u]-->n]) --> K(1.0) = Log[S[U, u]-->n]
3. p = 0,0 ; Sp[U, u] = 0 = S[U, u]^(-infini) --> K(0, 0) = -infini
4. q = 0,5 ; Sp[D, d] = S[D, d] --> K(0,5) = 1 ,
5. q = 1.0 ; Sp[D, d] = n = S[D, d]^(Log[S[U, u]-->m]) --> K(1.0) = Log[S[D, d]-->m]
6. q = 0,0 ; Sp[D, d] = 0 = S[D, d]^(-infini) --> K(0, 0) = -infini

Les première et quatrième expressions montrent que la puissance doit être égale à 1 au point de marche aléatoire. Les deuxième et cinquième expressions indiquent que la puissance doit être telle que, lorsqu'on lui élève une valeur, on obtient soit "n", soit "m", comme le montre le tableau de résultats ci-dessus. Les troisième et sixième expressions montrent que la puissance doit tendre vers moins l'infini pour donner 0. Ce fait implique également que les valeurs p et q doivent figurer au dénominateur du prototype, car la division par zéro conduit à des valeurs telles que l'infini. Nous avons déjà eu l'occasion de construire un prototype de loi de puissance pour une fonction. Nous pouvons l'utiliser comme base et la réviser. Après une analyse approfondie du problème, j'en suis arrivé à ce prototype :

• K(p) = 1 + D * Somme(N) (Kn[0] * | (( p - 0.5 )/(0.5*p)) | ^ A[0] (( p - 0,5 )/(0,5*p)) ^ A[0] + Kn[1] * (( p - 0,5 )/(0,5*p)) | ^ A[1] + .... + Kn[N] * (( p - 0,5 )/(0,5*p)) | ^ A[N])
• Kn[0] + Kn[1] + .... Kn[N] = Log[S[U, u]-->n] - 1
• D = (( p - 0,5 )/(0,5*p)) / (( p - 0,5 )/(0,5*p)) |
• K(q) = 1 + C * Somme(N) (Km[0] * (( q - 0,5 )/(0,5*q)) ^ B[0] + Km[1] * (( q - 0,5 )/(0,5*q)) ^ B[1] + .... + Km[N] * (( q - 0,5 )/(0,5*q)) ^ B[N])
• Km[0] + Km[1] + .... Km[N] = Log[S[D,d]-->m] - 1
• C = (( q - 0,5 )/(0,5*q)) / (( q - 0,5 )/(0,5*q)) |
• Kn, Km – le poids des termes appropriés
• A, B – la sensibilité des termes

La fonction semble compliquée, mais elle est basée sur une logique simple. Si "p=0,5, q=0,5", tout ce qui se trouve sous le signe de la somme devient nul et il ne reste que 1, ce qui donne les conditions "1", "4". Si "p=1, q=1", les fractions correspondantes de la somme, qui sont élevées à une puissance, deviennent 1 : |(( p - 0,5 )/(0,5*p)) |. Ces termes sont écrits avec le signe du modulo pour exclure les valeurs complexes de la fonction lorsqu'elle est élevée à une puissance. Au lieu de cela, le signe correspondant est fourni comme un facteur supplémentaire. La puissance n'affecte plus ces termes, et la somme entière devient Log[S[U, u]-->n] - 1, Log[S[D, D]-->m] - 1. En ajoutant ce nombre à 1, nous obtenons les valeurs requises de la fonction : Log[S[U, u]-->n], Log[S[D, d]-->m].

Les polynômes d'interpolation sont construits selon une logique similaire, comme par exemple le célèbre polynôme de Lagrange. Notre polynôme est conçu pour une tâche spécifique, pour laquelle il peut être appliqué. Son avantage est qu'il s'adapte parfaitement à la tâche. Pour trouver la fonction souhaitée à partir de cette famille de courbes, il suffit de trouver 2 tableaux de nombres.

Mise en œuvre et test du modèle mathématique

Avec les expressions trouvées, nous pouvons facilement mettre en œuvre la fonctionnalité nécessaire pour calculer n'importe quelle fractale. Nous n'aurons besoin que d'une seule structure qui servira de conteneur pour toutes les données que la fonction principale renverra. Les autres fonctions seront auxiliaires. Nous n'avons besoin que de la dernière fonction :

struct MathModel1//structure for the first mathematical model
   {
   double S;//the average number of any steps
   double pU;//the probability that the price will first reach the upper border
   double pD;//the probability that the price will first reach the lower border
   double SUu;//the average number of steps up if the price first reaches the upper border
   double SUd;//the average number of steps down if the price first reaches the upper border
   double SDu;//the average number of steps up if the price first reaches the lower border
   double SDd;//the average number of steps down if the price first reaches the lower border
   
   double SPUu;//the average probable number of steps up if the price first reaches the upper border
   double SPUd;//the average probable number of steps down if the price first reaches the upper border
   double SPDu;//the average probable number of steps up if the price first reaches the lower border
   double SPDd;//the average probable number of steps down if the price first reaches the lower border
   
   double SPUud;//the average probable number of steps in any direction if the price first reaches the upper border
   double SPDud;//the average probable number of steps in any direction if the price first reaches the lower border
   
   double SUDu;//the average number of steps up when reaching any of the borders
   double SUDd;//the average number of steps down when reaching any of the borders
   };

double Ss(int n, int m,double p, double K)//prototype of the function of the average number of steps in any direction when reaching any border
   {
   if (p>=0.5) return n*MathPow(m,MathPow((1-p)/0.5,K));
   else return MathPow(n,MathPow(p/0.5,K))*m;
   }

double Log(double a, double b)//logarithm function for any base
   {
   if (MathLog(a) != 0) return MathLog(b)/MathLog(a);
   else return 0.0;
   }

double SUu(int n,int m)//average number of steps up to the upper border if p=0.5
   {
   double rez=0.0;
   if (m>n)
      { 
      for (int i=0;i<=n;i++) rez+=double(i);
      rez+=(m-1)/3.0;
      }
   if (m==n) for (int i=0;i<=n;i++) rez+=double(i);
   return rez;
   }
   
double SDd(int n,int m)//average number of steps down to the lower border if p=0.5
   {
   double rez=0.0;
   if (n>m)
      { 
      for (int i=0;i<=m;i++) rez+=double(i);
      rez+=(n-1)/3.0;
      }   
   if (m==n) for (int i=0;i<=m;i++) rez+=double(i);
   return rez;
   }   

double KpnEasy(int n,int m, double p,double A)//power prototype for steps up m>=n
   {
   double D;
   if ( p-0.5 != 0 ) D=(p-0.5)/MathAbs(p-0.5);
   else D=1.0;
   return 1.0 + D*(Log(SUu(n,m),n) - 1)*MathPow(((p-0.5)/(0.5*p)),A);
   }

double KpmEasy(int n,int m,double p,double A)//power prototype for steps down m<n
   {
   double D;
   if ( 0.5-p != 0 ) D=(0.5-p)/MathAbs(0.5-p);
   else D=1.0;
   return 1.0 + D*(Log(SDd(n,m),m) - 1)*MathPow(((0.5-p)/(0.5*(1.0-p))),A);
   }
   
double SUuS(int n,int m,double p, double A)//full prototype for average steps up m>=n
   {
   return MathPow(SUu(n,m),KpnEasy(n,m,p,A));
   }
   
double SDdS(int n,int m,double p, double A)//full prototype for average steps down  n>m
   {
   return MathPow(SDd(n,m),KpmEasy(n,m,p,A));
   }      
   
MathModel1 CalculateMathModel(int n, int m, double p,double K=0.582897,double A=2.189246)//calculating the entire mathematical model
   {
   MathModel1 Mt;
   if ( m >= n )
      {
      Mt.S=Ss(n,m,p,K);
      Mt.pU=(2*p*Mt.S-Mt.S+m)/(n+m);
      Mt.pD=1.0-Mt.pU;
      Mt.SUu=SUuS(n,m,p,A);
      Mt.SUd=Mt.SUu-n;
      if (1.0-Mt.pU != 0.0) Mt.SDu=(Mt.S*p-Mt.SUu*Mt.pU)/(1.0-Mt.pU);
      else Mt.SDu=0.0;
      if (1.0-Mt.pU != 0.0) Mt.SDd=(Mt.S*(1.0-p)-Mt.SUd*Mt.pU)/(1.0-Mt.pU);
      else Mt.SDd=0.0;
      }
   else
      {
      Mt.S=Ss(n,m,p,K);
      Mt.pU=(2*p*Mt.S-Mt.S+m)/(n+m);
      Mt.pD=1.0-Mt.pU;
      Mt.SDd=SDdS(n,m,p,A);
      Mt.SDu=Mt.SDd-m;
      if (Mt.pU != 0.0) Mt.SUd=(Mt.S*(1.0-p)-Mt.SDd*(1.0-Mt.pU))/Mt.pU;
      else Mt.SUd=0.0;
      if (Mt.pU != 0.0) Mt.SUu=(Mt.S*p-Mt.SDu*(1.0-Mt.pU))/Mt.pU;
      else Mt.SUu=0.0;      
      }
   
   Mt.SPUu=Mt.SUu*Mt.pU;
   Mt.SPUd=Mt.SUd*Mt.pU;
   Mt.SPDu=Mt.SDu*Mt.pD;
   Mt.SPDd=Mt.SDd*Mt.pD;
   
   Mt.SPUud=Mt.SPUu+Mt.SPUd;
   Mt.SPDud=Mt.SPDu+Mt.SPDd;
   
   Mt.SUDu=Mt.SPUu+Mt.SPDu;
   Mt.SUDd=Mt.SPUd+Mt.SPDd;
   
   return Mt;
   }

Pour vérifier le modèle mathématique, j'ai implémenté un code analogue dans MathCad15. Si le modèle mathématique est composé correctement, les résultats du tableau doivent coïncider avec le résultat obtenu par le modèle mathématique. La liste des programmes est jointe à l'article, vous pouvez donc la consulter vous-même. J'ai décidé de ne pas ajouter le code de présentation directement dans l'article car il prendrait trop de place, mais vous devriez certainement voir le résultat. Comparons les matrices et assurons-nous que le modèle mathématique est viable :

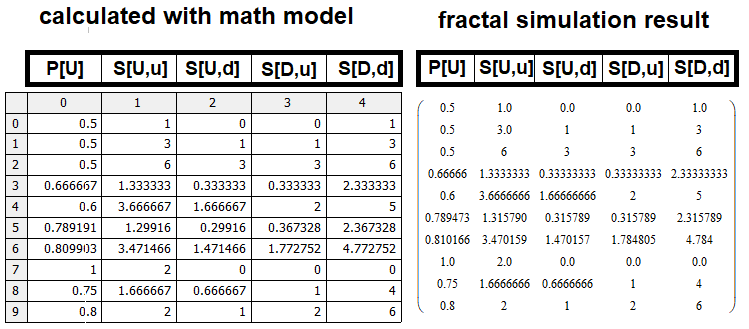
Bien sûr, il y a quelques imprécisions, qui sont dues à l'efficacité de nos prototypes trouvés pour les valeurs S, S[U, u], S[D, d]. Un autre facteur de différences mineures peut être lié aux imprécisions de la simulation, qui sont plus importantes pour des valeurs plus grandes de n et m simulés, car nous devons limiter la profondeur de la simulation en raison de la puissance de calcul limitée.

Conclusion

J'ai passé beaucoup de temps à développer ce modèle mathématique, car j'ai dû concevoir toutes les mathématiques à partir de zéro. Mais quoi qu’il en soit, je suis satisfait du résultat. Dans les prochains articles, j'essaierai de développer des modèles mathématiques plus universels qui, une fois combinés, permettraient de calculer n'importe quelle configuration de trading en fonction de ses principales caractéristiques. Le modèle mathématique convient aussi non seulement pour décrire les processus de fixation des prix, mais il peut également être utilisé pour décrire les signaux de trading et pour simplifier les stratégies complexes, en les ramenant à des stratégies plus simples. Cela prendra un certain temps. 

Références

• Combinatoire et théorie des probabilités pour le trading (Partie I) : L'essentiel

• Combinatoire et théorie des probabilités pour le trading (Partie II) : Fractale universelle