Algorithme de rebuy (rachat) : Modèle mathématique pour accroître l'efficacité

Sommaire

• Introduction
• Méthodes d'affinage des caractéristiques de trading basées sur l'algorithme de calcul de la moyenne
• "Help me get out of the drawdown"
• Réflexions générales sur l'algorithme de calcul de la moyenne
• Les subtilités d'une évaluation plus précise des systèmes de rachat
• Compréhension approfondie et universelle de la rentabilité
• Évaluation universelle
• Exemples de méthodes de clarification
• Accroître l'efficacité des systèmes grâce à la diversification
• Limites utiles
• Fonctionnalités utiles pour l'utilisation d'outils parallèles
• Distribution normale d'une variable aléatoire
• Beauté de la courbe de profit dans le cadre de la loi de distribution des valeurs aléatoires
• Conclusion

Introduction

Cette méthode de trading est activement utilisée dans une grande variété d'Expert Advisors. Il existe également de nombreuses variétés et de versions hybrides. A en juger par le nombre de références à ces systèmes, il est également évident que ce sujet est très populaire non seulement sur ce site, mais aussi sur toutes les autres ressources web. Toutes les méthodes ont un concept commun qui consiste à trader contre les mouvements du marché. En d'autres termes, l'EA utilise les rachats (rebuys) pour pouvoir acheter le plus bas possible et vendre le plus haut possible.

Il s'agit d'un système de trading classique, vieux comme le monde. Dans l'un des articles précédents, j'ai partiellement abordé ce sujet, tout en soulignant les possibilités d'hybridation de ces méthodes. Dans cet article, nous allons examiner le concept de plus près, en allant plus loin que les utilisateurs des forums. Toutefois, l'article sera plus général et beaucoup plus vaste, car l'algorithme de rachat est tout à fait adapté pour mettre en évidence certaines caractéristiques très intéressantes et très utiles.

Méthodes d'affinage des caractéristiques de trading basées sur l'algorithme de calcul de la moyenne

"Help me get out of the drawdown" (des auteurs de "my EA makes good money, but sometimes blows up the entire account")

Il s'agit d'un problème commun à de nombreux traders algorithmiques et de traders manuels. Au moment d'écrire cet article, j'ai eu une conversation avec une personne de ce genre, mais elle n'a pas saisi l'intégralité de mon point de vue. Malheureusement, il me semble qu'il n'a pratiquement aucune chance de comprendre le côté comique d'une telle situation. Après tout, si je pouvais un jour poser une question similaire à mon moi plus âgé et plus expérimenté, il est fort probable que je serais également incapable de comprendre la réponse. Je sais même ce que je ressentirais si je me répondais vraiment à moi-même. Je penserais que je suis humilié ou dissuadé de continuer à m'engager dans le trading algorithmique.

En réalité, tout est beaucoup plus simple. J'ai simplement eu la patience de suivre un certain chemin et d'acquérir une certaine sagesse, si l'on peut dire. Il ne s'agit pas d'une idéalisation et d'un éloge de soi, mais plutôt d'un minimum nécessaire. Il est dommage que ce chemin ait pris des années au lieu de semaines et de mois.

Il y a ici tout un monde de rêves et d'illusions, et pour être honnête, je commence déjà à me lasser de la simplicité de certaines personnes. Arrêtez de faire n'importe quoi et de vous prendre pour les rois du marché. Contactez plutôt une personne expérimentée et demandez-lui de choisir un EA adapté à votre budget. Croyez-moi, vous économiserez ainsi beaucoup de temps et d'argent, sans parler de votre santé mentale. L'une de ces personnes a écrit cet article. Les preuves sont fournies ci-dessous.

Réflexions générales sur l'algorithme de calcul de la moyenne

Si l'on examine l'algorithme de rebuy, ou "moyennage", on peut d'abord penser que ce système ne présente aucun risque de perte. Il fut un temps où je ne connaissais pas encore ces astuces et où j'étais surpris par les énormes espérances mathématiques qui surpassaient tous les écarts. Il est clair que ce n'est qu'une illusion, mais cette approche a un côté rationnel. Mais nous y reviendrons plus tard. Tout d'abord, pour pouvoir évaluer objectivement ces systèmes, nous devons connaître certains paramètres indirects qui peuvent nous en dire un peu plus que la simple image d'une croissance des bénéfices.

Les paramètres les plus pertinents du rapport du testeur de stratégie peuvent même aider à comprendre que le système est manifestement en train de perdre, même si la courbe d'équilibre semble excellente. Comme vous l'avez peut-être déjà compris, il s'agit en fait de la courbe de rentabilité. En fait, tous les indicateurs importants du système de trading sont secondaires par rapport aux caractéristiques mathématiques premières et les plus fondamentales, qui sont, bien entendu, l'espérance mathématique et ses caractéristiques primaires. Mais il convient de noter que l'espérance mathématique est une valeur tellement flexible que l'on peut toujours tomber dans le piège de l'illusion.

En effet, pour utiliser correctement un concept tel que l'espérance mathématique, il faut tout d'abord comprendre qu'il s'agit de la terminologie de la théorie des probabilités, et que tout calcul de cette quantité doit être effectué selon les règles de la théorie des probabilités, à savoir :

• Les calculs sont d'autant plus précis que l'échantillon analysé est grand. Idéalement, la valeur exacte est calculée à partir d'un échantillon infini.
• Si l'on décompose l'infini en plusieurs parties, on obtient plusieurs infinis

Quelqu'un pourrait se demander comment calculer l'espérance mathématique exacte d'une stratégie particulière, si nous ne disposons que d'un échantillon limité de cotations réelles. Et quelqu'un se demandera pourquoi nous avons besoin de ces infinis. En effet, toutes les estimations de certaines valeurs moyennes, telles que l'espérance mathématique, n'ont de poids que dans le domaine où ces calculs ont été effectués, mais n'ont rien à voir avec un autre domaine. Toute caractéristique mathématique n'a de poids que là où elle est calculée. Mais certaines techniques peuvent être distinguées pour affiner les caractéristiques de la rentabilité d'une stratégie particulière, ce qui permettra d'obtenir les valeurs les plus proches des valeurs réelles des paramètres requis.

Ceci est directement lié à notre tâche. Après s'être rendu compte que nous ne pouvons pas voir l'avenir d'une stratégie infiniment longue, ce qui en soi semble déjà être un non-sens complet. Il s'agit néanmoins d'un fait mathématique et d'une condition nécessaire et suffisante pour calculer les véritables caractéristiques mathématiques. Nous en arrivons à l'idée de rapprocher le nombre calculé sur un échantillon limité du nombre qui pourrait être calculé sur un échantillon infini. Les personnes familiarisées avec les mathématiques savent qu'il existe 2 concepts mathématiques permettant de calculer des sommes infinies :

• L’intégrale
• La somme de séries infinies

Je pense qu'il est clair pour tout le monde que pour calculer l'intégrale, ainsi que la somme de la série, il est nécessaire d'obtenir soit tous les points de la fonction dont l'intégrale doit être calculée dans le domaine d'intégration considéré, soit tous les éléments de la séquence de nombres dans la série considérée. Il reste l'option la plus parfaite : obtenir les expressions mathématiques appropriées pour la fonction que nous allons intégrer, et l'expression pour générer les éléments de la série. Dans de nombreux cas, si nous disposons des expressions mathématiques appropriées, nous pouvons obtenir les équations exactes de l'intégrale finie ou de la somme de la série. Mais dans le cas du trading réel, nous ne serons pas en mesure d'appliquer le calcul différentiel et, en général, cela ne nous aidera pas beaucoup, mais il est important de le comprendre.

La conclusion de tout ceci est que pour l'évaluation directe d'un système, nous ne disposons que d'un échantillon limité et de certains paramètres que nous obtenons dans le testeur de stratégie. En fait, leur importance est largement exagérée. La question se pose de savoir s'il est possible de juger de la rentabilité d'une stratégie particulière en utilisant les paramètres du testeur de stratégie, si ces paramètres sont suffisants pour obtenir une réponse sans ambiguïté et, surtout, comment utiliser ces paramètres correctement et si nous les utilisons vraiment correctement.

Nous devons également comprendre que pour chaque stratégie, tout paramètre permettant d'évaluer correctement la rentabilité et la sécurité réelles de la stratégie peut être complètement différent. Ceci est directement lié à l'évaluation de la courbe de profit. Pour le comprendre, dessinons d'abord une vue générale approximative de la courbe de trading que nous obtenons en utilisant l'algorithme de rachat :

Fig. 1

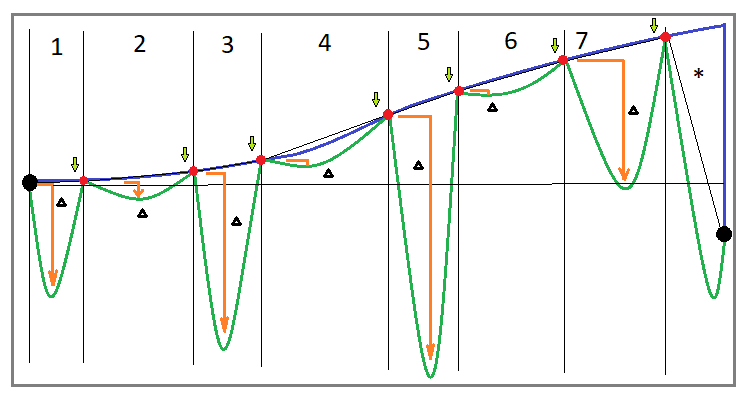
Commençons par la mise en œuvre d'un rachat pour un instrument. Si vous mettez correctement en œuvre cet algorithme, votre activité de trading consistera dans tous les cas en des cycles. Idéalement, tous les cycles devraient être positifs. Si certains cycles se terminent dans la zone négative, alors soit vous mettez en œuvre cet algorithme de manière incorrecte, soit il ne s'agit plus d'un algorithme pur et il comporte déjà des modifications. Mais nous allons considérer le rebuy classique. Définissons quelques paramètres caractéristiques de la courbe de trading pour indiquer un rachat classique :

• La courbe d'équilibre doit être croissante et comporter N cycles
• Tous les cycles ont un bénéfice positif
• Lorsque les échanges sont interrompus, il est probable que nous nous trouvions dans le dernier cycle incomplet.
• Un cycle incomplet a une rentabilité négative
• Les cycles sont caractérisés par des baisses en termes de capital.

Il semble que l'aspect général de la courbe devrait indiquer clairement au premier coup d'œil qu'un tel système est rentable. Mais tout n'est pas si simple. Si vous regardez le dernier cycle de trading inachevé, que j'ai spécifiquement clôturé en dessous du point de départ, vous verrez que dans certains cas vous aurez de la chance et vous attendrez la fin du cycle, tandis que dans d'autres cas vous n'attendrez pas jusqu'à la fin et vous ferez face à une grosse perte ou vous perdrez complètement votre dépôt. Mais pourquoi cela arrive-t-il ? En effet, l'image peut donner l'impression, à tort, que le montant des drawdowns des fonds est limité en valeur absolue et que, par conséquent, le temps consacré à ce drawdown devrait également être limité.

En réalité, plus la zone de test est longue, plus la zone moyenne de drawdown est longue. Il n'y a absolument aucune limite. La limite n'existe que sous la forme de votre dépôt et de la qualité de votre gestion de l'argent. Mais une approche compétente de la mise en place de votre système, basée sur ce principe, ne peut que conduire à une augmentation de la durée de vie de votre dépôt avant qu'il ne soit finalement détruit ou, au mieux, qu'il ne fasse qu'un très faible profit.

Lorsqu'il s'agit de tester des systèmes basés sur l'algorithme de rebuy (calcul de la moyenne), afin d'évaluer correctement leur capacité de survie, leur fiabilité et leur rentabilité réelle, il convient d'adhérer à une structure de test spécifique. Le fait est que lavaleur d'un seul test dans cette approche est minimisée pour une raison simple : lorsque vous testez une stratégie "normale", votre bénéfice pour l'ensemble du test dans le testeur de stratégie est très proche de la valeur distribuée "normalement". Cela signifie que lorsque vous testez une stratégie moyenne sans maintenir une position pendant une longue période, vous obtiendrez un nombre à peu près égal de zones de test rentables et non rentables, ce qui vous indiquera très rapidement que la stratégie est instable ou que la stratégie a une compréhension correcte du marché et qu'elle fonctionne sur l'ensemble de l'historique.

Lorsqu'il s'agit d'une stratégie de rachat, cette distribution peut être fortement déformée, car pour tester correctement ce système, il faut fixer le dépôt maximum possible. le résultat du test dépend aussi fortement de la longueur de la section de test. En effet, dans cette approche, toutes les opérations sont basées sur des cycles d'opérations. Chaque paramètre unique de ce système peut avoir à la fois un paramètre complètement différent du drawdown moyen et le paramètre de la durée moyenne du drawdown qui lui est associé. En fonction de ces indicateurs, des sections de test trop courtes peuvent donner lieu à des résultats de test trop élevés ou trop faibles. En règle générale, peu de tests de ce type sont effectués, ce qui peut dans la plupart des cas être à l'origine d'une confiance excessive dans le fonctionnement de ces systèmes.

Les subtilités d'une évaluation plus précise des systèmes de rachat

Voyons maintenant comment évaluer correctement les performances des systèmes utilisant l'algorithme de rachat, tout en appliquant les paramètres connus des systèmes de trading. Tout d'abord, dans le cadre d'une telle évaluation, je conseillerais d'utiliser une seule caractéristique : le facteur de récupération. Voyons comment le calculer :

• Facteur de Récupération = Profit Total / Réduction Maximale des Fonds Propres
• Profit Total - profit total par zone de trading
  
• Réduction Maximale des Fonds Propres - réduction maximale des fonds propres (drawdown) par rapport au point de jonction précédent pour l'équilibre et les fonds propres (pic d'équilibre).
  

Comme on peut le voir, il s'agit du bénéfice final divisé par le drawdown (ou réduction maximale) des fonds. La signification mathématique de cet indicateur au sens classique est que, selon l'idée, il devrait montrer la capacité du système à restaurer son drawdown. La condition limite pour la rentabilité d'un système de trading utilisant cette caractéristique est la suivante :

• Facteur de Récupération > 1
  

Si on le traduit en langage humain compréhensible, cela signifie que pour faire un profit, on ne peut pas risquer plus que le même montant du dépôt. Dans de nombreux cas, ce paramètre fournit une évaluation précise de la qualité des échanges pour un système particulier. Utilisez-le, mais soyez très prudent, car il s'agit d'une valeur assez controversée quant à sa signification mathématique.

Mais je vais devoir vous révéler tous ses inconvénients pour que vous compreniez que ce paramètre est également très arbitraire et que le niveau de sa signification mathématique est également très faible. Bien sûr, vous pourriez dire que si vous critiquez quelque chose, vous devez proposer une alternative. Je le ferai certainement, mais seulement après avoir analysé ce paramètre. Ce paramètre est lié au drawdown maximal qui, à son tour, peut être lié à n'importe quel point de la courbe de trading. Ceci signifie que si nous recalculons ce drawdown par rapport au solde de départ et que nous le remplaçons par le drawdown maximal, nous obtenons presque toujours un facteur de récupération surestimé. Formalisons tout cela correctement :

• Variation du Facteur de Recouvrement 1 = Profit Total / Réduction Maximale des Fonds Propres depuis le début de l'opération
• Réduction Maximale des Fonds Propres depuis le début de l'opération - drawdown maximal à partir du solde de départ (et non du maximum précédent)
  

Bien sûr, il ne s'agit pas d'un facteur de récupération classique, mais dans son essence, il détermine la rentabilité beaucoup plus correctement par rapport à la condition limite généralement acceptée. Commençons par représenter visuellement les deux options de calcul de cet indicateur - l'option classique et la mienne : 

Fig. 2

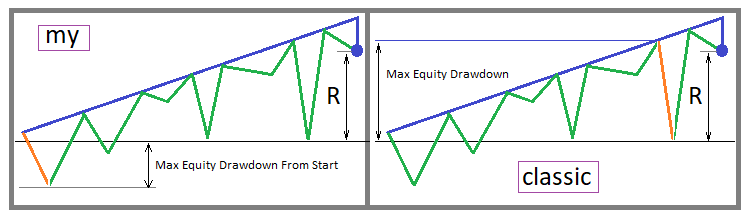
On peut constater que dans le premier cas, ce paramètre prendra des valeurs plus élevées, ce qui est bien sûr ce que nous souhaitons. Mais du point de vue de l'évaluation de la rentabilité, deux approches peuvent être suivies. Le paramètre classique est plus adapté à l'approche, dans laquelle il est préférable d'allonger le plus possible la durée de la section de test. Dans ce cas, une valeur plus élevée du Max Equity Drawdown compense le fait que ce drawdown ne commence pas au tout début de la courbe de trading, et donc ce paramètre est dans la plupart des cas proche de l'estimation réelle. Mon paramètre est plus efficace lorsqu'il s'agit d'évaluer plusieurs backtests.

En d'autres termes, ce paramètre est d'autant plus précis que votre stratégie a été testée plusieurs fois. Votre stratégie doit être testée dans le plus grand nombre de domaines possible. Cela signifie que les points de départ et d'arrivée doivent être choisis avec une variabilité maximale. Pour une évaluation correcte, il est nécessaire de sélectionner "N" des domaines les plus différents et de les tester, puis de calculer la moyenne arithmétique de cet indicateur pour tous les domaines testés. Cette règle nous permettra d'affiner les deux versions du facteur de récupération, la mienne et la classique, avec pour seul différence que moins de backtests indépendants devront être réalisés pour affiner la version classique.

Néanmoins, dire que ces manipulations de clarification sont peu nombreuses pour clarifier ces paramètres serait un euphémisme. J'ai présenté ma propre version du facteur de récupération afin de montrer que tout le monde peut créer son propre paramètre, et qu'il peut même être ajouté comme l'une des caractéristiques calculées pour le backtesting dans MetaTrader. Mais aucun de ces paramètres ne fait l'objet d'une preuve mathématique et chacun comporte ses propres erreurs et limites d'applicabilité. Tout cela signifie qu'à l'heure actuelle, il n'existe pas d'indicateur mathématique exact permettant une évaluation absolument précise de l'un ou l'autre algorithme utilisant le rebuy. Mais mon paramètre tendra vers la précision absolue avec l'augmentation du nombre de tests. Je fournirai plus de détails dans la section suivante.

Compréhension approfondie et universelle de la rentabilité

Évaluation universelle

Je pense que tout le monde sait que des paramètres tels que l'espérance mathématique de gain et le facteur de gain existent dans tous les rapports du testeur de stratégie ou dans les caractéristiques d'un signal de trading. Mais je pense que personne ne vous a dit que ces caractéristiques peuvent également être utilisées pour calculer la rentabilité d’un système de trading où il n'y a pas suffisamment d'analyse des transactions. Vous pouvez donc utiliser ces paramètres en remplaçant l'unité "position" par "test sur le segment". Pour calculer cet indicateur, vous devrez effectuer de nombreux tests indépendants sans tenir compte de la structure à l'intérieur. Cette approche vous aidera à évaluer les perspectives réelles du système de trading en utilisant uniquement les deux paramètres les plus courants. Elle peut également vous donner une habitude extrêmement utile : les tests multiples. Pour utiliser cette approche, il suffit de connaître l'équation suivante :

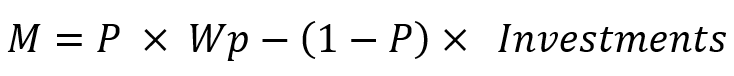
avec :

• M - la valeur attendue du gain
• Wp - le bénéfice souhaité
• Investments - le montant que vous êtes prêt à investir pour réaliser le profit souhaité
• P - la probabilité que l'investissement soit suffisant jusqu'à ce que le bénéfice soit atteint
• (1-P) - la probabilité que nous n'ayons pas assez d'investissements jusqu'à ce que le profit soit atteint (perte de dépôt)

Vous trouverez ci-dessous une équation similaire pour le facteur de profit :

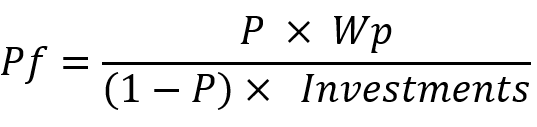
Tout ce que vous devez savoir, c'est qu'en cas de trading aléatoire et en l'absence d'obstacles tels que le spread, la commission et le swap ou le slippage, ces variables prendront toujours les valeurs suivantes pour n'importe quel système de trading :

M=0

Pf=1

Ces caractéristiques ne peuvent évoluer dans votre sens que si un moment prédictif se présente. Par conséquent, la probabilité que nous fassions un profit sans perdre le dépôt prendra la valeur suivante :

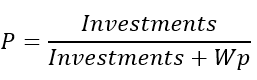
Si vous remplacez cette expression par la probabilité dans nos équations, vous obtiendrez les identités que j'ai fournies. Si nous prenons en compte le spread, la commission et le swap, nous obtenons ceci :

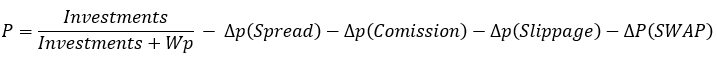
Le spread, la commission et le swap réduisent la probabilité finale, ce qui fait perdre aux identités leur validité. Les inégalités suivantes apparaissent à la place :

• M < 0
• Pf < 1

C'est le cas avec n'importe quel système de trading, et l'algorithme de rebuy ici n'est absolument pas meilleur que n'importe quel autre système. Lors du test ou de l'exploitation d'un tel système, il est possible dedéformer fortement la fonction de distribution de la valeur aléatoire du signal ou du profit final du backtest. Mais ce scénario ne se produit généralement que lors des tests ou d'une exploitation sur le court terme.

En effet, la probabilité de subir une baisse importante est beaucoup plus faible si vous testez sur une courte section. Mais lorsque vous commencez à effectuer ces tests sur des segments plus longs, vous verrez généralement des choses que vous n'aviez pas vues auparavant. Mais je suis sûr que la plupart d'entre nous pourront se rassurer en se disant que ce n'est qu'un accident et qu'il suffit de contourner ces zones dangereuses d'une manière ou d'une autre. Il en va généralement de même pour les essais multiples sur des segments courts.

Il n'y a qu'une seule façon de surmonter la non-rentabilité d'un système. Ajoutons une composante supplémentaire à l'équation de calcul des probabilités :

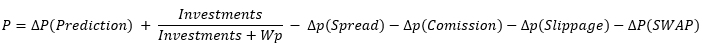
Comme nous pouvons le voir, la nouvelle composante "dP(Prediction)" est apparue dans l'équation. Il comporte un signe plus, ce qui est fait exprès pour montrer que seule cette composante est en mesure de compenser l'effet des spreads, des commissions et des swaps. Cela signifie que nous devons avant tout disposer d'une qualité de prédiction suffisante pour surmonter les effets négatifs et réaliser des bénéfices :

Nous ne pouvons obtenir les inégalités souhaitées que si nous fournissons cette inégalité particulière :

• M > 0
• Pf > 1

Comme vous pouvez le constater, ces expressions sont très faciles à comprendre et je suis sûr que personne ne mettra en doute leur exactitude. La sous-section suivante sera plus facile à comprendre si l'on utilise ces équations. En effet, je vous conseille de vous en souvenir, ou du moins de vous souvenir de leur logique, afin de pouvoir toujours les remettre en mémoire en cas de besoin. L'essentiel est de bien les comprendre. En général, une seule de ces équations suffit, mais j'ai pensé qu'il serait préférable d'en montrer deux à titre d'exemple. Quant aux autres paramètres, je pense qu'ils sont redondants dans le cadre de cette section.

Exemples de méthodes de clarification

Dans cette sous-section, je vous propose quelques manipulations supplémentaires qui vous permettront d'obtenir une valeur plus correcte du facteur de récupération. Je suggère de revenir à la "Figure 1" et d'examiner les segments numérotés. Pour affiner le facteur de récupération, il faut imaginer que ces segments sont des tests indépendants. De cette manière, nous pouvons nous passer de tests multiples, en supposant que nous avons déjà effectué ces tests. Nous pouvons le faire parce que ces segments sont des cycles qui ont à la fois un point de départ et un point d'arrivée, ce qui assure une équivalence avec le backtest. 

Dans le cadre de cette section, je pense qu'il est également utile de compléter la première image par son équivalent, compte tenu du fait que nous testons ou que nous tradons sur plusieurs instruments à la fois. Voici à quoi ressemblera la courbe de trading en utilisant l'algorithme de rachat pour une utilisation en parallèle sur plusieurs instruments :

Fig. 3

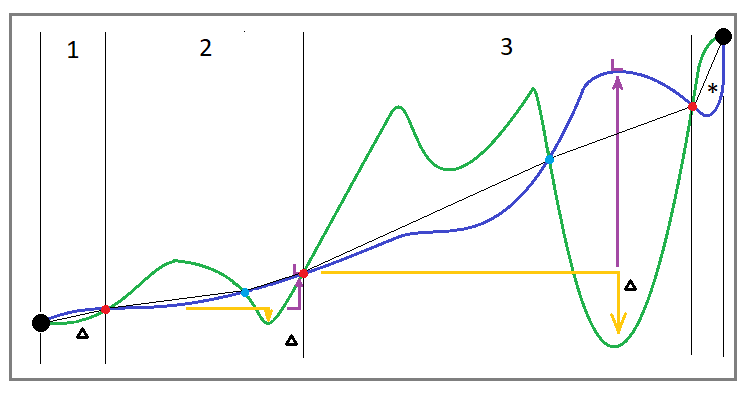
On constate que cette courbe diffère dans sa structure de la courbe de rebuy sur un seul instrument. J'ai ajouté ici des points bleus intermédiaires, ce qui signifie qu'avant la baisse, il peut y avoir des segments qui ont une "baisse inversée". Le fait est que nous ne pouvons pas considérer cela comme un drawdown. Néanmoins, nous n'avons pas le droit de considérer ces segments en dehors de l'analyse. C'est pourquoi ils doivent faire partie d'un cycle.

Je pense qu'il serait plus correct de reporter chaque nouveau cycle à la fin du précédent. Dans ce cas, la fin du cycle précédent doit être considérée comme le point de récupération de la dernière baisse (drawdown) des capitaux propres. Sur l'image, ces cycles sont séparés par des points rouges. Mais en fait, cette définition du cycle n'est pas suffisante. Il est également important de déterminer qu'il ne suffit pas de fixer le drawdown par les fonds propres, mais qu'il est important qu'il soit inférieur au début du cycle actuel. Sinon, de quel type de drawdown s'agit-il ?

Après avoir mis en évidence ces cycles, vous pouvez les considérer comme des tests indépendants distincts et calculer le facteur de récupération pour chacun d'entre eux. Cela peut se faire de la manière suivante :

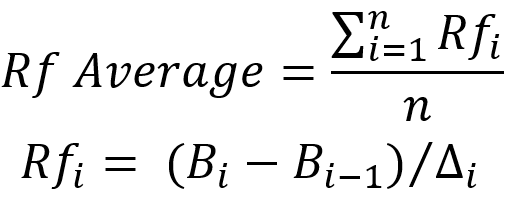
Dans cette équation, les points correspondants sur la courbe d'équilibre (la valeur finale du solde sur la section et la valeur initiale) sont représentés avec "B", et delta représente notre réduction. J'aimerais également que le lecteur revienne sur la dernière image. J'y ai représenté le delta à partir du point de départ rouge de chaque cycle, et non à partir du point de départ bleu, comme c'est généralement le cas, pour les raisons que j'ai énumérées plus haut. Mais si vous avez besoin de clarifier le facteur de récupération original, le delta doit être tracé à partir du point bleu. Dans ce cas, la méthode d'affinage des paramètres est plus importante que les paramètres eux-mêmes. La moyenne arithmétique simple est utilisée pour calculer la moyenne.

Néanmoins, même après avoir clarifié l'un ou l'autre paramètre, qu’il soit personnalisé ou classique, vous ne devez pas considérer le fait que la valeur de cet indicateur soit supérieure à 1, voire à 2 ou 3, comme le signe d'un système de trading rentable.

Il convient d'appliquer exactement la même équation à plusieurs backtests. Dans ce cas, tout backtest équivaut à un cycle. On peut même commencer par calculer les moyennes des cycles, et calculer ensuite la moyenne de la moyenne par rapport aux backtests. Nous pouvons aussi le faire beaucoup plus facilement en maximisant la durée du segment de test. Cette approche vous évitera au moins de multiplier les essais, car le nombre de cycles sera maximal, ce qui signifie que le facteur de récupération moyen sera calculé aussi précisément que possible.

Accroître l'efficacité des systèmes grâce à la diversification

Limites utiles

Après avoir examiné les possibilités d'affiner certaines caractéristiques des backtests, vous êtes sans doute mieux armé, mais vous ne connaissez toujours pas l'essentiel. La base est la réponse à la question suivante : pourquoi est-il nécessaire d'effectuer tous ces tests multiples ou de les diviser en cycles ? La question est vraiment complexe si l'on n'y consacre pas autant d'efforts que j'y consacre de temps. C'est malheureusement nécessaire. Mais avec mon aide, vous pouvez réduire considérablement le temps nécessaire à cette tâche.

Cette section vous permettra d'évaluer l'objectivité d'un paramètre particulier. J'essaierai de l'expliquer à la fois théoriquement et à l'aide des équations. Commençons par l'équation générale :

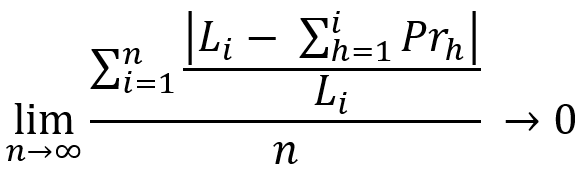
Considérons une équation similaire avec quelques légères modifications :

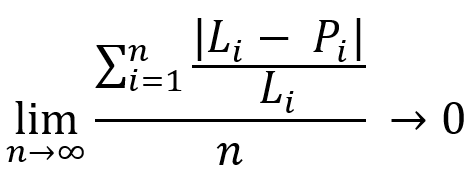
L'essence de ces équations est la même. Ces équations démontrent que danstout système de trading rentable, lorsque la durée de la section de test tend vers l'infini, nous obtiendrons une fusion complète des lignes de solde et de profit actuel, avec une certaine ligne représentant notre profit moyen. Dans la plupart des cas, la nature de cette ligne est déterminée par la stratégie que nous avons choisie. Regardons l'image suivante pour mieux comprendre :

Fig. 4

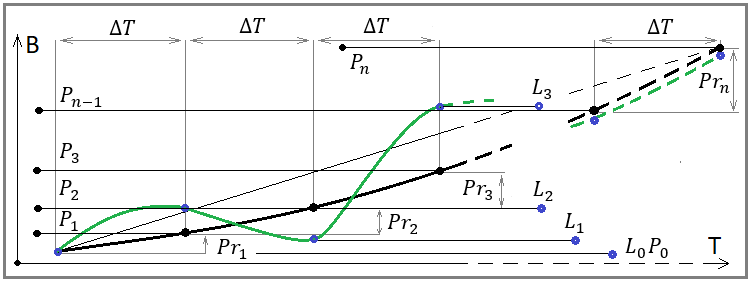
Si vous regardez attentivement cette image, vous y verrez toutes les quantités présentes dans nos équations. Il révèle le sens géométrique de nos limites mathématiques. La seule chose qui manque dans nos équations est l'intervalle de temps dT. Avec cet intervalle, nous discrétisons les pas de notre solde et nous donnons naissance à tous les points de notre série de nombres pour calculer le solde et le bénéfice de ces intervalles, et nous calculons également les valeurs de la ligne médiane en ces mêmes points. Ces équations sont l'équivalent mathématique de l'énoncé suivant :

• Plus nous combinons de tests multiples ou de courbes de trading, plus elles ressemblent à une ligne ascendante lisse (uniquement si le système est vraiment rentable).

En d'autres termes, tout système de trading rentable semble plus beau dans la partie graphique du testeur de stratégie ou du signal, plus la zone de test que nous choisissons est longue. Certains pourraient dire qu'aucun système ne peut atteindre de tels indicateurs. Mais il existe pourtant de nombreux exemples sur le Market, et il serait donc stupide de le nier. Tout dépend de l'universalité de l'algorithme et de votre compréhension de la physique du marché. Si vous connaissez les mathématiques qui sont toujours inhérentes au marché que vous négociez, vous obtenez en fait une courbe de profit qui croît à l'infini et vous n'avez pas besoin d'attendre l'infini pour confirmer l'efficacité du système. Il est évident qu'il s'agit d'une tâche extrêmement difficile, mais elle est néanmoins réalisable dans le cadre de nombreux algorithmes.

Terminons cette introduction théorique en apprenant à utiliser correctement les techniques discutées. On peut se demander comment utiliser ces techniques avec des sommes infinies, puisque nous ne disposons que d'échantillons limités et, par conséquent, de sommes incomplètes inévitables.

1. La réponse se trouve dans la division de l’historique entier en segments
2. Sélectionner plusieurs segments dont la longueur augmente constamment pendant la durée du test jusqu'à un segment de l'historique complet.
3. Choisir une méthodologie de test
4. Exécuter le test
5. Rechercher une amélioration du facteur de récupération et/ou du drawdown relatif.

L'essence de ce test délicat est de révéler des signes indirects que nos limites tendent réellement vers l'infini et zéro, respectivement. Pour accroître l'efficacité de notre système de test, nous devons comprendre que la section de test la plus longue doit au moins être plus belle que la plus courte et que, idéalement, chaque section suivante doit être à la fois plus grande et plus belle. Je n'utilise le concept de "plus beau" que pour faire comprendre à tout le monde qu'il s'agit en fait de l'équivalent de nos limites.

Mais nos limites ne sont valables que pour les considérations théoriques ou les préparations (comme vous voulez). À cet égard, la question se pose de savoir comment découvrir ces faits sans avoir recours à une "analyse à vue d'œil" ? Nous devons d'une manière ou d'une autre adapter nos limites aux paramètres que nous avons dans le rapport du testeur de stratégie. Autrement dit, nous avons besoin de limites alternatives pour certains paramètres du rapport ou du signal du testeur de stratégie afin que notre structure de test puisse être utilisée. Permettez-moi de vous montrer l'ensemble nécessaire et suffisant de limites alternatives :

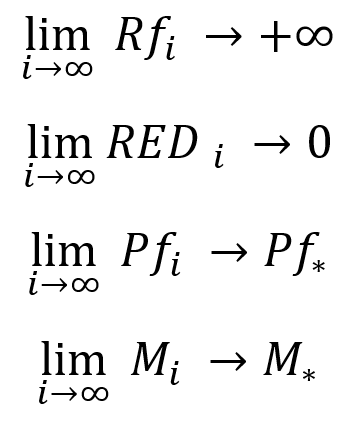
Ce qu'il faut comprendre ici :

1. Au cours d'un test infini, le facteur de récupération de toute stratégie rentable tend vers l'infini.
2. Au cours d'un test infini, l'écart relatif par action (de toute stratégie rentable) tend vers zéro.
3. Au cours d'un test infini, le facteur de profit des transactions de toute stratégie rentable tend vers sa valeur moyenne et a une limite réelle finie.
4. Au cours d'un test infini, l'espérance mathématique de toute stratégie rentable sans lot automatique activé (avec un lot fixe) tend vers sa valeur moyenne et a une limite réelle finie.

Tout ceci concerne des tests infinis, mais il est utile de comprendre la signification mathématique de ces limites avant de les adapter à un échantillon fini. L'adaptation de ces expressions à notre méthodologie devrait commencer par le fait que nous devrions sélectionner plusieurs segments de test, chacun d'entre eux devant être significativement plus grand que le précédent, de préférence au moins deux fois. Cela est nécessaire pour pouvoir remarquer la différence de lecture entre des tests plus courts et plus longs. Si nous numérotons nos tests de manière à ce que la longueur de l'indice augmente avec le temps, nous obtenons l'adaptation suivante pour le cas des échantillons finis :

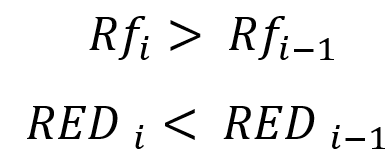
En d'autres termes, une augmentation du facteur de récupération et une diminution du drawdown relatif en termes de fonds sont des preuves indirectes que, très probablement, l'augmentation supplémentaire du segment de test ou de la durée de vie du signal rend notre courbe visuellement plus belle. Cela signifie que nous avons confirmé la réalisation de nos limites infinies. Dans le cas contraire, si la courbe de profit ne se redresse pas, on peut affirmer que le résultat obtenu est très proche du hasard et que la probabilité de pertes dans le futur est extrêmement élevée.

Bien sûr, beaucoup diront qu'il suffit d'optimiser le système plus souvent pour que tout aille bien. Dans certains cas extrêmement rares, cela est possible, mais cette approche nécessitera une méthodologie de test complètement différente. Je ne conseille à personne de recourir à cette approche, car dans ce cas vous n'avez pas de mathématiques, alors qu'ici vous avez tout de manière claire.

Toutes ces nuances devraient vous convaincre que tester l'algorithme de rebuy nécessite d'autant plus l'utilisation de cette approche. En particulier, nous pouvons même simplifier la tâche et tester le système de rebuy immédiatement sur le segment de longueur maximale. Nous pouvons inverser cette logique. Si nous n'apprécions pas les performances de trading sur le segment le plus long, des performances encore meilleures sur les segments courts indiqueront que nos inégalités ne sont plus satisfaites et que le système n'est pas prêt pour le trading à ce stade.

Caractéristiques utiles en termes d'utilisation parallèle de plusieurs instruments

Lorsque les tests portent sur un historique limité, la question se pose certainement : l'historique est-il suffisant pour nous permettre d'utiliser correctement notre méthodologie de test ? Dans de nombreux cas, la stratégie a du poids, mais sa qualité n'est pas suffisante pour une utilisation confortable. Pour commencer, nous devrions au moins comprendre si elle a réellement un début prédictif et si nous pouvons commencer à nous engager dans sa modernisation. Dans certains cas, nous ne disposons pas d'un historique de trading suffisant. Que devons-nous faire ? Comme beaucoup l'ont déjà deviné, à en juger par le titre de la sous-section, nous devrions utiliser plusieurs instruments à cette fin. 

Cela semble évident, mais malheureusement, comme toujours, il n'y a pas de mathématiques. L'essence des tests sur plusieurs instruments est équivalente à la même essence pour l'augmentation de la durée des tests. La seule modification est que votre système doit être multidevises. Le système peut avoir des paramètres différents selon les instruments de trading, mais il est souhaitable que tous les paramètres soient similaires. La similitude des paramètres indique que le système utilise des principes physiques qui fonctionnent sur le plus grand nombre possible d'instruments de trading.

Avec cette approche et la mise en œuvre correcte de ces tests, l'indice "i" devrait déjà être compris comme le nombre d'instruments testés simultanément sur un segment d'essai fixe. Les expressions signifient alors ce qui suit :

1. Lorsque l'on augmente le nombre d'instruments négociés, plus il y a d'instruments, plus le facteur de recouvrement est important.
2. Lorsque l'on augmente le nombre d'instruments négociés, plus il y a d'instruments, plus la baisse relative de chaque courbe de fonds est faible.

En fait, une augmentation du nombre de tests peut, pour simplifier, être interprétée comme une augmentation de la durée totale des tests, comme si nous considérions chaque test pour chaque outil comme faisant partie d'un énorme test global. Cette abstraction ne fera que vous aider à comprendre pourquoi cette approche a la même puissance. Mais si nous considérons cette question avec plus de précision et si nous comprenons mieux pourquoi une ligne composée de plusieurs autres sera beaucoup plus belle, nous devrions utiliser les concepts suivants de la théorie des probabilités :

• Valeur aléatoire
• Variance d'une variable aléatoire
• Espérance mathématique d'une variable aléatoire
• La loi de distribution normale d'une variable aléatoire

Pour bien expliquer pourquoi nous avons besoin de tout cela, nous avons d'abord besoin d'une image qui nous aidera à regarder un backtest ou un signal de trading d'une manière un peu différente :

Fig. 5

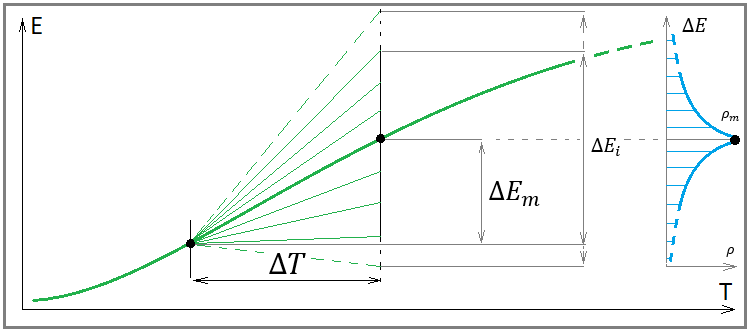
Je ne dessine pas de ligne du solde ici, car elle ne décide de rien, et nous avons seulement besoin d'une ligne de profit. La signification de cette image est que pourchaque ligne de profit, il est possible de sélectionner un nombre infini de segments indépendants d'une longueur fixe, dans lesquels il est possible de construire la loi de distribution d'une variable aléatoire de l'incrément de la ligne de profit. La présence d'une variable aléatoire signifie qu'à l'avenir, l'augmentation des bénéfices dans le domaine sélectionné peut avoir des valeurs complètement différentes dans la fourchette la plus large.

Cela semble compliqué, mais en fait tout est simple. Je pense que beaucoup de gens ont entendu parler de la loi de distribution normale. Elle est censée décrire la quasi-totalité des processus aléatoires dans la nature. Je pense que ce n'est qu'une illusion inventée pour vous empêcher de "penser". Blague à part, la popularité de la loi de distribution s'explique par le fait qu'il s'agit d'une équation compilée artificiellement et très pratique pour décrire des distributions symétriques par rapport à l'espérance mathématique d'une variable aléatoire. Elle nous sera utile pour d'autres transformations et expériences mathématiques.

Mais avant de commencer à travailler avec cette loi, nous devons définir la propriété principale de toute loi de distribution d'une variable aléatoire :

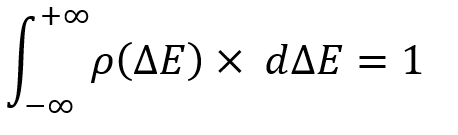
Toute loi de distribution de variables aléatoires est essentiellement l'analogue du groupe complet d'événements non conjoints. La seule différence est que nous n'avons pas un nombre fixe de ces événements et que nous pouvons à tout moment sélectionner un événement d'intérêt comme celui-ci :

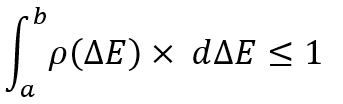
Au sens strict, cette intégrale considère la probabilité de trouver une variable aléatoire dans l'intervalle indiqué d'une variable aléatoire, et naturellement, elle ne peut pas être supérieure à 1. Aucun événement total d'un espace d'événements donné ne peut avoir une probabilité supérieure à 1. Mais ce n'est pas le plus important. La seule chose importante ici est que vous devez comprendre que l'événement dans ce cas est déterminé uniquement par un ensemble de 2 nombres. Il s'agit d'exemples de variables aléatoires de dimension minimale.

Il existe des analogues de ces équations pour la dimension "N", lorsqu'un événement peut être déterminé par "N*2" nombres, et des constructions encore plus complexes (dans le cadre des intégrales de région multidimensionnelles). Il s'agit de sections mathématiques assez complexes, mais ici elles sont redondantes. Toutes les lois obtenues ici se suffisent à elles-mêmes pour la variante unidimensionnelle.

Avant de passer à des constructions plus complexes, rappelons quelques caractéristiques des paramètres les plus courants des lois de distribution des valeurs aléatoires :

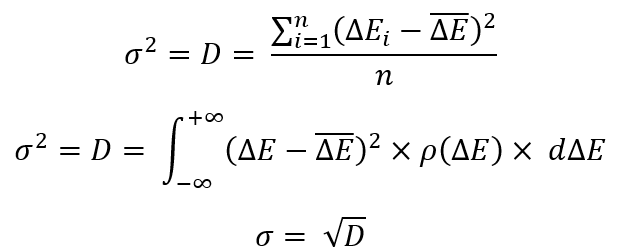
Pour définir l'une de ces équations, nous devons déterminer l'élément le plus important : l'espérance mathématique d'une variable aléatoire. Dans notre cas, elle se présente comme suit :

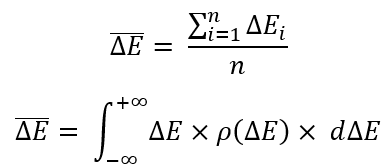
L'espérance mathématique est simplement la moyenne arithmétique. Les mathématiciens aiment donner des noms très intelligents à des choses simples afin que personne n'y comprenne rien. J'ai fourni deux équations. Leur seule différence est que la première fonctionne sur un nombre fini de variables aléatoires (quantité limitée de données), et que dans le second cas, l'intégrale sur la "densité de probabilité" est utilisée.

Une intégrale est l'équivalent d'une somme, à la seule différence qu'elle résume un nombre infini de variables aléatoires. La loi de distribution d'une variable aléatoire, qui se situe sous l'intégrale et contient toute l'infinité des variables aléatoires. Il y a quelques différences, mais en général l'essence est la même.

Reprenons maintenant les équations précédentes. Il ne s'agit là que de quelques manipulations des lois de distribution des variables aléatoires qui sont pratiques pour la plupart des mathématiciens. Comme dans le dernier exemple, il existe deux implémentations - l'une pour un ensemble fini de variables aléatoires, l'autre pour un ensemble infini (la loi de distribution d'une variable aléatoire). Elle stipule que "D" est le carré moyen de la différence entre toutes les variables aléatoires et la variable aléatoire moyenne (l'espérance mathématique de la variable aléatoire). Cette valeur est appelée "dispersion". La racine de cette valeur est appelée "écart-type".

Distribution normale d'une variable aléatoire

Ce sont ces valeurs qui sont généralement acceptées dans les mathématiques des variables aléatoires. Elles sont considérées comme les plus pratiques pour décrire les caractéristiques les plus importantes des lois de distribution aléatoire. Je ne suis pas d'accord avec cette idée, mais je suis néanmoins obligé de vous montrer comment elles sont calculées. Au final, ces quantités seront nécessaires pour comprendre la loi de distribution normale. Il est peu probable que vous trouviez facilement cette information, mais je vous dirai que la loi de distribution normale a été inventée artificiellement avec seulement quelques objectifs :

• Une manière simple de déterminer la loi de distribution symétrique à l'espérance mathématique
• La possibilité de définir la dispersion et l'écart-type
• La capacité à fixer des objectifs mathématiques

Toutes ces options nous permettent d'obtenir une équation toute faite pour la loi de distribution d'une variable aléatoire appelée loi de distribution normale :

Il existe d'autres variations des lois de distribution des variables aléatoires. Chaque implémentation est inventée pour une certaine gamme de problèmes. Mais comme la loi normale est la plus populaire et la plus connue, nous l'utiliserons comme exemple pour prouver et compiler l'équivalent mathématique des énoncés suivants :

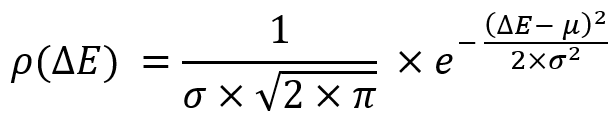
• Plus il y a d'instruments négociés en parallèle pour un système rentable, plus notre graphique de profit est beau et droit (un cas particulier de diversification).
• Plus la zone sélectionnée pour les tests ou les transactions est longue, plus notre graphique de profit est beau et droit.
• Plus il y a de systèmes négociés en parallèle avec une rentabilité prouvée, plus notre graphique de rentabilité globale est droit et beau.
• La combinaison de tous ces éléments donne lieu à une diversification idéale et au plus beau des graphiques

Tout ce qui vient d'être dit ne s'applique qu'aux systèmes de trading dont la rentabilité a été prouvée mathématiquement et de façon pratique. Commençons par définir ce que signifie "le plus beau graphe" en termes mathématiques. L'"écart-type", dont j'ai déjà montré l'équation ci-dessus, peut nous y aider.

Si l'on dispose d'une famille de courbes de densité de distribution d'une variable aléatoire d'incrément de profit ayant la même espérance mathématique, qui symbolisent deux segments de même durée dans le temps, pour deux graphiques pratiquement identiques, alors on préférera celle qui a l'écart-type le plus faible. La courbe parfaite dans cette famille pourrait être une courbe dont l'écart-type est nul. Cette courbe n'est réalisable que si l'on connaît l'avenir, ce qui est impossible. Mais il faut le comprendre pour comparer les courbes de cette famille.

Beauté de la courbe de profit dans le cadre de la loi de distribution des valeurs aléatoires

Ce fait est compréhensible lorsqu'il s'agit d'une famille de courbes, où les espérances mathématiques de l'augmentation des bénéfices au cours de la période choisie sont les mêmes, mais que faire lorsqu'il s'agit de courbes de distribution totalement arbitraires ? Il n'est pas évident de les comparer. Pour cela, l'écart-type n'est plus parfait et nous avons besoin d'une autre valeur de comparaison plus universelle qui tienne compte de la mise à l'échelle, ou nous devons trouver un algorithme pour réduire ces lois de distribution à une certaine valeur relative, où toutes les distributions auront la même espérance mathématique et, par conséquent, les critères classiques s'appliqueront à toutes les courbes. J'ai développé un algorithme de ce genre. L'une des astuces qu'il contient est la transformation suivante :

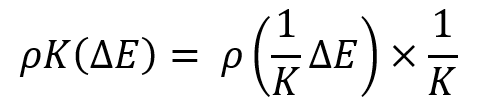
La famille de ces courbes se présente comme suit :

Fig. 6

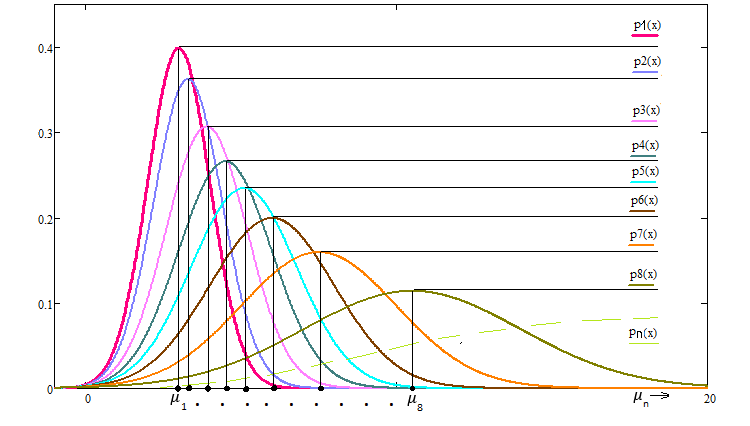
Un fait très intéressant est que si nous soumettons la loi de la distribution normale à cette transformation, elle est invariante par rapport à cette transformation et se présente comme suit :

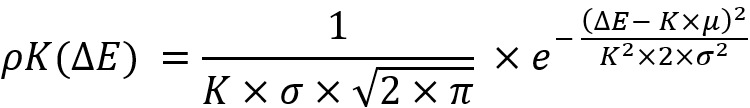
L'invariance consiste dans les remplacements suivants :

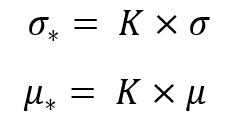
Si nous substituons ces remplacements dans l'équation précédente, nous obtenons la même loi de distribution fonctionnant avec les valeurs correspondantes marquées d'un astérisque :

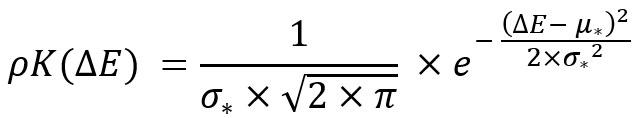
Cette transformation est nécessaire pour assurer non seulement l'invariance de la loi de transformation mais aussi l'invariance du paramètre suivant :

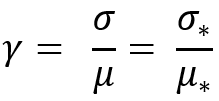
J'ai dû inventer ce paramètre. Il est impossible d'échelonner correctement la loi de distribution normale, comme toute autre loi, sans elle. Ce paramètre sera également invariant pour toute autre loi de distribution. En fait, la loi normale est plus facile à percevoir et à comprendre. L'idée est qu'elle peut être utilisée pour toutes les distributions ayant des espérances mathématiques différentes et que son essence sera similaire à l'écart-type, mais sans l'exigence que toutes les distributions comparées aient la même espérance mathématique. Il s'avère que notre transformation est conçue pour obtenir une famille de distributions où un paramètre donné a la même valeur. Cela semble assez pratique, n'est-ce pas ?

C'est l'une des façons de définir ce que l'on appelle la beauté d'un graphique. Le système ayant le plus petit paramètre est "le plus beau". C'est une bonne chose, mais nous avons besoin de ce paramètre pour une autre raison. Nous nous sommes donné pour mission de comparer la beauté des deux systèmes. Imaginons que nous ayons deux systèmes qui tradent indépendamment l'un de l'autre. Notre objectif est donc de fusionner ces systèmes et de comprendre si cette fusion aura un effet, ou plutôt, nous l'espérons, sur les points suivants :

 

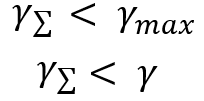
Ces rapports seront observés lors de l'utilisation de n'importe quelle loi de distribution. Cela signifie automatiquement qu'il est judicieux de diversifier si nos instruments ou systèmes négociés en parallèle ont une rentabilité similaire. Nous allons prouver ce fait d'une manière un peu différente. Comme je l'ai dit, j'ai mis au point un algorithme permettant de réduire toutes les distributions à une valeur aléatoire relative. Nous l'utiliserons, mais nous analyserons d'abord le processus général de fusion de plusieurs lignes, dans le cadre de la loi de distribution d'une variable aléatoire représentant la somme de deux deltas. Nous utiliserons la logique récurrente pour la fusion par paires. Pour ce faire, nous supposons que nous disposons de "n+1" courbes, chacune d'entre elles ayant une espérance mathématique définie. Mais pour arriver à la variable aléatoire qui symbolise la fusion, il faut comprendre ce qui suit :

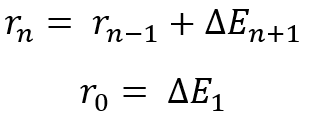
En fait, il s'agit d'une expression récurrente qui n'a aucun sens mathématique, mais qui montre la logique de la fusion de toutes les variables aléatoires présentes dans la liste. Pour simplifier, nous avons "n+1" courbes, que nous devons combiner en utilisant "n" transformations successives. En fait, cela signifie que nous devons obtenir la loi de distribution de la variable aléatoire totale à chacune des étapes en utilisant des opérateurs de transformation.

Je ne me lancerai pas dans de longues explications. A la place, je vais simplement montrer ces opérateurs de conversion afin que vous puissiez tirer vos propres conclusions. Ces équations mettent en œuvre la fusion de deux courbes de profit au cours de la période sélectionnée et calculent la probabilité que le profit total des deux segments des courbes "dE1 + dE2" soit inférieur (Pl) et supérieur (Pm) à la valeur "r" sélectionnée, respectivement :

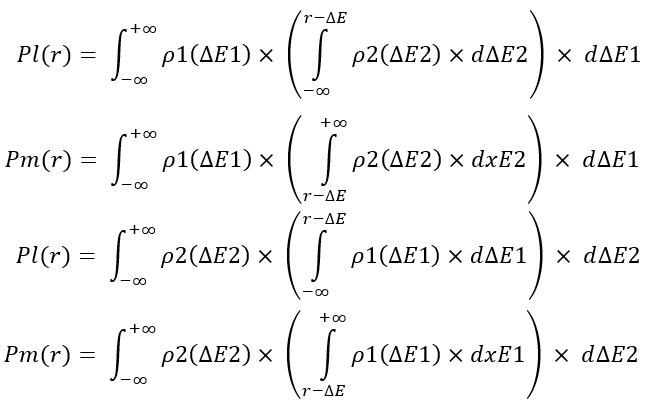
Il existe deux options pour mettre en œuvre ces quantités. Elles sont tout à fait similaires. Après avoir calculé ces valeurs, on peut les utiliser pour obtenir la loi de distribution de la variable aléatoire "r", ce qui est nécessaire pour élaborer l'ensemble de la chaîne de fusion récurrente. Par définition d'une variable aléatoire, nous pouvons obtenir les lois de distribution correspondantes à partir de ces équations comme suit :

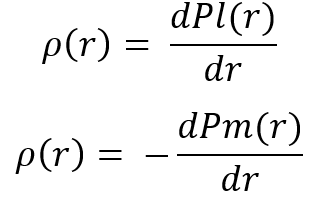
Comme vous l'avez peut-être deviné, après avoir obtenu la loi de distribution, nous pouvons passer à l'étape suivante de la chaîne de transformations récurrentes. Après avoir parcouru l'ensemble de la chaîne, nous obtenons la distribution finale, que nous pouvons déjà comparer à l'une des distributions que nous avons utilisées pour la chaîne de fusion récurrente. Créons quelques distributions basées sur les lois que nous avons obtenues, et exécutons une étape de fusion à titre d'exemple pour démontrer que chaque fusion est "plus belle que la précédente" :

Fig. 7

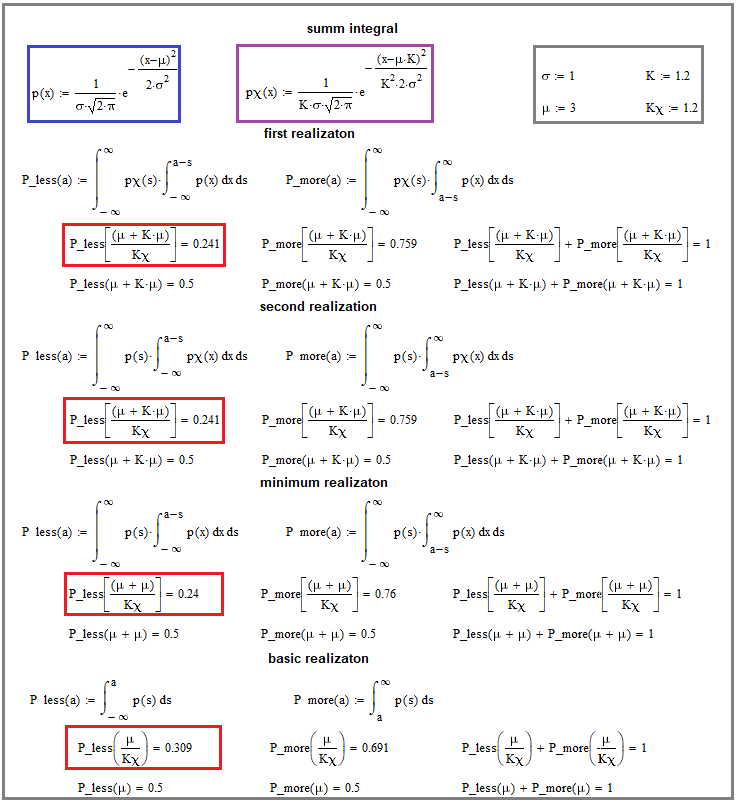
L'image montre la fusion mathématique qui applique nos équations de fusion. La seule chose qui n'est pas montrée ici est la différenciation pour transformer les intégrales en lois d'une distribution de valeurs de fusion aléatoire. Nous examinerons le résultat de la différenciation un peu plus tard, dans le cadre d'une idée plus générale, mais pour l'instant, occupons-nous de ce qui se trouve dans l'image.

Faites attention aux rectangles rouges. Ils constituent la base du présent document. L'intégrale la plus basse signifie que nous prenons l'intégrale selon la loi de distribution originale de manière à calculer la probabilité que la variable aléatoire prenne une valeur plus petite que l'espérance mathématique divisée par "Kx". Ci-dessus, vous verrez des intégrales similaires pour les fusions de deux distributions légèrement différentes. Dans tous les cas, il est important de maintenir ce rapport Kx entre l'espérance mathématique et la valeur limite choisie de l'intégrale, qui est exprimée dans le "Kx" correspondant. 

Notez que les deux options de fusion y sont présentées, conformément aux équations que je vous ai données plus haut. Il y a également une fusion de la distribution de base avec elle-même, comme si nous fusionnions deux courbes de profit similaires. Similaire ne veut pas dire identique dans l'image, mais plutôt ayant des lois de distribution identiques pour la variable aléatoire de l'augmentation de la courbe de profit dans la période de temps sélectionnée. La preuve en est que nous avons trouvé une probabilité plus faible d'un écart relatif de la variable aléatoire de la fusion par rapport à l'originale. Cela signifie que nous disposons d'une loi plus "belle" pour l'augmentation d'une valeur de profit aléatoire dans toute fusion. Bien sûr, il existe des exceptions qui nécessitent un examen plus approfondi du sujet, mais je pense que cette approche est suffisante pour cet article. Vous ne trouverez probablement rien de mieux nulle part, car il s'agit d'un matériau très spécifique.

L'autre façon de comparer la beauté consiste à transformer toutes les lois de distribution originales et le résultat de la chaîne récurrente examinée ci-dessus. Pour cela, il suffit d'utiliser notre transformation, qui nous a permis d'obtenir une famille de courbes de distribution évolutives, et de procéder comme suit :

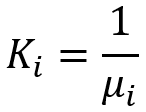
L'astuce de cette transformation est qu'avec cette approche, toutes les lois de distribution soumises à la transformation correspondante auront la même espérance mathématique et, par conséquent, nous pouvons utiliser uniquement l'écart-type pour évaluer leur "beauté" sans avoir à inventer des critères exotiques. Je vous ai montré deux méthodes. C'est à vous de choisir celle qui vous convient le mieux. Comme vous l'avez peut-être deviné, les lois de distribution de toutes ces courbes relatives ressemblent à ceci :

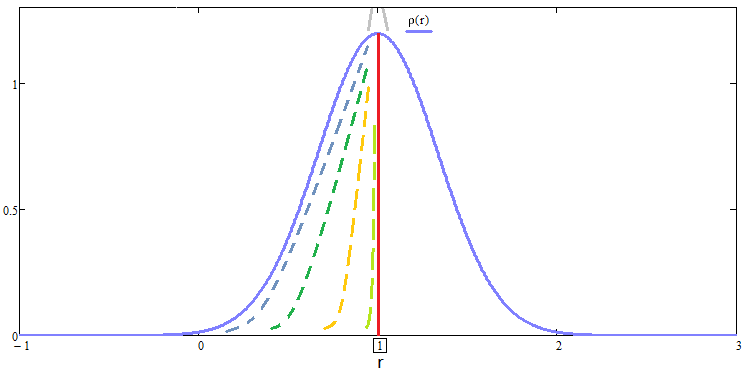
Cette approche est également applicable aux tests étendus. Par tests étendus, nous entendons ici des tests sur un segment plus long. Cette application ne sert qu'à confirmer le fait que plusle test est long, plus le graphique est beau. La seule astuce à appliquer pour cette preuve est d'accepter que si nous augmentons la durée du test, nous le faisons en multiples d'un nombre entier, alors qu'en multiples de ce nombre nous considérons déjà non pas 1 étape mais "n" et appliquons les équations de fusion. Cette fusion sera encore plus simple, puisque la chaîne de fusion récurrente ne contiendra qu'un seul élément dupliqué, et il sera possible de comparer le résultat uniquement avec cet élément.

Conclusion

Dans cet article, nous ne nous sommes pas intéressés à l'algorithme de rebuy lui-même, mais à un sujet beaucoup plus important qui vous donne les équations et les méthodes mathématiques nécessaires pour une évaluation plus précise et plus efficace des systèmes de trading. Plus important encore, vous obtenez la preuve mathématique de ce que vaut la diversification et de ce qui la rend efficace, et comment l'augmenter de manière naturelle et saine, en sachant que vous faites tout ce qu'il faut.

Nous avons également prouvé que le graphique d'un système rentable est d'autant plus beau que la zone de trading utilisée est longue et que les systèmes les plus rentables traitent simultanément sur un même compte. Jusqu'à présent, tout est formulé sous forme de théorie, mais dans le prochain article, nous examinerons les aspects appliqués. En d'autres termes, nous construirons un modèle mathématique fonctionnel pour la simulation des prix et la simulation du trading multidevises. Et nous confirmerons toutes nos conclusions théoriques. Vous ne trouverez probablement cette théorie nulle part, alors essayez d'approfondir ces mathématiques, ou au moins d'en comprendre l'essence.