Algorithme de rachat : Simulation de trading multi-devises

Sommaire

• Introduction
• Expliquer la nécessité d'une simulation de trading
• Modèle mathématique de simulation des prix utilisant la logique de discrétisation
• Essai du modèle
• EA de test
• Conclusion

Introduction

Dans l'article précédent, je vous ai montré un grand nombre de fonctions utiles que vous ne connaissiez probablement pas, mais la chose la plus intéressante est à venir : la recherche ou la simulation de trading. Parfois, un testeur de stratégie ne suffit pas. Bien qu'il s'agisse d'un outil très pratique pour connaître le marché, ce n'est qu'une première étape. Si vous avez lu attentivement l'article précédent, vous en connaissez probablement déjà la raison.

Expliquer la nécessité d'une simulation de trading

La raison d'être de la simulation de trading réside directement dans le fait que la quantité de données historiques de tout instrument de trading est limitée. Cette question ne peut être abordée que si vous comprenez le matériel que j'ai fourni dans l'article précédent, ou d'une autre manière.  

L'essence du problème est qu'un simple historique des cotations n'est pas toujours suffisant, car cet historique est formé à l'intersection de nombreux événements mondiaux aléatoires et non aléatoires. Il existe d'innombrables scénarios pour le déroulement de l'événement. Actuellement, j'essaie de décrire les choses le plus simplement possible. Mais si l'on passe au langage de la théorie des probabilités et que l'on utilise en même temps les acquis de l'article précédent, on comprend que l'histoire des cotations de tous les instruments que nous connaissons pourrait évoluer différemment.

Ce fait est évident si vous avez regardé le film "Retour vers le Futur". Il comporte beaucoup de maladresses et d'incohérences amusantes d'un point de vue scientifique, mais ce film transmet néanmoins l'idée principale du message fourni ici. L'essence du message est qu'une seule version des événements en cours ne nous suffit pas et que nous devrions envisager leur nombre maximal. L'histoire ne nous donne qu'une seule version, et sa taille peut parfois être insuffisante pour une évaluation objective. Par exemple, il n'y a pas si longtemps, de nombreux courtiers ont obtenu certains des symboles cryptographiques les plus populaires. C'est une très bonne chose en ce qui concerne la possibilité de tester et de négocier ces symboles. Mais l'inconvénient est qu'il n'y a pas assez de données historiques pour développer des systèmes de trading durables pour les EA qui travaillent sur les barres.

La simulation permettra de créer des instruments artificiels et de générer leurs cotations à chaque fois d'une manière complètement différente. Nous disposerons ainsi du cadre le plus large possible pour étudier le modèle mathématique de rachat et d'autres principes mathématiques importants dont j'ai parlé dans l'article précédent. Un autre avantage important est que nous pourrons simuler un nombre illimité d'instruments indépendants pour le trading en parallèle. En fin de compte, nous n'avons plus de limite à la durée des tests et au nombre d'instruments négociés de manière indépendante. Bien sûr, il ne s'agira pas de vraies cotations, mais elles ne différeront en rien des vraies en termes de législation sur les prix.

Modèle mathématique de simulation des prix utilisant la logique de discrétisation

Dans le contexte de notre tâche, l'utilisation de l'approche "discrétisation arbitraire" est plus que suffisante, car une forte discrétisation ne fera qu'augmenter l'efficacité de notre algorithme, ne serait-ce que parce que ce genre de systèmes résistent automatiquement aux propagations de manière plus efficace. Cependant, j'ai construit un algorithme qui permet également de simuler des ticks. Après tout, un tick est la plus petite période de temps. Le temps entre les arrivées des ticks est très différent, mais si vous calculez le temps moyen entre les ticks, vous pouvez imiter les ticks en première approximation.

Par barre, nous entendons ici une période de temps fixe, qu'il est commode de percevoir d'un point de vue visuel. Mais ce n'est pratique que parce qu'on vous a dit que c'était pratique, et vous ne pouvez pas y échapper, car tous les terminaux de trading sont conçus spécifiquement pour ce paradigme. Mais c'est loin d'être la meilleure façon de discrétiser les prix. Je pense que beaucoup d'entre vous connaissent le "renko". Cette approche de la discrétisation des prix n'a qu'un seul but : s'affranchir du temps. La valeur de cette approche peut être complètement différente selon les approches et selon les traders. Cependant, je n'utilise cet exemple que pour montrer l'une des autres façons de discrétiser les séries de prix. Cet exemple, selon moi, devrait vous indiquer que dans le contexte de notre tâche, nous utiliserons une logique de discrétisation complètement différente et peu familière, mais qui nous permettra de modéliser la tarification de manière très simple et efficace, sans coûts de calcul excessifs.

Pour la construction correcte d'un paradigme efficace et économique en termes de puissance de calcul, regardez l'image suivante :

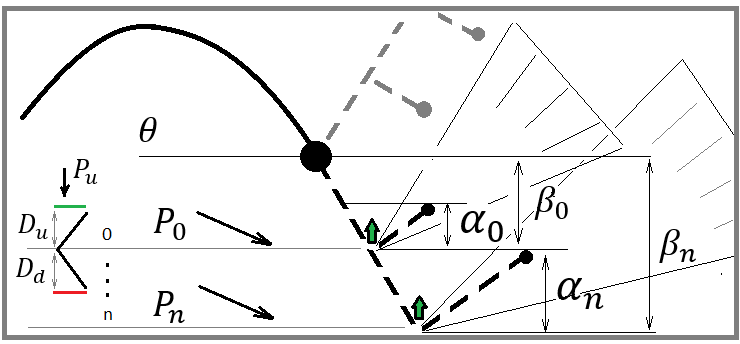
L'image montre 2 scénarios possibles pour la baisse des prix. Ces deux retours en arrière dénotent pour moi deux points arbitraires qui peuvent être choisis de n'importe quelle manière, et la méthode de choix n'a pas d'importance. L'important est que nous pouvons choisir arbitrairement n'importe quel point qui peut être considéré comme un point d'inversion probable.

Le mot "probable" devrait immédiatement indiquer à tout mathématicien qu'à un moment donné, il existe une certaine probabilité pour qu'un événement souhaité se produise. Dans notre cas, nous pouvons dire qu'un événement donné peut être arbitraire. L'événement de recul est caractérisé par les limites supérieure et inférieure de l'incrément de prix. La probabilité de cet événement peut être calculée de la manière suivante :

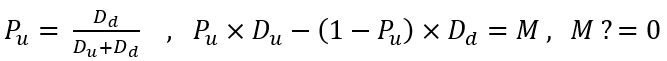
Voici la probabilité d'atteindre la borne supérieure et l'équation dont cette formule est dérivée. L'équation caractérise l'espérance mathématique de l'augmentation du prix s'il n'y a pas de moment prédictif. L'absence de moment prédictif se traduit par une attente nulle. Mais dans notre simulation, je souhaite pouvoir ajuster les paramètres du moment prédictif afin d'augmenter ou d'affaiblir les caractéristiques plates de notre pricing simulé. Enfin, vous verrez comment cela affecte l'algorithme de rachat et vous obtiendrez un modèle mathématique fonctionnel utilisant l'algorithme de rachat. Mais je veux d'abord vous donner tous les détails mathématiques de cette affaire.

Actuellement, nous pouvons constater que toutes ces équations sont belles et apparemment utiles. Mais jusqu'à présent il n'y a pas d'algorithme pratique pour ajuster la planéité (rollback) de l'instrument. Pour développer un tel algorithme, nous devons entrer les valeurs suivantes :

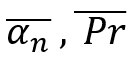
La première valeur est en fait la valeur "alpha" moyenne. On peut également l'appeler l'espérance mathématique de la valeur de retour du prix après un mouvement arbitraire à la baisse. La seconde valeur est l'espérance mathématique du pourcentage de recul exprimée en valeur relative par rapport à son mouvement précédent. L'essence de ces quantités est la même à la seule exception près :

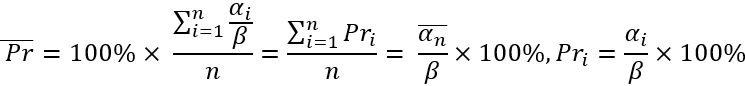
Je vous montre simplement comment ces quantités sont liées et comment elles sont calculées. Dans notre modèle, nous régulerons le recul moyen en fixant son pourcentage moyen. Et nous inverserons la logique en l'utilisant pour déterminer le recul moyen des prix. Il faut admettre que le pourcentage moyen de retour en arrière est très pratique comme valeur réglementaire pour le paramètre de planéité du marché. Si ce pourcentage est fixé à zéro, nous exigeons en fait un prix aléatoire (ce n'est qu'un exemple). La seule chose que je souhaite noter est que toutes les baisses de prix sont considérées par rapport au point "thêta". J'espère que vous me pardonnerez les libertés prises dans mes notations, car ce matériel est entièrement le mien, et il n'y a pas une goutte du travail de quelqu'un d'autre ici. Ces équations sont nécessaires pour comprendre ce que je vais faire ensuite.

La volatilité (taux de variation des prix) est une autre caractéristique importante de la fixation des prix (pricing). Ce paramètre est associé au temps, et nous devons trouver un moyen extrêmement pratique de définir cette valeur. Cela devrait nous permettre de contrôler facilement et efficacement le taux de fixation des prix et de calculer correctement le calendrier des cycles de trading. Actuellement, tout cela peut sembler trop compliqué. Mais ce sera beaucoup plus clair lorsque je passerai à la pratique et que je commencerai à vous montrer comment cela fonctionne. Commençons par la volatilité.

Dans l'interprétation classique, la volatilité est un peu différente. Il s'agit plutôt du degré de mouvement relatif possible du prix d'un minimum à un maximum et vice versa, d'un maximum à un minimum. Il s'agit d'une façon très peu pratique de définir le taux de fluctuation des prix. Il existe une méthode beaucoup plus pratique, qui consiste à mesurer l'évolution moyenne des prix sur une période donnée. Nous avons ces segments. On les appelle des barres. En effet, nous disposons de la loi de distribution d'une variable aléatoire du module de changement de prix par barre. Plus cette valeur est élevée, plus la volatilité des prix (taux de variation) est importante. Nous entrons les paramètres suivants :

Quant à savoir s'il faut simuler la distribution aléatoire de la valeur "S", je peux dire que ce n'est pas nécessaire. La seule chose que vous devez savoir est que le pricing réel sera différent de la méthode que nous utiliserons dans le modèle mathématique. Je propose de fixer la valeur "S" au niveau de sa valeur moyenne. Comme l’heure de chaque pas est déjà fixée, nous obtenons à la fois la taille du pas et sa durée dans le temps. Cela nous permettra par la suite d'évaluer la rentabilité annuelle du système de trading, ainsi que de mesurer la durée moyenne du cycle de trading. Regardons maintenant l'image suivante pour avancer :

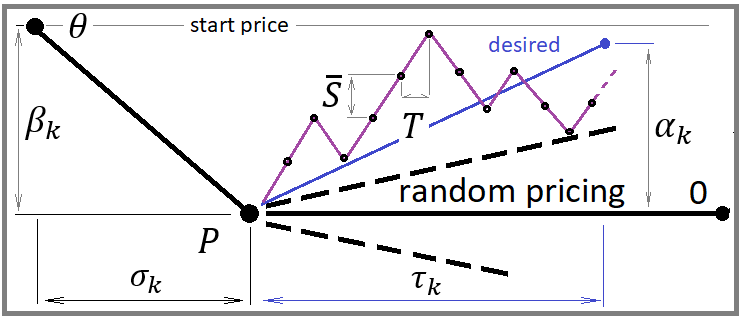
Comme nous devrons simuler le pricing pour chaque pas, il est évident que le pas peut être descendant ou ascendant. Si nous fixons un pas équiprobable dans les deux sens, nous obtenons un pricing aléatoire. Cela signifie que pour réguler la planéité, nous devons modifier ces probabilités de pas. Il s'agit de donner une sorte de "gravité" au point de départ du prix, à partir duquel le prix a commencé à évoluer à la hausse ou à la baisse. Dans notre cas, nous devrons réaliser ce qui suit :  

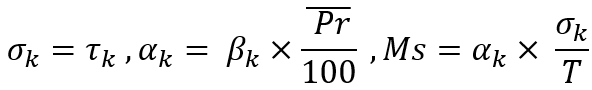
Dans ce cas, pour simplifier le modèle, j'ai supposé que le renversement de prix moyen choisi nécessite exactement le même temps que celui consacré à la hausse ou à la baisse précédente. Le but de ces calculs est de déterminer l'espérance instantanée d'un pas unique, afin de calculer la probabilité que le pas se produise vers le haut. Avec cette probabilité, la simulation du nouveau pas est ajusté. Cette valeur est recalculée après chaque étape pour chaque instrument de trading.

Voici un point très important : si nous décrivons chaque instrument séparément, nous devrons créer un tableau avec des données sur la variation moyenne du prix pour chacun d'entre eux. Mais dans le cadre de ma mission, tous les instruments se valent et il est donc possible d'introduire une caractéristique générale et plus pratique pour décrire un pas sous la forme d'un pourcentage moyen de variation de prix :

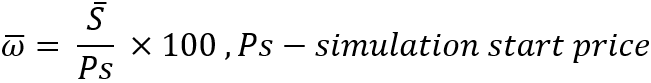
L'avantage de cette caractéristique est qu'elle est invariante par rapport à n'importe quel prix courant. En outre, si nous considérons des instruments idéaux, le prix auquel la simulation commence n'a pas d'importance, car il n'affectera pas le bénéfice ou la perte pendant le test. Une fois que nous avons compris cela, nous pouvons en toute sécurité commencer le trading en parallèle pour notre algorithme de rachat à partir d'un prix, disons, égal à 1. Après avoir déterminé cette valeur, il est déjà possible de calculer la valeur du pas lui-même :

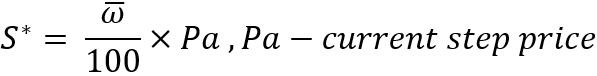
Maintenant que nous connaissons le pas, nous pouvons affirmer que nous avons recueilli toutes les données nécessaires pour calculer la probabilité qu'il y ait un pas vers le haut. Pour cela, nous utilisons notre formule originale pour l'espérance mathématique d'un pas avec quelques substitutions :

Après cette substitution, nous pouvons résoudre cette équation pour la probabilité d'un pas en avant et, finalement, obtenir la probabilité manquante :

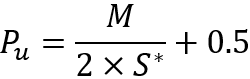
La seule chose à noter est que ces équations sont valables pour le cas où le prix de simulation tombe en dessous du point de départ. Mais que faire lorsque le prix augmente ? Tout est très simple. Il suffit de considérer le graphique miroir. Cela est possible parce que nous considérons des instruments parfaits. Si nous imaginons que le graphique des prix peut être décrit par une certaine expression "P = P(t)", alors le renversement de l'instrument se présentera comme suit :

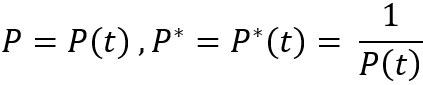
Ce renversement maintient les équations pour la situation où le prix a dépassé le point de départ. La seule chose que nous devons comprendre est que toutes les quantités dans nos expressions qui sont calculées à l'aide de prix (par exemple, les deltas) doivent utiliser le prix déjà converti élevé à la puissance moins un.

Construisons maintenant un modèle de trading. J'ai fait en sorte qu'il soit à sens unique, car il a été conçu à l'origine pour les opérations au comptant sur les crypto-monnaies. Mais ce modèle de trading est également adapté aux paires de devises du forex. En effet, si le modèle ne fonctionne, par exemple, que dans le cas d'un rachat, il fonctionnera tout aussi bien dans le cas d'une revente. La seule chose est que, pendant le test, nous sauterons les demi-vagues supérieures et ne travaillerons que sur les vagues inférieures. Pour gérer le modèle de trading, j'ai saisi les caractéristiques suivantes :

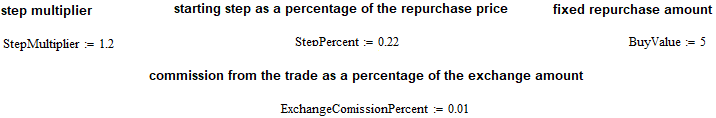
L'achat initial commence au prix "1-Step Percent/100", et le pas de rachat sera égal à "Step Percent/100". En fait, il devrait toujours y avoir une multiplication par le prix de départ, mais comme nous prenons ce prix égal à un, le calcul du pas est grandement simplifié. La possibilité d'une augmentation récurrente de l'échelon a également été introduite. Par exemple, nous pouvons soit augmenter chaque étape de rachat suivante par rapport à l'étape précédente de N fois, soit la diminuer de la même manière. Tout cela dépend de la valeur du coefficient correspondant. Le pas de rachat est mesuré dans la devise inférieure de l'instrument (et non dans la devise de base). Cette règle s'applique également aux crypto-monnaies.

Pour simplifier le modèle, on suppose que les instruments de trading appliqués dans ce cas sont approximativement les suivants : EURUSD, GBPUSD, NZDUSD et ainsi de suite, c'est-à-dire que la devise inférieure de l'instrument négocié doit être la même pour tous les instruments négociés. Cela simplifie un modèle déjà très complexe, mais c'est tout à fait suffisant pour tester les principes mathématiques du dernier article et pour optimiser les algorithmes de rachat. Dans notre cas, le spread est pris en compte sous la forme d'une commission, ce qui revient au même. En général, les paramètres sont suffisants pour le prototype du modèle mathématique. Examinons le processus de rachat :

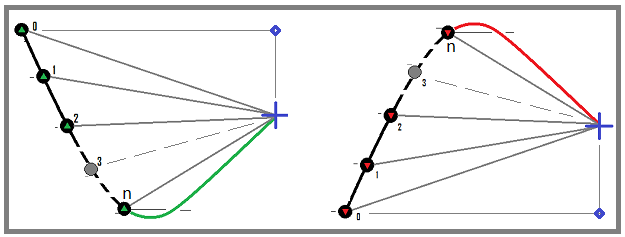
Nous utiliserons la première option (avec le mouvement de retour vert). Il s'agit en fait d'acheter la devise de base et de la vendre au point bleu. Avec cette approche, tout cycle de trading achevé sera rentable. Il en va de même pour le cycle de vente avec un mouvement de retour rouge. Mais nous les sauterons, comme je l'ai dit, afin que le modèle soit aussi multifonctionnel que possible et convienne à la fois au trading sur le marché du forex et au trading au comptant sur les bourses de crypto-monnaies.

Le modèle est conçu de manière à ce que l'effet de levier ne joue aucun rôle. Je pense vous avoir donné suffisamment d'informations théoriques pour que vous puissiez mieux comprendre la partie pratique, et cela peut aider quelqu'un à construire son propre modèle en utilisant mes réalisations.

Essai du modèle

Commençons par tester différentes variantes de génération des cotations. Pour vous montrer visuellement la différence dans la génération des cotations, plaçons d'abord le modèle dans la position suivante :

Avec ce réglage, nous obtiendrons un pricing aléatoire. Examinons quelques cotations générées de ce point de vue :

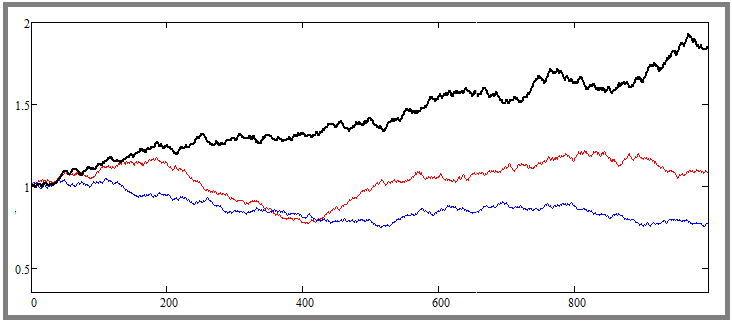
Il s'agit d'un graphique issu d'un modèle mathématique, qui montre deux cotations prises au hasard dans le jeu, et une courbe supplémentaire présentant l'écart le plus important par rapport au prix de départ. Dans le modèle mathématique, il est possible de définir le nombre requis d'instruments à simuler en parallèle, et il est naturel qu'il y en ait beaucoup, et qu'il y en ait toujours un qui soit le moins symétrique et le plus volatile. Mais j'espère que vous comprenez que ce n'est que le résultat de processus probabilistes. Plaçons maintenant le paramètre dans une position différente :

Comme vous l'avez peut-être déjà compris, cette étape crée une gravité de retour du prix au point de départ. Voici le résultat sur le graphique :

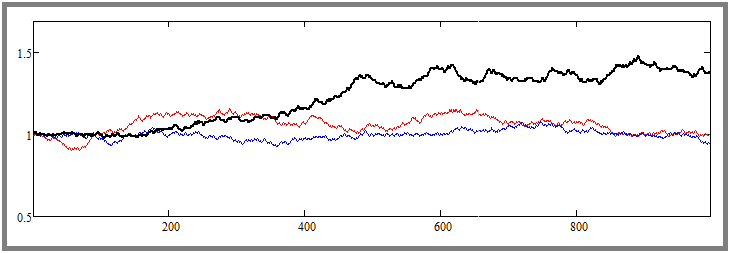
Remarquez la différence entre l'image précédente et l'image actuelle. Ici, nous avons déjà forcé l'ajustement plat dans la direction souhaitée. Nous pouvons voir que les courbes sont fortement pressées contre le prix de départ - la même chose s'est produite avec la cotation la plus volatile colorée en noir. Les deux exemples simulent exactement 1000 étapes pour chaque outil. Plus tard, j'augmenterai ces chiffres et je les manipulerai pour comprendre comment tout cela fonctionne et quels sont les paramètres exactement affectés.

Il convient à présent de déterminer les paramètres à utiliser pour tester le trading artificiel et la manière dont il doit être testé. Rappelons rapidement les questions auxquelles j'ai répondu dans l'article précédent. De manière plus simple et plus compréhensible, elles se présentent comme suit :

1. Condition de rentabilité des systèmes de trading avec rebuy.
2. La ligne de profit tend-elle vers une ligne droite parfaite lorsque l'on négocie sans cesse des instruments de trading idéaux ?
3. La ligne de profit tend-elle vers une ligne droite parfaite lorsque le nombre d'instruments augmente jusqu'à l'infini avec une période de temps de trading fixe ?

Découvrons l'état de la rentabilité. Pour ce faire, nous allons tout d'abord effectuer des transactions parallèles en utilisant des prix aléatoires et examiner les résultats. Il se présentera approximativement comme suit :

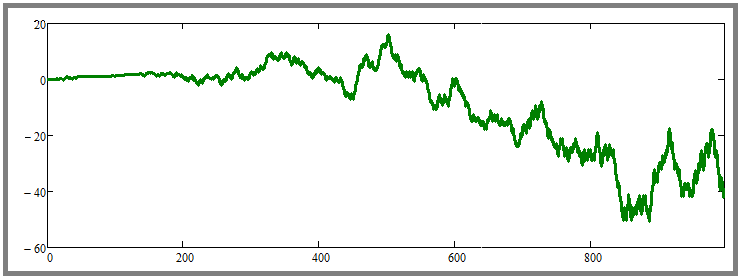
Selon les générations, des courbes rentables ou non rentables ont été obtenues. Ce n'est pas encore clair, mais la confirmation de l'inutilité des reconstructions en cas de pricing aléatoire pourrait être une augmentation extrême du nombre d'instruments négociés en parallèle. Voyons ce qui se passe si nous augmentons leur nombre à, disons, une centaine, et si nous augmentons en même temps le nombre de pas de simulation pour chaque outil à 10 000 :

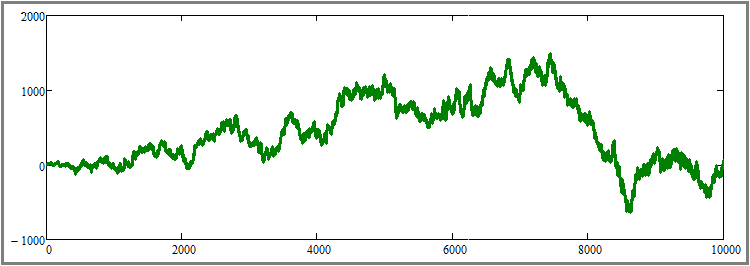
Comme vous pouvez le constater, ni l'augmentation du nombre d'instruments négociés en parallèle, ni l'augmentation de la durée des tests n'ont eu d'effet visible. Très probablement, cela confirme le fait mathématiquement prouvé dans l'article précédent : tout système de trading, y compris l'algorithme de rebuy, draine le compte en cas de prix complètement aléatoire et sans moment prédictif. À ce stade, je considère que le point 1 est théoriquement et pratiquement prouvé. Passons maintenant au deuxième point et définissons le paramètre suivant :

D'après mes tests, la gravité de retour s'est avérée tout à fait suffisante pour permettre une évaluation visuelle de l'effet pour n'importe quel lecteur. Bien sûr, nous pouvons fixer un pourcentage plus bas, mais l'effet sera moins prononcé. J'ai réinitialisé le nombre d'étapes de la simulation à la valeur d'origine de mille étapes. Voyons maintenant le résultat :

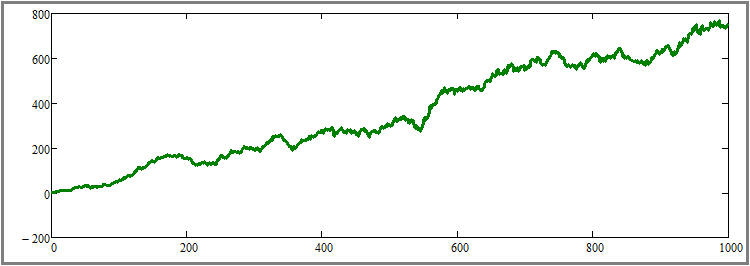
Je pense qu'il ne sera pas difficile de comprendre que ce graphique, entre autres, est un ajout à la preuve du paragraphe précédent, mais, en même temps, il est aussi un point de départ pour la preuve du paragraphe suivant. La prochaine étape de mon plan consiste à augmenter la durée de tous les segments de test sans modifier d'autres paramètres. Pour plus de clarté, j'ai multiplié le nombre d'étapes de simulation pour chaque outil par 50 - de 1000 à 50 000. Il s'agit d'une augmentation assez importante, mais c'est la seule façon de ressentir visuellement cet effet sans effectuer plusieurs tests et calculer la moyenne des résultats. Voyons le résultat :

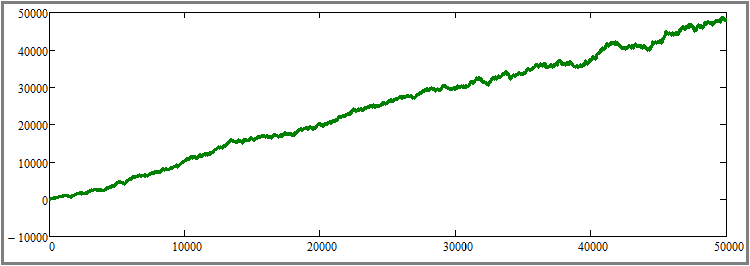
Comme nous pouvons le constater, la courbe est devenue beaucoup plus lisse et se rapproche d'une ligne droite, ce qui signifie que le deuxième principe d'augmentation du facteur de linéarité (beauté du graphique) avec l'augmentation de la durée du test fonctionne exactement comme prévu. Bien entendu, cela n'est vrai que dans l'hypothèse où l'on sait que la stratégie choisie est rentable. A ce stade, je considère que le deuxième paragraphe est théoriquement et pratiquement prouvé.

Ramenons maintenant le nombre de pas de simulation au niveau initial de 1000 pas et, inversement, augmentons le nombre d'instruments négociés en parallèle de dix fois, jusqu'à la valeur de 1000. Selon la légende, nous devrions obtenir une augmentation visible de la beauté du graphique. Voyons si c'est vrai :

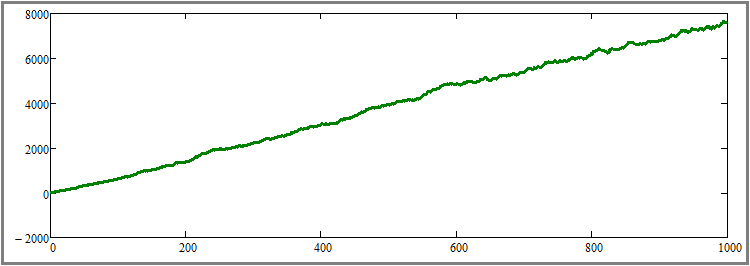
Comme nous pouvons le constater, cette hypothèse a été confirmée et l'effet est extrêmement prononcé. À ce stade, je pense que les trois hypothèses sont théoriquement et pratiquement prouvées. Les résultats sont les suivants :

1. La condition de la rentabilité de tout système de trading est la présence d'un moment prédictif.
2. Avec l'augmentation de la durée de trading ou de backtesting, toute courbe d'un système de trading rentable devient plus belle et plus droite (sans lot automatique) + [à condition que le point 1 soit rempli].
3. Avec l'augmentation du nombre de paires de devises négociées pour un système de trading multidevises ou l'augmentation du nombre de systèmes négociés simultanément, la courbe de rentabilité du système de trading devient plus belle et plus droite + [à condition que le point 1 pour chacun de ces systèmes soit rempli].

EA de Test

Nous avons compris comment utiliser correctement les systèmes de trading, y compris l'algorithme de rachat, afin de gagner de l'argent de la manière la plus efficace et la plus sûre possible, que ce soit en trading automatique ou manuel. Le calcul du money management et d'autres situations diverses pour la combinaison correcte de systèmes de trading méritent un article séparé que je vais écrire un peu plus tard.

J'ai ajouté cette section pour que vous puissiez voir clairement que l'algorithme de rebuy est une stratégie qui fonctionne. Pour ce faire, j'ai créé un EA de test qui reprend notre modèle mathématique, à la seule différence qu'il traite également les demi-vagues supérieures (cycles de vente). J'ai trouvé quelques paramètres qui prouvent la possibilité de créer un système de trading similaire pour MetaTrader 5. Voici l'un d'entre eux :

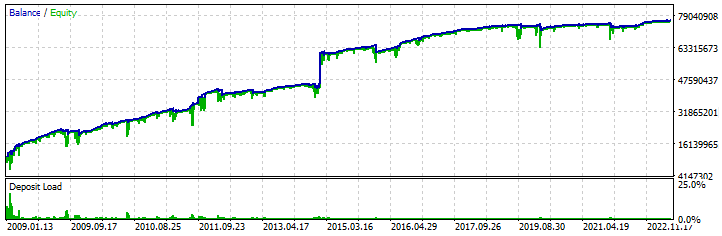
Les tests ont été effectués sur la période 2009-2023 en testant en parallèle les 28 paires de devises similaires à notre modèle mathématique. J'ai utilisé le modèle multibot que j'ai décrit dans l'un des articles précédents pour construire l'algorithme de test. Bien sûr, la courbe de profit est loin d'être idéale, et le dépôt initial pour ce type de trading doit être important. Mais, néanmoins, ma tâche dans cet article n'est pas de vous donner un robot prêt à l'emploi, mais de démontrer la proximité avec le modèle mathématique. La chose la plus importante à comprendre est qu'avec certaines modifications, cet algorithme sera beaucoup plus sûr, plus efficace et plus viable. Je vous propose de découvrir par vous-même l'essence des améliorations. Je pense que ce sera juste, étant donné que je montre des choses qui sont habituellement cachées.

L’Expert Advisor, avec l’ensemble des paramètres et le modèle mathématique, sont joints à l'article sous forme de fichier. Vous pouvez, si vous le souhaitez, étudier leur structure plus en détail et, peut-être, développer l'idée beaucoup plus loin. En fait, mon modèle mathématique est beaucoup plus utile que ce que j'ai décrit ici. Il calcule de nombreuses caractéristiques de trading importantes grâce à son propre ensemble de paramètres de sortie après le backtest. Bien entendu, sa fonctionnalité est très limitée, mais elle est suffisante pour la preuve et les estimations approximatives.

Conclusion

Dans cet article, j'ai achevé la partie pratique de la démonstration que le principe de diversification fonctionne et doit être utilisé. Plus important encore, en combinaison avec l'article précédent, j'ai prouvé à la fois théoriquement et pratiquement beaucoup de choses importantes vous permettant au moins d'augmenter l'efficacité de votre trading. La capacité de survie de l'algorithme de rachat pendant plus d'une décennie a également été prouvée à l'aide de l'EA créé.

Nous avons donc la confirmation de la théorie de la vague de la fixation des prix, ou de l'aplatissement du marché. Je vous conseille de lire cet article comme une confirmation supplémentaire. L'auteur y accorde une attention maximale à l'algorithme que j'ai décrit dans mon article. À partir de là, vous pouvez acquérir des connaissances supplémentaires sur la manière d'utiliser ces effets pour améliorer mon EA de test ou pour développer le vôtre.