El Take Profit debe ser alcanzable pero lo más grande posible y el Stop Loss debe ser inalcanzable pero lo más pequeño posible.
No estoy hablando de la práctica del comercio, sino de la teoría, por eso estoy considerando variantes extremas en aras del experimento.
Dado un EA con una entrada aleatoria, inicialmente establece un stop y un beneficio iguales.
Iteración 1 - el mercado ha dado un paso en la dirección de las probabilidades de beneficio han cambiado, vamos a disminuir las probabilidades y tirar de SL hasta el mercado.
Iteración 2 - el mercado ha dado un paso en dirección al stop las probabilidades han cambiado, escalamos las probabilidades y subimos el SL al mercado.
Si subimos el beneficio o el stop-loss al mercado, las probabilidades siempre se igualarán y esta operación devolverá un resultado nulo.
Para obtener un resultado favorable necesitamos desplazar la probabilidad, es decir, tirar de un lado más lentamente que del otro.
¿Cómo cambiará la probabilidad si el TP se tira más despacio que el SL?
Для господ чистых практиков перефразируем задачу в пошаговую :
Дано советник с рандомным входом, изначально выставляем равные стоп и профит.
Итерация 1 - рынок сделал шаг в сторону профита вероятности изменились, уровняем вероятности и подтянем СЛ к рынку.
Итерация 2 - рынок сделал шаг в сторону стопа вероятности изменились, уровняем вероятности и подтянем ТП к рынку.
Если подтягивать то профит то стоплосс к рынку то вероятности всегда будут уравниваться и такая торговля даст нулевой исход.
Для благоприятного исхода требуеться сдвинуть вероятность те подтягивать одну из сторон медленнее чем другую.
Как измениться вероятность если ТП подтягивать медленней чем СЛ ?
ITERACIÓN 1 y siguientes... ¿Quién dice que las probabilidades están niveladas?
¿De dónde viene esta hipótesis?
pero lo pondré por un tiempo.
Puente desde el centro hasta el...
si me preguntas.
Para los caballeros de la práctica pura, replanteemos el problema paso a paso:
Tenemos un EA con entrada aleatoria, inicialmente fijamos un stop y un profit iguales.
Iteración 1 - el mercado ha dado un paso en la dirección de las probabilidades de beneficio han cambiado, vamos a disminuir las probabilidades y tirar de SL hasta el mercado.
Iteración 2 - el mercado ha dado un paso en dirección al stop las probabilidades han cambiado, escalamos las probabilidades y tiramos del TP al mercado.
Si ahora subimos el beneficio y luego el stop loss al mercado, las probabilidades siempre serán iguales entre sí y esta operación devolverá un resultado nulo.
Para obtener un resultado favorable necesitamos desplazar la probabilidad, es decir, tirar de un lado más lentamente que del otro.
¿Cómo cambiará la probabilidad si el TP se mueve más lentamente que el SL?
En general, esto sólo se puede hacer para abstracciones tales como paseos aleatorios, o más específico - SB con una tendencia.
En el caso de la SB pura, las probabilidades serán inversamente proporcionales a la longitud hasta sl y tp. P(SL)=TP/(SL+TP), P(TP)=SL/(SL+TP) - sin considerar el diferencial
Para la SB con tendencia será más complicado y depende también del componente de tendencia y de la dispersión (volatilidad).
в общем виде это можно только для абстракций типа случайного блуждания посчитать, ну или более частные - СБ с трендом.
Для чистого СБ вероятности будут обратно пропорциональны длине до sl и tp. P(SL)=TP/(SL+TP), P(TP)=SL/(SL+TP) - без учета спреда
Для СБ с трендом все будет сложнее и зависит так же от трендовой составляющей и от дисперсии(волатильности).
Un tema vital, en mi opinión.
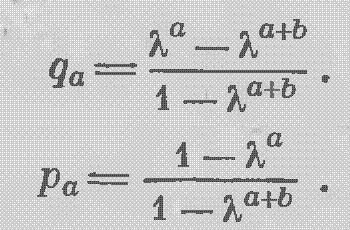 donde
donde  a y b son las distancias a TP y SL
a y b son las distancias a TP y SL
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
por lo tanto, la formulación del problema o más bien el problema previamente establecido tiempo_abierto|dirección|tiempo de cierre
se convierte en tiempo de apertura|dirección|(establecer TP y SL).
Ahora la esencia de la pregunta: ¿qué es mejor: un small_stop loss|big_stop profit o small_stop profit|big_stop loss ?
En teoría, cuanto menor sea la retirada, menor será la pérdida o el beneficio (por variaciones),
pero cuanto más lejos esté el nivel, menos probable será que se pueda alcanzar por acumulación.