Asesor Experto Grid-Hedge Modificado en MQL5 (Parte IV): Optimización de la estrategia de cuadrícula simple (I)

Introducción

En esta entrega de nuestra serie actual sobre el EA Grid-Hedge modificado en MQL5, nos adentramos en los entresijos del EA de cuadrícula. Basándonos en nuestra experiencia con Simple Hedge EA, ahora aplicamos técnicas similares para mejorar el rendimiento de Grid EA. Nuestro viaje comienza con un Grid EA existente, que sirve como lienzo para la exploración matemática. ¿El objetivo? Analizar la estrategia subyacente, desentrañar sus complejidades y descubrir los fundamentos teóricos que impulsan su comportamiento.

Pero reconozcamos el enorme desafío que tenemos por delante. El análisis que realizamos es multifacético y requiere una inmersión profunda en conceptos matemáticos y cálculos rigurosos. Por lo tanto, no sería práctico intentar cubrir tanto la optimización matemática como las mejoras posteriores basadas en código en un solo artículo.

Por ello, en esta entrega nos centraremos exclusivamente en los aspectos matemáticos. Prepárese para un examen exhaustivo de la teoría, las fórmulas y las complejidades numéricas. No se preocupe, no dejaremos piedra sin mover en nuestra búsqueda por comprender el proceso de optimización en su esencia.

En futuros artículos, centraremos nuestra atención en el aspecto práctico: la codificación propiamente dicha. Armados con nuestra base teórica, traduciremos los conocimientos matemáticos en técnicas de programación prácticas. Manténgase atento mientras unimos la teoría y la práctica para desbloquear todo el potencial del Grid EA.

Aquí está el plan para este artículo:

1. Resumen de la estrategia de cuadrícula
2. Optimización matemática
3. Simulación de cálculos en Python
4. Conclusión

Resumen de la estrategia de cuadrícula

Resumamos la estrategia. Primero tenemos dos opciones:

En el mundo del trading, nos enfrentamos a dos opciones básicas:

1. Comprar: Seguir comprando hasta alcanzar un punto determinado.
   
2. Vender: Seguir vendiendo hasta que se cumpla una condición específica.
   

En primer lugar, debemos decidir si realizar una orden de compra o de venta, dependiendo de ciertas condiciones. Digamos que vamos con una orden de compra. Realizamos el pedido y vigilamos el mercado. Si el precio del mercado sube, obtenemos ganancias. Una vez que el precio aumenta en una cierta cantidad que queremos que sea el objetivo (generalmente medido en pips), finalizamos el ciclo comercial y damos por finalizado el día. Pero si queremos empezar otro ciclo, también podemos hacerlo.

Ahora bien, si el precio se mueve en contra de nuestras expectativas y cae en una cierta cantidad, digamos 'x' pips, respondemos colocando otra orden de compra, pero esta vez con el doble del tamaño del lote. Este movimiento es estratégico porque duplicar el tamaño del lote reduce el precio promedio ponderado a '2x/3' (se puede calcular fácilmente matemáticamente) por debajo del precio de la orden inicial que está solo 'x/3' por encima de la segunda orden que se puede convertir por el precio fácilmente, que es exactamente lo que queremos. Este nuevo promedio es nuestro punto de equilibrio, donde nuestro beneficio neto es cero, teniendo en cuenta cualquier pérdida que hayamos sufrido.

En este punto de equilibrio, tenemos dos formas de obtener ganancias:

1. La primera orden, que ahora es la orden superior (se refiere a la orden que se abrió primero y tiene un nivel de precio más alto), inicialmente muestra una pérdida ya que el precio de mercado está por debajo de su precio de apertura. Pero a medida que el precio del mercado vuelve a subir hasta el precio de apertura de la primera orden, la pérdida de esa orden disminuye hasta llegar a cero y luego se vuelve positiva. Esto significa que nuestro beneficio neto sigue aumentando.
2. El segundo pedido, realizado con el doble de tamaño de lote, ya está generando ganancias. A medida que el precio del mercado continúa aumentando, el beneficio de esa orden también aumenta y el principal punto positivo es que tiene un tamaño de lote multiplicado.
   

Este enfoque es diferente de las estrategias de cobertura tradicionales porque nos brinda dos vías para obtener ganancias, lo que nos da más flexibilidad para establecer objetivos. Si seguimos aumentando el tamaño del lote de cada nueva orden mediante un determinado multiplicador (digamos duplicándolo), el efecto de reducir las pérdidas y aumentar las ganancias de la última orden se vuelve progresivamente más significativo. Esto se debe a que la orden más reciente y la orden anterior tienen un tamaño de lote mayor y este tamaño de lote sigue aumentando a medida que abrimos más órdenes. Si acumulamos una buena cantidad de órdenes, el beneficio que obtenemos de cada pip puede ser mucho mayor en comparación con la cobertura. Esto se vuelve especialmente importante cuando combinamos la cobertura con el comercio en red más adelante. En una estrategia híbrida de este tipo, el componente de red tiene el potencial de generar ganancias significativas.

El ejemplo proporcionado con dos pedidos se puede ampliar a un número mayor de pedidos. A medida que aumenta la cantidad de pedidos, particularmente cuando se realizan en un intervalo constante, el precio promedio acumulado tiende a disminuir. Al emplear un multiplicador de 2, el precio promedio —que representa el punto de equilibrio de las ganancias— converge hacia el precio de apertura de la tercera última orden. Exploraremos este concepto con prueba matemática en una discusión posterior.

A medida que profundizamos en las complejidades de esta estrategia comercial, es crucial comprender cómo funciona el tamaño de los lotes y cómo los movimientos de precios afectan nuestra posición. Al gestionar nuestros pedidos estratégicamente y ajustar el tamaño de los lotes, podemos navegar por los mercados con precisión, aprovechando las tendencias favorables y minimizando las pérdidas potenciales. La estrategia de doble beneficio que aplicaremos en el futuro cercano no sólo nos dará más flexibilidad, sino que también aumentará nuestras ganancias potenciales, creando un sistema comercial sólido que prospera gracias a la dinámica del mercado.

Optimización matemática

Primero echemos un vistazo a los parámetros que vamos a optimizar, es decir, los parámetros de la estrategia.

Parámetros de la estrategia:

1. Posición inicial (IP, Initial Position): La posición inicial es una variable binaria que establece el escenario para la dirección de nuestra estrategia comercial. Un valor de 1 significa una acción de compra, lo que indica que estamos ingresando al mercado con la expectativa de que los precios suban. Por el contrario, un valor de 0 representa una acción de venta, lo que sugiere que anticipamos una caída en los precios. Esta elección inicial puede ser un punto de decisión crítico, ya que determina el sesgo general de nuestra estrategia comercial y marca el tono para las acciones posteriores. Después de la optimización sabremos con certeza cuál es mejor comprar o vender.
2. Tamaño del lote inicial (IL, Initial Lot Size): El tamaño del lote inicial define la magnitud de nuestra primera orden dentro de un ciclo comercial. Establece la escala en la que participaremos en el mercado y sienta las bases para el tamaño de nuestras transacciones posteriores. Elegir un tamaño de lote inicial adecuado es crucial, ya que afecta directamente las ganancias y pérdidas potenciales asociadas con nuestras operaciones. Es esencial lograr un equilibrio entre maximizar nuestra rentabilidad potencial y gestionar nuestra exposición al riesgo. Depende en gran medida del multiplicador de tamaño de lote que elijamos, ya que si el multiplicador es mayor, este debería ser menor, de lo contrario, el tamaño de lote de las órdenes posteriores explotaría bastante rápido.
3. Distancia (D): La distancia es un parámetro espacial que determina el intervalo entre los niveles de precios de apertura de nuestras órdenes. Influye en los puntos de entrada en los que ejecutaremos nuestras operaciones y juega un papel importante en la definición de la estructura de nuestra estrategia comercial. Ajustando el parámetro Distancia, podemos controlar el espaciamiento entre nuestras órdenes y optimizar nuestras entradas en función de las condiciones del mercado y nuestra tolerancia al riesgo.
4. Multiplicador de tamaño de lote (M): El multiplicador de tamaño de lote es un factor dinámico que nos permite aumentar el tamaño de lote de nuestras órdenes posteriores en función de la progresión del ciclo comercial. Introduce un nivel de adaptabilidad a nuestra estrategia, permitiéndonos aumentar nuestra exposición a medida que el mercado se mueve a nuestro favor o reducirla cuando enfrentamos condiciones adversas. Al seleccionar cuidadosamente el multiplicador de tamaño de lote, podemos adaptar el tamaño de nuestras posiciones para capitalizar oportunidades rentables y al mismo tiempo gestionar el riesgo.
5. Número de pedidos (N): El número de pedidos representa el recuento total de pedidos que realizaremos dentro de un solo ciclo comercial/ciclo de cuadrícula. Este no es exactamente un parámetro de la estrategia, más bien es un parámetro que tendremos en cuenta al optimizar los parámetros reales de la estrategia.

Es fundamental tener una comprensión clara de los parámetros que serán el foco de nuestros esfuerzos de optimización. Estos parámetros sirven como base sobre la cual construiremos nuestra estrategia, y comprender sus roles e implicaciones es esencial para tomar decisiones informadas y lograr los resultados deseados.

Para simplificar, presentamos estos parámetros en sus formas básicas. Sin embargo, es importante tener en cuenta que en las ecuaciones matemáticas, algunas de estas variables se denotarían mediante notación de subíndice para distinguirlas de otras variables.

Estos parámetros sirven como base para construir nuestra función de ganancias. La función de beneficio es una representación matemática de cómo nuestra ganancia (o pérdida) se ve influenciada por los cambios en estas variables. Es un componente crucial de nuestro proceso de optimización, que nos permite evaluar cuantitativamente los resultados de varias estrategias comerciales en diferentes escenarios.

Con estos parámetros establecidos, ahora podemos proceder a definir los componentes de nuestra función de beneficio:

Calculemos la función de beneficio para un escenario simplificado donde elegimos comprar y tenemos solo dos pedidos. Supondremos que el multiplicador del tamaño del lote es 1, lo que significa que ambos pedidos tienen el mismo tamaño de lote de 0.01.

Para encontrar la función de beneficio, primero debemos determinar el punto de equilibrio. Supongamos que tenemos dos órdenes de compra, B1 y B2. B1 se coloca al precio 0, y B2 se coloca a una distancia D por debajo de B1, es decir, al precio -D. (Tenga en cuenta que el precio negativo aquí se utiliza para fines de análisis y no afecta el resultado, ya que el análisis depende del parámetro de distancia D en lugar de los niveles de precios exactos).

Ahora, digamos que el punto de equilibrio está a una distancia x por debajo de B1. En este punto, tendremos una pérdida de -x pips de B1 y una ganancia de +x pips de B2.

Si los tamaños de los lotes son iguales (es decir, el multiplicador del tamaño del lote es 1), el punto de equilibrio estaría exactamente en el medio de los dos pedidos. Sin embargo, si los tamaños de los lotes difieren, debemos considerar el multiplicador del tamaño del lote.

Por ejemplo, si el multiplicador del tamaño del lote es 2 y el tamaño del lote inicial es 0.01, entonces B1 tendrá un tamaño de lote de 0.01 y B2 tendrá un tamaño de lote de 0.02.

Para encontrar el punto de equilibrio en este caso, necesitamos encontrar el valor de x resolviendo la siguiente ecuación:

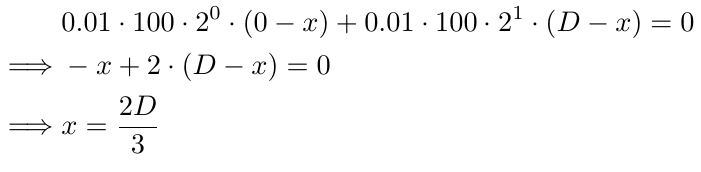
Analicemos los componentes de la ecuación. El tamaño del lote inicial, 0.01, se repite en cada parte de la ecuación (la segunda parte se refiere a la porción después del signo +). Multiplicamos esto por 100 para convertir el tamaño del lote a un número entero y, como aplicamos esta conversión de manera consistente en todas las ecuaciones, mantiene su importancia. Luego, lo multiplicamos por 2^0 en la primera parte y 2^1 en la segunda parte. Estos términos representan el multiplicador del tamaño del lote, con una potencia que comienza en 0 para el tamaño del lote inicial y se incrementa en 1 para cada orden posterior. Finalmente, utilizamos (0-x) en la primera parte, (D-x) en la segunda parte y ((i-1)D-x) en la i-ésima parte porque la i-ésima orden se coloca (i-1) veces D pips por debajo de B1. Resolver la ecuación para x da como resultado 2D/3, lo que significa que el punto de equilibrio se encuentra 2D/3 pips por debajo de B1 (como se define por x en nuestras ecuaciones). Si D es 10, el punto de equilibrio estaría 6.67 pips por debajo de B1, o 3.34 pips por encima de B2. Es más probable que se alcance este nivel de precio en comparación con el punto de equilibrio en B1 (si solo tuviéramos un pedido). Este es el concepto central detrás de la estrategia de cuadrícula: respaldar órdenes previas hasta que se logre un beneficio.

Ahora, consideremos un caso con 3 órdenes.

Para 3 pedidos, seguimos el mismo enfoque. La explicación de la 1ª y 2ª parte sigue siendo la misma. En la 3ª parte hay dos cambios: la potencia de 2 se incrementa en 1 y D ahora se multiplica por 2. Todo lo demás permanece sin cambios.

Resolviendo x aún más.

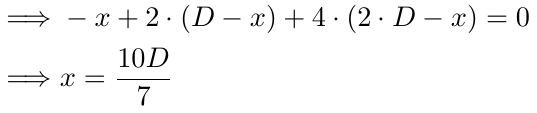
En el caso de 3 órdenes, encontramos que el punto de equilibrio se produce cuando el precio alcanza 10D/7 pips por debajo de B1. Si D es 10, el precio de equilibrio sería 14.28 pips por debajo de B1, 4.28 pips por debajo de B2 y 5.72 pips por encima de B3. Nuevamente, es más probable que el precio alcance este punto en comparación con el punto de equilibrio en B1 (con 1 orden) o el punto de equilibrio anterior. El punto de equilibrio continúa bajando, lo que aumenta la probabilidad de que el precio lo alcance, respaldando efectivamente nuestras órdenes anteriores si el precio se mueve en nuestra contra.

Generalicemos la fórmula para n pedidos.

Nota: Asumimos que todas las posiciones son órdenes de compra. El análisis de las órdenes de venta es simétrico, por lo que lo mantendremos simple.

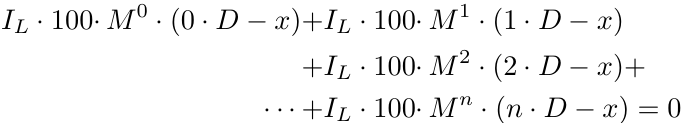
Sin embargo, resulta que esta generalización es incorrecta.

La razón de esto se puede explicar con un ejemplo sencillo. Tomemos como tamaño de lote inicial 0.01 y como multiplicador 1.5. Primero, abrimos una posición con un tamaño de lote de 0.01. Luego, abrimos una segunda posición con un tamaño de lote de 0.01 * 1.5 = 0.015. Sin embargo, después del redondeo, se convierte en 0.01, ya que el tamaño del lote debe ser un múltiplo de 0.01. Aquí hay dos cuestiones:

1. La ecuación se calcula basándose en la apertura de una posición con un tamaño de lote de 0.015, lo que prácticamente no es posible. En lugar de ello, abrimos una posición con un tamaño de lote de 0.01.
2. Este punto no es exactamente un problema sino más bien algo que debe tenerse en cuenta. Consideremos el mismo ejemplo. El primer orden fue 0.01 y el segundo orden también fue 0.01 por razones prácticas. ¿Cuál debería ser el tamaño del lote del tercer pedido? Multiplicamos el multiplicador del tamaño del lote por el tamaño del lote del último pedido, pero ¿deberíamos multiplicar 1.5 por 0.01 o 0.015? Si multiplicamos por 0.01, quedamos atrapados en un bucle que hace que el sentido de tener un multiplicador sea inútil. Entonces, vamos con 0.015 * 1.5 = 0.0225, que prácticamente se convierte en 0.02, y así sucesivamente.

Como ya hemos dicho, el segundo punto no supone exactamente un problema. Solucionemos el primer problema usando el Factor Entero Máximo (GIF, Greatest Integer Factor) o función piso en matemáticas, que dice que simplemente eliminamos la parte decimal de cualquier número positivo (no entraremos en detalles para los números negativos ya que el tamaño del lote no puede ser negativo). Notación: floor(.) o [.]. Ejemplos: floor(1.5) = [1.5] = 1; floor(5.12334) = [5.12334] = 5; floor(2.25) = [2.25] = 2; floor(3.375) = [3.375] = 3.

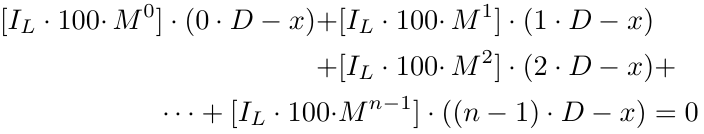
Donde, [.] representa GIF, es decir, el mayor factor entero. Resolviendo más, obtenemos:

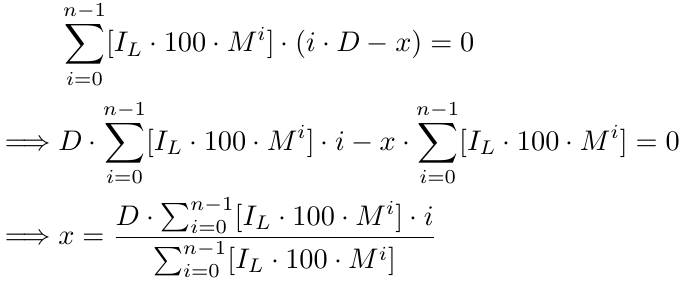
Más formalmente, para x número de pedidos tenemos una función de equilibrio b(x).

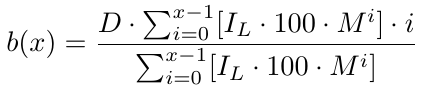
Ahora tenemos una función de equilibrio que nos da el precio de equilibrio. Devuelve cuántos pips por debajo de B1 se encuentra el precio de equilibrio. Con el precio de equilibrio, necesitamos determinar el nivel de Take Profit (TP), que es simplemente TP pips por encima de b(x). Como b(x) es el nivel de precio B1 menos el nivel de precio de equilibrio, para el nivel de toma de ganancias, debemos restar TP de b(x). Por lo tanto, tenemos nuestro nivel de toma de beneficios, que denotamos como t(x):

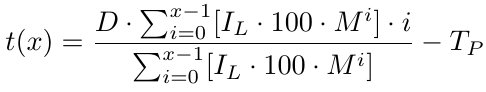
Dado x, es decir, el número de pedidos, tenemos nuestro nivel de toma de ganancias. Ahora necesitamos calcular la ganancia dada x. Intentemos encontrar la función de beneficio.

Suponiendo que el precio alcanza t(x), es decir, el nivel de toma de ganancias, y el ciclo se cierra, la ganancia/pérdida que recibimos de B1 es el nivel de precio de B1 menos t(x), con pips como unidad. Un valor negativo significa que tenemos una pérdida, mientras que un valor positivo muestra que tenemos una ganancia. De manera similar, la ganancia/pérdida que recibimos de B2 es el nivel de precio de B2 menos t(x), con pips como unidad, y sabemos que el nivel de precio de B2 está exactamente D pips por debajo del nivel de precio de B1. Para B3, la ganancia/pérdida es el nivel de precio de B3 menos t(x), con pips como unidad, y sabemos que el nivel de precio de B3 es exactamente 2 veces D pips por debajo del nivel de precio de B1. Tenga en cuenta que también debemos considerar el tamaño del lote inicial y el multiplicador del tamaño del lote.

Matemáticamente, dado x (es decir, el número de pedidos es 3), tenemos:

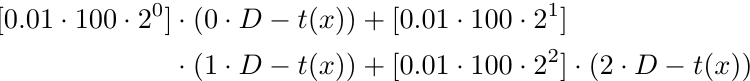
Más formalmente, para x número de pedidos tenemos una función de beneficio p(x).

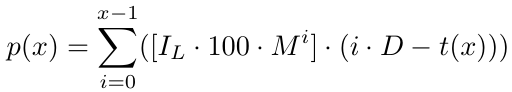
Entendamos qué significa esto. Dado cualquier número de órdenes, asumiendo que el ciclo se cierra en x número de órdenes (donde "cierra" significa que alcanzamos el nivel de toma de ganancias), tendremos una ganancia dada por la ecuación anterior p(x). Ahora que tenemos la función de ganancia, intentemos calcular la función de costo, que se refiere a la pérdida que sufriremos si perdemos un ciclo de red con x número de órdenes (donde "perdido" significa que no podemos abrir más órdenes para continuar el ciclo de red debido a fondos insuficientes, ya que la estrategia de red requiere muchas inversiones o cualquier otra razón).

La función de costo se vería así: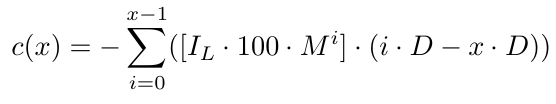

En esta ecuación, la parte [.] tiene en cuenta el tamaño del lote inicial y el multiplicador del tamaño del lote. La otra parte (i.D-x.D) considera x.D, que es la distancia entre el nivel de precio B1 y D pips por debajo de la orden con el precio más bajo. Usamos x.D porque es precisamente ahí donde abrimos un nuevo pedido. Si por alguna razón, probablemente por falta de fondos, no logramos continuar el ciclo, ese es el punto exacto en el que podemos decir con certeza que no podríamos continuar el ciclo si no podemos abrir la orden en ese nivel de precio (cuando el precio llegue allí). En esencia, cuando sabemos con certeza que no hemos logrado continuar el ciclo, el nivel de precio estaría x.D pips por debajo del nivel de precio B1. Como resultado, tendremos una pérdida de (0.D-x.D) del orden B1, (1.D-x.D) del orden B2, y así sucesivamente hasta el último orden, que es el orden Bx, del cual tendremos una pérdida de ((x-1).D-x.D)=-D. Esto tiene sentido porque estamos D pips por debajo de la última orden (la orden con el nivel de precio más bajo).

Más formalmente, para x número de pedidos tenemos una función de costo c(x).

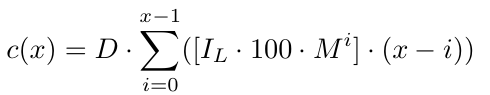
También debemos considerar el spread, que asumiremos como un spread constante para simplificar, ya que tomar un spread dinámico sería bastante complejo. Digamos que S es el spread estático, que mantendremos igual a 1-1,5 para EURUSD. El spread puede cambiar dependiendo del par de divisas, pero esta estrategia funcionará mejor con divisas que tienen menor volatilidad, como EURUSD.

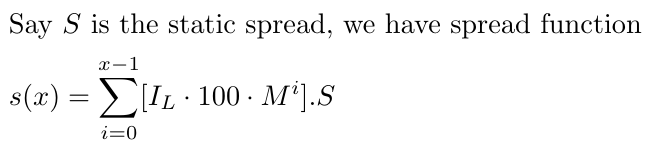
Es importante tener en cuenta que nuestro ajuste tiene en cuenta todas las operaciones, desde cero hasta x-1, reconociendo que el spread afecta a cada operación, sea rentable o no. Para simplificar, actualmente tratamos el spread (denotado como S) como un valor constante. Se tomó esta decisión para evitar complicar nuestro análisis matemático con la variabilidad añadida de un spread fluctuante. Aunque esta simplificación limita el realismo de nuestro modelo, nos permite centrarnos en los aspectos centrales de nuestra estrategia sin empantanarnos en una complejidad excesiva.

Ahora que tenemos todas las funciones necesarias, podemos trazarlas en Desmos.

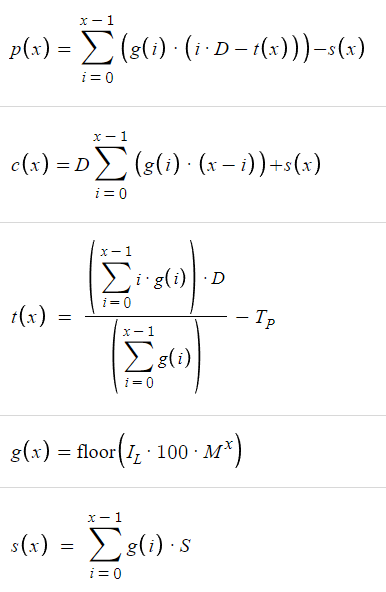
Dados los parámetros anteriores, tenemos la siguiente tabla, donde cambiando x obtenemos diferentes valores de p(x) y c(x):

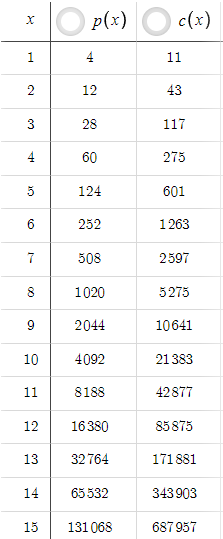
En este escenario, p(x) siempre es menor que c(x), pero esto se puede cambiar fácilmente aumentando el TP. Por ejemplo, si aumentamos el TP de 5 a 50:

Ahora, p(x) siempre es mayor que c(x). Un trader novato podría pensar que si podemos obtener niveles tan altos de relación riesgo-recompensa con TP=50, ¿por qué mantener TP=5? Sin embargo, debemos tener en cuenta la probabilidad. El incremento de TP de 5 a 50 ha disminuido drásticamente la probabilidad de que el precio alcance el nivel de toma de ganancias. Tenemos que darnos cuenta de que no tiene sentido tener una buena relación riesgo-recompensa si nunca o muy raramente alcanzamos el take profit. Para tener en cuenta las probabilidades, necesitamos datos de precios y optimización basada en codificación en lugar de solo ecuaciones, que exploraremos en otras partes de la serie.

Puedes usar esto; Enlace gráfico de Desmos para ver la gráfica de estas funciones y jugar con los parámetros para comprender mejor esta estrategia.

Con esto hemos completado la parte matemática de la optimización. En las siguientes secciones, profundizaremos en los aspectos prácticos de la implementación de esta estrategia, considerando las condiciones reales del mercado y los desafíos que conlleva. Al combinar la base matemática que hemos establecido aquí con técnicas de análisis y optimización basadas en datos, podemos refinar la estrategia de comercio de red para adaptarla mejor a nuestras necesidades y maximizar su potencial de rentabilidad.

Reflexiones finales: Como se mencionó anteriormente, numerosos parámetros indican un alto potencial de ganancias. Sin embargo, es fundamental entender que estas cifras sirven principalmente como ilustraciones. La razón detrás de esto es la ausencia de un componente vital en la optimización matemática: la probabilidad. Incorporar la probabilidad a nuestro modelo matemático es una tarea compleja, pero es un factor indispensable que no se puede ignorar. Para abordar esto, realizaremos simulaciones sobre datos de precios, lo que nos permitirá considerar la probabilidad en nuestros cálculos y mejorar la precisión de nuestro modelo.

Simulación de cálculos en Python

En esta simulación, calcularemos y graficaremos p(x) y c(x) frente a x, donde x representa el número de pedidos. Los valores de p(x) y c(x) se representarán en el eje y, mientras que x estará en el eje x. Esta visualización proporcionará información rápida sobre los cambios en p(x) y c(x), y ayudará a identificar qué función es mayor en diferentes puntos. Además, generaremos una tabla que muestre los valores exactos de p(x) y c(x) para cada x, ya que estos valores podrían no ser fácilmente legibles solo desde el gráfico. Esta combinación de la gráfica y la tabla ofrecerá una comprensión integral del comportamiento de p(x) y c(x).

Código Python:

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import FuncFormatter

# Parameters
D = 10     # Distance
I_L = 0.01 # Initial Lot Size
M = 2      # Lot Size Multiplier
S = 1      # Spread
T_P = 50   # Take Profit

# Values of x to evaluate
x_values = range(1, 21)  # x from 1 to 20

def g(x, I_L, M):
    return np.floor(I_L * 100 * M ** x)

def s(x, I_L, M, S):
    return sum(g(i, I_L, M) * S for i in range(x))

def t(x, D, I_L, M, T_P):
    numerator = sum(i * g(i, I_L, M) for i in range(x)) * D
    denominator = sum(g(i, I_L, M) for i in range(x))
    return (numerator / denominator) - T_P

def p(x, D, I_L, M, S, T_P):
    return sum(g(i, I_L, M) * (i * D - t(x, D, I_L, M, T_P)) for i in range(x)) - s(x, I_L, M, S)

def c(x, D, I_L, M, S):
    return D * sum(g(i, I_L, M) * (x - i) for i in range(x)) + s(x, I_L, M, S)

# Calculate p(x) and c(x) for each x
p_values = [p(x, D, I_L, M, S, T_P) for x in x_values]
c_values = [c(x, D, I_L, M, S) for x in x_values]

# Formatter to avoid exponential notation
def format_func(value, tick_number):
    return f'{value:.2f}'

# Plotting
fig, axs = plt.subplots(2, 1, figsize=(12, 12))

# Combined plot for p(x) and c(x)
axs[0].plot(x_values, p_values, label='p(x)', marker='o')
axs[0].plot(x_values, c_values, label='c(x)', marker='o', color='orange')
axs[0].set_title('p(x) and c(x) vs x')
axs[0].set_xlabel('x')
axs[0].set_ylabel('Values')
axs[0].set_xticks(x_values)
axs[0].grid(True)
axs[0].legend()
axs[0].yaxis.set_major_formatter(FuncFormatter(format_func))

# Create table data
table_data = [['x', 'p(x)', 'c(x)']] + [[x, f'{p_val:.2f}', f'{c_val:.2f}'] for x, p_val, c_val in zip(x_values, p_values, c_values)]

# Plot table
axs[1].axis('tight')
axs[1].axis('off')
table = axs[1].table(cellText=table_data, cellLoc='center', loc='center')
table.auto_set_font_size(False)
table.set_fontsize(10)
table.scale(1.2, 1.2)

plt.tight_layout()
plt.show()

Explicación del código:

1. Importar bibliotecas:

   • numpy se importa como np para operaciones numéricas.
   • matplotlib.pyplot se importa como plt para el trazado.
   • FuncFormatter se importa de matplotlib.ticker para formatear las etiquetas de las marcas de los ejes.

2. Establecer parámetros:

   • Defina las constantes D, I_L, M, S y T_P que representan la distancia, el tamaño de lote inicial, el multiplicador del tamaño de lote, el diferencial y la toma de beneficios, respectivamente.

3. Defina el rango para x:

   • x_values se establece en un rango de enteros de 1 a 20.

4. Definir funciones:

   • g(x, I_L, M): Calcula el valor de g a partir de la fórmula dada.
   • s(x, I_L, M, S): Calcula la suma de g(i, I_L, M) * S para i de 0 a x-1.
   • t(x, D, I_L, M, T_P): Calcula el valor de t a partir de la fórmula dada, utilizando un numerador y un denominador.
   • p(x, D, I_L, M, S, T_P): Calcula p(x) utilizando la fórmula dada.
   • c(x, D, I_L, M, S): Calcula c(x) utilizando la fórmula dada.

5. Calcule los valores p(x) y c(x):

   • p_values es una lista de p(x) para cada x en x_values.
   • c_values es una lista de c(x) para cada x en x_values.

6. Definir formateador:

   • format_func(value, tick_number): Define una función formateadora para dar formato a las etiquetas de marca del eje y con dos decimales.

7. Graficando:

   • fig, axs = plt.subplots(2, 1, figsize=(12, 12)): Crea una figura y dos subgráficas dispuestas en una sola columna.

   Primer subtrazado (trazado combinado para p(x) y c(x)):

   • axs[0].plot(x_values, p_values, label='p(x)', marker='o'): Traza p(x) frente a x con marcadores.
   • axs[0].plot(x_values, c_values, label='c(x)', marker='o', color='orange'): Traza c(x) frente a x con marcadores en color naranja.
   • axs[0].set_title('p(x) and c(x) vs x'): Establece el título de la primera subgráfica.
   • axs[0].set_xlabel('x'): Establece la etiqueta del eje x.
   • axs[0].set_ylabel('Values'): Establece la etiqueta del eje y.
   • axs[0].set_xticks(x_values): Asegura que los ticks del eje x se muestren para cada valor x.
   • axs[0].grid(True): Añade una cuadrícula al gráfico.
   • axs[0].legend(): Muestra la leyenda.
   • axs[0].yaxis.set_major_formatter(FuncFormatter(format_func)): Aplica el formateador al eje y para evitar la notación exponencial.

   Segunda Subgráfica (Tabla):

   • table_data: Prepara los datos de la tabla con las columnas x , p(x) , y c(x) , y sus valores correspondientes.
   • axs[1].axis('tight'): Ajusta el eje de la subgráfica para que se ajuste perfectamente a la tabla.
   • axs[1].axis('off'): Desactiva el eje para la subgráfica de la tabla.
   • table = axs[1].table(cellText=table_data, cellLoc='center', loc='center'): Crea una tabla en la segunda subgráfica con el texto de las celdas centrado.
   • table.auto_set_font_size(False): Desactiva el ajuste automático del tamaño de letra.
   • table.set_fontsize(10): Establece el tamaño de la fuente de la tabla.
   • table.scale(1.2, 1.2): Escala el tamaño de la tabla.

8. Diseño y visualización:

   • plt.tight_layout(): Ajusta la disposición para evitar solapamientos.
   • plt.show(): Muestra los gráficos y la tabla.

Hemos utilizado los siguientes parámetros por defecto (se pueden cambiar fácilmente para ver los diferentes resultados):

# Parameters
D = 10     # Distance
I_L = 0.01 # Initial Lot Size
M = 2      # Lot Size Multiplier
S = 1      # Spread
T_P = 50   # Take Profit

Resultado:

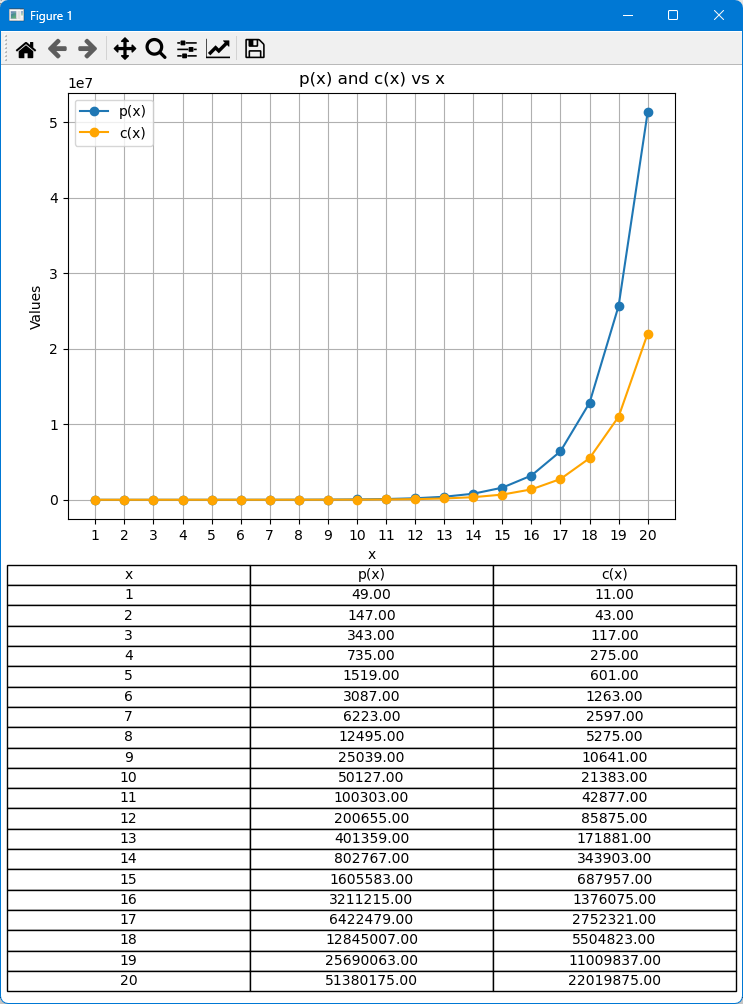
Nota: Al final del artículo se ha adjuntado un archivo Python que contiene el código comentado anteriormente.

Conclusión

En la cuarta entrega de nuestra serie, nos centramos en la optimización de la estrategia de rejilla simple mediante el análisis matemático y el papel de la probabilidad, que a menudo se pasa por alto en las estrategias de rejilla y cobertura. Los próximos artículos pasarán de la teoría a las aplicaciones prácticas basadas en código, aplicando nuestros conocimientos a escenarios de negociación reales para ayudar a los operadores a mejorar la rentabilidad y gestionar los riesgos de forma eficaz. Agradecemos sus continuos comentarios y le animamos a seguir interactuando mientras exploramos, perfeccionamos y triunfamos juntos en las estrategias comerciales.

¡Feliz codificación! ¡Feliz comercio!