MQL5 Programming Basics: Lists

MetaTrader 5 — Examples | 17 February 2014, 12:11

19 944

Introduction

The new version of the MQL language has provided developers of automated trading systems with effective tools for the implementation of complex tasks. One cannot deny the fact that the programming functionalities of the language have been considerably expanded. The MQL5 OOP features alone are worth a lot. Furthermore, the Standard Library should not go unmentioned. Judging by the error code number 359, class templates will be supported soon.

In this article, I would like to bring up what may in some way be an expansion or continuation of the subjects describing data types and their sets. Here, I would like to make reference to an article published on the MQL5.community website. A very detailed comprehensive description of the principles and logic of working with arrays was provided by Dmitry Fedoseev (Integer) in his article "MQL5 Programming Basics: Arrays".

So, today I propose to turn to lists, and more precisely, to linked linear lists. We will start with list structure, meaning and logic. After that, we will consider the related tools already available in the Standard Library. In conclusion, I'll provide examples of how lists can be used when working with MQL5.

Concept of List and Node: Theory

Concept of List and Node: Programming

1. Concept of List and Node: Theory

So what is a list for a developer and how do you go about it? I am going to make reference to the public source of information, Wikipedia, for a generic definition of this term:

In computer science, a list is an abstract data type that implements a finite ordered collection of values, where the same value may occur more than once. An instance of a list is a computer representation of the mathematical concept of a finite sequence - a tuple. Each instance of a value in the list is usually called an item, entry, or element of the list; if the same value occurs multiple times, each occurrence is considered a distinct item.

The term 'list' is also used for several concrete data structures that can be used to implement abstract lists, especially linked lists.

I believe you will agree that this definition is somewhat too scholarly.

For the purpose of this article, we are more interested in the last sentence of this definition. So let's dwell on it:

In computer science, a linked list is a basic dynamic data structure consisting of nodes, where each node is composed of data and one or two references ('links') to the next and/or previous node of the list.[1] The principal benefit of a linked list over a conventional array is a structural flexibility: the sequence of items of the linked list need not match the sequence of data elements in the computer memory, while internal links of the list items are always maintained for list traversal.

Let's try to look into it step by step.

In computer science, a list in itself is some data type. We have established that. It is rather a synthetic data type as it includes other data types. A list is somewhat similar to an array. If an array of one-type data was ever classified as a new data type, that would be a list. But not entirely so.

The principal benefit of a list is that it allows insertion or removal of nodes at any point in the list, as required. Here, the list is similar to a dynamic array, except that for a list you don't need to use the ArrayResize() function all the time.

Speaking in terms of the order of memory elements, list nodes are not stored and need not be stored the same way as array elements are stored in adjacent memory areas.

And that's more or less it. Moving further down the list.

1.1 Node in a Singly Linked List

Lists allow you to store nodes, instead of items. Node is a data type consisting of two parts.

The first part is a data field and the second part is used for links with other node(s) (Fig. 1). The first node in the list is called 'head', and the last node in the list is called 'tail'. The tail link field contains a NULL reference. It is basically used to indicate the lack of further nodes in the list. Other specialized sources refer to the rest of the list after the head as 'tail'.

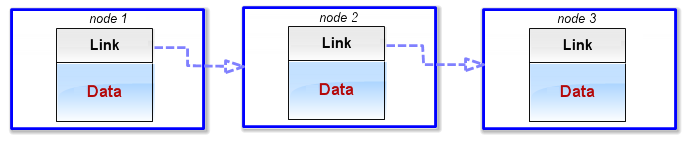
Fig. 1 Nodes in a singly linked list

Apart from singly linked list nodes, there are other types of nodes. A node in a doubly linked list is perhaps the most common one.

1.2 Node in a Doubly Linked List

We will also need a node that will serve the needs of a doubly linked list. It is different from the previous type in that it contains another link pointing to the previous node. And naturally, the node of the head of the list will contain a NULL reference. In the diagram showing the structure of the list containing such nodes (Fig. 2), links pointing to the previous nodes are displayed as red arrows.

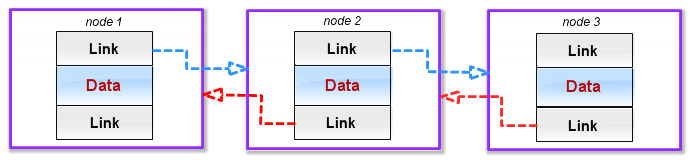
Fig. 2 Nodes in a doubly linked list

So the capabilities of a node in a doubly linked list will be similar to those of a singly linked list node. You will just need to handle one more link to the previous node.

1.3 Node in a Circular Doubly Linked List

There are cases where the above nodes can also be used in non-linear lists. And although the article will primarily describe linear lists, I will give an example of a circular list, as well.

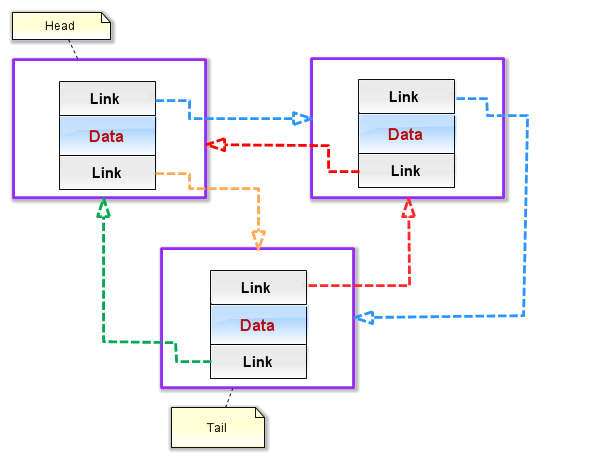
Fig. 3 Nodes in a circular doubly linked list

The diagram of a circular doubly linked list (Fig. 3) shows that nodes with two link fields are simply circularly linked. This is done using the orange and green arrows. Thus, the head node will be linked to the tail (as the previous element). And the link field of the tail node will not be empty as it will point to the head.

1.4 Major List Operations

As set out in specialized literature, all list operations can be divided into 3 base groups:

Addition (of a new node to the list);
Deletion (of a node from the list);
Checking (data of a node).

Addition methods include:

adding a new node to the beginning of the list;
adding a new node to the end of the list;
adding a node to the specified position in the list;
adding a node to an empty list;
parameterized constructor.

As far as deletion operations are concerned, they virtually mirror the corresponding operations of the addition group:

deleting the head node;
deleting the tail node;
deleting a node from the specified position in the list;
destructor.

Here, I would like to note that destructor serves to not only complete and terminate the list operation correctly, but also to properly delete all its elements.

The third group of various check operations in fact gives access to nodes or node values in the list:

searching for a given value;
checking the list for being empty;
getting the value of the ith node in the list;
getting the pointer to the ith node in the list;
getting the list size;
printing values of the list elements.

In addition to the base groups, I would also separate out the fourth, service group. It services the previous groups:

assignment operator;
copy constructor;
working with dynamic pointer;
copying the list by values;
sorting.

That's about it. The developer can of course expand the functionality and features of a list class at any time, as required.

2. Concept of List and Node: Programming

In this part, I suggest that we should proceed directly to programming nodes and lists. Illustrations to the code will be provided, where necessary.

2.1 Node in a Singly Linked List

Let's lay the groundwork for the node class (Fig. 4) serving the needs of a singly linked list. You can familiarize yourself with the class diagram notation (model) in the article entitled "How to Develop an Expert Advisor using UML Tools" (see Fig. 5. UML model of CTradeExpert class).

CiSingleNode class model

Fig. 4 CiSingleNode class model

Let's now try to work with the code. It is based on the example provided in the book by Art Friedman and other authors. "C/C++ Annotated Archives".

//+------------------------------------------------------------------+
//|                     CiSingleNode class                           |
//+------------------------------------------------------------------+
class CiSingleNode
  {
protected:
   int               m_val;   // data
   CiSingleNode     *m_next;  // pointer to the next node
public:
   void              CiSingleNode(void);                             // default constructor
   void              CiSingleNode(int _node_val);                    // parameterized constructor
   void             ~CiSingleNode(void);                             // destructor
   void              SetVal(int _node_val);                          // set-method for data
   void              SetNextNode(CiSingleNode *_ptr_next);           // set-method for the next node
   virtual void      SetPrevNode(CiSingleNode *_ptr_prev){};         // set-method for the previous node
   virtual CiSingleNode *GetPrevNode(void) const {return NULL;};     // get-method for the previous node
   CiSingleNode     *GetNextNode(void) const;                        // get-method for the next node 
   int               GetVal(void){TRACE_CALL(_t_flag) return m_val;} // get-method for data 
  };

I am not going to explain each method of the CiSingleNode class. You will be able to take a closer look at them in the file CiSingleNode.mqh attached. However, I would like to draw your attention to an interesting nuance. The class contains virtual methods that work with the previous nodes. They are in fact dummies and their presence is rather for the purposes of polymorphism for future descendants.

The code uses TRACE_CALL(f) preprocessor directive required for tracing calls of each method used.

#define TRACE_CALL(f) if(f) Print("Calling: "+__FUNCSIG__);

With only CiSingleNode class available, you are in a position to create a singly linked list. Let me give you an example of the code.

//=========== Example 1 (processing the CiSingleNode type )
 
   CiSingleNode *p_sNodes[3];                             // #1
   p_sNodes[0]=NULL;
   srand(GetTickCount()); // initialize a random number generator
//--- create nodes
   for(int i=0;i<ArraySize(p_sNodes);i++)
      p_sNodes[i]=new CiSingleNode(rand());               // #2
//--- links
   for(int j=0;j<(ArraySize(p_sNodes)-1);j++)
      p_sNodes[j].SetNextNode(p_sNodes[j+1]);             // #3
//--- check values
   for(int i=0;i<ArraySize(p_sNodes);i++)
     {
      int val=p_sNodes[i].GetVal();                       // #4
      Print("Node #"+IntegerToString(i+1)+                // #5
            " value = "+IntegerToString(val));
     }
//--- check next-nodes
   for(int j=0;j<(ArraySize(p_sNodes)-1);j++)
     {
      CiSingleNode *p_sNode_next=p_sNodes[j].GetNextNode(); // #9
      int snode_next_val=p_sNode_next.GetVal();             // #10
      Print("Next-Node #"+IntegerToString(j+1)+             // #11
            " value = "+IntegerToString(snode_next_val));
     }
//--- delete nodes
   for(int i=0;i<ArraySize(p_sNodes);i++)
      delete p_sNodes[i];                                   // #12

In string #1, we declare an array of pointers to objects of CiSingleNode type. In string #2, the array is filled with the pointers created. For data of each node, we take a pseudorandom integer in the range of 0 to 32767 using the rand() function. The nodes are linked with the next pointer in string #3. In strings #4-5, we check values of the nodes, and in strings #9-11 we check the performance of links. The pointers are deleted in string #12.

This is what has been printed to the log.

DH      0       23:23:10        test_nodes (EURUSD,H4)  Node #1 value = 3335
KP      0       23:23:10        test_nodes (EURUSD,H4)  Node #2 value = 21584
GI      0       23:23:10        test_nodes (EURUSD,H4)  Node #3 value = 917
HQ      0       23:23:10        test_nodes (EURUSD,H4)  Next-Node #1 value = 21584
HI      0       23:23:10        test_nodes (EURUSD,H4)  Next-Node #2 value = 917

The resulting node structure can be schematically shown as follows (Fig. 5).

Fig. 5 Links between the nodes in the CiSingleNode *p_sNodes[3] array

Let's now proceed to nodes in a doubly linked list.

2.2 Node in a Doubly Linked List

First, we need to brush up on the fact that a node in a doubly linked list is distinct in that it has two pointers: next-node pointer and previous-node pointer. I.e. besides the next-node link, you need to add a pointer to the previous node to a singly linked list node.

In doing this, I propose to use inheritance as a class relationship. Then the class model for a node in a doubly linked list may look as follows (Fig. 6).

CDoubleNode class model

Fig. 6 CDoubleNode class model

Now, it is time to take a look at the code.

//+------------------------------------------------------------------+
//|                    CDoubleNode class                             |
//+------------------------------------------------------------------+
class CDoubleNode : public CiSingleNode
  {
protected:
   CiSingleNode     *m_prev;  // pointer to the previous node 

public:
   void              CDoubleNode(void);                     // default constructor
   void              CDoubleNode(int node_val);             // parameterized constructor
   void             ~CDoubleNode(void){TRACE_CALL(_t_flag)};// destructor
   virtual void      SetPrevNode(CiSingleNode *_ptr_prev);  // set-method for the previous node
   virtual CiSingleNode *GetPrevNode(void) const;           // get-method for the previous node CDoubleNode
  };

There are very few additional methods - they are virtual and are related to working with the previous node. The complete class description is provided in CDoubleNode.mqh.

Let's try to create a doubly linked list based on the CDoubleNode class. Let me give you an example of the code.

//=========== Example 2 (processing the CDoubleNode type)

   CiSingleNode *p_dNodes[3];                             // #1
   p_dNodes[0]=NULL;
   srand(GetTickCount()); // initialize a random number generator
//--- create nodes
   for(int i=0;i<ArraySize(p_dNodes);i++)
      p_dNodes[i]=new CDoubleNode(rand());                // #2
//--- links
   for(int j=0;j<(ArraySize(p_dNodes)-1);j++)
     {
      p_dNodes[j].SetNextNode(p_dNodes[j+1]);             // #3
      p_dNodes[j+1].SetPrevNode(p_dNodes[j]);             // #4
     }
//--- check values
   for(int i=0;i<ArraySize(p_dNodes);i++)
     {
      int val=p_dNodes[i].GetVal();                       // #4
      Print("Node #"+IntegerToString(i+1)+                // #5
            " value = "+IntegerToString(val));
     }
//--- check next-nodes
   for(int j=0;j<(ArraySize(p_dNodes)-1);j++)
     {
      CiSingleNode *p_sNode_next=p_dNodes[j].GetNextNode(); // #9
      int snode_next_val=p_sNode_next.GetVal();             // #10
      Print("Next-Node #"+IntegerToString(j+1)+             // #11
            " value = "+IntegerToString(snode_next_val));
     }
//--- check prev-nodes
   for(int j=0;j<(ArraySize(p_dNodes)-1);j++)
     {
      CiSingleNode *p_sNode_prev=p_dNodes[j+1].GetPrevNode(); // #12
      int snode_prev_val=p_sNode_prev.GetVal();               // #13
      Print("Prev-Node #"+IntegerToString(j+2)+               // #14
            " value = "+IntegerToString(snode_prev_val));
     }
//--- delete nodes
   for(int i=0;i<ArraySize(p_dNodes);i++)
      delete p_dNodes[i];                                     // #15

In principle, this is similar to creating a singly linked list, yet there are a few peculiarities. Note how the array of pointers p_dNodes[] is declared in string #1. The type of pointers can be set identical to the base class. The principle of polymorphism in string #2 will help us to recognize them in the future. Previous nodes are checked in strings #12-14.

The following information was added to the log.

GJ      0       16:28:12        test_nodes (EURUSD,H4)  Node #1 value = 17543
IQ      0       16:28:12        test_nodes (EURUSD,H4)  Node #2 value = 1185
KK      0       16:28:12        test_nodes (EURUSD,H4)  Node #3 value = 23216
DS      0       16:28:12        test_nodes (EURUSD,H4)  Next-Node #1 value = 1185
NH      0       16:28:12        test_nodes (EURUSD,H4)  Next-Node #2 value = 23216
FR      0       16:28:12        test_nodes (EURUSD,H4)  Prev-Node #2 value = 17543
LI      0       16:28:12        test_nodes (EURUSD,H4)  Prev-Node #3 value = 1185

The resulting node structure can be schematically shown as follows (Fig. 7):

Fig. 7 Links between the nodes in the CDoubleNode *p_sNodes[3] array

I now suggest we consider a node that will be required in creating an unrolled doubly linked list.

2.3 Node in an Unrolled Doubly Linked List

Think of a node that would contain a data member which, instead of a single value, is attributable to the entire array, i.e. it contains and describes the entire array. Such node can then be used to create an unrolled list. I have decided not to provide any illustration here as this node is exactly the same as a standard node in a doubly linked list. The only difference is that the 'data' attribute encapsulates the entire array.

I am going to use inheritance again. The CDoubleNode class will serve as the base class for a node in an unrolled doubly linked list. And the class model for a node in an unrolled doubly linked list will look as follows (Fig. 8).

CiUnrollDoubleNode class model

Fig. 8 CiUnrollDoubleNode class model

The CiUnrollDoubleNode class can be defined using the following code:

//+------------------------------------------------------------------+
//|                    CiUnrollDoubleNode class                      |
//+------------------------------------------------------------------+
class CiUnrollDoubleNode : public CDoubleNode
  {
private:
   int               m_arr_val[]; // data array

public:
   void              CiUnrollDoubleNode(void);               // default constructor 
   void              CiUnrollDoubleNode(int &_node_arr[]);   // parameterized constructor
   void             ~CiUnrollDoubleNode(void);               // destructor
   bool              GetArrVal(int &_dest_arr_val[])const;   // get-method for data array
   bool              SetArrVal(const int &_node_arr_val[]);  // set-method for data array
  };

You can look into each method in more detail in CiUnrollDoubleNode.mqh.

Let's consider a parameterized constructor as an example.

//+------------------------------------------------------------------+
//|                   Parameterized constructor                      |
//+------------------------------------------------------------------+
void CiUnrollDoubleNode::CiUnrollDoubleNode(int &_node_arr[])
   : CDoubleNode(ArraySize(_node_arr))
  {
   ArrayCopy(this.m_arr_val,_node_arr);
   TRACE_CALL(_t_flag)
  }

Here, using the initialization list, we enter the size of a one-dimensional array in the data member this.m_val.

After that we 'manually' create an unrolled doubly linked list and check the links within it.

//=========== Example 3 (processing the CiUnrollDoubleNode type)

//--- data arrays
   int arr1[],arr2[],arr3[];                                  // #1
   int arr_size=15;
   ArrayResize(arr1,arr_size);
   ArrayResize(arr2,arr_size);
   ArrayResize(arr3,arr_size);
   srand(GetTickCount()); // initialize a random number generator
   
//--- fill the arrays with pseudorandom integers   
   for(int i=0;i<arr_size;i++)
     {
      arr1[i]=rand();                                         // #2
      arr2[i]=rand();
      arr3[i]=rand();
     }
//--- create nodes
   CiUnrollDoubleNode *p_udNodes[3];                          // #3
   p_udNodes[0]=new CiUnrollDoubleNode(arr1);
   p_udNodes[1]=new CiUnrollDoubleNode(arr2);
   p_udNodes[2]=new CiUnrollDoubleNode(arr3);
//--- links
   for(int j=0;j<(ArraySize(p_udNodes)-1);j++)
     {
      p_udNodes[j].SetNextNode(p_udNodes[j+1]);               // #4
      p_udNodes[j+1].SetPrevNode(p_udNodes[j]);               // #5
     }
//--- check values
   for(int i=0;i<ArraySize(p_udNodes);i++)
     {
      int val=p_udNodes[i].GetVal();                          // #6
      Print("Node #"+IntegerToString(i+1)+                    // #7
            " value = "+IntegerToString(val));
     }
//--- check array values
   for(int i=0;i<ArraySize(p_udNodes);i++)
     {
      int t_arr[]; // destination array 
      bool isCopied=p_udNodes[i].GetArrVal(t_arr);            // #8
      if(isCopied)
        {
         string arr_str=NULL;
         for(int n=0;n<ArraySize(t_arr);n++)
            arr_str+=IntegerToString(t_arr[n])+", ";
         int end_of_string=StringLen(arr_str);
         arr_str=StringSubstr(arr_str,0,end_of_string-2);
         Print("Node #"+IntegerToString(i+1)+                 // #9
               " array values = "+arr_str);
        }
     }
//--- check next-nodes
   for(int j=0;j<(ArraySize(p_udNodes)-1);j++)
     {
      int t_arr[]; // destination array 
      CiUnrollDoubleNode *p_udNode_next=p_udNodes[j].GetNextNode(); // #10
      bool isCopied=p_udNode_next.GetArrVal(t_arr);
      if(isCopied)
        {
         string arr_str=NULL;
         for(int n=0;n<ArraySize(t_arr);n++)
            arr_str+=IntegerToString(t_arr[n])+", ";
         int end_of_string=StringLen(arr_str);
         arr_str=StringSubstr(arr_str,0,end_of_string-2);
         Print("Next-Node #"+IntegerToString(j+1)+
               " array values = "+arr_str);
        }
     }
//--- check prev-nodes
   for(int j=0;j<(ArraySize(p_udNodes)-1);j++)
     {
      int t_arr[]; // destination array 
      CiUnrollDoubleNode *p_udNode_prev=p_udNodes[j+1].GetPrevNode(); // #11
      bool isCopied=p_udNode_prev.GetArrVal(t_arr);
      if(isCopied)
        {
         string arr_str=NULL;
         for(int n=0;n<ArraySize(t_arr);n++)
            arr_str+=IntegerToString(t_arr[n])+", ";
         int end_of_string=StringLen(arr_str);
         arr_str=StringSubstr(arr_str,0,end_of_string-2);
         Print("Prev-Node #"+IntegerToString(j+2)+
               " array values = "+arr_str);
        }
     }
//--- delete nodes
   for(int i=0;i<ArraySize(p_udNodes);i++)
      delete p_udNodes[i];                                            // #12
  }

The amount of code has become slightly bigger. This has to do with the fact that we need to create and fill an array for each node.

Working with data arrays begins in string #1. It is basically similar to what we had in the previous nodes considered. It is just that we need to print data values of each node for the entire array (e.g., string #9).

This is what I have got:

IN      0       00:09:13        test_nodes (EURUSD.m,H4)        Node #1 value = 15
NF      0       00:09:13        test_nodes (EURUSD.m,H4)        Node #2 value = 15
CI      0       00:09:13        test_nodes (EURUSD.m,H4)        Node #3 value = 15
FQ      0       00:09:13        test_nodes (EURUSD.m,H4)        Node #1 array values = 31784, 4837, 25797, 29079, 4223, 27234, 2155, 32351, 12010, 10353, 10391, 22245, 27895, 3918, 12069
EG      0       00:09:13        test_nodes (EURUSD.m,H4)        Node #2 array values = 1809, 18553, 23224, 20208, 10191, 4833, 25959, 2761, 7291, 23254, 29865, 23938, 7585, 20880, 25756
MK      0       00:09:13        test_nodes (EURUSD.m,H4)        Node #3 array values = 18100, 26358, 31020, 23881, 11256, 24798, 31481, 14567, 13032, 4701, 21665, 1434, 1622, 16377, 25778
RP      0       00:09:13        test_nodes (EURUSD.m,H4)        Next-Node #1 array values = 1809, 18553, 23224, 20208, 10191, 4833, 25959, 2761, 7291, 23254, 29865, 23938, 7585, 20880, 25756
JD      0       00:09:13        test_nodes (EURUSD.m,H4)        Next-Node #2 array values = 18100, 26358, 31020, 23881, 11256, 24798, 31481, 14567, 13032, 4701, 21665, 1434, 1622, 16377, 25778
EH      0       00:09:13        test_nodes (EURUSD.m,H4)        Prev-Node #2 array values = 31784, 4837, 25797, 29079, 4223, 27234, 2155, 32351, 12010, 10353, 10391, 22245, 27895, 3918, 12069
NN      0       00:09:13        test_nodes (EURUSD.m,H4)        Prev-Node #3 array values = 1809, 18553, 23224, 20208, 10191, 4833, 25959, 2761, 7291, 23254, 29865, 23938, 7585, 20880, 25756

I suggest we should draw a line under working with nodes and proceed directly to class definitions of different lists. Examples 1-3 can be found in the script test_nodes.mq5.

2.4 Singly Linked List

It is about time we make a class model of a singly linked list out of the major list operation groups (Fig. 9).

CiSingleList class model

Fig. 9 CiSingleList class model

It is easy to see that the CiSingleList class uses the node of CiSingleNode type. Speaking of types of relationships between classes, we can say that:

the CiSingleList class contains the CiSingleNode class (composition);
the CiSingleList class uses CiSingleNode class methods (dependency).

The illustration of the above relationships is provided in Fig. 10.

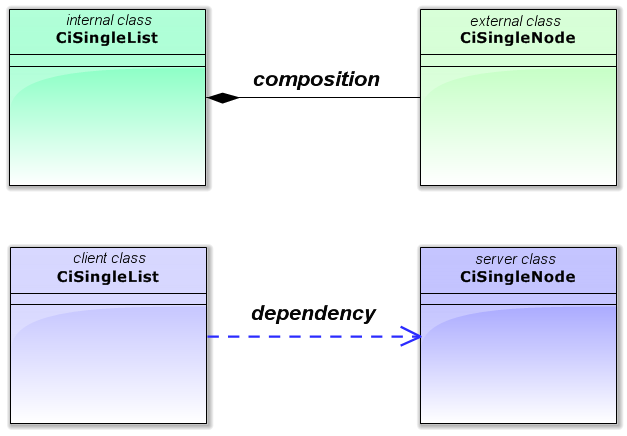
Fig. 10 Types of relationships between CiSingleList class and CiSingleNode class

Let's create a new class - CiSingleList. Looking ahead, all other list classes used in the article, will be based on this class. This is why it is so 'rich'.

//+------------------------------------------------------------------+
//|                     CiSingleList class                           |
//+------------------------------------------------------------------+
class CiSingleList
  {
protected:
   CiSingleNode     *m_head;    // head
   CiSingleNode     *m_tail;    // tail
   uint              m_size;    // number of nodes in the list
public:
   //--- constructor and destructor
   void              CiSingleList();                              // default constructor 
   void              CiSingleList(int _node_val);                 // parameterized constructor 
   void             ~CiSingleList();                              // destructor                

   //--- adding nodes   
   void              AddFront(int _node_val);                         // add a new node to the beginning of the list
   void              AddRear(int _node_val);                          // add a new node to the end of the list   
   virtual void      AddFront(int &_node_arr[]){TRACE_CALL(_t_flag)}; // add a new node to the beginning of the list
   virtual void      AddRear(int &_node_arr[]){TRACE_CALL(_t_flag)};  // add a new node to the end of the list
   //--- deleting nodes     
   int               RemoveFront(void);                           // delete the head node       
   int               RemoveRear(void);                            // delete the node from the end of the list
   void              DeleteNodeByIndex(const uint _idx);          // delete the ith node from the list

   //--- checking   
   virtual bool      Find(const int _node_val) const;             // find the required value    
   bool              IsEmpty(void) const;                         // check the list for being empty
   virtual int       GetValByIndex(const uint _idx) const;        // value of the ith node in the list
   virtual CiSingleNode *GetNodeByIndex(const uint _idx) const;   // get the ith node in the list
   virtual bool      SetNodeByIndex(CiSingleNode *_new_node,const uint _idx); // insert the new ith node in the list
   CiSingleNode     *GetHeadNode(void) const;                     // get the head node
   CiSingleNode     *GetTailNode(void) const;                     // get the tail node
   virtual uint      Size(void) const;                            // list size
   //--- service
   virtual void      PrintList(string _caption=NULL);             // print the list
   virtual bool      CopyByValue(const CiSingleList &_sList);     // copy the list by values
   virtual void      BubbleSort(void);                            // bubble sorting
   //---templates
   template<typename dPointer>
   bool              CheckDynamicPointer(dPointer &_p);           // template for checking a dynamic pointer
   template<typename dPointer>
   bool              DeleteDynamicPointer(dPointer &_p);          // template for deleting a dynamic pointer

protected:
   void              operator=(const CiSingleList &_sList) const; // assignment operator
   void              CiSingleList(const CiSingleList &_sList);    // copy constructor
   virtual bool      AddToEmpty(int _node_val);                   // add a new node to an empty list
   virtual void      addFront(int _node_val);                     // add a new "native" node to the beginning of the list
   virtual void      addRear(int _node_val);                      // add a new "native" node to the end of the list
   virtual int       removeFront(void);                           // delete the "native" head node
   virtual int       removeRear(void);                            // delete the "native" node from the end of the list
   virtual void      deleteNodeByIndex(const uint _idx);          // delete the "native" ith node from the list
   virtual CiSingleNode *newNode(int _val);                       // new "native" node
   virtual void      CalcSize(void) const;                        // calculate the list size
  };

The complete definition of the class methods is provided in CiSingleList.mqh.

When I only started developing this class, there were only 3 data members and just a few methods. But since this class served as the basis for other classes, I had to add several virtual member functions. I am not going to describe this methods in detail. An example of using this singly linked list class can be found in the script test_sList.mq5.

If it is run without the trace flag, the following entries will appear in the log:

KG      0       12:58:32        test_sList (EURUSD,H1)  =======List #1=======
PF      0       12:58:32        test_sList (EURUSD,H1)  Node #1, val=14 
RL      0       12:58:32        test_sList (EURUSD,H1)  Node #2, val=666 
MD      0       12:58:32        test_sList (EURUSD,H1)  Node #3, val=13 
DM      0       12:58:32        test_sList (EURUSD,H1)  Node #4, val=11 
QE      0       12:58:32        test_sList (EURUSD,H1)  
KN      0       12:58:32        test_sList (EURUSD,H1)  
LR      0       12:58:32        test_sList (EURUSD,H1)  =======List #2=======
RE      0       12:58:32        test_sList (EURUSD,H1)  Node #1, val=14 
DQ      0       12:58:32        test_sList (EURUSD,H1)  Node #2, val=666 
GK      0       12:58:32        test_sList (EURUSD,H1)  Node #3, val=13 
FP      0       12:58:32        test_sList (EURUSD,H1)  Node #4, val=11 
KF      0       12:58:32        test_sList (EURUSD,H1)  
MK      0       12:58:32        test_sList (EURUSD,H1)  
PR      0       12:58:32        test_sList (EURUSD,H1)  =======renewed List #2=======
GK      0       12:58:32        test_sList (EURUSD,H1)  Node #1, val=11 
JP      0       12:58:32        test_sList (EURUSD,H1)  Node #2, val=13 
JI      0       12:58:32        test_sList (EURUSD,H1)  Node #3, val=14 
CF      0       12:58:32        test_sList (EURUSD,H1)  Node #4, val=34 
QL      0       12:58:32        test_sList (EURUSD,H1)  Node #5, val=35 
OE      0       12:58:32        test_sList (EURUSD,H1)  Node #6, val=36 
MR      0       12:58:32        test_sList (EURUSD,H1)  Node #7, val=37 
KK      0       12:58:32        test_sList (EURUSD,H1)  Node #8, val=38 
MS      0       12:58:32        test_sList (EURUSD,H1)  Node #9, val=666 
OF      0       12:58:32        test_sList (EURUSD,H1)  
QK      0       12:58:32        test_sList (EURUSD,H1)

The script has filled 2 singly linked lists and then extended and sorted the second list.

2.5 Doubly Linked List

Let's now try to create a doubly linked list based on the list of the previous type. The illustration of the class model of a doubly linked list is provided in Fig. 11:

CDoubleList class model

Fig. 11 CDoubleList class model

The descendant class contains much fewer methods, while the data members are absent altogether. Below is the CDoubleList class definition.

//+------------------------------------------------------------------+
//|                      CDoubleList class                           |
//+------------------------------------------------------------------+
class CDoubleList : public CiSingleList
  {
public:
   void              CDoubleList(void);                  // default constructor    
   void              CDoubleList(int _node_val);         // parameterized constructor   
   void             ~CDoubleList(void){};                // destructor                  
   virtual bool      SetNodeByIndex(CiSingleNode *_new_node,const uint _idx); // insert the new ith node in the list  

protected:
   virtual bool      AddToEmpty(int _node_val);          // add a node to an empty list
   virtual void      addFront(int _node_val);            // add a new "native" node to the beginning of the list
   virtual void      addRear(int _node_val);             // add a new "native" node to the end of the list 
   virtual int       removeFront(void);                  // delete the "native" head node
   virtual int       removeRear(void);                   // delete the "native" tail node
   virtual void      deleteNodeByIndex(const uint _idx); // delete the "native" ith node from the list
   virtual CiSingleNode *newNode(int _node_val);         // new "native" node
  };

The complete description of the CDoubleList class methods is provided in CDoubleList.mqh.

Generally speaking, virtual functions are used here only to service the needs of the pointer to the previous node which does not exist in singly linked lists.

An example of using the list of CDoubleList type can be found in the script test_dList.mq5. It demonstrates all common list operations relevant to this list type. The script code contains one peculiar string:

CiSingleNode *_new_node=new CDoubleNode(666);     // create a new node of CDoubleNode type

There is no error because such construction is quite acceptable in cases where the base class pointer describes an object of the descendant class. This is one of the advantages of inheritance.

In MQL5, as well as in С++, the pointer to the base class can point to the object of the subclass derived from that base class. But the reverse is invalid.

If you write the string as follows:

CDoubleNode*_new_node=new CiSingleNode(666);

the compiler will not report an error or a warning but the program will run until it reaches this string. In this case, you will see a message about wrong casting of types referred to by pointers. Since the late binding mechanism only comes in action when the program is running, we need to carefully consider the hierarchy of relationships between classes.

After running the script, the log will contain the following entries:

DN      0       13:10:57        test_dList (EURUSD,H1)  =======List #1=======
GO      0       13:10:57        test_dList (EURUSD,H1)  Node #1, val=14 
IE      0       13:10:57        test_dList (EURUSD,H1)  Node #2, val=666 
FM      0       13:10:57        test_dList (EURUSD,H1)  Node #3, val=13 
KD      0       13:10:57        test_dList (EURUSD,H1)  Node #4, val=11 
JL      0       13:10:57        test_dList (EURUSD,H1)  
DG      0       13:10:57        test_dList (EURUSD,H1)  
CK      0       13:10:57        test_dList (EURUSD,H1)  =======List #2=======
IL      0       13:10:57        test_dList (EURUSD,H1)  Node #1, val=14 
KH      0       13:10:57        test_dList (EURUSD,H1)  Node #2, val=666 
PR      0       13:10:57        test_dList (EURUSD,H1)  Node #3, val=13 
MI      0       13:10:57        test_dList (EURUSD,H1)  Node #4, val=11 
DO      0       13:10:57        test_dList (EURUSD,H1)  
FR      0       13:10:57        test_dList (EURUSD,H1)  
GK      0       13:10:57        test_dList (EURUSD,H1)  =======renewed List #2=======
PR      0       13:10:57        test_dList (EURUSD,H1)  Node #1, val=11 
QI      0       13:10:57        test_dList (EURUSD,H1)  Node #2, val=13 
QP      0       13:10:57        test_dList (EURUSD,H1)  Node #3, val=14 
LO      0       13:10:57        test_dList (EURUSD,H1)  Node #4, val=34 
JE      0       13:10:57        test_dList (EURUSD,H1)  Node #5, val=35 
HL      0       13:10:57        test_dList (EURUSD,H1)  Node #6, val=36 
FK      0       13:10:57        test_dList (EURUSD,H1)  Node #7, val=37 
DR      0       13:10:57        test_dList (EURUSD,H1)  Node #8, val=38 
FJ      0       13:10:57        test_dList (EURUSD,H1)  Node #9, val=666 
HO      0       13:10:57        test_dList (EURUSD,H1)  
JR      0       13:10:57        test_dList (EURUSD,H1)

As in the case with a singly linked list, the script has filled the first (doubly linked) list, copied it and passed it to the second list. Then it increased the number of nodes in the second list, sorted and printed the list.

2.6 Unrolled Doubly Linked List

This list type is convenient in that it allows you to store not just a value but an entire array.

Let's lay the groundwork for the list of CiUnrollDoubleList type (Fig. 12).

CiUnrollDoubleList class model

Fig. 12 CiUnrollDoubleList class model

Since here we are going to deal with a data array, we will have to redefine the methods defined in the indirect base class CiSingleList.

Below is the CiUnrollDoubleList class definition.

//+------------------------------------------------------------------+
//|                     CiUnrollDoubleList class                     |
//+------------------------------------------------------------------+
class CiUnrollDoubleList : public CDoubleList
  {
public:
   void              CiUnrollDoubleList(void);                      // default constructor
   void              CiUnrollDoubleList(int &_node_arr[]);          // parameterized constructor
   void             ~CiUnrollDoubleList(void){TRACE_CALL(_t_flag)}; // destructor
   //---
   virtual void      AddFront(int &_node_arr[]);                    // add a new node to the beginning of the list
   virtual void      AddRear(int &_node_arr[]);                     // add a new node to the end of the list
   virtual bool      CopyByValue(const CiSingleList &_udList);      // copy by values
   virtual void      PrintList(string _caption=NULL);               // print the list
   virtual void      BubbleSort(void);                              // bubble sorting

protected:
   virtual bool      AddToEmpty(int &_node_arr[]);                  // add a node to an empty list
   virtual void      addFront(int &_node_arr[]);                    // add a new "native" node to the beginning of the list
   virtual void      addRear(int &_node_arr[]);                     // add a new "native" node to the end of the list
   virtual int       removeFront(void);                             // delete the "native" node from the beginning of the list
   virtual int       removeRear(void);                              // delete the "native" node from the end of the list
   virtual void      deleteNodeByIndex(const uint _idx);            // delete the "native" ith node from the list
   virtual CiSingleNode *newNode(int &_node_arr[]);                 // new "native" node
  };

The complete definition of the class methods is provided in CiUnrollDoubleList.mqh.

Let's run the script test_UdList.mq5 to check the operation of the class methods. Here, node operations are similar to those used in the previous scripts. We should perhaps say a few words about the sorting and printing methods. The sorting method sorts nodes by the number of elements so that the node containing the array of values of the smallest size is at the head of the list.

The printing method prints a string of array values contained in a certain node.

After running the script, the log will have the following entries:

II      0       13:22:23        test_UdList (EURUSD,H1) =======List #1=======
FN      0       13:22:23        test_UdList (EURUSD,H1) List node #1, array: 55, 12, 1, 2, 11, 114, 33, 113, 14, 15, 16, 17, 18, 19, 20
OO      0       13:22:23        test_UdList (EURUSD,H1) List node #2, array: 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
GG      0       13:22:23        test_UdList (EURUSD,H1) 
GP      0       13:22:23        test_UdList (EURUSD,H1) 
GR      0       13:22:23        test_UdList (EURUSD,H1) =======List #2 before sorting=======
JO      0       13:22:23        test_UdList (EURUSD,H1) List node #1, array: 55, 12, 1, 2, 11, 114, 33, 113, 14, 15, 16, 17, 18, 19, 20
CH      0       13:22:23        test_UdList (EURUSD,H1) List node #2, array: 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
CF      0       13:22:23        test_UdList (EURUSD,H1) List node #3, array: -89, -131, -141, -139, -129, -25, -105, -24, -122, -120, -118, -116, -114, -112, -110
GD      0       13:22:23        test_UdList (EURUSD,H1) 
GQ      0       13:22:23        test_UdList (EURUSD,H1) 
LJ      0       13:22:23        test_UdList (EURUSD,H1) =======List #2 after sorting=======
FN      0       13:22:23        test_UdList (EURUSD,H1) List node #1, array: 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
CJ      0       13:22:23        test_UdList (EURUSD,H1) List node #2, array: 55, 12, 1, 2, 11, 114, 33, 113, 14, 15, 16, 17, 18, 19, 20
II      0       13:22:23        test_UdList (EURUSD,H1) List node #3, array: -89, -131, -141, -139, -129, -25, -105, -24, -122, -120, -118, -116, -114, -112, -110
MD      0       13:22:23        test_UdList (EURUSD,H1) 
MQ      0       13:22:23        test_UdList (EURUSD,H1)

As you can see, after being sorted, the udList2 list has been printed starting from the node with the smallest array to the node containing the biggest array.

2.7 Circular Doubly Linked List

Although non-linear lists are not considered in this article, I suggest we work with them too. How you can circularly link nodes has already been shown above (Fig. 3).

Let's create a model of the CiCircleDoubleList class (Fig. 13). This class will be a descendant class of the CDoubleList class.

CiCircleDoubleList class model

Fig. 13 CiCircleDoubleList class model

Due to the fact that nodes in this list are of specific character (the head and the tail are linked), almost all methods of the source base class CiSingleList will have to be made virtual.

//+------------------------------------------------------------------+
//|                      CiCircleDoubleList class                    |
//+------------------------------------------------------------------+
class CiCircleDoubleList : public CDoubleList
  {
public:
   void              CiCircleDoubleList(void);                       // default constructor
   void              CiCircleDoubleList(int _node_val);              // parameterized constructor
   void             ~CiCircleDoubleList(void){TRACE_CALL(_t_flag)};  // destructor
   //---
   virtual uint      Size(void) const;                                        // list size
   virtual bool      SetNodeByIndex(CiSingleNode *_new_node,const uint _idx); // insert the new ith node in the list
   virtual int       GetValByIndex(const uint _idx) const;           // value of the ith node in the list
   virtual CiSingleNode *GetNodeByIndex(const uint _idx) const;      // get the ith node in the list
   virtual bool      Find(const int _node_val) const;                // find the required value
   virtual bool      CopyByValue(const CiSingleList &_sList);        // copy the list by values

protected:
   virtual void      addFront(int _node_val);                        // add a new "native" node to the beginning of the list
   virtual void      addRear(int _node_val);                         // add a new "native" node to the end of the list
   virtual int       removeFront(void);                              // delete the "native" head node
   virtual int       removeRear(void);                               // delete the "native" tail node
   virtual void      deleteNodeByIndex(const uint _idx);             // delete the "native" ith node from the list

protected:
   void              CalcSize(void) const;                           // calculate the list size
   void              LinkHeadTail(void);                             // link head to tail
  };

The complete class description is provided in CiCircleDoubleList.mqh.

Let's consider some methods of the class. The CiCircleDoubleList::LinkHeadTail() method links the tail node to the head node. It should be called when there is either a new tail or head and the previous link is lost.

//+------------------------------------------------------------------+
//|                  Linking head to tail                            |
//+------------------------------------------------------------------+
void CiCircleDoubleList::LinkHeadTail(void)
  {
   TRACE_CALL(_t_flag)
   this.m_head.SetPrevNode(this.m_tail);      // link head to tail
   this.m_tail.SetNextNode(this.m_head);      // link tail to head
  }

Think what this method would be like if we were dealing with a circular singly linked list.

Consider, for instance, the CiCircleDoubleList::addFront() method.

//+------------------------------------------------------------------+
//|                New "native" node to the beginning of the list    |
//+------------------------------------------------------------------+
void CiCircleDoubleList::addFront(int _node_val)
  {
   TRACE_CALL(_t_flag)
   CDoubleList::addFront(_node_val); // call a similar method of the base class
   this.LinkHeadTail();              // link head and tail
  }

You can see in the method body that a similar method of the base class CDoubleList is called. At this point, we could complete the method operation (the method as such is basically not needed here), if it was not for one thing. The link between the head and the tail is lost and the list cannot be circularly linked without it. This is why we have to call the method of linking the head and tail.

Working with the circular doubly linked list is checked in the script test_UdList.mq5.

In terms of tasks and objectives, other methods used are the same as in the previous examples.

As a result, the log contains the following entries:

PR      0       13:34:29        test_CdList (EURUSD,H1) =======List #1=======
QS      0       13:34:29        test_CdList (EURUSD,H1) Node #1, val=14 
QI      0       13:34:29        test_CdList (EURUSD,H1) Node #2, val=666 
LQ      0       13:34:29        test_CdList (EURUSD,H1) Node #3, val=13 
OH      0       13:34:29        test_CdList (EURUSD,H1) Node #4, val=11 
DP      0       13:34:29        test_CdList (EURUSD,H1) 
DK      0       13:34:29        test_CdList (EURUSD,H1) 
DI      0       13:34:29        test_CdList (EURUSD,H1) =======List #2 before sorting=======
MS      0       13:34:29        test_CdList (EURUSD,H1) Node #1, val=38 
IJ      0       13:34:29        test_CdList (EURUSD,H1) Node #2, val=37 
IQ      0       13:34:29        test_CdList (EURUSD,H1) Node #3, val=36 
EH      0       13:34:29        test_CdList (EURUSD,H1) Node #4, val=35 
EO      0       13:34:29        test_CdList (EURUSD,H1) Node #5, val=34 
FF      0       13:34:29        test_CdList (EURUSD,H1) Node #6, val=14 
DN      0       13:34:29        test_CdList (EURUSD,H1) Node #7, val=666 
GD      0       13:34:29        test_CdList (EURUSD,H1) Node #8, val=13 
JK      0       13:34:29        test_CdList (EURUSD,H1) Node #9, val=11 
JM      0       13:34:29        test_CdList (EURUSD,H1) 
JH      0       13:34:29        test_CdList (EURUSD,H1) 
MS      0       13:34:29        test_CdList (EURUSD,H1) =======List #2 after sorting=======
LE      0       13:34:29        test_CdList (EURUSD,H1) Node #1, val=11 
KL      0       13:34:29        test_CdList (EURUSD,H1) Node #2, val=13 
QS      0       13:34:29        test_CdList (EURUSD,H1) Node #3, val=14 
NJ      0       13:34:29        test_CdList (EURUSD,H1) Node #4, val=34 
NQ      0       13:34:29        test_CdList (EURUSD,H1) Node #5, val=35 
NH      0       13:34:29        test_CdList (EURUSD,H1) Node #6, val=36 
NO      0       13:34:29        test_CdList (EURUSD,H1) Node #7, val=37 
NF      0       13:34:29        test_CdList (EURUSD,H1) Node #8, val=38 
JN      0       13:34:29        test_CdList (EURUSD,H1) Node #9, val=666 
RJ      0       13:34:29        test_CdList (EURUSD,H1) 
RE      0       13:34:29        test_CdList (EURUSD,H1)

So the final diagram of inheritance between the introduced list classes is as follows (Fig. 14).

I am not sure if all the classes need to be related by inheritance but I decided to leave it all as is.

Inheritance between the list classes

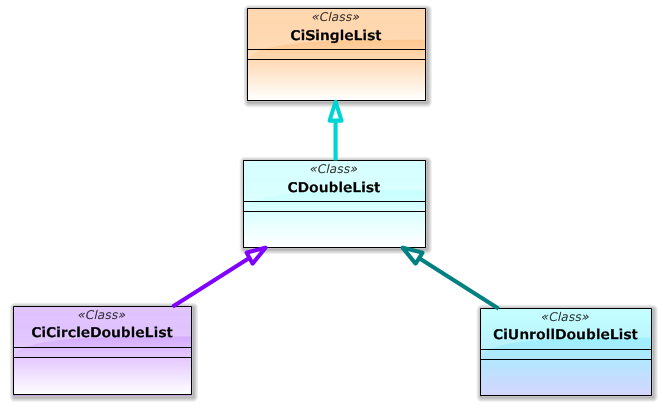
Fig. 14 Inheritance between the list classes

Drawing the line under this section of the article that has dealt with the description of custom lists, I would like to note that we have barely touched upon the group of non-linear lists, multiply linked lists and others. As I collect the relevant information and gain more experience working with such dynamic data structures, I will try to write another article.

3. Lists in the MQL5 Standard Library

Let's take a look at the list class available in the Standard Library (Fig. 15).

It belongs to Data Classes.

CList class model

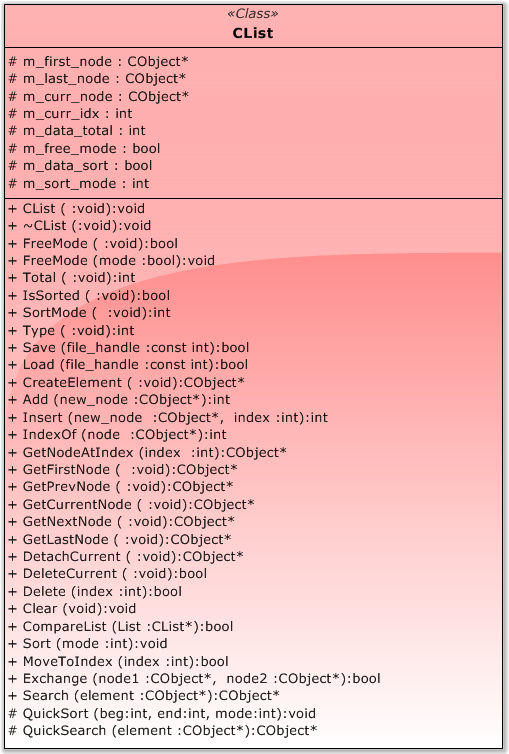
Fig. 15 CList class model

Curiously enough, CList is a descendant of the CObject class. I.e. the list inherits data and methods of the class, which is a node.

The list class contains an impressive set of methods. To be honest, I did not expect to find such a big class in the Standard Library.

The CList class has 8 data members. I would like to point out a couple of things. The class attributes contain the index of the current node (int m_curr_idx) and the pointer to the current node (CObject* m_curr_node). One can say that the list is "smart" - it can indicate the place where the control is localized. Further, it features memory management mechanism (we can physically delete a node or simply exclude it from the list), sorted list flag and sorting mode.

Speaking of methods, all methods of the CList class are divided into the following groups:

Attributes;
Create methods;
Add methods;
Delete methods;
Navigation;
Ordering methods;
Compare methods;
Search methods;
Input/Output.

As usual, there is a standard constructor and destructor.

The first one empties (NULL) all pointers. The memory management flag state is set to deleting. The new list will be unsorted.

In its body, the destructor only calls the Clear() method to empty the list of the nodes. The end of the list's existence does not necessarily entail "death" of its elements (nodes). Thus, the memory management flag set when deleting the list elements turns the class relationship from composition to aggregation.

We can handle this flag using set- and get-methods FreeMode().

There are two methods in the class which allow you to extend the list: Add() and Insert(). The first one is similar to the AddRear() method used in the first section of the article. The second method is similar to the SetNodeByIndex() method.

Let's start with a small example. We need to first create a CNodeInt node class, a descendant of the interface class CObject. It will store the value of integer type.

//+------------------------------------------------------------------+
//|                        CNodeInt class                            |
//+------------------------------------------------------------------+
class  CNodeInt : public CObject
  {
private:
   int               m_val;  // node data

public:
   void              CNodeInt(void){this.m_val=WRONG_VALUE;}; // default constructor
   void              CNodeInt(int _val);                      // parameterized constructor
   void             ~CNodeInt(void){};                        // destructor
   int               GetVal(void){return this.m_val;};        // get-method for node data
   void              SetVal(int _val){this.m_val=_val;};      // set-method for node data
  };
//+------------------------------------------------------------------+
//|                    Parameterized constructor                     |
//+------------------------------------------------------------------+
void CNodeInt::CNodeInt(int _val):m_val(_val)
  {

  };

We will work with the CList list in the script test_MQL5_List.mq5.

Example 1 demonstrates a dynamic creation of the list and nodes. The list is then filled with nodes and the value of the first node is checked before and after deleting the list.

//--- Example 1 (testing memory management)
   CList *myList=new CList;
// myList.FreeMode(false);  // reset flag
   bool _free_mode=myList.FreeMode();
   PrintFormat("\nList \"myList\" - memory management flag: %d",_free_mode);
   CNodeInt *p_new_nodes_int[10];
   p_new_nodes_int[0]=NULL;
   for(int i=0;i<ArraySize(p_new_nodes_int);i++)
     {
      p_new_nodes_int[i]=new CNodeInt(rand());
      myList.Add(p_new_nodes_int[i]);
     }
   PrintFormat("List \"myList\" has as many nodes as: %d",myList.Total());
   Print("=======Before deleting \"myList\"=======");
   PrintFormat("The 1st node value is: %d",p_new_nodes_int[0].GetVal());
   delete myList;
   int val_to_check=WRONG_VALUE;
   if(CheckPointer(p_new_nodes_int[0]))
      val_to_check=p_new_nodes_int[0].GetVal();
   Print("=======After deleting \"myList\"=======");
   PrintFormat("The 1st node value is: %d",val_to_check);

If the string resetting the flag remains commented-out (inactive), we will get the following entries in the log:

GS      0       14:00:16        test_MQL5_List (EURUSD,H1)      
EO      0       14:00:16        test_MQL5_List (EURUSD,H1)      List "myList" - memory management flag: 1
FR      0       14:00:16        test_MQL5_List (EURUSD,H1)      List "myList" has as many nodes as: 10
JH      0       14:00:16        test_MQL5_List (EURUSD,H1)      =======Before deleting "myList"=======
DO      0       14:00:16        test_MQL5_List (EURUSD,H1)      The 1st node value is: 7189
KJ      0       14:00:16        test_MQL5_List (EURUSD,H1)      =======After deleting "myList"=======
QK      0       14:00:16        test_MQL5_List (EURUSD,H1)      The 1st node value is: -1

Please note that after dynamically deleting the myList list, all nodes in it have also been deleted from the memory.

However if we uncomment the reset flag string:

// myList.FreeMode(false); // reset flag

the output to the log will be as follows:

NS      0       14:02:11        test_MQL5_List (EURUSD,H1)      
CN      0       14:02:11        test_MQL5_List (EURUSD,H1)      List "myList" - memory management flag: 0
CS      0       14:02:11        test_MQL5_List (EURUSD,H1)      List "myList" has as many nodes as: 10
KH      0       14:02:11        test_MQL5_List (EURUSD,H1)      =======Before deleting "myList"=======
NL      0       14:02:11        test_MQL5_List (EURUSD,H1)      The 1st node value is: 20411
HJ      0       14:02:11        test_MQL5_List (EURUSD,H1)      =======After deleting "myList"=======
LI      0       14:02:11        test_MQL5_List (EURUSD,H1)      The 1st node value is: 20411
QQ      1       14:02:11        test_MQL5_List (EURUSD,H1)      10 undeleted objects left
DD      1       14:02:11        test_MQL5_List (EURUSD,H1)      10 objects of type CNodeInt left
DL      1       14:02:11        test_MQL5_List (EURUSD,H1)      400 bytes of leaked memory

It is easy to notice that the head node retains its value both before and after the list has been deleted. In this case, there will also be undeleted objects remaining if the script does not contain the code to delete them correctly.

Let's now try to work with the sorting method.

//--- Example 2 (sorting)

   CList *myList=new CList;
   CNodeInt *p_new_nodes_int[10];
   p_new_nodes_int[0]=NULL;
   for(int i=0;i<ArraySize(p_new_nodes_int);i++)
     {
      p_new_nodes_int[i]=new CNodeInt(rand());
      myList.Add(p_new_nodes_int[i]);
     }
   PrintFormat("\nList \"myList\" has as many nodes as: %d",myList.Total());
   Print("=======List \"myList\" before sorting=======");
   for(int i=0;i<myList.Total();i++)
     {
      CNodeInt *p_node_int=myList.GetNodeAtIndex(i);
      int node_val=p_node_int.GetVal();
      PrintFormat("Node #%d is equal to: %d",i+1,node_val);
     }
   myList.Sort(0);
   Print("\n=======List \"myList\" after sorting=======");
   for(int i=0;i<myList.Total();i++)
     {
      CNodeInt *p_node_int=myList.GetNodeAtIndex(i);
      int node_val=p_node_int.GetVal();
      PrintFormat("Node #%d is equal to: %d",i+1,node_val);
     }
   delete myList;

As a result, the log contains the following entries:

OR      0       22:47:01        test_MQL5_List (EURUSD,H1)      
FN      0       22:47:01        test_MQL5_List (EURUSD,H1)      List "myList" has as many nodes as: 10
FH      0       22:47:01        test_MQL5_List (EURUSD,H1)      =======List "myList" before sorting=======
LG      0       22:47:01        test_MQL5_List (EURUSD,H1)      Node #1 is equal to: 30511
CO      0       22:47:01        test_MQL5_List (EURUSD,H1)      Node #2 is equal to: 17404
GF      0       22:47:01        test_MQL5_List (EURUSD,H1)      Node #3 is equal to: 12215
KQ      0       22:47:01        test_MQL5_List (EURUSD,H1)      Node #4 is equal to: 31574
NJ      0       22:47:01        test_MQL5_List (EURUSD,H1)      Node #5 is equal to: 7285
HP      0       22:47:01        test_MQL5_List (EURUSD,H1)      Node #6 is equal to: 23509
IH      0       22:47:01        test_MQL5_List (EURUSD,H1)      Node #7 is equal to: 26991
NS      0       22:47:01        test_MQL5_List (EURUSD,H1)      Node #8 is equal to: 414
MK      0       22:47:01        test_MQL5_List (EURUSD,H1)      Node #9 is equal to: 18824
DR      0       22:47:01        test_MQL5_List (EURUSD,H1)      Node #10 is equal to: 1560
OR      0       22:47:01        test_MQL5_List (EURUSD,H1)      
OM      0       22:47:01        test_MQL5_List (EURUSD,H1)      =======List "myList" after sorting=======
QM      0       22:47:01        test_MQL5_List (EURUSD,H1)      Node #1 is equal to: 26991
RE      0       22:47:01        test_MQL5_List (EURUSD,H1)      Node #2 is equal to: 23509
ML      0       22:47:01        test_MQL5_List (EURUSD,H1)      Node #3 is equal to: 18824
DD      0       22:47:01        test_MQL5_List (EURUSD,H1)      Node #4 is equal to: 414
LL      0       22:47:01        test_MQL5_List (EURUSD,H1)      Node #5 is equal to: 1560
IG      0       22:47:01        test_MQL5_List (EURUSD,H1)      Node #6 is equal to: 17404
PN      0       22:47:01        test_MQL5_List (EURUSD,H1)      Node #7 is equal to: 30511
II      0       22:47:01        test_MQL5_List (EURUSD,H1)      Node #8 is equal to: 31574
OQ      0       22:47:01        test_MQL5_List (EURUSD,H1)      Node #9 is equal to: 12215
JH      0       22:47:01        test_MQL5_List (EURUSD,H1)      Node #10 is equal to: 7285

Even if any sorting has been done at all, the sorting technique remained a mystery to me. I will explain why. Without going into much detail regarding the call order, the CList::Sort() method calls the virtual method CObject::Compare() which is not implemented in the base class in any way. So, the programmer has to deal with the implementation of a sorting method on his own.

And now, a few words about the Total() method. It returns the number of elements (nodes) for which the data member m_data_total is responsible. It is a very short concise method. The element count in this implementation will be much faster than in the one I proposed earlier. Indeed, why every time pass through the list and count nodes, whereas the exact number of nodes in the list can be set when adding or deleting nodes.

Example 3 compares the speed of filling lists of CList and CiSingleList type and calculates time for getting the size of each list.

//--- Example 3 (nodes number)

   int iterations=1e7;   // 10 million iterations
//--- the new CList 
   CList *p_mql_List=new CList;
   uint start=GetTickCount(); // starting value
   for(int i=0;i<iterations;i++)
     {
      CNodeInt *p_node_int=new CNodeInt(rand());
      p_mql_List.Add(p_node_int);
     }
   uint time=GetTickCount()-start; // time spent, msec
   Print("\n=======the CList type list=======");
   PrintFormat("Filling the list of %.3e nodes has taken %d msec",iterations,time);
//--- get the size
   start=GetTickCount();
   int list_size=p_mql_List.Total(); 
   time=GetTickCount()-start;
   PrintFormat("Getting the size of the list has taken %d msec",time);

   delete p_mql_List;

//---  the new CiSingleList 
   CiSingleList *p_sList=new CiSingleList;

   start=GetTickCount(); // starting value
   for(int i=0;i<iterations;i++)
      p_sList.AddRear(rand());
   time=GetTickCount()-start; // time spent, msec
   Print("\n=======the CiSingleList type list=======");
   PrintFormat("Filling the list of %.3e nodes has taken %d msec",iterations,time);
//--- get the size
   start=GetTickCount();
   list_size=(int)p_sList.Size();  
   time=GetTickCount()-start;
   PrintFormat("Getting the size of the list has taken %d msec",time);
   delete p_sList;

This is what I have got in the log:

KO      0       22:48:24        test_MQL5_List (EURUSD,H1)      
CK      0       22:48:24        test_MQL5_List (EURUSD,H1)      =======the CList type list=======
JL      0       22:48:24        test_MQL5_List (EURUSD,H1)      Filling the list of 1.000e+007 nodes has taken 2606 msec
RO      0       22:48:24        test_MQL5_List (EURUSD,H1)      Getting the size of the list has taken 0 msec
LF      0       22:48:29        test_MQL5_List (EURUSD,H1)      
EL      0       22:48:29        test_MQL5_List (EURUSD,H1)      =======the CiSingleList type list=======
KK      0       22:48:29        test_MQL5_List (EURUSD,H1)      Filling the list of 1.000e+007 nodes has taken 2356 msec
NF      0       22:48:29        test_MQL5_List (EURUSD,H1)      Getting the size of the list has taken 359 msec

The method for getting the size works instantly in the CList list. By the way, adding nodes to the list is also quite fast.

In the next block (Example 4), I suggest paying attention to one of the major downsides of the list as a data container - the speed of access to elements. The thing is that list elements are accessed linearly. In the CList class, they are accessed in a binary way, which slightly decreases the algorithm laboriousness.

When searching linearly, laboriousness is O(N). A search implemented in a binary way results in laboriousness of log2(N).

This is an example of the code for accessing elements of a data set:

//--- Example 4 (speed of accessing the node)

   const uint Iter_arr[]={1e3,3e3,6e3,9e3,1e4,3e4,6e4,9e4,1e5,3e5,6e5};
   for(uint i=0;i<ArraySize(Iter_arr);i++)
     {
      const uint cur_iterations=Iter_arr[i]; // iterations number     
      uint randArr[];                        // array of random numbers
      uint idxArr[];                         // array of indexes
      //--- set the arrays size    
      ArrayResize(randArr,cur_iterations);
      ArrayResize(idxArr,cur_iterations);
      CRandom myRand;                        // random number generator
      //--- fill the array of random numbers
      for(uint t=0;t<cur_iterations;t++)
         randArr[t]=myRand.int32();
      //--- fill the array of indexes with random numbers (from 0 to 10 million)
      int iter_log10=(int)log10(cur_iterations);
      for(uint r=0;r<cur_iterations;r++)
        {
         uint rand_val=myRand.int32(); // random value (from 0 to 4 294 967 295)
         if(rand_val>=cur_iterations)
           {
            int val_log10=(int)log10(rand_val);
            double log10_remainder=val_log10-iter_log10;
            rand_val/=(uint)pow(10,log10_remainder+1);
           }
         //--- check the limit
         if(rand_val>=cur_iterations)
           {
            Alert("Random value error!");
            return;
           }
         idxArr[r]=rand_val;
        }
      //--- time spent for the array
      uint start=GetTickCount();
      //--- accessing the array elements 
      for(uint p=0;p<cur_iterations;p++)
         uint random_val=randArr[idxArr[p]];

      uint time=GetTickCount()-start; // time spent, msec
      Print("\n=======the uint type array=======");
      PrintFormat("Random accessing the array of elements %.1e has taken %d msec",cur_iterations,time);

      //--- the CList type list
      CList *p_mql_List=new CList;
      //--- fill the list
      for(uint q=0;q<cur_iterations;q++)
        {
         CNodeInt *p_node_int=new CNodeInt(randArr[q]);
         p_mql_List.Add(p_node_int);
        }
      start=GetTickCount();
      //--- accessing the list nodes
      for(uint w=0;w<cur_iterations;w++)
         CNodeInt *p_node_int=p_mql_List.GetNodeAtIndex(idxArr[w]);
      time=GetTickCount()-start; // time spent, msec
      Print("\n=======the CList type list=======");
      PrintFormat("Random accessing the list of nodes %.1e has taken %d msec",cur_iterations,time);

      //--- free the memory
      ArrayFree(randArr);
      ArrayFree(idxArr);
      delete p_mql_List;
     }

Based on the block operation results, the following entries have been printed to the log:

MR      0       22:51:22        test_MQL5_List (EURUSD,H1)      
QL      0       22:51:22        test_MQL5_List (EURUSD,H1)      =======the uint type array=======
IG      0       22:51:22        test_MQL5_List (EURUSD,H1)      Random accessing the array of elements 1.0e+003 has taken 0 msec
QF      0       22:51:22        test_MQL5_List (EURUSD,H1)      
IQ      0       22:51:22        test_MQL5_List (EURUSD,H1)      =======the CList type list=======
JK      0       22:51:22        test_MQL5_List (EURUSD,H1)      Random accessing the list of nodes 1.0e+003 has taken 0 msec
MJ      0       22:51:22        test_MQL5_List (EURUSD,H1)      
QD      0       22:51:22        test_MQL5_List (EURUSD,H1)      =======the uint type array=======
GO      0       22:51:22        test_MQL5_List (EURUSD,H1)      Random accessing the array of elements 3.0e+003 has taken 0 msec
QN      0       22:51:22        test_MQL5_List (EURUSD,H1)      
II      0       22:51:22        test_MQL5_List (EURUSD,H1)      =======the CList type list=======
EP      0       22:51:22        test_MQL5_List (EURUSD,H1)      Random accessing the list of nodes 3.0e+003 has taken 16 msec
OR      0       22:51:22        test_MQL5_List (EURUSD,H1)      
OL      0       22:51:22        test_MQL5_List (EURUSD,H1)      =======the uint type array=======
FG      0       22:51:22        test_MQL5_List (EURUSD,H1)      Random accessing the array of elements 6.0e+003 has taken 0 msec
CF      0       22:51:22        test_MQL5_List (EURUSD,H1)      
GQ      0       22:51:22        test_MQL5_List (EURUSD,H1)      =======the CList type list=======
CH      0       22:51:22        test_MQL5_List (EURUSD,H1)      Random accessing the list of nodes 6.0e+003 has taken 31 msec
QJ      0       22:51:22        test_MQL5_List (EURUSD,H1)      
MD      0       22:51:22        test_MQL5_List (EURUSD,H1)      =======the uint type array=======
MO      0       22:51:22        test_MQL5_List (EURUSD,H1)      Random accessing the array of elements 9.0e+003 has taken 0 msec
EN      0       22:51:22        test_MQL5_List (EURUSD,H1)      
MJ      0       22:51:22        test_MQL5_List (EURUSD,H1)      =======the CList type list=======
CP      0       22:51:22        test_MQL5_List (EURUSD,H1)      Random accessing the list of nodes 9.0e+003 has taken 47 msec
CR      0       22:51:22        test_MQL5_List (EURUSD,H1)      
KL      0       22:51:22        test_MQL5_List (EURUSD,H1)      =======the uint type array=======
JG      0       22:51:22        test_MQL5_List (EURUSD,H1)      Random accessing the array of elements 1.0e+004 has taken 0 msec
GF      0       22:51:22        test_MQL5_List (EURUSD,H1)      
KR      0       22:51:22        test_MQL5_List (EURUSD,H1)      =======the CList type list=======
MK      0       22:51:22        test_MQL5_List (EURUSD,H1)      Random accessing the list of nodes 1.0e+004 has taken 343 msec
GJ      0       22:51:22        test_MQL5_List (EURUSD,H1)      
GG      0       22:51:22        test_MQL5_List (EURUSD,H1)      =======the uint type array=======
LO      0       22:51:22        test_MQL5_List (EURUSD,H1)      Random accessing the array of elements 3.0e+004 has taken 0 msec
QO      0       22:51:24        test_MQL5_List (EURUSD,H1)      
MJ      0       22:51:24        test_MQL5_List (EURUSD,H1)      =======the CList type list=======
NP      0       22:51:24        test_MQL5_List (EURUSD,H1)      Random accessing the list of nodes 3.0e+004 has taken 1217 msec
OS      0       22:51:24        test_MQL5_List (EURUSD,H1)      
KO      0       22:51:24        test_MQL5_List (EURUSD,H1)      =======the uint type array=======
CP      0       22:51:24        test_MQL5_List (EURUSD,H1)      Random accessing the array of elements 6.0e+004 has taken 0 msec
MG      0       22:51:26        test_MQL5_List (EURUSD,H1)      
ER      0       22:51:26        test_MQL5_List (EURUSD,H1)      =======the CList type list=======
PG      0       22:51:26        test_MQL5_List (EURUSD,H1)      Random accessing the list of nodes 6.0e+004 has taken 2387 msec
GK      0       22:51:26        test_MQL5_List (EURUSD,H1)      
OG      0       22:51:26        test_MQL5_List (EURUSD,H1)      =======the uint type array=======
NH      0       22:51:26        test_MQL5_List (EURUSD,H1)      Random accessing the array of elements 9.0e+004 has taken 0 msec
JO      0       22:51:30        test_MQL5_List (EURUSD,H1)      
NK      0       22:51:30        test_MQL5_List (EURUSD,H1)      =======the CList type list=======
KO      0       22:51:30        test_MQL5_List (EURUSD,H1)      Random accessing the list of nodes 9.0e+004 has taken 3619 msec
HS      0       22:51:30        test_MQL5_List (EURUSD,H1)      
DN      0       22:51:30        test_MQL5_List (EURUSD,H1)      =======the uint type array=======
RP      0       22:51:30        test_MQL5_List (EURUSD,H1)      Random accessing the array of elements 1.0e+005 has taken 0 msec
OD      0       22:52:05        test_MQL5_List (EURUSD,H1)      
GS      0       22:52:05        test_MQL5_List (EURUSD,H1)      =======the CList type list=======
DE      0       22:52:05        test_MQL5_List (EURUSD,H1)      Random accessing the list of nodes 1.0e+005 has taken 35631 msec
NH      0       22:52:06        test_MQL5_List (EURUSD,H1)      
RF      0       22:52:06        test_MQL5_List (EURUSD,H1)      =======the uint type array=======
FI      0       22:52:06        test_MQL5_List (EURUSD,H1)      Random accessing the array of elements 3.0e+005 has taken 0 msec
HL      0       22:54:20        test_MQL5_List (EURUSD,H1)      
PD      0       22:54:20        test_MQL5_List (EURUSD,H1)      =======the CList type list=======
FN      0       22:54:20        test_MQL5_List (EURUSD,H1)      Random accessing the list of nodes 3.0e+005 has taken 134379 msec
RQ      0       22:54:20        test_MQL5_List (EURUSD,H1)      
JI      0       22:54:20        test_MQL5_List (EURUSD,H1)      =======the uint type array=======
MR      0       22:54:20        test_MQL5_List (EURUSD,H1)      Random accessing the array of elements 6.0e+005 has taken 15 msec
NE      0       22:58:48        test_MQL5_List (EURUSD,H1)      
FL      0       22:58:48        test_MQL5_List (EURUSD,H1)      =======the CList type list=======
GE      0       22:58:48        test_MQL5_List (EURUSD,H1)      Random accessing the list of nodes 6.0e+005 has taken 267589 msec

You can see that random access to list elements takes more time as the list size gets bigger (Fig. 16).

Time spent for random access to array and list elements

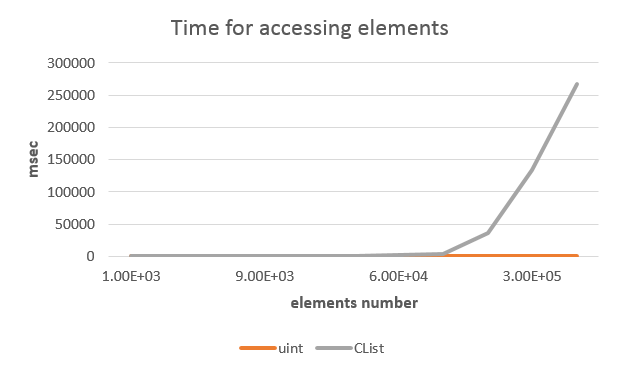
Fig. 16 Time spent for random access to array and list elements

Let's now consider methods for saving and loading data.

The base list class CList contains such methods but they are virtual. So, in order to test their operation using an example, we need to do some preparation.

We should inherit the CList class capabilities using the descendant class CIntList. The latter will only have 1 method to create a new element CIntList::CreateElement().

//+------------------------------------------------------------------+
//|                      CIntList class                              |
//+------------------------------------------------------------------+
class CIntList : public CList
  {

public:
   virtual CObject *CreateElement(void);
  };
//+------------------------------------------------------------------+
//|                    New element of the list                       |
//+------------------------------------------------------------------+
CObject *CIntList::CreateElement(void)
  {
   CObject *new_node=new CNodeInt();
   return new_node;
  }

We will also need to add the virtual methods CNodeInt::Save() and CNodeInt::Load() to the derived node type CNodeInt. They will be called from the member functions CList::Save() and CList::Load(), respectively.

As a result, the example will be as follows (Example 5):

//--- Example 5 (saving list data)
//--- the CIntList type list
   CList *p_int_List=new CIntList;
   int randArr[1000];                        // array of random numbers
   ArrayInitialize(randArr,0);
//--- fill the array of random numbers 
   for(int t=0;t<1000;t++)
      randArr[t]=(int)myRand.int32();
//--- fill the list
   for(uint q=0;q<1000;q++)
     {
      CNodeInt *p_node_int=new CNodeInt(randArr[q]);
      p_int_List.Add(p_node_int);
     }
//--- save the list to the file 
   int  file_ha=FileOpen("List_data.bin",FILE_WRITE|FILE_BIN);
   p_int_List.Save(file_ha);
   FileClose(file_ha);             
   p_int_List.FreeMode(true);    
   p_int_List.Clear();           
//--- load the list from the file  
   file_ha=FileOpen("List_data.bin",FILE_READ|FILE_BIN);
   p_int_List.Load(file_ha);
   int Loaded_List_size=p_int_List.Total();
   PrintFormat("Nodes loaded from the file: %d",Loaded_List_size);
//--- free the memory     
   delete p_int_List;

After running the script on the chart, the following entry will be added to the Log:

ND      0       11:59:35        test_MQL5_List (EURUSD,H1)      As many as 1000 nodes loaded from the file.

Thus, we have seen the implementation of input/output methods for a data member of the CNodeInt node type.

In the next section, we will see examples of how lists can be used to solve problems when working with MQL5.

4. Examples of Using Lists in MQL5

In the previous section when considering the methods of the Standard Library class CList, I have given a few examples.

Now, I am going to consider cases where the list is used to solve a specific problem. And here I cannot but once again point out the benefit of the list as a container data type. We can make working with the code more efficient by taking advantage of the flexibility of a list.

4.1 Handling Graphical Objects

Imagine that we need to programmatically create graphical objects in the chart. These can be different objects that may appear in the chart due to various reasons.

I remember how once the list helped me to sort out a situation with graphical objects. And I would like to share this memory with you.

I had a task to create vertical lines by the specified condition. According to the condition, the vertical lines served as limits for a given time interval which varied in length on a case to case basis. That said, the interval was not always completely formed.

I was studying the behavior of EMA21 and for that purpose had to collect statistics.

I was particularly interested in the length of the slope of the moving average. For example, in a downward movement the starting point was identified by registering the negative movement of the moving average (i.e. value decrease) whereby a vertical line was drawn. Fig. 17 shows such point identified for EURUSD, H1 as September 5, 2013 16:00, upon opening of a candlestick.

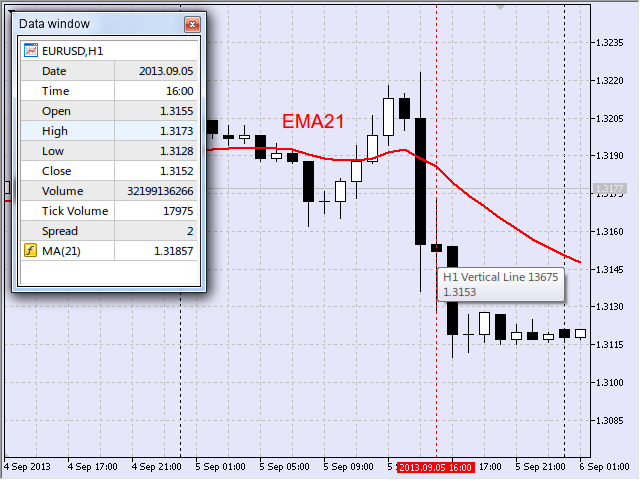
Fig. 17 First point of the downward interval

The second point suggesting the end of the downward movement was identified based on the reverse principle - by registering a positive movement of the moving average, i.e. value increase (Fig. 18).

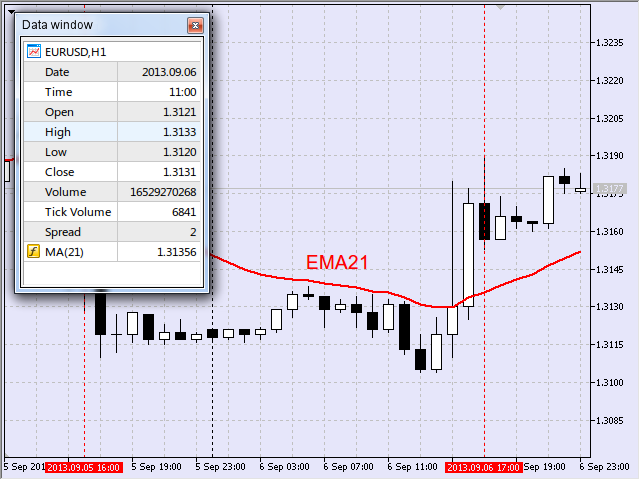
Fig. 18 Second point of the downward interval

Thus, the target interval was from September 5, 2013 16:00 to September 6, 2013 17:00.

The system for identification of different intervals can be more complex or more simple. This is not the point. What is important is the fact that this technique for working with graphical objects and concurrently collecting statistical data involves one of the major advantages of the list - flexibility of composition.

As for the current example, I first created a node of CVertLineNode type which is responsible for 2 graphical "Vertical line" objects.

The class definition is as follows:

//+------------------------------------------------------------------+
//|                      CVertLineNode class                         |
//+------------------------------------------------------------------+
class CVertLineNode : public CObject
  {
private:
   SVertLineProperties m_vert_lines[2];      // array of structures of vertical line properties
   uint              m_duration;             // frame duration
   bool              m_IsFrameFormed;        // flag of frame formation

public:
   void              CVertLineNode(void);
   void             ~CVertLineNode(void){};
   //--- set-methods   
   void              SetLine(const SVertLineProperties &_vert_line,bool IsFirst=true);
   void              SetDuration(const uint _duration){this.m_duration=_duration;};
   void              SetFrameFlag(const bool _frame_flag){this.m_IsFrameFormed=_frame_flag;};
   //--- get-methods   
   void              GetLine(SVertLineProperties &_vert_line_out,bool IsFirst=true) const;
   uint              GetDuration(void) const;
   bool              GetFrameFlag(void) const;
   //--- draw the line
   bool              DrawLine(bool IsFirst=true) const;
  };

Basically, this node class describes a frame (here interpreted as a number of candlesticks confined within two vertical lines). Frame limits are represented by a couple of structures of vertical line properties, duration and formation flag.

Apart from the standard constructor and destructor, the class has several set- and get-methods, as well as the method for drawing the line in the chart.

Let me remind you that the node of vertical lines (frame) in my example can be deemed formed when there is a first vertical line indicating the beginning of the downward movement and the second vertical line indicating the beginning of the upward movement.

Using the script Stat_collector.mq5, I displayed all the frames in the chart and counted how many nodes (frames) correspond to a certain duration limit over the last 2 thousand bars.

For illustration, I created 4 lists that could contain any frame. The first list contained frames with the number of candlesticks up to 5, the second - up to 10, the third - up to 15 and the fourth - unlimited number.

NS      0       15:27:32        Stat_collector (EURUSD,H1)      =======List #1=======
RF      0       15:27:32        Stat_collector (EURUSD,H1)      Duration limit: 5
ML      0       15:27:32        Stat_collector (EURUSD,H1)      Nodes number: 65
HK      0       15:27:32        Stat_collector (EURUSD,H1)      
OO      0       15:27:32        Stat_collector (EURUSD,H1)      =======List #2=======
RI      0       15:27:32        Stat_collector (EURUSD,H1)      Duration limit: 10
NP      0       15:27:32        Stat_collector (EURUSD,H1)      Nodes number: 15
RG      0       15:27:32        Stat_collector (EURUSD,H1)      
FH      0       15:27:32        Stat_collector (EURUSD,H1)      =======List #3=======
GN      0       15:27:32        Stat_collector (EURUSD,H1)      Duration limit: 15
FG      0       15:27:32        Stat_collector (EURUSD,H1)      Nodes number: 6
FR      0       15:27:32        Stat_collector (EURUSD,H1)      
CD      0       15:27:32        Stat_collector (EURUSD,H1)      =======List #4=======
PS      0       15:27:32        Stat_collector (EURUSD,H1)      Nodes number: 20

As a result, I got the following chart (Fig. 19). For convenience, the second vertical frame line is displayed in blue.

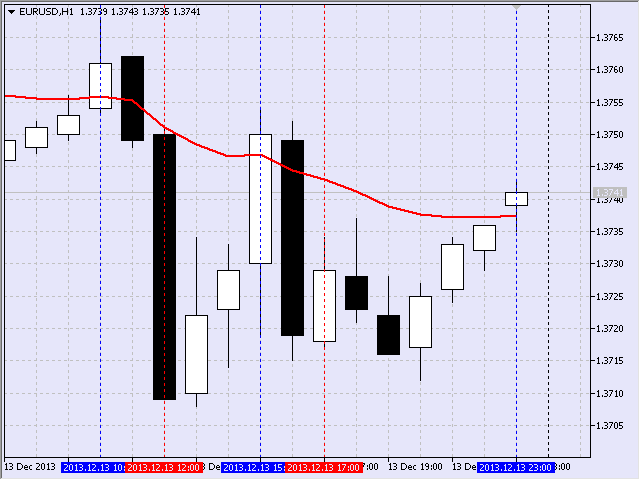
Fig. 19 Displaying frames

Curiously enough, the last frame was formed during the last hour on Friday, December 13, 2013. It fell under the second list since it was 6 hours in duration.

4.2 Dealing with Virtual Trading

Imagine that you need to create an Expert Advisor that would implement several independent strategies with respect to one instrument in a tick flow. It is clear that in reality only one strategy can be implemented at a time with respect to one instrument. All other strategies will be of virtual nature. So, it can be implemented solely for the purposes of testing and optimizing a trading idea.

Here, I must make a reference to a fundamental article that provides a detailed description of basic concepts related to trading in general and, particularly, to the MetaTrader 5 terminal: "Orders, Positions and Deals in MetaTrader 5".

So, if in solving this problem we use the trading concept, trading object management system and methodology of storing information about trading objects that are customary in the MetaTrader 5 environment, we should probably think of creating a virtual database.

Let me remind you that a developer classifies all trading objects into orders, positions, deals and history orders. A critical eye might notice that the term 'trading object' has been brought into use here by the author himself. This is true...

I propose to use a similar approach in virtual trading and get the following virtual trading objects: virtual orders, virtual positions, virtual deals and virtual history orders.

I believe that this subject is worth an in-depth and more detailed discussion. In the meantime, getting back to the subject of the article, I would like to say that container data types, including lists, can make the programmer's life easier when implementing virtual strategies.

Think of a new virtual position that, naturally enough, cannot be on the trade server side. This means that the information about it should be saved on the terminal side. Here, a database can be represented by a list which in turn consists of several lists, one of which will contain nodes of the virtual position.

Using the developer's approach, there will be the following classes of virtual trading:

Class/Group	Description
CVirtualOrder	Class for working with virtual pending orders
CVirtualHistoryOrder	Class for working with virtual "history" orders
CVirtualPosition	Class for working with virtual open positions
CVirtualDeal	Class for working with virtual "history" deals
CVirtualTrade	Class for performing virtual trading operations

Table 1. Classes of virtual trading

I will not discuss the composition of any of the virtual trading classes. But it will probably contain all or almost all methods of a standard trading class. I just want to note that what the developer uses is not a class of a given trading object itself but a class of its properties.

In order to use lists in your algorithms, you will also need nodes. Therefore, we need to wrap up the class of a virtual trading object in a node.

Assume that the node of a virtual open position is of CVirtualPositionNode type. The definition of this type could initially be as follows:

//+------------------------------------------------------------------+
//|                Class CVirtualPositionNode                        |
//+------------------------------------------------------------------+
class CVirtualPositionNode : public CObject
  {
protected:
   CVirtualPositionNode *m_virt_position;         // pointer to the virtual function

public:
   void              CVirtualPositionNode(void);  // default constructor
   void             ~CVirtualPositionNode(void);  // destructor
  };

Now, when the virtual position opens, it can be added to the list of virtual positions.

I would also like to note that this approach to working with virtual trading objects does not require the use of cache memory because the database is stored in the random access memory. You can, of course, arrange for it to be stored on other storage media.

Conclusion

In this article, I've tried to demonstrate the advantages of a container data type, such as list. But I could not go without mentioning its drawbacks. Anyway, I hope that this information will be useful for those who study OOP in general, and particularly, one of its fundamental principles, polymorphism.

Location of files:

In my opinion, it would be best to create and store files in the project folder. For example, like this: %MQL5\Projects\UserLists. This is where I saved all the source code files. If you use default directories, you will need to change the include file designation method (replace quotation marks with angle brackets) in the code of some files.

#	File	Location	Description
1	CiSingleNode.mqh	%MQL5\Projects\UserLists	Class of a singly linked list node
2	CDoubleNode.mqh	%MQL5\Projects\UserLists	Class of a doubly linked list node
3	CiUnrollDoubleNode.mqh	%MQL5\Projects\UserLists	Class of an unrolled doubly linked list node
4	test_nodes.mq5	%MQL5\Projects\UserLists	Script with examples of working with nodes
5	CiSingleList.mqh	%MQL5\Projects\UserLists	Class of a singly linked list
6	CDoubleList.mqh	%MQL5\Projects\UserLists	Class of a doubly linked list
7	CiUnrollDoubleList.mqh	%MQL5\Projects\UserLists	Class of an unrolled doubly linked list
8	CiCircleDoublList.mqh	%MQL5\Projects\UserLists	Class of a circular doubly linked list
9	test_sList.mq5	%MQL5\Projects\UserLists	Script with examples of working with a singly linked list
10	test_dList.mq5	%MQL5\Projects\UserLists	Script with examples of working with a doubly linked list
11	test_UdList.mq5	%MQL5\Projects\UserLists	Script with examples of working with an unrolled doubly linked list
12	test_CdList.mq5	%MQL5\Projects\UserLists	Script with examples of working with a circular doubly linked list
13	test_MQL5_List.mq5	%MQL5\Projects\UserLists	Script with examples of working with the CList class
14	CNodeInt.mqh	%MQL5\Projects\UserLists	Class of the node of integer type
15	CIntList.mqh	%MQL5\Projects\UserLists	List class for CNodeInt nodes
16	CRandom.mqh	%MQL5\Projects\UserLists	Class of a random number generator
17	CVertLineNode.mqh	%MQL5\Projects\UserLists	Node class for handling the frame of vertical lines
18	Stat_collector.mq5	%MQL5\Projects\UserLists	Script with a statistics collection example

References:

Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/709

Attached files |

Download ZIP

files.zip (22.75 KB)

Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.