Erhöhen der Effizienz Ihrer linearen Handelssysteme
613
14
Einleitung
Der heutige Beitrag zeigt durchschnittlichen MQL5-Programmierern, wie sie mithilfe der sogenannten Potenzierungstechnik mehr Gewinn aus ihren linearen Handelssystemen (Fixed Lot) herausholen können. Der Begriff "Potenzierung" wird hier in Bezug auf Kapitalverwaltungsmodelle angewendet, die die Größe oder Menge der Positionen im Markt gemäß dem eingegangenen Risiko anpassen. Der Grund dafür ist, dass die resultierende Kurve des Eigenkapitals geometrisch, oder exponentiell, ist und die Form einer Parabel annimmt. Der Begriff "linear" wird ebenfalls im vorliegenden Kontext verwendet, der sich in der Mitte zwischen Mathematik und Programmierung befindet. Speziell implementieren wir eine praktische MQL5-Variante der Positionsgrößenbestimmung Fixed Fractional von Ralph Vince.
Abbildung 1. Parabel
Fassen wir Kapitalverwaltungsmodelle kurz zusammen und finden heraus, wie wir eine Variante der Fixed-Fractional-Positionsgrößenbestimmung von Ralph Vince implementieren können. Sind Sie bereit? Verpassen Sie nicht die Gelegenheit, viel mehr aus Ihren Handelsstrategien herauszuholen!
1. Was sind Kapitalverwaltungsmodelle?
Kurz gesagt, sind Kapitalverwaltungsmodelle konzeptionelle Rahmen, innerhalb derer Sie Entscheidungen in Bezug auf die Größen Ihrer Positionen, die Verwendung Ihrer Stop Losses und Ihre Margenberechnungen und Handelskosten treffen. Es gibt zahlreiche Kapitalverwaltungsmodelle. Wenn Sie möchten, können Sie Fixed Lot, Fixed Fractional, Fixed Ratio, Kelly's Percentage oder Effective Cost googeln, um Ihre Kenntnis dieser klassischen Grundgerüste zu vertiefen. Wie ich bereits sagte, deckt dieser Beitrag nur eine Variante von Fixed Fractional ab.
1,2. Fixed Fractional
Die Grundidee hinter diesem Kapitalverwaltungssystem ist die Dimensionierung von Positionen in Abhängigkeit vom geschätzten mit ihnen verbundenen Risiko. Das Risiko ist bei jedem Abschluss der gleiche Bruchteil der Nettosumme.
Die Gleichung für die Anzahl der Kontrakte bei der Positionsgrößenbestimmung mit festem Bruchteil ist die folgende:
N = f * Equity / Trade Risk
N ist die Anzahl der Kontrakte, f ist der feste Bruchteil (eine Zahl zwischen 0 und 1), Equity ist der aktuelle Wert des Kapitals des Kontos und Trade Risk ist das Risiko des Abschlusses je Kontrakt, für das die Anzahl der Kontrakte berechnet wird. Bitte lesen Sie den Artikel Fixed Fractional Position Sizing von Michael R. Bryant, um mehr über dieses Modell zu erfahren.
Eine interessante Eigenschaft des Fixed-Fractional-Modells ist, dass die Größe der Operationen proportional zur Nettobilanz des Kontos bleibt und es somit theoretisch unmöglich ist, Ihr gesamtes Kapital zu verlieren. Das Risiko eines vollständigen Verlusts ist Null. Da allerdings die Anteile des Risikokapitals geringer sind, wirkt sich eine Serie von gewinn- oder verlustbringenden Operationen nicht drastisch auf die Gewinnkurve aus.
2. Hinzufügen von Fixed Fractional zu Ihrem Handelssystem
2,1. Lineares Handelssystem
Natürlich brauchen Sie zuallererst ein lineares Handelssystem, um in den Genuss des geringen Risikos zu kommen. Dieses System dient sozusagen als Machtbasis. Mit einem linearen System meine ich ein Handelssystem, das sich über einen bestimmten Zeitraum als gewinnbringend erweist und dessen Eigenkapitalkurve einer geraden Linie gleicht. In der Code Base steht beispielsweise mit HawaiianTsunamiSurfer ein sogenanntes lineares Handelssystem zur Verfügung. Seine Eigenkapitalkurve sieht von Januar 2012 bis März 2012 wie eine gerade Linie aus.
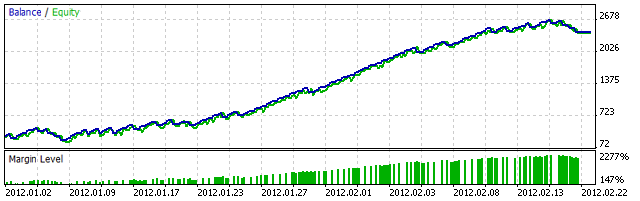
Abbildung 2. Eigenkapitalkurve von HawaiianTsunamiSurfer von Januar 2012 bis März 2012
Das Ziel dieses Beitrags ist nicht die Entwicklung eines linearen Handelssystems von Anfang an, sondern, Ihnen die benötigten Werkzeuge zur Verfügung zu stellen, sodass Sie mehr aus Ihren Systemen herausholen können. Ab jetzt werde ich also annehmen, dass Sie bereits mithilfe des objektorientierten Paradigmas ein solches Handelssystem entwickelt haben. In diesem Fall müssen Sie Ihr Programm um das nachfolgend dargelegte objektorientierte Codestück erweitern.
2,2. CEvolution, die wichtigste MQL5-Klasse zum Erhöhen der Effizienz Ihres Systems
Wir gehen also erneut objektorientiert an das Schreiben unseres EAs heran. Ich empfehle, dass Sie zuerst die Beiträge Eine weitere OOP-Klasse in MQL5 und Erstellung eines nachrichtenbasierten Expert Advisors lesen, um eine technische Grundlage für die Arbeit auf diese objektorientierte Weise zu bilden. Haben Sie die Beiträge bereits gelesen, dann denken Sie daran, dass die in diesen Beiträgen besprochenen Konzepte ein sehr wichtiges Element namens CEvolution beinhalten. Dadurch wird es uns ermöglicht, einige wichtige zeitliche Informationen wie den Status des Roboters zu jedem Zeitpunkt, die Historie der durchgeführten Operationen usw. zu verfolgen.
Diesmal erweitern wir CEvolution um die erforderliche Logik zum Verwalten unseres Kapitals. Da der risikobehaftete Anteil proportional zum Eigenkapital bleibt, das seinerseits nicht konstant ist, muss diese Logik in CEvolution hineinkodiert werden. Oder, vereinfacht ausgedrückt, die Eigenkapitalkurve verändert sich mit der Zeit, was in CEvolution wiedergegeben werden muss. Das ist die abstrahierte Idee hinter unserem objektorientierten Konzept. Ihre Aufgabe ist es nun, die folgende objektorientierte Klasse in Ihr objektorientiertes Handelssystem zu integrieren.
Klasse CEvolution.mqh:
//+------------------------------------------------------------------+ //| CEvolution.mqh | //| Copyright © 2013, Jordi Bassagañas | //+------------------------------------------------------------------+ #include <Mine\Enums.mqh> //+------------------------------------------------------------------+ //| CEvolution Class | //+------------------------------------------------------------------+ class CEvolution { protected: ENUM_STATUS_EA m_status; // The current EA's status ENUM_EXP_EQUITY_CURVE_LEVEL m_expEquityLevel; // The current exponential equity level double m_originalEquity; // The original equity value double m_lotSize; // The current lot size public: //--- Constructor and destructor methods CEvolution(ENUM_STATUS_EA status,ENUM_EXP_EQUITY_CURVE_LEVEL exp_equity_level); ~CEvolution(void); //--- Getter methods ENUM_STATUS_EA GetStatus(void); ENUM_EXP_EQUITY_CURVE_LEVEL GetExpEquityLevel(void); double GetOriginalEquity(void); double GetLotSize(void); //--- Setter methods void SetStatus(ENUM_STATUS_EA status); void SetExpEquityLevel(ENUM_EXP_EQUITY_CURVE_LEVEL exp_equity_level); void SetOriginalEquity(double equity); void SetLotSize(double size); //--- CEvolution specific methods double CalcEquityGrowth(double currentEquity); void RefreshExpEquityLevel(double currentEquity); void RefreshLotSize(); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ CEvolution::CEvolution(ENUM_STATUS_EA status,ENUM_EXP_EQUITY_CURVE_LEVEL exp_equity_level) { m_status=status; m_expEquityLevel=exp_equity_level; RefreshLotSize(); m_originalEquity=AccountInfoDouble(ACCOUNT_EQUITY); } //+------------------------------------------------------------------+ //| Destructor | //+------------------------------------------------------------------+ CEvolution::~CEvolution(void) { } //+------------------------------------------------------------------+ //| GetStatus | //+------------------------------------------------------------------+ ENUM_STATUS_EA CEvolution::GetStatus(void) { return m_status; } //+------------------------------------------------------------------+ //| GetExpEquityLevel | //+------------------------------------------------------------------+ ENUM_EXP_EQUITY_CURVE_LEVEL CEvolution::GetExpEquityLevel(void) { return m_expEquityLevel; } //+------------------------------------------------------------------+ //| GetEquity | //+------------------------------------------------------------------+ double CEvolution::GetOriginalEquity(void) { return m_originalEquity; } //+------------------------------------------------------------------+ //| GetLotSize | //+------------------------------------------------------------------+ double CEvolution::GetLotSize(void) { return m_lotSize; } //+------------------------------------------------------------------+ //| SetStatus | //+------------------------------------------------------------------+ void CEvolution::SetStatus(ENUM_STATUS_EA status) { m_status=status; } //+------------------------------------------------------------------+ //| SetExpEquityLevel | //+------------------------------------------------------------------+ void CEvolution::SetExpEquityLevel(ENUM_EXP_EQUITY_CURVE_LEVEL exp_equity_level) { m_expEquityLevel=exp_equity_level; } //+------------------------------------------------------------------+ //| SetEquity | //+------------------------------------------------------------------+ void CEvolution::SetOriginalEquity(double equity) { m_originalEquity=equity; } //+------------------------------------------------------------------+ //| SetLotSize | //+------------------------------------------------------------------+ void CEvolution::SetLotSize(double lot_size) { m_lotSize=lot_size; } //+------------------------------------------------------------------+ //| CalcEquityGrowth | //+------------------------------------------------------------------+ double CEvolution::CalcEquityGrowth(double currentEquity) { return NormalizeDouble(currentEquity * 100 / m_originalEquity - 100,2); } //+------------------------------------------------------------------+ //| RefreshExpEquityLevel | //+------------------------------------------------------------------+ void CEvolution::RefreshExpEquityLevel(double currentEquity) { double growth = CalcEquityGrowth(currentEquity); //--- is the current equity less than 10% of the original amount? if(growth <= 10) { SetExpEquityLevel(LEVEL_ONE); } //--- is the current equity more than 10% of the original amount and less than 20%? else if(growth > 10 && growth <= 20) { SetExpEquityLevel(LEVEL_TWO); } //--- is the current equity more than 20% of the original amount and less than 30%? else if(growth > 20 && growth <= 30) { SetExpEquityLevel(LEVEL_THREE); } //--- is the current equity more than 30% of the original amount and less than 40%? else if(growth > 30 && growth <= 40) { SetExpEquityLevel(LEVEL_FOUR); } //--- is the current equity more than 40% of the original amount and less than 50%? else if(growth > 40 && growth <= 50) { SetExpEquityLevel(LEVEL_FIVE); } //--- is the current equity more than 50% of the original amount and less than 60%? else if(growth > 50 && growth <= 60) { SetExpEquityLevel(LEVEL_SEVEN); } //--- is the current equity more than 60% of the original amount and less than 70%? else if(growth > 60 && growth <= 70) { SetExpEquityLevel(LEVEL_EIGHT); } //--- is the current equity more than 70% of the original amount and less than 80%? else if(growth > 70 && growth <= 80) { SetExpEquityLevel(LEVEL_NINE); } //--- is the current equity more than 90% of the original amount? else if(growth > 90) { SetExpEquityLevel(LEVEL_TEN); } } //+------------------------------------------------------------------+ //| RefreshLotSize | //+------------------------------------------------------------------+ void CEvolution::RefreshLotSize() { switch(m_expEquityLevel) { case LEVEL_ONE: SetLotSize(0.01); break; case LEVEL_TWO: SetLotSize(0.02); break; case LEVEL_THREE: SetLotSize(0.03); break; case LEVEL_FOUR: SetLotSize(0.04); break; case LEVEL_FIVE: SetLotSize(0.05); break; case LEVEL_SIX: SetLotSize(0.06); break; case LEVEL_SEVEN: SetLotSize(0.07); break; case LEVEL_EIGHT: SetLotSize(0.08); break; case LEVEL_NINE: SetLotSize(0.09); break; case LEVEL_TEN: SetLotSize(0.1); break; } } //+------------------------------------------------------------------+
Sehen wir uns nun einige wichtige Bestandteile dieser Klasse an.
Bei der Erstellung des Expert Advisors wird der Wert der ursprünglichen Eigenkapitalkurve in m_originalEquity gespeichert:
//+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ CEvolution::CEvolution(ENUM_STATUS_EA status,ENUM_EXP_EQUITY_CURVE_LEVEL exp_equity_level) { m_status=status; m_expEquityLevel=exp_equity_level; RefreshLotSize(); m_originalEquity=AccountInfoDouble(ACCOUNT_EQUITY); }
Die Methode CEvolution::CalcEquityGrowth dient der Berechnung des Wachstums der Eigenkapitalkurve in Bezug auf ihren ursprünglichen Wert:
//+------------------------------------------------------------------+ //| CalcEquityGrowth | //+------------------------------------------------------------------+ double CEvolution::CalcEquityGrowth(double currentEquity) { return NormalizeDouble(currentEquity * 100 / m_originalEquity - 100,2); }
Zuletzt dient CEvolution::RefreshExpEquityLevel der Aktualisierung der Eigenkapitalebene bei jedem Tick (beachten Sie, wie die Methode vollständig vom Wachstum des Eigenkapitals abhängt) und CEvolution::RefreshLotSize der Aktualisierung der Losgröße bei jedem Tick. Der Grund dafür ist, dass Sie diese Informationen in der Methode OnTick Ihres EAs auf folgende Weise aktualisieren müssen:
GetEvolution().RefreshExpEquityLevel(AccountInfoDouble(ACCOUNT_EQUITY)); GetEvolution().RefreshLotSize();
Übrigens, diese Lösung erfordert die Nutzung der folgenden benutzerdefinierten MQL5-Aufzählung:
//+------------------------------------------------------------------+ //| Exponential equity curve level enumeration | //+------------------------------------------------------------------+ enum ENUM_EXP_EQUITY_CURVE_LEVEL { LEVEL_ONE, LEVEL_TWO, LEVEL_THREE, LEVEL_FOUR, LEVEL_FIVE, LEVEL_SIX, LEVEL_SEVEN, LEVEL_EIGHT, LEVEL_NINE, LEVEL_TEN };Diese Umsetzung gilt als Variante von Fixed Fractional, bringt aber einige Besonderheiten mit sich. Beispielsweise wird die Eigenkapitalkurve exponentiell steigen, bis sie die sogenannte zehnte Ebene erreicht, woraufhin sie linear wird. Dennoch behält CEvolution die Grundidee des konstanten Erhöhens der Größe der Positionen im Verhältnis zur Eigenkapitalkurve bei.
2,3. Ihre Entscheidungsfindung
Mit allem, was bisher gesagt wurde, können Sie Ihre Entscheidungen über die Kapitalverwaltung bereits basierend auf dem aktuellen Status Ihres Roboters treffen.
Fügen Sie den folgenden Code in die Methode OnTick Ihres EAs ein:
switch(GetEvolution().GetStatus()) { case BUY: tp = ask + m_takeProfit * _Point; sl = bid - m_stopLoss * _Point; GetTrade().PositionOpen(GetBrain().GetSymbol(),ORDER_TYPE_BUY,m_evolution.GetLotSize(),ask,sl,tp); break; case SELL: sl = ask + m_takeProfit * _Point; tp = bid - m_stopLoss * _Point; GetTrade().PositionOpen(GetBrain().GetSymbol(),ORDER_TYPE_SELL,m_evolution.GetLotSize(),bid,sl,tp); break; case DO_NOTHING: // Nothing... break; }
Ich habe mein neues potenziertes System in ExponentialHawaiian umbenannt.
3. Backtesting Ihres potenzierten Systems
Vergessen Sie nicht, Tests durchzuführen, sobald Sie Ihr System um die oben dargelegte objektorientierte Logik erweitert haben! Ich führe jetzt das Backtesting von ExponentialHawaiian, der Fixed-Fractional-Variante von HawaiianTsunamiSurfer, durch:
Abbildung 3. Eigenkapitalkurve von ExponentialHawaiian von Januar 2012 bis März 2012
Die oben aufgeführte Kurve bleibt exponentiell, während das zugrunde liegende System linear bleibt. Wenn diese Bedingung nicht länger erfüllt wird, wird das System instabil und birgt ein theoretisches Risiko eines vollständigen Verlustes.
Fazit
Wir haben heute gelernt, wie wir größere Gewinne aus unseren linearen Handelssystemen herausholen können – solchen, die ein Fixed-Lot-Kapitalverwaltungssystem nutzen – indem wir sie potenzieren.
Wir haben mit der Vorstellung einiger klassischer Kapitalverwaltungssysteme begonnen (Fixed Lot, Fixed Fractional, Fixed Ratio, Kelly's Percentage, Effective Cost) und beschlossen, uns auf Fixed Fractional zu konzentrieren, ein einfaches Modell, in dem die Größe der Operationen proportional zur Nettobilanz des Kontos bleibt. Letztendlich haben wir ein Handelssystem genommen, das über einen gewissen Zeitraum lineare Ergebnisse zeigte, implementierten eine Variante von Fixed Fractional in MQL5 und testeten die Ergebnisse im Strategietester von MetaTrader.
Erneut haben wir einen objektorientierten Ansatz zum Schreiben unserer Expert Advisors genutzt. Ich empfehle, dass Sie zuerst die Beiträge Eine weitere OOP-Klasse in MQL5 und Erstellung eines nachrichtenbasierten Expert Advisors lesen, um eine technische Grundlage für die Arbeit auf diese objektorientierte Weise zu bilden.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/734
Versetzen Sie Ihre MQL5-Kunden mit einem Mix an verschiedenen Technologien ins Staunen!
Technische Indikatoren und digitale Filter
Der MQL5-Assistent: Wie man einem EA beibringt, einen bedingten Auftrag (Pending Order) eines beliebigen Preises zu platzieren
Erweiterung der MQL5-Standardbibliothek und Wiederverwendung von Code
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Okay, Sie sind ein guter Leser, also lassen Sie uns dieses Thema ein wenig vertiefen! Ich möchte, dass Sie nachdenken.
Sie denken , dass der Handel ist wie Mathematik, aber mein Artikel öffnet eine Tür für Sie zu arbeiten Ihre kritischen Fähigkeiten, wie Sie jetzt tun. IMHO erfordertder Handel genau das von Ihnen.Es ist eigentlich absurd , dass Sie irgendein System zur Macht erheben und Sie zum Millionär machen ! In diesem Fall wären wir alle reich.
Das Lustige daran ist, dass die Grundtheorie wahr bleibt. Deshalb sage ich:"Sobald Sie die oben erläuterte OO-Logik in Ihr System eingebaut haben, vergessen Sie nicht, Ihre Tests durchzuführen! Jetzt teste ich ExponentialHawaiian, die Fixed Fractional Variante von HawaiianTsunamiSurfer".
Dieser Satz oben ist wahr. Streng genommen muss ich also sagen, dass Sie vielleicht eine falsche logische Schlussfolgerunggezogen haben. Ich möchte nicht, dass der Leser denkt, dass er/sie zum Millionär wird, indem er/sie irgendein lineares Handelssystem an die Macht bringt. Ich ermutige Sie, CEvolution zusammen mit Ihrem System zu verwenden und Ihre eigenen Ergebnisse zu beobachten. Das ist Trading!, denke ich.
Das Lustige ist, dass Sie, wenn Sie Edward Thorp und nicht Vince studiert hätten, wüssten, dass ein fester Bruchteil nicht für alle Strategien geeignet ist, weil man unter bestimmten Umständen eine Menge Transaktionen braucht, bevor man bessere Ergebnisse erzielt.
Siehe: Edward O. Thorp. Das Kelly-Kriterium bei Blackjack, Sport, Wetten und dem Aktienmarkt
Lesen Sie hier mehr: 4. Der lange Lauf: Wann wird die Kelly-Strategie "dominieren"?
Man kann nicht für jede Strategie einen festen Bruchteil anwenden. Denn sie führt nicht immer zu besseren Ergebnissen als andere Strategien für das Kapital- und Risikomanagement.
E. Thorp ist ein guter Mathematiker, Glücksspieler und erfahrener Trader. Er hat sich seine Praxis verdient.
R. Vince - Theoretiker, kein Praktiker. Er verdient, indem er die Ideen anderer Leute in seinen Büchern falsch kopiert und dafür Tantiemen erhält.
Die Anhänger von Vince machen oft Fehler, die in der Handelspraxis schon lange bekannt sind, über die aber in den Büchern von Vince nichts gesagt wird. Sie versuchen, mathematische Methoden anzuwenden, wo sie nicht angewendet werden können.
Ich habe die Bücher von Vince weggeworfen, weil sie eine Menge Ungenauigkeiten enthalten und wenig praktischen Nutzen haben.
Meiner Meinung nach ist es keine gute Idee, den Vorteil einer Innovation anhand der Ergebnisse eines 3-Monats-Tests aufzuzeigen. Wenn ich einen Vergleich anstellen würde, würde ich ihn über einen Zeitraum von 10 Jahren anstellen.
Durch die Skalierung eines Preisdiagramms (oder sogar eines Random Walk) mit einer nicht-linearen Funktion (Exponent, einfach und klar) können Sie einen "Gral" TS in ein oder zwei Zeiten machen. Eine solche Skalierung läuft letztlich auf die Verwaltung der Positionsgröße hinaus. Aber das ganze Problem ist, dass der Markt diskret ist: Sie haben eine Mindestmenge und es gibt eine Mindestpreisbewegung (Pip). In diesen diskreten Abschnitten degeneriert schließlich jede Nichtlinearität zur Linearität.
Ich spreche hier ohne Berücksichtigung der Provisionen und des Spreads - eine so abstrakte Preislinie für langfristige Investoren)).