MetaTrader 5 / Statistiques et analyses
English Русский 中文 Español Deutsch 日本語 Português 한국어 Italiano Türkçe
Analyse des Principales Caractéristiques des Séries Chronologiques

Analyse des Principales Caractéristiques des Séries Chronologiques

MetaTrader 5 — Statistiques et analyses | 12 janvier 2022, 14:47
84 0
Victor
Victor


Introduction

L'analyse des processus représentés par les séries de prix est une tâche assez difficile nécessitant souvent un important volume de temps et d'efforts. Cela tient aux spécificités des séquences étudiées ainsi qu'au fait que malgré un grand nombre de publications diverses, il est parfois difficile de trouver une solution de programmation adéquate à un certain problème.

Même si un script ou un indicateur approprié a été trouvé, cela ne signifie pas que son code source n'aurait pas besoin d'être ajusté à la tâche en question.

De plus, même pour résoudre des problèmes simples, ces programmes peuvent nécessiter l'utilisation de paramètres d'entrée dont le point est bien connu des développeurs mais n'est pas toujours parfaitement clair pour un utilisateur.

Ces difficultés ne peuvent certainement pas devenir un obstacle insurmontable dans une recherche sérieuse mais quand on veut prouver une hypothèse ou simplement satisfaire sa curiosité, cette curiosité restera le plus souvent insatisfaite. C'est pourquoi j'ai eu l'idée de créer un outil de programmation universel permettant une analyse préliminaire facile des principales caractéristiques et paramètres d'une séquence d'entrée.

Un tel outil doit être tout à fait simple dans son installation sans nécessiter de paramètres d'entrée pour simplifier au maximum son utilisation. Dans le même temps, les paramètres et caractéristiques estimés doivent refléter de manière adéquate et claire la nature de la séquence en cours d’examen.

Une estimation préliminaire des caractéristiques pourrait aider à déterminer les moyens d'une étude plus approfondie ou à rejeter toute hypothèse donnée à un stade précoce et à éviter la perte de temps à l’égard d’ une étude plus approfondie.

Il est bien connu que les logiciels universels sont souvent médiocres par rapport aux logiciels personnalisés en termes de caractéristiques. C'est le prix régulier de l'universalité qui s'obtient presque toujours par tout le système des compromis. Cet article représente cependant un effort pour créer un outil universel qui permet de faciliter au maximum l'analyse préliminaire des caractéristiques des séquences.


Installation et Capacité

Le fichier TSAnalysis.zip qui se trouve à la fin de l'article comprend le répertoire \TSAnalysis comportant tous les fichiers nécessaires au travail. Après décompression, le répertoire avec tout son contenu (sans le renommer) doit être copié dans le répertoire \MQL5\Scripts. Le répertoire copié \TSAnalysis comporte un script de test TSAexample.mq5 qui peut être exécuté après la compilation.

Ce script doit préparer les données et appeler le navigateur par défaut pour les afficher à l'aide de la classe TSAnalysis. Il est à noter que l'utilisation de DLL externes doit être activée dans le Terminal pour le fonctionnement normal de la classe TSAnalysis. Pour désinstaller, il suffit de supprimer simplement le répertoire \TSAnalysis.

L'intégralité du code source utilisée dans l'analyse des séquences est représentée par la classe TSAnalysis et se trouve uniquement dans le fichier TSAnalysis.mqh.

Lorsque vous utilisez cette classe pour une séquence d'entrée, elle estime et peut afficher les informations suivantes :

  • Nombre d'éléments dans la séquence
  • Valeur maximale et minimale de la séquence (max, min);
  • Médiane,
  • Moyenne
  • variance
  • Écart-type
  • Variance non biaisée ;
  • Écart-type non biaisé ;
  • coefficient de dissymétrie,
  • kurtose
  • Excès d'aplatissement ;
  • Test Jarque-Bera;
  • valeur p du test de Jarque-Bera ;
  • Test de Jarque-Bera ajusté ;
  • Valeurs p ajustées du test de Jarque-Bera ;
  • Limites pour les valeurs n'appartenant pas à la séquence donnée (valeurs aberrantes) ;
  • Données d'histogramme ;
  • Données du Diagramme de Probabilité Normale ;
  • Données du corrélogramme ;
  • Bandes de confiance à 95 % pour la fonction d'auto-corrélation ;
  • Données du Spectral Plot calculées via la fonction d'auto-corrélation ;
  • Fonction d'auto-corrélation partielle Tracer les données ;
  • Données du Graphique d'Estimation Spectrale calculées à l'aide de la méthode d'entropie maximale.

Afin d'afficher visuellement les résultats obtenus dans la classe TSAnalysis en cours d’examen, une méthode d'exposition virtuelle est utilisée qui prend en charge une méthode d'affichage d'informations pré-préparée uniquement.

Par conséquent, en redéfinissant cette méthode dans les descendants de la classe TSAnalysis,nous pouvons organiser la sortie des résultats de toutes les manières possibles, non seulement en utilisant un fichier HTML comme dans la classe de base où, lors de la génération d'un fichier de données pour afficher des graphiques, un navigateur Web est appelé.

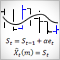
Avant de passer en revue la classe TSAnalysis, nous allons illustrer le résultat de son utilisation à travers une séquence de test de données. La figure ci-dessous montre le résultat d'exploitation du script TSAexample.mq5.

Figure 1. Résultat d’exploitation du script TSAexample.mq5

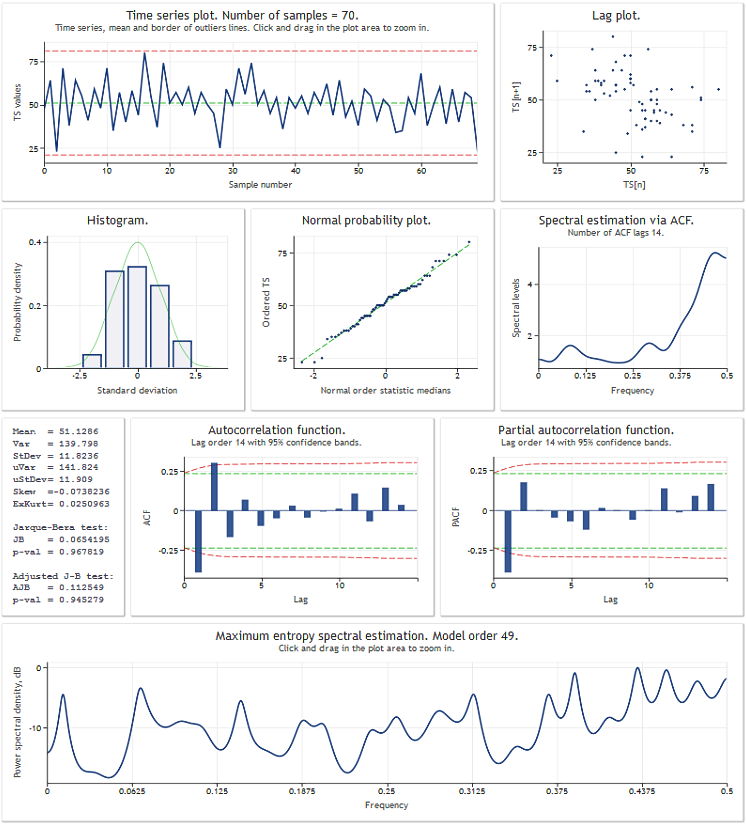
Figure 1. Résultat d'exploitation du script TSAexample.mq5

Après une brève familiarisation avec la capacité de la classe TSAnalysis, nous allons maintenant passer à un examen plus en détail de la classe elle-même.


Classe TSAnalysis

La classe TSAnalysis (voir TSAnalysis.mqh) comprend une seule méthode disponible (publique) Calc qui est en charge de tous les calculs nécessaires à la suite desquels la méthode virtuelle show est appelée. La méthode show sera brièvement revue par la suite, et nous allons maintenant procéder à une clarification étape par étape du point principal des calculs effectués.

Lors de l'utilisation de la classe TSAnalysis, certaines contraintes sont imposées sur la séquence d'entrée à l'étude.

Premièrement, la séquence doit comprendre au moins huit éléments. Une telle contrainte n'est probablement pas très rigide car il ne sera guère nécessaire d'étudier des séquences aussi courtes à des fins pratiques.

En plus de la contrainte de longueur de séquence minimale, la valeur de variance de séquence d'entrée doit être autre que proche de zéro. Cette exigence est due au fait que la valeur de la variance est utilisée dans les calculs ultérieurs et ne peut pas être inférieure à une certaine valeur pour un résultat stable.

Les séquences avec une valeur de variance très faible ne sont pas si courantes, donc cette contrainte ne sera probablement pas non plus un inconvénient majeur. Lorsque la séquence est trop courte et qu'il existe une valeur de variance proche de zéro, les calculs seront interrompus et un message d'erreur correspondant apparaîtra dans le journal.

Il existe encore une autre contrainte implicite concernant la longueur maximale autorisée d'une séquence d'entrée. Cette contrainte n'est pas explicitement définie et dépend des performances d'un ordinateur en cours d'utilisation et de sa capacité mémoire et est déterminée de manière purement subjective par le temps nécessaire à l'exécution du script et la vitesse de dessin des résultats dans un navigateur web. Il est admis que le traitement de séquences composées de 2 à 3 000 éléments ne devrait pas entraîner de sérieux soucis.

Le calcul des paramètres statistiques de la séquence sera basé sur le fragment ci-dessous du code source de la méthode Calc (voir TSAnalysis.mqh).

La description de l’algorithme utilisé est disponible en suivant ce lien"Algorithmes de Calcul de la Variance".

. . .
Mean=0; sum2=0; sum3=0; sum4=0;
for(i=0;i<NumTS;i++)
  {
  n=i+1; delta=TS[i]-Mean;
  a=delta/n; Mean+=a;                                       // Mean (average)
  sum4+=a*(a*a*delta*i*(n*(n-3.0)+3.0)+6.0*a*sum2-4.0*sum3); // sum of fourth degree
  b=TS[i]-Mean;
  sum3+=a*(b*delta*(n-2.0)-3.0*sum2);                       // sum of third degree
  sum2+=delta*b;                                            // sum of second degree
  }
. . .

À la suite de l'exécution de ce fragment, les valeurs suivantes sont calculées

où n = NumTS est le nombre d'éléments dans la séquence.

En utilisant les valeurs obtenues, nous calculons les paramètres suivants.

Variance and écart type:


Variance non-biaisée et écart type:


Dissymétrie:

Kurtose. L'aplatissement minimum est 1, l'aplatissement de la séquence normalement distribuée sera 3.

Excès de kurtose:

Dans ce cas, le kurtose minimum est de -2, et le kurtose de la séquence normalement distribuée sera de 0.

Par convention, lors de l'exécution du premier test préliminaire d'adéquation sur une séquence, la statistique de Jarque-Bera est utilisée, qui est facilement calculée en utilisant les valeurs connues de dissymétrie et d'aplatissement. La signification statistique (valeur p) de la statistique de Jarque-Bera, lors de l'augmentation de la longueur de la séquence, tend asymptotiquement vers la fonction de distribution du chi carré inverse avec deux degrés de liberté.

Ainsi,

Lorsque la séquence est courte, la p-valeur obtenue de cette manière a forcément une erreur appréciable. Cette même option de calcul est pourtant très souvent utilisée. Il est difficile de dire pourquoi - cela a peut-être a un rapport avec des formules simples et claires utilisées ou cela pourrait être le fait que la statistique de Jarque-Bera en elle-même ne représente pas un test d'adéquation idéal et qu'il est donc inutile de faire des calculs plus précis.

Dans notre cas, la statistique de Jarque-Bera et la valeur p correspondante sont calculées dans la méthode Calc (TSAnalysis.mqh) conformément aux formules ci-dessus.

En outre, un test de Jarque-Bera ajusté est calculé en complément :

Où :

La version ajustée du test de Jarque-Bera pour les séquences courtes réduit l'erreur de la valeur p calculée de la manière spécifiée mais ne l'élimine pas complètement.

Le résultat final de l'analyse est censé comporter un graphe de séquence d'entrée affichant la ligne correspondant à la moyenne et les lignes définissant les limites en dehors desquelles les valeurs peuvent être considérées comme invalides et n'appartenant pas à la séquence donnée (valeurs aberrantes).

Ces limites sont dans ce cas calculées comme suit :

Cette formule est fournie dans le livre par S.V. Bulashev "Statistics for Traders" avec une référence au livre de P.V. Novitsky et I.A Zograf "Estimation of Error in Measurement Results". Après détermination des limites, aucun traitement de la séquence d'entrée n'est prévu ; les limites sont censées être affichées à titre indicatif.

En plus du diagramme de séquence d'entrée, un histogramme reflétant une estimation empirique de la distribution de séquence d'entrée est destiné à être affiché. Le nombre d'intervalles pour l'histogramme est défini comme suit (SV Bulashev "Statistics for Traders") :


Le résultat est arrondi à la valeur entière impaire la plus proche. Si la valeur obtenue est inférieure à cinq, la valeur de 5 est utilisée.

Le nombre d'éléments dans les tableaux de données pour l'axe X et l'axe Y de l'histogramme correspond au nombre d'intervalles obtenu plus deux, puisqu'une colonne de valeur zéro est ajoutée à gauche et à droite de l'histogramme.

Un fragment du code (voir TSAnalysis.mqh) préparant les données pour la construction d'un histogramme est présenté ci-dessous.

. . .
n=(int)MathRound((Kurt+1.5)*MathPow(NumTS,0.4)/6.0);
if((n&0x01)==0)n--; if(n<5)n=5;                         // Number of bins
ArrayResize(XHist,n);
ArrayResize(YHist,n);
ArrayInitialize(YHist,0.0);
a=MathAbs(TSort[0]-Mean); b=MathAbs(TSort[NumTS-1]-Mean);
if(a<b)a=b; v=Mean-a;
delta=2.0*a/n;
for(i=0;i<n;i++)XHist[i]=(v+(i+0.5)*delta-Mean)/StDev; // Histogram. X-axis
for(i=0;i<NumTS;i++)
  {
  k=(int)((TS[i]-v)/delta);
  if(k>(n-1))k=n-1;
  YHist[k]++;
  }
for(i=0;i<n;i++)YHist[i]=YHist[i]/NumTS/delta*StDev;   // Histogram. Y-axis
. . .

Dans le code ci-dessus :

  • NumTS est le nombre d'éléments dans la séquence,
  • XHist[] et YHist[] sont des tableaux contenant respectivement des valeurs pour les axes X et Y.
  • TSort[] est le tableau contenant une séquence d'entrée triée.

En utilisant cette méthode de calcul, les valeurs de l'axe X seront exprimées en unités d'écart type et les valeurs de l'axe Y correspondront à la densité de probabilité.

Pour créer un graphique avec l'axe de distribution normal, la séquence d'entrée triée par ordre croissant est utilisée comme valeurs de l'axe Y. Le nombre de valeurs des axes Y et X est censé être égal. Pour calculer les valeurs de l'axe X, il faut d'abord trouver les valeurs médianes comme dans la loi de distribution uniforme :

Ils sont en outre utilisés pour calculer les valeurs de l'axe X au moyen de la fonction de distribution normale inverse (voir méthode ndtri).

Afin de créer un tracé de fonction d'auto-corrélation (ACF), un tracé de fonction d'auto-corrélation partielle (PACF) et de calculer l'estimation spectrale à l'aide de la méthode d'entropie maximale, les valeurs de la fonction d'auto-corrélation doivent être trouvées pour la séquence d'entrée.

Nous allons définir le nombre de valeurs qui sont censées être affichées sur les tracés ACF et PACF comme suit :


 

Le nombre de valeurs déterminées de la manière spécifiée sera tout à fait suffisant pour l'affichage de la fonction d'auto-corrélation sur le tracé mais pour un calcul ultérieur de l'estimation spectrale, il est conseillé d'avoir un plus grand nombre de valeurs ACF calculées qui dans notre cas seront égales à la ordre du modèle auto-régressif employé.

L'ordre du modèle IP sera défini par la valeur NLags obtenue :

 

Il est assez difficile de formaliser le processus de détermination de l'ordre optimal du modèle pour l'estimation spectrale. Un modèle d'ordre faible apportera des résultats extrêmement lissés tandis qu'un modèle d'ordre élevé aboutira très probablement à une estimation spectrale instable avec une large plage de valeurs.

En outre, l'ordre du modèle est également affecté par la nature de la séquence d'entrée, par conséquent l'ordre IP déterminé à l'aide de la formule ci-dessus sera dans certains cas trop élevé et dans d'autres cas trop faible. Malheureusement, aucune approche efficace pour déterminer l'ordre des modèles requis n'a été trouvée.

Ainsi, pour la séquence d'entrée, il faut déterminer le nombre de valeurs ACF égal à l'ordre du modèle IP qui est utilisé pour l'estimation spectrale de la séquence. 

. . .
ArrayResize(cor,IP);
a=0;
for(i=0;i<NumTS;i++)a+=TSCenter[i]*TSCenter[i];    
for(i=1;i<=IP;i++)
  {  
  c=0;
  for(k=i;k<NumTS;k++)c+=TSCenter[k]*TSCenter[k-i];
  cor[i-1]=c/a;                                   // Autocorrelation
  }
. . .

Ce fragment du code source (voir TSAnalysis.mqh) illustre le processus de calcul de la fonction d'auto-corrélation (ACF). Le résultat du calcul est placé dans le tableau cor[]. Comme on peut le voir, un coefficient d'auto-corrélation nul est calculé en premier, suivi du calcul et de la normalisation des coefficients restants dans la boucle. Après une telle normalisation, le coefficient zéro sera toujours égal à un, il n'est donc pas nécessaire de le sauvegarder dans le tableau cor[].

Ce tableau comporte le nombre de coefficients égal à IP à partir du premier. Lors du calcul de l' ACF, le tableau TSCenter[] est utilisé ; il comporte la séquence d'entrée des éléments de tous dont la valeur moyenne a été soustraite.

Afin de réduire le temps nécessaire dans le calcul de l’ ACF, nous pouvons faire usage des méthodes s’appuyant sur les algorithmes rapides de transformation ex:FFT Mais dans ce cas le temps nécessaire au calcul de l’ ACF est tout à fait acceptable donc il n'est probablement pas nécessaire de compliquer le code de programmation.

Un tracé ACF (corrélogramme) peut facilement être créé en utilisant les valeurs obtenues des coefficients de corrélation. Afin de pouvoir afficher les bandes de confiance à 95 % sur ce graphique, leurs valeurs peuvent être calculées à l'aide des formules ci-dessous.

Pour les bandes utilisées dans le test du caractère aléatoire :

 

Pour les bandes utilisées dans la détermination de l'ordre du modèle ARIMA :

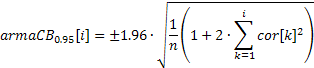
La valeur de la bande de confiance dans le premier cas sera constante et augmentera avec la hausse du coefficient d'auto-corrélation dans le second cas.

Une réponse en fréquence très lissée de la séquence d'entrée reflétant uniquement la tendance générale de la distribution de fréquence peut parfois être intéressante. Par exemple, remontées considérables des fréquences basses ou hautes, prédominance des fréquences moyennes, etc.

Il est conseillé d'afficher une telle réponse en fréquence en échelle linéaire pour fermement souligner les gammes de fréquences dominantes. Une telle réponse amplitude-fréquence (AFR) peut être tracée sur la base des coefficients d'auto-corrélation précédemment obtenus. Pour le calcul de l' AFR, nous utiliserons le nombre de coefficients égal au nombre affiché sur le graphique ACF.

Étant donné que ce nombre n'est pas grand, les estimations spectrales obtenues en conséquence devraient être assez lisses.

La réponse en fréquence de la séquence dans ce cas peut être exprimée au moyen de coefficients d'auto-corrélation comme suit :

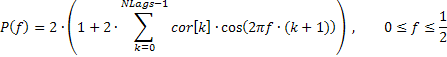
Un fragment du code (voir TSAnalysis.mqh) utilisé dans le calcul de l' AFR sur la base de la formule fournie, est présenté ci-dessous

. . .
n=320;                                              // Number of X-points
ArrayResize(Spect,n);
v=M_PI/n;
for(i=0;i<n;i++)
  {
  a=i*v; b=0;
  for(k=0;k<NLags;k++)b+=((double)NLags-k)/(NLags+1.0)*ACF[k]*MathCos(a*(k+1));
  Spect[i]=2.0*(1+2*b);                             // Spectrum Y-axis
  }
. . .

Il convient de noter que les valeurs de coefficient de corrélation dans le code ci-dessus sont, pour un lissage supplémentaire, multipliées par la fonction de fenêtre triangulaire.

Pour une analyse spectrale plus détaillée, la méthode de l'entropie maximale a été choisie comme autre compromis. Le choix d'une méthode d'estimation spectrale universelle est assez difficile. Les inconvénients associés aux méthodes non paramétriques classiques d'analyse spectrale sont bien connus.

Les méthodes de périodogramme et de corrélogramme peuvent servir d'exemples de telles méthodes qui sont facilement implémentées à l'aide d'algorithmes de transformée rapides de Fourier Mais malgré la grande stabilité des résultats, ces méthodes nécessitent des séquences d'entrée très longues afin d'obtenir un pouvoir de résolution adéquat. En revanche, les méthodes paramétriques d'estimation spectrale (par exemple les méthodes auto-régressives) peuvent assurer une résolution beaucoup plus élevée pour des séquences courtes.

Malheureusement, lors de leur utilisation, il faut prendre en considération non seulement les spécificités d'une certaine implémentation de ces méthodes mais aussi la nature de la séquence d'entrée. Dans le même temps, il est assez difficile de déterminer l'ordre optimal du modèle AR dont la remontée entraîne une augmentation de la puissance de résolution mais des résultats dispersés obtenus. Si des modèles d'ordre très élevé sont utilisés, ces méthodes commencent à donner des résultats instables.

Les caractéristiques comparatives de différents algorithmes d'estimation spectrale peuvent être trouvées dans le livre de S.L. Marple "Digital Spectral Analysis with Applications". Comme déjà mentionné, la méthode du maximum d'entropie a été choisie dans ce cas. Cette méthode donne probablement la puissance de résolution la plus faible par rapport à d'autres méthodes auto-régressives, mais elle a été sélectionnée en vue d'obtenir des estimations spectrales plus stables.

Examinons l'ordre des calculs d'estimation spectrale auto-régressive. Le choix de l'ordre du modèle a été évoqué plus tôt, nous admettrons donc que l'ordre du modèle a déjà été sélectionné étant égal à IP et que les coefficients d'auto-corrélation IP cor[] ont été calculés.

Afin d'obtenir les coefficients auto-régressifs en utilisant les coefficients d'auto-corrélation connus, l'algorithme de Levinson-Durbin est utilisé comme méthode LevinsonRecursion.

//-----------------------------------------------------------------------------------
// Calculate the Levinson-Durbin recursion for the autocorrelation sequence R[]
// and return the autoregression coefficients A[] and partial autocorrelation
// coefficients K[]
//-----------------------------------------------------------------------------------
void TSAnalysis::LevinsonRecursion(const double &R[],double &A[],double &K[])
  {
  int p,i,m;
  double km,Em,Am1[],err;

  p=ArraySize(R);
  ArrayResize(Am1,p);
  ArrayInitialize(Am1,0);
  ArrayInitialize(A,0);
  ArrayInitialize(K,0);
  km=0;
  Em=1;
  for(m=0;m<p;m++)
    {
    err=0;
    for(i=0;i<m;i++)err+=Am1[i]*R[m-i-1];
    km=(R[m]-err)/Em;
    K[m]=km; A[m]=km;
    for(i=0;i<m;i++)A[i]=(Am1[i]-km*Am1[m-i-1]);
    Em=(1-km*km)*Em;
    ArrayCopy(Am1,A);
    }
  return;
  }

La méthode dispose de trois paramètres d'entrée. Les trois paramètres sont des références à des tableaux. Lors de l'appel de cette méthode, les coefficients d'auto-corrélation d'entrée doivent être placés dans le premier tableau R[]. Au cours des calculs, ces valeurs demeurent inchangées.

Les coefficients d'auto-corrélation obtenus seront placés dans le tableau A[]. En plus de cela, le tableau K[] comportera des valeurs de fonction d'auto-corrélation partielles égales aux coefficients de réflexion du modèle auto-régressif pris avec un signe opposé. L'ordre du modèle n'est pas passé en tant que paramètre d'entrée ; il est admis qu’il soit égal au nombre d'éléments du tableau d'entrée R[].

Les tailles du tableau de sortie ne doivent donc pas être inférieures à la taille du tableau d'entrée ; le respect de cette exigence n'est pas vérifié à l'intérieur de la fonction. A l'issue des calculs, le coefficient auto-régressif nul et le coefficient nul de la fonction d'auto-corrélation partielle ne sont pas enregistrés dans les tableaux A[] et K[].

Il est admis qu'ils sont toujours égaux à un. Ainsi, les tableaux de sortie comporteront, comme dans la séquence d'entrée, des coefficients d'indices de 1 à IP (à ne pas confondre avec les indices de tableaux qui partent de 0).

Les valeurs obtenues de la fonction d'auto-corrélation partielle ne sont en outre utilisées que pour l'affichage sur un graphique respectif, et les coefficients auto-régressifs servent de base au calcul de l'estimation de la réponse en fréquence qui est définie par la formule suivante :

La réponse en fréquence est calculée pour 4096 valeurs de fréquence normalisées sur la plage de 0 à 0,5. Le calcul direct des valeurs AFR à l'aide de la formule ci-dessus prend trop de temps, ce qui peut être considérablement réduit en utilisant l'algorithme de transformée rapide de Fourier pour calculer la somme des exponentielles complexes.

À cette fin, la méthode Calc utilise la transformée rapide de Hartley (FHT) au lieu de la transformée rapide de Fourier.

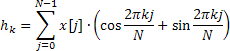
La transformée de Hartley n'implique pas d'opérations complexes et les séquences d'entrée et de sortie sont valides. La transformée de Hartley inverse est calculée en utilisant la même formule n’exigeant qu'un facteur supplémentaire 1/N.

Dans une séquence d'entrée valide, il existe un lien simple entre les coefficients de cette transformée et les coefficients de la transformée de Fourier

 

Des informations sur les algorithmes de transformée rapide de Hartley peuvent être disponibles ici "FXT algorithm library" et "Discrete Fourier et Hartley Transforms".

Dans l'implémentation donnée, la fonction de transformée rapide de Hartley est représentée par la méthode fht.

//-----------------------------------------------------------------------------------
// Radix-2 decimation in frequency (DIF) fast Hartley transform (FHT).
// Length is N = 2 ** ldn
//-----------------------------------------------------------------------------------
void TSAnalysis::fht(double &f[], ulong ldn)
  {
  const ulong n = ((ulong)1<<ldn);
  for (ulong ldm=ldn; ldm>=1; --ldm)
    {
    const ulong m = ((ulong)1<<ldm);
    const ulong mh = (m>>1);
    const ulong m4 = (mh>>1);
    const double phi0 = M_PI / (double)mh;
    for (ulong r=0; r<n; r+=m)
      {
      for (ulong j=0; j<mh; ++j)
        {
        ulong t1 = r+j;
        ulong t2 = t1+mh;
        double u = f[t1];
        double v = f[t2];
        f[t1] = u + v;
        f[t2] = u - v;
        }
      double ph = 0.0;
      for (ulong j=1; j<m4; ++j)
        {
        ulong k = mh-j;
        ph += phi0;
        double s=MathSin(ph);
        double c=MathCos(ph);
        ulong t1 = r+mh+j;
        ulong t2 = r+mh+k;
        double pj = f[t1];
        double pk = f[t2];
        f[t1] = pj * c + pk * s;
        f[t2] = pj * s - pk * c;
        }
      }
    }
  if(n>2)
    {
    ulong r = 0;
    for (ulong i=1; i<n; i++)
      {
      ulong k = n;
      do {k = k>>1; r = r^k;} while ((r & k)==0);
      if (r>i) {double tmp = f[i]; f[i] = f[r]; f[r] = tmp;}
      }
    }
  }

Lors de l'appel de cette méthode, une référence au tableau de données d'entrée f[] et l'entier non signé ldn définissant la longueur de transformation N = 2 ** ldn sont transmis en entrée . La taille du tableau f[] ne doit pas être inférieure à la longueur de transformée N. Gardez à l'esprit qu'il n'y a pas de contrôle pour cela à l'intérieur de la fonction. N'oubliez pas non plus que le résultat de la transformation est stocké dans le tableau où les données d'entrée ont été placées.

Après la transformée, les données d'entrée elles-mêmes ne sont pas stockées. Dans la méthode Calc à l’examen, une transformée de longueur N=8192 est utilisée afin de calculer 4096 valeurs AFR. Après le calcul de la magnitude de transformée au carré et en prenant l'inverse, le résultat obtenu est normalisé à sa valeur maximale et mis à l'échelle logarithmique.

A part cela, il n'y a pas de spécificités majeures de la méthode Calc ; si nécessaire,nous pouvons regarder de plus près son implémentation en se référant à TSAnalysis.mqh.

Toutes les valeurs obtenues et préparées pour l'affichage à la suite des calculs sont enregistrées dans des variables faisant partie de la classe TSAnalysis. Par conséquent, elles n'ont pas besoin d'être transmises en arguments lors de l'appel de la méthode virtuelle show pour afficher les résultats.


Visualisation

Comme déjà mentionné, la méthode show est déclarée comme virtuelle. Ainsi, en la redéfinissant,nous pouvons implémenter la méthode requise pour afficher les résultats du calcul qui seraient différents de celui proposé. La visualisation dans la classe TSAnalysis proposée est réalisée au moyen de la préparation du fichier de données et de l'appel d'un navigateur Web pour l'affichage des données.

Pour qu'un navigateur Web puisse afficher de telles données, le fichier TSA.htm est utilisé et se trouve dans le même répertoire que le reste des fichiers du projet. Cette méthode d’affichage d’informations graphiques était précédemment décrite dans l’article "Graphes et Diagrammes en HTML".

La classe TSAnalysis de la méthode show est chargée de formater et d'enregistrer tous les résultats de calcul destinés à l’affichage dans une variable de type chaîne (voir TSAnalysis.mqh). Une longue ligne générée de cette manière est enregistrée dans TSDat.txt en une seule étape. La création de ce fichier et l'enregistrement des données dans celui-ci sont effectués à l'aide des outils standard MQL5, le fichier est donc créé dans le répertoire \MQL5\Files.

Ce fichier est ensuite déplacé dans le répertoire de ce projet en appelant les fonctions externes du système. Ceci est suivi d'un appel d'un navigateur Web affichant TSA.htm qui utilise les données de TSDat.txt. Étant donné que les fonctions système sont appelées dans la méthode show, l'utilisation de DLL externes doit être activée dans le terminal pour travailler avec la classe TSAnalysis.


Exemples

TSAexample.mq5 inclus dans l'archive TSAnalysis.zip est un exemple d'utilisation de la classe TSAnalysis.

//-----------------------------------------------------------------------------------
//                                                                     TSAexample.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include "TSAnalysis.mqh"
//-----------------------------------------------------------------------------------
// Script program start function
//-----------------------------------------------------------------------------------
void OnStart()
  {
  double bd[]={47,64,23,71,38,64,55,41,59,48,71,35,57,40,58,44,80,55,37,74,51,57,50,
  60,45,57,50,45,25,59,50,71,56,74,50,58,45,54,36,54,48,55,45,57,50,62,44,64,43,52,
  38,59,55,41,53,49,34,35,54,45,68,38,50,60,39,59,40,57,54,23};

  TSAnalysis *tsa=new TSAnalysis;

  tsa.Calc(bd);

  delete tsa;

  }

Comme nous pouvons le voir, la référence à la classe est assez simple ; s'il existe un tableau préparé comportant la séquence d'entrée, il ne faudra pas beaucoup d'efforts pour le transmettre vers la méthode Calc pour analyse. De plus, n'oubliez pas de libérer de la mémoire en appelant delete. Le résultat de l'exécution de ce script a déjà été fourni au début de l'article.

Afin de démontrer l'efficacité des estimations spectrales produites, tournons-nous vers des exemples supplémentaires où les séquences générées seront utilisées.

Pour commencer, nous utiliserons une séquence composée de deux sinusoïdes.

int i,n;
double a,x[];
  
n=400;
ArrayResize(x,n);
a=2*M_PI;
for(i=0;i<n;i++)x[i]=MathSin(0.064*a*i)+MathSin(0.071*a*i);

La figure ci-dessous montre l'estimation de la réponse en fréquence de cette séquence.

Fig. 2

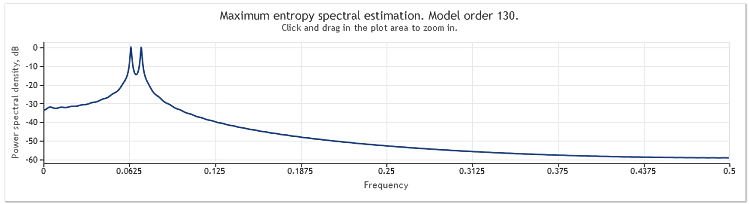
Figure 2. Estimation spectrale. Deux sinusoïdes

Bien que les deux sinusoïdes soient bien observables, un zoom avant sur la zone d'intérêt du graphique nous a permis de découvrir que les pics sont situés à des fréquences de 0,0637 et 0,0712. En d'autres termes, elles sont quelque peu différentes des vraies valeurs. Où une séquence se compose d'une seule sinusoïde, un tel biais d'estimation n'est pas observé. Examinons cette occurrence comme étant l'effet de la méthode d'analyse spectrale choisie.

Nous allons davantage compliquer la tâche en ajoutant un composant aléatoire à notre séquence. A cet effet, un générateur de séquence pseudo-aléatoire sera utilisé représenté par la classe RNDXor128 que l'on peut retrouver dans l'archive RNDXor128.zip en fin d'article.

Le fragment de code ci-dessous a été utilisé pour générer un signal de test.

int i,n;
double a,x[];
  
RNDXor128 *rnd=new RNDXor128;
n=800;
ArrayResize(x,n);
a=2*M_PI;
for(i=0;i<n;i++)x[i]=MathSin(0.064*a*i)+MathSin(0.071*a*i)+rnd.Rand_Norm();
delete rnd;

Dans cet exemple, un signal aléatoire avec une distribution normale et une variance unitaire a été ajouté à deux sinusoïdes.

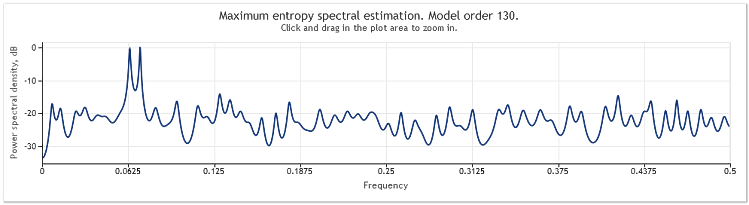
Figure 3. Estimation spectrale. Deux sinusoïdes plus un signal aléatoire

Dans ce cas, les composants sinusoïdaux demeurent bien discernables.

Une multiplication par cinq de l'amplitude du composant aléatoire entraîne des sinusoïdes sensiblement masquées.

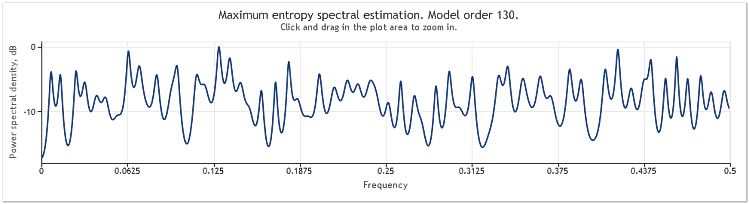
Figure 4. Estimation spectrale. Deux sinusoïdes plus un signal aléatoire avec une plus grande amplitude

Lorsque la longueur de la séquence passe de 400 à 800 éléments, les sinusoïdes redeviennent bien visibles.

 

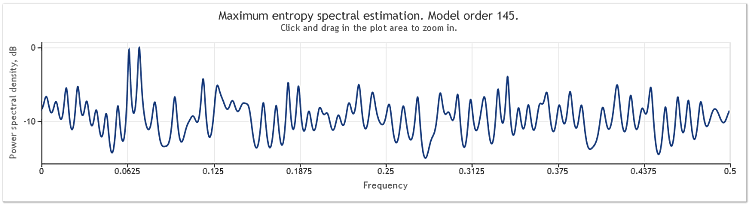
Figure 5. Deux sinusoïdes plus un signal aléatoire avec une plus grande amplitude. N=800

L'ordre des modèles auto-régressifs est ainsi passé de 130 à 145. L'augmentation de la longueur de la séquence a conduit à un ordre plus élevé du modèle et, par conséquent, la puissance de résolution de l'estimation spectrale a augmenté - les pics du graphique sont devenus sensiblement plus nets.

L'estimation spectrale des cotations de l' EURUSD, D1 sur deux ans (2009 et 2010) peut être présentée comme suit.

Figure 6. Cotations EURUSD. 2009-2010. Period D1

La séquence d'entrée se composait de 519 valeurs et l'ordre du modèle, comme indiqué sur la figure, semblait être de 135.

Comme nous pouvons le voir, cette estimation spectrale comporte un certain nombre de pics distincts. Mais cette estimation n’est pas suffisante à elle seule pour déterminer si ces pics sont des composants périodiques des cotations.

La survenance de pics de réponse en fréquence peut être causée par un composant aléatoire de haut niveau présente dans les cotations ou par une non-stationnarité explicite de la séquence en question.

Il est donc toujours conseillé de vérifier le résultat obtenu à partir des données d'une autre fraction de la séquence ou d'un autre intervalle de temps avant de tirer une conclusion définitive sur la présence du composant périodique. En outre, lors de l'étude de la récurrence cyclique, nous pouvons essayer d'utiliser les différences de séquence au lieu de la séquence elle-même.

 

Conclusion

La méthode d'estimation spectrale employée dans l'article étant basée sur des coefficients d'auto-corrélation, la moyenne de la séquence d'entrée apparaît toujours supprimée de la séquence après l'application de la méthode. Il est souvent absolument nécessaire de supprimer un composant constant de la séquence d'entrée mais, lors de l'utilisation de méthodes auto-régressives, une telle suppression peut, dans certains cas, provoquer une distorsion de l'estimation spectrale dans le domaine des basses fréquences.

Un exemple de telles distorsions est présenté à la fin du chapitre « Summary of Results Regarding Spectral Estimates » dans le livre de S.L. Marple "Digital Spectral Analysis with Applications". Dans notre cas, la méthode d'analyse spectrale employée ne nous laisse pas d'autre choix alors rappelons simplement que l'estimation spectrale est toujours réalisée par rapport à une séquence avec une moyenne supprimée.


Références


Traduit du russe par MetaQuotes Ltd.
Article original : https://www.mql5.com/ru/articles/292

Fichiers joints |
Télécharger ZIP
RNDXor.zip (54.87 KB)
TSAnalysis.zip (79.7 KB)
Avertissement: Tous les droits sur ces documents sont réservés par MetaQuotes Ltd. La copie ou la réimpression de ces documents, en tout ou en partie, est interdite.

Autres articles par cet auteur

Aller à la discussion
Prévision de Séries Chronologiques à l'Aide du Lissage Exponentiel Prévision de Séries Chronologiques à l'Aide du Lissage Exponentiel
L'article familiarise le lecteur avec les modèles de lissage exponentiel utilisés dans la prévision à court terme des séries chronologiques. De plus, il aborde les questions liées à l'optimisation et à l'estimation des résultats prévisionnels et fournit quelques exemples de scripts et d'indicateurs. Cet article sera utile pour une première prise de connaissance des principes de prévision à partir de modèles de lissage exponentiel.
Théorie et Implémentation des Indicateurs Adaptatifs Avancés dans MQL5 Théorie et Implémentation des Indicateurs Adaptatifs Avancés dans MQL5
Cet article décrira les indicateurs adaptatifs avancés et leur implémentation dans MQL5 : Cyber Cycle Adaptatif, Centre de Gravité Adaptatif et RVI Adaptatif. Tous les indicateurs ont été initialement présentés dans "Cybernetic Analysis for Stocks and Futures" par John F. Ehlers.
Analyse des Paramètres Statistiques des Indicateurs Analyse des Paramètres Statistiques des Indicateurs
L’analyse technique met largement en œuvre les indicateurs montrant les cotations de base « plus clairement » et permettant aux traders d’effectuer une analyse et de prévoir l’évolution des prix du marché. Il est tout à fait évident qu’il n’y a aucun sens à utiliser les indicateurs, et encore moins les appliquer dans la création de systèmes de trading, à moins que nous ne puissions résoudre les problèmes liés à la transformation des cotations initiales et la crédibilité des résultats obtenus. Dans cet article, nous montrons qu’il existe des réels motifs pour une telle conclusion.
Assistant MQL5 pour les Nuls Assistant MQL5 pour les Nuls
Début 2011, nous avons publié la première version de l'assistant MQL5. Cette nouvelle application fournit un outil simple et pratique pour générer automatiquement des robots de trading. Tout utilisateur de MetaTrader 5 peut créer un Expert Advisor personnalisé sans même savoir comment programmer en MQL5.