Kombinatorik und Wahrscheinlichkeitsrechnung für den Handel (Teil I): Die Grundlagen

Inhalt

• Einführung
• Wie kann die Wahrscheinlichkeitstheorie bei der Marktanalyse helfen?
• Besonderheiten der angewandten Wahrscheinlichkeitstheorie für den manuellen und automatisierten Handel
• Wahrscheinlichkeitsbäume und Hypothesen
• Über Fraktale
• Bernoulli-Schema
• Erstellen des ersten Fraktals
• Zusammenfassung
• Schlussfolgerung

Einführung

Meines Erachtens kann die Sprache der Wahrscheinlichkeitstheorie ein völlig anderes Verständnis der Prozesse auf dem Markt vermitteln. Nachdem Sie die Besonderheiten der Wahrscheinlichkeitstheorie verstanden haben, werden Sie anfangen, auf eine völlig neue Art zu denken. Vage Ideen oder einige unbewiesene Tipps werden nicht mehr den Wunsch hervorrufen, sich zu beeilen und mit einem echten Konto zu handeln. Andererseits verstehe ich, dass dieser neue Ansatz vielleicht nicht für jeden angenehm ist. In dieser Serie möchte ich Ihnen einen echten und korrekten Ansatz für den Handel zeigen. Alle Entscheidungen sollten ausschließlich auf Zahlen beruhen und Annahmen wie "vielleicht", "was wäre wenn", "es scheint" und ähnliches vermeiden.

Wie kann die Wahrscheinlichkeitstheorie bei der Marktanalyse helfen?

Ich habe mich lange Zeit meines Lebens mit technischen Wissenschaften beschäftigt, wobei mir die Wahrscheinlichkeitstheorie am schwersten fiel. Das lag daran, dass ich nicht verstanden habe, wie weitreichend ihre Möglichkeiten sind. Ein unbestreitbarer Vorteil sind ihre unbegrenzten Möglichkeiten, die nur von Ihrem Einfallsreichtum und Ihrem Fleiß und natürlich Ihrer Intelligenz abhängen. Nach jahrelangem technischem Studium wurde mir klar, dass es bei der Intelligenz nicht um die Schnelligkeit und Aufmerksamkeit bei der Durchführung der gleichen Operationen geht, sondern um die Flexibilität des Geistes. Wenn wir zum Beispiel die Differentialmathematik, die Theorie der Vektor- und Skalarfelder oder auch die Schulalgebra betrachten, so implizieren sie alle eine bestimmte Reihe von Regeln oder Empfehlungen, mit deren Hilfe man fast jedes Problem lösen kann. Jede nicht standardisierte Aufgabe ist ein Schock für unser Gehirn. In der Wahrscheinlichkeitstheorie gibt es eine unendliche Anzahl solcher Momente — hier lassen sich viele Probleme nur durch völlig andere Ansätze lösen. Mit anderen Worten: Intelligenz kann nur durch Fleiß und Bereitschaft zur Lösung eines bestimmten Problems entwickelt werden, und die Wahrscheinlichkeitstheorie kann Ihnen dabei helfen.

Der Rahmen der Wahrscheinlichkeitstheorie beschreibt so grundlegende Handelskonzepte wie die mathematische Erwartung, mögliche Wahrscheinlichkeiten verschiedener Ereignisse, Durchschnittswerte, Perzentile und mehr. Die Wahrscheinlichkeitstheorie besagt, dass es kein perfektes Handelssystem gibt und dass jedes System seine eigenen Risiken hat. Wir können nur das Handelssystem wählen, dessen Risiken nicht zu viele Unannehmlichkeiten verursachen. Noch wichtiger ist es, diese Risiken richtig zu interpretieren. Mit anderen Worten, wir gehen von der ungenauen Sprache der Empfindungen oder visuellen Annäherungen zu klaren quantitativen Kriterien über. Natürlich sind auch visuelle Einschätzungen wichtig, aber sie funktionieren besser, wenn sie mit quantitativen Variablen kombiniert werden. Es ist unmöglich, alle Details und Nuancen in einem Artikel zu beschreiben, aber ich werde versuchen, einige interessante Informationen hier aufzunehmen. Ich hoffe, dass Sie hier etwas Nützliches finden werden.

Besonderheiten der angewandten Wahrscheinlichkeitstheorie für den manuellen und automatisierten Handel

Bevor wir die Wahrscheinlichkeitstheorie für die Marktanalyse nutzen können, müssen wir uns zunächst mit Ereignissen und ihren Wahrscheinlichkeiten vertraut machen. Ein Ereignis ist eine Reihe von Ergebnissen, die bestimmte Kriterien erfüllen oder die nach einem bestimmten Kriterium zu einer bestimmten Menge zusammengefasst werden. Ein Ergebnis ist ein bestimmtes, elementares Element, das mit jedem anderen Element der gegebenen Gruppe übereinstimmt. Die Gruppe bezieht sich auf alle möglichen Ergebnisse eines Prozesses. Es ist nicht so wichtig, um welche Art von Prozess es sich handelt, wie seine Physik aussieht oder wie lange der Prozess dauert. Wichtig ist nur, dass wir als Ergebnis dieses Prozesses etwas erhalten, das vor Abschluss des Prozesses noch nicht existierte. Die Ergebnisse, die sich auf unser Ereignis beziehen, sind im Wesentlichen unser Ereignis — der Einfachheit halber fassen wir sie zu einem einzigen Objekt zusammen. Die obige Idee kann wie folgt visualisiert werden:

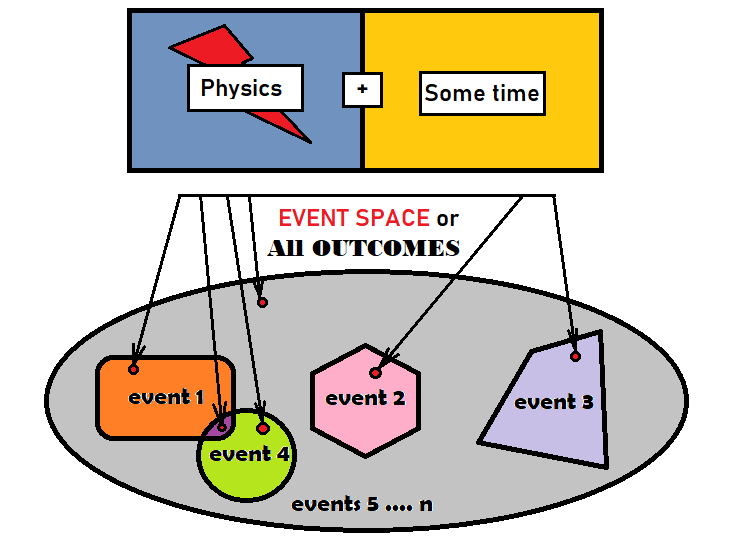
Die graue Ellipse in der obigen Abbildung stellt alle Ereignisse dar. In der Mathematik wird das Ereignisraum genannt. Das bedeutet nicht, dass der Ereignisraum eine geometrische Form hat, aber er ist durchaus geeignet, diese Konzepte zu beschreiben. Innerhalb der Ellipse gibt es 4 Ereignisse. Wie in der Abbildung zu sehen ist, befindet sich innerhalb jedes Ereignisses ein kleiner roter Punkt. Es kann eine begrenzte oder eine unbegrenzte Anzahl solcher Punkte geben — das hängt von dem betrachteten Prozess ab. Zwei der in der Abbildung gezeigten Ereignisse überschneiden sich. Solche Ereignisse werden als Überschneidungen bezeichnet. Es gibt also einige Ergebnisse, die zu beiden Ereignissen gehören. Alle anderen Ereignisse sind nicht überlappend, da sie sich in verschiedenen Teilen der Ellipse befinden und sich geometrisch nicht überschneiden. Der Rest der grauen Fläche kann als letztes Ereignis betrachtet werden, er kann aber auch in kleinere Teile zerlegt werden, bis keine grauen Flächen mehr vorhanden sind.

Jedes Ereignis hat mindestens eine entsprechende Zahl, die gewöhnlich Wahrscheinlichkeit genannt wird. Die Wahrscheinlichkeit gibt an, wie oft dieses Ereignis bei Wiederholungen desselben Prozesses auftreten würde, wenn man dasselbe Experiment unendlich oft durchführen könnte. Es gibt zwei Arten von Ereignisräumen:

1. Mit einer endlichen Anzahl von möglichen Ergebnissen
2. Mit einer unendlichen Anzahl von möglichen Ergebnissen

Wenn die Anzahl der Ergebnisse endlich ist, kann die Wahrscheinlichkeit wie folgt berechnet werden:

• P = S/N , S ist die Anzahl der Resultate, die das Ereigniskriterium erfüllen, N ist die Gesamtzahl aller Resultate im Ereignisraum

In einigen Fällen, wenn die Anzahl der Ergebnisse in einem bestimmten Raum unendlich ist, kann diese Wahrscheinlichkeit auch bestimmt werden, zum Beispiel mit Hilfe von Integralen. Für den Fall in der obigen Abbildung können die Werte "S" und "N" durch die Flächen ihrer geometrischen Formen ersetzt werden.

Es ist nicht immer möglich, den Ereignisraum, die Anzahl der Ergebnisse und die von den Ereignissen beschriebene Physik eindeutig zu definieren. Diese grafischen Darstellungen sollen unserem Gehirn helfen, Daten zu analogisieren, so dass es sich, anstatt mit einer Geometrie zu arbeiten und zu versuchen zu verstehen, was vor sich geht, an die Vorstellung gewöhnen kann, dass wir nur mit Wahrscheinlichkeiten und zusätzlichen Zahlen arbeiten, die diesen Wahrscheinlichkeiten entsprechen. Ereignisse können auch als Zustände bezeichnet werden. Wenn wir die Logik der Zustände verwenden, dann ist die Wahrscheinlichkeit genau die Häufigkeit des Auftretens eines bestimmten Zustands als Ergebnis der Wiederholung der gleichen Experimente. 

In Analogie zu den Flächen der Figuren ist die Summe der Flächen aller Figuren, die in der Ellipse enthalten sind, genau gleich der Fläche dieser Ellipse. In der Mathematik ist die Fläche die Anzahl der Ergebnisse, die darauf fallen. Daraus folgt:

• N = S[1] + S[2] + ... + S[n]
  
• S ist die Anzahl der Resultate eines bestimmten Ereignisses
• N ist die Gesamtheit der Resultate des Ereignisraums

Dividiert man beide Seiten der Gleichheit durch den Wert N, erhält man eine interessante und sehr wichtige Beziehung, die der gesamten Wahrscheinlichkeitstheorie zugrunde liegt:

• 1 = S[1]/N   +   S[2]/N   +   ...   +S[n]/N

Bitte beachten Sie, dass dieses Verhältnis nur für nicht überlappende Ereignisse gilt. Denn wenn Ereignisse verbunden werden, überlappen sich die Flächen der Formen, und die Summe ihrer Flächen ist größer als die Fläche der ursprünglichen Ellipse. Es ist ähnlich wie bei einem Puzzle, bei dem die Fläche aller Puzzleteile genau dem resultierenden Bild entspricht. In diesem Fall steht ein Puzzleteil für eines der Ereignisse. Alle diese Brüche stellen die Wahrscheinlichkeiten bestimmter Ereignisse dar:

• 1  = P[1]   +   P[2]   +   ...   +P[n]

Dieses Verhältnis dient als Grundlage für den Begriff Kollektiv erschöpfende Ereignismenge (collectively exhaustive event set). Eine kollektiv erschöpfende Ereignismenge ist die Gesamtheit aller sich nicht überschneidenden Ereignisse, die einen bestimmten Ereignisraum bilden. Für ein Puzzle ist die kollektiv erschöpfende Menge die aller Puzzleteile. Die Gesamtwahrscheinlichkeit all dieser Ereignisse muss gleich eins sein, was bedeutet, dass eines dieser Ereignisse notwendigerweise als Ergebnis des Experiments eintreten muss. Wir wissen nicht, welches Ereignis eintreten wird, aber wir werden es durch das Ergebnis des Experiments herausfinden.

Demnach kann jede Menge von Resultaten aus dem gewählten Ereignisraum als Ereignis dienen. Dies bedeutet, dass eine kollektiv erschöpfende Menge auf alle möglichen Arten und Kombinationen gesammelt werden kann. Wenn es sich um eine endliche Anzahl von Resultaten handelt, kann es eine begrenzte Anzahl solcher Kombinationen geben; bei einer unendlichen Anzahl von Resultaten wäre die Anzahl der Kombinationen immer unendlich. Wenn bekannt ist, dass die Anzahl der Resultate gleich unendlich ist, denken Mathematiker an das Konzept eines Zufallswertes. In manchen Fällen kann es bequemer sein, mit Zufallswerten zu arbeiten, wenn die Aufgabenstellung dies zulässt. Ein Zufallswert ist eine etwas andere Methode, den Ereignisraum zu beschreiben. In diesem Fall ist das Resultat die eindeutige Menge von einer oder mehreren Zahlen. Wir können sagen, dass dies ein Vektor ist. Dieses Betrachtungsmodell impliziert das Konzept der Wahrscheinlichkeitsdichte. 

Diese Konzepte werden im weiteren Verlauf der Untersuchung dieses Themas verwendet, also lassen Sie uns sie jetzt betrachten. Die Wahrscheinlichkeitsdichte ist eine Funktion, die den gesamten Ereignisraum beschreibt. Die Dimension dieser Funktion entspricht genau der Anzahl der Zahlen, die erforderlich sind, um jedes Resultat in diesem Ereignisraum zu beschreiben. Betrachten wir zum Beispiel das Problem des Schießens auf eine Zielscheibe in einem Schießstand, so ist die Dimension dieser Funktion gleich zwei, da die Zielscheibe flach (zweidimensional) ist. In diesem Fall wird ein bestimmtes Resultat durch X- und Y-Koordinaten charakterisiert. Diese Zahlen sind unsere Zufallsvariablen, so dass wir die folgende Formel aufstellen können:

• R = R(X,Y)
• R ist die Wahrscheinlichkeitsdichte eines Geschosses, das einen Punkt mit den Koordinaten (X,Y) trifft

Die Eigenschaften dieser Funktion sind so, dass das vollständige Integral von minus bis plus unendlich für alle Variablen dieser Funktion gleich eins ist, was die obige Gleichung beweist. Die Wahrscheinlichkeiten werden hier nur durch die Integrale des Bereichs bestimmt, in dem die Funktion dargestellt wird. Verschiedene Ereignisse können aus stückweise integrierten Bereichen zusammengesetzt sein. Es ist also möglich, so viele Ereignisse zu beschreiben, wie wir brauchen, denn ihre Anzahl ist unendlich. Diese Definition ist im Rahmen dieses Artikels ausreichend.

Ich möchte noch einige Details zu überlappenden Ereignissen hinzufügen. Solche Ereignisse sind ebenfalls sehr wichtig für das allgemeine Verständnis des Gesamtbildes. Es ist klar, dass nicht überlappende Ereignisse im Vergleich zu überlappenden Ereignissen einfacher zu handhaben sind. Die Wahrscheinlichkeitstheorie muss sich manchmal mit der Kombination oder Aufteilung von Ereignissen befassen. Hier sind wir jedoch nur an den Wahrscheinlichkeiten interessiert, die sich aus diesen Transformationen ergeben. Zu diesem Zweck werden wir die Begriffe der Ereignisse Summe und Produkt sowie die Operation Inversion verwenden. Diese Operationen haben nicht ganz dieselbe Bedeutung wie in der Mathematik. Außerdem operieren sie nur mit Wahrscheinlichkeiten. Die Wahrscheinlichkeiten von verbundenen Ereignissen können nicht addiert werden, da dies die Integrität der Menge verletzen würde. Im Allgemeinen können diese 3 Operationen, die auf Quellereignisse angewendet werden, alle möglichen Ereignisse beschreiben, die aus Teilen von Quellereignissen zusammengesetzt werden können. Anhand des Beispiels von zwei sich überschneidenden Ereignissen kann ich zeigen, wie das auf der Ebene aussehen kann:

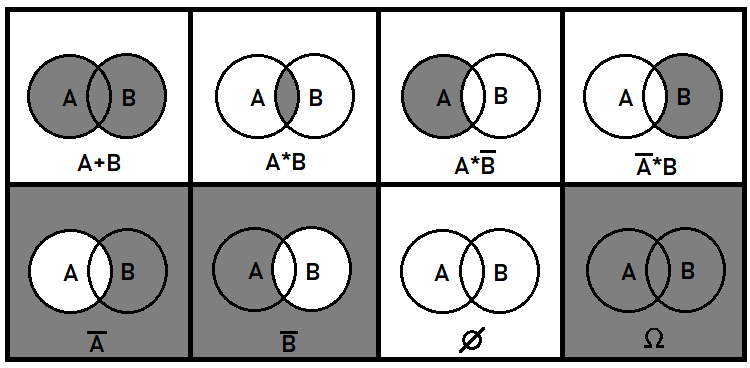
Weitere algebraische Operationen können aus den oben dargestellten zusammengesetzt werden. So entspricht beispielsweise die boolesche Division der dritten und vierten Situation in der obigen Abbildung, da die Division der Multiplikation mit dem Kehrwert des ausgewählten Ereignisses entspricht. Streng genommen reichen die ersten beiden Ereignisse aus, um alle möglichen Ereignisse zu beschreiben, die aus Teilen von Quellereignissen zusammengesetzt werden können. Fälle mit mehr als zwei sich überschneidenden Ereignissen sind wesentlich schwieriger. In diesem Artikel werden wir uns nur mit nicht überlappenden Ereignissen befassen.

Die Marktmathematik basiert in erster Linie auf dem Konzept des Zufallslaufs. Wir werden dieses Konzept betrachten, und dann wird es möglich sein, diese Ereignisse durch das Vorhandensein von Mustern zu verallgemeinern. Nehmen wir an, wir eröffnen eine Position mit Stop-Loss und Take-Profit in gleichem Abstand zu den Eröffnungskursen. Dabei werden Spreads, Kommissionen und Swaps nicht berücksichtigt. Wenn wir also eine Position kostenlos eröffnen und nach dem Zufallsprinzip in verschiedene Richtungen und an verschiedenen Chartpunkten handeln, ist das Gewinn-Verlust-Verhältnis gleich eins. Mit anderen Worten: Die Anzahl der gewinnbringenden Positionen ist gleich der Anzahl der Verlustpositionen beim Endloshandel. Demnach wäre der Gewinn gleich Null, egal wie lange wir handeln. Wenn Sie alle Provisionen, Spreads und Swaps berücksichtigen, wird das Endergebnis negativ sein.

Der Random Walk mag sinnlos erscheinen, da die Mathematik dieses Prozesses immer zu Verlusten führt. Aber der Random Walk kann bei der Berechnung der Wahrscheinlichkeiten verschiedener Ereignisse helfen. Dazu gehören die Schließung durch asymmetrische Stopps oder der Durchschnittspreis, den das Diagramm in einer bestimmten Preisspanne passieren wird. Wir können auch die Lebensdauer von Positionen und andere nützliche Variablen berechnen, die bei der Berechnung von Risiken oder bei Ihren Versuchen, Gewinne zu maximieren oder Verluste zu minimieren, hilfreich sein können.

Wahrscheinlichkeitsbäume und Hypothesen

Ein sehr nützliches Beispiel für die Entwicklung Ihrer Frontallappen sind Ereignisbäume, oder Wahrscheinlichkeitsbäume. Dieses Thema geht auf das Bernoulli-Schema zurück, das die Grundlage aller Wahrscheinlichkeitsbäume ist. Dieses Schema untersucht die Ketten von sich nicht überschneidenden Ereignissen, die aufeinander folgen. Doch zuvor wollen wir die Formel für die Gesamtwahrscheinlichkeit betrachten. Wenn wir diese wichtige Konstruktion studieren, können wir zum Bernoulli-Schema und damit zu den Wahrscheinlichkeitsbäumen übergehen. Die Formel sieht wie folgt aus:

• P(A) = Summe(0 ... i .... n) [ P(H[i]) * P(A|H[i]) ] — Wahrscheinlichkeit des Ereignisses A
• P(H[i]) — Wahrscheinlichkeit der Hypothese H[i]
  
• P(A|H[i]) — Wahrscheinlichkeit, dass das Ereignis A im Rahmen der Hypothese H[i] eintritt

Ich möchte anmerken, dass es bei der Arbeit mit Wahrscheinlichkeiten besser ist, sie im Stil der Hypothese zu schreiben. Zum Beispiel würde der Ausdruck P(H[k]|H[i]) folgendes bedeuten:

1. Die Wahrscheinlichkeit des Ereignisses H[k] berechnet relativ zum Raum H[i]

Auf diese Weise ist klar, welches Ereignis als Raum betrachtet wird und welches Ereignis verschachtelt ist. Denn jedes Ereignis ist ein kleinerer Ereignisraum, innerhalb dessen es weitere Ereignisse geben kann, die ebenfalls als Ereignisräume dienen können, und so weiter. Nach dieser Logik kann der Ausdruck P(H[i]) wie folgt geschrieben werden:

• P(H[i]|O) — denn diese Wahrscheinlichkeit wird relativ zu O geschätzt.
  

Zerlegen wir nun die Formel für die Gesamtwahrscheinlichkeit in Teile, um zu verstehen, was dahinter steckt. Die Formel mag auf den ersten Blick schwierig erscheinen, also machen wir sie klarer. Zunächst werde ich die Formel in einer etwas anderen Form umschreiben:

• P(A) = (S[0] + ... + S[i] + ... + S[n]) / O   =   S[0]/O + ... + S[i]/O + ... + S[n]/O  =  (S[0]/N[0]) * ( N[0]/O ) + ... + (S[i]/N[i]) * ( N[i]/O ) + ... + (S[n]/N[n]) * ( N[n]/O )
• S[i] — die Fläche des spezifischen Segments des Schnittpunkts der Hypothese H[i]
• N[i]  — die Fläche der gesamten Hypothese H[i] (einschließlich S[i])
• O  — alle Resultate oder die Fläche der gesamten Ellipse

Nach kleinen Umformungen, die darin bestehen, den Zähler und den Nenner mit dem Wert N[i] zu multiplizieren, können wir die Wahrscheinlichkeiten sehen, die in der ursprünglichen Formel vorhanden sind:

• S[i]/N[i] ----> P(A|H[i])
• N[i]/O ----> P(H[i])

Sie kann wie folgt grafisch dargestellt werden:

 

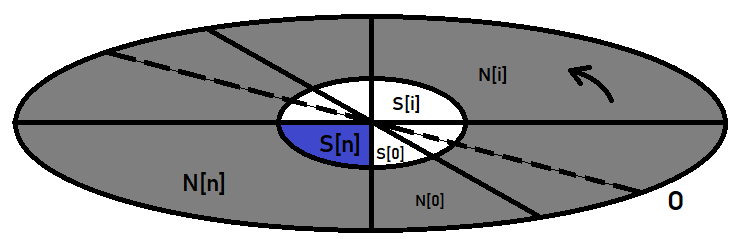
Die äußere Ellipse ist der Ereignisraum. Die zentrale Ellipse ist unser Ereignis, nach dessen Wahrscheinlichkeit wir suchen. Angenommen, es handelt sich um eine Uhr: Zeichnen Sie den Durchmesser der Ellipse, drehen Sie sie gegen den Uhrzeigersinn und schneiden Sie die Ellipse in Segmente, die Hypothesen darstellen. Eine Hypothese ist nur ein besonderer Name für Ereignisse. In Wirklichkeit handelt es sich jedoch um dieselben Ereignisse, die sich nicht von den Ereignissen unterscheiden, für die wir die Wahrscheinlichkeit berechnen.

Diese Formel hat einen Sonderfall, der beim Aufbau des Bernoulli-Schemas hilfreich sein wird. Stellen Sie sich vor, dass die zentrale Ellipse vollständig innerhalb einer dieser Hypothesen liegt. Dann stellt sich heraus, dass alle Terme dieser Summe, die sich auf die übrigen Hypothesen beziehen, automatisch auf Null gesetzt werden, weil die Wahrscheinlichkeit des Eintretens des Ereignisses A innerhalb dieser Hypothesen unmöglich oder gleich Null ist, was diese Terme schließlich zu Null macht. Daraus ergibt sich, dass:

• P(A) = P(H) * P(A|H)
• H  — die Wahrscheinlichkeit der Hypothese, in der das ausgewählte Ereignis vollständig enthalten ist.

Und was ist, wenn wir annehmen, dass das Ereignis A auch als Hypothese bezeichnet wird? Und warum nicht? Eine Hypothese ist ein Ereignis, also ist jedes Ereignis eine Hypothese. Nehmen wir nun an, es gibt ein weiteres Ereignis B, das sich innerhalb von A befindet. Dann ist A eine Hypothese in Bezug auf B, und die vorstehende Formel ist auf diese beiden Ereignisse anwendbar:

• P(B) = P(A) * P(B|A) = P(H) *  P(A|H) *  P(B|A)

Wenn wir stattdessen das vorherige Verhältnis P(A) einfügen, können wir ein gewisses Muster beim Aufbau einer allgemeinen Formel für eine beliebige Anzahl von verschachtelten Hypothesen oder Ereignissen erkennen. Was ist der Zweck davon? Dies ist der direkte Prototyp der Bernoulli-Formel, die wir etwas später besprechen werden. Nun gibt es noch eine weitere interessante Tatsache zu besprechen.

Über Fraktale

Wenn P(A) + P(B) = 1 ist, dann handelt es sich nach der obigen Formel um eine kollektiv erschöpfende Menge von Ereignissen. Das bedeutet, dass eine vollständige Gruppe aus zwei beliebigen Ketten von Hypothesen bestehen kann, die ineinander verschachtelt sind. Diese Hypothesen können sich aber auch überschneiden. Wenn wir verlangen, dass alle möglichen verschachtelten Hypothesen sich nicht mit den Hypothesen der anderen Ketten überschneiden, dann werden automatisch alle Ketten sich nicht mit allen Ketten in diesem Ereignisraum überschneiden. Eine grafische Darstellung dieses Musters ist recht interessant:

Dieses Muster wird Fraktal genannt, weil eine solche Struktur nicht zu Ende gebaut werden kann; sie kann unendlich oft erstellt werden. In der obigen Abbildung ist die Struktur nur 3 Ebenen tief. Die blauen Rechtecke stellen das Ende einer separaten Kette von Wahrscheinlichkeiten dar. Wenn wir die Wahrscheinlichkeiten all dieser Ketten addieren, bilden sie eine kollektiv erschöpfende Menge von Ereignissen.

Solche Fraktale lassen sich gut durch Kombinationen beschreiben. Kombinationen beruhen auf dem Konzept der Fakultät einer Zahl. Es gibt ein weiteres Konzept, die Permutation, das zwischen Fakultät und Kombination liegt. Die Permutationsformel ist von der Fakultät abgeleitet, und der Begriff der Kombination ist von der Permutationsformel abgeleitet. Hier sind die entsprechenden Formeln:

• n! - Fakultät der Zahl n
• P(n,k) = n! / ( n - k )!  — Permutationen von N Elementen durch K Elemente
• С(n,k) = n! / ( k! * ( n - k )! )  — Kombinationen von N Elementen durch K Elemente

Eine Fakultät ist das Produkt aller natürlichen Zahlen, die mit 1 beginnen und mit n enden, wobei "0! = 1". Das heißt, die Fakultät von Null ist gleich Eins. In diesem Fall handelt es sich nur um eine Ausnahme von der Regel, aber ich habe noch keinen einzigen Fall gesehen, in dem diese Ausnahme die Berechnungen beeinträchtigt oder die Algorithmen verkompliziert hätte.

Permutationen sind ein wenig komplizierter. Stellen Sie sich vor, Sie haben ein Kartenspiel, und dieses Kartenspiel hat eine bestimmte Anzahl von Karten. Führen Sie ein einfaches Experiment durch: Mischen Sie den Stapel und nehmen Sie einige Karten auf völlig willkürliche Weise aus dem Stapel und legen Sie sie in der Reihenfolge auf den Tisch, in der wir sie aus dem Stapel genommen haben. Permutationen sind also die Anzahl aller möglichen Resultate dieses Experiments, während die Reihenfolge der Karten auch als eindeutiger Identifikator eines bestimmten Resultats betrachtet wird. Eine solche Permutation ist auf jedes beliebige Element anwendbar.

Die erste Karte kann auf n verschiedene Arten vom Stapel genommen werden, die zweite kann auf "n-1" Arten genommen werden, da die erste Karte nicht mehr im Stapel ist. Und so weiter, bis zur Karte "n-k-1". Um die Anzahl aller möglichen Permutationen zu erhalten, müssen wir alle Zahlen von "n-k-1" mit "n" multiplizieren. Dieses Verfahren ähnelt einer Fakultät. Nimmt man "n!" und teilt es durch "n-k" Faktoren, so erhält man das ursprüngliche Produkt, das genau "(n-k)!" entspricht. Auf diese Weise erhalten wir die Permutationsformel.

Die Kombinationsformel ist ein wenig komplizierter, aber auch sehr einfach herzuleiten. Wir haben alle möglichen Permutationen, aber die Reihenfolge der Elemente spielt keine Rolle — nur die Karten in dieser Menge sind wichtig. Nun müssen wir die Anzahl dieser Fälle herausfinden, wobei jeder Fall eine andere Menge von Karten hat. In der Tat enthält jede Permutation bereits eine dieser einzigartigen Mengen, aber wir brauchen nicht alle. Ändern wir die Logik und versuchen wir, alle Permutationen aller möglichen Kombinationen zu sammeln: Es stellt sich heraus, dass eine Kombination, egal wie wir die Elemente in ihr anordnen, einzigartig ist. Wenn wir außerdem alle eindeutigen Kombinationen nehmen und alle möglichen Permutationen innerhalb dieser Kombinationen erzeugen, erhalten wir Folgendes:

• P(n,k) = C(n,k) * P(k,k)

Die Anzahl aller möglichen eindeutigen Permutationen innerhalb einer Kombination ist gleich "P(k,k)", denn wir müssen aus "k" Varianten alle möglichen Permutationen für diese "k" Varianten sammeln. Dividiert man beide Teile der Gleichung durch "P(k,k)", erhält man die erforderliche Kombinationsformel:

• C(n,k) = P(n,k)/P(k,k) = n! / ( k! * ( n - k )! )
  

Sowohl Permutationen als auch Kombinationen werden häufig für verschiedene wahrscheinlichkeitstheoretische Probleme verwendet. Wenn es um praktische Anwendungen geht, sind es die Kombinationen, die für uns äußerst nützlich sind. Kombinationen werden bei der Konstruktion von fraktalen Funktionen für eine Vielzahl von Zwecken verwendet. Vielleicht wäre es korrekter, sie als rekurrent zu bezeichnen, aber aus irgendeinem Grund nenne ich solche Funktionen fraktal (wahrscheinlich, weil sie wirklich fraktal sind, also nicht nur eine Rekursion, sondern einen ganzen Baum von Aufrufen darstellen).

Bernoulli-Schema

Bevor wir mit der Untersuchung solcher fraktalen Funktionen fortfahren, wollen wir die bekannte Bernoulli-Formel betrachten. Angenommen, wir haben eine Kette von identischen Experimenten, die wir mehrmals wiederholen müssen. Das Experiment soll dazu führen, dass ein Ereignis mit einer bestimmten Wahrscheinlichkeit eintritt oder nicht eintritt. Nehmen wir weiter an, wir wollten die Wahrscheinlichkeit finden, dass in einer Kette von "n" Experimenten unser Ereignis genau "k" Mal auftritt. Die Bernoulli-Formel kann diese Frage beantworten:

• P = C(n,k)*Pow(p,k)*Pow(q,n-k)   — Bernoulli-Formel
  
• p  —die Wahrscheinlichkeit des Auftretens des Ereignisses als Ergebnis eines einzigen Experiments
• q = 1 - p   — die Wahrscheinlichkeit, dass das Ereignis als Ergebnis des Experiments nicht eintritt

Erinnern Sie sich an die zuvor abgeleitete Formel für probabilistische Ketten? Erweitern wir sie für eine beliebig große Kettenlänge:

• P(n) = P(H[1]|O) *  P(H[2]|H[1]) *  P(H[3]|H[2]) * ... * P(H[k]|H[k-1]) * ... *P(H[n]|H[n-1])
• n  — die Anzahl der Segmente in der Kette
• O  — die gesamte Menge der Resultate; kann als H[0] bezeichnet werden

Diese Formel berechnet die Wahrscheinlichkeit für das Eintreten der genau erforderlichen Kette von Hypothesen. Die Formel kann wie folgt visuell dargestellt werden:

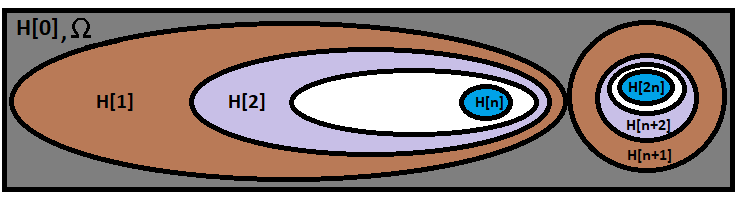
Unsere Formel befindet sich in der ersten und größten Ellipse, während eine andere Kette auf der rechten Seite sich nicht mit unserer Kette überschneidet und einen anderen Zweig aus einer anderen Kombination symbolisiert. Es gibt genau so viele solcher Zweige, wie es Varianten zur Berechnung von Kombinationen in unserer Formel gibt. Verwechseln Sie also nicht die Kombinationen mit den Kombinationsberechnungsvarianten. Die Anzahl der Varianten zur Berechnung der Kombinationen ist gleich:

• n+1 (weil auch die erfolgreichen Resultate mit der Kombinationen "0" gezählt werden)
• n ist die Anzahl der unabhängigen Versuche in der Versuchskette

Stellen Sie sich nun vor, dass die Wahrscheinlichkeiten all dieser Hypothesen entweder gleich "p" oder "q" sind. Dann wird die Formel vereinfacht:

• P(n) = Pow(p,k)*Pow(q,n-k)
• k  — wie viele Faktoren gleich "p" sind im Produkt enthalten
• n-k  — wie viele Faktoren gleich "q" sind in dem Produkt enthalten

Sie ähnelt bereits der Bernoulli-Formel, aber ihr fehlt die Kombination. Wenn man genau nachdenkt, wird klar, dass die Varianten von Ketten mit ähnlicher Wahrscheinlichkeit und der Menge von "k" und "n-k" genau gleich "C(n,k)" sind. Da sich alle Wahrscheinlichkeitsketten nicht überschneiden, ist die Wahrscheinlichkeit, eine dieser Ketten zu erhalten, die Summe der Wahrscheinlichkeiten aller dieser Ketten. Da alle diese Wahrscheinlichkeiten gleich sind, können wir die Wahrscheinlichkeit einer Kette mit ihrer Anzahl multiplizieren, um die Bernoulli-Formel zu erhalten:

• P = C(n,k)*Pow(p,k)*Pow(q,n-k)

Diese Formel lässt sich weiter ausbauen, zum Beispiel, wenn wir die Wahrscheinlichkeit nicht für eine streng festgelegte Kombination, sondern für das k-malige und mehrmalige Auftreten eines Ereignisses, für das k-malige und weniger-malige Auftreten eines Ereignisses sowie für alle ähnlichen Kombinationen ermitteln wollen. In diesem Fall handelt es sich um die Summe der Wahrscheinlichkeiten für alle erforderlichen Kombinationen. Die Wahrscheinlichkeit, dass das Ereignis mehr als k-mal auftritt, wird beispielsweise wie folgt berechnet:

• P = Summ(k+1 ... i ... n)[C(n,i)*Pow(p,i)*Pow(q,n-i)]

Es ist wichtig zu verstehen, dass:

• P = Summ(0 ... i ... n)[C(n,i)*Pow(p,i)*Pow(q,n-i) ] = 1

mit anderen Worten, alle möglichen Ketten bilden eine kollektiv erschöpfende Ereignismenge. Eine weitere wichtige Gleichung ist:

• Summe(0 ... i ... n)[C(n,i)] = Pow(2,n)
  

Das ist logisch, da jedes Segment der Wahrscheinlichkeitskette nur zwei Zustände hat: "Das Ereignis ist eingetreten" und "Das Ereignis ist nicht eingetreten". Der Zustand, in dem das Ereignis nicht eingetreten ist, ist ebenfalls ein Ereignis, was impliziert, dass ein anderes Ereignis eingetreten ist.

Kombinationen haben eine weitere interessante Eigenschaft:

• C(n,k) =  C(n,n-k)
  

Sie wird wie folgt hergeleitet: Man berechne "C(n,n-k)" und vergleiche es mit "C(n,k)". Nach einigen kleinen Umformungen können wir sehen, dass beide Ausdrücke identisch sind. Ich habe ein kleines Programm auf der Basis von MathCad 15 erstellt, um alle oben genannten Aussagen zu überprüfen:

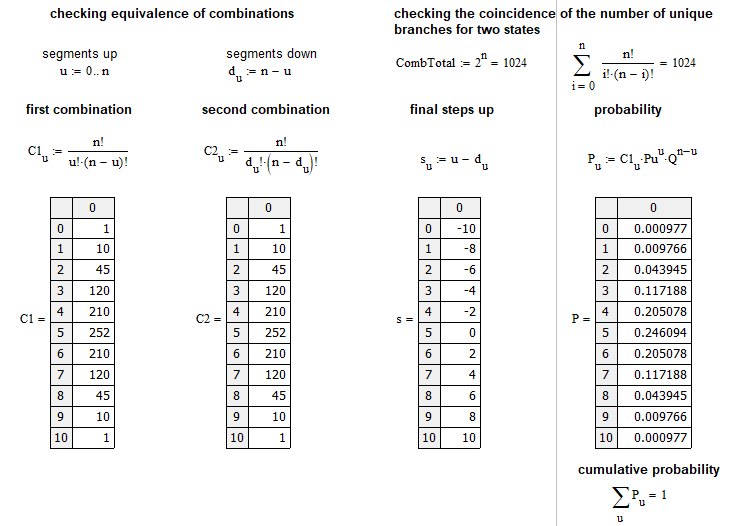
Dieses Beispiel ist nahe am Markt. Es berechnet die Wahrscheinlichkeit, dass sich der Markt in n Schritten um u Schritte nach oben bewegt. Ein Schritt ist die Kursbewegung um eine bestimmte Anzahl von Punkten nach oben oder unten, bezogen auf den vorherigen Schritt. Die grafische Anordnung der Wahrscheinlichkeiten für jedes "u" kann wie folgt dargestellt werden:

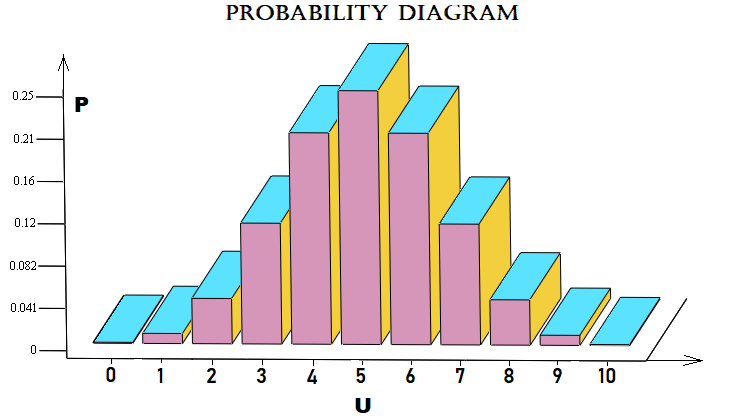
Der Einfachheit halber habe ich ein Bernoulli-Schema mit 10 Schritten verwendet. Die Datei ist unten angehängt, damit Sie sie testen können. Sie müssen dieses Schema nicht unbedingt auf die Preisgestaltung anwenden. Es kann auch auf Aufträge oder alles andere angewendet werden.

Erstellen des ersten Fraktals

Besondere Aufmerksamkeit sollte den Problemen im Zusammenhang mit Stop-Loss- und Take-Profit-Level gewidmet werden. Wir sollten irgendwie die Wahrscheinlichkeit berechnen, dass eine Position durch Stop-Loss oder Take-Profit geschlossen wird, wenn wir die Werte von Stop-Loss und Take-Profit in Punkten (Abstand vom aktuellen Kurs) kennen. Dieser Wert kann zu jedem beliebigen Zeitpunkt berechnet werden, auch wenn es sich nicht mehr um den offenen Kurs handelt, da alle diese Aspekte direkt von den Preisbildungsmechanismen abhängen. In diesem Beispiel möchte ich den Beweis der Formel anhand von Fraktalen demonstrieren. Im Falle eines Random Walk kann diese Wahrscheinlichkeit wie folgt berechnet werden:

• P(TP) = SL / ( TP + SL ) - die Wahrscheinlichkeit, den Take-Profit zu erreichen
• P(SL) = TP / ( TP + SL ) - die Wahrscheinlichkeit des Erreichens von Stop-Loss
• SL  — Punktabstand zum Stop-Loss
  
• TP  — Punktabstand zum Take-Profit

Diese beiden Wahrscheinlichkeiten bilden eine kollektiv erschöpfende Ereignismenge:

• P(TP) + P(SL) = 1
  

Nach dieser Formel ist der mathematische Erwartungswert solcher Strategien für den Zufallshandel gleich Null, wenn wir Spread, Kommission und Swap ausschließen:

• M =  P(TP) * TP - P(SL) * SL = 0

Dies ist der einfachste Fall, wenn wir einen festen Stopp-Level festlegen. Es ist jedoch möglich, diese Formel auf jede beliebige Strategie zu verallgemeinern. Nun wollen wir die Formel mit demselben MathCad 15 beweisen. Ich arbeite schon seit langem mit diesem Programm. Es ist in der Lage, Berechnungen von fast beliebiger Komplexität durchzuführen, sogar mit Hilfe von Programmierung. In diesem Beispiel werden wir nicht nur die obigen Formeln beweisen, sondern auch das erste Beispiel für die Konstruktion einer fraktalen Formel sehen. Beginnen wir damit, den Prozess der Preisbewegung zu skizzieren. Wir können hier keine kontinuierlichen Funktionen verwenden, sondern nur diskrete. Nehmen wir dazu unsere bedingte Order und berechnen wir die Abstände der Stopp-Levels nach oben und nach unten, dann teilen wir diese Segmente in Teile mit gleichen Schritten auf, so dass jeder Schritt eine ganzzahlige Anzahl von Schritten umfasst. Stellen Sie sich vor, dass sich der Kurs um diese Schritte bewegt. Da die Schritte gleich sind, ist die Wahrscheinlichkeit eines Schrittes in eine der beiden Richtungen 0,5. Wir brauchen eine grafische Darstellung, um das entsprechende Fraktal zu implementieren:

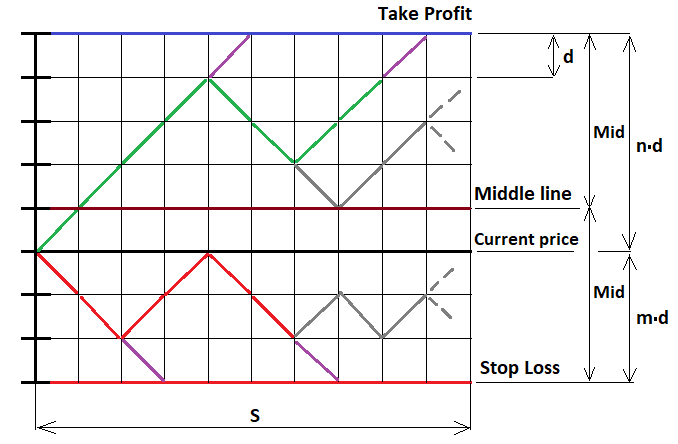
Um dieses Problem zu lösen, betrachten wir drei mögliche Fälle der fraktalen Fortsetzung:

1. Wir befinden uns oberhalb der Mittellinie ( U > MiddleLine )
2. Wir befinden uns unterhalb der Mittellinie ( U < MiddleLine )
3. Wir befinden uns auf der Höhe der Mittellinie ( U = MiddleLine )

"U" ist die Gesamtzahl der Schritte "u-d" nach oben im Verhältnis zum Eröffnungskurs. Wenn der Punkt, von dem aus wir das Fraktal weiter aufbauen wollen, unter dem Preis liegt, dann nimmt U entsprechend der Funktion negative Werte an. Wenn wir uns an der Mittellinie befinden, ist die Anzahl der Schritte, die wir machen können, ohne zu befürchten, die Linie zu überschreiten, um einen weniger als Mid. Bevor wir jedoch mit der Konstruktion fortfahren, müssen wir die fraktale Konstruktion auf die Anzahl der Schritte beschränken, die der Preis oder die Aufträge machen können. Wenn die Anzahl der Schritte die erforderliche Anzahl überschreitet, müssen wir die weitere Konstruktion unterbrechen. Andernfalls entsteht eine unendliche Rekursion, aus der man nicht mehr herauskommt. Die Berechnungszeit wird gleich unendlich sein.

In der Abbildung habe ich mehrere lilafarbene Schritte eingezeichnet — an diesen Punkten sammeln wir die Wahrscheinlichkeiten und summieren sie zu einer gemeinsamen Variablen. Danach müssen wir unsere Kette nach oben oder unten drehen, je nachdem, welche Grenze die Kette berührt hat, damit sie sich weiterbewegen kann, um neue verschachtelte fraktale Ebenen zu bilden. An anderen Stellen können wir auf der Grundlage des Bernoulli-Schemas ganze fraktale Ebenen bilden.

Wenn es möglich ist, einen Baum auf der Grundlage des Bernoulli-Schemas zu erstellen, müssen wir zunächst die Anzahl der Schritte bestimmen, die wir machen können, wobei wir die Extremfälle berücksichtigen, in denen alle Schritte nur nach oben oder nur nach unten gehen. Für alle drei Fälle ist der Wert gleich:

• (n - 1) - U  — wenn sich unsere Kette bereits oberhalb der Mittellinie befindet (da eine Erhöhung von U eine Verringerung des Abstands zur oberen Grenze bewirkt)
• (m - 1) + U  — wenn sich unsere Kette bereits unterhalb der Mittellinie befindet (da eine Verringerung von U eine Verringerung des Abstands zur unteren Begrenzung bewirkt)
• (floor(Mid)-1)  — wenn unsere Kette genau auf der Mittellinie liegt
• n  — die Anzahl der oberen Segmente
• m  — die Anzahl der unteren Segmente
• floor  — die Funktion verwirft den Dezimalteil (dies ist möglicherweise nicht notwendig)

Zunächst müssen wir zwei Hilfswerte berechnen:

• Mid = (m+n)/2  — die Hälfte der Bereichsbreite (in Schritten)
• Middle = (m+n)/2 - m   — der "U"-Wert für die mittlere Linie (in Schritten)

Diese Werte werden später verwendet, um die fraktale Verzweigungslogik zu beschreiben. Vorerst werden wir das Fraktal nur für die Fälle erstellen, in denen "n>=m" ist. Diese Daten reichen jedoch nicht aus, um ein Fraktal zu erstellen. Um tiefere Fraktalebenen erstellen zu können, muss "U" für jede neue Kombination aus dem Bernoulli-Schema neu definiert und an eine neue Fraktalebene übergeben werden. Außerdem muss die Anzahl der durchgeführten Schritte korrekt inkrementiert und korrekt weitergegeben werden. In ähnlicher Weise müssen wir die Wahrscheinlichkeit der gesamten Kette mit Hilfe der Multiplikatoren der nächsten fraktalen Ebene sammeln und die Wahrscheinlichkeit der Zwischenkette an die nächste Ebene weitergeben, bis dieser Prozess mit einem erfolgreichen Überschreiten der erforderlichen Grenze endet. Die folgende Abbildung erklärt diese drei Varianten:

  

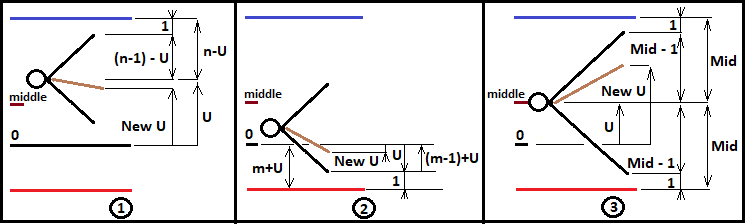
Anhand dieses Diagramms können wir nun aufschreiben, wie die Werte "NewU" und andere Hilfswerte für jeden vorgestellten Fall aussehen werden. Betrachten wir ein Beispiel für die Konstruktion eines Fraktals, um die Wahrscheinlichkeit des Überschreitens der oberen Grenze zu berechnen:

Für den Fall 1:

Schauen wir uns das obere Bild an und beschreiben wir mathematisch, was dort passiert. Diese Abbildung zeigt einen Auszug aus meinem Programm in MathCad 15. Der gesamte Code des Programms ist unten angehängt. Hier gebe ich die wichtigsten Details an, die die Grundlage des Fraktals sind. Das erste Rechteck befindet sich in einer Schleife, die "i" durchläuft, um alle möglichen Kombinationen zu beschreiben. Diese Logik kann in der MetaEditor-IDE wiederholt werden. Beginnen wir mit dem ersten Bild im Diagramm. Um "NewU" zu definieren, müssen wir zunächst einige grundlegende Formeln definieren:

• ( n - 1 ) - U = f — dies ist die Anzahl der Schritte des zukünftigen Kombinationsbaums (der Abstand wird durch den Abstand zur nächsten Grenze des fraktalen Bereichs bestimmt)
• u + d = f  — derselbe Wert, aber ausgedrückt durch die Anzahl der steigenden und fallenden Segmente
• s = u - d  — die Anzahl der letzten Schritte, ausgedrückt durch die Anzahl der fallenden und steigenden Segmente
• u = i  — dies liegt daran, dass mein Programm zur Iteration "i" verwendet (sollte man sich merken)

Um alle erforderlichen Werte zu berechnen, müssen wir "s" durch "U" und "i" ausdrücken. Zu diesem Zweck müssen wir die Variable "d" eliminieren. Man drückt sie zunächst aus und setzt sie dann in den Ausdruck für "s" ein:

1. d = f - u = f - i = ( n - 1 ) - U - i
2. s = i -( n - 1 ) + U + i = -( n - 1 ) + 2*i + U

Als Nächstes verwenden wir das gefundene "s", um "NewU" zu ermitteln, und alle Werte, die dem nächsten Fraktal-Level übergeben werden müssen:

• NewU = s + U = -( n - 1 ) + 2*i + 2*U   — unser neues "U", das dem nächsten Fraktal-Level übergeben werden muss.
• NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i) = P * C( ( n - 1 ) - U ,i) * Pow(p,i) * Pow(1-p, ( n - 1 ) - U -i) — unsere neue Wahrscheinlichkeit "P" m die dem nächsten Fraktal-Level übergeben werden muss (erhalten durch Multiplikation mit der Wahrscheinlichkeit des neuen Segments der Kette).
• NewS = S + f = S + ( n - 1 ) - U — neues "S" , dem nächsten Fraktal-Level übergeben werden muss.

Schauen wir uns nun das untere Rechteck an. Hier behandeln wir die Fälle, in denen die Schrittkette die obere Grenze des Bereichs erreicht hat. Zwei Fälle sollten hier behandelt werden:

1. Sammeln der Wahrscheinlichkeit, mit der die Kette den Rand schneidet (rot unterstrichen).
2. Ähnliche Aktionen, wobei neue Werte inkrementiert werden, die wir an die nächste fraktale Ebene weitergeben.

Dieser Fall ist sehr einfach, da es nur zwei mögliche Varianten gibt:

1. Berühren des Randes
2. Beachten des Randes

Für diese Aktionen ist das Bernoulli-Schema nicht erforderlich, da in jedem Fall nur ein Schritt erforderlich ist. Die Wahrscheinlichkeit der Umkehrung wird zusätzlich mit "(1-p)" multipliziert, da die Wahrscheinlichkeit der Überschneidung "p" ist und diese beiden Ereignisse eine kollektiv erschöpfende Menge bilden sollten, wie aus den vorherigen Berechnungen hervorgeht. Die Schritte werden um 1 erhöht, und "U" wird um "1" vermindert, da es sich um eine absteigende Reflexion handelt. Jetzt haben wir alles, um diesen Fall korrekt zu konstruieren. Diese Regeln werden für die Konstruktion der Hauptfraktale identisch sein, die wir für ganz andere Fälle benötigen.

Für den Fall 2:

Die Berechnung ist in diesem Fall fast gleich. Der einzige Unterschied besteht darin, dass "f" einen anderen Wert annimmt:

• ( m - 1 ) + U = f

Wiederum ist "s" durch "U" und "i" auszudrücken, wobei die gleichen Formeln wie im vorherigen Fall zu verwenden sind:

1. d = f - u = f - i = ( m - 1 ) + U - i
2. s = i -( m - 1 ) - U + i = -( m - 1 ) + 2*i - U

Auf ähnliche Weise finden wir alle anderen Werte, die wir an den nächsten Fraktal-Level weitergeben müssen:

• NewU = s + U = -( m - 1 ) + 2*i  — unser neues "U", das dem nächsten Fraktal-Level übergeben werden muss.
• NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i) = P * C( ( m - 1 ) + U ,i) * Pow(p,i) * Pow(1-p,( m - 1 ) + U -i)  — unsere neue Wahrscheinlichkeit "P" der Kette, die dem nächsten Fraktal-Levenübergeben werden muss.
• NewS = S + f = S + ( m - 1 ) + U  — unser neues "S", das dem nächsten Fraktal-Level übergeben werden muss.

Das untere Rechteck ist fast identisch mit dem vorherigen Fall, außer dass wir "U" um eins erhöhen, weil die Reflexion zunimmt und dies eine Erhöhung von "U" bedeutet. Es ist auch erwähnenswert, dass in diesem Fall keine Wahrscheinlichkeiten gesammelt werden, da wir nicht an den Fällen interessiert sind, in denen die untere Grenze in diesem Fraktal überschritten wird. Bleibt nur noch der jüngste Fall zu betrachten, bei dem die Kette die Mittellinie des Korridors erreicht hat.

Für den Fall 3:

Definition von "f":

• floor(Mid) - 1 = f

Ermitteln von "s":

1. d = f - i =  floor(Mid) - 1 - i
2. s = i - d = -(floor(Mid) - 1) + 2*i

Ermitteln wir schließlich die Werte, die an die nächste fraktale Ebene weitergegeben werden sollen:

• NewU = s + U = -(floor(Mid) - 1) + 2*i + U
  
• NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i) = P * C( floor(Mid) - 1 ,i) * Pow(p,i) * Pow(1-p,floor(Mid) - 1 - i)  — unsere neue Kettenwahrscheinlichkeit "P", die an die nächste fraktale Ebene weitergegeben werden muss.
• NewS = S + f = S + (Floor(Mid) - 1) — unser neues "S", das an die nächste fraktale Ebene weitergegeben wird.

Eine Besonderheit in diesem Fall ist, dass der Block keine Wahrscheinlichkeiten sammelt, denn Wahrscheinlichkeiten können nur an den Grenzwerten von "U" gesammelt werden, wo Wahrscheinlichkeitsketten auch wieder in die Kette zurückgespiegelt werden, damit sie sich weiter ausbreiten können. Die Erstellung eines Fraktals zur Berechnung der Wahrscheinlichkeit, die obere Grenze zu überschreiten, ist identisch, aber die Wahrscheinlichkeiten werden im zweiten Fall gezählt, nicht im ersten.

Ein interessantes Merkmal bei der Konstruktion solcher Fraktale ist das obligatorische Vorhandensein der Bernoulli-Formel in solchen Funktionen. Die Kombinationen sind rosa hervorgehoben, und die Produkte der Wahrscheinlichkeiten sind gelb dargestellt. Diese beiden Multiplikatoren bilden zusammen die Bernoulli-Formel.

Überprüfen wir nun zwei Dinge gleichzeitig: die Korrektheit der Konstruktion des gesamten Fraktals und die Annahme, dass die erwartete Auszahlung nur von der Vorhersagefähigkeit abhängt. Die Schritte können als Punkte oder als Geschäfte dargestellt werden. Im letzteren Fall sollten die Punkte mit dem entsprechenden Proportionalitätskoeffizienten multipliziert werden, der von den Lots und der Tickgröße abhängt. Hier werden wir Punkte verwenden — diese Darstellung ist universell:

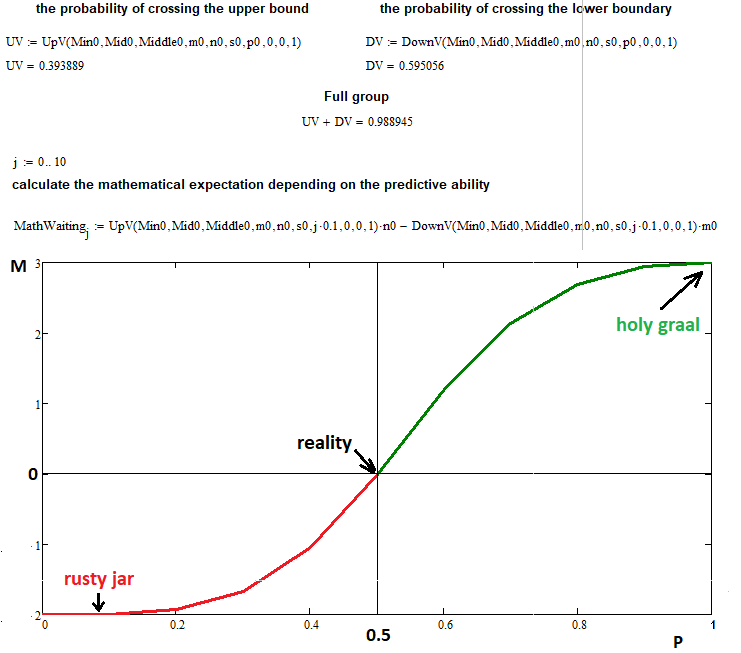
In diesem Beispiel habe ich die folgenden Eingabedaten verwendet, um die mathematische Erwartung gegenüber der Wahrscheinlichkeit eines Anstiegs darzustellen:

• n = 3 — Anzahl der oberen Segmente
• m = 2  — Anzahl der unteren Segmente
• s = 22  — Anzahl der zulässigen Schritte für eine Kettenreaktion der fraktalen Funktion (wenn Sie diesen Wert erhöhen, wird der Computer zusätzlich belastet, daher ist diese Anzahl von Schritten völlig ausreichend)
• 0 ... 0.1 ... 0.2 ...... 1.0   — Unterteilung des Bereichs der Aufwärtswahrscheinlichkeiten in 10 Teile mit einer Schrittweite von 0.1

Wie Sie sehen, ist für die Wahrscheinlichkeit von 0,5 die mathematische Erwartung für unsere Geschäfte gleich Null, wie zuvor durch die Formel vorhergesagt. Bei den Extrempunkten 0 und 1 tendiert der Funktionswert zu "n" und "-m", was unsere Annahmen bestätigt. Das Fraktal hat seine Aufgabe erfolgreich erfüllt, auch wenn es einen Nachteil aufweist: einen starken Anstieg der Berechnungszeit und der Komplexität. Es ist jedoch durchaus akzeptabel, für ähnliche Aufgaben ein paar Stunden oder sogar einen Tag zu warten.

Dieses Fraktal funktioniert nur für Fälle, in denen n >= m ist, d.h. wenn der Abstand zur oberen Grenze größer ist als der Abstand zur unteren Grenze, aber es ist nicht notwendig, dies im Fraktal anzugeben. Diese Konstruktion kann gespiegelt werden: Wenn n < m, können wir das Fraktal berechnen, indem wir m anstelle von n und n anstelle von m einsetzen. Dann vertauscht man die Wahrscheinlichkeiten und erhält das gewünschte Ergebnis. Solche Fraktale können nicht nur zum Beweisen von Formeln verwendet werden, sondern auch für einen umgekehrten Prozess. Einige Formeln können nur durch die Verwendung von Fraktalen erhalten werden.

Zusammenfassung

Ich denke, dass die folgenden, sehr wichtigen Schlussfolgerungen in diesem Artikel gezogen wurden:

• Die Wahrscheinlichkeitstheorie in Verbindung mit der Programmierung kann eine theoretische Grundlage für die Beschreibung vieler Marktprozesse liefern.
• Fraktale in Verbindung mit den wichtigsten Bestimmungen der Wahrscheinlichkeitsrechnung können die schwierigsten Fragen beantworten.
• Wir haben ein Beispiel für die Erstellung eines ziemlich komplexen Fraktals gesehen.
• Die gesamte Theorie wurde in der Praxis durch Programmierung in der MathCad 15 Umgebung getestet.
• Der Artikel hat gezeigt, dass das Bernoulli-Schema die Möglichkeit bietet, beliebige Fraktale mit zweistufigen Zuständen zu erzeugen.

Schlussfolgerung

Ich hoffe, der Leser konnte in diesem Material etwas Neues erkennen, das in der Praxis für den Handel verwendet werden kann. Bei der Arbeit an diesem Artikel habe ich versucht, die ganze Kraft der diskreten Mathematik und der Wahrscheinlichkeitstheorie zu vermitteln, um Sie auf eine weitere schwierige Aufgabe vorzubereiten — die Beschreibung von Marktprozessen mit Hilfe von Fraktal-Wahrscheinlichkeitsketten. Ich habe versucht, alle wichtigen Bestimmungen der Wahrscheinlichkeitstheorie in einem Material zusammenzufassen, das bei der Lösung komplexer Aufgaben für den praktischen Handel weiterhelfen kann. Außerdem habe ich versucht, alle irrelevanten Details zu entfernen. Der nächste Artikel wird neue Beispiele für die praktische Anwendung von Fraktalen und Antworten auf andere wichtige Fragen enthalten.