Kombinatorik und Wahrscheinlichkeitsrechnung für den Handel (Teil II): Das universelle Fraktal

Inhalt

• Einführung
• Bewertung der Nutzungsmöglichkeiten von Fraktalen im Handel
• Theoretische Grundlage für den Aufbau eines universellen Fraktals
• Schreiben des Codes zur Implementierung eines universellen Fraktals
• Ableitung der ersten Formel auf der Grundlage eines symmetrischen Fraktals
• Bewertung der Leistung der abgeleiteten Formel für alle positiven und reellen Argumente
• Fortgeschrittenes Fraktal, entwickelt aus dem universellen Fraktal
• Zusammenfassen der Ergebnisse
• Schlussfolgerung
• Referenzen

Einführung

Im vorigen Artikel haben wir die Grundlagen der Wahrscheinlichkeitstheorie erörtert, die uns helfen werden, die Besonderheiten der Verwendung fraktaler Funktionen für Handelsaufgaben zu verstehen. Als Fortsetzung dieses Themas werde ich einige autarke fraktale Funktionen vorstellen, die alle erforderlichen Preisbildungsprozesse beschreiben können. Wir werden versuchen, sie zu verallgemeinern und zu vereinfachen sowie Formeln zu erstellen, um verschiedene Fragen zu beantworten, für die es keine klaren quantitativen Schätzungen und eindeutigen Antworten gibt. 

Bewertung der Nutzungsmöglichkeiten von Fraktalen im Handel

Lassen Sie uns das Thema fortsetzen, indem wir die Ergebnisse des vorherigen Artikels zusammenfassen und das Material in einer kompakteren und universelleren Form präsentieren. Erinnern Sie sich an das Beispiel der Konstruktion eines Fraktals aus dem vorigen Artikel? Ein solches Fraktal ist von geringem praktischen Nutzen, aber in diesem Fall sind wir vor allem an den Regeln für den Aufbau der Struktur interessiert, die wir ermittelt haben. Wie sich herausstellte, lassen sich diese Regeln auf drei Arten von Fraktalen anwenden:

1. Fraktal mit symmetrischen Rändern
2. Fraktal mit asymmetrischen Rändern
3. Fraktal mit oberem oder unterem Rand

Solche Fraktale können zur Beschreibung der folgenden Prozesse verwendet werden:

• Beschleunigte Nachahmung des Handels mit der Fähigkeit, die Wahrscheinlichkeiten verschiedener Szenarien zu bewerten, unter Berücksichtigung von Einzahlungsbeschränkungen (da die untere Grenze die Einzahlungshöhe symbolisieren kann, bei der ein weiterer Handel unmöglich ist).
• Schätzung der durchschnittlichen Anzahl von Schritten innerhalb eines Fraktals (z.B. können Sie schätzen, wie viele Aufträge wir im Durchschnitt haben, bevor wir entweder den gewünschten Gewinn oder Verlust erzielen).
• Schätzung der durchschnittlichen Gesamtwerte für jeden Schritt (z. B. können Sie die durchschnittliche Haltedauer einer Position auf der Grundlage von Statistiken für eine kleinere Position, d. h. eine Position mit kleineren Stopp-Levels in Punkten oder in Preisdifferenzen, berechnen).
• Bewertung der Rentabilität von Optionen auf der Grundlage eines einzelnen umrandeten Fraktals.
• Andere Möglichkeiten.

Theoretische Grundlage für den Aufbau eines universellen Fraktals

Verwenden wir die Konstruktionsregeln, die wir im vorherigen Artikel abgeleitet haben, und ergänzen sie, um zu verstehen, wie ein Fraktal konstruiert wird. Außerdem habe ich einen kleinen Fehler in meinen Formeln gefunden, durch den eine Asymmetrisierung der Ränder nach oben oder unten unmöglich war. Die abgeleiteten Formeln erwiesen sich als korrekt und funktionieren daher für absolut jedes Fraktal. Eigentlich handelt es sich um eine Funktion zur Umsetzung eines beliebigen Fraktals. Alle möglichen Fraktale sind ein Spezialfall eines allgemeinen Fraktals. Wenn wir die drei oben definierten Fraktaltypen nehmen, sind die Bedingungen des allgemeinen Fraktals für die Implementierung dieser drei Spezialfälle wie folgt:

1. m = n & [ m > s & n > s ]
2. ( m > n || n > m )  & [ m > s & n > s ]
3. ( m > S && n <= S ) || ( n > S && m <= S )

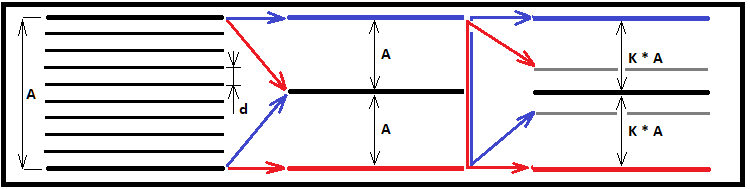
Schematisch sehen diese drei Arten von Fraktalen wie folgt aus:

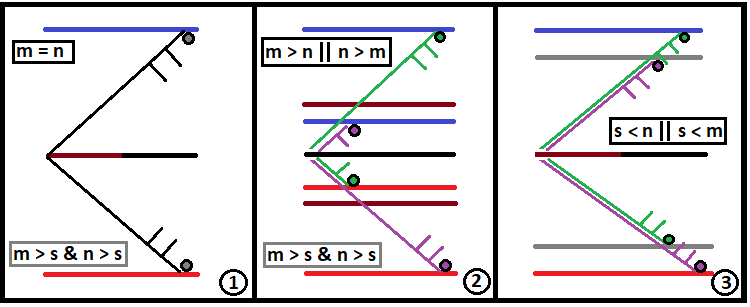
Im Idealfall sollte "S" gegen Unendlich tendieren. Die folgenden Variablen wurden in meinem vorherigen Artikel noch nicht beschrieben. Ich werde hier die entsprechenden Beschreibungen geben, um ein vollständiges Bild davon zu bekommen, wie man die allgemeine Formel verwendet, um die Spezialfälle zu erhalten. Das Fraktal ist eine Funktion, die nach dem Prinzip einer Kettenreaktion funktioniert, wie bei einer Atombombe. Wenn die eingestellte Kettenreaktion zu tief ist, kann der Computer mit solch massiven Berechnungen überfordert sein. Wenn der Fall nicht besonders kritisch ist, wird er einfach sehr lange rechnen — Minuten, Stunden oder sogar Tage. Um eine Kettenreaktion in einem Fraktal korrekt auszulösen, sollten wir zwei grundlegende Werte finden:

• Half - die Hälfte der Kanalbreite
• Middle - der "U"-Wert, der der mittleren Linie entspricht

Der Wert von Half lässt sich für alle drei Fälle, die wir im vorigen Artikel ermittelt haben, leicht berechnen: Er ist das arithmetische Mittel von m und n:

• Half = ( n + m ) / 2

Um den zweiten Wert zu realisieren, müssen wir drei Logikvarianten verwenden. Allerdings können die erste und die zweite Variante zu einer kombiniert werden. Wir haben also zwei Varianten:

1. n >= m
2. n < m

Da die "U"-Achse nach oben gerichtet ist und der Wert n der obere Teil der Kanäle ist, während m der untere Teil ist, erhalten wir zwei Verhältnisse für zwei Fälle mit möglichen m und n:

1. Middle = Half - m
2. Middle = - ( Half - n )

Diese Werte werden der Fraktalfunktion zur internen Verwendung übergeben, da die im vorigen Artikel beschriebene interne Verzweigungslogik ohne sie nicht implementiert werden kann. Der Funktionsprototyp lautet wie folgt:

• double Fractal(double Half, double Middle, int m, int n, int s,double p,int S, int U, double P)

Wir müssen also drei obligatorische Werte für den korrekten Fraktalstart übergeben:

1. Half - die Hälfte der Kanalbreite
   
2. Middle - der "U"-Wert, der der mittleren Linie entspricht
   
3. m - die Anzahl der Schritte bis zur unteren Grenze
4. n - die Anzahl der Schritte bis zum oberen Rand
5. s - die maximal zulässige Anzahl von Schritten in jeder Richtung für eine einzelne Kette

Andere Werte werden mit Großbuchstaben angegeben, um zu verdeutlichen, dass diese Werte dynamisch sind und auf verschiedenen fraktalen Ebenen unterschiedlich sein werden. Hier ist ihre Definition:

• S - die Anzahl der Schritte, die in der aktuellen Wahrscheinlichkeitskette akkumuliert wurden; die an die nächste fraktale Ebene weitergegeben werden
• U - aktueller Abstand zwischen dem Startpunkt der Kette und ihrem Ende; wird an die nächste fraktale Ebene weitergegeben
• P - akkumuliertes Produkt der Wahrscheinlichkeiten der gesamten Kette auf der Grundlage des Bernoulli-Schemas; zur Weiterleitung an die nächste fraktale Ebene

Für einen korrekten Start des Fraktals sollten wir also die folgenden Werte in die Funktion eingeben:

• S = 0 (da es sich um einen Start handelt, also noch keine Schritte stattgefunden haben)
• U = 0 (aus demselben Grund)
• P = 1 (da es sich um eine Nullkette handelt und alle nächsten Schritte eine vollständige Gruppe bilden sollten)

Um die Entwicklung der allgemeinen Regeln für Fraktale, die die Preisbildung oder den Handel simulieren, abzuschließen, lassen Sie uns kurz die Regeln umschreiben, die im vorherigen Artikel ermittelt wurden. Diese Regeln werden innerhalb des Fraktals verwendet. Die Regeln beruhen auf mehreren Formeln für die gleichen Schritte:

• f = u + d  — das ist die Anzahl der Schritte des Baums der zukünftigen Kombinationen (der Abstand wird durch den Abstand zur nächsten Grenze des fraktalen Bereichs bestimmt)
• s = u - d  — die Anzahl der letzten Schritte, ausgedrückt durch die Anzahl der fallenden und steigenden Segmente

Wir haben festgelegt, dass wir eine Schleife durch "u" machen. Darüber hinaus werden wir den "s"-Wert als neues "U" verwenden, das an die nächste fraktale Ebene weitergegeben wird, wenn die Anzahl der verbleibenden Schritte dies zulässt. Zu diesem Zweck müssen wir eine Formel für "u" definieren, die kein "d" enthält. Dazu wird "d" aus der ersten Gleichung herausgenommen und in die zweite Gleichung eingesetzt:

• s = 2*u - f

Dieser Wert könnte auch als der neue Wert von "U" verwendet werden, um weiterzugehen, wenn der aktuelle Wert gleich Null wäre. Wir müssen also dieses "s" zu "U" addieren, um den Wert zu erhalten, der weitergegeben werden soll:

• NewU = s + U  - unser neues "U", das an die nächste fraktale Ebene weitergegeben werden soll

Wie bereits im vorigen Artikel definiert, nimmt dieser Ausdruck drei mögliche Werte an, die auf den drei möglichen Werten der Zahl "f" basieren. Ich habe ein Diagramm aus dem vorherigen Artikel überarbeitet, um die Idee zu veranschaulichen:

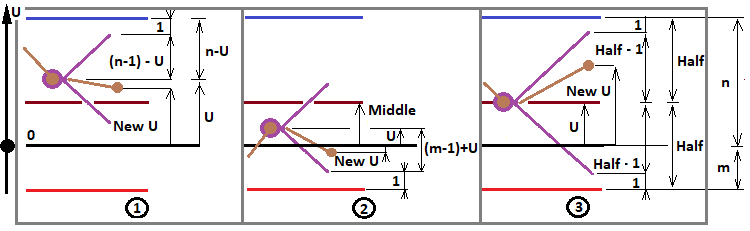
Dieses Diagramm ist hier sehr geeignet, da wir nun alle möglichen fraktalen Konfigurationen bestimmen, die uns bei der Lösung der meisten Probleme nützlich sein können. Nach diesem Diagramm definieren wir drei Fälle für "f":

1. f = ( n - 1 ) - U
2. f = ( m - 1 ) + U
3. f = Half - 1

Diese drei Fälle treten auf, wenn die folgenden Bedingungen erfüllt sind:

1. U > Middle
2. U < Middle
3. U = Middle

Nun müssen wir die letzten beiden Werte beschreiben, die an die nächste Fraktalebene weitergegeben werden, und besprechen, wie die Zahlen im Fraktal gesammelt werden. Die letzten beiden Werte werden wie folgt berechnet:

• NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i)  — unsere neue Kettenwahrscheinlichkeit "P", die an die nächste fraktale Ebene weitergegeben wird
• NewS = S + f = S + (floor(Mid) - 1) — unser neues "S", das an die nächste fraktale Ebene weitergegeben wird

Bevor wir mit dem Sammeln von Zahlen in einer gemeinsamen Variablen beginnen, sollten wir darauf achten, dass die Zahlen in einem ähnlichen Block gesammelt werden — aber in diesem Fall machen wir nur einen Schritt, so dass wir das Bernoulli-Schema nicht brauchen. Die Reihenfolge der Anweisungen ist nicht wichtig; sie sollten nur im selben Block stehen. Zahlen können nur in den Fällen "1" und "2" gesammelt werden, mit einigen Klarstellungen:

1. U = n - 1
2. U = - ( m - 1 )

Für den ersten Fall sind die drei vorherigen Werte einfacher zu berechnen, da wir nur einen Schritt haben:

• NewU = U - 1
• NewP = P * p
• NewS = S + 1

Für den zweiten Fall gibt es einen kleinen Unterschied:

• NewU = U + 1
• NewP = P * ( 1 - p )
• NewS = S + 1

Auf der Grundlage der Verallgemeinerung aller Fraktale wird jedes dieser Fraktale in 2 Typen unterteilt:

• Fraktal, das die Gesamtwahrscheinlichkeit des Überschreitens der oberen Grenze des Korridors berechnet.
• Fraktal zur Berechnung der Gesamtwahrscheinlichkeit für das Überschreiten der unteren Grenze des Korridors.

Jeder dieser Typen entspricht einem weiteren Fraktaltyp, der mit dem ursprünglichen Fraktal in Verbindung steht:

• Fraktal, das die durchschnittliche Anzahl von Schritten berechnet, um die obere Grenze zu überschreiten.
• Fraktal, das die durchschnittliche Anzahl der Schritte bis zum Überschreiten der unteren Grenze berechnet.

Diese vier Fraktaltypen unterscheiden sich durch die Form der summierten Zahlen. Wenn wir die Wahrscheinlichkeiten sammeln, können wir nur "P*p" und "P*(1-p)" addieren. Für die anderen beiden Fraktale benötigen wir zusätzliche Variablen, um die nächsten Fraktalebenen zu erreichen. In diesen Fraktalen verwenden wir gleich große Schritte, die in entgegengesetzter Richtung verlaufen, so dass ihre Wahrscheinlichkeiten entweder "p" oder "1-p" sind. Wenn "p" jedoch nicht gleich 0,5 ist, bedeutet dies, dass es sich um zwei verschiedene Ereignisse handelt, die unterschiedliche Eigenschaften haben können. Unter Merkmalen verstehe ich eine Reihe von Zufallsvariablen, die einem bestimmten Ereignis entsprechen. Einer dieser Werte ist die Positionsdauer. Es kann eine beliebige Anzahl solcher Werte geben, und wir können sie bei Bedarf als Zeit besprechen. Dieser Teil lässt sich mit ein paar einfachen Schritten vereinfachen. Die zu summierenden Zahlen haben die folgende Form:

1.  P * p * NewS
2.  P * ( 1 - p ) * NewS

Wie man sieht, werden die Wahrscheinlichkeiten mit der Anzahl der Schritte in dieser abgeschlossenen Kette von Schritten multipliziert. Diese Formel gilt jedoch nur, wenn die Aufwärts- und Abwärtsschritte gleich wahrscheinlich sind. In anderen Fällen müssen wir zwei verschiedene Strukturen verwenden, um die Aufwärts- und die Abwärtsschritte zu beschreiben, oder eine Struktur bereitstellen, um beide Zahlen zu speichern. Im zweiten Fall gibt die fraktale Funktion keine Zahl, sondern einen Datencontainer zurück. Der Container muss nicht erweitert werden. Außerdem habe ich einen Container bereitgestellt, in dem alle erforderlichen Parameter gespeichert werden können, so dass es nicht notwendig ist, mehrere Funktionen mit ähnlichem Code zu beschreiben. Stattdessen habe ich alle Funktionen in einer einzigen zusammengefasst, die alle erforderlichen Parameter beschreiben kann. Der Typ des Fraktals und die von ihm gelöste Aufgabe hängen direkt von den Eingabeparametern der Funktion ab. Um das Konzept zu erweitern, sollte das erste "S" und sein Äquivalent "NewS" durch die folgenden Werte ersetzt werden:

1. SU - die letzten Schritte der ausgewählten Wahrscheinlichkeitskette nach oben
2. SD - die letzten Schritte der ausgewählten Wahrscheinlichkeitskette nach unten
3. NewSU und NewSD - Werte, die an die nächste fraktale Ebene weitergegeben werden
4. SU + SD = S

Diese Werte sollten ähnlich wie die Definition von "S" definiert werden. Wenn "U > Middle":

• NewSU = SU
• NewSD = SD + 1

Wenn "U < Middle":

• NewSU = SU + 1
• NewSD = SD

Sechs weitere Werte werden für die endgültige Aufwertung des Fraktals benötigt:

1. UpperMidSDown - die durchschnittliche wahrscheinliche Gesamtzahl der Schritte nach unten, bevor der obere Rand erreicht wird
2. UpperMidSUp - die durchschnittliche wahrscheinliche Gesamtzahl der Schritte nach oben, bevor die obere Grenze erreicht wird
3. UpperSummProbability - die Wahrscheinlichkeit, die obere Grenze zu überschreiten
4. LowerMidSDown - die durchschnittliche Gesamtzahl der wahrscheinlichen Schritte nach unten, bevor die untere Grenze erreicht wird
5. LowerMidSUp - die durchschnittliche Gesamtzahl der wahrscheinlichen Schritte nach oben, bevor die untere Grenze erreicht wird
6. LowerSummProbability - die Wahrscheinlichkeit des Überschreitens der unteren Grenze

Die Werte "1", "2", "4", "5" geben die Summe der Produkte aus der entsprechenden Anzahl von Schritten und ihrer Wahrscheinlichkeit an. Diese Werte sind an sich bedeutungslos, aber sie sind Bestandteile von Formeln mit nützlichen Werten, auf die wir noch eingehen werden. Die Werte "3" und "6" sind die Wahrscheinlichkeiten der Hypothese, dass zwei Grenzen überschritten werden, die eine vollständige Gruppe bilden. Mit Hilfe dieser Werte können wir eine Fülle von anderen Dingen bestimmen.

Schreiben des Codes zur Implementierung eines universellen Fraktals

Um das Fraktal korrekt zu starten, benötigen wir eine Funktion, die alle vorbereitenden Operationen vor dem Start des Fraktals ausführt und danach das Fraktal auf der Grundlage vordefinierter Regeln korrekt startet. Ich habe eine Implementierung dieses Algorithmus im MQL5-Stil vorbereitet:

Container StartFractal(int m, int n, int s,double p)//preparing all variables and starting the fractal
   {
   int Minimum;
   if ( m <= n ) Minimum=m;
   else Minimum=n;
   double Middle;
   if ( n >= m ) Middle = (m+n)/2.0 - Minimum;
   else Middle = -((m+n)/2.0 - Minimum);   
   double Half = (m+n)/2.0;
   return Fractal(Half,Middle,m,n,s,p,0,0,0,1.0);
   }

Nach der Fraktalberechnung gibt die Funktion unseren Container mit allen erforderlichen Daten zurück:

struct Container//a container for collecting all the necessary data about the fractal
   {
   //values to be summed, for the upper bound
   double UpperMidSUp;//the sum of probabilities multiplied by the number of steps up of a specific chain (to cross the upper bound)
   double UpperMidSDown;//the sum of probabilities multiplied by the number of steps down of a specific chain (to cross the upper bound
   double UpperSummProbability;//the sum of the probabilities (to cross the upper border)
   //values to be summed, for the lower border
   double LowerMidSUp;//the sum of probabilities multiplied by the number of steps up of a specific chain (to cross the lower border)
   double LowerMidSDown;//the sum of probabilities multiplied by the number of steps down of a specific chain (to cross the lower border)
   double LowerSummProbability;//the sum of the probabilities (to cross the lower border)
   
   Container()//default constructor
      {
      UpperMidSUp=0.0;
      UpperMidSDown=0.0;
      UpperSummProbability=0.0;     
      LowerMidSUp=0.0;
      LowerMidSDown=0.0;
      LowerSummProbability=0.0;
      }
   
   //
   void Summ(Container &c0,const Container &c1) const//full sum for operator overloading
      {
      c0.UpperMidSUp=c0.UpperMidSUp+c1.UpperMidSUp;
      c0.UpperMidSDown=c0.UpperMidSDown+c1.UpperMidSDown;
      c0.UpperSummProbability=c0.UpperSummProbability+c1.UpperSummProbability;      
      c0.LowerMidSUp=c0.LowerMidSUp+c1.LowerMidSUp;
      c0.LowerMidSDown=c0.LowerMidSDown+c1.LowerMidSDown;
      c0.LowerSummProbability=c0.LowerSummProbability+c1.LowerSummProbability;
      }            
   void operator+=(Container &c) { Summ(this,c); }//operator += overload
   };

Dieser Container enthält eine Überladung des "+="-Operators, um zwei identische Strukturen zu kombinieren. Dieser Teil wird für die Hauptfunktion verwendet. Hier ist die fraktale Funktion:

Container Fractal(double Half, double Middle, int m, int n, int s,double p,int SU,int SD, int U, double P)//Fractal
   {
   Container C;
   ///to pass to the next fractal level
   int NewU;
   int NewSU;
   int NewSD;
   double NewP;
   ///
   
   if ( U > Middle && SU + SD < s )//case 1
      {
      if ( (n-1) - U > 0 )
         {
         for ( int u=0 ; u <= (n-1) - U; u++ )
            {
            NewU = -(n-1) + 2*u + 2*U;
            NewP = P * (Factorial((n-1) - U)/(Factorial(u)*Factorial((n-1) - U - u))) * pow(p,u)*pow(1.0-p,(n-1) - U - u);
            NewSU = SU + u;
            NewSD = SD + ((n-1) - U - u);
            C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
            }         
         }
      if ( (n-1) - U == 0 )
         {
         NewU = U - 1;
         NewP = P * (1.0 - p);
         NewSU = SU;
         NewSD = SD + 1;
         Container ct;

         ct.UpperMidSDown=P*p*SD;
         ct.UpperMidSUp=P*p*(SU+1);
         ct.UpperSummProbability=P*p;
         
         C+=ct;
         C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
         }         
      }   
   
   if ( U < Middle && SU + SD < s )//case 2
      {
      if ( (m-1) + U > 0 )
         {
         for ( int u=0 ; u <= (m-1) + U; u++ )
            {
            NewU = -(m-1) + 2*u;
            NewP = P * (Factorial((m-1) + U)/(Factorial(u)*Factorial((m-1) + U - u))) * pow(p,u)*pow(1.0-p,(m-1) + U - u);
            NewSU = SU + u;
            NewSD = SD + ((m-1) + U - u);
            C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
            }         
         }
      if ( (m-1) + U == 0 )
         {
         NewU = U + 1;
         NewP = P * p;
         NewSU = SU + 1;
         NewSD = SD;  
         Container ct;

         ct.LowerMidSDown=P*(1.0 - p)*(SD+1);
         ct.LowerMidSUp=P*(1.0 - p)*SU;
         ct.LowerSummProbability=P*(1.0 - p);
         
         C+=ct;
         C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
         }         
      }
  
   if ( U == Middle && SU + SD < s )//case 3
      {
      if ( int(MathFloor(Half))-1 > 0 )
         {
         for ( int u=0 ; u <= int(MathFloor(Half))-1; u++ )
            {
            NewU = -(int(MathFloor(Half))-1) + 2*u + U;
            NewP = P * (Factorial(int(MathFloor(Half))-1)/(Factorial(u)*Factorial(int(MathFloor(Half))-1 - u))) * pow(p,u)*pow(1.0-p,int(MathFloor(Half))-1 - u);
            NewSU = SU + u;
            NewSD = SD + (int(MathFloor(Half))-1 - u);
            C+=Fractal(Half,Middle,m,n,s,p,NewSU,NewSD,NewU,NewP);
            }         
         }
      }
   
   return C;
   }

Der Code wurde in MetaTrader 5 getestet - er funktioniert ziemlich gut. Diese Logik kann bei Bedarf weiter ausgebaut werden, wobei es noch eine Menge fortgeschrittener Möglichkeiten gibt. Ich habe mich jedoch entschieden, die Liste der Funktions-Eingabeparameter vorerst kurz zu halten, da die implementierte Funktionalität für unsere Zwecke völlig ausreichend ist. Wenn Sie den Code sorgfältig studieren, werden Sie sehen, dass er den oben skizzierten mathematischen Prinzipien voll entspricht. Obwohl er kurz ist, kann dieses Stück Code Wunder bewirken. Ich bin der Meinung, dass der Code so viel Logik und Mathematik wie möglich enthalten sollte. Das ist es, was wir letztendlich brauchen werden. Selbst ein schöner Code ist nutzlos, wenn er nicht für den vorgesehenen Zweck verwendet werden kann. In unserem Fall ist der Verwendungszweck die Anwendbarkeit für den Handel. Hier ist das Protokoll als Bestätigung:

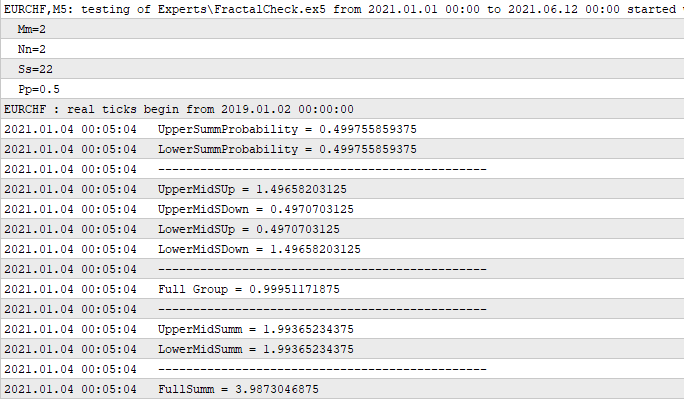
In diesem Fall habe ich einen einfachen Expert Advisor erstellt, der das gesamte Fraktal beim ersten erhaltenen Tick berechnet. Diese Berechnung wird einmal durchgeführt, sodass keine weiteren Neuberechnungen erforderlich sind. Die ersten sechs Zahlen sind Teil des Containers, während der Rest von ihnen abgeleitet wird. Ich zeige hier nur die wichtigsten Ableitungen, die zum Verständnis beitragen können, dass diese sechs Variablen es ermöglichen, alle anderen Variablen zu erhalten, die wir benötigen. Schauen Sie sich zum Beispiel die "Full Group" (Volle Gruppe) an. Sie wird so genannt, weil die Summe der Wahrscheinlichkeiten von zwei sich nicht überschneidenden Hypothesen einer der Grenzübergänge nach der vorherigen Berechnung gleich eins sein muss. Dies wird durch unseren Code bestätigt. Es folgen zwei identische Zahlen, die die Summen von "1", "2" und "3", "4" sind. Die letzte Zahl ist die Summe der vorletzten Zahlen - dies ist die durchschnittliche Anzahl der Schritte, die die Kette durchläuft. Der Grund, warum ich diese Eingabeparameter der Mengenfunktion gesetzt habe, wobei "m" und "n" gleich und symmetrisch sind, wird später gezeigt.

Ableitung der ersten Formel auf der Grundlage eines symmetrischen Fraktals

Nach dem Log-Ergebnis tendiert die durchschnittliche Anzahl der Schritte, die die Kette durchläuft, zu "4". Der Korridor verdoppelt sich im Verhältnis zu einem Einheitsschritt. Ein Einheitsschritt liegt vor, wenn "n" und "m" auf eins gesetzt werden. Mit anderen Worten, wenn wir die durchschnittliche Anzahl der Schritte in einem Korridor berechnen wollen, der aus kleineren Korridoren besteht (in diesem Fall passt eine ganzzahlige Anzahl kleinerer Korridore in einen größeren und der neue Korridor ist ebenfalls symmetrisch), dann können wir annehmen, dass:

• P[n] = P[n-1] * 2  - ist der rekursive Ausdruck für die neue Korridorbreite in Schritten, ausgehend von der Breite des vorherigen, kleineren Korridors, aus dem der neue Korridor zusammengesetzt ist.
• S[n] = S[n-1] * 4 - ist der rekursive Ausdruck für die Berechnung der durchschnittlichen Anzahl der Schritte des neuen Korridors, ausgedrückt durch den Durchschnittswert eines kleineren Korridors.

Wenn wir annehmen, dass "P[0]=1" und "S[0]=1", und wenn wir die Rekursionsnummerierung beim Index "0" beginnen, dann kann diese Rekursion als zwei sehr ähnliche Reihen dargestellt werden:

• P[n] = 2^n , n = 0 ... + Unendlich
• S[n] = 4^n = (2^2)^n = (2^n)^2 = P[n]^2

Wenn man sich die erste Reihe genau ansieht und die zweite Reihe korrekt umformt, stellt sich heraus, dass die zweite Reihe durch die Elemente der ersten Reihe ausgedrückt werden kann. Mit anderen Worten, wir erhalten die folgende Abhängigkeit: S = S(P) = P^2. Diese Abhängigkeit gilt jedoch nur für die rekursive Verdoppelung der Kanalbreite. Als ich diese Formel sah, beschloss ich, ihre Anwendbarkeit für jede beliebige große Zahl "n" und "m" zu überprüfen. Logischerweise setzen wir im zweiten Schritt "n=3", "m=3" und berechnen die gleichen Variablen. Mit diesen Eingabeparametern tendiert die durchschnittliche Anzahl der Schritte gegen die Zahl "9". Sie können diesen Teil selbst überprüfen, indem Sie den obigen Code oder die unten beigefügten MathCad 15 Programme verwenden. Die gleiche Reihe kann für diese Parameter erstellt werden:

• P[n] = 3^n , n = 0 ... + Unendlich
• S[n] = 9^n = (3^2)^n = (3^n)^2 = P[n]^2

Wie Sie sehen können, ergibt sich die gleiche Beziehung "S=S(P)=P^2". Wir könnten das Gleiche für alle anderen möglichen Szenarien im Zusammenhang mit der Intervallaufteilung wiederholen, aber das ist nicht notwendig. Diese Tatsache bedeutet, dass wir, wenn wir, sagen wir, die durchschnittliche Lebensdauer eines Preises in einem symmetrischen Kanal kennen, die durchschnittliche Lebensdauer eines Preises in einem beliebigen anderen Kanal berechnen können. Sie kann wie folgt berechnet werden:

• S = S0 * K^2 - die durchschnittliche Anzahl der Schritte in einem neuen Korridor
• T = S * T0 - die durchschnittliche Lebensdauer des neuen Korridors
• T = T0 * K^2- die durchschnittliche Lebensdauer des neuen Korridors, ausgedrückt als durchschnittliche Lebensdauer eines anderen Korridors (vorausgesetzt, dass S0 = 1)
• S0 - die durchschnittliche Anzahl der Schritte des alten Korridors
• T0 - die durchschnittliche Lebensdauer einer Stufe des alten Korridors
• P = K * P0  --> K = P/P0 - wie oft der neue Korridor größer ist als der alte
• P - die Breite des neuen Korridors
• P0 - die Breite des alten Korridors

Nun können wir die Hypothese mit MathCad 15 testen. Prüfen wir zunächst die Annahmen bezüglich der quadratischen Beziehung:

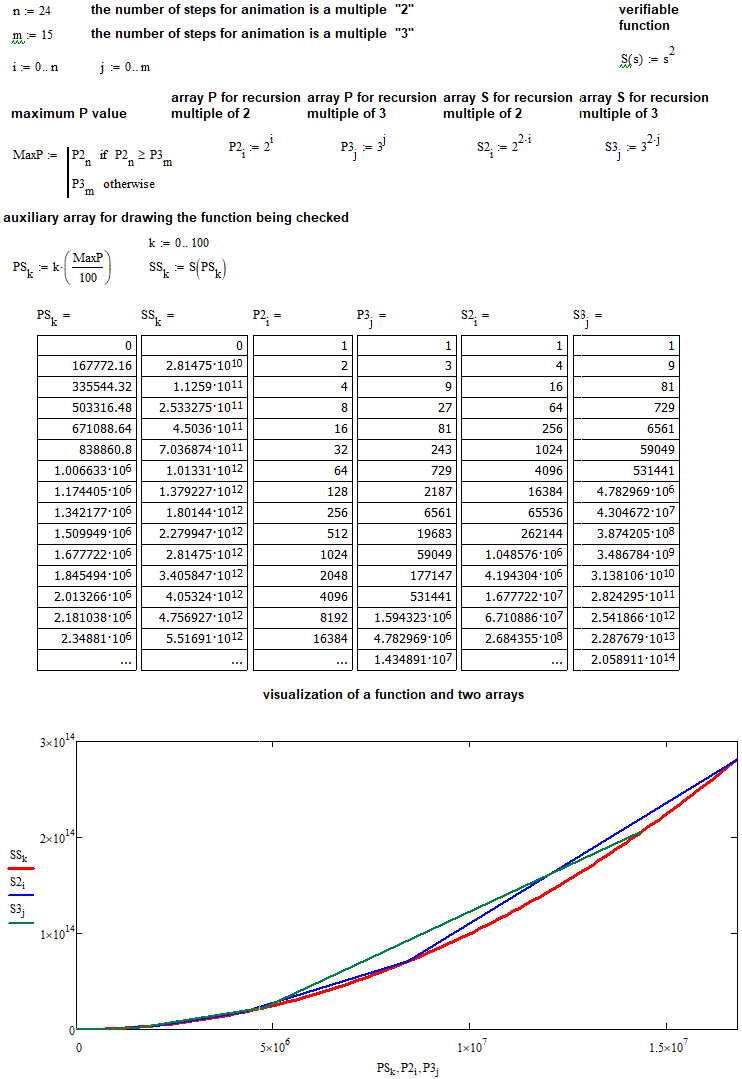
Jetzt sollte es ganz klar sein.

Bewertung der Leistung der abgeleiteten Formel für alle positiven und reellen Argumente

Die Formel funktioniert für alle ganzen Zahlen "P". Aber kann sie auch für eine Fließkommazahl "K" verwendet werden? Wir müssen einen Trick anwenden, um eine Fließkommazahl "K" bereitzustellen. Angenommen, wir haben einen Preiskorridor mit einer bekannten durchschnittlichen Lebensdauer, und wir haben einen Korridor, der "N" Mal in unseren Korridor passt, aber wir kennen seine durchschnittliche Lebensdauer noch nicht. Wir werden ihn mit der gleichen Formel finden. Nach dieser Logik:

• T = T0 * N^2 ---> T0 = T / N^2
• T - ist die Lebensdauer unseres Korridors, für den wir die durchschnittliche Lebensdauer kennen
• T0 - ist die durchschnittliche Lebensdauer eines kleineren Korridors, aus dem unser Korridor besteht

Das bedeutet, dass wir die Lebensdauer eines kleineren Korridors ermitteln können, die wir für die Berechnung der Lebensdauer des dritten Korridors mit einem gebrochenen Steigerungsfaktor benötigen. Nachdem wir nun die Lebensdauer des kleinsten Korridors ermittelt haben, können wir seine Breite in Punkten bestimmen:

• d = P / N

Anschließend können wir berechnen, wie viele solcher Korridore in einen verbreiterten Korridor passen, indem wir das folgende Verhältnis verwenden:

• Smin = MathFloor( K * P / d ) = MathFloor( K * N )
• Lim( N --> +Unendlich ) [ K * N/MathFloor( K * N ) ] = 1

Wie Sie sehen können, verringert sich die Korridorbreite, ohne dass dies das Ergebnis beeinflusst. Die zweite Zeile zeigt ein sehr wichtiges Verhältnis, das uns helfen wird zu verstehen, was wir als Nächstes tun müssen. Sie zeigt, dass wir, wenn wir den Quellkorridor in so viele Segmente wie möglich unterteilen, den Bruchteil vernachlässigen können, der als Ergebnis der Funktion MathFloor verworfen wird. Dies zeigt sich daran, dass der Grenzwert gegen Eins tendiert. Wenn diese Ungenauigkeit verwirrend ist, können wir einen anderen Wert finden:

• Smax = MathFloor( K * P / d ) + 1 = MathFloor( K * N ) + 1 = Smin + 1

Es ist nun klar, dass der wahre Wert von "K * N" genau zwischen "Smin" und "Smax" liegt. Wenn "N" gegen unendlich geht, erhalten wir zwei sehr ähnliche Korridore und ihre durchschnittliche Lebensdauer wird tendenziell gleich sein, da sich ihre Größe nur um ein Segment unterscheidet. Die durchschnittliche Lebensdauer des erforderlichen Korridors lässt sich daher besser durch das arithmetische Mittel der durchschnittlichen Lebensdauer dieser Korridore bestimmen:

• T1 =( T0 * Smin^2 + T0 * Smax^2 ) / 2 =  T0 *( Smin^2 + Smax^2 ) / 2
• T1 - die durchschnittliche Lebensdauer des Korridors, die wir bestimmen müssen

Die folgende Abbildung veranschaulicht meine Ideen:

Nachdem wir nun einen alternativen Ausdruck für die Berechnung der Lebensdauer des Korridors gefunden haben, können wir dessen Ergebnis mit dem Wert der Funktion für die Ganzzahl "K" vergleichen, wobei wir stattdessen die Fließkommazahl "K" einsetzen. Wenn die resultierenden Werte der beiden Ausdrücke identisch sind, können wir daraus schließen, dass die gefundene Funktion für ganzzahlige "K"-Werte absolut für alle Ganz- und Fließkommazahlen im Bereich von "0 ... +Unendlich". Führen wir die erste Prüfung für "N = 1000" durch. Ich denke, dass diese Aufteilung ausreicht, um die Identität von zwei Zahlen zu erkennen, falls es eine gibt:

Wie Sie sehen können, sind die beiden Zahlen praktisch identisch. Logischerweise sollten sie bei größeren "N"-Werten noch identischer sein. Dies kann auch durch die folgende Annahme bewiesen werden:

• Lim( N --> +infinity ) [  (T0 *( Smin^2 + Smax^2 ) / 2) / ( T * K^2 )  ] = 1

Der Zähler dieses Grenzwertes ist unser Näherungsausdruck für die Berechnung der durchschnittlichen Lebensdauer des neuen Korridors, und der Nenner ist ein Ausdruck, der vermutlich genau denselben Wert beschreibt. Ich habe eine einfache Funktion erstellt, die die gleichen Berechnungen durchführt wie im vorherigen Screenshot. Diesmal wird sie jedoch auf den gesamten Bereich der Zahl "N" angewendet, beginnend mit "1". Schauen wir uns nun das Ergebnis der Programmausführung an:

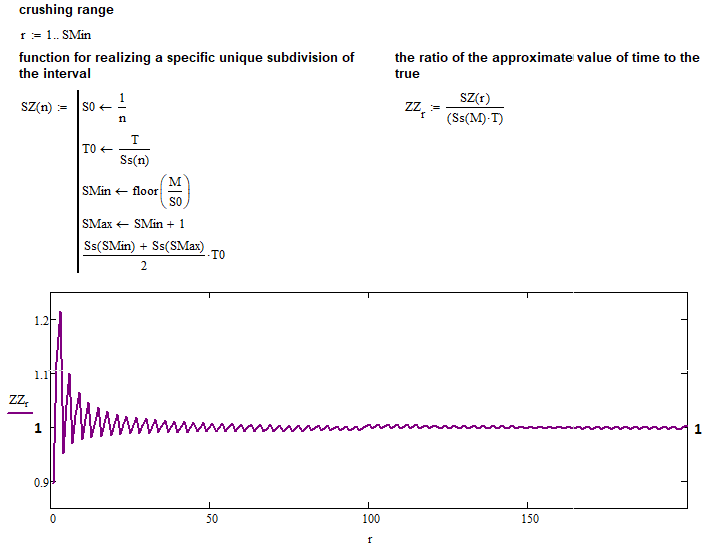
Alle Annahmen werden vollständig bestätigt: die Funktion, die wir für die ganze Zahl "K" gefunden haben, ist absolut für jedes positive "K" anwendbar. Jetzt haben wir eine einzige, sehr nützliche Funktion, die als Grundlage für weitere Aktionen verwendet werden kann, zum Beispiel als Grundlage für weitere Mathematik zur Beschreibung des gesamten universellen Fraktals.

Fortgeschrittenes Fraktal, entwickelt aus dem universellen Fraktal

Als nützliches und zusätzliches Beispiel für die weitere Anwendung eines universellen Fraktals können wir ein einseitiges Fraktal nehmen, mit, sagen wir, "n=1", "m ---> +unendlich", "s = m+1", "p=0,5". Bisher besprachen wir Fraktale mit gleichwahrscheinlichen Schritten in beide Richtungen, was nur für den Random Walk gilt. Aber dieses Fraktal bietet alle Möglichkeiten. Um zu einer tieferen Analyse einer solch komplexen Struktur zu gelangen, müssen zunächst die Grundlagen besprochen werden. Außerdem erhalten wir in diesem ersten Schritt nützliche Formeln und können grundlegende Schlussfolgerungen zu diesen fraktalen Prozessen ziehen. Ich habe das Fraktal mit verschiedenen "s"-Werten getestet und die folgenden Daten erhalten:

• s = 22 , FullSumm = 2.868 , UpperSummProbability = 0.831
• s = 32 , FullSumm = 3.618 , UpperSummProbability = 0.860
• s = 42 , FullSumm = 4.262 , UpperSummProbability = 0.877
• s = 45 , FullSumm = 4.499 , UpperSummProbability = 0.882

Eine weitere Erhöhung der Anzahl zulässiger Schritte führt zur Rechenzeitsingularität, d.h. die Rechenzeit steigt so stark an, dass sie Stunden oder sogar Tage benötigen würde. Betrachtet man jedoch die Geschwindigkeit, mit der die durchschnittliche Wahrscheinlichkeitssumme ansteigt, so wird deutlich, dass es nicht möglich ist, die Konvergenz dieser Reihe anhand dieser Art von Fraktal zu bewerten. Auf der Grundlage der zuvor abgeleiteten Formel können wir die Konvergenz jedoch mit einem anderen, aber sehr nützlichen Fraktaltyp bewerten. Dieses Fraktal kann auch bei der Berechnung der Zeit für eine sehr beliebte und gewinnbringende Strategie namens "Carry Trade" helfen. Zunächst zeige ich eine Abbildung, und dann erkläre ich sie:

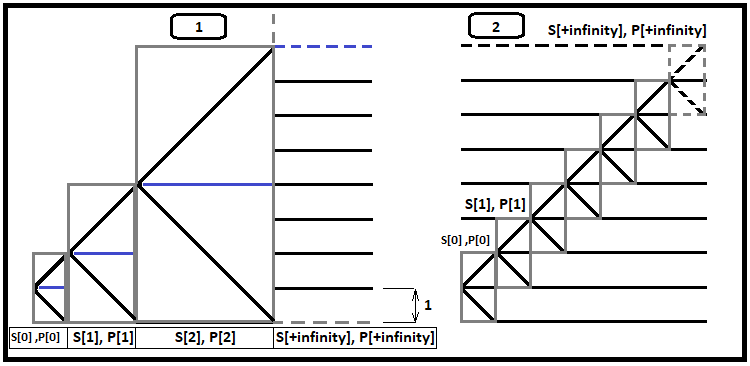
Stellen Sie sich vor, dass der Preisbildungsprozess einen Schritt von der Grenze entfernt beginnt, unabhängig davon, wo die Grenze liegt, nach oben oder nach unten. Die obige Abbildung zeigt ein Beispiel mit einem unteren Rand, da dies leichter zu erkennen ist. Schauen Sie sich das erste Fraktal genauer an. Jedes graue Kästchen enthält zwei Szenarien für weitere Ereignisse:

1. Der Kurs erreicht den oberen Rand des Rechtecks
2. Der Kurs erreicht den unteren Rand des Rechtecks

Wenn der Kurs den oberen Rand des Korridors erreicht, beginnt an dieser Stelle automatisch ein neues, größeres Fraktal, und so weiter. Wenn wir diesen Prozess genauso besprechen wie beim universellen Fraktal, werden wir wieder die Wahrscheinlichkeitsketten sehen. Aber jetzt sagt unsere Formel die Anzahl der Schritte, die in einem symmetrischen Korridor gemacht werden, basierend darauf, wie viele Schritte in den Korridor passen (jetzt sehen wir, dass ein Schritt ein kleinerer Korridor ist, der in den ursprünglichen Korridor passt).

Um die durchschnittliche Anzahl der Schritte zu berechnen, müssen Sie nicht das gesamte Fraktal besprechen. Wenden Sie stattdessen die abgeleitete Formel auf jedes der Fraktale an. Der Schritt ist hier nicht derselbe Wert, sondern er wird gemacht, wenn wir die obere oder untere Grenze des nächsten verschachtelten Fraktals erreichen. Auf dieser Grundlage können wir Wahrscheinlichkeitsketten erstellen, die sehr einfach sein werden. Die Wahrscheinlichkeit, die Grenze beim allerersten Fraktal P[0] zu erreichen, ist gleich 0,5. Das bedeutet, dass es einen zweiten möglichen Fall gibt, in dem wir das nächste Fraktal erstellen müssen, in der Hoffnung, dass der Preis die Grenze erreicht. Alle diese Ereignisse sind ineinander verschachtelt, und alle diese Ketten bilden eine vollständige Gruppe.

Die Wahrscheinlichkeit, die Grenze beim zweiten Fraktal P[1] zu erreichen, ist gleich der vorherigen Wahrscheinlichkeit multipliziert mit 0,5. Dieser Prozess kann unbegrenzt fortgesetzt werden. Die durchschnittliche Anzahl der Schritte kann mit Hilfe der abgeleiteten Formel und der Kettenwahrscheinlichkeiten bestimmt werden. Dazu wird zunächst eine Formel für die Wahrscheinlichkeit jeder einzelnen Kette definiert, wobei berücksichtigt wird, dass die durchschnittliche Anzahl der Schritte zum Überschreiten der oberen und der unteren Grenze gleich ist. Es stellt sich heraus, dass:

• PUp = PDown = P - das Verhältnis, das zeigt, dass die Wahrscheinlichkeiten, die obere und untere Grenze eines Fraktals zu berühren, für alle Grenzen aller verschachtelten Fraktale gleich wahrscheinlich sind
• P[j] = 0,5^(j+1) , j = 0 ... + Unendlich- die Wahrscheinlichkeit, dass die Kette j eintreten wird
• S[i] = S[i-1] + P[i] * ( S[i-1]/P[i-1] + F(D[i]) ), i = 1 ... + Unendlich - eine wiederkehrende Formel zur Berechnung der gesamten durchschnittlich wahrscheinlichen Anzahl von Schritten für alle fraktalen Ebenen (während S[0] = 1*0,5 = 0,5)
• F(K) = K^2 - unsere abgeleitete Formel zur Berechnung der durchschnittlichen Anzahl der Schritte
• D(i) = 2^i - wie viele Schritte passen in die nächste fraktale Ebene
• S[i-1]/P[i-1] - die durchschnittliche Anzahl der Schritte im verbleibenden nicht berücksichtigten Zweig, sofern der aktuelle Zweig stattgefunden hat (da zusätzlich zum aktuellen verschachtelten Fraktal alle Schritte berücksichtigt werden müssen, die vorher stattgefunden haben)
  

Das zweite Fraktal ist eigentlich identisch mit dem ersten, d.h. die Wahrscheinlichkeiten ihrer Ketten (das P[]-Array) sind identisch. Brauchen wir das? Nehmen wir an, wir haben die Strategie "Carry Trade". Wir haben zwei Konten, ein Swap-Konto und ein Swap-freies Konto, um Positionen mit einem positiven Swap abzuschließen. Außerdem benötigen wir eine Formel zur Berechnung der durchschnittlichen profitablen Haltedauer einer Position. Diese durchschnittliche Haltedauer ergibt sich direkt aus der Formel für die durchschnittliche Anzahl von Schritten. Ich werde dieses Thema in diesem Artikel nicht im Detail behandeln. Ich möchte nur die Bedeutung der Mathematik aufzeigen. Dieses Thema wird später im Detail besprochen. Definieren wir nun eine Formel für die durchschnittlichen Wahrscheinlichkeitsschritte für das zweite Fraktal:

• S[j] = S[j-1] + P[j] * ( S[i-1]/P[i-1] + F(1) ) - eine wiederkehrende Formel zur Berechnung der gesamten durchschnittlich wahrscheinlichen Anzahl von Schritten für alle fraktalen Stufen (während S[0] = 1*0. 5 = 0.5)

In diesem Fall ist diese Formel nur ein Spezialfall der wertvollen Formel, denn im zweiten Fraktal ist K=1, immer, für alle fraktalen Ebenen. Wir wollen nun herausfinden, wo die Grenzen der Summen dieser Größen für beide Fraktale liegen:

Die erste Reihe divergiert, was bedeutet, dass, wenn es keine Obergrenze gibt und der Handel endlos ist, die durchschnittliche Zeit sich Unendlich nähert. Im zweiten Fall erhalten wir eine klare Grenze bei 2. Das bedeutet, dass wir, wenn wir eine Position mit einem positiven Swap eröffnen, diese Position im Durchschnitt nach zwei Schritten schließen müssen (die durchschnittliche Positionshaltezeit ist also gleich 2*T, wobei T die durchschnittliche Positionshaltezeit ist, vorausgesetzt, wir schließen die Position, wenn sie eine der Grenzen erreicht). Im zweiten und einfachsten Fall schließen wir einfach beide Positionen auf beiden Konten, auch wenn das Swap-Konto eine positive Zahl anzeigt. Die erste Option ist natürlich viel attraktiver, aber ihre Umsetzung würde eine schnelle und reibungslose Abhebung und Einzahlung auf beiden Konten erfordern. Wenn diese Option nicht möglich ist, müssen wir auf eine klassische Option zurückgreifen, die zwar weniger Gewinn abwirft, dafür aber eine größere Stabilität aufweist.

Zusammenfassen der Ergebnisse

Im zweiten Teil der Artikelserie haben wir sehr interessante Ergebnisse erzielt, auch für die praktische Anwendung im Handel. Und was noch wichtiger ist: Es ist jetzt klar, dass die Anwendungsmöglichkeiten von Fraktalen riesig sind. Was wir in diesem Artikel getan haben:

• die Definition klarer mathematischer Regeln für den Aufbau eines universellen Fraktals,
• einen funktionierenden Code im MQL5-Stil auf der Grundlage der genannten mathematischen Prinzipien erstellt,
• erfolgreich die Prinzipien mit zwei Plattformen, MetaTrader 5 und MathCad 15 überprüft,
• mit Hilfe der Algorithmen die erste Formel zur Berechnung der Lebensdauer eines beliebigen Korridors erstellt,
• die Formel durch Programmierung für alle möglichen Fälle getestet und validiert,
• den neuen Typ eines schnelleren Fraktals, basierend auf der erhaltenen Formel ermittelt,
• mit dem Ergebnis können wir die Berechnungen beschleunigen und bestimmen, was nicht durch ein universelles Fraktal bestimmt werden konnte,
• einen Spezialfall der Verwendung eines fortgeschrittenen Fraktals für Swap-Probleme tuschiert,
• Werkzeuge für die weitere Entwicklung der Theorie entwickelt.

Außerdem möchte ich anmerken, dass sich mein Werkzeugkasten stark erweitert hat. Jetzt können wir Fraktale mit unterschiedlichen Wahrscheinlichkeitsstufen analysieren (Trendsituationen und Situationen im Zusammenhang mit der Analyse von Handelsstatistiken). Bitte beachten Sie noch einmal, dass wir in diesem Artikel nur Fälle besprochen haben, in denen "p = 1 - p = q = 0,5". Das bedeutet, dass alle Berechnungen nur auf Situationen anwendbar sind, die einen Random Walk beschreiben. Es gibt also viel mehr potenzielle Möglichkeiten.

Im Folgenden finden Sie die Formel, die nach dem Studium des Fraktals ermittelt wurde. Ich werde sie noch einmal kurz erläutern:

1. S = K^2 - die durchschnittliche Anzahl der Schritte des neuen Korridors, basierend auf der Tatsache, dass ein Schritt gleich einem anderen Korridor ist,
2. T = S * T0 = T0 * K^2 - durchschnittliche Lebensdauer eines unbekannten Korridors,
3. T0 - durchschnittliche Lebensdauer eines bekannten Korridors,
4. P = K * P0 --> K = P/P0 - wievielmal der bekannte Korridor größer ist als der unbekannte,
5. P - die Breite des Korridors mit einer unbekannten Lebensdauer,
6. P0 - die Breite des bekannten Korridors,

Indem wir 4 durch 1 ersetzen, können wir die durchschnittliche Anzahl der Schritte, die sich in dem unbekannten Korridor befinden, durch die bekannten Werte ausdrücken, und indem wir 1 durch 2 ersetzen, erhalten wir die durchschnittliche Lebensdauer dieses Korridors, die auf der Grundlage der bekannten Werte berechnet wird:

• T0, P0, P

Ich werde auch eine Antwort auf eine Frage hinzufügen, die Leser zu Beginn dieses Artikels gestellt haben könnten:

• Warum brauchen wir Formeln, wenn wir Handelsstatistiken vom MetaTrader 5 Strategietester sammeln können?

Antwort:

• Nun, es ist nicht immer möglich, Statistiken zu sammeln, da nicht alle Finanzsymbole über eine ausreichende Handelshistorie verfügen, die für solche Bewertungen erforderlich ist. Bei großen Korridoren ist dies nicht möglich, da man einen Korridor auswählen könnte, der seine Grenzen nie überschritten hat. Durch die Verwendung von Korridoren mit geringerer Breite und der Formel können wir die Daten erhalten, die nicht aus Statistiken gewonnen werden können. Außerdem bietet diese Art von Mathematik eine unübertroffene Genauigkeit und Flexibilität. Es gibt noch viele andere Vorteile.

Schlussfolgerung

In diesem Artikel habe ich versucht, die Berechnungslogik zu beschreiben, die für die weitere Erforschung von Preisbildungsprozessen genutzt werden kann. Bislang gibt es noch nicht viel für die praktische Anwendung. Aber ich bin sicher, dass wir alle Varianten des universellen Fraktals untersuchen können und mögliche Formeln zur Beschreibung asymmetrischer und einseitiger Preiskorridore erhalten. Im nächsten Artikel werde ich die Erforschung des universellen Fraktals fortsetzen und versuchen, alle Ergebnisse in Form einfacher Formeln darzustellen. Außerdem werde ich eine neue, sehr interessante Mathematik einbeziehen, die es ermöglicht, die erhaltenen Formeln nicht nur für Preisbildungsprozesse, sondern auch für die Beschreibung von Backtests und Handelssignalen zu verwenden. Dies wird es uns ermöglichen, jede Strategie in Bezug auf Zeit und Wahrscheinlichkeiten absolut genau zu analysieren, was letztlich der wichtigste Aspekt des Handels ist.

Referenzen

• Kombinatorik und Wahrscheinlichkeitsrechnung für den Handel (Teil I): Die Grundlagen