Kombinatorik und Wahrscheinlichkeitsrechnung für den Handel (Teil III): Das erste mathematische Modell

MetaTrader 5 — Handel | 11 Oktober 2021, 09:27

532

Evgeniy Ilin

Inhalt

Einführung

Im vorigen Artikel habe ich die erste Formel für Fraktale gefunden. Dies ermöglichte die Annahme, dass alle wichtigen fraktalbezogenen Werte durch ein mathematisches Modell beschrieben werden können. Die Simulation ist nicht dazu gedacht, solche Werte zu beschreiben, sondern diente nur dazu, die ersten Daten zu sammeln, um eine tiefere Analyse solcher Strukturen zu ermöglichen. In diesem Artikel habe ich mich entschlossen, ein besonderes Augenmerk auf die Beschreibung des gesamten Prozesses der Entwicklung des ersten mathematischen Modells zu legen, bis hin zum Erhalt des mathematischen Modells, das in verschiedenen Expert Advisors angewendet werden kann.

Neue Ideen

Bei der Betrachtung eines symmetrischen Fraktals im vorangegangenen Artikel haben wir eine allgemeine Formel für die Berechnung der durchschnittlichen Anzahl von Schritten erhalten, die der Kurs infolge einer Bewegung innerhalb eines bestimmten Korridors macht, der durch die Anzahl der gleichen symmetrischen, kleineren Korridore bestimmt wird. Diese Formel lautet wie folgt:

S = K^2 - die durchschnittliche Anzahl der Schritte des neuen Korridors, basierend auf der Tatsache, dass ein Schritt ein weiterer Korridor ist
P = K * P0 --> K = P/P0 - wievielmal der bekannte Korridor größer ist als der unbekannte
P - die Breite des Korridors, dessen durchschnittliche Anzahl von Schritten nicht bekannt ist (die Schritte sind halb so groß wie die des ursprünglichen Korridors)
P0 - die Breite des bekannten Korridors,

Um einen asymmetrischen Korridor beschreiben zu können, müssen wir einige der zuvor genannten Begriffe neu definieren, um sie verständlicher zu machen. Der wichtigste von ihnen ist K. Dieser Wert gibt die Anzahl der Schritte an, die der Preis in dem neuen Korridor machen sollte, vorausgesetzt, dass die Schritte nur nach oben oder nur nach unten gemacht werden. Bei einem symmetrischen Korridor ist die Anzahl der Schritte gleich, unabhängig davon, welche Grenze wir betrachten (überschreiten), die obere oder die untere. Dies liegt daran, dass das Problem sowohl für die obere als auch für die untere Grenze spiegelbildlich ist. Was die Asymmetrie anbelangt, so haben wir als Ergebnis der Code-Experimente im vorherigen Artikel herausgefunden, dass die durchschnittliche Anzahl der Schritte für diesen Fall wie folgt bestimmt wird:

S = n * m - durchschnittliche Anzahl der Schritte für die asymmetrischen Hälften des Korridors
n - die Anzahl der Schritte, die in die obere Hälfte des Korridors passen
m - die Anzahl der Schritte, die in die untere Hälfte des Korridors passen

Für den symmetrischen Korridor gilt also "m = n". Ausgehend von dem oben Gesagten bedeutet dies:

S = n * n = m * m = m * n = n^2 = m^2 = K^2
K = n = m

Das bedeutet, dass die erste abgeleitete Formel nur ein Spezialfall der vorherigen ist und K somit nicht mehr benötigt wird.

Eine interessante Eigenschaft dieser Funktion ist, dass S(a*k, b*k) = S(a,b) * S(k,k) ist, was sehr einfach zu beweisen ist:

S(n*k ,m*b) = m*k*n*b = n*m * k*b
S(n ,m) * S(k ,b) = n*m * k*b

Diese Eigenschaft ist sehr interessant. Mit zusätzlichen Überlegungen kann sie die Ableitung aller notwendigen Formeln zur Beschreibung des gesamten Fraktals liefern. Diese Eigenschaft spiegelt eine sehr wichtige Eigenschaft eines jeden Fraktals wider: die Fähigkeit zur Verschachtelung. Mit anderen Worten: Jedes endliche Fraktal von großer Komplexität kann als zwei oder mehr einfachere Fraktale dargestellt werden, die als Stufen ineinander dienen. Diese Eigenschaft wird genutzt, um die Formel für komplexere Fälle zu verallgemeinern.

Bevor wir mit den Fraktalen fortfahren, möchte ich Sie daran erinnern, dass die oben definierten Formeln nur funktionieren, wenn p=0,5 ist. Sobald der Markt oder die fraktalen Parameter von einem Random Walk abzuweichen beginnen, ändert sich diese Formel auf sehr interessante Weise, nämlich:

Ss[n,m,p] - eine allgemeinere Formel für die durchschnittliche Anzahl der Schritte (in jeder Richtung)
S(n ,m) = Ss[n,m,0,5] - Formel für einen Random Walk ist ein Spezialfall der allgemeinen Formel

Allgemeine Formel für die durchschnittliche Anzahl von Schritten

Um die Form einer allgemeineren Formel zu bestimmen, habe ich die Invarianz des fraktalen Verschachtelungsprinzips genutzt. Wenn wir jede einzelne fraktale Verschachtelungsebene relativ zur vorhergehenden betrachten, müssen wir nicht darüber nachdenken, welche Schritte in einem bestimmten Schritt vorkommen. So treten die primären Auf- und Abwärtsschritte mit genau denselben Häufigkeitsverhältnissen auf, die der Situation der vorherigen Stufe entsprachen. Mit anderen Worten: Das Überschreiten einer Grenze der entsprechenden Verschachtelungsebene ist entweder ein Schritt nach oben oder ein Schritt nach unten für die nächste Verschachtelungsebene. Es ist aber auch bekannt, dass das Verhältnis der Häufigkeit des Auftretens von Stufen für die aktuelle Verschachtelungsebene nicht von der Konfiguration der aktuellen Ebene abhängt. Das bedeutet, dass das fraktale Verschachtelungsprinzip für jede Wahrscheinlichkeit "p" gilt. Das heißt, wenn sich der "p"-Wert ändert, sollte sich auch die Formel ändern, aber sie sollte irgendwie ihre Verschachtelungseigenschaft beibehalten. Eine einfache Erfahrung kann uns dabei helfen, die allgemeine Formel zu bestimmen. Wir wissen, dass die Wahrscheinlichkeit p einen Random-Walk-Punkt und zwei Extrempunkte mit Null und Eins hat. Schauen wir uns an, welche Werte die Funktion an diesen drei Punkten annehmen wird. So erhalten wir das Folgende:

Ss[n,m,1] = Sn[n] = n
Ss[n,m,0] = Sm[m] = m
Ss[n,m,0.5] = Sn[n] * Sm[m] = m*n
Sn[n,p] - die Anzahl der Schritte in einer Richtung bis zur oberen Grenze
Sn[m,p] - die Anzahl der Schritte in eine Richtung bis zur unteren Grenze

Im ersten Fall gibt es keine Schritte nach unten — alle Ketten folgen demselben Weg. Im zweiten Fall ist das Gegenteil der Fall, und alle Schritte sind abwärts gerichtet, ohne Schritte nach oben. Bei extremen Werten verschwindet einer der Faktoren vollständig aus der Formel. Dies ist möglich, wenn man ihn auf Null erhöht. Jede Zahl hoch Null ist gleich 1. Darüber hinaus hat der Grad eine Invarianz der folgenden Form:

A^X * B^X = (A*B)^X

Ersetzt man die Zahlen durch Durchschnittsschritte, so bleibt das Prinzip der fraktalen Verschachtelung erhalten. Außerdem zeigt dies, dass die Potenz nicht von n und m abhängt. Die sich daraus ergebende allgemeine Formel für die durchschnittliche Anzahl der Schritte lautet wie folgt:

Ss[m,n,p] = ( Sn[n] ^ Pn[p] ) * ( S[m] ^ Pm[p] ) = (n ^ Pn[p] ) * ( m ^ Pm[p] )

Das Prinzip der fraktalen Verschachtelung lässt sich schematisch wie folgt darstellen:

Ketten

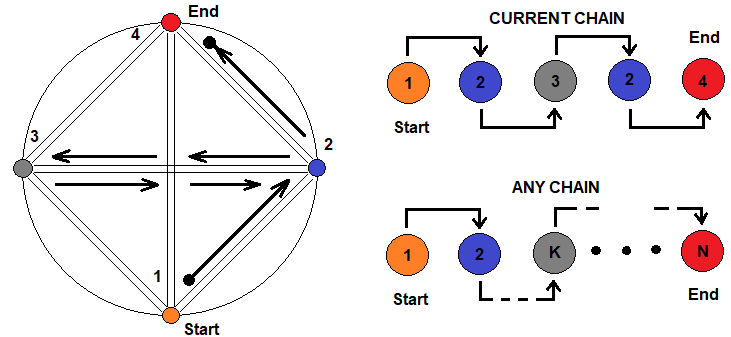
Die Abbildung zeigt vier Zustände, die verschiedene Fraktale symbolisieren, die durch einander ausgedrückt werden können. Der Übergang von einem Zustand zum anderen ist durch eine beliebige Kette möglich. Rechts ist eine willkürlich gewählte Kette dargestellt. Etwas weiter unten wird gezeigt, dass diese Kette beliebig lang und komplex sein kann, und dass man denselben Zustand beliebig oft durchlaufen kann. Das bedeutet, dass die Formel für die durchschnittliche Anzahl von Schritten in einem Fraktal als eine Kette von Produkten dargestellt werden kann, die fraktale Verschachtelungsebenen darstellen.

Aufbau eines Prototyps einer Potenzfunktion

Weitere Ideen ergeben sich aus der fraktalen Verschachtelungseigenschaft und aus der Invarianz von Potenzfunktionen gleicher Potenz in Bezug auf die Basis. Aus all diesen mathematischen Prinzipien lassen sich weitere Formeln zur tieferen Beschreibung der Fraktale ableiten. So erhalten wir zusätzlich zwei Funktionen, deren Form wir nicht kennen:

Pn[p] - Potenz für den oberen Grenzmultiplikator
Pm[p] - Potenz für den unteren Grenzmultiplikator

Wir wissen Folgendes:

Pn[0.5] = 1 , Pn[1] = 1 , Pn[0] = 0
Pm[0.5] = 1 , Pm[1] = 1 , Pm[0] = 0

Durch die Analyse von Potenzfunktionen ist es möglich, einen geeigneten Funktionsprototyp zu erstellen. Ich habe den folgenden Prototyp ausgewählt:

Pn[p] = 1 , if p >= 0.5
Pn[p] = ( (1 – p)/0.5 ) ^ K
Pm[p] = 1 , if p <= 0.5
Pm[p] = ( p/0.5 ) ^ K
K ist die Potenz, die die Flachheit der Funktion regelt

Es wäre genauer, "2" und "4" in Form von Polynomen darzustellen, die den glatten Übergang einer bestimmten Potenz genau beschreiben können, aber ich denke, dass dies hier überflüssig ist. Wenn Sie genauere Polynome definieren möchten, finden Sie hier die Prototypen:

Pn[p] = C1 * ( (1 – p)/0.5 ) ^ K1 + C2 * ( (1 – p)/0.5 ) ^ K2 … + … + CN * ( (1 – p)/0.5 ) *KN
Pm[p] = C1 * ( p/0.5 ) ^ K1 + C2 * ( p/0.5 ) ^ K2 … + … + CN * ( p/0.5 ) ^ KN
С1 + С2 + ... + ... СN = 1 sind die Gewichte für die jeweilige Potenz
KN ist die Potenz des entsprechenden Terms

Das Polynom, das ich gewählt habe, ist die einfachste Version des allgemeinen Polynoms mit nur einem Term. Alle erklärten Prinzipien können für jede gebrochene Zahl "n, m" überprüft werden.

Ich habe das folgende Programm erstellt, um die obigen Annahmen zu überprüfen:

Prüfen der Formel

Wie aus den Programmergebnissen ersichtlich ist, funktioniert alles wie es sollte. Um sicher zu gehen, vergleicht man einfach zwei Zahlen. Wenn sie gleich sind, sind das Schachtelungsprinzip und die Möglichkeit der Verwendung von Bruchzahlen n und m bestätigt.

Das allgemeine Schema zur Ermittlung der besten Funktion aus der prototypisch begrenzten Familie

Nun müssen wir festlegen, wie wir nach den benötigten Koeffizienten für den Prototyp suchen wollen. Ich habe mich für die einfachste Art der Suche entschieden - die Erzeugung von Zufallszahlen im gewünschten Bereich. Das Methodenschema sieht wie folgt aus:

Schema der Annäherung

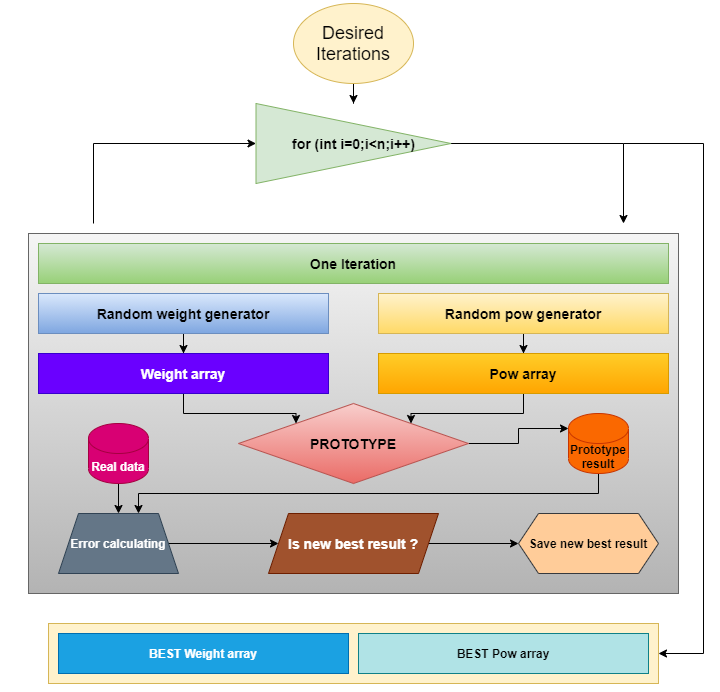
Es ist für jeden Funktionsprototyp geeignet, wenn wir Koeffizienten für die beste Übereinstimmung von realen Daten mit dem mathematischen Modell finden müssen. Das gleiche Schema wird auch weiterhin gelten, denn am Ende des Artikels werden wir die gleiche Methode anwenden, um einen anderen Prototyp zu bearbeiten.

Vertiefte Analyse

Lassen Sie uns nun die Struktur dieser Formel genauer analysieren. Das Ergebnis der Formel ist die durchschnittliche Anzahl der Schritte, die der Preis macht, bevor er eine der Grenzen überschreitet. Die Schritte nach oben und nach unten werden als gleich angesehen, aber diese Gleichheit ist nur im Falle eines Random Walk möglich. Um ein asymmetrisches Fraktal vollständig zu beschreiben, muss zusätzlich bestimmt werden, woraus der angegebene Wert eigentlich besteht. Logischerweise hängt die durchschnittliche Anzahl von Schritten jeder Art sowohl von der durchschnittlichen Anzahl von Schritten beim Überschreiten der oberen Grenze als auch von der durchschnittlichen Anzahl von Schritten beim Überschreiten der unteren Grenze ab. Ermitteln wir die entsprechenden Werte für den oberen Grenzübergang:

SP[U,ud] = S[U,u] * P[U] + S[U,d] * P[U] = (S[U,u] + S[U,d]) * P[U] = S[U] * P[U]
S[U] - die durchschnittliche Anzahl beliebiger Schritte, sofern die Kette von Schritten zuerst die obere Grenze erreicht
S[U,u] - die durchschnittliche Anzahl der Schritte nach oben, sofern die Schrittkette zuerst die obere Grenze erreicht
S[U,d] - die durchschnittliche Anzahl der Schritte nach unten, sofern die Schrittkette zuerst die obere Grenze erreicht
P[U] - die Wahrscheinlichkeit, dass der Preis zuerst die obere Grenze überschreitet
SP[U,ud] - die durchschnittliche wahrscheinliche Anzahl von Schritten bis zum Überschreiten der oberen Grenze

Die Formeln für die untere Grenze sind ähnlich:

SP[D,ud] = S[D,u] * P[D] + S[D,d] * P[D] = (S[D,u] + S[D,d]) * P[D] = S[D] * P[D]
S[D] - die durchschnittliche Anzahl der Schritte, sofern die Kette von Schritten zuerst die untere Grenze erreicht
S[D,u] - die durchschnittliche Anzahl der Schritte nach oben, sofern die Schrittkette zuerst die untere Grenze erreicht
S[D,d] - die durchschnittliche Anzahl der Schritte nach unten, sofern die Schrittkette zuerst die untere Grenze erreicht
P[D] - die Wahrscheinlichkeit, dass der Preis zuerst die untere Grenze überschreitet
SP[D,ud] - die durchschnittliche wahrscheinliche Anzahl von Schritten bis zum Überschreiten der unteren Grenze

Es wird deutlich, dass:

S = SP[U,ud] + SP[D,ud]

Letztendlich hängen alle Werte, die wir schließlich erhalten und verwenden können, von fünf Grundwerten ab:

S[U,u] = SP[U,u]/P[U] - die durchschnittliche Anzahl der Schritte nach oben, vorausgesetzt, die Kette von Schritten erreicht zuerst die obere Grenze
S[U,d] = SP[U,d]/P[U] - die durchschnittliche Anzahl der Schritte nach unten, vorausgesetzt, die Schrittkette erreicht zuerst die obere Grenze
S[D,u] = SP[D,u]/P[D] - die durchschnittliche Anzahl der Stufen nach oben, sofern die Stufenkette zuerst den unteren Rand erreicht
S[D,d] = SP[D,d]/P[D] - die durchschnittliche Anzahl der Schritte nach unten, vorausgesetzt, die Schrittkette erreicht zuerst die untere Grenze
P[U] - die Wahrscheinlichkeit, dass der Preis zuerst die obere Grenze überschreitet

Wir werden die Formeln für diese Werte auf der Grundlage der Ergebnisse der fraktalen Operation mit verschiedenen Eingangsparametern suchen. Im vorigen Artikel habe ich die folgenden Werte für den fraktalen Ausgang gewählt:

SP[U,u] - die durchschnittliche Anzahl der Schritte nach oben, vorausgesetzt, dass die Schrittkette zuerst die obere Grenze erreicht
SP[U,d] - die durchschnittliche Anzahl der Schritte nach unten, vorausgesetzt, die Schrittkette erreicht zuerst den oberen Rand
SP[D,u] - die durchschnittliche Anzahl der Schritte nach oben, sofern die Schrittkette zuerst den unteren Rand erreicht
SP[D,d] - die durchschnittliche Anzahl der Schritte nach unten, sofern die Schrittkette zuerst die untere Grenze erreicht
P[U] - die Wahrscheinlichkeit, dass der Preis zuerst die obere Grenze überschreitet
P[D] - die Wahrscheinlichkeit, dass der Preis zuerst die untere Grenze überschreitet
S = SP - die durchschnittliche Anzahl beliebiger Schritte

Hier ist eine separate Gruppe von Elementen, die in Form von Grundwerten ausgedrückt werden können:

SP[U]
S[U,ud] = S[U,u] + S[U,d]
S[D,ud] = S[D,u] + S[D,d]
P[D] = 1 - P[U]
S = SP[U,ud] + SP[D,ud]

Im Rahmen meiner Beschäftigung mit der Mathematik der Fraktale habe ich umfangreiche Analysen durchgeführt, die in einem kompakten Diagramm kurz dargestellt werden können. Das Diagramm zeigt den daraus resultierenden Prozess der Suche nach einem mathematischen Modell:

Sequenz der Suche nach einem mathematischen Modell

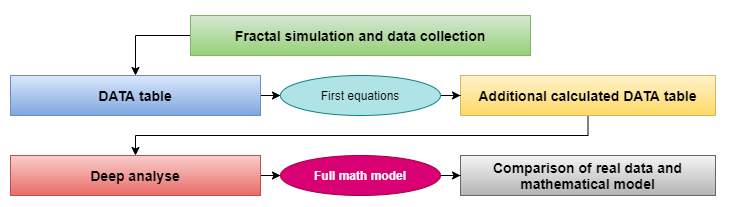
Datenerfassung und Schlussfolgerungen

Bei einer genaueren Betrachtung der Ergebnisse der Fraktalberechnungen stellte ich fest, dass die sechs Werte, die bei der Konstruktion des Konzepts eines universellen Fraktals zunächst ermittelt wurden, mathematisch zusammenhängen. Zunächst habe ich Tests für symmetrische Grenzen durchgeführt und versucht, Abhängigkeiten zwischen diesen Werten zu erkennen. Ich habe einige Ergebnisse erhalten. Ich habe die Berechnungen für zehn verschiedene Fälle durchgeführt, und es stellte sich heraus, dass dies ausreichend ist:

Test-Index	Schritte in der oberen Hälfte des Korridors (n)	Schritte in der unteren Hälfte des Korridors ( m )	Wahrscheinlichkeit des ersten Schrittes ( p )	Durchschnittliche wahrscheinliche Anzahl von Aufwärtsschritten für die obere Grenze ( SP[U,u] )	Durchschnittliche wahrscheinliche Anzahl von Abwärtsschritten für die obere Grenze ( SP[U,d] )	Durchschnittliche wahrscheinliche Anzahl von Aufwärtsschritten für die untere Grenze ( SP[D,u] )	Durchschnittliche wahrscheinliche Anzahl von Abwärtsschritten für die untere Grenze ( SP[D,d] )	Durchschnittliche wahrscheinliche Anzahl beliebiger Schritte für die obere Grenze ( SP[U,ud] )	Durchschnittliche wahrscheinliche Anzahl beliebiger Schritte für die untere Grenze ( SP[D,ud] )
1	1	1	0.5	0.5	0	0.0	0.5	0.5	0.5
2	2	2	0.5	1.5	0.5	0.5	1.5	2.0	2.0
3	3	3	0.5	3.0	1.5	3.0	1.5	4.5	4.5
4	1	2	0.5	0.888888	0.2222222	0.111111	0.777777	1.11111111	0.8888888
5	2	3	0.5	2.2	1.0	0.8	2.0	3.2	2.8
6	1	2	0.6	1.038781	0.249307	0.066481	0.487534	1.288088	0.554016
7	2	3	0.6	2.811405	1.191072	0.338217	0.906713	4.0024777	1.244931
8	2	3	1.0	2.0	0.0	0.0	0.0	2.0	0.0
9	1	3	0.5	1,25	0.5	0.25	1	1,75	1,25
10	1	4	0.5	1.6	0.8	0.4	1.2	2.4	1.6

Im Folgenden zeige ich eine Tabelle mit berechneten Werten, die im Fraktalprotokoll nicht angezeigt werden. Wir werden sie benötigen, um die Abhängigkeiten zwischen den Werten zu bewerten:

Test-Index	Schritte in der oberen Hälfte des Korridors (n)	Schritte in der unteren Hälfte des Korridors ( m )	Kreuzungswahrscheinlichkeit der oberen Grenze ( P(U) )	Kreuzungswahrscheinlichkeit der unteren Grenze ( P(D) )	Durchschnittliche Anzahl beliebiger Schritte beim Kreuzen der oberen Grenze (S[U,ud]) = SP[U,ud]/P[U]	Durchschnittliche Anzahl beliebiger Schritte beim Kreuzen der unteren Grenze (S[D,ud]) = SP[D,ud]/P[D]	Durchschnittliche Anzahl der Schritte nach oben für die obere Grenze ( S[U,u] ) = SP[U,u]/P[U]	Durchschnittliche Anzahl der Abwärtsschritte für die obere Grenze ( S[U,d] ) = SP[U,d]/P[U]	Durchschnittliche Anzahl der Aufwärtsschritte für die untere Grenze ( S[D,u] ) = SP[D,u]/(P[D])	Durchschnittliche Anzahl der Abwärtsschritte für den unteren Rand ( S[D,d] ) = SP[D,d]/(P[D])	Durchschnittliche Anzahl der Schritte ( S )
1	1	1	0.5	0.5	1.0	1.0	1.0	0.0	0.0	1.0	1
2	2	2	0.5	0.5	4.0	4.0	3.0	1	1	3	4
3	3	3	0.5	0.5	9.0	9.0	6	3	3	6	9
4	1	2	0.66666	0.3333333	1.6666666	2.6666666	1.3333333	0.33333333	0.33333333	2.33333333	2
5	2	3	0.6	0.4	5.3333333	7	3.6666666	1.66666666	2	5	6
6	1	2	0.789473	0.210526	1.631579	2.631579	1.315790	0.315789	0.315789	2.315789	1.842104
7	2	3	0.810166	0.189498	4.940318	6.569626	3.470159	1.470157	1.784805	4.784	5.2474087
8	2	3	1.0	0.0	2.0	0.0	2.0	0.0	0.0	0.0	2.0
9	1	3	0.75	0.25	2.3333333	5	1.6666666	0.6666666	1	4	3
10	1	4	0.8	0.2	3.0	8.0	2	1	2	6	4

Aus dieser Tabelle können Sie die ersten beiden Gleichungen entnehmen, die zur Berechnung aller vier unbekannten Werte benötigt werden (aus denen sich alle anderen Werte zusammensetzen). Um die Formeln zu erhalten, achten Sie auf die Spalten S[U,u], S[U,d], S[D,u], S[D,d]. Es ist sehr interessant, dass die Zahlen in dieser Spalte paarweise den gleichen Bruchteil in den Spalten S[U,u], S[U,d] und in S[D,u], S[D,d] haben. Außerdem kann man sehen, dass S[U,u] > S[U,d] und S[D,d] > S[D,u] ist. Wenn wir diese Werte paarweise subtrahieren und mit m, n vergleichen, stellt sich heraus, dass diese Differenz genau der entsprechenden Anzahl von Schritten zur oberen oder unteren Grenze entspricht:

S[U,u] – S[U,d] = n
S[D,d] – S[D,u] = m

So erhalten wir zwei sehr wichtige Werte, die bei der Bestimmung der Grundwerte helfen werden. Zwei Gleichungen sind nicht genug. Aber wir können zwei weitere Gleichungen aufstellen, die es ermöglichen, dieselben Werte auf der Grundlage einer etwas anderen Logik zu bestimmen. Wenn wir mit dem Fraktal unendlich lange experimentieren, dann wird das Verhältnis der Häufigkeit des Auftretens von Auf- und Abwärtsschritten proportional zu den entsprechenden Wahrscheinlichkeiten sein.

Diese Verhältnisse erhält man, wenn man annimmt, dass:

Lim[N0 -- > +Unendlich] (N0[U]/N0) = p
Lim[N0 -- > +Unendlich] (N0[D]/N0) = 1-p
Lim[N0 -- > +Unendlich] (N0[U]/N) = S[UD,u]
Lim[N0 -- > +Unendlich] (N0[D]/N) = S[UD,d]
Lim[N0 -- > +Unendlich] (N0/N) = S
N0 - die Anzahl der Elementarexperimente, die im Verhältnis zu den ersten Schritten durchgeführt werden (die ein komplexes Experiment bilden)
N - die Anzahl der komplexen Experimente, die sich aus einfachen Experimenten zusammensetzen

Wenn wir den Multiplikator N0/N0 = 1 in "3" und "4" einführen und die Brüche darin richtig anordnen, dann erhalten wir folgendes:

Lim[N0 -- > +Unendlich] (N0[U]/N) = Lim[N0 -- > +Unendlich] (N0[U]/N0 * N0/N) = Lim[N0 -- > +Unendlich] (N0[U]/N0) * Lim[N0 -- > +Unendlich] (N0/N) = p*S = S[UD,u]
Lim[N0 -- > +unendlich] (N0[D]/N) = Lim[N0 -- > +Unendlich] (N0[D]/N0 * N0/N) = Lim[N0 -- > +Unendlich] (N0[D]/N0) * Lim[N0 -- > +unendlich] (N0/N) = (p-1)*S = S[UD,d]

Die Produktgrenze kann als Produkt der Grenzen dargestellt werden, wenn jede dieser Grenzen eine endliche Zahl ist. Unsere Grenzwerte erfüllen diese Bedingung. Auf diese Weise werden diese Formeln abgeleitet. Die Formeln lauten wie folgt:

S[UD,u] = S*p
S[UD,d] = S*(1-p)

Es ist besser, diese Werte in Form von Fundamentalwerten auszudrücken — damit haben wir zwei fehlende Gleichungen, um alles zu bestimmen, was wir brauchen:

S[U,u] * P[U] + S[D,u] * ( 1 – P[U] ) = S*p
S[U,d] * P[U] + S[D,d] * ( 1 – P[U] ) = S*(1-p)

Infolgedessen haben vier Gleichungen fünf unbekannte Werte. Die fünfte Unbekannte ist eine der Wahrscheinlichkeiten, die die vollständige Gruppe bilden (Wahrscheinlichkeit, eine der Grenzen zu erreichen). Um alle fünf Unbekannten zu finden, benötigen wir die fünfte Gleichung, denn ein Gleichungssystem kann nur dann eine eindeutige Lösung haben, wenn die Anzahl der Gleichungen gleich der Anzahl der Unbekannten ist. Die fünfte Gleichung lässt sich intuitiv ermitteln, da sie die Differenz zwischen dem Aufwärts- und dem Abwärtsschritt ist. Im Idealfall ist sie der Grenzwert:

Lim[Nt[U] -- > +Unendlich] ((N0[U] - N0[D])/(Nt[U] - Nt[D]) = 1
Nt[U] = – die ideale Anzahl der Grundschritte nach oben, berechnet unter Verwendung einer Wahrscheinlichkeit für einen Grundschritt nach oben
Nt[D] - die ideale Anzahl von Grundschritten nach unten, berechnet mit der Wahrscheinlichkeit eines Grundschritts nach unten
N0[U] - reale Anzahl der Grundschritte nach oben
N0[D] - reale Anzahl von Grundschritten abwärts

Ein ähnlicher Grenzwert lässt sich mit Hilfe der Grenzüberschreitungswahrscheinlichkeiten ermitteln:

Lim[Nb[U] -- > +Unendlich] ((N0[U] - N0[D])/(Nb[U] - Nb[D]) = 1
Nb[U] - die ideale Anzahl von Basisschritten nach oben, berechnet anhand der Wahrscheinlichkeit, die obere Grenze zu überschreiten
Nb[D] - die ideale Anzahl von Basisschritten nach unten, berechnet anhand der Wahrscheinlichkeit des Überschreitens der unteren Grenze
N0[U] - reale Anzahl der Grundschritte nach oben
N0[D] - reale Anzahl von Grundschritten abwärts

Mit Hilfe dieser beiden Grenzwerte können wir einen komplexeren Grenzwert bilden, z. B. ihre Summe, ihre Differenz oder ihren Quotienten. Ich wähle den Quotienten, der den folgenden Ausdruck reduziert und den Grenzwert N0 [U] - N0 [D] vollständig eliminiert. Wenn man diese beiden Grenzwerte teilt und die Gleichung umformt, erhält man folgendes:

P[U] * n – (1 - P[U]) * m = p * S - (1 - p) *S

Dies ist die fünfte Gleichung, aus der wir die Wahrscheinlichkeiten für das Überschreiten der Grenzen ableiten können. Als Ergebnis erhalten wir ein System von fünf Gleichungen. Es sieht so aus:

S[U,u] – S[U,d] = n
S[D,d] – S[D,u] = m
S[U,u] * P[U] + S[D,u] * ( 1 – P[U] ) = S*p
S[U,d] * P[U] + S[D,d] * ( 1 – P[U] ) = S*(1-p)
P[U] * n – (1 - P[U]) * m = p * S - (1 - p) *S = 2*p*S - S

Das ursprüngliche Gleichungssystem mit vier Unbekannten liefert ebenfalls die gleiche resultierende Gleichung. Das System kann auf klassische Weise gelöst werden, indem man die Variablen nacheinander eliminiert:

--> S[U,u] = n + S[U,d] - eliminiert "S[U,u]"
--> S[D,d] = m + S[D,u] - eliminiert "S[D,d]"
(n + S[U,d]) * P[U] + S[D,u] * ( 1 - P[U] ) = S*p - alles in Gleichung 3 einsetzen
S[U,d] * P[U] + (m + S[D,u]) * ( 1 - P[U] ) = S*(1-p) - alles in Gleichung 4 einsetzen

Nach diesen Umformungen brauchen wir nur noch Gleichung 3 von 4 zu subtrahieren, und wir erhalten die gleiche Gleichung, die wir intuitiv erhalten haben. Leider erlaubt es uns dieses Gleichungssystem nicht, die vier verbleibenden Werte zu finden. Ich hatte gehofft, dass dieses System funktionieren würde, aber das tat es nicht. Um den Grund dafür zu verstehen, musste ich die Tabelle mit fraktalen Daten analysieren. Dadurch konnte ich eine Formel für eine dieser vier Größen erstellen. Mit dieser zusätzlichen Formel können wir alle übrigen Werte ermitteln. Das System hat sich also als nützlich erwiesen.

Der Algorithmus zur Berechnung des gesamten mathematischen Modells

Definieren wir zunächst die Umkehrgleichungen und die Reihenfolge ihrer Anwendung, um alle anderen zu finden, wobei wir S[U,u] kennen. Ich verwende diesen Wert, weil es mir gelungen ist, die entsprechenden Formeln für seine Berechnung zu finden. Mit diesem Wert können wir sofort S[U,d] mit Hilfe der ersten Gleichung finden:

S[U,d] = S[U,u] - n

Setzen Sie dann diese beiden Werte in die Gleichungen 3 und 4 ein, und Sie erhalten die verbleibenden Werte S[D,u] und S[D,d]. S[D,u] kann unmittelbar aus der dritten Gleichung berechnet werden:

S[D,u] = ( S*p - S[U,u] * P[U] ) / ( 1 - P[U] )

Jetzt müssen wir nur noch eine Formel für den letzten unbekannten Wert finden. Setzen wir den erhaltenen Ausdruck für S[U,d] in die vierte Gleichung ein:

S[D,d] = ( S*(1-p) - S[U,d] * P[U]) / ( 1 - P[U] ) = ( S*(1-p) - ( S[U,u] - n ) * P[U] ) / ( 1 - P[U] )

Das einzige fehlende Element ist der Wert von P[U], der sich leicht durch Lösen der fünften Gleichung ermitteln lässt. Tun wir dies:

P[U] * n – (1 - P[U]) * m = 2*p*S – S
--> P[U] * (n + m) = 2 * p * S – S + m
--> P[U] = ( 2 * p * S – S + m ) / (n + m)

Die bekannten Werte sind hier die folgenden:

n - die Anzahl der Schritte bis zur oberen Grenze
m - die Anzahl der Schritte nach unten bis zur unteren Grenze
p - die Wahrscheinlichkeit für den ersten Schritt nach oben
S[U,u] - die durchschnittliche Anzahl der Schritte nach oben unter der Voraussetzung, dass die obere Grenze überschritten wird
P[U] - die Wahrscheinlichkeit für das Überschreiten der oberen Grenze

Wert 4 kann berechnet werden:

S[U,u] = Ss[m,n,p] = (n ^ Pn[p] ) * ( m ^ Pm[p] )
Pn[p] = 1 , if p >= 0.5
Pn[p] = ( (1 – p)/0.5 ) ^ K
Pm[p] = 1 , if p <= 0.5
Pm[p] = ( p/0.5 ) ^ K
K ist die Potenz, die die Flachheit der Funktion regelt

Wir werden den Koeffizienten der Flachheit etwas später in einem separaten Programm berechnen. Jetzt müssen wir den wichtigsten Wert bestimmen. Durch die Analyse des Wertes S[U,u] aus der Tabelle ist es mir gelungen, Formeln für zwei Werte für symmetrische Grenzen herzuleiten:

S[U,u] = Summ[ i = 0, n] ( i ) ; wenn n == m
S[U,d] = Summ[ i = 0, n] ( i-1 ) ; wenn n == m

Das Problem ist, dass diese Formeln nur für p = 0,5 und symmetrische Grenzen funktionieren. Das Konzept der Formeln sollte auf asymmetrische Grenzen ausgedehnt werden. Danach können wir sie für verschiedene p-Werte verallgemeinern. Bevor wir zur Verallgemeinerung übergehen, ist zu beachten, dass die Testergebnisse in der Tabelle nur für "m > n" gelten. Wenn "m < n", funktionieren die Formeln für "S[D,d], S[D,u]". In diesem Fall ist es notwendig, ein Spiegelbild des Algorithmus zu erstellen, um alle anderen unbekannten Werte zu finden.

In ähnlicher Weise definieren wir die Umkehrgleichungen und die Reihenfolge, in der sie für den Fall von S[D,d] verwendet werden sollen. Auch hier wird der Wert S[D,u] mit Hilfe der zweiten Gleichung ermittelt:

S[D,u] = S[D,d] - m

Anschließend können beide Werte in die Gleichungen 3 und 4 eingesetzt werden, um S[U,u] und S[U,d] zu ermitteln. S[D,u] kann unmittelbar aus der vierten Gleichung berechnet werden:

S[U,d] = ( S*(1-p) - S[D,d] * ( 1 - P[U] ) ) / P[U]

Jetzt müssen wir nur noch eine Formel für den letzten unbekannten Wert finden. Wir setzen den erhaltenen Ausdruck für S[U,d] in die dritte Gleichung ein:

S[U,u] = ( S*p - ( S[D,d] - m ) * ( 1 - P[U] ) ) / P[U]

Damit haben wir alle erforderlichen Daten erhalten, um die Formeln S[U,u], S[D,d] für Fälle zu verallgemeinern, in denen "n != m" ist. Die folgenden Daten wurden durch die Analyse der Tabellendaten ermittelt:

m > n, p = 0,5
S[U,u] = Summ[ i = 0 … n] ( i ) + (m-1)/3

Für den umgekehrten Fall:

m < n, p = 0,5
S[D,d] = Summ[ i = 0 … m] ( i ) + (n-1)/3

Die Berechnungen sind einfacher für den Standardfall mit symmetrischen Rändern:

m = n, p = 0,5
S[U,u] = Summ[ i = 0 … n] ( i )
S[D,d] = Summ[ i = 0 … m] ( i )

Prototypen zur Ermittlung der letzten Gleichung

Nun wollen wir einen Prototyp der modifizierten Funktion definieren, der S[U,u], S[D,d] für alle möglichen p-Werte beschreibt. Um einen grundlegenden Prototyp zu erstellen, benötigen wir drei Punkte auf der p-Achse und einige Annahmen bezüglich der Gesamtstruktur. Ich glaube, dass es ausreicht, zwei Arten von generischen Funktionen zu betrachten:

Sp[U,u] = S[U,u] ^ K(p)
Sp[D,d] = S[D,d] ^ K(q)
q = 1-p

Der erste Typ kann ein echter funktionierender Prototyp sein oder eine bestimmte Markierung, die anzeigt, dass die Struktur anders ist und eine andere Logik erfordert. Es hat sich gezeigt, dass die Potenzfunktion in der Lage ist, alle Daten zusammenzuführen. Natürlich kann es komplexere Prototypen geben, die vielleicht genauer sind, aber ich denke, unsere Lösung ist völlig ausreichend. Das Wichtigste ist, die Logik zu verstehen. Wenn Sie das Modell jedoch feiner abstimmen wollen, können Sie dies anhand der in diesem Artikel vorgestellten Daten tun. Ich habe ein Testprogramm erstellt:

Die gefundenen Funktionen auf der Grundlage von Prototypen

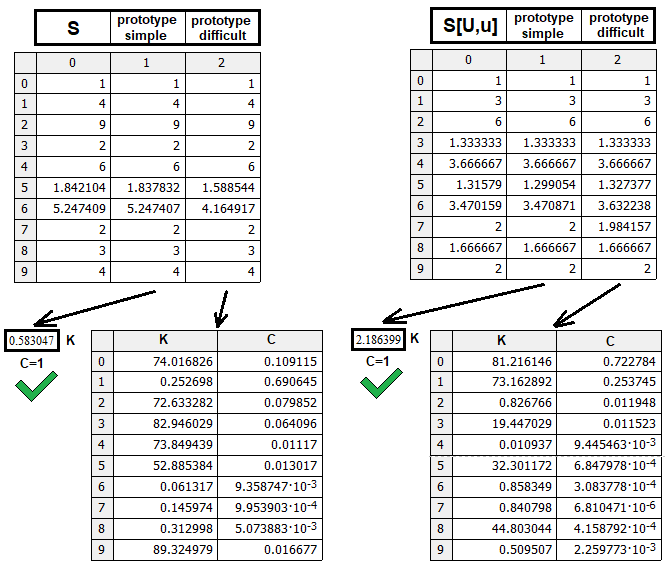
Das Programm prüft beide Prototypen, S(n,m,p) und S[U,u](n,m,p). Für S[D,d](n,m,p) ist keine Prüfung erforderlich, da diese Funktion auf S[U,u](n,m,p) gespiegelt ist und somit S[D,d](n,m,p) = S[U,u](m,n,p-1). Die Abbildung zeigt den Vergleich der gefundenen Prototypen in Bezug auf ihre Effizienz. Jeder Prototyp wurde mit der gleichen Anzahl von zufälligen Kombinationen von Gewichten und Potenzkoeffizienten in den Formeln getestet. Der einfachere Prototyp zeigt ein schöneres Ergebnis bei gleicher Anzahl von Suchzyklen. Bei Bedarf können zusätzliche Berechnungen durchgeführt werden, um zu sehen, wozu komplexere Prototypen in der Lage sind.

Nach der Überprüfung müssen wir die interne Struktur der verschachtelten Funktion "K(p)", "K(q)" definieren. Ihre interne Struktur muss die obligatorische Koinzidenz in den Punkten p=0, p=0,5, p=1, q=0, q=0,5, q=1 gewährleisten. Wir kennen die Funktionswerte in diesen Punkten, was die Auswahl des gewünschten Prototyps erleichtert:

p = 0.5 ; Sp[U,u] = S[U,u] --> K(0.5) = 1 ,
p = 1.0 ; Sp[U,u] = n = S[U,u]^(Log[S[U,u]-->n]) --> K(1.0) = Log[S[U,u]-->n]
p = 0.0 ; Sp[U,u] = 0 = S[U,u]^(-infinity) --> K(0.0) = -infinity
q = 0.5 ; Sp[D,d] = S[D,d] --> K(0.5) = 1 ,
q = 1.0 ; Sp[D,d] = n = S[D,d]^(Log[S[U,u]-->m]) --> K(1.0) = Log[S[D,d]-->m]
q = 0.0 ; Sp[D,d] = 0 = S[D,d]^(-Unendlich) --> K(0.0) = -Unendlich

Der erste und der vierte Ausdruck zeigen, dass die Potenz am Punkt des Random Walk gleich eins sein sollte. Die zweite und die fünfte Potenz zeigen, dass die Potenz so beschaffen sein sollte, dass man bei der Erhöhung eines Wertes entweder "n" oder "m" erhält, was in der obigen Ergebnistabelle zu sehen ist. Der dritte und der sechste Ausdruck zeigen, dass die Potenz gegen minus unendlich tendieren muss, um Null zu ergeben. Diese Tatsache impliziert zusätzlich, dass die Werte p und q im Nenner des Prototyps stehen sollten, da eine Division durch Null zu solchen Werten wie unendlich führt. Wir haben bereits Erfahrungen mit der Erstellung eines Potenzgesetz-Prototyps für eine Funktion gesammelt. Wir können ihn als Grundlage verwenden und überarbeiten. Nach einer eingehenden Analyse des Problems bin ich zu diesem Prototyp gekommen:

K(p) = 1 + D * Summ(N) (Kn[0] * | (( p – 0.5 )/(0.5*p)) | ^ A[0] + Kn[1] * | (( p – 0.5 )/(0.5*p)) | ^ A[1] + …. + Kn[N] * | (( p – 0.5 )/(0.5*p)) | ^ A[N])
Kn[0] + Kn[1] + …. Kn[N] = Log[S[U,u]-->n] – 1
D = (( p – 0.5 )/(0.5*p)) / | (( p – 0.5 )/(0.5*p)) |
K(q) = 1 + C * Summ(N) (Km[0] * (( q – 0.5 )/(0.5*q)) ^ B[0] + Km[1] * (( q – 0.5 )/(0.5*q)) ^ B[1] + …. + Km[N] * (( q – 0.5 )/(0.5*q)) ^ B[N])
Km[0] + Km[1] + …. Km[N] = Log[S[D,d]-->m] – 1
C = (( q – 0.5 )/(0.5*q)) / | (( q – 0.5 )/(0.5*q)) |
Kn, Km - Gewichte der entsprechenden Terme
A, B - Empfindlichkeit der Terme

Die Funktion sieht kompliziert aus, aber sie beruht auf einer einfachen Logik. Wenn "p=0,5, q=0,5", dann wird alles unter dem Summenzeichen zu Null und es bleibt nur 1 übrig, was die Bedingungen "1", "4" ergibt. Wenn "p=1, q=1", dann werden die entsprechenden Brüche innerhalb der Summe, die auf eine Potenz erhöht werden, zu 1: |(( p - 0,5 )/(0,5*p)) |. Diese Terme werden mit dem Moduluszeichen geschrieben, um komplexe Werte der Funktion beim Erhöhen auf eine Potenz auszuschließen. Stattdessen wird das entsprechende Vorzeichen als zusätzlicher Faktor angegeben. Die Potenz wirkt sich nicht mehr auf diese Terme aus, und die gesamte Summe wird zu Log[S[U,u]-->n] - 1, Log[S[D,D]-->m] - 1. Wenn wir diese Zahl zu 1 addieren, erhalten wir die erforderlichen Werte der Funktion: Log[S[U,u]-->n], Log[S[D,d]-->m].

Interpolationspolynome werden nach einer ähnlichen Logik konstruiert, ein Beispiel dafür ist das bekannte Lagrange-Polynom. Unser Polynom ist für eine bestimmte Aufgabe konzipiert, für die es eingesetzt werden kann. Sein Vorteil ist die volle Anpassungsfähigkeit an die Aufgabe. Um die gewünschte Funktion aus dieser Kurvenfamilie zu finden, müssen wir nur zwei Zahlenreihen finden.

Implementierung und Prüfung des mathematischen Modells

Mit den gefundenen Ausdrücken können wir die notwendige Funktionalität zur Berechnung eines beliebigen Fraktals leicht implementieren. Wir brauchen nur eine Struktur, die als Container für alle Daten dient, die die Hauptfunktion zurückgibt. Die anderen Funktionen werden Hilfsfunktionen sein. Wir brauchen nur die letzte Funktion:

struct MathModel1//structure for the first mathematical model
   {
   double S;//the average number of any steps
   double pU;//the probability that the price will first reach the upper border
   double pD;//the probability that the price will first reach the lower border
   double SUu;//the average number of steps up if the price first reaches the upper border
   double SUd;//the average number of steps down if the price first reaches the upper border
   double SDu;//the average number of steps up if the price first reaches the lower border
   double SDd;//the average number of steps down if the price first reaches the lower border
   
   double SPUu;//the average probable number of steps up if the price first reaches the upper border
   double SPUd;//the average probable number of steps down if the price first reaches the upper border
   double SPDu;//the average probable number of steps up if the price first reaches the lower border
   double SPDd;//the average probable number of steps down if the price first reaches the lower border
   
   double SPUud;//the average probable number of steps in any direction if the price first reaches the upper border
   double SPDud;//the average probable number of steps in any direction if the price first reaches the lower border
   
   double SUDu;//the average number of steps up when reaching any of the borders
   double SUDd;//the average number of steps down when reaching any of the borders
   };

double Ss(int n, int m,double p, double K)//prototype of the function of the average number of steps in any direction when reaching any border
   {
   if (p>=0.5) return n*MathPow(m,MathPow((1-p)/0.5,K));
   else return MathPow(n,MathPow(p/0.5,K))*m;
   }

double Log(double a, double b)//logarithm function for any base
   {
   if (MathLog(a) != 0) return MathLog(b)/MathLog(a);
   else return 0.0;
   }

double SUu(int n,int m)//average number of steps up to the upper border if p=0.5
   {
   double rez=0.0;
   if (m>n)
      { 
      for (int i=0;i<=n;i++) rez+=double(i);
      rez+=(m-1)/3.0;
      }
   if (m==n) for (int i=0;i<=n;i++) rez+=double(i);
   return rez;
   }
   
double SDd(int n,int m)//average number of steps down to the lower border if p=0.5
   {
   double rez=0.0;
   if (n>m)
      { 
      for (int i=0;i<=m;i++) rez+=double(i);
      rez+=(n-1)/3.0;
      }   
   if (m==n) for (int i=0;i<=m;i++) rez+=double(i);
   return rez;
   }   

double KpnEasy(int n,int m, double p,double A)//power prototype for steps up m>=n
   {
   double D;
   if ( p-0.5 != 0 ) D=(p-0.5)/MathAbs(p-0.5);
   else D=1.0;
   return 1.0 + D*(Log(SUu(n,m),n) - 1)*MathPow(((p-0.5)/(0.5*p)),A);
   }

double KpmEasy(int n,int m,double p,double A)//power prototype for steps down m<n
   {
   double D;
   if ( 0.5-p != 0 ) D=(0.5-p)/MathAbs(0.5-p);
   else D=1.0;
   return 1.0 + D*(Log(SDd(n,m),m) - 1)*MathPow(((0.5-p)/(0.5*(1.0-p))),A);
   }
   
double SUuS(int n,int m,double p, double A)//full prototype for average steps up m>=n
   {
   return MathPow(SUu(n,m),KpnEasy(n,m,p,A));
   }
   
double SDdS(int n,int m,double p, double A)//full prototype for average steps down  n>m
   {
   return MathPow(SDd(n,m),KpmEasy(n,m,p,A));
   }      
   
MathModel1 CalculateMathModel(int n, int m, double p,double K=0.582897,double A=2.189246)//calculating the entire mathematical model
   {
   MathModel1 Mt;
   if ( m >= n )
      {
      Mt.S=Ss(n,m,p,K);
      Mt.pU=(2*p*Mt.S-Mt.S+m)/(n+m);
      Mt.pD=1.0-Mt.pU;
      Mt.SUu=SUuS(n,m,p,A);
      Mt.SUd=Mt.SUu-n;
      if (1.0-Mt.pU != 0.0) Mt.SDu=(Mt.S*p-Mt.SUu*Mt.pU)/(1.0-Mt.pU);
      else Mt.SDu=0.0;
      if (1.0-Mt.pU != 0.0) Mt.SDd=(Mt.S*(1.0-p)-Mt.SUd*Mt.pU)/(1.0-Mt.pU);
      else Mt.SDd=0.0;
      }
   else
      {
      Mt.S=Ss(n,m,p,K);
      Mt.pU=(2*p*Mt.S-Mt.S+m)/(n+m);
      Mt.pD=1.0-Mt.pU;
      Mt.SDd=SDdS(n,m,p,A);
      Mt.SDu=Mt.SDd-m;
      if (Mt.pU != 0.0) Mt.SUd=(Mt.S*(1.0-p)-Mt.SDd*(1.0-Mt.pU))/Mt.pU;
      else Mt.SUd=0.0;
      if (Mt.pU != 0.0) Mt.SUu=(Mt.S*p-Mt.SDu*(1.0-Mt.pU))/Mt.pU;
      else Mt.SUu=0.0;      
      }
   
   Mt.SPUu=Mt.SUu*Mt.pU;
   Mt.SPUd=Mt.SUd*Mt.pU;
   Mt.SPDu=Mt.SDu*Mt.pD;
   Mt.SPDd=Mt.SDd*Mt.pD;
   
   Mt.SPUud=Mt.SPUu+Mt.SPUd;
   Mt.SPDud=Mt.SPDu+Mt.SPDd;
   
   Mt.SUDu=Mt.SPUu+Mt.SPDu;
   Mt.SUDd=Mt.SPUd+Mt.SPDd;
   
   return Mt;
   }

Um das mathematische Modell zu überprüfen, habe ich eine analoge Version dieses Codes in MathCad15 implementiert. Wenn das mathematische Modell richtig zusammengesetzt ist, dann sollten die Ergebnisse aus der Tabelle mit dem Ergebnis des mathematischen Modells übereinstimmen. Der Code des Programms ist dem Artikel beigefügt, sodass Sie es selbst überprüfen können. Ich habe mich entschieden, den Code nicht direkt in den Artikel zu präsentieren, da er zu viel Platz im Artikel einnehmen würde, aber Sie sollten das Ergebnis auf jeden Fall sehen. Vergleichen wir die Matrizen und vergewissern wir uns, dass das mathematische Modell brauchbar ist:

Überprüfen der Genauigkeit des mathematischen Modells

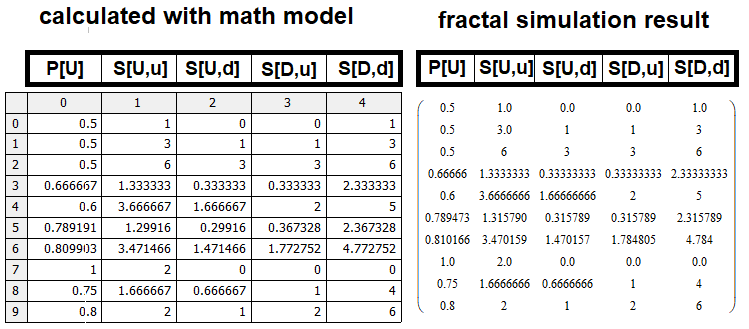
Natürlich gibt es einige Ungenauigkeiten, die aber auf die Effizienz der von uns gefundenen Prototypen für die Werte S, S[U,u], S[D,d] zurückzuführen sind. Ein weiterer Faktor für geringfügige Unterschiede kann mit Simulationsungenauigkeiten zusammenhängen, die bei größeren Werten von simuliertem n, m größer sind, da wir die Simulationstiefe aufgrund der begrenzten Rechenleistung begrenzen müssen.

Schlussfolgerung

Die Entwicklung dieses mathematischen Modells hat mich sehr viel Zeit gekostet, da ich die gesamte Mathematik von Grund auf neu entwickeln musste. Trotzdem bin ich mit dem Ergebnis zufrieden. In den nächsten Artikeln werde ich versuchen, universellere mathematische Modelle zu entwickeln, die in ihrer Kombination die Berechnung jeder beliebigen Handelskonfiguration in Bezug auf ihre Hauptmerkmale ermöglichen würden. Darüber hinaus eignet sich das mathematische Modell nicht nur zur Beschreibung von Preisbildungsprozessen, sondern auch zur Beschreibung von Handelssignalen und zur Vereinfachung komplexer Strategien, indem man sie auf einfachere Strategien reduziert. Dies wird einige Zeit in Anspruch nehmen.

Referenzen

Kombinatorik und Wahrscheinlichkeitsrechnung für den Handel (Teil I): Die Grundlagen

Kombinatorik und Wahrscheinlichkeitsrechnung für den Handel (Teil II): Das universelle Fraktal

Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/9570

Beigefügte Dateien |

ZIP herunterladen

Materials.zip (312.85 KB)

Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Andere Artikel von diesem Autor

Zur Diskussion im Händlerforum

Umgang mit Zeit (Teil 1): Die Grundlagen

Funktionen und Codeschnipsel, die den Umgang mit der Zeit, dem Broker-Offset und der Umstellung auf Sommer- oder Winterzeit vereinfachen und verdeutlichen. Genaues Timing kann ein entscheidendes Element beim Handel sein. Ist die Börse in London oder New York zur aktuellen Stunde bereits geöffnet oder noch nicht, wann beginnt und endet die Handelszeit für den Forex-Handel? Für einen Händler, der manuell und live handelt, ist dies kein großes Problem.

Grafiken in der Bibliothek DoEasy (Teil 82): Die Umgestaltung von Bibliotheksobjekten und Kollektion von grafischen Objekten

In diesem Artikel werde ich alle Bibliotheksobjekte verbessern, indem ich jedem Objekt einen eindeutigen Typ zuordne und die Entwicklung der Klasse der grafischen Bibliotheksobjekte Kollektion fortsetze.

Grafiken in der Bibliothek DoEasy (Teil 83): Die Klasse des abstrakten grafischen Standardobjekts

In diesem Artikel werde ich die Klasse des abstrakten grafischen Objekts erstellen. Dieses Objekt soll als Grundlage für die Erstellung der Klasse der grafischen Standardobjekte dienen. Grafische Objekte haben mehrere Eigenschaften. Daher muss ich vor der eigentlichen Erstellung der Klasse des abstrakten grafischen Objekts eine Menge Vorarbeit leisten. Dazu gehört das Festlegen der Eigenschaften in den Enumerationen der Bibliothek.

Kombinatorik und Wahrscheinlichkeitsrechnung für den Handel (Teil II): Das universelle Fraktal

In diesem Artikel werden wir das Studium der Fraktale fortsetzen und besonderes Augenmerk auf die Zusammenfassung des gesamten Materials legen. Zu diesem Zweck werde ich versuchen, alle früheren Entwicklungen in eine kompakte Form zu bringen, die für die praktische Anwendung im Handel geeignet und verständlich ist.