您应当知道的 MQL5 向导技术（第 18 部分）：配合本征向量进行神经架构搜索

前言

我们继续 MQL5 向导实现的系列文章，正在探查神经架构搜索，同时具体阐述了本征向量在加速网络训练过程中所能扮演的角色，令其更高效。神经网络理论上是一组数据的曲线拟合，以至于它们有助于提炼出一个公式表达式，当应用于输入数据（x）时，其会提供一个目标值（y），就像二次方程按曲线行事。尽管 x 和 y 数据点可以是、且事实上往往是多维的，这就是为何神经网络广受欢迎。无论如何，提炼公式化表达式的原则仍然存在，这就是为什么神经网络只是达此目标的一种手段，而非如此行事的唯一途径。

概述

如果我们选择利用神经网络来定义训练数据集与其目标之间的关系，如本文的情况，那么我们就必须正视一个问题，即这个网络将采用什么设置？网络有若干种类型，这意味着适用的设计和设置也很多。至于本文，我们研究一个非常基本的情况，往往被称为多层感知器。配以该类型，我们要详述的设置仅是隐藏层的数量、和每个隐藏层的大小。

NAS 典型情况下有助于识别这 2 个设置，以及更多。举例，即使配以简单 MLP，使用哪种激活类型、初始权重、以及初始背离等问题，仍旧是影响网络性能和准确性的敏感因素。不过，于此略过了这些内容，因为搜索空间拓展太广，即使是中等规模数据集，正向和反向传播所需的计算资源也会令人望而却步。

此处 NAS 适配的方式有点新颖，因为它在矩阵搜索空间中使用本征向量和数值来识别理想的设置。传统上，NAS 是通过强化学习、或进化算法、或贝叶斯优化、或随机搜索来执行的。

出于比较目的，这些传统方式的每一种都涉及经由来自目标的每项性能基准分数，依据选定的设置（也称为架构）来训练和交叉验证网络。它们的不同之处在于它们的穷举程度，或者它们的方式很高效，且无需在搜索空间内穷举。强化学习依赖于一种算法，即在搜索空间内基于其设置预先估算网络，且会随每次选择不断改进算法。进化算法在搜索空间内交叉或组合网络，以便到达在搜索空间中一开始也许就不一定会去的新网络，再次估算它们对目标的性能基准分数。贝叶斯优化（如随机搜索）依赖于以数组格式排序的搜索空间，或者其中不同的网络设置可被视为搜索空间内的坐标。例如，如果搜索空间是 2-维的，只有 2 个变量，隐藏层的标准大小、和隐藏层的数量，那么这些选项将以类似于下图的形式在该矩阵中呈对角线以升序（或降序）扩散。

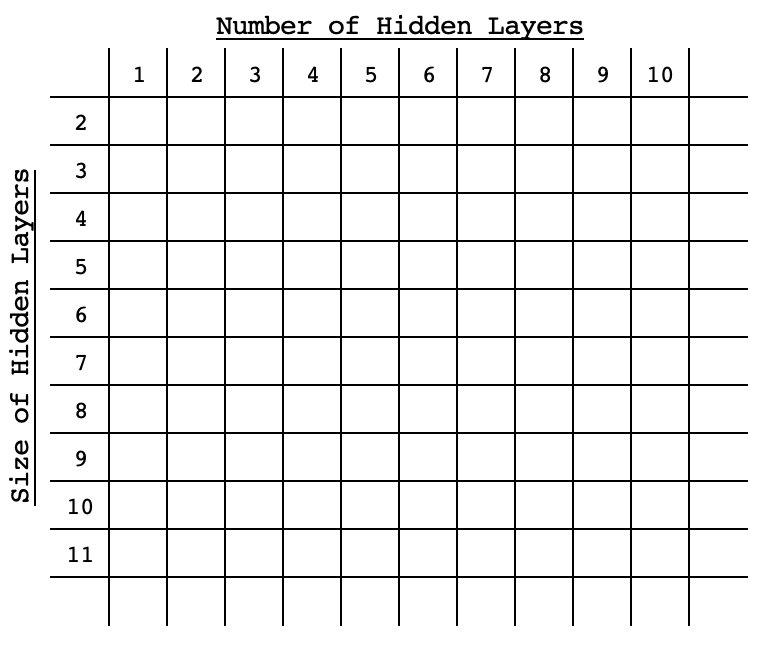
配以这种安排，任何网络的性能都将与其在空间内的“坐标”挂钩，因此每个后续选择均可运用统计方法，来优选网络产生最佳性能。几天前撰写的关于本征向量和 PCA 的文章，使用矩阵搜索空间来选择理想的工作日和指标应用价格，以便在采用 H4 时间帧时交易 EURUSD。这是来自价格变化的交叉矩阵，内含 5-周日的价格变化，及每个所参考的应用价格。

我们将在本文中研究类似的搜索方式。鉴于我们尝试“解决”的问题是所有网络的穷举训练，我们的基准分数只是正向通验得分，来自按标准权重和乖离初始化网络的目标值。我们仅在数据样本上进行前向运行，每个设置的平均分数将当作其在矩阵内的基准分数。

本征向量在 NAS 中的角色

为简洁起见，我们将用于 NAS 的本征矩阵将是 2-维的，如上暗示。如果我们研究一个简单的 MLP，其中所有隐藏层都具有相同的大小，那么我们要回答的仅有两个问题就是 MLP 应该有多少个隐藏层，以及每个隐藏层的大小。

这些问题的可能答案可以很容易地以矩阵形式呈现，每个网络的默认性能均记录在每个层大小、及层编号的组合上。如矩阵表格中所反映的，网络的设置会有所不同，但其输入和输出层都是标准的。至于本文，我们的输入层大小为 4，以及输出层大小为 1。我们正在研究一种普遍场景，其中我们基于 4 个最后收盘价来预测下一个收盘价。

测试品种为 EURJPY，将于 H4 时间帧上涵盖 2022 年。这意味着我们的数据将是 2022 年的 4 小时收盘价。在“训练”这个模型时，我们所做的只是记录所有网络设置下贯穿全年的实际价格距目标值的平均偏差。我们的设置跨度，沿矩阵行数从单一隐藏层直至 10-个隐藏层，而列数所拥有的隐藏层大小，其跨度从 2 到 11。这些测试设置是任意的，且鉴于本文末尾附有完整的源代码，故欢迎读者按自己的偏好自行定制它。

重申一下，该模型的“训练”将涉及每个可用网络的单次正向通验，所有网络都搭配涵盖 2022 年的标准默认权重和乖离，每根柱线预测基准分数都比之于实际收盘价。在“训练”期间，不会有反向传播、或典型的网络训练。

我们依靠本文中视察的网络类来实现 MLP。它只需一个整数型数组，其大小定义为层的总数，其中每个索引处的整数值设置层大小。

尽管本文和系列是着重于 MQL5 向导，但上面提到的“训练”将由脚本完成，就像上一篇本征向量一文中的情况一样，我们将取用它的结果/建议来编写信号类实例，可由向导组装的智能系统进行测试。我们组装好的智能系统测试将依据每根柱线、或每个新数据点上进行正常的网络训练。所推荐网络的策略测试器结果的基准分数，将比之于最差建议，作为对照，如此我们就可评估本征向量和数值在 NAS 中能否足智多谋。

如果我们回顾上一篇文章中涵盖的本征向量和数值的内容，那么所使用的降维为我们提供了来自所分析矩阵的单个向量。故此，在我们的例子中，我们在矩阵中记录的每个网络的性能将降低到一个向量。在上一篇文章中，我们想获得工作日和所应用价格，即在 H4 时间帧内捕捉到的 EURJPY 货币对涵盖一年的大部分方差。这意味着我们专注于投影矩阵中本征向量的最大值，因为它们与我们的目标呈正相关。

在这种情况下，尽管我们的矩阵记录了距目标值的偏差，这意味着我们在矩阵中拥有的是每个网络的误差因子。鉴于是为测试目的，我们希望使用误差最小的网络，我们按层数和每层大小选择网络将是来自投影矩阵中提取到的每个本征向量的最小值。所述预处理都是由脚本处理的，可以分为 5 个部分，即 a) 网络的初始化：

//initialise networks
   ArrayResize(__M.row, __SIZE);
   for(int r = 0; r < __SIZE; r++)
   {  for(int c = 0; c < __SIZE; c++)
      {  ArrayResize(__M.row[r].col, __SIZE);
         ArrayResize(__M.row[r].col[c].settings, 2 + __LEAST_LAYERS + r);
         ArrayFill(__M.row[r].col[c].settings, 0, __LEAST_LAYERS + r + 2, __LEAST_SIZE + c);
         __M.row[r].col[c].settings[0] = __INPUTS;
         __M.row[r].col[c].settings[__LEAST_LAYERS + r + 1] = __OUTPUTS;
         __M.row[r].col[c].n = new Cnetwork(__M.row[r].col[c].settings, __initial_weight, __initial_bias);
      }
   }

b) 网络基准测试：

//benchmark networks
   int _buffer_size = (52*PeriodSeconds(PERIOD_W1))/PeriodSeconds(Period());
   PrintFormat(__FUNCSIG__ + " buffered: %i", _buffer_size);
   if(_buffer_size >= __INPUTS)
   {  for(int i = _buffer_size - 1; i >= 0; i--)
      {  for(int r = 0; r < __SIZE; r++)
         {  for(int c = 0; c < __SIZE; c++)
            {  vector _in,_out;
               vector _in_new,_out_new,_in_old,_out_old;
               _in_new.CopyRates(Symbol(), Period(), 8, i + 1, __INPUTS);
               _in_old.CopyRates(Symbol(), Period(), 8, i + 1 + 1, __INPUTS);
               _out_new.CopyRates(Symbol(), Period(), 8, i, __OUTPUTS);
               _out_old.CopyRates(Symbol(), Period(), 8, i + 1, __OUTPUTS);
               _in = Norm(_in_new, _in_old);
               _out = Norm(_out_new, _out_old);
               __M.row[r].col[c].n.Set(_in);
               __M.row[r].col[c].n.Forward();
               __M.row[r].col[c].benchmark += fabs(__M.row[r].col[c].n.output[0]-_out[0]);
            }
         }
      }
   }

c) 复制基准分数到分析矩阵：

//copy benchmarks to analysis matrix
   matrix _m;
   _m.Init(__SIZE, __SIZE);
   _m.Fill(0.0);
   for(int r = 0; r < __SIZE; r++)
   {  for(int c = 0; c < __SIZE; c++)
      {  _m[r][c] = __M.row[r].col[c].benchmark;
      }
   }

d) 归一化矩阵，并生成本征向量和数值：

//generating eigens
   PrintFormat(" for: %s, with: %s", Symbol(), EnumToString(Period()));
   matrix _z = ZNorm(_m);
   matrix _cov_col = _z.Cov(false);
   matrix _e_vectors;
   vector _e_values;
   _cov_col.Eig(_e_vectors, _e_values);

e) 最后解释本征向量，从投影矩阵中提取理想和最差的网络层数和层大小：

//interpreting the eigens from projection
   matrix _t = _e_vectors.Transpose();
   matrix _p = _m * _t;
   vector _max_row = _p.Max(0);
   vector _max_col = _p.Max(1);
   string _layers[__SIZE];
   for(int i=0;i<__SIZE;i++)
   {  _layers[i] = IntegerToString(i + __LEAST_LAYERS)+" layer";
   }
   double _nr_layers[];
   _max_row.Swap(_nr_layers);
   //since network performance inversely relates to network deviation from target
   PrintFormat(" est. ideal nr. of layers is: %s", _layers[ArrayMinimum(_nr_layers)]);
   PrintFormat(" est. worst nr. of layers is: %s", _layers[ArrayMaximum(_nr_layers)]);
   string _sizes[__SIZE];
   for(int i=0;i<__SIZE;i++)
   {  _sizes[i] = "size "+IntegerToString(i + __LEAST_SIZE);
   }
   double _size_nr[];
   _max_col.Swap(_size_nr);
   PrintFormat(" est. ideal size of layers is: %s", _sizes[ArrayMinimum(_size_nr)]);
   PrintFormat(" est. worst size of layers is: %s", _sizes[ArrayMaximum(_size_nr)]);

执行上述脚本，在大小 100 的搜索空间中运行几秒钟，这是一个好兆头。不过，有人可能会争辩说空间不够全面，这是一个有效的论点，这就是为什么附加的脚本将空间的大小属性作为全局变量，用户可以修改该属性，从而创建更勤劳的东西。此外，我们还需要一个结构来处理网络实例，及其基准分数。这在头文件中定义如下：

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
struct Scol
{  int   settings[];
   Cnetwork *n;
   double benchmark;
   
   Scol()
   {  ArrayFree(settings);
      benchmark = 0.0;
   }
   ~Scol(){ delete n; };
};
struct Srow
{  Scol  col[];

   Srow(){};
   ~Srow(){};
};
struct Smatrix
{  Srow  row[];
   
   Smatrix(){};
   ~Smatrix(){};
};
Smatrix __M;   //matrix of networks

测试智能系统

如果我们运行上述脚本来帮助筛选理想的网络设置，那么附加到 EURJPY 的 H4 时间帧上，我们会得到以下日志：

2024.05.03 18:22:39.336 nas_1_changes (EURJPY.ln,H4) void OnStart() buffered: 2184

2024.05.03 18:22:42.209 nas_1_changes (EURJPY.ln,H4) for: EURJPY.ln, with: PERIOD_H4

2024.05.03 18:22:42.209 nas_1_changes (EURJPY.ln,H4) est. ideal nr. of layers is: 6 layer

2024.05.03 18:22:42.209 nas_1_changes (EURJPY.ln,H4) est. worst nr. of layers is: 9 layer

2024.05.03 18:22:42.209 nas_1_changes (EURJPY.ln,H4) est. ideal size of layers is: size 2

2024.05.03 18:22:42.209 nas_1_changes (EURJPY.ln,H4) est. worst size of layers is: size 4

推荐的网络设置是针对 6-层网络，其中每个的大小为 2！作为旁注，目标数据（y 值）用于基准测试，矩阵被归一化为 0.0 到 1.0 的范围内，其中 0.5 的读数意味着结果的价格变化为 0，而任何小于 0.5 的数值都代表结果价格下跌，高于 0.5 的值将指向价格上涨。执行归一化的函数代码如下所列：

//+------------------------------------------------------------------+
//| Normalization (0.0 - 1.0, with 0.5 for 0                         |
//+------------------------------------------------------------------+
vector Norm(vector &A, vector &B)
{  vector _n;
   _n.Init(A.Size());
   if(A.Size() > 0 && B.Size() > 0 && A.Size() == B.Size() && A.Min() > 0.0 && B.Min() > 0.0)
   {  int _size = int(A.Size());
      _n.Fill(0.5);
      for(int i = 0; i < _size; i++)
      {  if(A[i] > B[i])
         {  _n[i] += (0.5*((A[i] - B[i])/A[i]));
         }
         else if(A[i] < B[i])
         {  _n[i] -= (0.5*((B[i] - A[i])/B[i]));
         }
      }
   }
   return(_n);
}

该归一化是必要的，因为我们正在考虑采用给定小数据集训练一个网络，来拓展能够处理负值和正值的权重和乖离，作为输出将需要扩充的大型数据集、更复杂的网络设置，当然还需要更多的计算资源。本文不探讨这两种场景，但如果认为可行，可以大胆尝试。如此，通过我们的归一化，我们能够从适度训练和数据集的网络中获得敏感的结果。

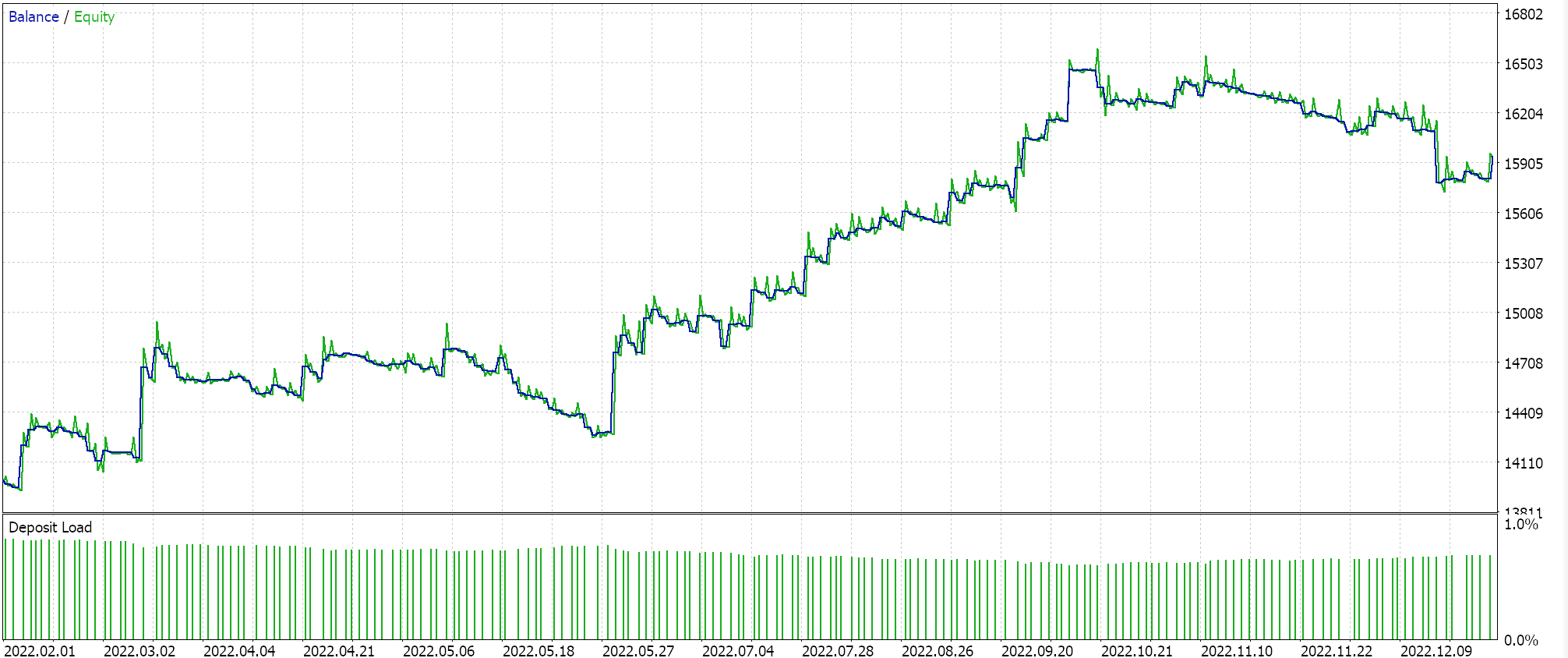
如果我们按推荐的 6 层、大小为 2 的网络配置运行测试，我们所做会得到如下所示的报告和净值曲线：

脚本日志结果中还标记了 9 层、大小为 4 的网络配置。如果我们运行测试，智能系统输入设置与该网络配置雷同，我们将得到以下结果：

令人震惊的是，结果也几乎雷同！为什么！？好吧，有几个理论原因可以解释这一点：

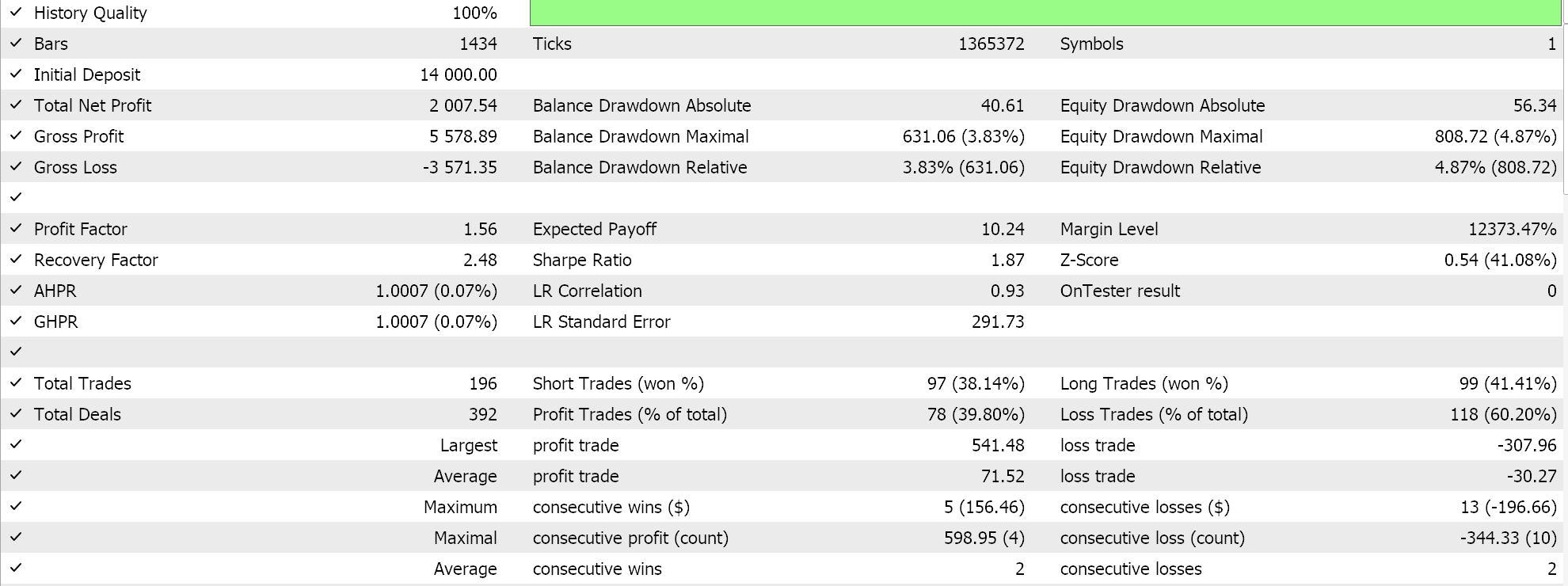
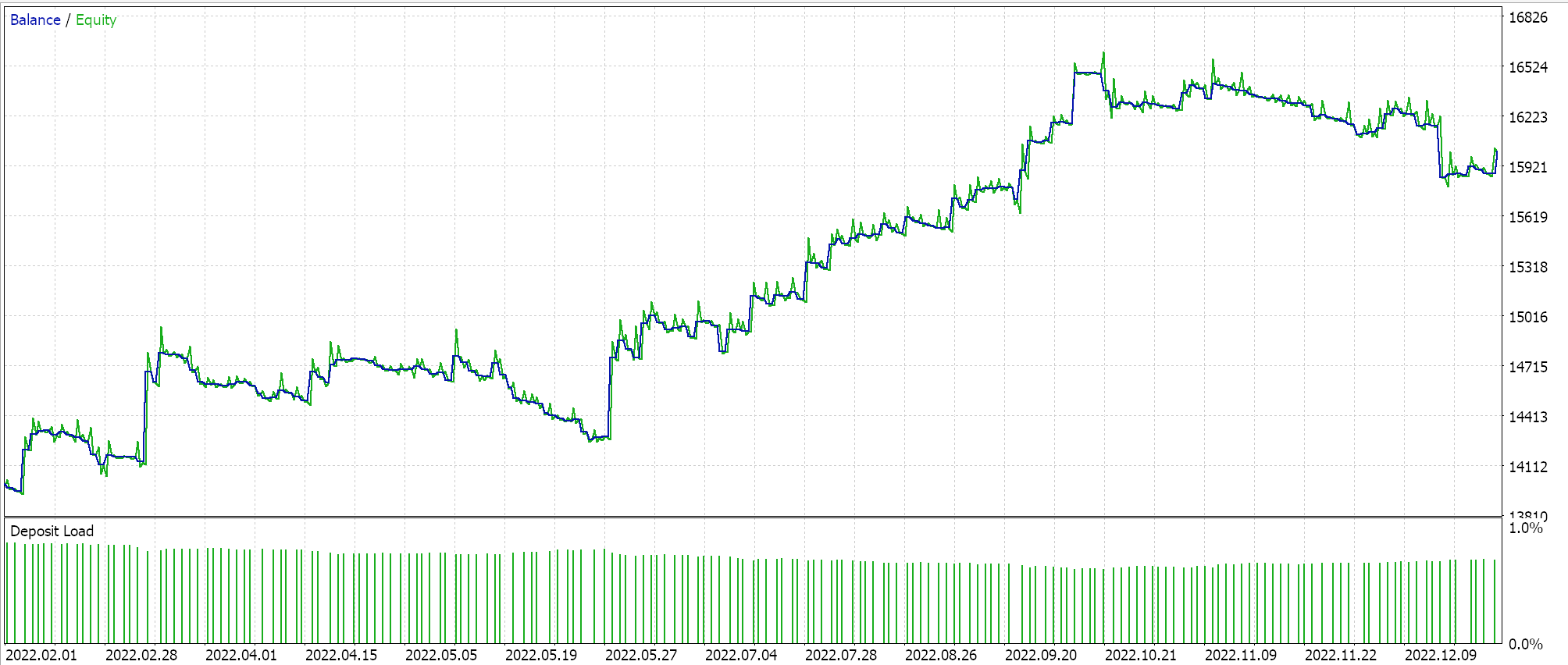
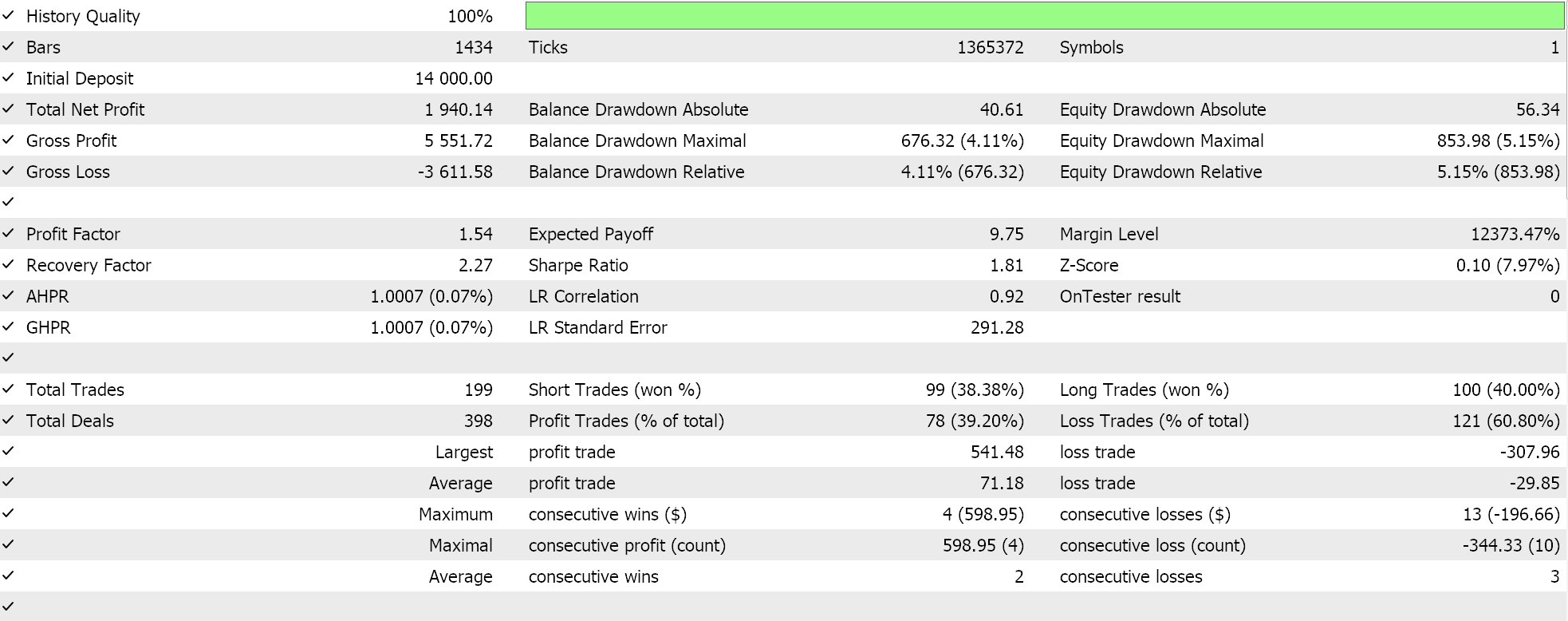
神经网络的能力可能会有冗余，其中不同的设置（或架构）学习数据中相同的底层关系，即使它们具有不同的结构。回想一下，在这两次通验中，网络都在训练，故权重和乖离两者都得到了改善。如此这般，方差较大的本征向量捕获了更广泛的特征集，而方差较小的本征向量则侧重于细节，任一网络配置都能学到基础知识以确保良好性能。

而在这种状况下，隐藏层的数量、及其大小是判定网络性能的关键因素，但可能还有其它主导因素在起作用，就像我们选择的激活函数（我们使用软性加强）、或所用的学习率。其一或所有这些都可能对网络的性能产生不成比例的影响。

另一种可能的解释就与搜索空间限制有关。我们研究了 10 种不同的层大小，和 10 种不同的隐藏层选项，它们都变形为矩形形式。当映射此特定数据集时，这本身就约束了可能的网络组合，如此这几个选项中的任何一个都可以轻松获得所需的方案。

结束语

我们已见识到，当面对可供选择的神经网络配置纵深适度时，如何搭配本征向量和数值以非正统的方式完成 NAS。该过程可以伸缩，或许甚至能延展到包括或参考非分析矩阵部分的其它因素，这是通过添加隐藏层形式（我们只看矩形），甚或激活类型。后者更容易添加到本文中视察的矩阵当中，因为只有 2 到 3 种主要的激活类型，这可能只是意味着将列数增加三倍，同时增加行数以确保维持方阵，这是本征向量分析的先决条件。如果要参考的不同形状以透明类型列举，额外的隐藏层形状也可类似行事 。 

注意：

附件可随同智能系统向导组装指南使用，这些都可在这里和此处找到。