Denis , makale hakkında şu yorumu yapacağım.
Teoriye gelince, soru yok, her şey ayrıntılı olarak sunulmuş.
Uygulamaya gelince, dikkatinizi ampirik histogramları gösterdiğiniz şekillere çekmek istiyorum, özellikle Şekil 2'ye. Mesele şu ki, analizinizde çok önemli iki yanlışlık yaptınız.
İlk olarak, histogramları oluşturan komut dosyası için çok az sayıda sınıf belirlediniz - sadece 9, bu da Pearson kriterinin gücüne büyük bir darbe vuruyor ve uygulamasını etkisiz hale getiriyor. Gelecek için, emin olmak için 200-300 sınıf alın, tabii ki örneklem büyüklüğü izin veriyorsa (ve veriyorsa), hata yapmazsınız. Tam olarak bunu yapmış olsaydınız, lognormal dağılım testinin ve hipersekans için getiri testinin negatif sonuç vereceğinden emin olabilirdiniz. Bu arada, bu tür iki dağılımın aynı anda belirli bir değeri ve onun modülünü temsil edemeyeceğinden emin olmak çok kolaydır, sadece hipersekansın "yarısını" alın ve kendisiyle konvolve edin (rastgele bir değişkenden modülü almaya benzer): kesinlikle lognormal bir dağılım elde edemezsiniz.
İkinci yanlışlık, getiri dağılımının tepesinin (diğer bir deyişle beklentisinin) tam olarak 0 olması gerektiğine dair a priori bilgiyi kullanmamış olmanızdır (aksi takdirde hepimiz uzun zaman önce milyarder olurduk). Şekil 2'deki histogramın, olmaması gerektiği halde sağa kaymış görünmesinin nedeni budur. Yine, histogramı çizerken bunu dikkate almak testleri daha güvenilir hale getirecektir.
Not: Modellemenin temelleri üzerine bir makale yazıyorum, bu nedenle bu kadar yoğun bir ilgi var. Makaleniz için teşekkür ederim, konu içinde. Saygılarımla.
...Öncelikle, histogramları oluşturan kod için çok az sayıda sınıf belirlemişsiniz - sadece 9, bu da Pearson kriterinin gücüne büyük bir darbe vuruyor ve uygulamasını etkisiz hale getiriyor. Gelecek için, emin olmak için 200-300 sınıf alın, tabii ki örneklem büyüklüğü izin veriyorsa (ve veriyorsa), hata yapmazsınız. Tam olarak bunu yapmış olsaydınız, lognormal dağılım testinin ve hipersekans için getiri testinin negatif sonuç vereceğinden emin olabilirdiniz. Bu arada, bu tür iki dağılımın aynı anda belirli bir değeri ve onun modülünü temsil edemeyeceğinden emin olmak çok kolaydır, sadece hipersekansın "yarısını" alın ve kendisiyle konvolve edin (rastgele bir değerden modülü almanın benzeri): kesinlikle lognormal bir dağılım elde edemezsiniz.
Sayın alsu, görüşünüz için teşekkürler!
Sırayla gidelim.
Sınıf sayısı isteğe bağlı olarak değil, bazı formüllere göre belirlenir. Benim durumumda bu Sturgis formülüdür. En popüler kurallardan biridir. Mükemmel değil, buna katılıyorum. Ama yine de...
Peki siz hangi kurala göre 200-300 sınıf alıyorsunuz?
İkinci yanlışlık, getiri dağılımının tepesinin (diğer bir deyişle beklentisinin) tam olarak 0 olması gerektiğine dair a priori bilgiyi kullanmamış olmanızdır (aksi takdirde hepimiz uzun zaman önce milyarder olurduk). Şekil 2'deki histogramın, olmaması gerektiği halde sağa kaymış gibi görünmesinin nedeni budur. Yine, histogramı oluştururken bu noktayı dikkate almak testleri daha güvenilir hale getirecektir.
Örneklemi olgusal bir temelde analiz ediyorum. Elimdekileri analiz ediyorum. Peki hangi temele dayanarak verim dağılımının tepesi tam olarak 0 noktasında olmalıdır? Belki bir şeyleri yanlış anlıyorum...
Ayrıca, uydurmanın uygulandığı dağılıma bakarsanız ( X~HS(-0.00, 1.00)), ilk parametrenin - kaydırma parametresi - tam olarak 0 olduğunu görmek kolaydır. Aslında, beklentiye eşittir.
İşte standart değerlerin örneklenmesine ilişkin bir başka html raporu. Umarım şekil az çok okunabilirdir. Ancak makaledekiyle aynı değil. En son verileri şimdi aldım.
Gördüğünüz gibi, Ortalama =0. Ve en iyi uyum Hiperbolik Sekant dağılımıdır: X~HS(0.00, 1.00).
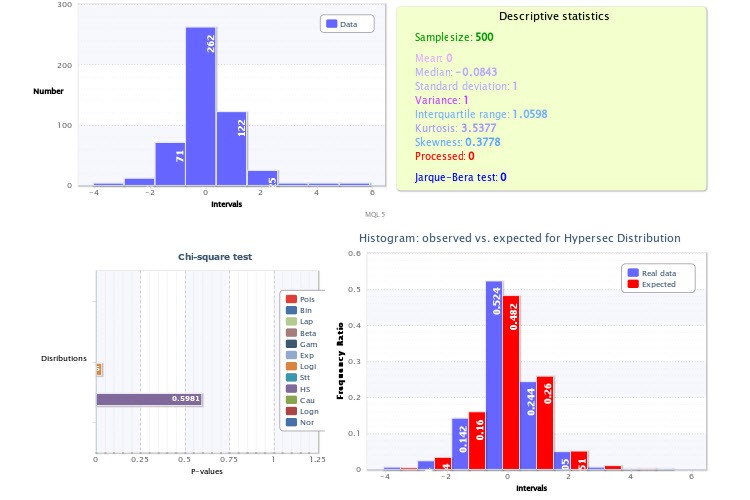
Kesinlikle, Sturges'in formülü tam olarak 9 sınıf vermiştir, ancak bu daha ziyade örneklem büyüklüğünü artırmayı düşünmek için bir nedendir (formülü tersine çevirerek, 256 civarında olduğunu görüyorum?).
Ayrıca, bu formül yalnızca normal dağılımdan gelen genel popülasyonlar için iyi çalışır (bunun için türetilmiştir) ve düşünüldüğü gibi, örneklem büyüklüğü 200 değerden fazla değildir. Alternatif formüller kullanabilirsiniz - Diakonis, Scott....
Genel olarak, Sturges formülünün mantıksal bir gerekçesini asla vermemiştir - evet, normal dağılımın binom dağılımına yaklaştırılmasına dayanmaktadır, ne olmuş yani? Bu, sınıf sayısını seçmenin verimliliği sorusunu nasıl etkileyebilir? Optimalite kriteri yazar tarafından hiçbir zaman tanımlanmamıştır ve formülün kendisi de rastgele yazılmıştır. Ancak mesele şu ki, Sturges'in yaklaşımı uzun bir süre boyunca herhangi bir şekilde resmileştirilmiş tek yaklaşımdı ve otomatik olarak (ve bence oldukça düşüncesizce!) tüm istatistik paketlerine dahil edildi; bu arada, bu formül neredeyse her zaman son derece düşük bir sınıf sayısı verdiği için oldukça can sıkıcıdır.
Bir kez daha, alternatif formüller vardır, ancak kişisel bir bilgisayarın varlığı, paradoksal bir şekilde, bize kendi kafamızı bir cihaz olarak kullanma fırsatı verir, yani bu göstergeyi sorunsuz bir şekilde değiştirdiğimizde, grafiğin düzgünlüğü ile histogramın çözünürlüğü arasında bir uzlaşma sağladığımızda, bu belirli örnek için az ya da çok optimal sınıf sayısını belirlemenin görsel bir yolu. Bu arada, bu yöntem genellikle herhangi bir formülden daha iyi ve daha hızlıdır.
Herkese her zaman şunu söylerim - sayıları formüllere koymadan önce, bunun ne anlama geldiğini ve nasıl (ve uygulanıp uygulanmayacağını) sorun. Kısacası, Sturges'in formülünün kullanılmasına karşıyım, modası geçmiş ve yetersiz olduğunu düşünüyorum).
Ortalama ile ilgili olarak. Getiri beklentisi 0 olmalıdır çünkü öyle olmasaydı, aptalca bir şekilde her zaman bu MO'nun işaretine karşılık gelen bir yönde bahis oynayabilir ve önceden belirlenmiş herhangi bir büyüklükte bir getiri elde etmeyi garanti edebilirdik. Üst kısım tamamen simetri nedeniyle MO ile çakışmalıdır: grafiğin sol yarısı sağ yarısının ayna görüntüsü olmalıdır (oran artışı ve azalışı istatistiksel olarak eşittir ve aralarında hiçbir fark olmamalıdır), bu nedenle simetri merkezi merkezle çakışır.
HS(0.00, 1.00) aldığınıza göre, sınıfları ortalamanız gerekir - yani sıfır sınıfı bazı simetrik aralıktaki (-x0;x0) indeks değerlerini içermelidir, aksi takdirde hesaplamalara sınıfların sıfıra göre kaymasıyla ilişkili sistematik bir hata ekleriz ve sonunda chi^2 testinin sonucuna sızar. Sizin 0 noktanız sıfır sınıfının ortasında değil.
Aslında, ayrık verilerde sınıfların nasıl simetrik hale getirileceği sorusu oldukça önemsizdir ve yine, her bir örnek için ayrı ayrı ve çok dikkatli bir şekilde çözmek iyidir, aksi takdirde sınıflara bölünmenin sınırlarının yanlış seçimi nedeniyle de yetersiz sonuçlar alma riskiyle karşı karşıya kalırız.
alsu, yazımın konusu olmasa da son derece ilginç bir konuya değinmişsiniz. Elimden geldiğince bu konuyu daha fazla araştıracağım.
Yapıcı eleştirileriniz için teşekkür ederim!
Bilimsel bilginin ticarette uygulanabilirliği hakkındaki görüşlerinizi beğendim.
Olasılık teorisi ve matematiksel istatistiğe aşina olan bir kişiye hangi kitapları tavsiye edeceğinizi söyleyebilir misiniz?
Denis, iyi günler.
Bilimsel bilginin ticarette uygulanabilirliği hakkındaki görüşünüzü beğendim.
Lütfen olasılık teorisi ve matematiksel istatistiğe aşina olan bir kişiye hangi kitapları tavsiye edeceğinizi söyleyin.
Fikriniz için teşekkür ederim!
Yeni başlayanlar için bir şeyler aramak gerektiğini düşünüyorum, biraz lit-rol. Önemli olan kitabın metninin sizi daha fazla okumaktan vazgeçirmemesidir :-))).
Gaidyshev ve Bulashev'in bir kitabını beğendim.....
- rsdn.org
İkinci yanlışlık, getiri dağılımının tepesinin (diğer bir deyişle beklentisinin) tam olarak 0 olması gerektiğine dair a priori bilgiyi kullanmamış olmanızdır (aksi takdirde hepimiz uzun zaman önce milyarder olurduk).
Hiç de değil. Dağılımın tepesinin 0'a göre kayması (bir enstrümanın büyümesi/azalması) gelecekte de aynı olacağı anlamına gelmez. Bu yüzden çoğu tüccar milyarder değildir, çünkü değil.
Saygılarımla.
...Dağılımın tepesinin 0'a (yükselen/düşen enstrüman) göre kayması, gelecekte de durumun böyle olacağı anlamına gelmez...
Katılıyorum.
Alsu için bir soru. Sıfır noktasından bahsederken piyasa etkinliğini mi kastettiniz?
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz
Yeni makale Satıcı Çalışmasında İstatistiksel Dağılımların Rolü yayınlandı:
Bu makale, bazı teorik istatistiksel dağılımlarla çalışmak için sınıfları ortaya koyan MQL5'te İstatistiksel Olasılık Dağılımları makalemin mantıklı bir devamıdır. Artık teorik bir temele sahip olduğumuza göre, doğrudan gerçek veri setlerine geçmemizi ve bu temelden bilgi amaçlı yararlanmaya çalışmamızı öneriyorum.
Ayrıca, bu betiğin istatistiksel sonuçları küçük bir HTML raporu şeklinde görselleştirmesi gerektiğine karar verdim, bunun bir örneği HTML formatında Grafikler ve Diyagramlar makalesinde bulunabilir (Şekil 8).
Şekil 8. Numune tahmini hakkında istatistiksel rapor
Yazar: Denis Kirichenko