Вы упускаете торговые возможности:
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Регистрация
Вход
Вы принимаете политику сайта и условия использования
Если у вас нет учетной записи, зарегистрируйтесь
Спасибо за ссылку, увлекся поиском связанных с ней идей. Не думаю, что Вам нужно подходить к вопросу как там, с позиций R-функций. Подход с обычными средствами:
Прямо из уравнения окружности радиусом R с координатами центра Xc, Yc, с игнорированием потери смысла у единиц измерения (номер, курс, расстояние)
R^2 = (X-Xc)^2 + (Y-Yc)^2
делаем функцию невязки в точке с номером i (Xi = i). Это разность между расстоянием от точки (Xi, Yi) до центра Xc, Yc и радиусом R:
Di = ((Xi-Xc)^2 + (Yi-Yc)^2)^0.5 - R.
Квадраты Di и складываем, чтобы получить целевую функцию, которую надо минимизировать. Искомых варьируемых параметров три: R, Xc, Yc. У крайних (первой и последней) точек влияние меньше, чем у промежуточных (нет соседних), думаю, лучше соответствующие Di^2 умножить на два. А для Ваших целей подгонки с акцентом на последние точки можно поиграть еще и весами нескольких последних точек, заведя для весов еще один столбец.
Если будет выходить криво, придется учесть единицы измерения. Для того, чтобы в подсчете расстояния влияние X и Y было почти одинаковым (а R ведь подвержен обоим влияниям), нужно к качестве X брать не номер i, а тот же номер, умноженный на выравнивающий масштаб, так, чтобы диапазоны X и Y были близки по размеру.
P.S. Оказывается, sernam.ru очень хитро избавился от обвинений в нарушении авторских прав, публикуя тексты книг только по частям и без указания выходных данных, в частности, наименований книг. В sernam.ru можно встретить тексты, которых больше нигде в инет не найдешь.
понял, что минимизировать нужно по формуле Di = ((Xi-Xc)^2 + (Yi-Yc)^2)^0.5 - R.
потом нужно будет по игрекам найденную окружность построить.
уравнение будет...
y=(R^2-(X-Xc)^2)^0.5+Yc
так что, не сильно тратьте время на это направление. хотя можете построить индикатор, основанный на дуге, а не на прямой, как машка. может он будет работать лучше, чем sma.
вот какую я формулу брал.
общее уравнение дуги:
(x - L)^2+ (y + (R - H))^2 = R^2
y = sqrt(R^2 - (x - L)^2) - (R - H) , где формула для R на рисунке.
Но это подходит только для положительной плоскости. для эксперимента брал "ценовой канал по дуге", который лежит в положительной плоскости.
может просто выбрано красивое название...
RRR5:
...
Но это подходит только для положительной плоскости. для эксперимента брал "ценовой канал по дуге", который лежит в положительной плоскости.
Что такое "положительная плоскость"?
Что такое "положительная плоскость"?
а для такой нет
ну для такой дуги сработает
а для такой нет
RRR5, Вы быстро делаете рисунки. Чем, интересно?
Почитал я здесь рассуждения о полиномах, МНК, различных методах аппроксимации, о возможности прогнозирования и т.д. ...
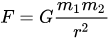
Кто-то верит в прогноз, кто-то нет.
Но то, что я надеялся найти, так и не увидел.
Чтобы попытаться объяснить, что я имею ввиду, я прибегну к аналогии с гравитацией во Вселенной.
Вот посмотрите на анимированную гифку, которую я записал.
Ответьте сами себе на вопрос. Можно ли спрогнозировать траекторию движения каждого объекта?
Ну конечно же можно.
Но только если вы знаете информацию о каждом объекте в данный момент: его массу, текущее положение и направление движения, время появление объекта и время его исчезновения.
А дальше дело математики и расчетов с применением по сути только одной формулы (для варианта классической механики для скоростей, далеких от скорости света):
сама программа - гравитационная залипалка вот здесь. Можете поиграться.
Нужно также понимать , что даже наша планета движется не по замкнутому кругу, а по сути по трехмерной синусоиде(спирали).
Вот в этом видео это наглядно продемонстрировано :
Ну а если у нас нет информации о всех объектах?
Можно ли прогнозировать траекторию, зная только саму траекторию в прошлом?
Вот здесь и начинается самое интересное.
Если кто-то скажет, что нет нельзя - то ответ будет не верным. Так же неверным будет утвердительный ответ.
Решение данной задачи будет только лишь вероятностным.
Задачу нужно решать от обратного. По прошлой траектории сначала нужно рассчитать вероятностные траектории основных "сгустков" объектов и их массу. Чтобы потом спрогнозировать вероятностные модели возможных траекторий.
Вот для этого и нужна базовая задача ИИ - распознание образов.
О чем, как я понял, и говорил Максим Дмитриевский.
Лет шесть назад я опубликовал в КБ свои первые наработки в этой области: https://www.mql5.com/ru/code/10882. Я как раз для распознания там каналов использовал полином 1 степени (Линейная регрессия). После этого я значительно продвинулся в этой области. Но ничего не публикую и не буду по очевидным причинам. Только лишь даю подсказки для пытливых умов.
Нахождение линейных каналов по сути и является нахождением центров этих гравитационных масс.
И, как правило, в любом инструменте (символе) существует от 5 до 10 таких центров (каналов). Для прогнозировании цены нужно учитывать их все одновременно. Только лишь в этом случае правильность прогноза вверх или вниз будет значительно превышать 50%.
Все же пытаются найти какой то особый набор чисел и наивно полагают что они будут прогнозировать будущее.
Дело в том, что этот "набор чисел" живой, динамичный, он постоянно меняется, так же как меняется и положение локальных центров масс множества объектов в аналогии с материальной гравитацией. И задача сводится в нахождении закона изменения этого "набора чисел" и даже нахождения закона изменения самого закона :))
В идеале этот "набор чисел" должен пересчитываться с каждым тиком. Вот именно поэтому я не однократно говорил, что то, что многие называют оптимизацией, находя конкретный "набор чисел" является банальной подгонкой под исторические данные.
Считаю аналогию с гравитацией весьма уместной. На рынке гравитацию создают деньги. Кто-то войдет со 100 долларами, кто-то с несколькими миллиардами. Здесь работают те же законы тяготения и даже та же самая формула, которую я давал выше. Сила притяжения обратно пропорциональна квадрату расстояния и прямо пропорциональна массам. Поэтому и полиномиальная регрессия 2 степени (парабола) самый уместный инструмент. Хотя логичнее было бы использовать гиперболу, ведь именно по законам гиперболы происходит взаимодействие двух гравитационных тел. Но, дело в том, что парабола гораздо удобней для расчетов, а так же парабола и гипербола очень похожи друг на друга на самом важном промежутке.
Вот здесь это наглядно видно. Красная линия - парабола, синяя - гипербола.
Главное отличие гравитации денег от гравитации небесных тел - это то, что деньги могут внезапно появляться и внезапно исчезать, создавая мощные гравитационные колебания. Но для вычисления этого события и существует такое понятие как пробой канала.
Решение данной задачи будет только лишь вероятностным.
Задачу нужно решать от обратного. По прошлой траектории сначала нужно рассчитать вероятностные траектории основных "сгустков" объектов и их массу. Чтобы потом спрогнозировать вероятностные модели возможных траекторий.
Боюсь, "вероятностным решением" здесь будет все множество любых траекторий в заданном пространстве - и какая ценность этого решения ?
Это все равно, что "с высокой вероятностью" утверждать, что евродоллар в этом году не будет иметь отрицательное значение, не больше 100. Заметь, вероятность этого утверждения близка к 100%. Но много ли пользы ты получишь от такого "прогноза" ?
В теории вероятности доказывается, что когда на состояние объекта влияют много независимых сил - вероятность состояния начинает подчиняться закону Гаусса. Но, ход и значение цен этому распределению не подчиняется по той простой причине, что входы и выходы участников рынка - зависимы.
RRR5:
понял, что минимизировать нужно по формуле Di = ((Xi-Xc)^2 + (Yi-Yc)^2)^0.5 - R.
...
Но это подходит только для положительной плоскости. для эксперимента брал "ценовой канал по дуге", который лежит в положительной плоскости.
Так и не понял, чем тебе не нравится МНК. Он ведь нормально строит любую из указанных кривых.
Люблю на мелких ТФ работать, но вот такие закидоны не люблю.
Чем их можно предсказать?