Algorithmes d'optimisation de la population

MetaTrader 5 — Exemples | 7 juin 2023, 09:36

833

Andrey Dik

"Rien ne se passe dans l'univers
sans qu’un minimum ou un maximum apparaisse"
Leonhard Euler, 18e siècle

Sommaire :

1. Perspective historique

Les algorithmes d'optimisation sont des algorithmes permettant de trouver des points extrêmes dans le domaine d'une fonction, où la fonction atteint sa valeur minimale ou maximale.

Les experts grecs de l'Antiquité le savaient déjà :

- De toutes les formes ayant un périmètre donné, le cercle a la plus grande surface.

- De tous les polygones ayant un nombre donné de côtés et un périmètre donné, le polygone régulier est celui qui a la plus grande surface.

- De toutes les figures tridimensionnelles ayant une surface donnée, la sphère est celle qui a le plus grand volume.

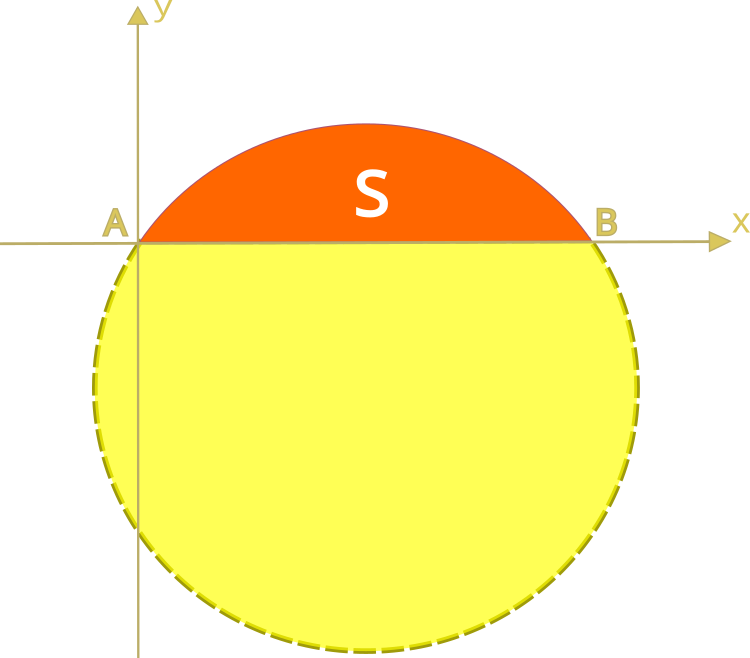
Le premier problème ayant des solutions variationnelles a été proposé à peu près à la même époque. Selon la légende, cela s'est produit vers l’an -825. Didon, la sœur du roi de la ville phénicienne de Tyr, s'est installée sur la côte sud de la Méditerranée et a demandé à une tribu locale un terrain qui pourrait tenir dans une peau de taureau. Les habitants lui ont donné une peau de bête. La jeune fille débrouillarde l'a découpé en bandes fines et les a attachées pour en faire une corde. Avec cette corde, elle couvre le territoire au large de la côte et y fonde la ville de Carthage.

Le problème consiste à trouver la courbe la plus efficace, couvrant la surface maximale, parmi les courbes planes fermées d'une longueur donnée. L'aire maximale dans ce problème est représentée par l'aire circonscrite par un demi-cercle.

didon 1

Passons sur une grande partie de l'histoire, y compris l'ancienne culture de la Méditerranée, l'oppression de l'Inquisition et le charlatanisme au Moyen-Âge, jusqu'à la Renaissance avec sa libre circulation de la pensée et ses nouvelles théories. En juin 1696, Jean Bernoulli publie le texte suivant à l'intention des lecteurs des Acta Eruditorum : "Moi, Johann Bernoulli, je m'adresse aux plus brillants mathématiciens du monde. Rien n'est plus attrayant pour les personnes intelligentes qu'un problème honnête et difficile, dont la solution possible apportera la célébrité et restera un monument durable. Suivant l'exemple de Pascal, Fermat, etc., j'espère gagner la gratitude de toute la communauté scientifique en plaçant devant les meilleurs mathématiciens de notre temps un problème qui mettra à l'épreuve leurs méthodes et la force de leur intelligence. Si quelqu'un me communique la solution du problème proposé, je le déclarerai publiquement digne d'éloges".

Le problème du brachistochrone de Jean Bernoulli :

"Étant donné deux points A et B dans un plan vertical, quelle est la courbe tracée par un point soumis à la seule action de la pesanteur, qui part de A et atteint B en un minimum de temps ? Fait remarquable, Galilée a tenté de résoudre un problème similaire en 1638, bien avant la publication de Bernoulli. La réponse : le chemin le plus rapide, d'un point à un autre, n'est pas le chemin le plus court, comme il semble l'être à première vue, ni une ligne droite, mais une courbe - une cycloïde qui détermine la courbure de la courbe en chaque point.

Brachistochrone 9

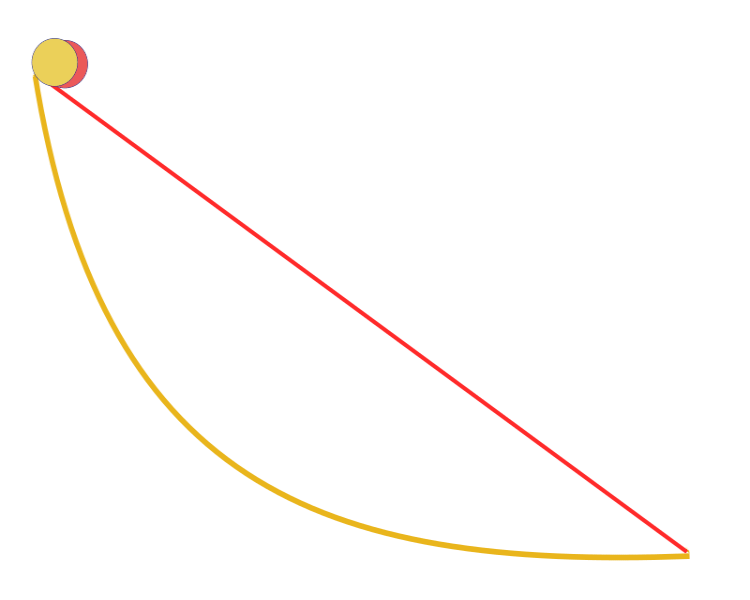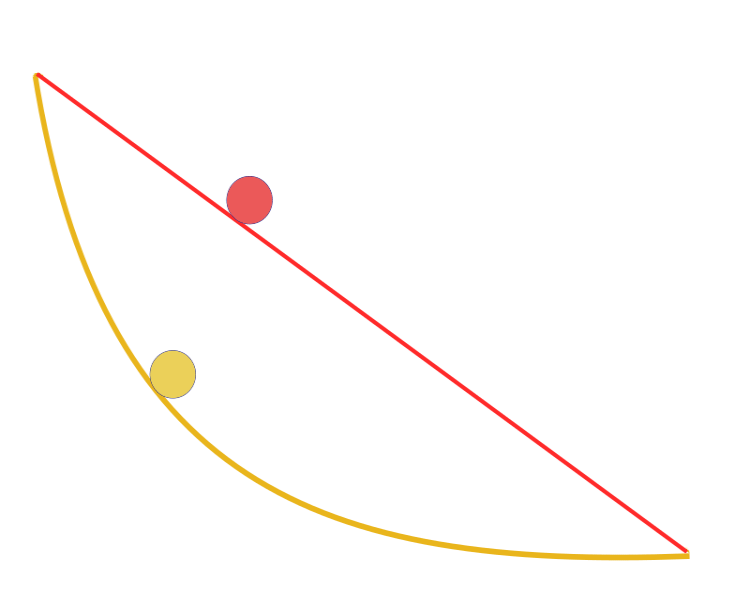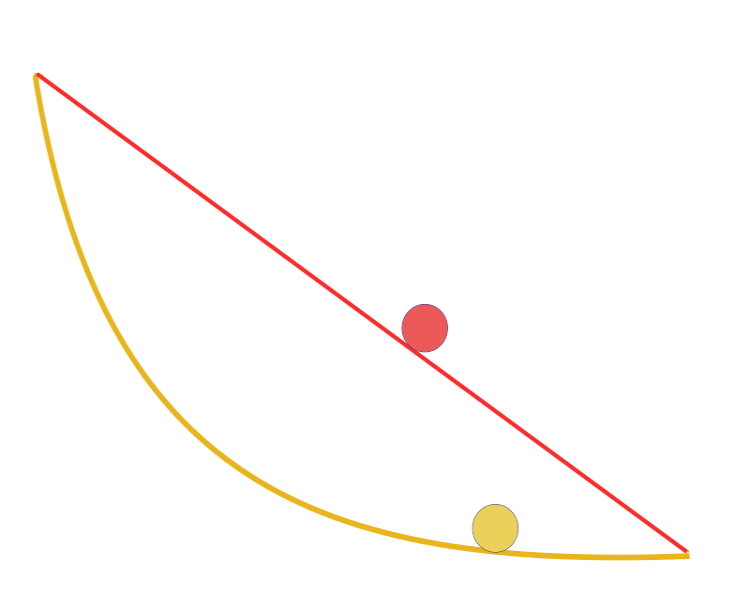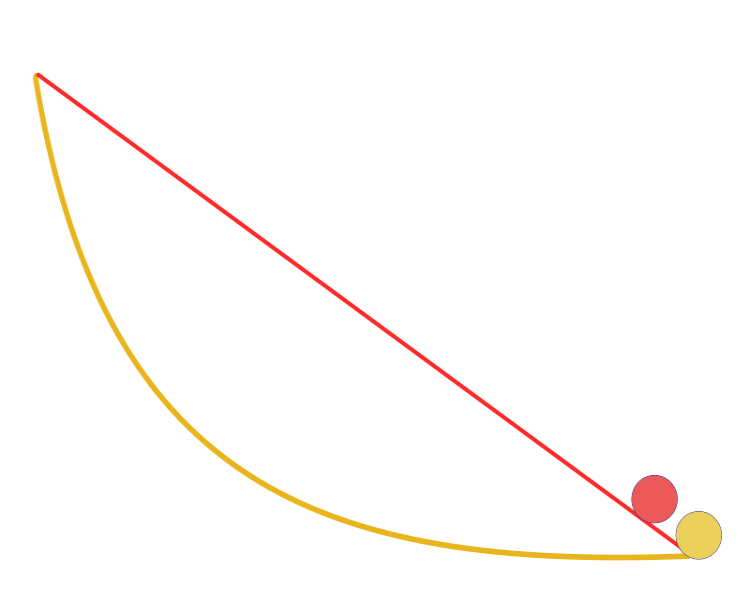
Courbe brachistochrone

Toutes les autres solutions, y compris celle de Newton (qui n'a pas été révélée à l'époque), sont basées sur la recherche du gradient en chaque point. La méthode de la solution proposée par Isaac Newton est à la base du calcul variationnel. Les méthodes de calcul variationnel sont généralement appliquées à la résolution de problèmes dont les critères d'optimalité sont présentés sous la forme de fonctions et dont les solutions sont des fonctions inconnues. Ces problèmes se posent généralement dans l'optimisation statique des processus avec des paramètres distribués ou dans les problèmes d'optimisation dynamique.

Les conditions d'extrémité du premier ordre dans le calcul variationnel ont été obtenues par Léonard Euler et Joseph-Louis Lagrange (les équations d'Euler-Lagrange). Ces équations sont largement utilisées dans les problèmes d'optimisation et, avec le principe de l'action stationnaire, sont appliquées dans les calculs de trajectoires en mécanique. Il est cependant rapidement apparu que les solutions de ces équations ne donnaient pas toujours un véritable extremum, ce qui signifie que des conditions suffisantes garantissant sa découverte sont nécessaires. Le travail s'est poursuivi et des conditions d'extrémité du second ordre ont été dérivées par Legendre et Jacobi, puis par l'élève de ce dernier, Hesse. La question de l'existence d'une solution dans le calcul variationnel a été soulevée pour la première fois par Weierstrass dans la seconde moitié du 19ème siècle.

Dès la seconde moitié du XVIIIe siècle, la recherche de solutions optimales aux problèmes a constitué les fondements mathématiques et les principes de l'optimisation. Malheureusement, les méthodes d'optimisation ont été peu utilisées dans de nombreux domaines scientifiques et technologiques jusqu'à la seconde moitié du 20e siècle, car l'utilisation pratique des méthodes mathématiques nécessitait d'énormes ressources informatiques. L'avènement des nouvelles technologies informatiques dans le monde moderne a finalement rendu possible la mise en œuvre de méthodes d'optimisation complexes, donnant lieu à une grande variété d'algorithmes disponibles.

Les années 1980 ont vu le début du développement intensif de la classe des algorithmes d'optimisation stochastiques, qui sont le résultat d'une modélisation empruntée à la nature.

2. Classification des OA

Classe

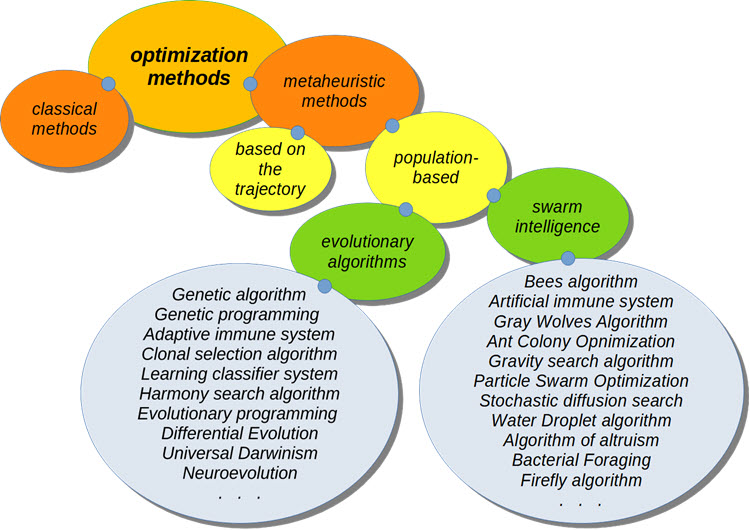
Classification des AO

Lors de l'optimisation des systèmes de trading, les algorithmes d'optimisation métaheuristiques sont les plus excitants. Ils ne nécessitent pas de connaître la formule de la fonction à optimiser. Leur convergence vers l'optimum global n'a pas été prouvée, mais il a été établi expérimentalement qu’ils donnent une assez bonne solution dans la plupart des cas, ce qui est suffisant pour un certain nombre de problèmes.

De nombreux AO sont apparus comme des modèles empruntés à la nature. Ces modèles sont également appelés modèles comportementaux, d'essaimage ou de population, tels que le comportement des oiseaux en vol (algorithme de l'essaim de particules) ou les principes du comportement des colonies de fourmis (algorithme de la fourmi).

Les algorithmes de population impliquent le traitement simultané de plusieurs options pour résoudre le problème d'optimisation et représentent une alternative aux algorithmes classiques basés sur les trajectoires de mouvement dont la zone de recherche n'a qu'un seul candidat évoluant lors de la résolution du problème.

3. Convergence et taux de convergence : Stabilité de la convergence - Évolutivité des algorithmes d'optimisation

L'efficacité, la vitesse, la convergence, ainsi que les effets des conditions du problème et des paramètres de l'algorithme nécessitent une analyse minutieuse pour chaque implémentation algorithmique et pour chaque classe de problèmes d'optimisation.

3.1) Convergence et taux de convergence

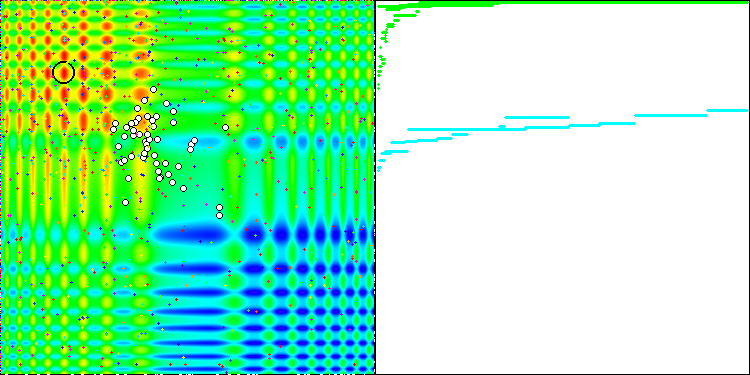
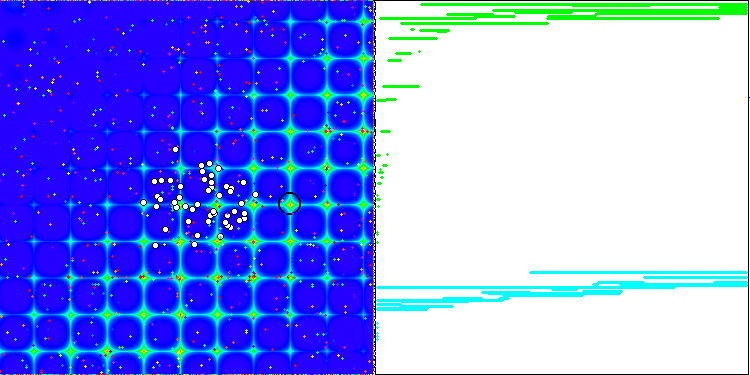
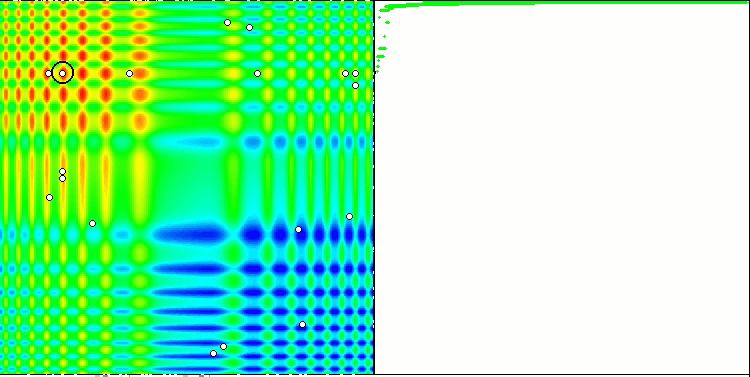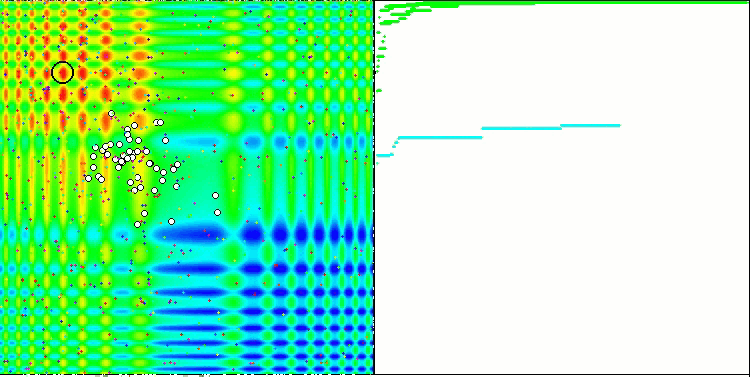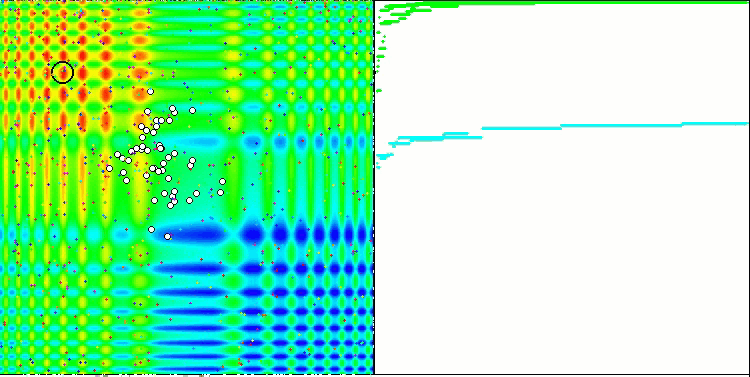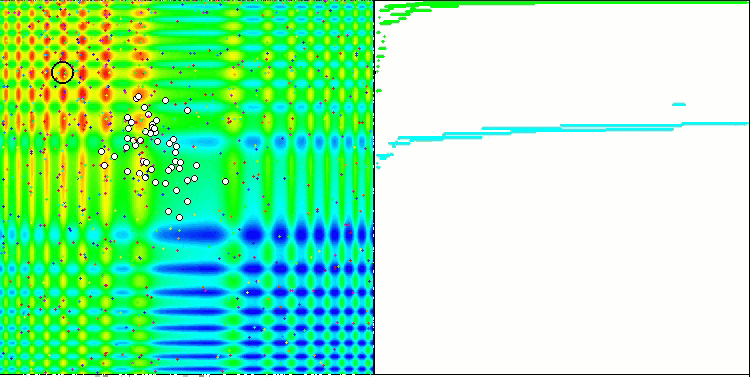
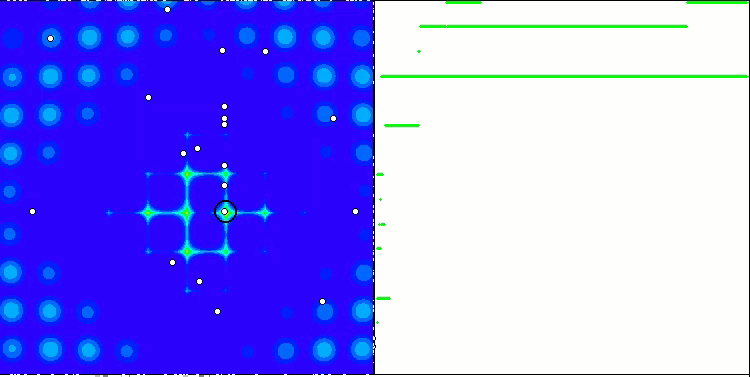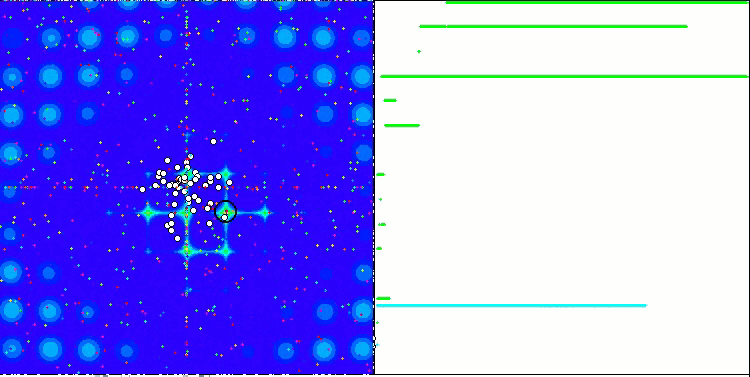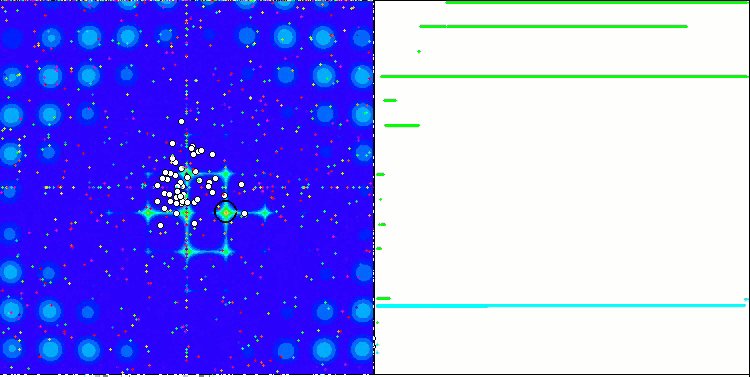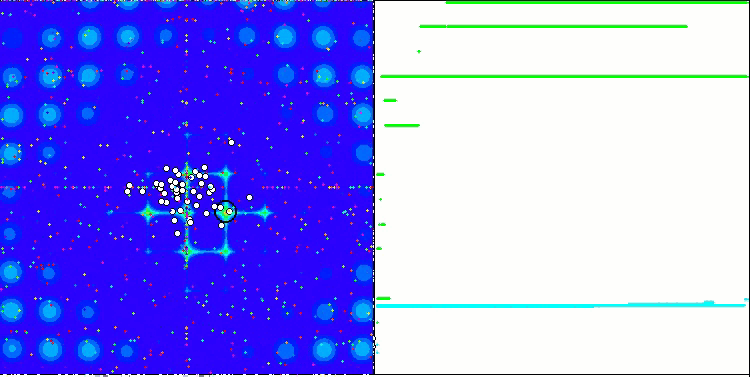
La convergence est la propriété d'un algorithme itératif d'atteindre l'optimum de la fonction objective ou de s'en approcher suffisamment en un nombre fini d'étapes. Sur le côté droit des captures d'écran ci-dessus, nous pouvons voir le graphique (construit itérativement) des résultats obtenus par la fonction de test calculée. Grâce à ces deux images, nous pouvons conclure que la convergence est affectée par la complexité de la surface de la fonction. Plus il est complexe, plus il est difficile de trouver l'extremum global.

Le taux de convergence des algorithmes est l'un des indicateurs les plus importants de la qualité d'un algorithme d'optimisation et l'une des principales caractéristiques des méthodes d'optimisation. Lorsqu'on entend dire qu'un algorithme est plus rapide qu'un autre, il s'agit dans la plupart des cas du taux de convergence. Plus le résultat est proche de l'extremum global et plus il est obtenu rapidement (c'est-à-dire plus les itérations de l'algorithme sont précoces), plus ce paramètre est élevé. Il convient de noter que le taux de convergence des méthodes ne dépasse généralement pas le taux quadratique. Dans de rares cas, la méthode peut avoir un taux de convergence cubique.

3.2) Stabilité de la convergence

Le nombre d'itérations nécessaires pour atteindre le résultat dépend non seulement de la capacité de recherche de l'algorithme lui-même, mais aussi de la fonction étudiée. Si la fonction est caractérisée par une grande complexité de la surface (présence de courbes prononcées, de discrétions, de discontinuités), l'algorithme peut s'avérer instable et incapable de fournir une précision acceptable. De plus, la stabilité de la convergence peut être comprise comme étant la répétabilité des résultats de l'optimisation lorsque plusieurs tests consécutifs sont effectués. Si les résultats présentent des écarts importants entre les valeurs, la stabilité de l'algorithme est faible.

3.3) Évolutivité des algorithmes d'optimisation

convergence 7 convergence 6

L'évolutivité des algorithmes d'optimisation est la capacité à maintenir la convergence avec une augmentation de la dimension du problème. En d'autres termes, avec l'augmentation du nombre de variables de la fonction optimisée, la convergence devrait rester à un niveau acceptable pour des raisons pratiques. Les algorithmes de population pour l'optimisation de la recherche présentent des avantages indéniables par rapport aux algorithmes classiques, en particulier lorsqu'il s'agit de résoudre des problèmes de grande dimension et mal formalisés. Dans ces conditions, les algorithmes de population peuvent offrir une forte probabilité de localiser l'extrémité globale de la fonction optimisée.

Dans le cas d'une fonction optimisée lisse et unimodale, les algorithmes de population sont généralement moins efficaces que n'importe quelle méthode de gradient classique. Les inconvénients des algorithmes de population incluent également une forte dépendance de leur efficacité par rapport aux degrés de liberté (le nombre de paramètres de réglage), qui sont assez nombreux dans la plupart des algorithmes.

4. Fonctions de test, construction d'un critère d'évaluation OA complexe

Il n'existe pas de méthodologie généralement acceptée pour tester et comparer les algorithmes d'optimisation. Toutefois, de nombreuses fonctions d'essai ont été proposées par les chercheurs au fil des ans. Nous utiliserons les fonctions que j'ai créées avant la publication du premier article. Ces fonctions se trouvent dans \MQL5\Experts\Exemples\Math 3D\Functions.mqh et \MQL5\Experts\Exemples\Math 3D Morpher\Functions.mqh. Ces fonctions répondent à tous les critères de complexité pour les tests des AO. De plus, les fonctions Forest et Megacity ont été développées pour fournir une étude plus complète des capacités de recherche des AO.

Fonction de test de Skin :

La fonction est lisse sur l'ensemble de son domaine et présente de nombreuses valeurs locales min/max qui diffèrent de manière insignifiante (pièges de convergence), ce qui bloque les algorithmes qui n'atteignent pas l'extremum global.

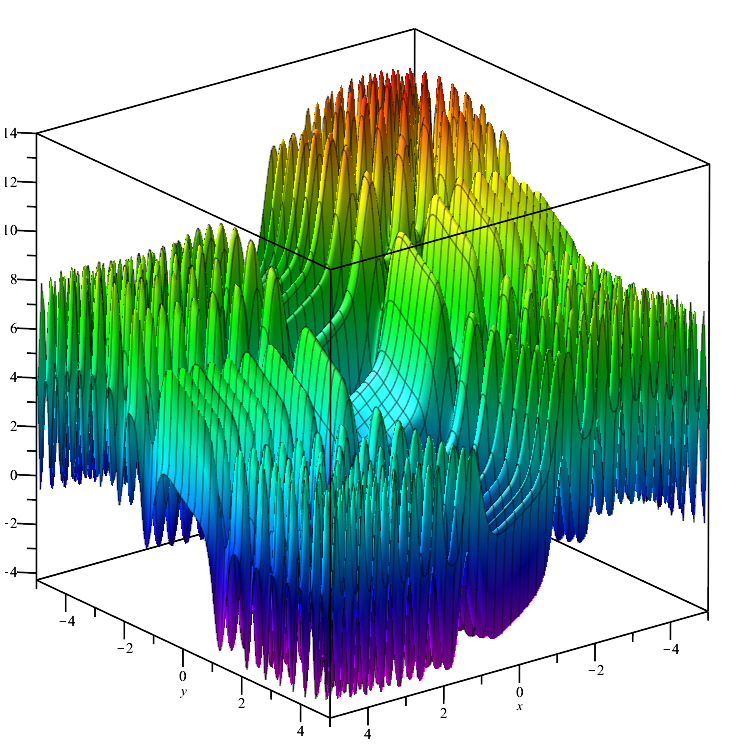
Skin

Fonction de test de Forest :

La fonction représente plusieurs maximums qui n'ont pas de différentiel en leurs points. Elle peut donc s'avérer difficile pour les algorithmes d'optimisation, dont la robustesse dépend essentiellement du caractère lisse de la fonction étudiée.

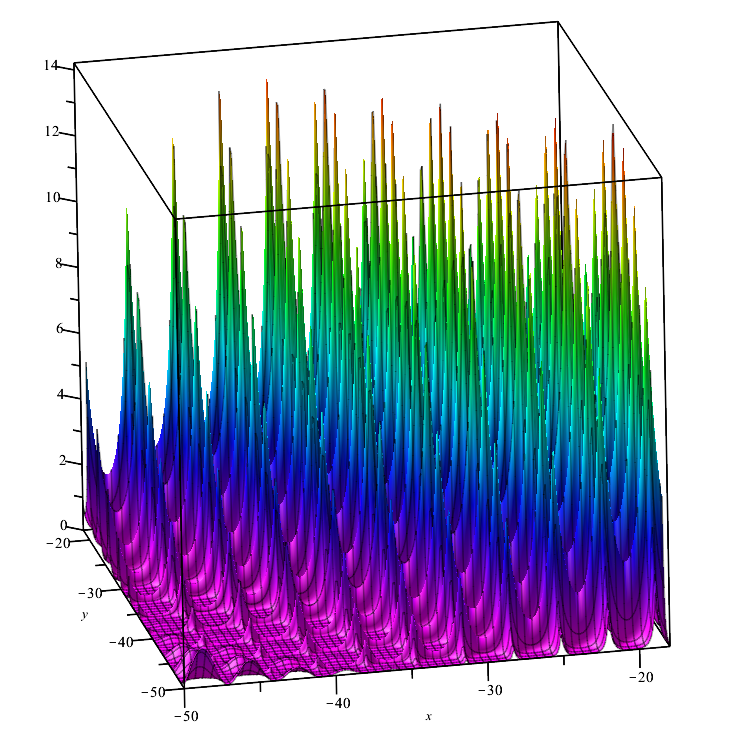
Forest

Fonction de test de Megacity :

Une fonction discrète qui forme des "zones" (où la modification des variables n'entraîne pas de changement significatif dans la valeur de la fonction). Elle pose donc un problème pour les algorithmes qui nécessitent un gradient.

Chinatown

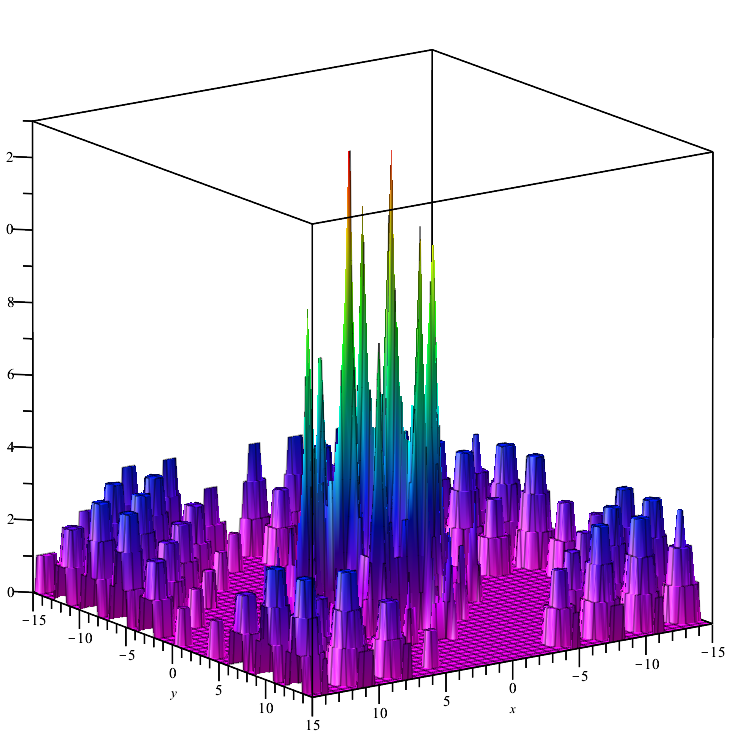
Megacity

5. Banc d'essai

Pour une comparaison complète des algorithmes d'optimisation, on a tenté de créer un critère d'évaluation général. La complexité de cette idée réside dans le fait qu'il n'est pas évident de comparer les algorithmes. Chacun d'entre eux est bon à sa manière pour la classe de problèmes correspondante. Par exemple, un algorithme converge rapidement mais ne s'adapte pas bien, tandis qu'un autre s'adapte bien mais est instable.

Convergence : Pour étudier la convergence, nous utilisons les 3 fonctions présentées ci-dessus. Leur minimum et leur maximum sont convertis en une fourchette allant de 0,0 (pire résultat) à 1,0 (meilleur résultat), ce qui nous permet d'évaluer la capacité des algorithmes à assurer la convergence sur différents types de problèmes.
Taux de convergence : Les meilleurs résultats de l'algorithme sont mesurés à la 1000ème et à la 10 000ème exécution de la fonction testée. Nous pouvons ainsi voir à quelle vitesse l'AO converge. Plus la convergence est rapide, plus le graphique de convergence est incurvé vers le maximum.
Stabilité : Effectuez 5 cycles d'optimisation pour chacune des fonctions et calculez la valeur moyenne dans l'intervalle de 0,0 à 1,0. Cela est nécessaire car les résultats de certains algorithmes peuvent varier considérablement d'une exécution à l'autre. Plus la convergence est élevée dans chacun des 5 tests, plus la stabilité est grande.
Évolutivité : Certains AO ne peuvent montrer des résultats pratiques que sur des fonctions avec un petit nombre de variables : par exemple, moins de 2 variables, et certains ne sont même pas capables de travailler avec plus d’1 variable. Il existe aussi des algorithmes capables de travailler avec des fonctions comportant un millier de variables. Ces algorithmes d'optimisation peuvent être utilisés comme AO pour les réseaux neuronaux.

Pour faciliter l'utilisation des fonctions de test, écrivons une classe mère et un énumérateur qui nous permettra de sélectionner un objet de la classe enfant de la fonction de test correspondante à l'avenir :

//——————————————————————————————————————————————————————————————————————————————
class C_Function
{
  public: //====================================================================
  double CalcFunc (double &args [], //function arguments
                   int     amount)  //amount of runs functions
  {
    double x, y;
    double sum = 0.0;
    for (int i = 0; i < amount; i++)
    {
      x = args [i * 2];
      y = args [i * 2 + 1];

      sum += Core (x, y);
    }

    sum /= amount;

    return sum;
  }
  double GetMinArg () { return minArg;}
  double GetMaxArg () { return maxArg;}
  double GetMinFun () { return minFun;}
  double GetMaxFun () { return maxFun;}
  string GetNamFun () { return fuName;}

  protected: //==================================================================
  void SetMinArg (double min) { minArg = min;}
  void SetMaxArg (double max) { maxArg = max;}
  void SetMinFun (double min) { minFun = min;}
  void SetMaxFun (double max) { maxFun = max;}
  void SetNamFun (string nam) { fuName = nam;}

  private: //====================================================================
  virtual double Core (double x, double y) { return 0.0;}
  
  double minArg;
  double maxArg;
  double minFun;
  double maxFun;
  string fuName;
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
enum EFunc
{
  Skin,
  Forest,
  Megacity,
  
};
C_Function *SelectFunction (EFunc f)
{
  C_Function *func;
  switch (f)
  {
    case  Skin:
      func = new C_Skin (); return (GetPointer (func));
    case  Forest:
      func = new C_Forest (); return (GetPointer (func));
    case  Megacity:
      func = new C_Megacity (); return (GetPointer (func));
    
    default:
      func = new C_Skin (); return (GetPointer (func));
  }
}
//——————————————————————————————————————————————————————————————————————————————

Les classes enfants ressembleront alors à ceci :

//——————————————————————————————————————————————————————————————————————————————
class C_Skin : public C_Function
{
  public: //===================================================================
  C_Skin ()
  {
    SetNamFun ("Skin");
    SetMinArg (-5.0);
    SetMaxArg (5.0);
    SetMinFun (-4.3182);  //[x=3.07021;y=3.315935] 1 point
    SetMaxFun (14.0606);  //[x=-3.315699;y=-3.072485] 1 point
  }

  private: //===================================================================
  double Core (double x, double y)
  {
    double a1=2*x*x;
    double a2=2*y*y;
    double b1=MathCos(a1)-1.1;
    b1=b1*b1;
    double c1=MathSin(0.5*x)-1.2;
    c1=c1*c1;
    double d1=MathCos(a2)-1.1;
    d1=d1*d1;
    double e1=MathSin(0.5*y)-1.2;
    e1=e1*e1;

   double res=b1+c1-d1+e1;
   return(res);
  }
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
class C_Forest : public C_Function
{
  public: //===================================================================
  C_Forest ()
  {
    SetNamFun ("Forest");
    SetMinArg (-50.0);
    SetMaxArg (-18.0);
    SetMinFun (0.0);             //many points
    SetMaxFun (15.95123239744);  //[x=-25.132741228718345;y=-32.55751918948773] 1 point
  }

  private: //===================================================================
  double Core (double x, double y)
  {
    double a = MathSin (MathSqrt (MathAbs (x - 1.13) + MathAbs (y - 2.0)));
    double b = MathCos (MathSqrt (MathAbs (MathSin (x))) + MathSqrt (MathAbs (MathSin (y - 2.0))));
    double f = a + b;

    double res = MathPow (f, 4);
    if (res < 0.0) res = 0.0;
    return (res);
  }
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
class C_Megacity : public C_Function
{
  public: //===================================================================
  C_Megacity ()
  {
    SetNamFun ("Megacity");
    SetMinArg (-15.0);
    SetMaxArg (15.0);
    SetMinFun (0.0);   //many points
    SetMaxFun (15.0);  //[x=`3.16;y=1.990] 1 point
  }

  private: //===================================================================
  double Core (double x, double y)
  {
    double a = MathSin (MathSqrt (MathAbs (x - 1.13) + MathAbs (y - 2.0)));
    double b = MathCos (MathSqrt (MathAbs (MathSin (x))) + MathSqrt (MathAbs (MathSin (y - 2.0))));
    double f = a + b;

    double res = floor (MathPow (f, 4));
    return (res);
  }
};
//——————————————————————————————————————————————————————————————————————————————

Pour vérifier la validité des résultats des tests AO obtenus sur le banc d'essai, nous pouvons utiliser un script énumérant les fonctions X et Y avec la taille de pas « Step ». Faites attention au choix du pas, car un pas très petit rendra le calcul très long. Par exemple, la fonction Skin a pour plage d'arguments [-5 ; 5]. Avec un pas de 0,00001 le long de l'axe X, il y aura (5 - (-5)) / 0,00001 = 1.000.000 de pas, le même nombre le long de l'axe Y, respectivement, le nombre total d'exécutions de la fonction de test pour calculer la valeur de chacun des points sera égal à 1.000.000 х 1.000.000 = 1.000.000.000.000 (10^12, trillion).

Il est nécessaire de comprendre à quel point la tâche est difficile pour l’AO, puisqu'il doit trouver le maximum en seulement 10 000 étapes (c'est approximativement cette valeur qui est utilisée dans l'optimiseur de MetaTrader 5). Veuillez noter que ce calcul est effectué pour une fonction à 2 variables, et que le nombre maximum de variables qui seront utilisées dans les tests est de 1.000.

Gardez à l'esprit ce qui suit : les tests d'algorithmes dans cet article et les suivants utilisent un pas de 0,0 (zéro !), soit le pas minimum possible pour une implémentation spécifique de l'OA correspondant.

//——————————————————————————————————————————————————————————————————————————————
input EFunc  Function          = Skin;
input double Step              = 0.01;

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  C_Function *TestFunc = SelectFunction (Function);

  double argMin = TestFunc.GetMinArg ();
  double argMax = TestFunc.GetMaxArg ();

  double maxFuncValue = 0;
  double xMaxFunc     = 0.0;
  double yMaxFunc     = 0.0;
  
  double minFuncValue = 0;
  double xMinFunc     = 0.0;
  double yMinFunc     = 0.0;
  
  double fValue       = 0.0;

  double arg [2];

  arg [0] = argMin;
  arg [1] = argMin;

  long cnt = 0;

  while (arg [1] <= argMax && !IsStopped ())
  {
    arg [0] = argMin;

    while (arg [0] <= argMax && !IsStopped ())
    {
      cnt++;

      fValue = TestFunc.CalcFunc (arg, 1);

      if (fValue > maxFuncValue)
      {
        maxFuncValue = fValue;
        xMaxFunc = arg [0];
        yMaxFunc = arg [1];
      }
      if (fValue < minFuncValue)
      {
        minFuncValue = fValue;
        xMinFunc = arg [0];
        yMinFunc = arg [1];
      }

      arg [0] += Step;
      
      if (cnt == 1)
      {
       maxFuncValue = fValue;
       minFuncValue = fValue;
      }
    }

    arg [1] += Step;
  }
  
  Print ("======", TestFunc.GetNamFun (), ", launch counter: ", cnt);
  Print ("MaxFuncValue: ", DoubleToString (maxFuncValue, 16), " X: ", DoubleToString (xMaxFunc, 16), " Y: ", DoubleToString (yMaxFunc, 16));
  Print ("MinFuncValue: ", DoubleToString (minFuncValue, 16), " X: ", DoubleToString (xMinFunc, 16), " Y: ", DoubleToString (yMinFunc, 16));
         
  delete TestFunc;
}

//——————————————————————————————————————————————————————————————————————————————

Écrivons un banc d'essai :

#include <Canvas\Canvas.mqh>
#include <\Math\Functions.mqh>
#include "AO_RND.mqh"

//——————————————————————————————————————————————————————————————————————————————
input int    Population_P       = 50;
input double ArgumentStep_P     = 0.0;
input int    Test1FuncRuns_P    = 1;
input int    Test2FuncRuns_P    = 20;
input int    Test3FuncRuns_P    = 500;
input int    Measur1FuncValue_P = 1000;
input int    Measur2FuncValue_P = 10000;
input int    NumberRepetTest_P  = 5;
input int    RenderSleepMsc_P   = 0;

//——————————————————————————————————————————————————————————————————————————————
int WidthMonitor = 750;  //monitor screen width
int HeighMonitor = 375;  //monitor screen height

int WidthScrFunc = 375 - 2;  //test function screen width
int HeighScrFunc = 375 - 2;  //test function screen height

CCanvas Canvas;  //drawing table
C_AO_RND AO;     //AO object

C_Skin       SkiF;
C_Forest     ForF;
C_Megacity  ChiF;

struct S_CLR
{
    color clr [];
};

S_CLR FunctScrin []; //two-dimensional matrix of colors
double ScoreAll = 0.0;

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  //creating a table -----------------------------------------------------------
  string canvasName = "AO_Test_Func_Canvas";
  if (!Canvas.CreateBitmapLabel (canvasName, 5, 30, WidthMonitor, HeighMonitor, COLOR_FORMAT_ARGB_RAW))
  {
    Print ("Error creating Canvas: ", GetLastError ());
    return;
  }
  ObjectSetInteger (0, canvasName, OBJPROP_HIDDEN, false);
  ObjectSetInteger (0, canvasName, OBJPROP_SELECTABLE, true);

  ArrayResize (FunctScrin, HeighScrFunc);
  for (int i = 0; i < HeighScrFunc; i++)
  {
    ArrayResize (FunctScrin [i].clr, HeighScrFunc);
  }
  
  //============================================================================
  //Test Skin###################################################################
  Print ("=============================");
  CanvasErase ();
  FuncTests (SkiF, Test1FuncRuns_P, SkiF.GetMinFun (), SkiF.GetMaxFun (), -3.315699, -3.072485, clrLime);
  FuncTests (SkiF, Test2FuncRuns_P, SkiF.GetMinFun (), SkiF.GetMaxFun (), -3.315699, -3.072485, clrAqua);
  FuncTests (SkiF, Test3FuncRuns_P, SkiF.GetMinFun (), SkiF.GetMaxFun (), -3.315699, -3.072485, clrOrangeRed);
  
  //Test Forest#################################################################
  Print ("=============================");
  CanvasErase ();
  FuncTests (ForF, Test1FuncRuns_P, ForF.GetMinFun (), ForF.GetMaxFun (), -25.132741228718345, -32.55751918948773, clrLime);
  FuncTests (ForF, Test2FuncRuns_P, ForF.GetMinFun (), ForF.GetMaxFun (), -25.132741228718345, -32.55751918948773, clrAqua);
  FuncTests (ForF, Test3FuncRuns_P, ForF.GetMinFun (), ForF.GetMaxFun (), -25.132741228718345, -32.55751918948773, clrOrangeRed);
  
  //Test Megacity#############################################################
  Print ("=============================");
  CanvasErase ();
  FuncTests (ChiF, Test1FuncRuns_P, ChiF.GetMinFun (), ChiF.GetMaxFun (), 3.16, 1.990, clrLime);
  FuncTests (ChiF, Test2FuncRuns_P, ChiF.GetMinFun (), ChiF.GetMaxFun (), 3.16, 1.990, clrAqua);
  FuncTests (ChiF, Test3FuncRuns_P, ChiF.GetMinFun (), ChiF.GetMaxFun (), 3.16, 1.990, clrOrangeRed);
  
  Print ("All score for C_AO_RND: ", ScoreAll / 18.0);
}
//——————————————————————————————————————————————————————————————————————————————

void CanvasErase ()
{
  Canvas.Erase (XRGB (0, 0, 0));
  Canvas.FillRectangle (1,                1, HeighMonitor - 2, HeighMonitor - 2, COLOR2RGB (clrWhite));
  Canvas.FillRectangle (HeighMonitor + 1, 1, WidthMonitor - 2, HeighMonitor - 2, COLOR2RGB (clrWhite));
}

//——————————————————————————————————————————————————————————————————————————————
void FuncTests (C_Function &f,
                int        funcCount,
                double     minFuncVal,
                double     maxFuncVal,
                double     xBest,
                double     yBest,
                color      clrConv)
{
  DrawFunctionGraph (f.GetMinArg (), f.GetMaxArg (), minFuncVal, maxFuncVal, f);
  SendGraphToCanvas (1, 1);
  int x = (int)Scale (xBest, f.GetMinArg (), f.GetMaxArg (), 0, WidthScrFunc - 1, false);
  int y = (int)Scale (yBest, f.GetMinArg (), f.GetMaxArg (), 0, HeighScrFunc - 1, false);
  Canvas.Circle (x + 1, y + 1, 10, COLOR2RGB (clrBlack));
  Canvas.Circle (x + 1, y + 1, 11, COLOR2RGB (clrBlack));
  Canvas.Update ();
  Sleep (1000);

  int xConv = 0.0;
  int yConv = 0.0;

  int EpochCmidl = 0;
  int EpochCount = 0;

  double aveMid = 0.0;
  double aveEnd = 0.0;

  //----------------------------------------------------------------------------
  for (int test = 0; test < NumberRepetTest_P; test++)
  {
    InitAO (funcCount * 2, f.GetMaxArg (), f.GetMinArg (), ArgumentStep_P);

    EpochCmidl = Measur1FuncValue_P / (ArraySize (AO.S_Colony));
    EpochCount = Measur2FuncValue_P / (ArraySize (AO.S_Colony));

    // Optimization-------------------------------------------------------------
    AO.F_EpochReset ();


    for (int epochCNT = 1; epochCNT <= EpochCount && !IsStopped (); epochCNT++)
    {
      AO.F_Preparation ();

      for (int set = 0; set < ArraySize (AO.S_Colony); set++)
      {
        AO.A_FFcol [set] = f.CalcFunc (AO.S_Colony [set].args, funcCount);
      }

      AO.F_Sorting ();

      if (epochCNT == EpochCmidl) aveMid += AO.A_FFpop [0];

      SendGraphToCanvas  (1, 1);

      //draw a population on canvas
      for (int i = 0; i < ArraySize (AO.S_Population); i++)
      {
        if (i > 0) PointDr (AO.S_Population [i].args, f.GetMinArg (), f.GetMaxArg (), clrWhite, 1, 1, funcCount);
      }
      PointDr (AO.S_Population [0].args, f.GetMinArg (), f.GetMaxArg (), clrBlack, 1, 1, funcCount);

      Canvas.Circle (x + 1, y + 1, 10, COLOR2RGB (clrBlack));
      Canvas.Circle (x + 1, y + 1, 11, COLOR2RGB (clrBlack));

      xConv = (int)Scale (epochCNT,       1,          EpochCount, 2, WidthScrFunc - 2, false);
      yConv = (int)Scale (AO.A_FFpop [0], minFuncVal, maxFuncVal, 1, HeighScrFunc - 2, true);

      Canvas.FillCircle (xConv + HeighMonitor + 1, yConv + 1, 1, COLOR2RGB (clrConv));

      Canvas.Update ();
      Sleep (RenderSleepMsc_P);
    }

    aveEnd += AO.A_FFpop [0];

    Sleep (1000);
  }

  aveMid /= (double)NumberRepetTest_P;
  aveEnd /= (double)NumberRepetTest_P;

  double score1 = Scale (aveMid, minFuncVal, maxFuncVal, 0.0, 1.0, false);
  double score2 = Scale (aveEnd, minFuncVal, maxFuncVal, 0.0, 1.0, false);
  
  ScoreAll += score1 + score2;

  Print (funcCount, " ", f.GetNamFun (), "'s; Func runs ", Measur1FuncValue_P, " result: ", aveMid, "; Func runs ", Measur2FuncValue_P, " result: ", aveEnd);
  Print ("Score1: ", DoubleToString (score1, 5), "; Score2: ", DoubleToString (score2, 5));
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void InitAO (const int    params,  //amount of the optimized arguments
             const double max,     //maximum of the optimized argument
             const double min,     //minimum of the optimized argument
             const double step)    //step of the optimized argument
{
  AO.F_Init (params, Population_P);
  for (int idx = 0; idx < params; idx++)
  {
    AO.A_RangeMax  [idx] = max;
    AO.A_RangeMin  [idx] = min;
    AO.A_RangeStep [idx] = step;
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void PointDr (double &args [], double Min, double Max, color clr, int shiftX, int shiftY, int count)
{
  double x = 0.0;
  double y = 0.0;
  
  double xAve = 0.0;
  double yAve = 0.0;
  
  int width  = 0;
  int height = 0;
  
  color clrF = clrNONE;
  
  for (int i = 0; i < count; i++)
  {
    xAve += args [i * 2];
    yAve += args [i * 2 + 1];
       
    x = args [i * 2];
    y = args [i * 2 + 1];
    
    width  = (int)Scale (x, Min, Max, 0, WidthScrFunc - 1, false);
    height = (int)Scale (y, Min, Max, 0, HeighScrFunc - 1, false);
    
    clrF = DoubleToColor (i, 0, count - 1, 0, 360);
    Canvas.FillCircle (width + shiftX, height + shiftY, 1, COLOR2RGB (clrF));
  }
  
  xAve /= (double)count;
  yAve /= (double)count;

  width  = (int)Scale (xAve, Min, Max, 0, WidthScrFunc - 1, false);
  height = (int)Scale (yAve, Min, Max, 0, HeighScrFunc - 1, false);

  Canvas.FillCircle (width + shiftX, height + shiftY, 3, COLOR2RGB (clrBlack));
  Canvas.FillCircle (width + shiftX, height + shiftY, 2, COLOR2RGB (clr));
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void SendGraphToCanvas (int shiftX, int shiftY)
{
  for (int w = 0; w < HeighScrFunc; w++)
  {
    for (int h = 0; h < HeighScrFunc; h++)
    {
      Canvas.PixelSet (w + shiftX, h + shiftY, COLOR2RGB (FunctScrin [w].clr [h]));
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void DrawFunctionGraph (double     min,
                        double     max,
                        double     fMin,
                        double     fMax,
                        C_Function &f)
{
  double ar [2];
  double fV;

  for (int w = 0; w < HeighScrFunc; w++)
  {
    ar [0] = Scale (w, 0, HeighScrFunc, min, max, false);
    for (int h = 0; h < HeighScrFunc; h++)
    {
      ar [1] = Scale (h, 0, HeighScrFunc, min, max, false);
      fV = f.CalcFunc (ar, 1);
      FunctScrin [w].clr [h] = DoubleToColor (fV, fMin, fMax, 0, 250);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
//Scaling a number from a range to a specified range
double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool Revers = false)
{
  if (OutMIN == OutMAX) return (OutMIN);
  if (InMIN == InMAX) return ((OutMIN + OutMAX) / 2.0);
  else
  {
    if (Revers)
    {
      if (In < InMIN) return (OutMAX);
      if (In > InMAX) return (OutMIN);
      return (((InMAX - In) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
    }
    else
    {
      if (In < InMIN) return (OutMIN);
      if (In > InMAX) return (OutMAX);
      return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
color DoubleToColor (const double in,    //input value
                     const double inMin, //minimum of input values
                     const double inMax, //maximum of input values
                     const int    loH,   //lower bound of HSL range values
                     const int    upH)   //upper bound of HSL range values
{
  int h = (int)Scale (in, inMin, inMax, loH, upH, true);
  return HSLtoRGB (h, 1.0, 0.5);
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
color HSLtoRGB (const int    h, //0   ... 360
                const double s, //0.0 ... 1.0
                const double l) //0.0 ... 1.0
{
  int r;
  int g;
  int b;
  if (s == 0.0)
  {
    r = g = b = (unsigned char)(l * 255);
    return StringToColor ((string)r + "," + (string)g + "," + (string)b);
  }
  else
  {
    double v1, v2;
    double hue = (double)h / 360.0;
    v2 = (l < 0.5) ? (l * (1.0 + s)) : ((l + s) - (l * s));
    v1 = 2.0 * l - v2;
    r = (unsigned char)(255 * HueToRGB (v1, v2, hue + (1.0 / 3.0)));
    g = (unsigned char)(255 * HueToRGB (v1, v2, hue));
    b = (unsigned char)(255 * HueToRGB (v1, v2, hue - (1.0 / 3.0)));
    return StringToColor ((string)r + "," + (string)g + "," + (string)b);
  }
}
//——————————————————————————————————————————————————————————————————————————————
//——————————————————————————————————————————————————————————————————————————————
double HueToRGB (double v1, double v2, double vH)
{
  if (vH < 0) vH += 1;
  if (vH > 1) vH -= 1;
  if ((6 * vH) < 1) return (v1 + (v2 - v1) * 6 * vH);
  if ((2 * vH) < 1) return v2;
  if ((3 * vH) < 2) return (v1 + (v2 - v1) * ((2.0f / 3) - vH) * 6);
  return v1;
}
//——————————————————————————————————————————————————————————————————————————————

Pour convertir un nombre double d'une plage en une couleur, l'algorithme de conversion de HSL en RGB a été utilisé (le système de couleurs de MetaTrader 5).

Le banc d'essai affiche une image sur le graphique. Il est divisé en 2 :

La fonction de test est affichée sur le côté gauche. Son graphique tridimensionnel est projeté sur un plan, où le bleu correspond au minimum et le rouge au maximum. La position des points dans la population est affichée (la couleur correspond au numéro ordinal de la fonction test avec le nombre de variables 40 et 1000, la coloration n'est pas effectuée pour une fonction à deux variables), les points dont les coordonnées sont moyennées sont marqués en blanc, et le meilleur est marqué en noir.
Le graphique de convergence est affiché sur le côté droit, les tests avec 2 variables sont marqués en vert, les tests avec 40 variables sont en bleu, et les tests avec 1.000 variables sont en rouge. Chacun des tests est effectué cinq fois (5 graphiques de convergence de chaque couleur). Nous pouvons observer ici à quel point la convergence de l’AO se détériore avec l'augmentation du nombre de variables.

6. AO simple utilisant un RNG

Mettons en œuvre la stratégie de recherche la plus simple à titre d'exemple. Il n'a aucune valeur pratique, mais il constituera d'une certaine manière une norme pour comparer les algorithmes d'optimisation. La stratégie génère un nouvel ensemble de variables de fonction selon un choix aléatoire 50/50 : soit copier la variable à partir d'un ensemble parent sélectionné au hasard dans la population, soit générer une variable à partir de la plage min/max. Après avoir récupéré les valeurs des fonctions de test, le nouvel ensemble de variables qui en résulte est copié dans la seconde moitié de la population et est trié. De nouveaux ensembles remplacent ainsi constamment une moitié de la population, alors que les meilleurs ensembles sont concentrés dans l'autre moitié.

Vous trouverez ci-dessous le code d’un AO basé sur le RNG :

//+————————————————————————————————————————————————————————————————————————————+
class C_AO_RND
{
  public: //||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

  struct ArrColony
  {
      double args [];
  };

  //----------------------------------------------------------------------------
  double    A_RangeStep []; //Step ranges of genes
  double    A_RangeMin  []; //Min ranges of genes
  double    A_RangeMax  []; //Max ranges of genes

  ArrColony S_Population []; //Population
  ArrColony S_Colony     []; //Colony

  double    A_FFpop [];      //Values of fitness of individuals in population
  double    A_FFcol [];      //Values of fitness of individuals in colony

  //----------------------------------------------------------------------------
  // Initialization of algorithm
  void F_Init (int argCount,       //Number of arguments

               int populationSize) //Population size
  {
    MathSrand ((int)GetMicrosecondCount ()); //reset of the generator

    p_argCount  = argCount;
    p_sizeOfPop = populationSize;
    p_sizeOfCol = populationSize / 2;

    p_dwelling  = false;

    f_arrayInitResize (A_RangeStep, argCount, 0.0);
    f_arrayInitResize (A_RangeMin,  argCount, 0.0);
    f_arrayInitResize (A_RangeMax,  argCount, 0.0);

    ArrayResize (S_Population, p_sizeOfPop);
    ArrayResize (s_populTemp, p_sizeOfPop);
    for (int i = 0; i < p_sizeOfPop; i++)
    {
      f_arrayInitResize (S_Population [i].args, argCount, 0.0);
      f_arrayInitResize (s_populTemp [i].args, argCount, 0.0);
    }

    ArrayResize (S_Colony, p_sizeOfCol);
    for (int i = 0; i < p_sizeOfCol; i++)
    {
      f_arrayInitResize (S_Colony [i].args, argCount, 0.0);
    }

    f_arrayInitResize (A_FFpop, p_sizeOfPop, -DBL_MAX);
    f_arrayInitResize (A_FFcol, p_sizeOfCol, -DBL_MAX);

    f_arrayInitResize (a_indexes, p_sizeOfPop, 0);
    f_arrayInitResize (a_valueOnIndexes, p_sizeOfPop, 0.0);
  }

  //----------------------------------------------------------------------------
  void F_EpochReset ()   //Reset of epoch, allows to begin evolution again without initial initialization of variables
  {
    p_dwelling = false;
    ArrayInitialize (A_FFpop, -DBL_MAX);
    ArrayInitialize (A_FFcol, -DBL_MAX);
  }
  //----------------------------------------------------------------------------
  void F_Preparation ();  //Preparation
  //----------------------------------------------------------------------------
  void F_Sorting ();      //The settling of a colony in population and the subsequent sorting of population

  private: //|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
  //----------------------------------------------------------------------------
  void F_PopulSorting ();

  //----------------------------------------------------------------------------
  ArrColony          s_populTemp      []; //Temporal population
  int                a_indexes        []; //Indexes of chromosomes
  double             a_valueOnIndexes []; //VFF of the appropriate indexes of chromosomes

  //----------------------------------------------------------------------------
  template <typename T1>
  void f_arrayInitResize (T1 &arr [], const int size, const T1 value)
  {
    ArrayResize     (arr, size);
    ArrayInitialize (arr, value);
  }

  //----------------------------------------------------------------------------
  double f_seInDiSp         (double In, double InMin, double InMax, double step);
  double f_RNDfromCI        (double min, double max);
  double f_scale            (double In, double InMIN, double InMAX, double OutMIN, double OutMAX);

  //---Constants----------------------------------------------------------------
  int  p_argCount;   //Quantity of arguments in a set of arguments
  int  p_sizeOfCol;  //Quantity of set in a colony
  int  p_sizeOfPop;  //Quantity of set in population
  bool p_dwelling;   //Flag of the first settling of a colony in population
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void C_AO_RND::F_Preparation ()
{
  //if starts of algorithm weren't yet - generate a colony with random arguments
  if (!p_dwelling)
  {
    for (int person = 0; person < p_sizeOfCol; person++)
    {
      for (int arg = 0; arg < p_argCount; arg++)
      {
        S_Colony [person].args [arg] = f_seInDiSp (f_RNDfromCI (A_RangeMin [arg], A_RangeMax [arg]),
                                                    A_RangeMin  [arg],
                                                    A_RangeMax  [arg],
                                                    A_RangeStep [arg]);
      }
    }

    p_dwelling = true;
  }
  //generation of a colony using with copying arguments from parent sets--------
  else
  {
    int parentAdress = 0;
    double rnd       = 0.0;
    double argVal    = 0.0;

    for (int setArg = 0; setArg < p_sizeOfCol; setArg++)
    {
      //get a random address of the parent set
      parentAdress = (int)f_RNDfromCI (0, p_sizeOfPop - 1);

      for (int arg = 0; arg < p_argCount; arg++)
      {
        if (A_RangeMin [arg] == A_RangeMax [arg]) continue;

        rnd = f_RNDfromCI (0.0, 1.0);

        if (rnd < 0.5)
        {
          S_Colony [setArg].args [arg] = S_Population [parentAdress].args [arg];
        }
        else
        {
          argVal = f_RNDfromCI (A_RangeMin [arg], A_RangeMax [arg]);
          argVal = f_seInDiSp (argVal, A_RangeMin [arg], A_RangeMax [arg], A_RangeStep [arg]);

          S_Colony [setArg].args [arg] = argVal;
        }
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void C_AO_RND::F_Sorting ()
{
  for (int person = 0; person < p_sizeOfCol; person++)
  {
    ArrayCopy (S_Population [person + p_sizeOfCol].args, S_Colony [person].args, 0, 0, WHOLE_ARRAY);
  }
  ArrayCopy (A_FFpop, A_FFcol, p_sizeOfCol, 0, WHOLE_ARRAY);

  F_PopulSorting ();
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Ranging of population.
void C_AO_RND::F_PopulSorting ()
{
  //----------------------------------------------------------------------------
  int   cnt = 1, i = 0, u = 0;
  int   t0 = 0;
  double t1 = 0.0;
  //----------------------------------------------------------------------------

  // We will put indexes in the temporary array
  for (i = 0; i < p_sizeOfPop; i++)
  {
    a_indexes [i] = i;
    a_valueOnIndexes [i] = A_FFpop [i];
  }
  while (cnt > 0)
  {
    cnt = 0;
    for (i = 0; i < p_sizeOfPop - 1; i++)
    {
      if (a_valueOnIndexes [i] < a_valueOnIndexes [i + 1])
      {
        //-----------------------
        t0 = a_indexes [i + 1];
        t1 = a_valueOnIndexes [i + 1];
        a_indexes [i + 1] = a_indexes [i];
        a_valueOnIndexes [i + 1] = a_valueOnIndexes [i];
        a_indexes [i] = t0;
        a_valueOnIndexes [i] = t1;
        //-----------------------
        cnt++;
      }
    }
  }

  // On the received indexes create the sorted temporary population
  for (u = 0; u < p_sizeOfPop; u++) ArrayCopy (s_populTemp [u].args, S_Population [a_indexes [u]].args, 0, 0, WHOLE_ARRAY);

  // Copy the sorted array back
  for (u = 0; u < p_sizeOfPop; u++) ArrayCopy (S_Population [u].args, s_populTemp [u].args, 0, 0, WHOLE_ARRAY);

  ArrayCopy (A_FFpop, a_valueOnIndexes, 0, 0, WHOLE_ARRAY);
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Choice in discrete space
double C_AO_RND::f_seInDiSp (double in, double inMin, double inMax, double step)
{
  if (in <= inMin) return (inMin);
  if (in >= inMax) return (inMax);
  if (step == 0.0) return (in);
  else return (inMin + step * (double)MathRound ((in - inMin) / step));
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Random number generator in the custom interval.
double C_AO_RND::f_RNDfromCI (double min, double max)
{
  if (min == max) return (min);
  double Min, Max;
  if (min > max)
  {
    Min = max;
    Max = min;
  }
  else
  {
    Min = min;
    Max = max;
  }
  return (double(Min + ((Max - Min) * (double)MathRand () / 32767.0)));
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
double C_AO_RND::f_scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX)
{
  if (OutMIN == OutMAX) return (OutMIN);
  if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0));
  else
  {
    if (In < InMIN) return (OutMIN);
    if (In > InMAX) return (OutMAX);
    return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);
  }
}
//——————————————————————————————————————————————————————————————————————————————

7. Résultats

AO	Exécutions	Skin			Forest			Megacity (discrète)			Résultat final
AO	Exécutions	2 paramètres (1 F)	40 paramètres (20 F)	1.000 paramètres (500 F)	2 paramètres (1 F)	40 paramètres (20 F)	1.000 paramètres (500 F)	2 paramètres (1 F)	40 paramètres (20 F)	1.000 paramètres (500 F)	Résultat final
RND	1.000	0,98744	0,61852	0,49408	0,89582	0,19645	0,14042	0,77333	0,19000	0,14283	0,51254
RND	10.000	0,99977	0,69448	0,50188	0,98181	0,24433	0,14042	0,88000	0,20133	0,14283	0,51254

Après avoir été testés sur le banc d'essai, les résultats de l’AO RND se sont révélés tout à fait inattendus. L'algorithme est capable de trouver l'optimum des fonctions de deux variables avec une très grande précision, alors que pour Forest et Megacity, les résultats sont nettement moins bons. Mes hypothèses sur les propriétés de recherche faibles pour les fonctions avec de nombreuses variables ont été confirmées. Les résultats sont très médiocres avec 40 arguments. La valeur cumulative finale est de 0,51254.

Dans les articles suivants, j'analyserai et je testerai des algorithmes d'optimisation bien connus et largement utilisés. Je continuerai ainsi à remplir le tableau de résultats qui constitue la note de l’AO.

Traduit du russe par MetaQuotes Ltd.
Article original : https://www.mql5.com/ru/articles/8122

Fichiers joints |

Télécharger ZIP

MQL5.zip (9.71 KB)

Avertissement: Tous les droits sur ces documents sont réservés par MetaQuotes Ltd. La copie ou la réimpression de ces documents, en tout ou en partie, est interdite.

Autres articles par cet auteur

Aller à la discussion

Développer un Expert Advisor de trading à partir de zéro (partie 18) : Nouveau système d’ordres (I)

Ceci est la 1ère partie du nouveau système d’ordres. Depuis que nous avons commencé à documenter cet EA dans nos articles, il a subi divers changements et améliorations tout en conservant le même modèle de système d'ordres sur le graphique.

Algorithmes d'optimisation de la population : Essaim de Particules (OEP ou PSO en anglais)

Dans cet article, j'examinerai l'algorithme populaire d'Optimisation par Essaims Particulaires (OEP ou Particle Swarm Optimization - PSO). Précédemment, nous avons abordé les caractéristiques importantes des algorithmes d'optimisation telles que la convergence, le taux de convergence, la stabilité et l'évolutivité, et nous avons développé un banc d'essai et examiné l'algorithme RNG le plus simple.

Développer un Expert Advisor de trading à partir de zéro (Partie 19) : Nouveau système d'ordres (II)

Dans cet article, nous allons développer un système graphique de gestion des ordres du type "regardez ce qui se passe". Notez que nous ne partons pas de zéro cette fois-ci. Nous modifierons le système existant en ajoutant davantage d'objets et d'événements sur le graphique de l'actif.

Apprenez à concevoir un système de trading basé sur l'Oscillateur de Chaikin

Bienvenue dans ce nouvel article de notre série consacrée à l'apprentissage de la conception d'un système de trading à l'aide d’un indicateur technique parmi les plus populaires. Dans ce nouvel article, nous allons apprendre à concevoir un système de trading basé sur l'indicateur Chaikin Oscillator (Oscillateur de Chaikin).