Üçüncü Nesil Nöral Ağlar: Derin Ağlar
293
0
İçindekiler
- İkinci Nesil Nöral Ağlar
- 1.1. Bağlantıların Mimarisi
- 1.2. Nöral Ağların Ana Türleri
- 1.3. Çalışma Yöntemleri
- 1.4. Dezavantajlar
- Derin Öğrenme
- 2.1. Arkaplan
- 2.2. Otomatik kodlayıcılar. Otomatik Kodlayıcı ve Kısıtlı Boltzmann Makinesi. Farklılıklar ve Özellikler
- 2.3. Yığılmış Otomatik İlişkilendirme Ağları. Yığılmış Otomatik Kodlayıcı SAE, Yığılmış Kısıtlı Boltzmann Makinesi (Yığılmış RBM)
- 2.4. Derin Ağların Eğitimi (DN). Aşamalar. Özellikler
- Pratik Deneyler
- 3.1. R Dili
- 3.2. Uygulama Varyasyonları ve Ele Alınan Sorunlar
- 3.3. Deney için veri hazırlama
- 3.3.1. Kaynak Veri
- 3.3.2. Girdi Verileri (Öngörücüler)
- 3.3.2.1. Welles Wilder'ın Yönlü Hareket Endeksi - ADX(HLC, n)
- 3.3.2.2. aroon(HL, n)
- 3.3.2.3. Emtia Kanal Endeksi - CCI(HLC, n)
- 3.3.2.4. chaikinVolatilite (HLC, n)
- 3.3.2.5. Chande Momentum Osilatörü - CMO(Med, n)
- 3.3.2.6. MACD osilatörü
- 3.3.2.7. OsMA(Med,nFast, nSlow, nSig)
- 3.3.2.8. Göreceli Güç Endeksi - RSI(Med,n)
- 3.3.2.9. Stokastik Osilatör - stok(HLC, nFastK=14, nFastD=3, nSlowD=3)
- 3.3.2.10. Stokastik Momentum Endeksi - SMI(HLC, n = 13, nFast = 2, nSlow = 25, nSig = 9)
- 3.3.2.11. Volatilite (Yang ve Zhang) - volatilite(OHLC, n, calc="yang.zhang", N=96)
- 3.3.3. Çıktı Verileri (Hedef)
- 3.3.4. Takas Verileri
- 3.3.5. Eğitmek ve Test Etmek İçin Örnek Oluşturma
- 3.3.6. Sınıf Dengeleme
- 3.3.7. Ön İşleme
- 3.4. Modelleri Oluşturma, Eğitme ve Test Etme
- Uygulama (Gösterge ve Expert Advisor)
Giriş
Bu makale, Derin Öğrenme ve Derin Ağ gibi konunun ana fikirlerini mesleki olmayan terimlerle karmaşık hesaplamalar olmadan ele alacaktır.
Gerçek verilerle yapılan deneyler, metrik tanımlama ve karşılaştırma yoluyla derin nöral ağların sığ olanlara göre teorik avantajlarını doğrular (veya doğrulamaz). Görev hazırlanmakta olan sınıflandırmadır. Derin nöral ağ modeline dayalı ve istemci/sunucu şemasına göre birlikte çalışan bir gösterge ve Expert Advisor oluşturacağız, ardından bunları test edeceğiz.
Okuyucunun, nöral ağlarda kullanılan temel kavramlar hakkında doğru bir fikre sahip olduğu varsayılmaktadır.
1. İkinci Nesil Nöral Ağlar
Nöral ağlar, görüntü işleme ile bağlantılı geniş yelpazede soruna hitaben tasarlanmıştır.
Tipik olarak nöral ağlar tarafından çözülen sorunların listesi aşağıda bulunmaktadır:
- İşlevlerin bir küme nokta ile yaklaştırılması (regresyon);
- Belirtilen sınıf kümesine göre veri sınıflandırması;
- Önceden bilinmeyen prototip sınıflarının tanımlanmasıyla veri kümeleme;
- Sıkıştırma bilgilendirmesi;
- Kayıp verileri geri yükleme;
- İlişkili bellek;
- Optimizasyon, optimum kontrol vb.
Yukarıdaki listenin dışında, bu makalede sadece "Sınıflandırma" tartışılacaktır.
1.1. Bağlantıların Mimarisi
Bilgi işleme yöntemi, ağdaki geri bildirim döngülerinin yokluğundan veya varlığından büyük ölçüde etkilenir. Nöronlar arasında geri bildirim döngüleri yoksa (yani ağ, her nöronun yalnızca bir önceki katmandan bilgi aldığı sıralı katmanlardan oluşan bir yapıya sahipse), ağdaki bilgi işleme tek yönlüdür. Girdi sinyali, bir dizi katman tarafından işlenir ve katman sayısına eşit sayıda yanıt alınır.
Geri bildirim döngülerinin varlığı, nöral ağın dinamiğini (bu durumda yinelenen olarak adlandırılır) öngörülemez hale getirebilir. Aslında, bir ağ "sonsuza kadar döngü yapabilir" ve asla bir yanıt üretemez. Aynı zamanda Turing'e göre, rastgele yinelenen bir ağ için, öğelerinin denge durumuna gelip gelmeyeceğini belirleyen bir algoritma yoktur (sonlanma problemi).
Genel olarak konuşursak, tekrarlayan ağlardaki nöronların bilgi işlemeye birçok kez katılması, bu tür ağların bilgiyi farklı şekillerde daha derin bir seviyede işlemesine olanak tanır. Bu durumda, ağın sonsuza kadar döngüye girmemesi için özel önlemler alınmalıdır. Örneğin, Hopfield ağında olduğu gibi simetrik bağlantılar kullanın veya zorla yineleme sayısını sınırlayın.
| Eğitim türü Bağlantı türü | Bir "denetimci" ile | "Denetimci" olmadan |
|---|---|---|
| Geri bildirim döngüleri olmadan | Çok katmanlı algılayıcılar (işlev yaklaşımı, sınıflandırma) | Rekabetçi ağ, kendi kendini organize eden haritalar (veri sıkıştırma, özellik ayrıştırma) |
| Geri bildirim döngüleri ile | Tekrarlayan algılayıcı (zaman serisi öngörüsü, çevrimiçi eğitim) | Hopfield ağı (İlişkili bellek, veri kümeleme, optimizasyon) |
Tablo 1. Bağlantı türüne ve eğitim türüne göre nöral ağ sınıflandırması
1.2. Nöral Ağların Ana Türleri
Algılayıcı ile başlayan nöral ağlar, gelişimlerinde uzun bir yol kat etti. Günümüzde yapı ve eğitim yöntemleri bakımından farklılık gösteren çok sayıda nöral ağ kullanılmaktadır.
En yaygın olanları:
1.2.1. Çok Katmanlı Tam Bağlantılı İleri Bildirimli Ağlar MLP (Çok Katmanlı Algılayıcı)
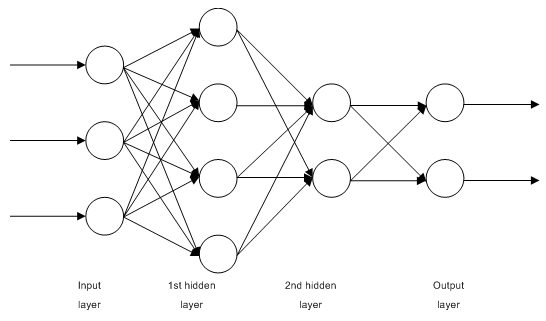
Şek. 1. Çok katmanlı bir nöral ağın yapısı
1.2.2. Jordan Ağları kısmen tekrarlayan ağlardır ve Elman ağlarına benzer.
Girdi katmanında ek bağlam nöronları ile ileri bildirimli bir ağ olarak ele alınabilir.
Bu bağlam nöronları kendileri tarafından (doğrudan geri bildirim) ve girdi nöronlarından beslenir. Bağlam nöronları ağın mevcut durumunu korur. Bir Jordan ağında bağlam ve girdi nöronlarının sayısı aynı olmalıdır.
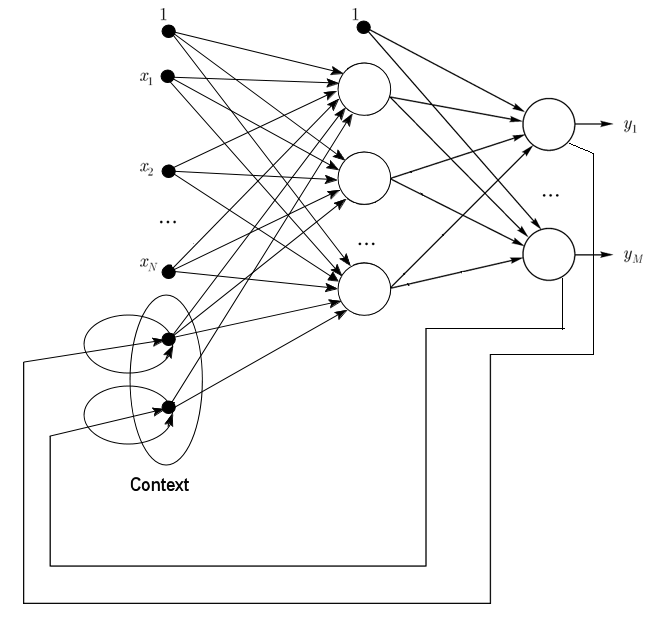
Şek. 2. Jordan ağının yapısı
1.2.3. Elman Ağları kısmen tekrarlayan ağlardır ve Jordan ağlarına benzer. Elman ve Jordan ağları arasındaki fark, Elman ağı bağlamı nöronlarının çıktı nöronları tarafından değil, gizli olanlarla beslenmesidir. Öte yandan, bağlam nöronlarında doğrudan geri bildirim yoktur.
Elman ağında, bağlam ve gizli nöronların sayısı aynı olmalıdır. Elman ağlarının temel avantajı, bağlam nöronlarının sayısının Jordan ağındaki gibi çıktı sayısıyla değil, ağı daha esnek hale getiren gizli nöron sayısıyla tanımlanmasıdır. Gizli nöronlar, çıktı sayısının aksine kolayca eklenebilir veya çıkarılabilir.
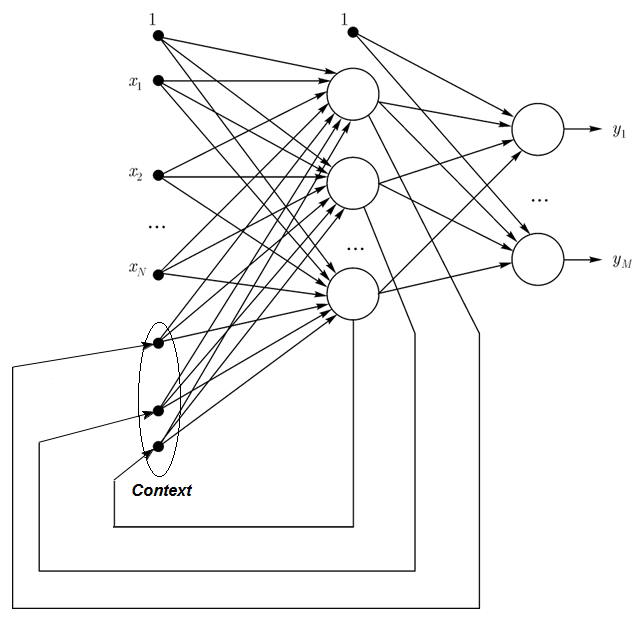
Şek. 3. Elman ağının yapısı
1.2.4. Radyal Temel İşlev Ağı (RBF) - radyal olarak simetrik nöronlardan oluşan bir ara (gizli) katman içeren ileri bildirimli bir nöral ağdır. Böyle bir nöron, genellikle Gauss olarak kabul edilen bazı doğrusal olmayan yasalarla belirli bir girdi vektöründen karşılık gelen merkezine olan mesafeyi dönüştürür.
RBF ağlarının çok katmanlı ileri bildirimli ağlara göre birçok avantajı vardır. Her şeyden önce, yalnızca bir ara katmanla rastgele doğrusal olmayan bir işlevi öykünürler (kelimeden emin değiller), bu da geliştiriciyi katman sayısına karar verme gereğinden kurtarır. Daha sonra, çıktı katmanındaki doğrusal kombinasyon içindeki parametreler, yaygın olarak bilinen doğrusal optimizasyon yöntemlerinin yardımıyla optimize edilebilir. İkincisi hızlı çalışır ve geri yayılıma büyük ölçüde müdahale eden yerel minimumlar konusunda zorluk çekmez. RBF ağının geri yayılımı kullanırken olduğundan çok daha hızlı öğrenmesinin nedeni budur.
RBF'nin Dezavantajları: Bu ağlar zayıf ekstrapolasyon özelliklerine sahiptir ve girdi vektörü büyük olduğunda külfetli hale gelir.
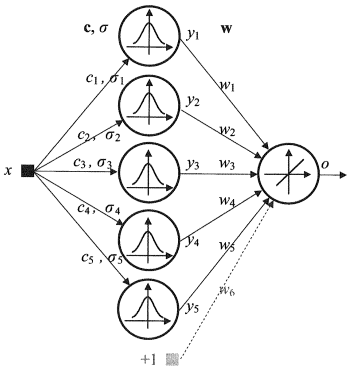
Şek. 4. RBF'nin Yapısı
1.2.5. Dinamik Öğrenme Vektörü Niceleme, DLVQ Ağları kendi kendini organize eden haritalara (SOM) çok benzer. SOM'dan farklı olarak, DLVO denetimli öğrenme kapasitesine sahiptir ve prototipler arasında komşuluk ilişkisi yoktur. Vektör niceleme, kümelemeden daha geniş bir kullanıma sahiptir.
1.2.6. Hopfield Ağı, simetrik bir bağlantı matrisine sahip tam bağlantılı bir ağdır. Operasyon sırasında, bu tür ağların dinamikleri denge durumlarından birine yakınsar. Bu denge durumları, ağın enerjisi olarak bilinen işlevselliğin yerel minimumlarıdır. Bu şekilde bir ağ, bir filtre olarak ve bazı optimizasyon zorluklarını ele almak için içerik adresli bir ilişkili bellek sistemi olarak kullanılabilir.
Belirli sayıda taktikle yanıt alana kadar çalışan birçok nöral ağın aksine Hopfield ağları, bir ağın sonraki durumunun bir öncekiyle tamamen aynı olduğu denge durumuna ulaşana kadar çalışır. Bu durumda, başlangıç durumu bir girdi formasyonudur ve denge durumunda çıktı resmi alınır. Bir Hopfield ağının eğitimi, girdi ve çıktı katmanlarında aynı anda sunulacak bir eğitim formasyonu gerektirir.
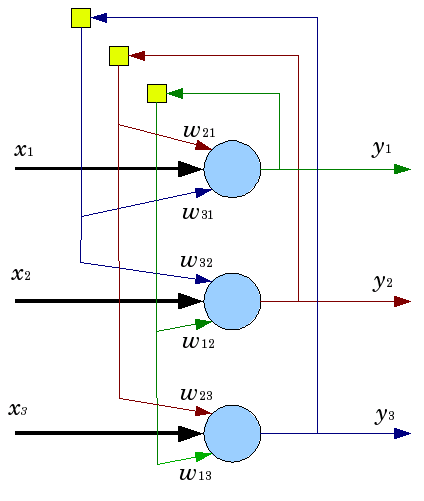
Şek. 5. Üç nöronlu bir Hopfield ağının yapısı
Çekici özelliklerine rağmen, klasik bir Hopfield ağı ideal olmaktan çok uzaktır. N ağındaki nöron sayısının yaklaşık %15'i kadar sınırlı bir belleğe sahiptir, oysa adresli bellek sistemleri N bit kullanarak 2N'ye kadar farklı resmi depolayabilir.
Öte yandan, Hopfield ağları resmin ilk saklama pozisyonuna göre kaydırıldığını veya döndürüldüğünü tanıma kapasitesine sahip değildir. Bu ve diğer dezavantajlar, bir Hopfield ağının günlük kullanım için pratik bir araçtan ziyade çalışmaya uygun teorik bir model olarak algılanmasını tanımlar.
Diğerlerinin çoğu (Hemming tekrarlayan ağı, Grossberg ağı, uyarlamalı rezonans teorisi ağları (ART-1, ART-2) vb.) ilgi alanımızın dışında olduğu için bu makalede bahsedilmemiştir.
1.3. Eğitim Yöntemleri
Yeni şeyler öğrenme kabiliyeti, insan beyninin temel özelliğidir. Yapay nöral ağların durumunda öğrenim, hazırlanmakta olan görevde etkili bir çözüm elde etmek için ağ mimarisini (nöronlar arasındaki bağlantıların yapısı) ve sinaptik bağlantıların ağırlıklarını (katsayı sinyallerini etkileyen) yapılandırma sürecidir. Genellikle bir nöral ağın eğitimi veri örneğinde gerçekleştirilir. Eğitim süreci belirli bir algoritmayı takip eder ve bu süreç devam ettikçe ağın tepkisi girdi sinyallerine doğru iyileşmelidir.
Üç ana öğrenme paradigması vardır: denetimli, denetimsiz ve birleşik. İlk durumda, her girdi örneği için doğru cevaplar bilinir ve ağırlıklar hatayı en aza indirmeye çalışır. Denetimsiz öğrenme, verilerin iç yapısını ve doğasını açıklayarak örnekleri kategorilere ayırmaya olanak tanır. Birleşik eğitimde yukarıdaki yaklaşımların her ikisi de kullanılır.
1.3.1. Nöral Ağ Öğrenmenin Temel Kuralları
Bunlarla bağlantılı ağ mimarisine dayalı dört ana öğrenme kuralı vardır: hata düzeltme, Boltzmann yasası, Hebb kuralı ve rekabetçi öğrenme.
1.3.1.1. Hata Düzeltme
Her girdi örneğinin istenen ve gerçek (tahmini) değerle uyuşmayabilen belirli bir çıktı değeri (hedef değer) vardır. Hata düzeltim öğrenme kuralı, hata azaltırken ağırlıkların doğrudan ayarlanması için hedef ve tahmin değerleri arasındaki farkı kullanmaktır. Eğitim sadece hatalı bir sonuç durumunda gerçekleştirilir. Bu öğrenme kuralının çok sayıda modifikasyonu vardır.
1.3.1.2. Boltzmann Kuralı
Boltzmann kuralı, termodinamik ilkelerine benzer şekilde stokastik bir öğrenme kuralıdır. Bu, nöronların ağırlık katsayılarının istenen olasılık dağılımına göre ayarlanmasıyla sonuçlanır. Boltzmann kuralını öğrenme, bir hatanın iki mod durumlarındaki korelasyon tutarsızlığını üreten bir hata ile izole edilmiş bir düzeltme durumu olarak düşünülebilir.
1.3.1.3. Hebb Kuralı
Hebb kuralı, nöral ağ öğreniminin en ünlü algoritmasıdır. Bu yöntemin amacı, bir sinapsın her iki tarafındaki nöronların aynı anda ve düzenli olarak aktive olması durumunda sinaptik bağlantının gücünün artmasıdır. Buradaki önemli bir özellik, sinaptik ağırlık değişiminin sadece bu sinaps ile bağlantılı nöronların aktivitesine bağlı olmasıdır. Bu kuralın, sinaptik ağırlık modifikasyonundaki özellikleri içinde farklılık gösteren birçok varyasyonu vardır.
1.3.1.4. Rekabetçi Öğrenme
Burada, bir dizi çıktı nöronunun aynı anda etkinleşebildiği Hebb öğrenme kuralından farklı olarak çıktı nöronları birbirleriyle rekabet eder. Ağırlıklı toplamın maksimum değerine sahip bir çıktı nöronu "kazanan" ve "kazanan hepsini alır" olmaktadır. Diğer çıktı nöronlarının çıktıları inaktif olarak ayarlanır. Öğrenmede, yalnızca "kazanan" ağırlıklar geçerli girdi örneğine yakınlığı artıracak şekilde hedeflenir.
Farklı problemleri ele alan birçok öğrenme algoritması vardır. En verimli modern algoritmalardan biri olan geri yayılım bunlardan biridir. Arkasındaki ilke, sinaptik ağırlık değişiminin hata işlevinin yerel gradyanı dikkate alınarak gerçekleşmesidir.
Çıktı katmanında değerlendirilen bir nöral ağın gerçek ve doğru yanıtları arasındaki fark, sinyal akışına doğru geri yayılır (Şek. 5). Bu şekilde her nöron, ağırlığının ağın kümülatif hatasına olan katkısını tanımlayabilir. En basit öğrenme kuralı, kümülatif hataya katkılarıyla orantılı olarak sinaptik ağırlık değişimi olan en dik iniş yöntemidir.
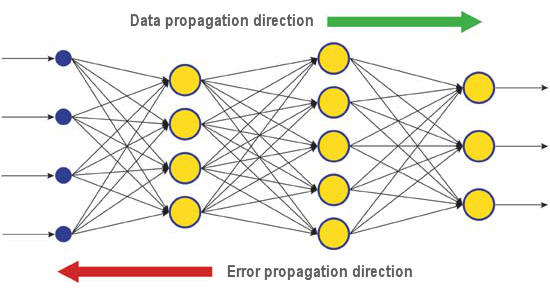
Şek. 6. Ağ geri yayılım yoluyla öğrenirken veri ve hata yayılım formasyonu
Elbette bu tür bir nöral ağ öğrenimi, daima algoritmanın yerel minimuma girme olasılığı bulunduğu için en iyi öğrenme sonucunu sağlamaz. Bulunan çözümü yerel bir uç noktadan çıkarmaya olanak tanıyan özel teknikler vardır. Nöral ağ bu tekniğin birkaç uygulamasından sonra aynı kararı verirse, büyük olasılıkla bulunan çözümün optimal olduğu sonucuna varılabilir.
1.4. Dezavantajlar
- Nöral ağları kullanmanın ana zorluğu "boyutsallık laneti" olarak adlandırılır. Girdi boyutları ve katman sayısı artırıldığında, ağın karmaşıklığı ve öğrenme süresi de katlanarak artar ve alınan sonuç her zaman optimal değildir.
- Nöral ağları kullanmanın bir başka zorluğu da, geleneksel nöral ağların görevleri nasıl çözdükleri açıklayamamasıdır. Tıp gibi bazı uygulama alanlarında bu açıklama sonucun kendisinden daha önemlidir. Dahili sonuç temsili çoğu zaman o kadar karmaşıktır ki, genellikle ilgili olmayan en basit durumlar dışında analiz edilmesi imkansızdır.
2. Derin Öğrenme
Bugün makine öğrenimi teorisi ve pratiği, üçüncü nesil nöral ağları temsil eden derin öğrenme yöntemlerinin başarılı bir şekilde uygulanmasının neden olduğu "derin bir devrimden" geçmektedir. Yeni öğrenme paradigmaları, geçen yüzyılın 80'li ve 90'lı yıllarında kullanılan klasik ikinci nesil ağların aksine geleneksel nöral ağların genişlemesini ve başarılı bir şekilde uygulanmasını kısıtlayan bir dizi sorunu çözmektedir.
Derin öğrenme algoritmalarıyla eğitilen ağlar, doğruluk açısından en iyi alternatif yöntemleri basitçe mükemmelleştirmekle kalmamıştır, aynı zamanda bazı durumlardaki girdi bilgisinin mantığını anlamanın en temel kurallarını ortaya çıkarmıştır. Resim tanıma ve metin bilgisi analizi en parlak örnekleridir.
Günümüzde en gelişmiş endüstriyel bilgisayar görme ve konuşma tanıma yöntemleri derin ağlara dayanmaktadır. Apple, Google, Facebook gibi bilişim sektörünün devleri, derin nöral ağlar geliştiren araştırmacıları istihdam etmektedir.
2.1. Arkaplan
Toronto Üniversitesi'nde okuyan Profesör Geoffrey E. Hinton liderliğindeki lisansüstü öğrencilerden oluşan bir ekip, Merck'in sponsor olduğu bir yarışmada birincilik ödülünü kazandı. G. Hinton'un grubu, 15 molekülün kimyasal yapısını tanımlayan sınırlı bir veri seti kullanarak bu moleküllerden hangisinin en etkili ilaç olacağını tanımlayan özel bir program sistemi oluşturmayı ve uygulamayı başardı.
Bu çalışmanın özelliği, geliştiricilerin derin öğrenmeye dayalı yapay bir nöral ağ kullanmasıydı. Sonuç olarak, normalde sistem çok sınırlı bir dizi kaynak veriye dayalı olarak hesaplamaları ve araştırmayı yerine getirirken bir nöral ağı eğitmek sisteme önemli miktarda bilgi girmesini gerektirir.
Hinton'ın ekibinin başarısı özellikle etkileyiciydi, çünkü ekip yarışmaya son dakikada girmeye karar verdi. Buna ek olarak derin öğrenme sistemi, moleküllerin hedeflerine nasıl bağlandığına dair özel bir bilgi olmadan geliştirildi. Derin öğrenmenin başarılı bir şekilde uygulanması, yapay zeka geliştirmesinde hareketli bir 2012 yılında gerçekleşen diğer bir başarıydı.
2012 yazında Google'dan Jeff Dean ve Andrew Y. Ng, %15,8 doğruluk oranına sahip yeni bir resim tanıma sistemi sundu; burada 16.000 düğümden oluşan bir küme sistemini eğitmek için 20.000 farklı nesnenin 14 milyon resminden oluşan bir kitaplık içeren ImageNet ağını kullandılar. Geçen yıl İsviçreli bilim adamları tarafından oluşturulan bir program, trafik işaretlerinin resimlerini tanıma konusunda bir insanı geride bıraktı. Kazanan program 50.000'lik bir kümedeki resimlerin yüzde 99.46'sını doğru bir şekilde tanımladı; 32 kişiden oluşan gruptaki en yüksek oran yüzde 99.22 ve insanlar için ortalama yüzde 98.84 idi. Ekim 2012'de, Microsoft bilimsel programlarının koordinatörü Richard F. Rashid, Çin'in Tianjin kentindeki bir konferansta, kendi sesinin bir simülasyonu eşliğinde Mandarin'e İngilizceden eşzamanlı çeviri teknolojisini sundu.
Yapay zeka alanında çığır açan tüm bu teknolojiler, belirli bir ölçüde derin öğrenme yöntemine dayanmaktadır. Derin öğrenme teorisine ana katkı, çağdaş bilgisayarların altında yatan Boole cebirinin kurucusu İngiliz bilim adamı George Boole'un büyük-büyük torunu olan profesör Hinton tarafından yapılmıştır.
Derin öğrenme teorisi, çeşitli sunum seviyelerindeki girdi bilgisi analizi için özel algoritmalarla sıradan makine öğrenimi yöntemlerini tamamlar. Bu yeni yaklaşımın özelliği, derin öğrenmenin söz konusu nesnenin parametrelerini etkileyebilecek tüm faktörleri hesaba katacak yeterli bilgilendirici sunum seviyeleri hakkındaki unsuru bulana kadar incelemesidir.
Bu şekilde, böyle bir yaklaşıma dayalı bir nöral ağ, öğrenim için daha az girdi bilgisi gerektirir ve eğitilmiş bir ağ, bilgiyi normal nöral ağlardan daha yüksek bir doğruluk seviyesinde analiz edebilir. Profesör Hinton ve meslektaşları, teknolojilerinin özellikle çoklu boyutlu, iyi yapılandırılmış bilgi dizileri içindeki özellikleri aramak için iyi olduğunu belirtmektedirler.
Yapay zeka teknolojileri (AI), özellikle derin öğrenme, Nuance Communications teknolojilerine dayanan akıllı kişisel asistan Apple Siri ve Google Street View'daki adresleri tanıma dahil olmak üzere farklı sistemlerde yaygın olarak kullanılmaktadır. Yine de, yapay zeka yaratmanın tarihi iyimser vaatler ve hayal kırıklıklarıyla dolu olduğundan, bilim adamları bu alandaki başarıyı çok dikkatli şekilde tahmin hesaplamaktadırlar.
1960'larda bilim adamları, tam özellikli bir yapay zeka yaratmanın sadece 10 yıl alacağına inanıyorlardı. Daha sonra 1980'lerde, genç şirketlerden "hazır yapay zeka" öneri dalgaları, ardından da bu sahada yakın zamana kadar devam eden "buz devri" geldi. Günümüzde bulut hizmetlerinde bulunan geniş hesaplama imkanları, yeni teorik ve algoritmik temelleri kullanarak yeni ve güçlü bir nöral ağ uygulama seviyesi sağlar.
Unutulmamalıdır ki nöral ağların, hatta evrişimli nöral ağlar gibi üçüncü nesillerin, otomatik ilişkilendirme ağlarının, Boltzmann makinelerinin bile biyolojik nöronlarla isim dışında hiçbir ortak yanı yoktur.
Yeni öğrenme paradigması, öğrenme fikrini iki aşamada uygular. İlk aşamada, girdi verilerinin iç yapısı hakkında bilgi, katman katman denetimsiz eğitim yolu üzerinden otomatik ilişkilendirici ile biçimlendirilmemiş büyük bir veri dizisinden ayıklanır. Daha sonra çoklu katmanlı nöral ağ içindeki bilginin kullanımı, biçimlendirilmiş veriler kullanılarak bilinen yöntemlerle denetimli eğitimden geçer. Aynı zamanda, biçimlendirilmemiş veri miktarı mümkün olduğunca büyük olmalıdır. Biçimlendirilmiş veriler boyut olarak çok daha küçük olabilir. Bizim durumumuzda bu birincil bir öneme sahip değildir.
2.2. Otomatik kodlayıcılar. Otomatik Kodlayıcı ve Kısıtlı Boltzmann Makinesi. Farklılıklar ve Özellikler
2.2.1. Otomatik kodlayıcı
İlk oto ilişkilendirici (АА) bir Fukushima nöral ağıydı.
Yapısı Şekil 7'de sunulmuştur.
Şek. 7. Fukushima nöral ağı
Bir otomotik ilişkilendiricinin (АА) amacı, çıktıdaki girdinin mümkün olduğu kadar kesin görüntüsünü almaktır.
İki tür АА vardır - üreten ve sentezleyen. Kısıtlı Boltzmann makinesi birinci türe aittir ve otomatik kodlayıcı ikinci türü temsil eder.
Bir otomatik kodlayıcı açık katmana sahip bir nöral ağdır. Denetimsiz öğrenme algoritması ve geri yayılım kullanarak girdi vektörüne eşit bir hedef değer belirler, yani y = x.
Otomatik kodlayıcıya bir örneğ Şekil 8'de sunulmuştur.
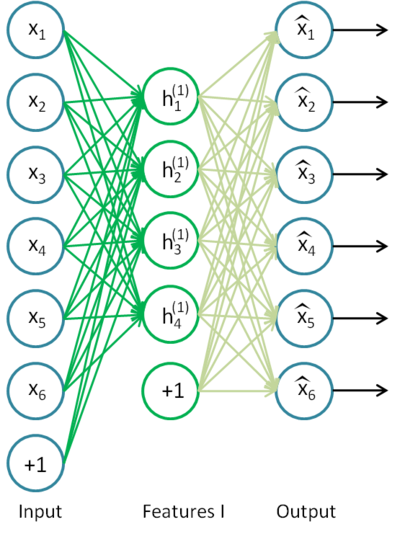
Şek. 8. Otomatik kodlayıcı yapısı
Otomatik kodlayıcı h(x)=x işlevini oluşturmaya çalışıyor. Başka bir deyişle, nöral ağ geri bildiriminin yaklaşık olarak girdi parametrelerinin değerlerine eşit olmasını sağlayan bir işlev yaklaşıklığı bulmaya çalışmaktadır. Problem çözümünün için açık katmandaki nöron sayısının girdi verisinin boyutundan (resimdeki gibi) az olması gerekir.
Girdi sinyali ağ çıkışına iletildiğinde verilerin sıkıştırılmasına izin verir. Örneğin, girdi vektörü 10x10 piksel boyutunda (100 karakteristik) bir resmin parlaklık seviyeleri kümesiyse, gizli katmanın nöron sayısı 50 ise, ağ görüntüyü sıkıştırmayı öğrenmek zorunda kalır. h(x)=x gerekliliği gizli katmanın elli nöronunun aktivasyon seviyelerine dayalı olarak, çıktı katmanının ilk resmin 100 pikselini geri yükleyeceği anlamına gelir. Böyle bir sıkıştırma, gizli ara bağlantılar, karakteristik korelasyon veya herhangi bir yapı varsa mümkündür. Bu şekilde bir otomatik kodlayıcı işlemi, girdi verilerinin azalması anlamında temel bileşen analiz yöntemini (PCA) hatırlatır.
Şaşırtıcı bir şekilde, Bengio ve diğerleri (2007), stokastik gradyan inişi ile eğitim yaparken, gizli nöronların sayısı girdi sayısından daha fazla ("süper bol" olarak da adlandırılır) olan doğrusal olmayan otomatik kodlama ağlarının, ağın girişten sunum alan uyum hatası ışığında yararlı bir sunuma sahip olduğunu göstermiştir.
Daha sonra seyreklik fikri ortaya çıktığında, seyrek otomatik kodlayıcı yaygın olarak kullanıldı.
Bir seyrek otomatik kodlayıcı, girdi boyutundan önemli ölçüde daha fazla sayıda gizli nörona sahip olan bir otomatik kodlayıcıdır, ancak bunların aktivasyonu seyrektir. Seyrek aktivasyon, gizli katmandaki aktif olmayan nöronların sayısının aktif olanların sayısından önemli ölçüde fazla olmasıdır. Seyrekliği gayri resmi olarak tanımlarsak, işlevin değeri 1'e yakınsa nöron aktif olarak kabul edilebilir. Sigmoid işlevi kullanılıyorsa, aktif olmayan nöron için değer 0'a yakın olmalıdır (hiperbolik tanjant işlevi için değer -1'e yakın olmalıdır).
Gürültü giderici otomatik kodlayıcı adı verilen otomatik kodlayıcının bir varyasyonu vardır (Vincent ve diğerleri, 2008). Bu aynı otomatik kodlayıcıdır ancak bu eğitiminin bazı özellikleri vardır. Bu ağı eğitirken, "bozuk" veriler girilir (bazı değerler 0 ile değiştirilir). Aynı zamanda, çıktı verileriyle karşılaştırılacak "doğru" veriler vardır. Bu şekilde otomatik kodlayıcı hasarlı verileri geri yükleyebilir.
2.2.2. Kısıtlı Boltzmann Makinesi, RBM.
Kısıtlı bir Boltzmann makinesinin (RBM) tarihine odaklanmayacağız. Tüm bilmemiz gereken bunun, eğitilmesi çok zor tekrarlayan geri bildirimli nöral ağlarla başladığıdır. Bu öğrenme zorluğu nedeniyle daha fazla kısıtlı tekrarlayan model ortaya çıktı, böylece daha basit öğrenme algoritmaları uygulanabildi. Bir Hopfield nöral ağı bu tür modellerden biriydi. John Hopfield nöral ağ dinamiklerini termodinamik ile karşılaştırarak ağ enerjisi kavramını tanıtan kişiydi.
RBM yolunda bir sonraki adım, normal Boltzmann makineleriydi. Bunlar stokastik bir yapıya sahip olmaları bakımından Hopfield ağından farklıdırlar ve nöronları, görünür ve gizli durumlarını tanımlayan iki gruba ayrılır (gizli bir Markov modeline benzer). Sınırlı bir Boltzmann makinesi, bir katmanın nöronları arasında bağlantı olmadığı zaman standart olandan farklıdır.
Şek. 9 RBM yapısını temsil etmektedir.
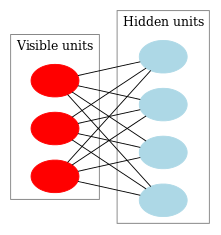
Şek. 9. Bir RBM yapısı
Bu modelin özelliği, bir grubun nöronlarının mevcut durumlarında, diğer grubun nöron durumları ile birbirinden bağımsız olmasıdır. Şimdi bu özelliğin kilit role sahip olduğu teoriye geçebiliriz.
Yorumlama ve amaç
Bir RBM gizli bir Markov modeline benzer şekilde yorumlanır. Gözlemleyebildiğimiz bir dizi durumumuz (görünür nöronlar) ve doğrudan göremediğimiz bir dizi gizli durumumuz (gizli nöronlar) vardır. Gözlemleyebildiğimiz durumlara dayanarak, gizli durumlar hakkındaki olasılığa dayalı bir sonuca varabiliriz. Böyle bir model eğitildikten sonra, gizli olanların Bayes teoremini izlediğini bilerek görünür durumlarla ilgili sonuçlar çıkarma fırsatı elde ederiz. Bu, modeli eğitmek için kullanılan olasılık dağılımından veri üretilmesine olanak tanır.
Bu şekilde model eğitiminin amacını formüle edebiliriz: model parametreleri, başlangıç durumundan geri yüklenen bir vektör orijinale en yakın olacak şekilde ayarlanmalıdır. Geri yüklenen vektör, olasılıksal çıkarımla gizli durumlardan alınan vektördür, bu da sırasıyla görünür durumlardan, yani orijinal vektörden olasılıksal bir çıkarımla alınır.
Eğitim algoritması Karşıtsal Farklılık CD-k'dir
Bu algoritma 2002 yılında Profesör Hinton tarafından icat edilmiştir ve oldukça basittir. Ana fikir, matematiksel beklenti değerlerinin tanımlanmış değerlerle değiştirilmesidir. Gibbs örneklemesi fikri tanıtıldı.
CD-k şu şekilde görünmektedir:
- Görünür nöronların durumu, girdi formasyonuna eşit olarak ayarlanır;
- Çizili gizli katman durumlarının olasılıkları;
- Gizli katmanın her bir nöronuna, mevcut durumuna eşit olasılıkla "1" durumu atanır;
- Görünür katman durumlarının olasılıkları, gizli katmana dayalı olarak çizilir;
- Geçerli yineleme k'den küçükse, 2. adıma dönün;
- Çizili gizli katman durumlarının olasılıkları;
Hinton'un derslerinde şu şekilde görünmektedir:
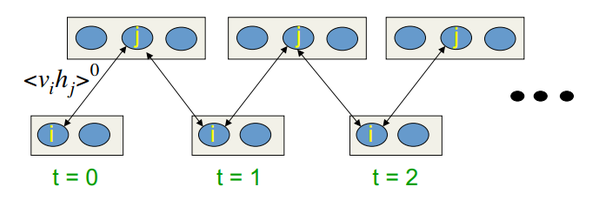
Şek.10. CD-k öğrenim algoritması
Başka bir deyişle, örneklemeyi ne kadar uzun süre yaparsak, gradyan o kadar kesin olur. Profesör CD-1 için alınan sonucun, yani sadece bir örnekleme yinelemesinin zaten iyi olduğunu belirtiyor.
2.3. Yığılmış Otomatik İlişkilendirme Ağları. Yığılmış Otomatik Kodlayıcı SAE, Yığılmış Kısıtlı Boltzmann Makinesi (Yığılmış RBM)
Otomatik ilişkilendiriciler girdi veri setinden yüksek seviyeli soyutlamaları ayıklamak için tek bir ağda birleştirilir.
Şekil 11, yığınlanmış otomatik kodlayıcı tarafından başlatılan ağırlıklarla derin nöral ağı temsil eden yığınlanmış otomatik kodlayıcı yapısını ve nöral ağı temsil eder
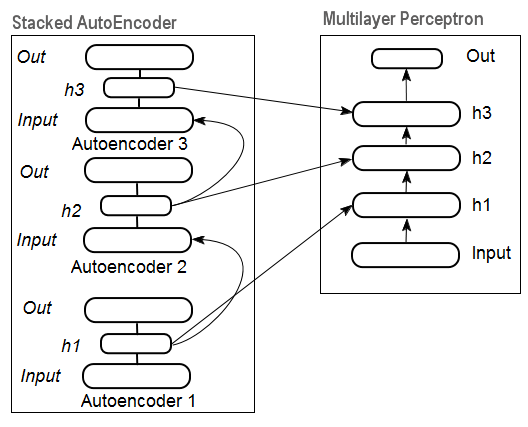
Şek. 11. Bir DN SAE Yapısı
Şekil 12'de, ağırlıkları SRBM tarafından başlatılan birlikte derin nöral ağı temsil eden yığılmış bir RBM (SRBM) ve bir nöral ağ modeli vardır.
Derin ağ yapılarının bu çizimleri, bilginin aşağıdan yukarıya ayıklanma olgusunu vurgulamaktadır.
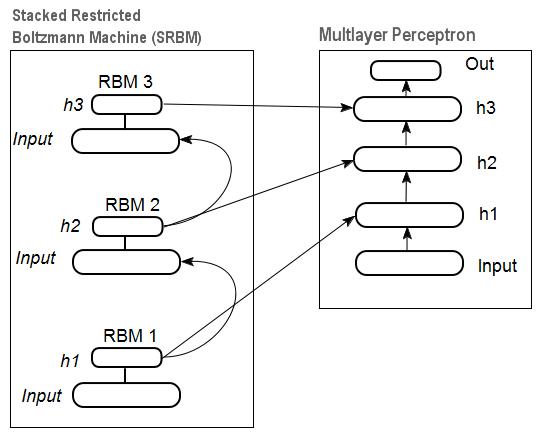
Şek. 12. DN SRBM Yapısı
2.4. Derin Ağların Eğitimi (DN). Aşamalar. Özellikler
Derin ağların eğitimi iki aşamadan oluşur. İlk aşamada, bir otomatik ilişkilendirme ağı (DN türüne bağlı olarak SAE veya SRBM), biçimlendirilmemiş bir veri dizisi üzerinde denetimsiz eğitim alır. Ondan sonra, sıradan MLP gizli katman nöronları, eğitimden sonra alınan gizli katman ağırlıkları tarafından başlatılır. Şekil 11 ve Şekil 12, öğrenme ve transfer süreçlerinin bir formasyonunu temsil etmektedir. İlk АЕ/RBM'nin eğitiminden sonra, gizli katmanın nöron ağırlıkları ikincisinin vb. girdileri olur. Bu şekilde yapı hakkında genelleştirilmiş bilgiler (çizgi, kontur, formasyon vb.) veriden ayıklanmış olur.
İkinci aşama, MLP'nin iyi bilinen yöntemler kullanılarak biçimlendirilmiş veri kümesi üzerinde (denetimli eğitim) ince ayarının yapılma zamanıdır. Uygulama, bu şekilde yapılan başlatmanın MLP'nin gizli katmanlarının nöron ağırlıklarını global minimuma ayarladığını ve sonraki ince ayarın çok kısa bir zaman aldığını kanıtladı.
Daha da fazlası D. Hinton, katman sayısı üçten fazla olan derin ağlar için ince ayarın iki aşamada yapılması gerektiğini önerdi. İlk aşamada sadece iki üst katman ve ikinci aşamada ağın geri kalanı eğitilmelidir.
SRBM'nin SAE'den daha az kararlı denetimsiz eğitim sonuçlarına sahip olduğu belirtilmelidir.
Not. Çoğu zaman bu terimler karıştırılır. SRBM derin inanç ağı DBN ile tanımlanır. RBM DBN'den türetilmesine rağmen, bunlar tamamen farklı yapılardır. DBN, gizli katmanların nöron ağırlıkları ikili formasyonlar tarafından rastgele başlatıldığı çok katmanlı bir nöral ağdır.
3. Pratik Deneyler
Derin ağlar R'de gerçekleştirilecektir.
3.1. R Dili
Geçmiş. R, 1996 yılında Aokland Üniversitesi'nden Yeni Zelandalı bilim adamları Ross Ihaka ve Robert Gentleman tarafından geliştirilen bir programlama dili ve istatistik hesaplamaları ve grafikleme ortamıdır.
R, ücretsiz bir yazılım olan bir GNU projesidir ve felsefesi aşağıdaki prensiplere dayanmaktadır:
- herhangi bir amaç için program başlatma özgürlüğü (özgürlük 0);
- bir programın nasıl çalıştığını öğrenme ve onu kendi ihtiyaçlarına göre uyarlama özgürlüğü (özgürlük 1);
- başkalarına yardım etmek için kopyaları dağıtma özgürlüğü (özgürlük 2);
- programı iyileştirme ve toplumun iyileştirmelerden faydalanmasına izin verme özgürlüğü.
Tarihsel perspektifte R, S'nin uygulanması için bir alternatiftir. İkincisi, 1976'da Bell Labs şirketinde John Chambers ve meslektaşları tarafından geliştirilmiştir. Bugün R, John Chambers dahil olmak üzere R Geliştirme Çekirdek Ekibi tarafından hala geliştirilmektedir.
Deneyleri tekrarlamak için R ve Rstudio'yu kurmanız gerekli olacaktır. İnternette nereden indirileceği ve nasıl indirileceği ile ilgili bilgiler. Herhangi bir sorunuz varsa, bunları makalenin yorumlarında tartışabiliriz.
R'nin Avantajları:
- Bugün R istatistik hesaplamalarında bir standarttır.
- Üniversitelerin global bilim topluluğu tarafından geliştirilmekte ve desteklenmektedir.
- Tüm gelişmiş veri madenciliği alanları için geniş paketler. Fikrin yayınlanması ve R paketinde uygulanması arasındaki süre genellikle 2 haftayı geçmez.
- Ve son olarak az bir kısmı değil tamamı ücretsizdir. Ücretsiz bir işletim sisteminin ünlü geliştiricisi bir keresinde şunları söylemiştir: "Programlar seks gibidir - ücretsiz olduğunda daha iyidir".
3.2. Uygulama Varyasyonları ve Ele Alınan Sorunlar
İki olası uygulama yolu vardır.
Birincisi John Hinton'un benzersiz programlarını Matlab için kullanmaktır. Bunun için "R.matlab" gereklidir. Bu paket, MAT dosyalarını okumak ve yazmak için writeMat() ve readMat() yöntemlerine sahiptir. Yerel olarak veya istemci-sunucu bağlantısındaki uzak ana bilgisayarda başlatılan Matlab v6 ve daha yüksek sürümlerden iletişimi (kod uygulaması, nesne gönderme ve alma vb.) sağlar. Ayrıntılar paketin açıklamasında bulunabilir. Bu Matlab'ı rahat kullananlar için bir yoldur. Bu yöntemi kullanmayı denemedim ama Matlab ve MQL'yi bu şekilde bağlama olasılığı vardır.
İkinci uygulama yöntemi bu konuda R paketlerini kullanmaktır. Şimdi keşfedeceğiz.
Bu makalenin konusuyla bağlantılı olduğunu bildiğim üç paket var:
"deepnet", DN SAE ve DN SRBM modellerini uygulayan basit bir pakettir. Denetimli ve denetimsiz öğrenimde girdi veri kümesinin uzunluğu aynıdır. Sistemin ince ayarını iki aşamada gerçekleştirme imkanı vermemektedir. Başlangıçta modellerin araştırılması ve test edilmesi için kullanılır.
"darh" DN SRBM modellemesi için gelişmiş ve geniş kapsamlı bir pakettir. DN SAE için bir model var ama başlatamadım. Bu paket deneyimli kullanıcılar içindir, herhangi karmaşıklık seviyesindeki bir modeli oluşturmaya ve ayarlamaya olanak tanır. Hinton'un MatLab için m dilindeki benzersiz programlarına dayanmaktadır.
"H2O", csv dosyaları içinde yazılmış büyük (>1 Гб) veri kümeleri üzerindeki derin ağları (sadece onları değil) eğitme amaçlı olan kapsamlı bir pakettir.
Aşağıdaki deneylerde "deepnet" paketini kullanacağız.
3.3. Deney için Girdi ve Hedef Verilerinin Hazırlanması
Günümüzde veri madenciliği belirli bir iş düzenine sahiptir:
- Girdi verilerinin seçilmesi (çalışma, analiz, ön hazırlık, değerlendirme). Verileri eğitim, doğrulama ve test kümeleriene (örneklerine) bölme;
- Eğitim veri kümesindeki bir modelin eğitilmesi ve validasyonda bir modelin/modellerin seçilmesi;
- Model/model kalitesinin test örneği üzerinde değerlendirilmesi ve optimal model parametrelerinin veya küme dışındaki en iyi modelin belirli ölçülerle tanımlanması;
- Modelin/modellerin çalışmaya başlamasına izin verilmesi.
İlk aşama en çok zaman alan ve sonuç için çok önemli olan aşamadır. Dürüst olmak gerekirse bu aşama resmileştirilmemiştir ve genel olarak konuşmak gerekirse neredeyse bir görsel formudur. Çokça şey araştırmacının deneyimine bağlıdır. Ama yine de! Girdi veri kümesinin nicel değerlendirmelerinin elde edilmesi, en önemlilerini seçmek için çok önemlidir. Bu durumda belirli bir model için en iyi değişkenlerin otomatik seçimi daha da iyidir. R, her aşamada zorlukların üstesinden gelmek için kapsamlı işlevsellik sağlar.
Kaynak veriler sadece çok önemli olmakla kalmaz, aynı zamanda dikkate alınması gereken birçok yönü vardır. Bu konu ayrı bir makaleyi hak ediyor. Bu makalenin amacı, karmaşık bir şeyi çok basit kelimelerle anlatmak olduğu için önemli noktaları tartışacağız ancak fazla ayrıntıya girmeyeceğiz.
3.3.1. Kaynak Veri
Sınıflandırmamız için bir küme bağımsız (girdi) değişkene ve bir hedef değişkene ihtiyacımız vardır. Derin ağların en belirgin avantajı, büyük girdi örnekleri üzerinde hızlı bir şekilde öğrenme kabiliyetleri olduğu için, 17 öngörücüden (11 gösterge) oluşan bir küme girdi verisi oluşturalım. ZigZag, hedef değişkenin bir rolüne sahiptir. Açık, Yüksek, Düşük, Kapat tekliflerinin 4000 çubuk derinliğinde olan R ortamında vektörlerini indirin. Bunu yapmanın yolu, aşağıdaki gösterge yazma yöntemi açıklamasında tartışılmaktadır. Bu aşamada önemli değildir. Diğer tüm hesaplamalar R'de yapılacaktır.
Çubuk gövdesinin ortalama fiyatını ve boyutunu içeren 4 vektörden oluşan bir matris oluşturun. Bunu bir işleve dönüştürün:
pr.OHLC <- function (o, h, l, c)
{
#Unite quote vectors into a matrix having previously expanded them
#Indexing of time series of vectors in R starts with 1.
#Direction of indexing is from old to new ones.
price <- cbind(Open = rev(o), High = rev(h), Low = rev(l), Close = rev(c))
Med <- (price[, 2] + price[, 3])/2
CO <- price[, 4] - price[, 1]
#add Med and CO to the matrix
price <- cbind(price, Med, CO)
} Sonuca bakın (08.10. 14 12:00'de belirtin)
> head(price)
Open High Low Close Med CO
[1,] 1.33848 1.33851 1.33824 1.33844 1.338375 -4e-05
[2,] 1.33843 1.33868 1.33842 1.33851 1.338550 8e-05
[3,] 1.33849 1.33862 1.33846 1.33859 1.338540 1e-04
[4,] 1.33858 1.33861 1.33856 1.33859 1.338585 1e-05
[5,] 1.33862 1.33868 1.33855 1.33855 1.338615 -7e-05
[6,] 1.33853 1.33856 1.33846 1.33855 1.338510 2e-05 3.3.2. Girdi Verileri (Öngörücüler)
Göstergeleri listeleyin. Göstergeler, girdi boyutlarının maksimum farkını elde etmek için herhangi bir tercih olmadan rastgele seçilmiştir.
Tüm göstergelerin hesaplanması, çok sayıda gösterge içeren "TTR" paketi kullanılarak gerçekleştirilir.
3.3.2.1. Welles Wilder'ın Yönlü Hareket Endeksi - ADX(HLC, n) - 4 çıkış (Dip, Din,DX, ADX)
Hesaplayın ve ilk 200 çubukta nasıl göründüğüne bakın:
> library(TTR)
> adx<-ADX(price, n = 16)
> plot.ts(head(adx, 200))
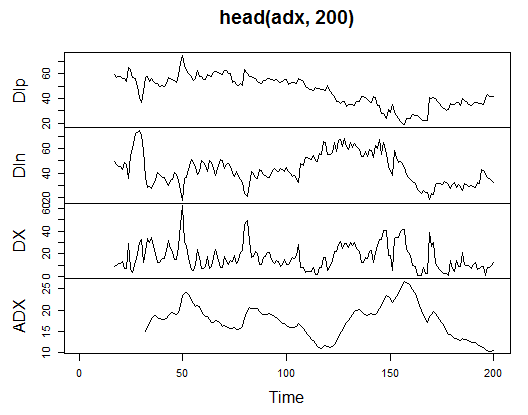
Şek. 13. Gösterge Welles Wilder'ın Yönlü Hareket Endeksi - ADX(HLC, n)
> summary(adx) DIp DIn DX ADX Min. :15.90 Min. : 5.468 Min. : 0.00831 Min. : 5.482 1st Qu.:41.21 1st Qu.: 33.599 1st Qu.: 8.05849 1st Qu.:14.046 Median :47.36 Median : 43.216 Median :16.95423 Median :18.099 Mean :47.14 Mean : 46.170 Mean :19.73032 Mean :19.609 3rd Qu.:53.31 3rd Qu.: 55.315 3rd Qu.:27.97471 3rd Qu.:23.961 Max. :80.12 Max. :199.251 Max. :81.08751 Max. :52.413 NA's :16 NA's :16 NA's :16 NA's :31
Matrisin başında 31 tanımsız değer (NA) vardır. Daha sonra tüm göstergeler için ayrıntılı açıklamalar olmadan aynı hesaplamaları yapın.
3.3.2.2. aroon(HL, n) - 1 çıkış (osilatör)
Yalnızca bir değişken "osilatör"ün ilk 200 çubuğunu hesaplayın ve BAKIN
> ar<-aroon(price[ , c('High', 'Low')], n = 16)[ ,'oscillator']
> plot(head(ar, 200), t = "l")
> abline(h = 0)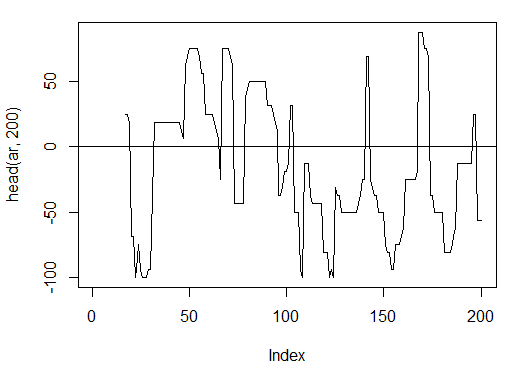 
Şek. 14. Gösterge aron(HL, n)
> summary(ar) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -100.00 -56.25 -18.75 -7.67 43.75 100.00 16
3.3.2.3. Emtia Kanal Endeksi - CCI(HLC, n) - 1 çıkış
> cci<-CCI(price[ ,2:4], n = 16)
> plot.ts(head(cci, 200))
> abline(h = 0)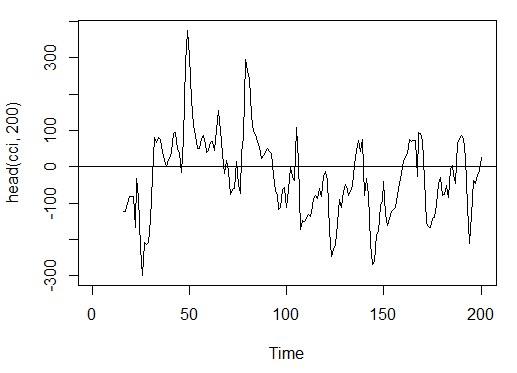 
Şek. 15. Gösterge Emtia Kanal Endeksi - CCI(HLC, n)
> summary(cci) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -469.10 -90.95 -18.74 -14.03 66.91 388.20 15
3.3.2.4. Chaikin Volatilite - chaikinVolatility (HLC, n) - 1 çıkış
> chv<-chaikinVolatility(price[ , 2:4], n = 16)
> summary(chv)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
-0.67570 -0.29940 0.02085 0.12890 0.41580 5.15700 31
> plot(head(chv, 200), t = "l")
> abline(h = 0)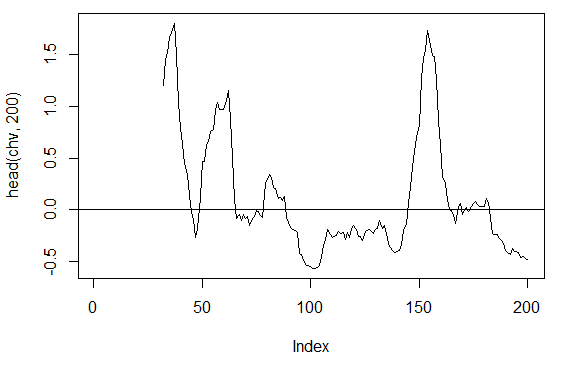 
Şek. 16. Gösterge chaikinVolatility (HLC, n)
3.3.2.5. Chande Momentum Osilatörü - CMO(Med, n) - 1 çıkış
> cmo<-CMO(price[ ,'Med'], n = 16)
> plot(head(cmo, 200), t = "l")
> abline(h = 0)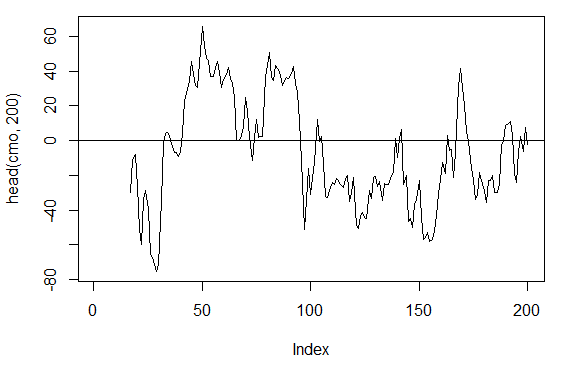 
Şek. 17. Gösterge Chande Momentum Osilatörü - CMO(Med, n)
> summary(cmo) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -97.670 -32.650 -5.400 -6.075 19.530 93.080 16
3.3.2.6. MACD osilatörü - MACD(Med, nFast, nSlow, nSig) 1 çıkış kullanılır (macd)
> macd<-MACD(price[ ,'Med'], 12, 26, 9)[ ,'macd'] > plot(head(macd, 200), t = "l") > abline(h = 0)
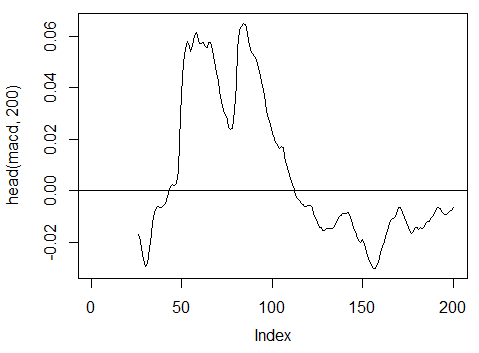
Şek. 18. Gösterge MACD osilatörü
> summary(macd) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -0.346900 -0.025150 -0.005716 -0.011370 0.013790 0.088880 25
3.3.2.7. OsMA(Med,nFast, nSlow, nSig) – 1 çıkış
> osma<-macd - MACD(price[ ,'Med'],12, 26, 9)[ ,'signal'] > plot(head(osma, 200), t = "l") > abline(h = 0)
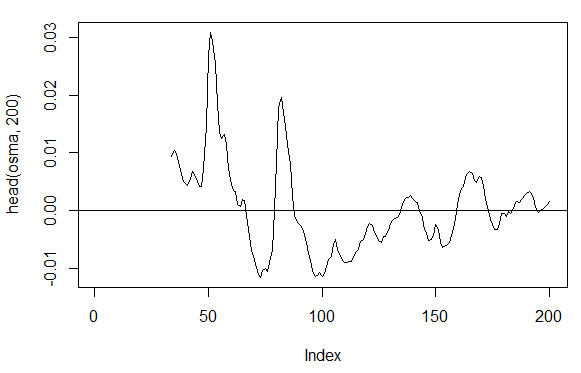
Şek. 19. Gösterge OsMA(Med,nFast, nSlow, nSig)
> summary(osma) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's -0.10560 -0.00526 0.00034 0.00007 0.00646 0.05922 33
3.3.2.8. Göreceli Güç Endeksi - RSI(Med,n) – 1 çıkış
> rsi<-RSI(price[ ,'Med'], n = 16)
> plot(head(rsi, 200), t = "l")
> abline(h = 50) 
Şek. 20. Gösterge Göreceli Güç Endeksi - RSI(Med,n)
> summary(rsi) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's 5.32 37.33 47.15 46.53 55.71 84.82 16
3.3.2.9. Stokastik Osilatör - stoch(HLC, nFastK=14, nFastD=3, nSlowD=3) - 3 çıkış
> stoh<-stoch(price[ ,2:4], 14, 3, 3) > plot.ts(head(stoh, 200))
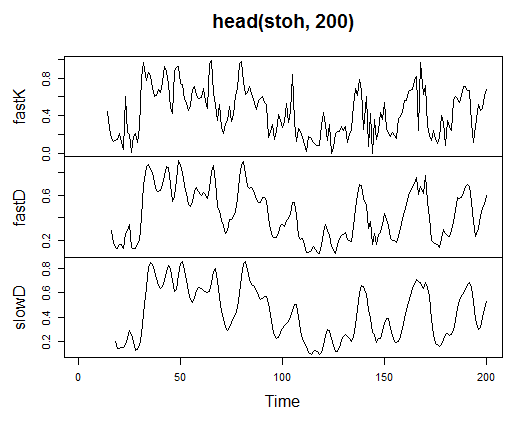
Şek. 21. Gösterge Stokastik Osilatör - stoch(HLC, nFastK=14, nFastD=3, nSlowD=3)
> summary(stoh) fastK fastD slowD Min. :0.0000 Min. :0.01782 Min. :0.02388 1st Qu.:0.2250 1st Qu.:0.23948 1st Qu.:0.24873 Median :0.4450 Median :0.44205 Median :0.44113 Mean :0.4622 Mean :0.46212 Mean :0.46207 3rd Qu.:0.6842 3rd Qu.:0.67088 3rd Qu.:0.66709 Max. :1.0000 Max. :0.99074 Max. :0.97626 NA's :13 NA's :15 NA's :17
3.3.2.10. Stokastik Momentum Endeksi - SMI(HLC, n = 13, nFast = 2, nSlow = 25, nSig = 9) — 2 çıkış
> smi<-SMI(price[ ,2:4],n = 13, nFast = 2, nSlow = 25, nSig = 9) > plot.ts(head(smi, 200))
Şek. 22. Gösterge Stokastik Momentum Endeksi - SMI(HLC, n = 13, nFast = 2, nSlow = 25, nSig = 9)
> summary(smi) SMI signal Min. :-82.185 Min. :-78.470 1st Qu.:-33.392 1st Qu.:-31.307 Median : -9.320 Median : -8.839 Mean : -8.942 Mean : -8.985 3rd Qu.: 15.664 3rd Qu.: 14.069 Max. : 71.878 Max. : 63.865 NA's :25 NA's :33
3.3.2.11. Volatilite (Yang ve Zhang) - volatility(OHLC, n, calc="yang.zhang", N=96)- 1 çıkış
> vol<-volatility(price[ ,1:4],n = 16,calc = "yang.zhang", N =96) > plot.ts(head(vol, 200))
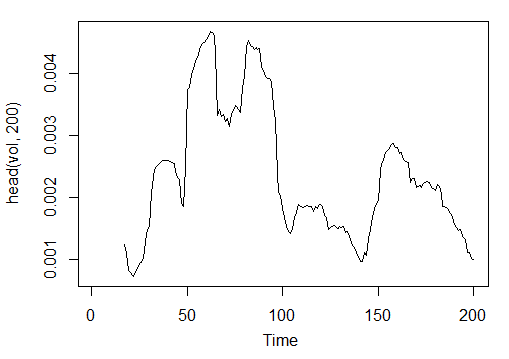
Şek. 23. Gösterge Volatilite (Yang ve Zhang) - volatility(OHLC, n, calc="yang.zhang", N=96)
> summary(vol) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's 0.000599 0.001858 0.002638 0.003127 0.004015 0.012840 16
4000 bar derinliğindeki OHLC örneği için М15 zaman diliminde EURUSD için 11 göstergeden 17 değişkenimiz var.
Bunları bir matris biçimi oluşturmak için kullanın ve yukarıdaki parametreleri, optimizasyon için gerekli olacak bir biçimsel parametre р ile tek bir işlevde yazın.
Aşağıdaki formülü kullanarak girdi parametrelerinin matrisini hesaplayın:
In<-function(p = 16){
adx<-ADX(price, n = p);
ar<-aroon(price[ ,c('High', 'Low')], n=p)[ ,'oscillator'];
cci<-CCI(price[ ,2:4], n = p);
chv<-chaikinVolatility(price[ ,2:4], n = p);
cmo<-CMO(price[ ,'Med'], n = p);
macd<-MACD(price[ ,'Med'], 12, 26, 9)[ ,'macd'];
osma<-macd - MACD(price[ ,'Med'],12, 26, 9)[ ,'signal'];
rsi<-RSI(price[ ,'Med'], n = p);
stoh<-stoch(price[ ,2:4],14, 3, 3);
smi<-SMI(price[ ,2:4],n = p, nFast = 2, nSlow = 25, nSig = 9);
vol<-volatility(price[ ,1:4],n = p,calc="yang.zhang", N=96);
In<-cbind(adx, ar, cci, chv, cmo, macd, osma, rsi, stoh, smi, vol);
return(In)
}
> X<-In()
> tail(X)
DIp DIn DX ADX ar cci chv
[3995,] 46.49620 36.32411 12.28212 18.17544 25.0 168.0407 0.1835102
[3996,] 52.99009 31.61164 25.26952 18.61882 37.5 227.7030 0.3189822
[3997,] 58.11948 28.16241 34.72000 19.62515 37.5 145.2337 0.3448520
[3998,] 56.00323 30.48687 29.50206 20.24245 37.5 118.5831 0.3068059
[3999,] 55.96197 28.78737 32.06467 20.98134 37.5 116.5376 0.3517668
[4000,] 54.97777 26.85440 34.36713 21.81795 62.5 160.0767 0.6169701
cmo macd osma rsi fastK
[3995,] 29.71342 -0.020870825 0.01666593 52.91932 0.8832685
[3996,] 41.89526 -0.009654368 0.02230591 61.49793 0.8833819
[3997,] 30.98237 -0.002051532 0.02392699 58.94513 0.7259475
[3998,] 33.84813 0.003454534 0.02354645 58.00549 0.7930029
[3999,] 38.84892 0.009590136 0.02374564 60.63806 0.8367347
[4000,] 54.71698 0.019303110 0.02676689 66.64815 0.9354120
fastD slowD SMI signal vol
[3995,] 0.7773581 0.7735064 -35.095406 -47.27712 0.003643196
[3996,] 0.7691688 0.7761507 -26.482951 -43.11828 0.003858942
[3997,] 0.8308660 0.7924643 -19.699762 -38.43458 0.003920541
[3998,] 0.8007775 0.8002707 -13.141932 -33.37605 0.003916109
[3999,] 0.7852284 0.8056239 -6.569699 -28.01478 0.003999789
[4000,] 0.8550499 0.8136852 2.197810 -21.97226 0.004293766 İşlenmemiş girdi verileri hazırlanmakta.
3.3.3. Çıktı Verileri (Hedef)
Şimdi çıktı (hedef veri) oluşturacağız. Daha önce de belirttiğimiz gibi ZigZag kullanacağız.
37 büyük nokta kanal genişliğinde ZigZag kullanacağız. ZigZag ortalama fiyat üzerinden hesaplanacaktır. Gösterge HL fiyatları ile hesaplanabilir ancak bu durumda gösterge daha kararlı olduğu için ortalama fiyat tercih edilir. Sinyali (0 - Al, 1-Sat) ayıkladıktan sonra, onu ağ modelini varsayan bir girdi matrisine dönüştürün.
Bir işlev yazın:
Out<-function(ch=0.0037){ # ZigZag has values on each bar and not only in the points zz<-ZigZag(price[ ,'Med'], change = ch, percent = F, retrace = F, lastExtreme = T); n<-1:length(zz); # On the last bars substitute the undefined values for the last known ones for(i in n) { if(is.na(zz[i])) zz[i] = zz[i-1];} #Define the speed of ZigZag changes and move one bar forward dz<-c(diff(zz), NA); #If the speed >0 - signal = 0(Buy), if <0, signal = 1 (Sell) otherwise NA sig<-ifelse(dz>0, 0, if else(dz<0, 1, NA)); return(sig); }
Sinyalleri hesaplayın.
> Y<-Out() > table(Y) Y 0 1 1567 2423
Sınıf orantısı dengesizdir. Bir sınıfın örnek sayısı diğerinden fazladır. Bu tür kümelere karşı tüm sınıflandırma modelleri, düşmanca bir tutum sergiler.
Verileri eğitim ve test örneklerine ayırırken bu durumu düzelteceğiz.
3.3.4. Takas Verileri
Veri kümelerimizi tanımsız verilerden temizleyin. Bu durumda takas, daha geniş bir görev döngüsü anlamına gelir. Bu "Neredeyse sıfır değişkenleri", yüksek ilintili olanları ve ayrıca burada tartışmayacağımız diğer bazı görevleri temizlemeyi içerir.
Bir işlev yazın ve verileri temizleyin
Clearing<-function(x, y){
dt<-cbind(x,y);
n<-ncol(dt)
dt<-na.omit(dt)
return(dt);
}
> dt<-Clearing(X,Y); nrow(dt)
[1] 3957 Matris 43 çubuk kısaldı.
3.3.5. Eğitmek ve Test Etmek İçin Örnek Oluşturma
Kaynak verileri eğitim ve test örneklerine göre ayırmanın birkaç yolu vardır. Kaynak verinin eğitime düzenli rastgele bölünmesini uygulayacağız ve birini 8/10 oranında test edeceğiz. Örneklerin katmanlara ayrılması önemlidir; bu, eğitim ve test örneklerindeki sınıf örneklerinin orantısının, kaynak veri kümesindeki sınıf orantısına karşılık gelmesi gerektiği anlamına gelir. Kaynak veri kümesindeki sınıf eşitsizliğinin düzeltilmesi de faydalı olacaktır. Bunu yapmanın iki yolu vardır - ya daha büyük ya da daha küçük sınıf ile dengeleme. Daha fazla örneğe gerek duyduğumuz için, daha büyük olan "1" sınıfı ile seviye atlayacağız. Bu durumda "caret" paketini kullanacağız.
Her iki sınıfın örnek sayısının aynı ve büyük olana eşit olduğu yeni dengeli bir küme oluşturalım.
3.3.6. Sınıf Dengeleme
Aşağıda, sınıf sayısını büyük tarafa göre dengeleyen (eğer farklılık %15'ten büyükse) ve dengeli bir matris döndüren işlev verilmiştir
Balancing<-function(DT){
#Calculate a table with a number of classes
cl<-table(DT[ ,ncol(DT)]);
#If the divergence is less than 15%, return the initial matrix
if(max(cl)/min(cl)<= 1.15) return(DT)
#Otherwise level by the greater side
DT<-if(max(cl)/min(cl)> 1.15){
upSample(x = DT[ ,-ncol(DT)],y = as.factor(DT[ , ncol(DT)]), yname = "Y")
}
#Convert у (factor) into a number
DT$Y<-as.numeric(DT$Y)
#Recode у from 1,2 into 0,1
DT$Y<-ifelse(DT$Y == 1, 0, 1)
#Convert dataframe to matrix
DT<-as.matrix(DT)
return(DT);
} Açıklama. İlk dizede her sınıfın örnek sayısını hesaplayın (boyut sınıfların sayısına eşit olan vektördür).
Büyük vektörün küçük olana orantısını bulun ve belirlenen eşik değerinden küçükse çıkın. Orantı daha büyükse, х ve y'yi ayrı ayrı yerleştirerek işlevi hesaplayın. Y önce bir faktöre dönüştürülmelidir.
Bu upSample() işlevinin biçimsel parametrelerinin gerekliliğidir. Bir faktör olarak hedef değişkene ihtiyacımız olmadığından, onu 0 ve 1 değerleriyle sayısal bir değişkene dönüştürüyoruz. Sayısal değişkeni (0,1) bir faktöre dönüştürdüğümüzde, "0" ve "1" metin değişkenlerini aldığımızı lütfen unutmayın. Sayısal değişkenlere ters çevrilmiş dönüşümde 1 ve 2 (!) elde ederiz. Onları 0 ve 1 ile değiştiriyoruz. Veri kümemiz "veri çerçevesi''nden "matris" sınıfına dönüştürülür. Hesaplayın:
dt.b<-Balancing(dt) x<-dt.b[ ,-ncol(dt.b)] y<-dt.b[ , ncol(dt.b)]
Bu şekilde, kaynak dt veri kümesine (girdi ve çıktı) ve dengeli dt.b kümesine sahip oluruz.
Eğitime bölün ve örnekleri test edin
"rminer" paketinden holdout() işlevini kullanarak eğitim endekslerini alın ve örnekleri test edin.
> library('rminer')
> t<-holdout(y, ratio = 8/10, mode = "random") t nesnesi, eğitim (t$tr) ve test (t$ts) veri kümesinin endekslerini içeren bir listedir. Alınan kümeler katmanlara ayrılmıştır.
3.3.7. Ön İşleme
Girdi veri kaynağımız farklı değer aralıklarına sahip değişkenler içerir. Esasen derin ağlar, ağırlıkları başlatmanın kendine özgü yolu olan düzenli ağlardır.
Nöral ağlar (-1; 1) veya (0, 1) aralığındaki girdi değişkenlerini alabilir. Girdi değişkenlerini [-1, 1] aralığında normalleştirin.
Bunun için "caret" paketindeki preProcess() işlevini kullanın. Lütfen ön işleme parametrelerinin eğitim veri kümesinde hesaplanacağını ve test veri kümesinin ve yeni girilen verilerin daha fazla ön işleme için kaydedileceğini unutmayın.
> spSign<-preProcess(x[t$tr, ], method = "spatialSign") > x.tr<-predict(spSign, x[t$tr, ]) > x.ts<-predict(spSign, x[t$ts, ])
Artık derin bir nöral ağ oluşturmak, eğitmek ve test etmek için her şeye sahibiz.
3.4. Modelleri Oluşturma, Eğitme ve Test Etme
Şimdi DN SAE modelini oluşturup eğiteceğiz. Modelin formülü ve değişkenlerin açıklaması:
sae.dnn.train(x, y, hidden = c(10), activationfun = "sigm", learningrate = 0.8, momentum = 0.5, learningrate_scale = 1, output = "sigm", sae_output = "linear", numepochs = 3, batchsize = 100, hidden_dropout = 0, visible_dropout = 0)
burada:
- х girdi verilerinin matrisidir;
- y hedef değişkenlerin vektörü veya matrisidir;
- gizli her gizli katmanda bir dizi nöron içeren bir vektördür. Varsayılan olarak с(10);
- activationfun, gizli nöronları etkinleştirme işlevidir. "Sigm", "lineer", "tanh" olabilir. Varsayılan olarak "sigm";
- learningrate gradyan inişi için bir eğitim seviyesidir. Varsayılan olarak = 0.8;
- momentum gradyan inişi için bir momentumdur. Varsayılan olarak = 0,5;
- learningrate_scale eğitim seviyesi, her yinelemeden sonra bu değerle çarpılabilir. Varsayılan olarak =1.0;
- numepochs eğitim için bir dizi yinelemedir. Varsayılan olarak =3;
- batchsize eğitilmekte olan küçük miktardaki verinin boyutudur. Varsayılan olarak =100;
- çıktı "sigm", "doğrusal", "softmax" olabilen çıktı nöronları için aktivasyon işlevidir. Varsayılan olarak "sigm";
- sae_output, "sigm", "doğrusal", "softmax" olabilen SAE'nin çıkış nöronlarının aktivasyon işlevidir. Varsayılan olarak "doğrusal";
- hidden_dropout gizli katmanlar için silinebilir bir parçasıdır. Varsayılan olarak =0;
- visible_dropout görünür (girdi) katmanının silinebilir bir parçasıdır. Varsayılan olarak =0.
Aşağıdaki boyutlarda (17, 100, 100, 100, 1) bir model oluşturacağız, onu eğiteceğiz, öğrenme zamanını not edeceğiz ve tahmini gözlemleyeceğiz.
> system.time(SAE<-sae.dnn.train(x= x.tr, y= y[t$tr], hidden=c(100,100,100), activationfun = "tanh", learningrate = 0.6, momentum = 0.5, learningrate_scale = 1.0, output = "sigm", sae_output = "linear", numepochs = 10, batchsize = 100, hidden_dropout = 0, visible_dropout = 0)) begin to train sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae has been trained. begin to train deep nn ...... deep nn has been trained. user system elapsed 12.92 0.00 13.09
Gördüğümüz gibi bu iki aşamada gerçekleşir. İlk önce otomatik kodlayıcı, katman katman eğitilir ve ardından nöral ağı alır.
Üç katman içindeki az sayıda eğitim süresi ve çok sayıda gizli nöron bilerek ayarlanmıştır. Tüm süreç 13 saniye sürdü!
Tahminleri, öngörücülerin test kümesinde değerlendirelim.
> pr.sae<-nn.predict(SAE, x.ts); > summary(pr.sae) V1 Min. :0.2649 1st Qu.:0.2649 Median :0.5881 Mean :0.5116 3rd Qu.:0.7410 Max. :0.7410
0,1 seviyelerine dönüştürün ve ölçümleri hesaplayın
> pr<-ifelse(pr.sae>mean(pr.sae), 1, 0) > confusionMatrix(y[t$ts], pr) Confusion Matrix and Statistics Reference Prediction 0 1 0 316 128 1 134 378 Accuracy : 0.7259 95% CI : (0.6965, 0.754) No Information Rate : 0.5293 P-Value [Acc > NIR] : <2e-16 Kappa : 0.4496 Mcnemar's Test P-Value : 0.7574 Sensitivity : 0.7022 Specificity : 0.7470 Pos Pred Value : 0.7117 Neg Pred Value : 0.7383 Prevalence : 0.4707 Detection Rate : 0.3305 Detection Prevalence : 0.4644 Balanced Accuracy : 0.7246 'Positive' Class : 0
Bu üstün bir katsayı değildir. Katsayı ile değil, bu sinyalleri kullanarak elde edeceğimiz kârla daha çok ilgileniyoruz. Son 500 çubuk üzerinden kontrol edin (yaklaşık bir hafta). Eğitimli ağımızdan son 500 sıralı çubuk üzerinden sinyaller alacağız.
Giriş verilerinin son 500 çubuğunu normalleştirin, eğitimli nöral ağdan tahminleri alın ve bunları sinyallere dönüştürün -1= (Sat) ve 1 = (Satın Al)
> new.x<-predict(spSign,tail(dt[ ,-ncol(dt)], 500)) > pr.sae1<-nn.predict(SAE, new.x) > pr.sig<-ifelse(pr.sae1>mean(pr.sae1), -1, 1) > table(pr.sig) pr.sig -1 1 235 265 > new.y<-ifelse(tail(dt[ , ncol(dt)], 500) == 0, 1, -1) > table(new.y) new.y -1 1 201 299 > cm1<-confusionMatrix(new.y, pr.sig) > cm1 Confusion Matrix and Statistics Reference Prediction -1 1 -1 160 41 1 75 224 Accuracy : 0.768 95% CI : (0.7285, 0.8043) No Information Rate : 0.53 P-Value [Acc > NIR] : < 2.2e-16 Kappa : 0.5305 Mcnemar's Test P-Value : 0.002184 Sensitivity : 0.6809 Specificity : 0.8453 Pos Pred Value : 0.7960 Neg Pred Value : 0.7492 Prevalence : 0.4700 Detection Rate : 0.3200 Detection Prevalence : 0.4020 Balanced Accuracy : 0.7631 'Positive' Class : -1
Doğruluk katsayısı fena değil ancak katsayı ile değil, daha çok kârla ilgileniyoruz.
Karı öngörülen sinyallerimizi kullanarak son 500 çubuk için test edin ve denge eğrisini alın:
> bal<-cumsum(tail(price[ , 'CO'], 500) * pr.sig) > plot(bal, t = "l") > abline(h = 0)
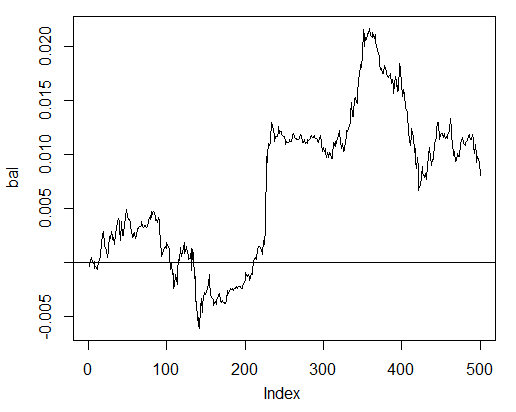
Şek. 24. Son 500 çubuktaki nöral ağ sinyallerine göre denge
Denge, canlı piyasanın spread, slipaj ve diğer gerçekleri dikkate alınmadan hesaplanmıştır.
Şimdi ZZ'nin ideal sinyallerinden elde edilecek olan denge ile karşılaştırın. Kırmızı çizgi, nöral ağ sinyallerinin dengesidir:
> bal.zz<-cumsum(tail(price[ , 'CO'], 500) * new.y) > plot(bal.zz, t = "l") > lines(bal, col = 2)
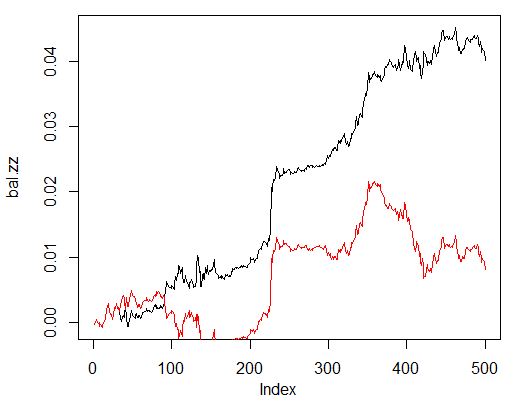
Şek. 25. Son 500 çubuktaki nöral ağ sinyallerine ve ZigZag sinyallerine göre denge
İyileştirme potansiyeli vardır.
Tahmin() ve Test() olmak üzere iki yardımcı işlevi kolaylaştırmak için iki işlev yazın. İlki Doğruluk/Err katsayılarını ve ikincisi Bal/BalZZ dengesini oluşturacaktır.
Bu, bazı ağ parametrelerini değiştirerek hemen bir sonuç elde etmeyi ve hangi parametrelerin ağın kalitesini etkilediğini görmeyi sağlar.
Bir uygunluk işlevi yazıldıktan sonra, işlem sürecinde herhangi bir kesinti olmaksızın evrimsel (genetik) algoritma kullanılarak optimal ağ parametreleri bulunabilir. Şu an bu makalede buna zaman ayırmayacağız ancak başka bir zaman ayrıntılı olarak ele alacağız.
Aşağıda Tahmin() katsayılarını hesaplayan Hata/Doğruluk işlevi verilmiştir:
Estimation<-function(X, Y, r = 8/10, m = "random", norm = "spatialSign", h = c(10), act = "tanh", LR = 0.8, Mom = 0.5, out = "sigm", sae = "linear", Ep = 10, Bs = 50, CM=F){ #Indices of the training and test data set t<-holdout(Y, ratio = r, mode = m) #Parameters of preprocessing prepr<-preProcess(X[t$tr, ], method = norm) #Divide into train and test data sets with preprocessing x.tr<-predict(prepr, X[t$tr, ]) x.ts<-predict(prepr, X[t$ts, ]) y.tr<- Y[t$tr]; y.ts<- Y[t$ts] #Train the model SAE<-sae.dnn.train(x = x.tr , y = y.tr , hidden = h, activationfun = act, learningrate = LR, momentum = Mom, output = out, sae_output = sae, numepochs = Ep, batchsize = Bs) #Obtain a forecast on the test data set pr.sae<-nn.predict(SAE, x.ts) #Recode it into signals 1,0 pr<-ifelse(pr.sae>mean(pr.sae), 1, 0) #Calculate the Accuracy coefficient or classification error if(CM) err<-unname(confusionMatrix(y.ts, pr)$overall[1]) if(!CM) err<-nn.test(SAE, x.ts, y.ts, mean(pr.sae)) return(err) }
Biçimsel parametreler:
- X – işlenmemiş girdi ön görücü matrisi;
- Y – hedef değişken vektörü;
- r – orantı dizisi/testi;
- m – örnek oluşturma modu (rastgele veya sıralı);
- norm – girdi parametrelerini normalleştirme modu ([ -1, 1]= "spatialSign";[0, 1]="range");
- h – gizli katmanlarda çok sayıda nöron içeren vektör;
- hareket – gizli nöronların aktivasyon işlevi;
- LR – eğitim seviyesi;
- Мом — momentum;
- out – çıktı katmanının aktivasyon işlevi;
- sae – otomatik kodlayıcının aktivasyon işlevi;
- Ep – eğitim dönemlerinin sayısı;
- Bs – küçük örneğin boyutu;
- СM– Boolean değişkeni, DOĞRU ise baskı Doğruluğu. Aksi halde Hatalı.
Örnek olarak, her biri 30 nöron içeren üç gizli katmana sahip ağ tarafından dengesiz veri kümesi dt üzerindeki sınıflandırma hatasını hesaplayacağız:
> Err<-Estimation(X = dt[ ,-ncol(dt)], Y = dt[ ,ncol(dt)], h=c(30, 30, 30), LR= 0.7) begin to train sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae has been trained. begin to train deep nn ...... deep nn has been trained. > Err [1] 0.1376263
Test() işlevi, tahmin sinyallerine veya ideal sinyallere (ZigZag) göre dengeyi hesaplar:
Testing<-function(dt1, dt2, r=8/10, m = "random", norm = "spatialSign", h = c(10), act = "tanh", LR = 0.8, Mom = 0.5, out = "sigm", sae = "linear", Ep = 10, Bs=50, pr = T, bar = 500){ X<-dt1[ ,-ncol(dt1)] Y<-dt1[ ,ncol(dt1)] t<-holdout(Y, ratio = r, mode = m) prepr<-preProcess(X[t$tr, ], method = norm) x.tr<-predict(prepr, X[t$tr, ]) y.tr<- Y[t$tr]; SAE<-sae.dnn.train(x = x.tr , y = y.tr , hidden = h, activationfun = act, learningrate = LR, momentum = Mom, output = out, sae_output = sae, numepochs = Ep, batchsize = Bs) X<-dt2[ ,-ncol(dt2)] Y<-dt2[ ,ncol(dt2)] x.ts<-predict(prepr, tail(X, bar)) y.ts<-tail(Y, bar) pr.sae<-nn.predict(SAE, x.ts) sig<-ifelse(pr.sae>mean(pr.sae), -1, 1) sig.zz<-ifelse(y.ts == 0, 1,-1 ) bal<-cumsum(tail(price[ ,'CO'], bar) * sig) bal.zz<-cumsum(tail(price[ ,'CO'], bar) * sig.zz) if(pr) return(bal) if(!pr) return(bal.zz) }
Biçimsel parametreler:
- dt1 – ağın eğitimi için kullanılan girdi ve hedef değişkenin matrisi;
- dt2 - ağı test etmek için kullanılan girdi ve hedef değişkenlerin matrisi;
- pr – Boolean değişkeni, DOĞRU ise denge tahmin sinyalleri ile, aksi takdirde ZigZag ile yazdırır;
- bar - dengeyi hesaplamak için kullanılacak son çubuk sayısı.
Nöral ağ tarafından yukarıdaki ile aynı parametrelerle dengeli dt.b veri kümesi üzerinde eğitim yaparken dt veri kümemizin son 500 çubuğundaki dengeyi hesaplayın:
> Bal<-Testing(dt.b, dt, h=c(30, 30, 30), LR= 0.7) begin to train sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae has been trained. begin to train deep nn ...... deep nn has been trained. > plot(Bal, t = "l") > abline(h = 0)
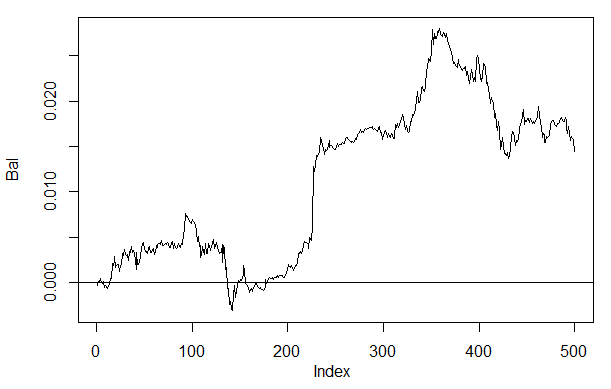
Şek. 26. Nöral ağ sinyallerindeki son 500 çubuktaki denge h(30,30,30)
Sonucu daha önce elde edilen denge ile karşılaştırırsak, önemli bir gelişme görebiliriz. Yine de buradaki en ilginç nokta bu değildir.
Son 500 çubuktaki fiyat grafiğine bakarsak, hangi kısımlarının ağımız (150-350 çubuk) tarafından en iyi kabul edilen olduğunu görebiliriz.
> plot(tail(price[ ,'Close'], 500), t = "l") > abline(v = c(150,350), col=2)
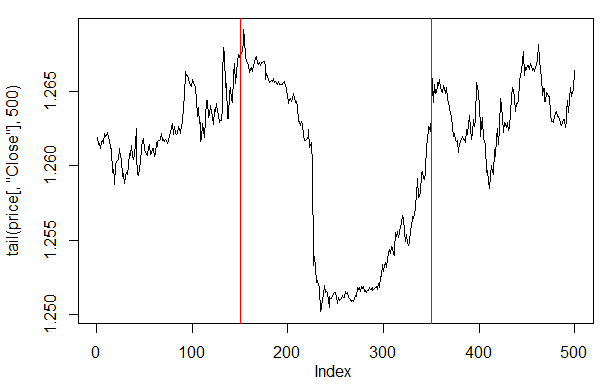
Şek. 27. Son 500 çubuktaki Kapanış fiyatı çizimi
Not: Tahmin çıktılarının kodunu çözerken ortalamadan daha az/fazla basitleştirilmiş bir sürüm kullandık ancak diğer sürümler de kullanılabilir.
Değerler 0,6'dan büyük veya 0,4'ten küçükse, kararsız 0,4-0,6 segmenti kesilir. Kalibrasyonda daha kesin sınıf sınırları elde edilebilir. Bu daha sonra tartışılacaktır.
Test() işlevimiz, ek bir dec parametresi tanıtılacaksa biraz değişecektir. Bu, bir şifre çözme yöntemi ("ortalama" veya "60/40") seçmemize ve bunun denge üzerinde ne gibi etkisi olacağını ön gören değerleri kontrol etmemizi sağlayacaktır.
Testing.1<-function(dt1, dt2, r = 8/10, m = "random", norm = "spatialSign", h = c(10), act = "tanh", LR = 0.8, Mom = 0.5, out = "sigm", sae = "linear", Ep = 10, Bs = 50, pr = T, bar = 500, dec=1){ X<-dt1[ ,-ncol(dt1)] Y<-dt1[ ,ncol(dt1)] t<-holdout(Y, ratio = r, mode = m) prepr<-preProcess(X[t$tr, ], method = norm) x.tr<-predict(prepr, X[t$tr, ]) y.tr<- Y[t$tr]; SAE<-sae.dnn.train(x = x.tr , y = y.tr , hidden = h, activationfun = act, learningrate = LR, momentum = Mom, output = out, sae_output = sae, numepochs = Ep, batchsize = Bs) X<-dt2[ ,-ncol(dt2)] Y<-dt2[ ,ncol(dt2)] x.ts<-predict(prepr, tail(X, bar)) y.ts<-tail(Y, bar) pr.sae<-nn.predict(SAE, x.ts) #Variant +/- mean if(dec == 1) sig<-ifelse(pr.sae>mean(pr.sae), -1, 1) #Variant 60/40 if(dec == 2) sig<-ifelse(pr.sae>0.6, -1, ifelse(pr.sae<0.4, 1, 0)) sig.zz<-ifelse(y.ts == 0, 1,-1 ) bal<-cumsum(tail(price[ ,'CO'], bar) * sig) bal.zz<-cumsum(tail(price[ ,'CO'], bar) * sig.zz) if(pr) return(bal) if(!pr) return(bal.zz) }
Birinci ve ikinci kod çözüm yöntemleriyle dengeyi hesaplayın ve değerlendirin.
Sonuçların tekrarlanması için yalancı rastgele sayı oluşturucusunu aynı pozisyona ayarlayın.
> set.seed<-1245 > Bal1<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 1) begin to train sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae has been trained. begin to train deep nn ...... deep nn has been trained. > set.seed<-1245 > Bal2<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 2) begin to train sae ...... training layer 1 autoencoder ... training layer 2 autoencoder ... training layer 3 autoencoder ... sae has been trained. begin to train deep nn ...... deep nn has been trained. > plot(Bal2, t = "l") > lines(Bal1, col = 2)
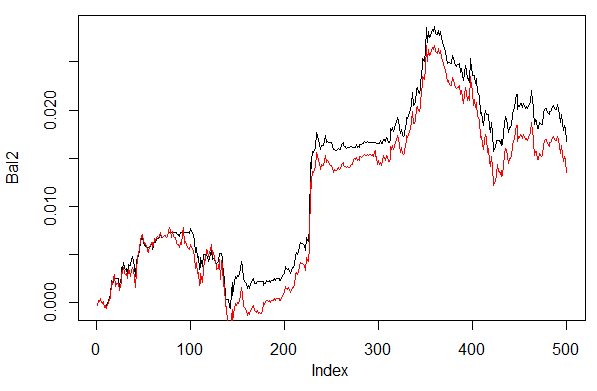
Şek. 28. Tahmini şifreleri çözmenin farklı yolları ile son 500 çubuktaki nöral ağ sinyallerine göre denge
Açıkça, ikinci yolla denge 60/40 daha iyi görünüyor. Geliştirme için bu bakımdan da alan vardır.
İşte kontrol edilecek son şey. Teorik olarak, birkaç nöral ağdan oluşan bir topluluk daha iyi ve daha kararlı bir sonuç verir. Bağımsız örnekler üzerinde eğitilebilseler de aynı örnekler üzerinde eğitilmiş birkaç ağdan oluşan bir topluluğu test edeceğiz. Topluluğun tahmin sonucu, tüm ağ tahminlerinin basit bir ortalamasıdır. Ortalama almanın daha karmaşık başka yolları da vardır.
Test() işlevimizi bir parametre daha ekleyerek iyileştireceğiz — ans=1 topluluktaki ağların sayısını belirtir.
3.4.1. Paralel Hesaplamalar
Çeşitli bağımsız model ile yapılan hesaplamalar kolaylıkla paralel hale getirilebildiğinden, R dilinin sağladığı fırsatı kullanacağız ve bu bilgisayarların hangi işletim sistemlerine sahip olduğuna bakmadan çeşitli işlemci çekirdeğinden veya yerel ağdaki bilgisayarlardan oluşan bir küme oluşturacağız.
Bunun için "foreach" ve "doParallel" paketlerine ihtiyacımız vardır. Aşağıda, işlemcimizin bütün çekirdekleri için küme başlatacak çok basit bir işlev bulunmaktadır.
library(doParallel) library(foreach) puskCluster<-function(){ cores<-detectCores() cl<-makePSOCKcluster(cores) registerDoParallel(cl) clusterSetRNGStream(cl) return(cl) }
Aşağıda birkaç nokta açıklığa kavuşturulmuştur. İlk iki dizede gerekli kitaplıkları yükleriz. Önceden bilgisayarınıza yüklenmiş olmaları gereklidir. Daha sonra işlemcide kaç tane çekirdek olduğunu tanımlarız, bir küme oluştururuz, paralel hesaplamalar için bir paket kaydederiz, her hesaplama akışına bağımsız bir yalancı rasgele sayı oluşturucusu kurar ve küme tanıtıcısını döndürürüz. Bu ayrı bir konu olsa da, yalancı rasgele sayı oluşturucunun kalitesi her model hesaplaması için son derece önemlidir.
Bunu, küme başlatıldıktan ve gerekli tüm hesaplamalar yapıldıktan sonra durdurmayı unutmamalıyız:
cl<-puskCluster() stopCluster(cl)
Paralel hesaplamalar "foreach" paketi üzerinden aşağıdaki formülle yapılacaktır:
SAE<-foreach(times(ans), .packages = "deepnet") %dopar% sae.dnn.train(x = x.tr , y = y.tr , hidden = h, activationfun = act, learningrate = LR, momentum = Mom, output = out, sae_output = sae, numepochs = Ep, batchsize = Bs)
burada time(ans) elde etmek istediğimiz ağ sayısıdır ve .packages hesaplanan işlevi almak için paketi işaret eder.
Sonuç liste biçimine sahiptir ve ihtiyacımız olan eğitimli ağ sayısını içerir.
Daha sonra her ağ üzerinden tahmine ve ortalama hesaplamaya gerek duyarız.
pr.sae<-(foreach(i = 1:ans, .combine = "+") %do% nn.predict(SAE[[i]], x.ts))/ans
Burada i, eğitimli ağ endekslerinin bir vektörüdür.combine="+" nöral ağlarda döndürülen bütün öngörülerin hangi biçimde döndürülmesi gerektiğini belirtir. Bu durumda bir toplamı döndürmemiz ve bu hesaplamaları paralel bir (operatör %do%) şekilde değil, sırayla gerçekleştirmemiz gerekliydi. Elde edilen toplam, nöral ağların sayısına bölünecek ve bu da sonuç olacaktır. Bu güzel ve basit bir yöntemdir.
3 ve 4 nöral ağdan oluşan topluluklardan elde edilen dengeyi yukarıdakilerle aynı parametrelerle ve 60/40 kod çözme yöntemini kullanarak hesaplayın. Nöral ağdaki sonuçlarla karşılaştırın. Paralel hesaplamaların etkinliğini değerlendirmek için, dönem sayısını 300'e yükseltin ve tahmini elde etme sürecini zamanlayın.
1. Bir nöral ağ:
> system.time(Bal21<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 2, Ep=300)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000057 ####loss on step 20000 is : 0.000043 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000081 ####loss on step 20000 is : 0.000086 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000072 ####loss on step 20000 is : 0.000066 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.069451 ####loss on step 20000 is : 0.079629 deep nn has been trained. user system elapsed 115.78 0.00 116.96 > plot(Bal21, t = "l") > abline(h = 0)
2. 3 nöral ağ topluluğu:
> system.time(Bal41<-Testing.2(dt.b, dt, h = c(30, 30, 30), LR = 0.7, Ep=300, dec = 2, ans=3)) user system elapsed 0.22 0.06 233.64 > lines(Bal41, col=4)
3. 4 nöral ağ topluluğu:
> system.time(Bal44<-Testing.2(dt.b, dt, h = c(30, 30, 30), LR = 0.7, Ep=300, dec = 2, ans=4)) user system elapsed 0.13 0.03 247.86 > lines(Bal44, col=2)
Akış sayısı çekirdek sayısından fazlaysa paralel hesaplamadaki yürütme süresi optimaldir. 2 çekirdek kullandım.
Demem o ki, dengede önemli bir avantaj sağlamaz. Aşağıdaki grafikte, mavi çizim 3 ağı, kırmızı olan - 4 ağı ve siyah olan - bir ağı göstermektedir.
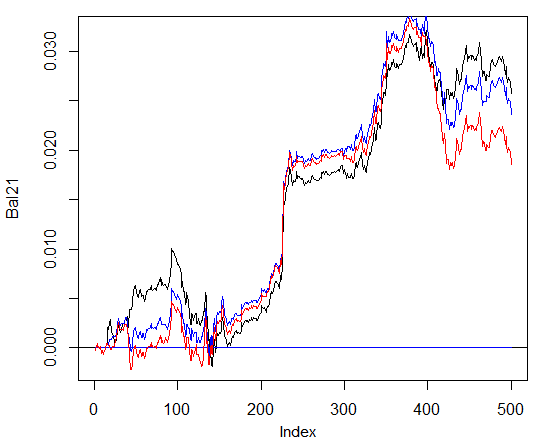
Şek. 29. Son 500 çubuktaki 3 ve 4 nöral ağdan ve bir ağdan oluşan toplulukların sinyallerine göre denge
Genel olarak sonuç, girdi ve çıktı verilerinden başlayarak, bunların normalleştirilme şekli, gizli katmanların sayısı ve bu katmanlardaki nöronların sayısı, eğitim seviyesi, eğitim dönemlerinin sayısı ve diğerleri gibi birçok parametreye bağlıdır.
Son üç örnek. Son 1000 çubuktaki üç gizli katmanda farklı sayıda gizli nöron içeren üç nöral ağın dengesini hesaplayın.
> system.time(Bal0<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 2, Ep=300, bar=1000)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000054 ####loss on step 20000 is : 0.000044 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000078 ####loss on step 20000 is : 0.000079 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000090 ####loss on step 20000 is : 0.000072 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.072633 ####loss on step 20000 is : 0.057917 deep nn has been trained. user system elapsed 116.09 0.02 116.26 > max(Bal0) [1] 0.04725 > plot(Bal0, t="l") > tail(Bal0,1) [1] 0.03514
Maksimum kar 472 puan, son çubukta 351 puan. Grafikte siyah olarak çizilmiştir.
> system.time(Bal0<-Testing.1(dt.b, dt, h = c(13, 8, 5), LR = 0.7, dec = 2, Ep=300, bar=1000)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.005217 ####loss on step 20000 is : 0.004846 training layer 2 autoencoder ... ####loss on step 10000 is : 0.051324 ####loss on step 20000 is : 0.046230 training layer 3 autoencoder ... ####loss on step 10000 is : 0.023292 ####loss on step 20000 is : 0.026113 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.057788 ####loss on step 20000 is : 0.056932 deep nn has been trained. user system elapsed 64.04 0.01 64.24 Warning message: In sae$encoder[[i - 1]]$W[[1]] %*% t(train_x) + sae$encoder[[i - : longer object length is not a multiple of shorter object length > lines(Bal0, col="blue")
Bu açıkça etkisiz bir varyasyondur.
Üçüncü varyasyon:
> system.time(Bal0<-Testing.1(dt.b, dt, h = c(50, 50, 50), LR = 0.7, dec = 2, Ep=300, bar=1000)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000018 ####loss on step 20000 is : 0.000013 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000062 ####loss on step 20000 is : 0.000048 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000053 ####loss on step 20000 is : 0.000055 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.096490 ####loss on step 20000 is : 0.084860 deep nn has been trained. user system elapsed 186.18 0.00 186.39 > lines(Bal0, col="red") > max(Bal0) [1] 0.0543
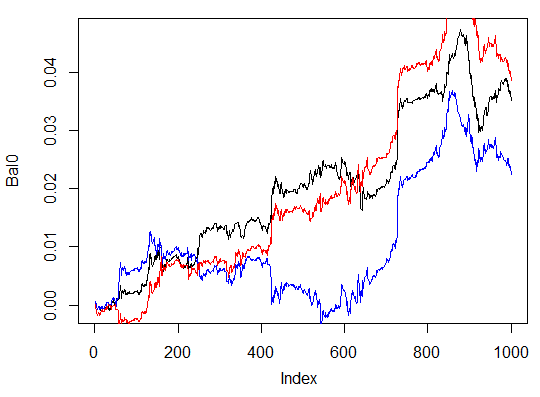
Şek. 30. Son 1000 çubuktaki farklı sayıda gizli nöron içeren üç nöral ağ sinyallerine göre denge
Sonuçlar üçüncü varyantın, 543 puanlık maksimum kârla üçünün içinden en iyisi olduğunu göstermektedir. Sadece gizli nöronların sayısını değiştirdik ve bu önemli bir gelişme sağladı. Optimal parametrelerin araması evrimsel algoritmalar aracılığıyla yapılmalıdır. Bunu keşfetmek okuyucuya kalmıştır.
Yazarın algoritmasının bu pakette tam olarak uygulanmadığı unutulmamalıdır.
4. Uygulama (Gösterge ve Expert Advisor)
Şimdi, derin ağ kullanarak alım satım sinyallerini almak için gösterge ve Expert Advisor için bir program yazacağız.
Bu şekilde bir uygulamanın iki yolu vardır:
- Birincisi. Nöral ağın eğitimi Rstudio içinde manuel olarak gerçekleştirilir. Kabul edilebilir sonuçlar elde ettikten sonra ağı uygun kataloğa kaydedin. Ardından EA'yı ve grafikteki göstergeyi başlatın. EA eğitilmiş ağı yükleyecektir. Gösterge, her yeni çubukta yeni bir girdi veri vektörü hazırlar ve bunu EA'ya iletir. EA ağ verilerini sunar, sinyal alır ve ardından buna göre hareket eder. EA bu gibi açılış ve kapanış talimatları, takip gibi olağan faaliyelerini yerine getirmektedir. Göstergenin amacı, her yeni çubukta yeni giriş verilerini hazırlamak ve EA'ya iletmek ve en önemlisi, ağ tarafından tahmin edilen sinyalleri bir grafik üzerinde sunmaktır. Pratik, bir nöral ağı değerlendirmenin en etkili yolunun görsel kontrol olduğunu göstermektedir.
- İkinci yol. EA'yı ve grafikteki göstergeyi başlatın. İlk başlatmada, gösterge EA'ya hazırlanmış geniş bir girdi ve çıktı veri kümesi iletir. EA eğitim, test etme ve en iyi nöral ağı seçim işlemini başlatır. Bundan sonra çalışma ilk şekilde olduğu gibi devam eder.
Şimdi ilk algoritmayı takip ederek bağlantı göstergesi-EA yazacağız. Minimum yay ve kıvrımlara sahip EA.
Neden bu kadar zordur? Bu uygulama yolu, farklı sembollere/zaman dilimlerine yerleştirilmiş birkaç göstergenin tek bir EA'ya bağlanmasına ve sonuç olarak onlarla birlikte çalışmasına olanak tanır. Bunun için EA'nın küçük bir modernizasyondan geçmesi gereklidir. Bunun hakkında daha sonra konuşacağız.
Aşağıda, gösterge ile EA arasındaki etkileşim yapısı yer almaktadır:
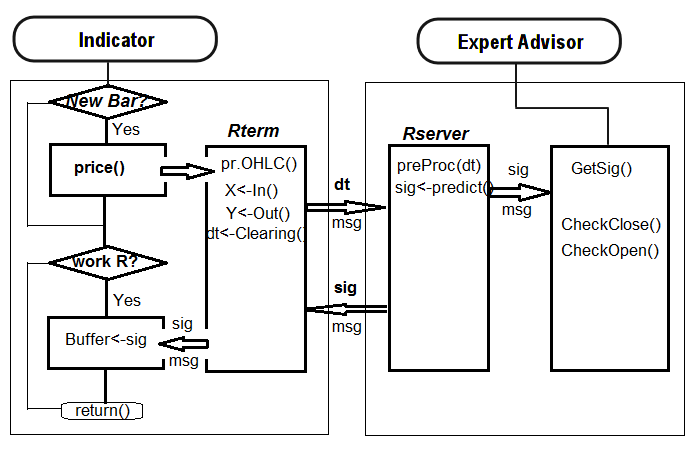
Şek. 31. Gösterge ve EA arasındaki etkileşim yapısı
4.1. Modeli Eğitme ve Kaydetme
İlgilendiğimiz grafikte yer alan göstergeyi kullanarak gerekli kaynak verileri elde edin. Bunun için, girdi değişkenini send=false ayarlayarak göstergeyi çizelgeye yerleştirin, yani görsel temsilin sunucuya gönderilmemesi gereklidir. Bu sembol veya zaman dilimindeki ilk başlatmada, gösterge terminalin (/MQL4/Files) adlı veri dosyasında aşağıdaki /Symbol/TF/Test_Data/ dizinlerini oluşturmaktır.
Böyle bir dizin organizasyonu, modellerin ön eğitiminde deney sonuçlarını bir araya getirmeme ve eski verilerin üzerine yenilerini yazmama fırsatı verir. Aracı sonuçlar /Symbol/TF/Test_Data/ dizininde saklanacak ve EA'nın iş için kullanacağı model /Symbol/TF/ dizininde bulunacaktır (oraya manuel olarak yerleştirilmesi gerekecektir). Aynı sonuç, yeni bir sembol veya EA'nın zaman dilimindeki ilk başlatmada da olacaktır.
Yani, EURUSD, М30 için 14.10.2014 tarihinde 4000 çubuk bulunmaktadır. dt[] veri çerçevesine ihtiyacımız vardır.
Denge sınıfları:
> dt.b<-Balancing(dt) > table(dt.b[ ,ncol(dt.b)]) 0 1 2288 2288
Şimdi, daha önce yazılmış olan Testing.1() işleviyle, 500 ve 300 dönem derin nöral ağı eğitin ve son 500 çubukta elde edilen dengeyi nöral ağ tarafından tahmin edilen sinyallerle değerlendirin.
> system.time(bal<-Testing.1(dt.b, dt, h = c(50, 50, 50), LR = 0.7, dec = 2, Ep=500, bar=500)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000017 ####loss on step 20000 is : 0.000015 ####loss on step 30000 is : 0.000015 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000044 ####loss on step 20000 is : 0.000041 ####loss on step 30000 is : 0.000039 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000042 ####loss on step 20000 is : 0.000042 ####loss on step 30000 is : 0.000036 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.089417 ####loss on step 20000 is : 0.043276 ####loss on step 30000 is : 0.069399 deep nn has been trained. user system elapsed 267.59 0.08 269.37 > plot(bal, t="l")
Nöral ağı farklı bir ad altında kaydedin ve başka bir tane eğitin
> SAE1<-SAE > system.time(bal<-Testing.1(dt.b, dt, h = c(50, 50, 50), LR = 0.7, dec = 2, Ep=300, bar=500)) begin to train sae ...... training layer 1 autoencoder ... ####loss on step 10000 is : 0.000020 ####loss on step 20000 is : 0.000016 training layer 2 autoencoder ... ####loss on step 10000 is : 0.000050 ####loss on step 20000 is : 0.000050 training layer 3 autoencoder ... ####loss on step 10000 is : 0.000051 ####loss on step 20000 is : 0.000043 sae has been trained. begin to train deep nn ...... ####loss on step 10000 is : 0.083888 ####loss on step 20000 is : 0.083941 deep nn has been trained. user system elapsed 155.32 0.02 156.25 > lines(bal, col=2)
Denge grafiklerine bir göz atın (son sonuç kırmızı ile vurgulanmıştır).
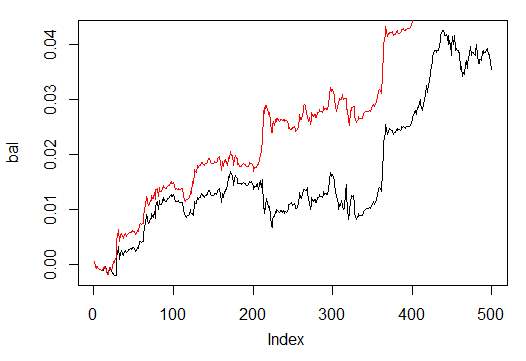
Şek. 32. Son 500 çubuktaki 500 ve 300 dönemde eğitilmiş nöral ağ sinyallerine denge
Görüldüğü gibi, 300 dönemde eğitilen nöral ağ, 500 çağda eğitilen ağa göre daha iyi sonuç vermiştir.
İkincinin eğitim süresi, bu zaman dilimindeki bir alım satım oturumu sırasında hızlı şekilde yeniden eğitme için uygundur.
Gerçek bir grafik üzerinde daha fazla çalışmak için iki nesneye ihtiyacımız var: eğitimli model "SAE" ve girdi verileri için normalleştirme parametreleri "prepr". Bunları ilgili dizine kaydedin, benim durumumda bu "D:/Alpari Limited MT4/MQL4/Files/EURUSD/M30/Test_2014-10-14" olur. Bu gösterge tarafından kaydedilen "i_SAE_EURUSD_30.Rdata" çalışma alanını Rstudio'da açtıysanız, çalışan olarak tanımlanır ve çalışır.
save(SAE, prepr, file="SAE.model") "SAE.model" dosyasına modelin kendisini ve normalizasyon parametrelerini kaydettik. Modeli bunlar olmadan kullanmak mantıklı değildir. Beğendiğiniz modelleri her gün deneyebilir ve kaydedebilirsiniz. "/File/Symbol/TF/Test_Data" klasörlerine kaydedileceklerdir. EA'nın modeli kullanması için, "SAE.model" dosyasını manuel olarak "File/Symbol/TF/" klasörüne koyun. Bu klasör yalnızca bir model içerebilir ve EA bunu çalışma için kullanacaktır.
"SAE.model" dosyasını yükledikten sonra, EA bu nesneleri çalışmada kullanmak üzere çalışma alanına yükler. Bu noktada işin manuel kısmı bitmiştir, göstergeyi-EA'yı grafiğe yerleştirebilir ve gerçek zamanlı olarak test edebilirsiniz.
EA'nın çalışma etkinliğini değerlendirmek için nicel kriterler gereklidir. Doğruluk katsayısı bu amaç için pek uygun değildir.
ZigZag tarafından alınan tahmini denge oranının ve son çubuktaki denge oranının çubuk sayısına ortalaması. Bizim durumumuzda bu, ZigZag'a göre dengedir:
sig.zz<-ifelse(tail(dt[ , ncol(dt)], 500) == 0, 1, -1) bal.zz<-cumsum(tail(price[ , 'CO'], 500) * sig.zz) Kzz<-mean(bal.zz / bal) > Kzz [1] 0.9173312
Bu çok yüksek bir puan ama göreceli.
Zamanla neye benzediğini görürsek, ilk 50-100 çubuk için bunun kararsız bir endeks olduğunu görebiliriz, ancak daha sonra neredeyse sabit hale gelmektedir. İstatistikler aşağıdadır:
> plot(bal/bal.zz, t="l") > summary(bal/bal.zz) Min. 1st Qu. Median Mean 3rd Qu. Max. -15.2500 0.7341 0.7844 0.9173 0.8833 55.0000
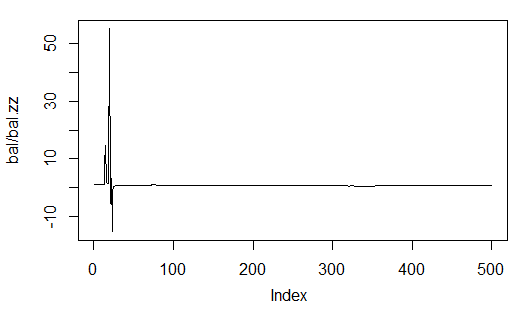
Şek. 33. Tahmini dengenin ZigZag tarafından elde edilen dengeye oranı
İkincisi, N çubuk uzunluğundaki bir streç üzerinde bir çubuk için kaç kar noktası olduğunu gösterdiği için daha kesindir.
Örneğin, 500 barlık bir sinir ağı tahminine göre denge için:
> Kb<-tail(bal,1)/length(bal)*10^Dig > Kb [1] 11.508
ZigZag sinyallerine göre:
> Kbz<-tail(bal.zz,1)/length(bal)*10^Dig > Kbz [1] 13.784
Parametrelerden birinin etkinliğinin alt sınırı tanımlandığında, nöral ağı yeniden eğitebileceğimiz veya parametrelerini optimize edebileceğimiz zamanı biliriz.
EA, grafikte aşağıdaki parametreleri gösterecektir: OP – yürütülen operasyon, Acc – Doğruluk, K – Kb daha önce tanımlanır, Kmax – Kb ile aynı parametredir ancak yüksek dengede tanımlanır ve bu parametrenin son çubuktaki maksimum olandan ne kadar farklı olduğu hakkında bir fikir verir.
4.2. Kurulum ve Başlatma Sırası
Ekli SAE.zip arşivinde şunları bulabilirsiniz:
- i_SAE.mq4 göstergesi, ~/MQL4/Indicators/ klasörüne yerleştirilir
- e_SAE.mq4 EA ~/MQL4/Experts/ klasörüne yerleştirilir
- mt4Rb7.dll kütüphanesi, ~/MQL4/Libraries/ klasörüne yerleştirilir.
- mt4Rb7.mqh başlık dosyası, ~/MQL4/Include/ klasörüne yerleştirilir. Kütüphane ve başlık dosyası Bernd Kreuss tarafından geliştirilmiş ve güzel bir şekilde sunulmuştur. Ad, son değişikliğin (b7) endeksini içerir. Aynı ada sahip çok sayıda sürüm olduğunda, düzeltilmesi çok zaman alan karışıklıklar olabilir.
- R üzerindeki script dosyaları: i_SAE.r (ana gösterge script'i), i_SAE_fun.r (gösterge script'i işlevleri), e_SAE.r (EA script'i), e_SAE_init.r (EA başlatma script'i), SAE_SetDir.r (gerekli dizinleri doğrulama ve oluşturma script'i). Script dosyaları ne sembole ne de bir zaman dilimine bağlı oldukları için ayrı bir dizinde bulunabilirler. Benim durumumda bu "C:Rdata/SAE/"dir. "C:Rdata/" dizini, belirli bir projeye eklenmemiş farklı script dosyaları içerir. Script dosyalarını benimkinden farklı bir klasöre koyarsanız, gösterge ve EA'da script dosyalarına giden yol için doğru olan uygun düzeltmeleri yapın.
- SAE.model, "SAE" modeline ve "prepr" normalleştirme parametrelerine sahip bir dosyadır. Model son tarih 14.10.14'te EURUSD (M30) üzerinde eğitilmiştir. Eğitim süreci yukarıda açıklanmıştır.
Ayrıca R dilinin bilgisayarınızda saklandığı dizine giden yolu da unutmayın.
Çalışmaya başlamak için aşağıdaki sırayı takip etmek tercih edilebilir. EA'yı grafiğe yerleştirin. EA'yı başka bir sembole yerleştirmeye karar verirseniz, daha önce başlatılan sunuculardan farklı bir bağlantı noktası belirtilir. Mesela, bağlantı noktası 8886'dır (varsayılan olarak bağlantı noktası 8888).
Not. Bu kesinlikle verimsiz bir yoldur. Her sunucunun boyutu 120-130 Mb'dir. Bugün olanlar bunlardır.
Normal EA başlatma işleminden sonra, "Hesaplama sonucu yoktur! Sembolü" uyarısı görünecektir. Ardından göstergeyi harici parametre send = true ve göstergenin bağlanacağı belirtilen sunucu bağlantı noktası ile kurun (yukarıya bakın). Her şey doğru çalışırsa, çıktı dizesinde gerçek veri olarak "operasyon", Doğruluk, K ve Kmax görünecek ve alım satım işlemi başlayacaktır.
Sürecin verimli kontrolü en iyi Windows Görev Yöneticisinden kolaylaştırılabilir. EA veya gösterge başlatıldıktan sonra Rterm listede görünmüyorsa, R süreci kesintiye uğramıştır. Bu tür kesintilerin ana nedeni, script dosyalarındaki sözdizimi hatası, alıcı MQL vektörünün uzunluğunun ve Rterm'den çıkarılan vektörün uyumsuzluğudur.
Script dosyaları, Rstudio'da baştan sona satır satır başlatılarak hataları ayıklanabilir.
Maalesef EA'yı test cihazında başlatamadım, bu nedenle bir deneme hesabında test edilmesi gereklidir.
4.3. Niteliksel Özellikleri Geliştirme Yolları ve Yöntemleri
- Girdide kullanılan gösterge kümesini değiştirin.
- Girdi verilerinin normalleştirilme yolunu değiştirin.
- "Denetimcinin" parametrelerini ve girdideki göstergeleri optimize edin.
- İki sütunlu matris için giriş değişkeni kodlamasını değiştirin. Tahmin sinyalini kalibre edin.
- Ağ parametrelerini optimize edin (gizli katmanlardaki nöron sayısı, katman sayısı, öğrenme düzeyi, dönem sayısı).
Sonuç
SAE üzerinden gizli katmanlardaki nöron ağırlıklarını başlatma ile derin ağ modelleri oluşturduk, eğittik ve test ettik. Ağlar çok hızlı bir şekilde yeniden eğitilir ve alım satım sürecini kesintiye uğratmadan ağların yeniden eğitilmesine olanak tanır.
Nöral ağlar tarafından gösterilen sonuçlar, metriklere göre ortalamadır. İdeal sonuç ilk hedef değildi.
Model ve verimlilik katsayısı için böyle kalıcı bir değerlendirme kullanılırsa, model alım satım sürecini kesintiye uğratmadan yeniden eğitilebilir ve optimize edilebilir.
Ek:
- SAE.zip - gösterge, EA ve beraberindeki dosyalar.
- R_intro.zip - Rusçada R ve Rstudio ile ilgili literatür.
- DeepLearning.zip - Derin Öğrenme literatürü.
MetaQuotes Ltd tarafından Rusçadan çevrilmiştir.
Orijinal makale: https://www.mql5.com/ru/articles/1103
MQL5 Cookbook: TradeTransaction Olayının İşlenmesi
MetaTrader Sinyalleri hizmetini ve Sosyal Alım Satımı nasıl geliştirdik?
MQL5 Cookbook: Özel Grafik Olaylarını İşleme
Makroekonomik Verilerin Döviz Fiyatı Dalgalanması Üzerindeki Etkisinin Regresyon Analizi
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz