Andrey Dik / プロファイル
- 情報
|
12+ 年
経験
|
5
製品
|
87
デモバージョン
|
|
15
ジョブ
|
0
シグナル
|
0
購読者
|
A group for communication on optimization and free product testing://t.me/+vazsAAcney4zYmZi
Attention! My Telegram doppelgangers have appeared, my real nickname is @JQS_aka_Joo
My github with optimization algorithms: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
All my publications: https://www.mql5.com/en/users/joo/publications
I have been developing systems based on machine learning technologies since 2007 and in the field of artificial
intelligence, optimization and forecasting.
I took an active part in the development of the MT5 platform, such as the introduction of support for universal parallel
computing on the GPU and CPU with OpenCL, testing and backtesting of distributed
computing in the LAN and cloud during optimization in MT5, my test functions are included in the standard delivery of the terminal.
⭐⭐ ⭐ ⭐ ⭐ ⭐ ⭐ ⭐ ⭐⭐ ⭐ ⭐ ⭐ ⭐ ⭐ ⭐ ⭐ ⭐ ⭐ ⭐ ⭐ ⭐ ⭐ ⭐ ⭐ ⭐ ⭐ ⭐ ⭐ ⭐ ⭐ ⭐ ⭐ ⭐ ⭐ ⭐
My Products:
https://www.mql5.com/en/users/joo/seller
Recommended Brokers:
https://rbfxdirect.com/ru/lk/?a=dnhp
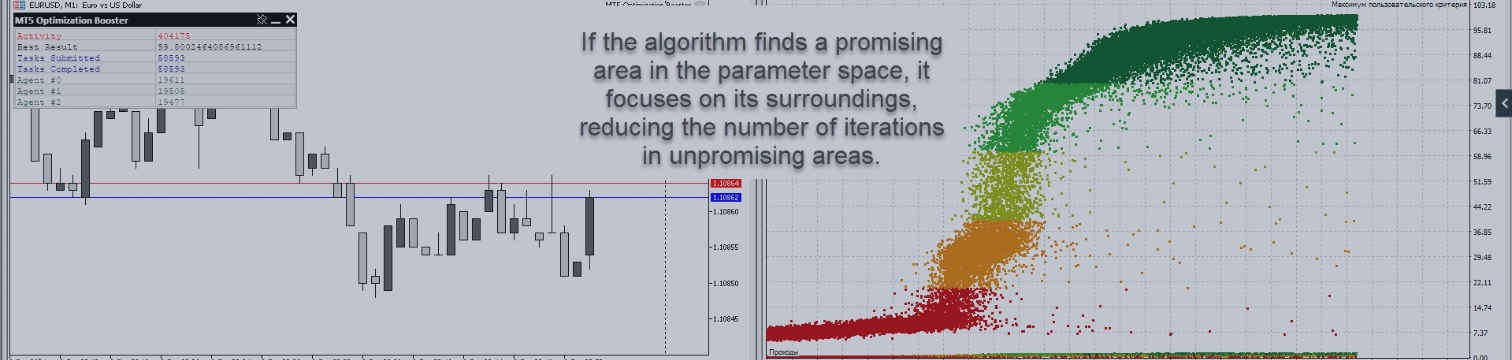

この記事では、細菌走化性最適化(BCO)アルゴリズムのオリジナルバージョンとその改良版を紹介します。新バージョン「BCOm」では、細菌の移動メカニズムを簡素化し、位置履歴への依78ytf存を軽減するとともに、計算負荷の大きかった元のバージョンに比べて、より単純な数学的手法を採用しています。この記事では両者の違いを詳しく検討し、とくにBCOmの特徴に焦点を当てます。また、テストを実施し、その結果をまとめます。


この記事では、最初期かつ最も広く知られているメタヒューリスティック手法の一つであるタブーサーチアルゴリズムについて解説します。初期解の選択や近傍解の探索から始め、特にタブーリストの活用に焦点を当てながら、アルゴリズムの動作を詳しく見ていきます。本記事では、タブーサーチの主要な特徴と要素について取り上げます。

本稿では、微細藻類に特徴的な生物学的プロセスに基づく人工藻類アルゴリズム(AAA)について考察します。このアルゴリズムには、螺旋運動、進化過程、適応過程が含まれており、最適化問題を解くことができます。この記事では、AAAが機能する原理と、数学的モデリングにおけるその可能性について詳しく分析し、自然とアルゴリズムによる解とのつながりを強調しています。
この記事では、無政府社会最適化(ASO)アルゴリズムに触れ、無政府社会(中央集権的な権力や様々な種類のヒエラルキーから解放された社会的相互作用の異常なシステム)の参加者の非合理的で冒険的な行動に基づくアルゴリズムが、解空間を探索し、局所最適の罠を回避できることを議論します。本稿では、連続問題にも離散問題にも適用可能な統一的なASO構造を提示します。

この記事は、生命と繁殖に最適な条件を求めて動物が季節的に移動する様子をモデル化するAMOアルゴリズムについて説明しています。AMOの主な機能には、トポロジカル近傍の使用と確率的更新メカニズムが含まれており、実装が容易で、さまざまな最適化タスクに柔軟に対応できます。

この記事では、人工蜂の巣アルゴリズム(ABHA)の探索を続け、コードの詳細を掘り下げるとともに、残りのメソッドについて考察します。ご存じのとおり、このモデルにおける各蜂は個別のエージェントとして表現されており、その行動は内部情報、外部情報、および動機付けの状態に依存します。さまざまな関数を用いてアルゴリズムをテストし、その結果を評価表としてまとめて提示します。

この記事では、2009年に開発された人工蜂の巣アルゴリズム(ABHA)について説明します。このアルゴリズムは、連続的な最適化問題を解決することを目的としています。この記事では、蜂がそれぞれの役割を担って効率的に資源を見つける蜂のコロニーの行動から、ABHAがどのようにインスピレーションを得ているかを探ります。

生物の社会的行動と、それが新しい数学モデルであるASBO(適応型社会的行動最適化)の開発に与える影響について、引き続き考察していきます。今回は、二段階の進化プロセスを詳しく分析し、アルゴリズムをテストした上で結論を導き出します。自然界において生物の集団が生存のために協力するのと同様に、ASBOも集団行動の原理を活用し、複雑な最適化問題を解決します。

この記事は、生物の社会的行動の世界と、それが新たな数学モデルであるASBO(適応型社会的行動最適化、Adaptive Social Behavior Optimization)の構築に与える影響について、興味深い洞察を提供します。生物社会におけるリーダーシップ、近隣関係、協力の原則が、革新的な最適化アルゴリズムの開発にどのように着想を与えるのかを探ります。

この記事では、クーロンの静電気力の法則に触発された人工電界アルゴリズム(AEFA: Artificial Electric Field Algorithm)を紹介します。このアルゴリズムは、荷電粒子とその相互作用を利用して複雑な最適化問題を解決するために電気現象をシミュレートします。AEFAは、自然法則に基づいた他のアルゴリズムと比較して、独自の特性を示します。

この記事では、問題の詳細と検索空間内の環境のダイナミクスを考慮できる柔軟でインテリジェントな最適化手法の開発における重要なステップとしてのANSアルゴリズムの可能性を明らかにします。
第2回では、化学演算子を1つのアルゴリズムに集め、その結果の詳細な分析を紹介します。化学反応最適化(CRO)法がテスト機能に関する複雑な問題の解決にどのように対処するかを見てみましょう。
この記事の最初の部分では、化学反応の世界に飛び込み、最適化への新しいアプローチを発見します。化学反応最適化(CRO)は、熱力学の法則から導き出された原理を使用して効率的な結果をもたらします。この革新的な方法の基礎となった分解、合成、その他の化学プロセスの秘密を明らかにします。

ここでは、ACSアルゴリズムの進化、つまり収束特性とアルゴリズムの効率性を向上させることを目的とした3つの変更について検討します。主要な最適化アルゴリズムの1つを変換します。行列の修正から母集団形成に関する革新的なアプローチまでをカバーします。

人工協調探索(ACS)は、バイナリ行列と、相互主義的関係と協調に基づく複数の動的な個体群を用いて、最適解を迅速かつ正確に探索する革新的な手法です。捕食者と被食者に対するACS独自のアプローチにより、数値最適化問題で優れた結果を出すことができます。

この記事では、コードロックを単なるセキュリティメカニズムとしてではなく、複雑な最適化問題を解くためのツールとして再考し、新たな視点から捉えます。セキュリティ装置にとどまらず、最適化への革新的アプローチのインスピレーション源となるコードロックの世界をご紹介します。各ロックが特定の問題の解を表す「ロック」の母集団を作り、機械学習や取引システム開発など様々な分野でこれらのロックを「ピッキング」し、最適解を見つけるアルゴリズムを構築します。

この記事では、ユニークな宇宙物体である彗星と、太陽に接近する際に形成されるその印象的な尾にインスパイアされた「彗尾最適化アルゴリズム(CTA: Comet Tail Algorithm)」について考察します。このアルゴリズムは、彗星とその尾の運動の概念に基づき、最適化問題の最適解を見つけることを目的としています。