じゅぎょう
とりあえず、コードを持ってくる必要があると思います。
1.コンパイル可能です。
2.読みやすい形。
3.解説
原則的に、このテーマは興味深く、緊急性の高いものです。
じゅぎょう
とりあえず、コードを持ってくる必要があると思います。
1.コンパイル可能です。
2.読みやすい形。
3.解説
オッケーです。
実数のソートされた配列があります。配列の中のセルを、仮想ルーレットのセクターの大きさに対応する確率で選ぶ必要がある。
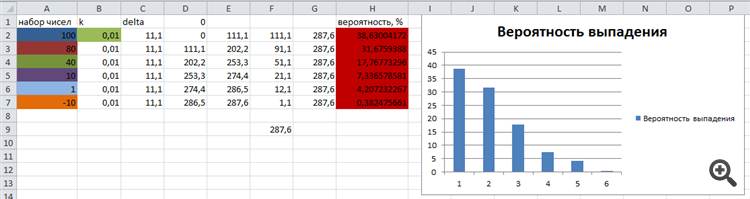
テストセットの数字とその理論的な抜け落ちの確率をエクセルで計算し、アルゴリズムの結果と比較するために、次の図のように表示します。
アルゴリズムを実行した結果。
2012.04.04 21:35:12 ルーレット(EURUSD,H1) h0 38618465 38.618465
2012.04.04 21:35:12 ルーレット(EURUSD,H1) h1 31685360 31.68536
2012.04.04 21:35:12 ルーレット(EURUSD,H1)h3 7.334754 7.334754
2012.04.04 21:35:12 ルーレット(EURUSD,H1) h4 4205492 4.205492
2012.04.04 21:35:12 ルーレット(EURUSD,H1) h5 385095 0.385095
2012.04.04 21:35:12 ルーレット(EURUSD,H1) 12028 ms - 実行時間
ご覧のように、対応するセクタに「ボール」が落ちる確率の結果は、理論的に計算されたものとほぼ同じであることがわかります。
#property script_show_inputs //--- input parameters input int StartCount=100000000; // Границы соответствующих секторов рулетки double select1[]; // начало сектора double select2[]; // конец сектора //—————————————————————————————————————————————————————————————————————————————— void OnStart() { MathSrand((int)TimeLocal());// сброс генератора // массив с тестовым набором чисел double array[6]={100.0,80.0,40.0,10.0,1.0,-10.0}; ArrayResize(select1,6);ArrayInitialize(select1,0.0); ArrayResize(select2,6);ArrayInitialize(select2,0.0); // счетчики для подсчета выпадений соответствующего числа из тестового набора int h0=0,h1=0,h2=0,h3=0,h4=0,h5=0; // нажмём кнопочку секундомера int time_start=(int)GetTickCount(); // проведём серию испытаний for(int i=0;i<StartCount;i++) { switch(Roulette(array,6)) { case 0: h0++;break; case 1: h1++;break; case 2: h2++;break; case 3: h3++;break; case 4: h4++;break; default: h5++;break; } } Print((int)GetTickCount()-time_start," мс - Время исполнения"); Print("h5 ",h5, " ",h5*100.0/StartCount); Print("h4 ",h4, " ",h4*100.0/StartCount); Print("h3 ",h3, " ",h3*100.0/StartCount); Print("h1 ",h1, " ",h1*100.0/StartCount); Print("h0 ",h0, " ",h0*100.0/StartCount); Print("----------------"); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Рулетка. int Roulette(double &array[], int SizeOfPop) { int i=0,u=0; double p=0.0,start=0.0; double delta=(array[0]-array[SizeOfPop-1])*0.01-array[SizeOfPop-1]; //------------------------------------------------------------------------------ // зададим границы секторов for(i=0;i<SizeOfPop;i++) { select1[i]=start; select2[i]=start+MathAbs(array[i]+delta); start=select2[i]; } // бросим "шарик" p=RNDfromCI(select1[0],select2[SizeOfPop-1]); // посмотрим, на какой сектор упал "шарик" for(u=0;u<SizeOfPop;u++) if((select1[u]<=p && p<select2[u]) || p==select2[u]) break; //------------------------------------------------------------------------------ return(u); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Генератор случайных чисел из заданного интервала. double RNDfromCI(double min,double max) {return(min+((max-min)*MathRand()/32767.0));} //——————————————————————————————————————————————————————————————————————————————
OKです。
実数のソートされた配列があります。配列の中のセルを、仮想ルーレットのセクターの大きさに対応する確率で 選択する必要がある。
セクタ幅」の設定原理を説明してください。 配列の値に対応していますか?それとも別に設定されているのでしょうか?
これが一番暗い問題で、あとは問題ない。
第二の質問:0.01という数字は何ですか? どこから来たのですか?
要するに、正しいセクターの脱落確率(円周に占める幅の割合)はどこで得られるのか教えてください。
各セクターのサイズだけでいいんです。 自然界には負のサイズは存在しないという前提(デフォルト)で。 カジノでも。;)
セクタ幅」の設定原理を説明してください。 配列の値に対応していますか?それとも別に設定されているのでしょうか?
セクタの幅は配列の値に対応することができません。そうでなければ、アルゴリズムはすべての数に対して機能しません。
重要なのは、数字同士の距離です。すべての数字が最初の数字から離れれば離れるほど、落ちにくくなる。本質的には、我々は最後の数字が落ちるの確率は0に等しくなかったように、0.01の要因によって調整され、数字間の距離に比例する直線の棒に延期第一から最も遠いとして。係数が高いほど、各セクターがより均等であることを示している。Excelファイルを添付しますので、実験してみてください。
MetaDriver。
1.要するに、正しいセクターの脱落確率(円周の端数での幅)がわかる場所を教えてください。
2.自然界には負のサイズは存在しないと(デフォルトで)仮定して、各セクタのサイズを決めればいいのです。;)1.理論的な確率の計算は、エクセルで行っています。最初の数字は最も高い確率、最後の数字は最も低い確率であるが0にはならない。
2) セクタの大きさが負になることは、どのような数の集合に対しても、集合が降順でソートされている場合、最初の数が最大となります(集合の中で最大の数でも負であれば動作します)。
セクタの幅は配列の値と一致してはいけません。そうでなければ、アルゴリズムはすべての数に対して機能しません。
hu:重要なのは、数字が離れている距離です。すべての数字が最初の数字から離れれば離れるほど、落ちにくくなる。要するに我々は、番号間の距離に比例する直線上のセグメントを、0.01のファクターで調整し、最後の番号が落ちない確率が、最初の番号から最も遠いものとして0であるように 延期 するのである。係数が高いほど、各セクターがより均等であることを示している。エクセルファイルが添付されていますので、実験してみてください。
1.理論的な確率の計算はエクセルに記載されている。最初の数字は最も高い確率、最後の数字は最も低い確率であるが0にはならない。
2. セクションが降順でソートされている場合、どのような数の集合に対しても、負のサイズのセクタは決して存在しません - 最初の数が最大です(集合の中で最大の数でも同様に負の数で動作します)。
あなたのスキームは「いきなり」最小の 数(vmh)の確率を 設定します。合理的な 正当性がない。
// 「正当化」はちょっと難しいので。大丈夫です。N個の釘の間にはN-1個のスペースしかありません。
つまり、「係数」に依存するわけです。
アルゴリズムを行う前に、全セクタの 「幅」の計算を決めておく必要があります。
zyu:「数値間の距離」の計算式をあげてください。ど の数字が「最初」なのでしょうか?自分との距離は?Excelに送らないでください、経験済みです。思想的なレベルで混乱する。補正係数はどこから来て、なぜそうなっているのか?
赤で示したものは、まったく事実ではありません。:)
は、非常に高速になります。
int Selection() { return(RNDfromCI(1,SizeOfPop); }
アルゴリズム全体の品質に影響を及ぼしてはならない。
また、仮にそうなったとしても、このオプションはスピードを犠牲にして品質を追い越すことになるでしょう。
1.あなたのスキームは「いきなり」最小の 数(vmh)の確率を 設定します。合理的な 正当性がない。つまり、(vmhは)「係数」にも依存するわけです。
2.アルゴリズムを行う前に、全セクタの 「幅」の計算を決めておく必要があります。
3.zu:「数値間の距離」の計算式をあげよ。 どの数字が「最初」なのでしょうか?自分との距離感は?Excelに送らないでください、経験済みです。思想レベルで混乱する。補正係数はどこから出てくるのか、また具体的になぜ出てくるのか。
4.赤で強調されているのは、まったく事実ではありません。:)
1.ええ、そんなことはないですよ。この係数がいいんです。アルゴリズムのスピードは変わりません。
2.確信に至る。
array[0]が最大の数で、0.0を始点とする正の方向に向かう数列の光線があります。このようにレイ上のセグメントを配置します。
start0=0=0 end0=start0+|array[0]+delta|
start1=end0 end1=start1+|array[1]+delta|とする。
start2=end1 end2=start2+|array[2]+delta|とする。
......
start5=end4 end5=start5+|array[5]+delta|となります。
どこで
delta=(array[0]-array[5])*0.01-array[5];
以上、算数でした。:)
ここで、印をつけた光線に「球」を投げると、ある区間に当たる確率は、その区間の長さに比例する。
4.間違っているところ(全てではない)を強調したため。最後の数字が0になる確率を持たないように0.01倍で補正した数字間の距離に比例する線分を数直線上にプロットして います」と強調してください。
は、非常に高速になります。
int Selection() { return(RNDfromCI(1,SizeOfPop); }
アルゴリズム全体の品質に影響を及ぼしてはならない。
そして、少しでも影響を受けると、スピードを犠牲にして品質を追い越してしまう。
:)
単純に配列の要素を ランダムに選べということでしょうか?- この場合、配列番号間の距離は考慮されないので、このオプションは役に立ちません。

- www.mql5.com
は、無価値であることが実験的に確認されているのでしょうか?
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
ここでは、最適アルゴリズムの論理の問題を議論することをお勧めします。
もし、自分のアルゴリズムが速度(あるいは明瞭さ)の点で最適なロジックを備えていると疑う人がいれば、それは歓迎すべきことです。
また、このスレッドでは、アルゴリズムを実践したい人、他の人の役に立ちたい人を歓迎します。
当初は、"Dummieからの質問 "ブランチに投稿したのですが、この質問は、そこに属するものではないことに気づきました。
そこで、これより高速な「ルーレット」アルゴリズムのバリエーションを提案してください。
明らかに、配列は関数から取り出すことができるので、毎回宣言してサイズを変更する必要はないのですが、もっと画期的な解決策が必要です。:)