От теории к практике - страница 622
Вы упускаете торговые возможности:
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Регистрация
Вход
Вы принимаете политику сайта и условия использования
Если у вас нет учетной записи, зарегистрируйтесь
Колмогоров - это дядька поумнее большинства пялящихся в монитор. И требования к прогнозированию ВР у него простые: матожидание = const и периодическая АКФ.
Теперь вот какую вещь надо сказать.
Смотрю я на распределения приращений и как они меняют свои стат.моменты в зависимости от интервалов считывания котировок и понимаю, что рыночные цены НЕ обладают свойством самоподобия. Это свойство присуще исключительно процессам с устойчивыми, бесконечно делимыми (к примеру, нормальными) распределениями приращений - таким как броуновское движение. На рынке этого не наблюдается.
Очевидно, Мандельброт и его подельники, не шаря в физике (а еще хуже - шаря, но тщательно это скрывая), специально ввели в заблуждение страждущих, чтобы те поскорее переходили на скальпинг на тиковых данных и мелких таймфреймах и, сливая свои депозиты, пополняли их бездонные карманы.
Вот так-то!
Исследование на тему
http://tpq.io/p/rough_volatility_with_python.html
то же самое https://hal.inria.fr/hal-01350915/documentТеперь вот какую вещь надо сказать.
Смотрю я на распределения приращений и как они меняют свои стат.моменты в зависимости от интервалов считывания котировок и понимаю, что рыночные цены НЕ обладают свойством самоподобия. Это свойство присуще исключительно процессам с устойчивыми, бесконечно делимыми (к примеру, нормальными) распределениями приращений - таким как броуновское движение. На рынке этого не наблюдается.
Очевидно, Мандельброт и его подельники, не шаря в физике (а еще хуже - шаря, но тщательно это скрывая), специально ввели в заблуждение страждущих, чтобы те поскорее переходили на скальпинг на тиковых данных и мелких таймфреймах и, сливая свои депозиты, пополняли их бездонные карманы.
Вот так-то!
ты уже и теорию заговора сюда приплёл... очередная чушь.
Ознакомься с предметом:
http://inis.jinr.ru/sl/vol2/Physics/Динамические%20системы%20и%20Хаос/Федер%20Е.,%20Фракталы,%201991.pdf
Чтобы было понятно, к чему я стремлюсь.
Только начал работать в потоке Эрланга 60-го порядка (считывание тиковых котировок, в среднем, 1 раз в минуту).
Имеем следующую гистограмму для приращений, к примеру, пары EURJPY:
Статистика:
Это - практически распределение Лапласа.
Сумма приращений (~цена) и модулей приращений (~дисперсия) имеют нормальное распределение при достаточно большом объеме выборки (сутки - для М1 или неделя - для М5) таких СВ.
Так вот задача - выйти на чистое распределение Лапласа, тогда реально будем иметь прямой аналог процесса Орнштейна-Уленбека с возвратом к средней.
еще бы угадать какие участки истории он использует для построения своих графиков, есть трендовые участки на несколько месяцев, есть боковики
как и не ясен принцип "перескакивания" с М1 на М5, тут как бы нужно постоянство или хотя бы обоснование, ему бы в гос.статистические учреждения. Там с такими бы талантами ему не было бы цены, там тоже удачно складывают то кварталы, то месяцы, то сезоны = на выходе нужные стат.данные
)))
Чтобы было понятно, к чему я стремлюсь.
Только начал работать в потоке Эрланга 60-го порядка (считывание тиковых котировок, в среднем, 1 раз в минуту).
Имеем следующую гистограмму для приращений, к примеру, пары EURJPY:
Статистика:
Это - практически распределение Лапласа.
Сумма приращений (~цена) и модулей приращений (~дисперсия) имеют нормальное распределение при достаточно большом объеме выборки (сутки - для М1 или неделя - для М5) таких СВ.
Так вот задача - выйти на чистое распределение Лапласа, тогда реально будем иметь прямой аналог процесса Орнштейна-Уленбека с возвратом к средней.
В общем понятно, уменьшается эксцесс, подбираются хвосты ---> от Лапласа переходим к нормальному, от нормального к равномерному. А что тогда в самом начале? Не Лаплас? Что? Ведь легко описывается экспонентой, если взять один бок.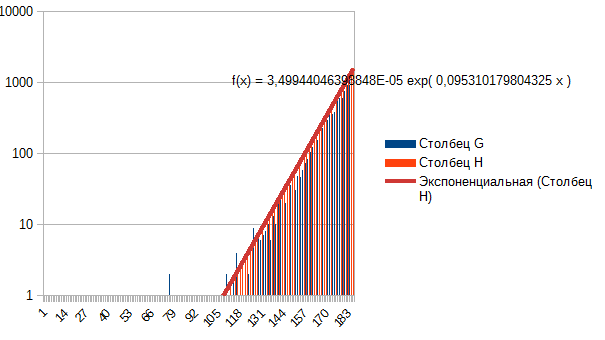
Это минутки EURUSD окно-месяц.