Вы упускаете торговые возможности:
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Регистрация
Вход
Вы принимаете политику сайта и условия использования
Если у вас нет учетной записи, зарегистрируйтесь
Нет, с помощью гусеницы нельзя оценить насколько изменилось состояние рынка.
Можно лишь оценить насколько новые ошибки предсказания изменили прогноз против старых ошибок.
То есть SSA ничего не говорит о правильности прогноза, разница SSA говорит лишь о разнице в ошибках. А уж куда пойдёт рынок SSA это не волнует от слова совсем.
Без оценки ошибок каждого из SSA ваша разность как бы висит в воздухе, ей не на что опереться.
да знаю я это уже давно, но надежда то есть, вот и выдумываю куда бы еще посмотреть )) , я хочу матрицу собственных чисел ковариационной матрицы прогнать на истории и проанализировать, насколько большие различия в ней - а вдруг как в теории расказывают, что цена учитывает все и пр. премудрости )))
ой не знаю не знаю, мне кажется что если Александр до конца не смог - то ничто уже не спасет такой подход. Прогнозировать случайное блуждание тяжко, и оценивать его какие-то мнимые состояния :)
тут в дополнение к моему посту выше, в особенности в части анекдота... если честно, то есть некая иллюзия, что закономерность то в ценовых графиках это как раз и не повторять свое предыдущие состояния, вот и в SSA будет время, сделаю набор всех возможных ковариационным матриц и попробую проанализировать на предмет неповторяемости в близлежащих состояниях, т.е. матрицы должны чередоваться в неповторяемом порядке
может вечером причешу код по SSA и выложу, код просто порт из Матлаба, не ожидал, но Алглиб очень помогает быстро портировать такие вещи делал как себе пример с целью научиться, может тоже кому поможет разобраться, вот матлаб SSA приатачил
выделю вопрос отдельно:
На какую функцию делать регрессию, чтобы последняя ее точка находилась в центре ценового канала?
Нужна функция, типа полинома, которая справлялась бы и с зигзагом и с половиной окружности (как видите на примерах, полином с этими темами не справляется).
(фигуру Максима Дмитриевского пока можно не рассматривать, она не вписывается в теорию, что цена - это торговый канал, который идет по определенной траектории. эта фигура - это торговый канал с выбросом в конце, ее можно рассмотреть позже.)
Другими примерами нелинейных функций служат показательные функции, логарифмические функции, тригонометрические функции, степенные функции, гауссова функция и кривые Лоренца.
Ну Смокчи, всех взбудоражил своими картинками! ))
ну и немного психологии, чтобы оценить насколько поиски Грааля успешны, понравилось видео, видимо девушка выглядит естественной и убедительной
ну и немного психологии, чтобы оценить насколько поиски Грааля успешны, понравилось видео, видимо девушка выглядит естественной и убедительной
увидев такие глаза ночью можно и гусеницу родить
ну и немного психологии, чтобы оценить насколько поиски Грааля успешны, понравилось видео, видимо девушка выглядит естественной и убедительной
Девчёнка умница-молодость видит невидимое для многих.
ну если психология интересна, так сказать вишенка на торте...
ну если психология интересна, так сказать вишенка на торте...
Самая интересная 30я минута фильма), но чтобы понять надо смотреть весь.
вам же уже написали что это бесполезное времяпрепровождение
пока свое время не потратишь - не поймешь.
Как сделать регрессию в экселе.
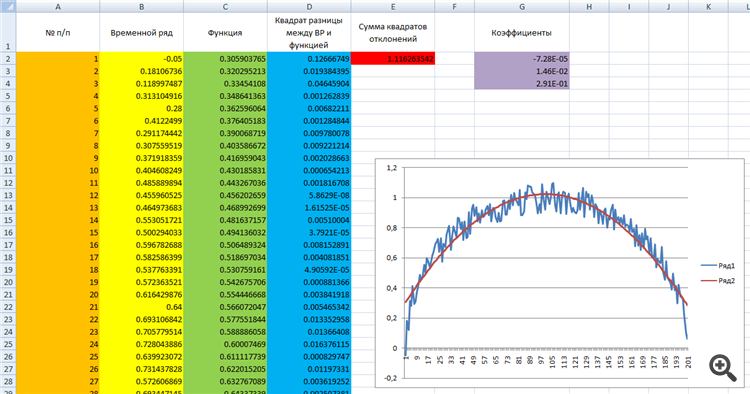
С помощью функции Данные/Поиск решения.
Во вложенной таблице:
первый столбец это номер п/п.
второй столбец - временной ряд.
третий - функция (в данном случае полинома).
четвертый - МНК. значение временного ряда минус значение функции, и взять в квадрат.
в красной ячейке - сумма по синему столбцу, то есть сумма квадратов отклонений.
в фиолетовых ячейках - коэффициенты, которые нужно подобрать.
Функция полинома это y=ax2+bx+c
где х - значения координат по оси x. оранжевый столбец. от 0 до 201.
у - это значения координат по оси у, которые будут у подобранного полинома.
a,b,c - коэффициенты, которые мы будем подбирать.
В экселе формула будет выглядеть вот так =a*A1^2+b*A1+c . То есть вместо иксов подставляем значения из столбца А. (смотреть зеленый столбец)
Для того чтобы подобрать коэффициенты функции, нажимаем "Данные", и потом "Поиск решения".

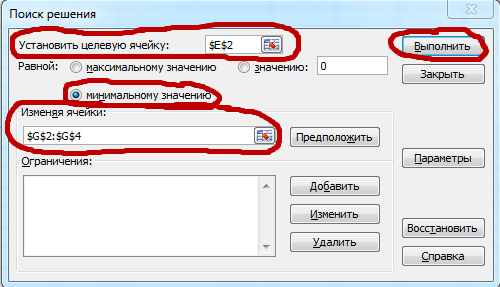
В открывшемся меню выбираем:
Установить целевую ячейку (красная ячейка в нашей таблице),
минимальному значению,
Изменяя ячейки (фиолетовые ячейки на нашей таблице)
и нажимаем "Выполнить".
То есть, мы минимизируем квадраты отклонений временного ряда от функции.
Попробуйте в зеленый столбец поподставлять свои функции.
показательные функции, логарифмические функции, тригонометрические функции, степенные функции, гауссова функция , кривые Лоренца, другие...
Задача остается прежней, нужно подобрать функцию, последняя точка которой будет лежать в центре ценового канала (и для фигуры зигзаг и для фигуры половина окружности).
...
То есть, мы минимизируем квадраты отклонений временного ряда от функции.
Попробуйте в зеленый столбец поподставлять свои функции.
показательные функции, логарифмические функции, тригонометрические функции, степенные функции, гауссова функция , кривые Лоренца, другие...
Задача остается прежней, нужно подобрать функцию, последняя точка которой будет лежать в в центре ценового канала (и для фигуры зигзаг и для фигуры половина окружности).
Заинтересовало. Во-первых, неточность, минимизируем не "квадраты", а "сумму квадратов". Во вторых, если нужно придать большее значение последним точкам, это делается просто, в минимизируемой сумме надо брать не просто квадраты, а взвешенные квадраты, то есть умноженные на какие-нибудь положительные весовые коэффициенты. Их значения в конце массива сделать бОльшими, в начале мЕньшими. Например, для номеров точек i от 1 до n веса, равные q^(n-i) при q < 1, дают квадратам отклонения множители, аналогичные весам курсов в экспоненциальной скользящей средней. Часто еще делают их сумму равной единице, если надо сравнивать разные аппроксимации по значению минимума взвешенной суммы квадратов отклонений.
А что такое "центр" для криволинейного канала, границы которого описываются различными типами формул? Или хотя бы для первого варианта, показательными функциями?
Если это просто середина отрезка от предпоследнего значения в ряде до последнего, то достаточно сделать очень большими веса отклонений в двух последних точках ряда. Или еще проще, найти эту середину, и все.
Нужны еще какие-то требования к отклонениям, иначе задача недопоставлена.
А польза-то какая от вычислений "центра" в последней точке?