Вот и вопрос, как их составить? Пока только в итерационной форме получается:
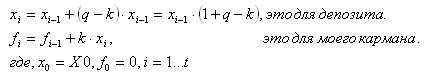
Надо это в аналитической форме представить (в виде функциональной зависимости от времени t).
Ага! тогда получается так:
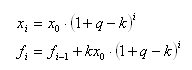
И выражение для суммы снятых за период t месяцев денежных средств можно записать в виде:
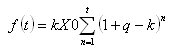
Если так, то уже лучше. Что дальше? Нужно от суммы избавиться...
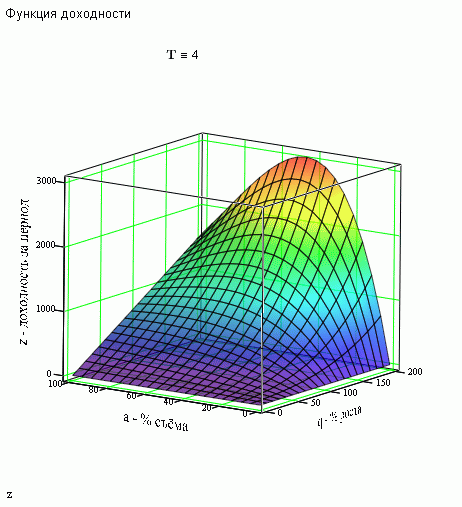
выглядеть будет где-то так.
Нефига-се!...
А можно подробнее? В смысле в виде формулы.
Т.е. действительно, виден оптимум по проценту съёма!
Если так, то уже лучше. Что дальше? Нужно от суммы избавиться...
вспоминаем формулу для суммы n первых членов геометрической прогрессии
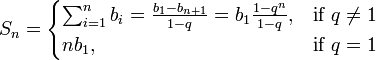
вспоминаем формулу для суммы n первых членов геометрической прогрессии
Шайтан! Действительно, 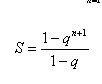 .
.
Тогда окончательно, выражение для суммы снятых средств будет представлено в виде:
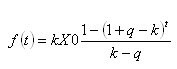
Осталось взять производную по времени и приравнять её к нулю... Мда-а-а.
Привет всем!
Мне позволили пользоваться депозитом размером в Х0 руб. в течении t месяцев. Ежемесячно на депозит начисляется фиксированный процент средств q от текущей величины депозита Х. Мне разрешается каждый месяц снимать некоторый процент k со счёта которая не превышает величину q.
Таким образом, стоит задача максимизировать снятую за период t месяцев денежную сумму.
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Привет всем!
Мне позволили пользоваться депозитом размером в Х0 руб. в течении t месяцев. Ежемесячно на депозит начисляется фиксированный процент средств q от текущей величины депозита Х. Мне разрешается каждый месяц снимать некоторый процент k со счёта которая не превышает величину q.
Таким образом, стоит задача максимизировать снятую за период t месяцев денежную сумму. Очевидным кажется, что снимать каждый месяц весь начисляемый процент q не самый лучший вариант, т.к. депозит в этом случае не растёт и при меньшей нагрузки на счёт, снятая в итоге сумма может быть больше... С другой стороны, величина k не должна стремиться к нулю, т.к. в этом случае сумма снятых денег тоже стремиться к нулю. Видимо, истина где-то по середине. Но, где именно?
Помогите аналитически решить эту задачку в общем виде.
P.S. Не стал постить в ветке задачки никак не связанные с торговлей, т.к. предложенная тема связана с последней.