Рантье - страница 6
Вы упускаете торговые возможности:
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Регистрация
Вход
Вы принимаете политику сайта и условия использования
Если у вас нет учетной записи, зарегистрируйтесь
Нет-нет. Не ошибаюсь. Вот зависимость суммы выводимых денег, которая следует из итерационной формулы (красным), и из аналитической зависимости (синим).
Видно, что совпадают и имеется максимум по к (на предыдущей странице топика).
ясно, у вас нет дискретного снятия а обязательно непрерывное снятие равными долями. Поэтому решения снимать в разные периоды по-разному у вас нет. Поэтому нет и решения снять все в конце не снимая до этого. Это вытекает не из условий задачи, а из формул вами применяемых (k фиксировано, а не переменное ki, i=0...T)
Суммарные выведенные средства
эффект становится ощутимым при достаточно большом коэффициенте роста
У меня похожие зависимости.
Сейчас пытаюсь разложить выражение для производной по степеням k, но ничего хорошего не получается - приходится удерживать аж шесть порядков. Понятно, что решить аналитически это нельзя. Может есть ещё идеи? Кто-то про дифурки вспоминал...
У меня похожие зависимости.
Сейчас пытаюсь разложить выражение для производной по степеням k, но ничего хорошего не получается - приходится удерживать аж шесть порядков. Понятно, что решить аналитически это нельзя. Может есть ещё идеи? Кто-то про дифурки вспоминал...
аналитически сложновато. От q и t. Зависит как-то хитро :) При увеличении q, как и при увеличении t доля оптимального снятия последовательно уменьшается
У меня похожие зависимости.
Сейчас пытаюсь разложить выражение для производной по степеням k, но ничего хорошего не получается - приходится удерживать аж шесть порядков. Понятно, что решить аналитически это нельзя. Может есть ещё идеи? Кто-то про дифурки вспоминал...
Можно идти от частного к общему. Например, если t = 1, то вывести деньги можно только один раз, а следовательно выводить нужно в размере q. Далее рассматриваем случай для t = 2, t = 3 и т.д.
Т.е. если при t = 2 оптимально выводить за раз менее q, то найти экстремум и обобщить для всех q при t = 2.
Точно также для t = 3, t = 4 и т.д.
По значению экстремума можно будет получить размер вывода денег, как f(t)
Для составления ДУ можно рассмотреть схему связанных сосудов.
Начальный объём первого сосуда B0
Можно идти от частного к общему. Например, если t = 1, то вывести деньги можно только один раз, а следовательно выводить нужно в размере q. Далее рассматриваем случай для t = 2, t = 3 и т.д.
По значению экстремума можно будет получить размер вывода денег, как f(t)
Возможно ты и прав. Только вот уже для t=3 мы имеем согласно уравнению
степень k - тройку в первой производной df(k)/dk=0, и нам нужно искать корни кубического уравнения со всеми вытекающими... Т.е. дальше t=3 нам по этому сценарию не пробиться. Напомню, что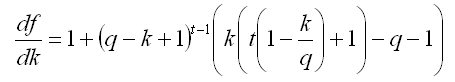 
, и для t=1 оптимальный размер k=q, для t=2 k=q, для t=3 k=q. А вот дальше увеличивать t и решать аналитически не получится. Если решать численно, то видно, что для скорости роста депозита q в пределах 10% в месяц, оптимальный процент вывода денег со счёта становится меньше q при t>30 месяцев.
Вывод отсюда таков: Если надёжность ТС такова, что среднее время жизни депозита не превышает 3 лет, то оптимальным поведением будет ежемесячный вывод всей полученной прибыли (депозит не растёт). В противном случае нужно искать аналитическое решение для оптимального процента вывода k и действовать согласно формуле. Этот сценарий гарантирует максимальное количество денежных средств положенных в карман за ожидаемое время жизни депозита.
avtomat:
Для составления ДУ можно рассмотреть схему связанных сосудов.Начальный объём первого сосуда B0
Если сосуды (течение жидкости) находятся в динамическом равновесии, (т.е. сколько жидкости за единицу времени втекает в первый сосуд, столько же вытекает из последнего) задача об уровне воды в каждом сосуде решается элементарно и не сводится к поставленной задаче о депозите. Если же рассматривать сосуды в процессе их наполнения то не совсем понятна аналогия с депозитом. avtomat, поясни, пожалуйста, что ты имел в виду предлагая такую интерпретацию?
P.S. Призыв получить приближённое аналитическое решение уравнения df/dk=0 остаётся в силе. Принимаются любые идеи.