
Что такое тренды и какова структура рынков — трендовая или флэтовая?
Введение
Прежде чем начать, посмотрим, какое определение тренда дает интернет. Вот такое определение написано в wikipedia:
Тренд (англицизм от trend) — основная тенденция изменения чего-либо: например, в математике — временного ряда. Тренды могут быть описаны различными уравнениями — линейными, логарифмическими, степенными и так далее. Фактический тип тренда устанавливают на основе подбора его функциональной модели статистическими методами либо сглаживанием исходного временного ряда.
Или такое определение:
Тренд в экономике — направление преимущественного движения показателей. Обычно рассматривается в рамках технического анализа, где подразумевают направленность движения цен или значений индексов. Чарльз Доу отмечал, что при восходящем тренде последующий пик на графике должен быть выше предыдущих, при нисходящем тренде последующие спады на графике должны быть ниже предыдущих (см. Теория Доу). Выделяют тренды восходящий (бычий), нисходящий (медвежий) и боковой (флэт). На графике часто рисуют линию тренда, которая на восходящем тренде соединяет две или более впадины цены (линия находится под графиком, визуально его поддерживая и подталкивая вверх), а на нисходящем тренде соединяет два или более пика цены (линия находится над графиком, визуально его ограничивая и придавливая вниз). Трендовые линии являются линиями поддержки (для восходящего тренда) и сопротивления (для нисходящего тренда).
Для нас намного важнее не то, как это звучит, а как заработать при помощи данного определения и что вообще это означает. Читая определения выше, не очень понятно, что нужно делать, чтобы заработать и как это все описать математически. Все широко известные определения созданы как будто специально расплывчатыми, чтобы их можно было трактовать более чем одним способом, и чтобы оставить людям возможность "додумать" что-то свое. Но в науке не нужно ничего додумывать, определение должно быть четким, понятным и иметь только одно толкование, без вариантов, чтобы каждый из тех, кто руководствуется методом, мог с точностью воспроизвести результаты другого человека, который использовал данный метод.
Основы прибыльной торговой стратегии
Для того чтобы перейти к понятиям трендов и флэтов, нужно сначала разобраться в основах, то есть что нужно сделать для того, чтобы заработать. Абсолютно любая торговая стратегия, хотите вы этого или нет, строится на том, что нам нужно получить матожидание прибыли больше 0. Для людей, знакомых с математикой, тут все понятно, и дальнейшие пояснения не нужны, но для остальных поясню, что такое матожидание, и дальше это будет важно. Простыми словами, матожидание — это средняя прибыль. Логично, что средняя прибыль должна быть больше 0, иначе если она будет 0, то мы не будем зарабатывать, если будет меньше 0, то будем терять деньги.
Матожидание складывается из вероятности прибыльной сделки, среднего размера прибыли и среднего размера убытка по сделкам. Формула простая: вероятность прибыли умножаем на среднюю прибыль и вычитаем из полученного результата вероятность убытка, умноженную на средний убыток.
m=(P(tp)*tp)-(P(sl)*sl),
где
- m — матожидание прибыли,
- P(tp) — вероятность прибыльной сделки,
- P(sl) — вероятность убыточной сделки,
- tp — средний размер прибыльной сделки,
- sl — средний размер убыточной сделки.
Это означает, что если вероятность прибыльной сделки 50%, и средний размер прибыльной сделки равен размеру убыточной, то матожидание будет равно 0, и мы ничего не заработаем. Например, средний размер прибыльной и убыточной сделки = 10$, тогда m=(50*10)-(50*10)=0. Нужно уточнить, что матожидание для нормально распределенной случайной величины равно 0 (это математический факт). В своей предыдущей статье Дискретизация ценового ряда, случайная составляющая и "шумы", я рассматривал, что распределение приращений на реальных рынках очень похоже на нормальное и подозрительно напоминает случайное блуждание.
Для того чтобы заработать, нам нужно либо повысить вероятность прибыльной сделки, либо повысить средний размер прибыльной сделки и понизить средний размер убыточной сделки. Допустим, мы повысим вероятность прибыльной сделки до 60%, и пусть средний размер прибыльной сделки будет равен среднему размеру убыточной сделки = 10$. Тогда совершив сто сделок, мы заработаем, m=(60*10)-(40*10)=200$. Так, если вероятность прибыльной сделки будет сохраняться, то мы будем стабильно выходить в плюс. Аналогично можно повысить средний размер прибыльной сделки, понизить средний размер убыточной сделки и оставить вероятность на уровне 50 %, так мы тоже будем выходить в плюс.
На этом месте часто возникает когнитивное искажение у многих трейдеров, особенно начинающих. Человек думает: "Хорошо, я просто сделаю средний размер прибыльной сделки в 2 раза больше среднего размера убыточной сделки и буду открывать позиции... скажем, по пересечению средних" (алгоритм входа не важен, подставьте свой). Человек подсознательно рассчитывает на результат: m=(50*20)-(50*10)=500$ прибыли, но по факту оказывается, что он получает матожидание m=(33,3*20)-(66,6*10)=0, точнее даже убыток из-за спреда и комиссий. В данной статье я не буду учитывать спред и комиссии, на текущем этапе это не так важно. Другой трейдер попадает в обратную "ловушку": он решает сделать прибыль в 2 раза меньше убытка, ведь тогда по его наблюдениям прибыль срабатывает чаще. В итоге он тоже получает убыток из-за комиссий и спреда, потому что оказывается, что реальное матожидание такой системы m=(66,6*10)-(33,3*20)=0. Так можно очень сильно увеличить стоплосс и уменьшить профит, доведя вероятность получения прибыли до 90%-99% и выше, но в итоге вся прибыль будет компенсирована убытками. Сюда можно отнести и все системы с мартингейлом, который не меняет матожидание и если оно было равно 0, то таким и останется, но получение убытка может быть сильно отложено во времени.
Данная ситуация получается потому, что реально человек не нашел никаких прибыльных закономерностей, а без рабочих закономерностей, он будет торговать случайное блуждание, и матожидание случайного блуждания = 0. Далее в тексте я буду говорить, что если матожидание равно 0, то значит вероятность совершить прибыльную сделку так и остается равна 50%, меняются только коэффициенты (введу термин "равновесие 50%"). У нас или повышается вероятность прибыльной сделки и пропорционально уменьшается размер прибыльной, или наоборот, вероятность прибыльной сделки падает, но и размер ее пропорционально растет. Нам нужно как-то нарушить это "равновесие 50%" и выйти за пределы нулевого матожидания. Тут нужно уточнить, что сделать убыточную систему так-же сложно, как и прибыльную, убытки трейдер терпит потому, что существуют комиссии и депозит конечен.
Переход от свечных графиков к блоковым
Так как торгуем мы изменение цен, а оно происходит в пунктах (под пунктом понимаю минимально возможное изменение цены), и прибыль зависит от того, сколько цена прошла пунктов, то для простоты понимания нужно отойти от стандартного способа представления цены в виде свечей/баров, потому что они сильно искажают картину и затрудняют понимание процесса. Перейдем к способу отображения, которое учитывает только движение цены в пунктах. В статье я буду использовать мой индикатор, который строит блоки после того, как цена пройдет определенное число пунктов. Индикатор прикрепил к статье. Но вы можете использовать любой другой способ. На рисунке 1 показан пример, как строятся блоки. Блок может быть любого размера, от 1 пункта до бесконечности, с шагом 1 пункт. Если размер блока 10 пунктов, то блок закрывается после того, как цена прошла 10 пунктов по вертикали и начинается формирование нового блока, который может закрываться с шагом в 10 пунктов вверх или вниз. У блока есть цены open, high, low, close и обозначают они все то же самое, что и у свечей. Будем считать, что 1 блок — это 1 шаг, и это будет важно далее.
Рисунок 1.
Чтобы перейти к понятию тренда, нужно от чего-то отталкиваться и иметь какой-то эталон. Нам известно, что для случайного блуждания характерно то, что каждый следующий шаг не зависит от предыдущего, у процесса отсутствует память и вероятность смены направления каждого следующего шага 50%. Но возникает вопрос: случайное блуждание трендовое или флэтовое? Посмотрим на график случайного блуждания на рисунке 2.
Рисунок 2.
Многие найдут на рисунке 2 и тренды и флэты, но реально это график случайного блуждания, продискретизированный часовыми свечами, вероятность сделать каждый следующий шаг вверх тут 50%, ровно как и шаг вниз, и не зависит от направления предыдущего шага. При разработке понятия трэнд, мы будем отталкиваться от случайного блуждания потому, что как я писал ранее, матожидание прибыли на случайном блуждании = 0. Это следует из того, что вероятность изменения или сохранения направления каждого следующего шага тут равно 50% и, открыв позицию, сколько бы шагов мы ее не держали, средний убыток будет равен средней прибыли, а вероятность угадать направление 50%. Поэтому мы будем считать, что график случайного блуждания не трендовый и не флэтовый, он случайный.
Так появился эталон, с которым можно сравнивать ценовой ряд, который мы исследуем, делать выводы — трендовый данный ценовой ряд или флетовый.
Разработка модели эталона
На рисунке 2 был показан график случайного блуждания, продискретизированный часовыми свечами, такое представление не очень наглядно и вносит искажения в восприятие процесса, перейдем к его исходному виду, которое показано на рисунке 3. Данный ряд я прикрепил к статье в формате CSV, и вы можете загрузить его в терминал.
Рисунок 3.
На рисунке 3 показан график случайного блуждания с шагом 1 пункт и тот же график в виде блоков, размером 1 пункт. Блоки нужны, чтобы шаги были лучше видны, по сути, это один и тот же график, отличия только визуальные. Так как мы считаем, что случайное блуждание будет эталоном для дальнейшего определения трендовости ценового ряда, то для того, чтобы сравнивать реальный ценовой ряд с эталоном, построим график распределения плотности вероятностей приращений для случайного блуждания. Данную задачу можно решить аналитически, при помощи функции Гаусса, но это не так наглядно, и даже не все люди, знакомые с математикой, до конца понимают, что означает та или иная форма полученного распределения. Поэтому для построения эталонной плотности распределения вероятностей, при помощи правил комбинаторики, создадим таблицу, фрагмент которой показан на рисунке 4. Полная таблица будет приложена к статье отдельным файлом в формате excel.
Рисунок 4.
При помощи таблицы будем оценивать, сколько случайное блуждание может пройти по вертикали за 40 шагов. При помощи коэффициента qs (в формуле таблицы) будем задавать число выборок, для которого строится таблица. В примере таблица построена для 100 000 выборок. В столбце, "vertical steps" указано, сколько шагов по вертикали проходит функция, а в столбце "probability of event %" отображается частота, с которой встречается это число шагов по вертикали. Например, всего процесс делает 40 шагов, максимум может уйти на 40 шагов вверх или вниз, у нас 100 000 выборок (измерений) и мы получаем, что из 100 000 раз, в среднем 0,00000009 раз процесс уйдет на 40 шагов по вертикали. При этом 38 шагов по вертикали он пройдет уже 0,0000036 раз из 100 000, а 36 шагов по вертикали он пройдет 0,00007 раз из 100 000. Так, набрав массив значений в столбце "probability of event %", можно построить график распределения плотности вероятностей приращений, который отображен на рисунке 5.
Рисунок 5.
При помощи таблицы получили эталонное распределение плотности вероятности приращений за 40 шагов для процесса, у которого вероятность изменения направления каждого следующего шага равна вероятности продолжения и равна 50%. Для того, чтобы проверить, что нигде нет ошибки, можно измерить распределение плотности вероятности для случайного блуждания и сравнить с эталоном. Измерения будем делать для случайного блуждания, фрагменты которого показаны на рисунках 2 и 3. Будем последовательно измерять, сколько функция прошла шагов по вертикали за 40 шагов и 100 000 выборок (измерений). Результаты показаны на рисунке 6. По оси Х отложены амплитуды -40...0...40 шагов по вертикали, по оси Y отложено количество событий для каждого числа шагов по вертикали.
Рисунок 6.
На рисунке 6 красным показано эталонное распределение для 100 000 выборок по 40 шагов (рассчитанные по таблице), а белой гистограммой показаны реально измеренные 100 000 выборок созданного случайного блуждания. Как видно, реально измеренное почти полностью совпадает с рассчитанным по таблице. Отклонения незначительны, и чем больше будет выборок, тем точнее реально измеренные значения будут соответствовать эталону. Теперь сравнивая распределение какого-то ряда с эталоном, можно говорить, насколько сильно оно отличается от эталонного распределения. На данный момент можно сделать вывод, что исходя из формы плотности распределений вероятности приращений, исследуемый ряд максимально похож на случайное блуждание. Зачем это нужно рассмотрим далее.
Распределение приращений на реальном рынке
Для измерений возьмем реальный график GBPUSD и преобразуем его в блоковый график с размером блока 0,00022. Как и в примере выше, посчитаем, сколько цена проходила по вертикали за 40 шагов, используя 100 000 выборок и сравним с эталоном на рисунке 7.
Рисунок 7.
Как и раньше, красным цветом показано эталонное распределение, а белым измеренное. Теперь и потребуется то упрощение, которое мы делали ранее, то есть использовали комбинаторику, вместо функции Гаусса, потому что даже не все люди, понимающие математику, могут сделать правильный вывод, а уж те, кто не понимают математику, вообще никакие выводы сделать бы не смогли. Мы видим, что распределение приращений GBPUSD симметрично относительно нуля. Симметричность относительно нуля указывает на то, что нет ярко выраженной склонности к восходящим или нисходящим трендам. То есть вероятность того, что после каждого блока вверх будет блок вниз равна вероятности того, что после каждого блока вниз будет блок вверх. Другими словами, нет ярко выраженной тенденции движения цены вверх или вниз.
Намного интереснее, что график распределения GBPUSD ниже и шире эталона. Это говорит о том, что за 40 шагов цена попадает в ноль намного реже, чем должна для случайного блуждания, и наоборот проходит по вертикали зачастую больше блоков, чем должна для случайного блуждания. А это означает, что вероятность смены направления каждого следующего шага не равна 50%, а немного меньше. Из данного графика можно сделать вывод, что если был растущий блок, то с вероятностью больше 50% после растущего блока появится растущий, и с вероятностью больше 50% после падающего блока, появится падающий.
Что дают нам эти знания? Вспомним формулу матожидания, по которой мы могли оценить прибыль. Там вся проблема получения прибыли крылась в том, что если бы вероятность "правильного" входа была больше 50%, то мы бы оставались в прибыли при условии, что средний убыток равен средней прибыли. Чтобы заработать, нужно было нарушить "равновесие 50%". Сейчас мы не оценивали точного значения вероятности разворота, его можно просто посчитать по графику, но если предположить, что на данном графике вероятность продолжения 55%, а вероятность разворота 45%, и средняя прибыль равна среднему убытку и равна 10 шагам (размер шага 0,00022*10=0,0022), то матожидание m=(55*0.0022)-(45*0.0022)=0.121-0.099=0.022. В свою очередь это означает, что, совершив 100 сделок, мы останемся в плюсе 0,022. Если торговать 0,1 лотом по GBPUSD, то это 220$ прибыли.
Зная, что вероятность продолжения тенденции больше 50%, можно использовать торговую стратегию на продолжение тренда, то есть если закрылся растущий блок, то открывая позицию Buy на продолжение тренда, мы заработаем. Другими словами, зная, что вероятность продолжения тенденции больше 50%, мы используем трендовую стратегию и остаемся в плюсе. И наоборот, если мы знаем, что вероятность разворота больше 50%, то есть вероятность того, что после растущего блока появится падающий блок, мы будем открывать позицию Sell каждый раз, когда закрывается растущий блок и, используя флэтовую (контртрендовую) стратегию, останемся в плюсе.
Определение: что такое тренд / флэт
Определение тренда и флэта напрямую вытекает из того, используя какую стратегию мы сможем заработать на том или ином рынке. Если на случайном блуждании вероятность продолжения тенденции равна 50% и случайное блуждание не трендовое и не флэтовое, то:
Трендовое движение — ситуация, при которой вероятность продолжения тенденции выше вероятности разворота тенденции. Если цена прошла 10 пунктов, то при трендовой ситуации с вероятностью больше 50% цена пройдет еще 10 пунктов в направлении предыдущего движения.
Флэтовое движение — ситуация, при которой вероятность смены направления движения выше вероятности продолжения тенденции. Если цена прошла 10 пунктов при флетовой ситуации, то с вероятностью выше 50% развернется и пройдет 10 пунктов в обратном направлении.
Если цена представлена в виде блоков (как я описывал выше) по 10 пунктов, то при трендовой ситуации выгодно открывать позицию Buy после закрытия каждого следующего растущего блока и открывать позицию Sell после каждого следующего падающего блока. При флэтовой ситуации, наоборот, после закрытия растущего блока выгодно открывать позицию Sell и после падающего блока открывать позицию Buy.
Другими словами, если рынок трендовый, то просто торгуй на продолжение тенденции и выйдешь в плюс. Если рынок флетовый, то торгуй на разворот тенденции и выйдешь в плюс. Если рынок не трендовый и не флэтовый, то не открывай позиции.
Тут я не утверждаю, что на случайном блуждании нельзя заработать, это тема отдельного и очень серьезного исследования.
Проверка утверждения
Не всегда, казалось бы, логичные утверждения, оказываются верными. Поэтому проверим наши выводы при помощи простой модели. Для этого создадим 2 процесса, у первого будет вероятность разворота больше 80%, он показан на рисунке 8. У второго процесса вероятность разворота будет 20%, и он показан на рисунке 9.
Рисунок 8.
Рисунок 9.
На рисунке 8 видно, что измеренное распределение плотности вероятности значительно уже эталона, процесс намного чаще возвращается в ноль. На рисунке 9 видно, что измеренное распределение плотности вероятности намного шире эталона, процесс намного реже возвращается в ноль, чем эталон. Отсюда можно сделать выводы, что ранее проделанные операции верные, и логика неошибочна. Если вероятность разворота меньше 50%, то распределение получается действительно шире эталонного, и дальше эту логику можно применять для анализа степени трендовости того или иного инструмента. Тут я введу понятие "трендовость", которое будет количественно отображать склонность процесса к продолжению тенденции.
Оценка степени трендовости инструмента
Имея эталонное значение, можно оценивать степень трендовости в абсолютных значениях как различных таймфреймов одного инструмента, так и разных инструментов между собой. Но для начала нужно разработать методику сравнения в абсолютных величинах. Я предлагаю 2 методики:
- По отклонению плотности. Выбираем диапазон амплитуд и считаем, сколько событий попало в этот диапазон для эталона, потом проделываем то же самое для измеренных значений. Делим эталонное значение на измеренное, получаем абсолютные единицы. Если значение больше 1, то ряд трендовый, если меньше 1, то флэтовый. Например, весь диапазон амплитуд у нас -40...0...40, смысла считать сколько попало в диапазон -40...40 нет, потому что туда попадет 100% значений, поэтому возьмем другое значение. В теории вероятности говорится что: "Около 68% значений из нормального распределения находятся на расстоянии не более одного стандартного отклонения σ от среднего; около 95 % значений лежат расстоянии не более двух стандартных отклонений; и 99,7 % не более трёх". То есть считается нормальным сравнивать сколько событий попадает в тот или иной диапазон и сравнивать с нормальным распределением. Но мы не измеряли стандартное отклонение в своей работе, да оно и не нужно, поэтому воспользуемся абсолютными цифрами. Я предлагаю следующую методику:
- Задаем на эталоне сколько процентов выборок нас интересует, например нас интересует 80% выборок, смотрим, в какой диапазон попадает 80% выборок. В нашем примере было 100 000 выборок, значит 80% это 80 000 выборок. Посчитаем, в какой диапазон амплитуд попадает 80 000 выборок. В диапазон от -8 до 8 на эталоне попадает 84,6% выборок, а в диапазон -6...6 попадает 73,18% выборок. Получилось, что 84,6% ближе к 80%, значит фиксируем сколько выборок попадает в диапазон -8...8 — и это 84614 выборки.
- Теперь измеряем, сколько выборок попадает в диапазон -8...8 на распределении, построенном для ряда с 80% вероятностью разворота. В нашем случае в этот диапазон попадает 100 000 выборок. Далее делим 84614/100000=0,8416. Получили степень трендовости 0,8416 для графика на рисунке 8.
- Проверим степень трендовости графика с рисунка 9. Там в диапазон -8...8 попало 52034 выборки и получаем степень трендовости ряда с 20% вероятностью разворота 84614/52325=1,617.
- По средней амплитуде. Можно использовать другой метод. Из центральной предельной теоремы можно сделать вывод, что средняя амплитуда по вертикали у случайного блуждания пропорциональна степени 0,5 из числа шагов. Мы ранее делали таблицу для построения эталонного распределения, часть которой показана на рисунке 4, и там была ячейка "average block vertically", в которой рассчитывалось какое в среднем число шагов по вертикали пройдет эталонное случайное блуждание. Это число находилось как сумма столбца "amplitude frequency" для диапазона 0...40 шагов по вертикали, деленная на число выборок (в данном случае 100 000). В таблице это значение 5,0148. Значит, в среднем случайное блуждание пройдет -5,0148...5,0148 шагов по вертикали для 40 шагов, это пропорционально степени 0,437 из числа шагов. Отклонение от степени 0,5 возникает из-за того, что берем всего 40 шагов, и в теореме о пьяном матросе говорится, что случайное блуждание должно пройти примерно пропорционально степени 0,5 из числа шагов. При помощи таблицы мы получили точное значение для данного числа шагов.
- Если мы измерим, какое среднее число шагов по вертикали проходит процесс с вероятностью разворота 50%, который изображен на рисунках 2 и 3, то получится значение 5,0363. Найдем степень трендовости ряда с 50% вероятностью разворота, для этого делим эталонное значение на измеренное 5,0148/5,0363=0,9957. Видно, что степень трендовости практически равна 1, что говорит о том, что ряд максимально близок к случайному блужданию, и мы не ошибаемся в логике.
- Посчитаем степень трендовости для процесса с вероятностью разворота 80%. Для этого измерим его среднюю амплитуду, и она равна 1,6495. Далее делим измеренное значение на эталонное 1,6495/5,0148=0,3289. Значение сильно ниже 1, значит исследуемый ряд имеет низкую трендовость.
- Посчитаем степень трендовости для процесса с вероятностью разворота 20%. Для этого измерим его среднюю амплитуду, и она равна 9,95. далее делим измеренное значение на эталонное 9,95/5,0148=1,98. Значение почти в 2 раза выше 1, что говорит о том, что исследуемый ряд имеет высокую степень трендовости.
Имея подобный инструмент, мы можем напрямую сравнивать степень трендовости на разных масштабах (таймфреймах) одного инструмента и наглядно оценивать статистические характеристики данного инструмента. Для примера возьмем все те же 2 процесса с вероятностью разворота 20% и 80% и оценим визуально их статистические характеристики на разных масштабах. До этого мы оперировали с размером блока, равным 1 пункту, но создадим блоки с большим размером, путем умножения каждого следующего размера блока на коэффициент 1,1. Так мы получим несколько масштабов с размерами блока 1; 1.1; 1.21; 1.33 ..... 6.12. На рисунке 10 показано, как изменяется трендовость с увеличением масштаба для процесса с вероятностью разворота 80%, а на рисунке 11 показано, как изменяется трендовость для процесса с вероятностью разворота 20%.
Рисунок 10.
Рисунок 11.
На рисунках 10 и 11 самый маленький масштаб, размером 1 пункт, расположен слева, а самый большой масштаб расположен справа по оси Х. По оси Y отложена степень трендовости инструмента, посчитанная методом "средней амплитуды". Видно, что на рисунке 10, где процесс изначально флетовый, с вероятностью разворота 80%, первый столбец гистограммы имеет низкую трендовость, но с увеличением масштаба трендовость стремится к 1, то есть к эталонному значению случайного блуждания. Можно сделать вывод, что несмотря на то, что вероятность разворота на самом маленьком масштабе высока, при переходе на большие масштабы, закономерность резко теряется, на больших масштабах процесс утрачивает память и превращается в случайное блуждание. На рисунке 11 можно увидеть аналогичную картину. Если изначально процесс имеет высокую степень трендовости 2.053, то с увеличением масштаба трендовость процесса уменьшается и стремится к эталонному значению для случайного блуждания.
Из рисунков 10 и 11 можно сделать вывод, что процесс имеет память только на самом маленьком масштабе, далее, при увеличении масштаба, процесс становится все сильнее похож на случайное блуждание. Этот вывод полностью подтверждает то, как были созданы эти ряды. При генерации этих двух процессов учитывалось только направление предыдущего шага, остальные шаги не учитывались, поэтому эффект "памяти" быстро исчезает с увеличением масштаба.
Построение зависимости степени трендовости от числа шагов
Реальные рынки отличаются от синтетически созданных рядов, и для выявления закономерностей необходимо иметь больше инструментов для анализа, чтобы находить скрытые в них закономерности. Поэтому полезным будет проводит анализ степени трендовости не только на фиксированном числе шагов, но и оценивать, как меняется трендовость рынка с увеличением числа пройденных шагов. Так как таблицы эталона мы можем строить для разного числа шагов, то одновременно можно просматривать не только как ведет себя инструмент с увеличением размера шага, но и как он ведет себя от увеличения числа шагов. На рисунке 12 показано, как меняется степень трендовости GBPUSD на 10 000 выборок при размере блока 0,00314, для количества шагов от 10 до 100. Самый левый столбец гистограммы построен для 10 шагов, самый правый для 100 шагов, на каждом столбце гистограммы число шагов увеличивается на 2.
Рисунок 12.
Из рисунка 12 видно, что на данном масштабе трендовость GBPUSD больше 1 и колеблется в диапазоне 1,133-1,166, в зависимости от числа шагов, для которого проведен анализ. На рисунке 13 показано, как изменяется степень трендовости с увеличением масштаба. График построен для 10 000 выборок по 40 шагов, для размеров шага от 0,00021 до 0,00495. Крайний левый столбец гистограммы построен для размера блока 0,00021, и каждый следующий столбец гистограммы больше предыдущего в 1,1 раза.
Рисунок 13.
На рисунке 13 видно, как степень трендовости уменьшается с увеличением масштаба, если для самого маленького масштаба трендовость 1,425, то для самого большого уже стремится к 1 и составляет 1,062. Можно заметить, что поведение GBPUSD, с увеличением масштаба, похоже не поведение синтетического ряда с вероятностью разворота 20%.
Благодаря такому подходу, можно в динамике оценивать, насколько быстро меняется степень трендовости торгового инструмента. На анимации ниже показано, как меняется распределение плотности вероятности приращений для акций компании AMD относительно эталонного распределения. За основу были взяты свечи тайм фрейма m1. Анимация построена для 40 шагов, 1000 выборок. Размер блока динамически меняется от текущей средней волатильности.
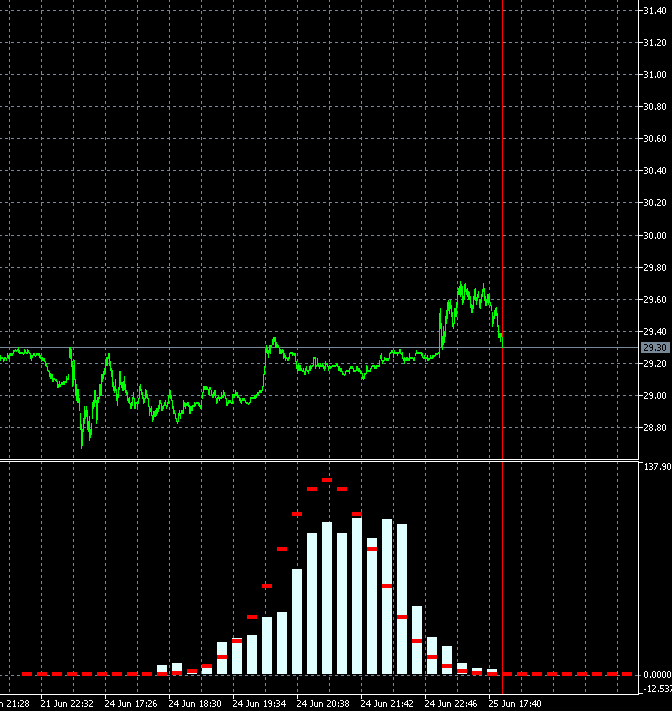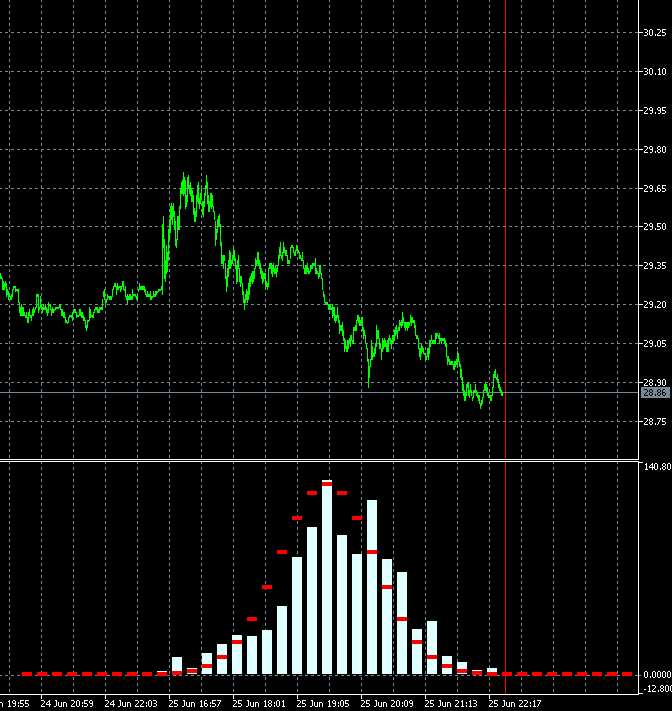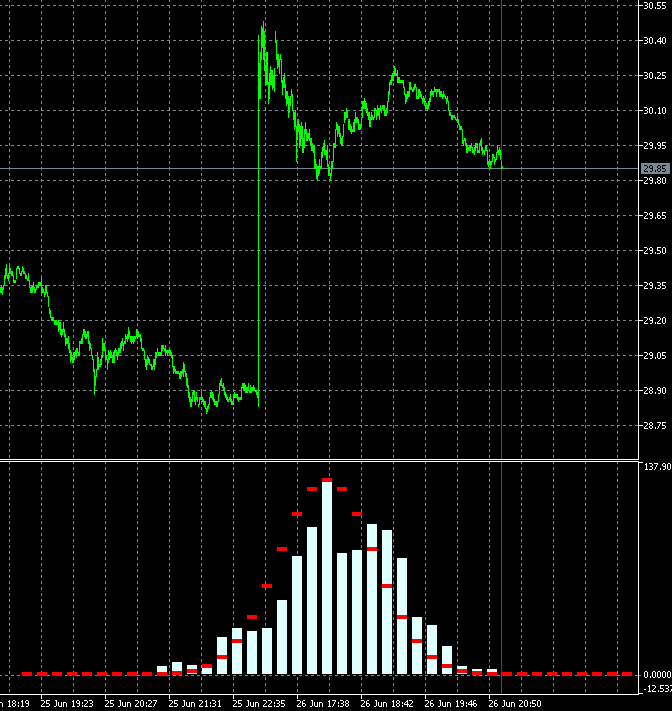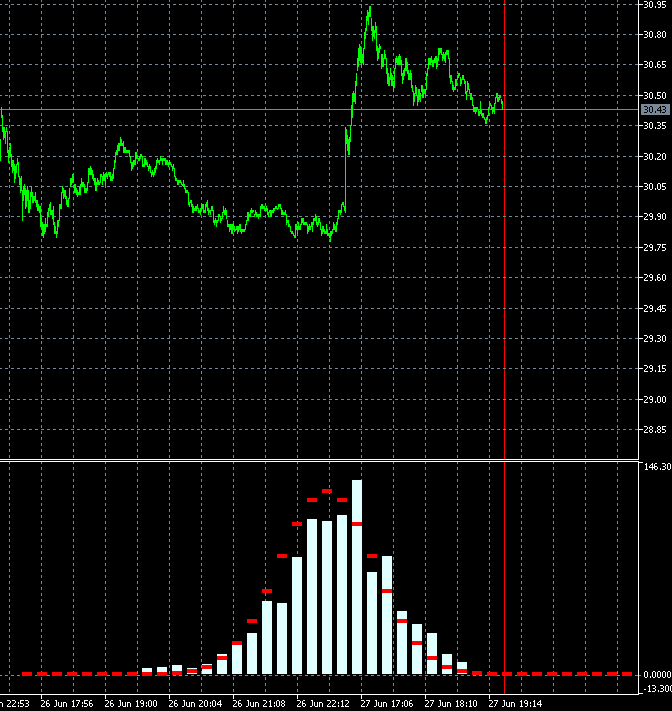
По анимации заметно, что в отличие от GBPUSD, распределение плотности вероятности приращений акций AMD, не симметрично относительно нуля, и присутствует выраженная трендовая составляющая в сторону роста акций. Это означает, что вероятность продолжения тенденции несколько выше для случая, когда после шага вверх, следует шаг вверх, чем для случая, когда после шага вниз следует шаг вниз. По такому инструменту выгодно торговать на повышение. Только лишь торгуя на повышение инструментами с подобными характеристиками, совершая входы в случайном месте, можно остаться в плюсе.
Какова структура рынков — трендовая или флэтовая?
Из всего выше сказанного должен возникнуть вопрос: "Рынки в среднем трендовые, флэтовые или случайные?". Потому что, ответив на этот вопрос, станет ясно, какую стратегию лучше применять и какое направление анализа нужно далее развивать. Я проанализировал более 30 валютных пар, более 50 акций, как Российского, так и Американского рынка, рынки криптовалют и сырьевые рынки. Среди сырьевых рынков были металлы, энергоносители, пищевые инструменты. На основе проделанных исследований могу сделать вывод, что:
- Большинство развитых валютных пар имеют слабую трендовую тенденцию, которая уменьшается с ростом масштаба и увеличением торгового объема по инструменту. Например, EURUSD менее трендовый, чем GBPUSD. Плотность распределения вероятностей на валютных рынках ближе всего к нормальному распределению.
- Рынок акций более трендовый, чем валюты, но склонность уменьшения трендовости от величины масштаба в среднем сохраняется. Активно развивающиеся активы имеют большую степень трендовости, чем активы развитых компаний. Чем меньше компания склонна к развитию и чем меньше у нее потенциал, тем менее трендовая у нее акция. У совсем "неинтересных" активов структура может превратиться во флэтовую. Чем выше ликвидность по инструменту, тем ниже степень трендовости. Анализируя распределение трендовости от размера масштаба, можно понять структуру движения капитала. Например, мы видим, что на малых масштабах акция трендовая, но на больших масштабах она флетовая. Данный факт будет говорить о том, что компания не развивается, а деньги вкладываются в акции с краткосрочной перспективой и затем изымаются из актива. То есть по форме распределений видно, какие инструменты имеют инвестиционный характер, а какие исключительно спекулятивный. Таким образом, косвенно через график можно оценить кредитный рейтинг компании.
- На рынке сырья встречаются трендовые и флетовые инструменты, зависит от текущей потребности в сырье и уровне его производства. Чем сильнее растет потребность при неизменном производстве, тем более трендовый инструмент. Аналогично и с обратной ситуацией, при падении спроса на сырье повышается степень его трендовости при неизменном уровне производства. Флэтовым становится сырье, у которого спрос и предложение близко к равновесию.
- Рынок криптовалют имеет трендовую тенденцию на стадии роста интереса к активу и увеличении торгового оборота, но становится флэтовым на стадии угасания интереса к активу. В итоге график цен за всю историю стремится к случайному блужданию, но как только начинается новая волна, инструмент снова становится трендовым.
Тут можно сделать более широкие выводы, но это не тема данной статьи и данного исследования.
Приведу несколько примеров на рисунках ниже, описывающих особенности торговых инструментов.
- BTCUSD на некоторых масштабах флэтовый, как я писал ранее, при уменьшении ажиотажа криптовалюты становятся флэтовыми. Что интересно, распределение плотности вероятности для биткоина симметричное относительно нуля, несмотря на то, что визуально кажется, как-будто на биткоине должен присутствовать восходящий тренд.
- Акции AMD и AAPL показывают устойчивую трендовость с незначительными провалами. Распределение плотности вероятности смещено вправо относительно нуля в сторону восходящих движений. Но и визуально видно, что эти акции имеют устойчивую восходящую тенденцию.
- Нефть имеет в целом трендовый характер, даже с увеличением масштаба.
- Видно, что на EURUSD трендовость на больших масштабах практически исчезает, и инструмент становится на некоторых масштабах флетовым, и в целом он больше остальных стремится к распределениям плотности вероятности случайного блуждания.
- Лидеры Российского рынка похожи друг на друга, устойчивые тренды на малых масштабах и практически отсутствующая трендовость на больших масштабах.
В следующей статье я постараюсь объяснить причины такого поведения инструментов, почему на малых масштабах инструмент более трендовый, и почему с ростом масштаба, как правило, степень трендовости падает. Разработаем алгоритм на базе данного исследования и посмотрим будет ли он зарабатывать.
Заключение
Понятиям тренд и флэт можно не только дать четкое и полное определение, но и сравнить степень трендовости инструментов между собой, а так же степень трендовости инструмента на разных масштабах. Подобный анализ позволяет полнее судить о характеристиках и особенностях того или иного инструмента, и строить торговые алгоритмы, учитывая особенности поведения каждого инструмента индивидуально.
Зная статистические характеристики инструмента и изменение их во времени, можно отказаться от оптимизации параметров при разработке торгового алгоритма, вместо этого можно проводить измерения и осознанно изменять параметры торгового алгоритма под статистические характеристики торгуемого инструмента.
К статье приложены файлы с историей для графиков с 20%, 50% и 80% вероятностью разворота, отдельно приложен файл Excel для построения эталонного распределения и индикатор, строящий блоки, использовавшиеся для анализа.
Автор алгоритма индикатора — Maxim Romanov, автор кода индикатора — Konstantin Gruzdev.
 Дискретизация ценового ряда, случайная составляющая и "шумы"
Дискретизация ценового ряда, случайная составляющая и "шумы"
 Нейросети — это просто (Часть 2): Обучение и тестирование сети
Нейросети — это просто (Часть 2): Обучение и тестирование сети
 Использование криптографии совместно с внешними приложениями
Использование криптографии совместно с внешними приложениями
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Как то подозрительно сильно скачут столбики гистограммы при изменении всего на 1 бар: по идее должен 1 бар из 1000 с конца убираться и 1 вначале добавляться. Т.е. изменение должно быть в пропорции 1/500 сразу на все столбики гистограммы, практически должны измениться 1 или 2 столбика.

Подумал, что может скорость большая и плавности не замечаю...
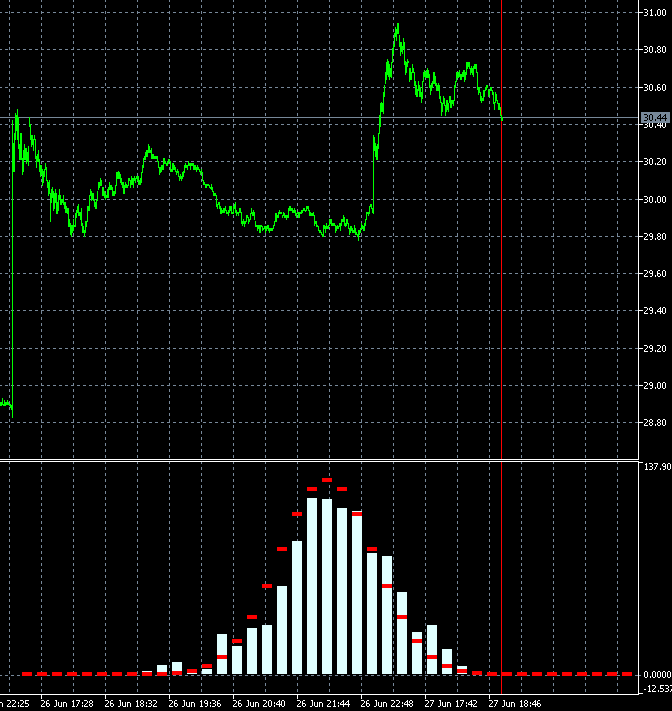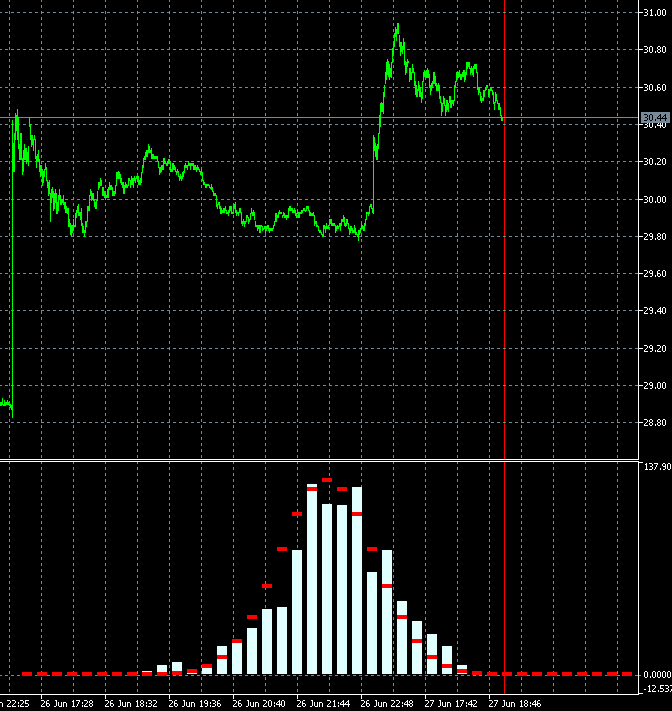
Скопировал 2 кадра 340 и 341 с соседними барами и сделал помедленнее:
Изменения очень сильные сразу во всех столбиках. Может где-то ошибка в их расчете? Не могут 2 бара из 1000 так менять картинку.
Такое ощущение, что в расчете не 2 бара сменилось, а все 1000, типа окно на 1000 (на неделю, месяц...) в прошлое сместилось, а не на 1 бар.
Как то подозрительно сильно скачут столбики гистограммы при изменении всего на 1 бар: по идее должен 1 бар из 1000 с конца убираться и 1 вначале добавляться. Т.е. изменение должно быть в пропорции 1/500 сразу на все столбики гистограммы, практически должны измениться 1 или 2 столбика.
Подумал, что может скорость большая и плавности не замечаю...
Скопировал 2 кадра 340 и 341 с соседними барами и сделал помедленнее:
Изменения очень сильные сразу во всех столбиках. Может где-то ошибка в их расчете? Не могут 2 бара из 1000 так менять картинку.
Такое ощущение, что в расчете не 2 бара сменилось, а все 1000, типа окно на 1000 (на неделю, месяц...) в прошлое сместилось, а не на 1 бар.
да, это может показаться подозрительно) Но тут особенность в построении блоков. Блоки строятся не в будущее, а в прошлое от последней даты. Соответственно когда приходит свеча, цена построения блоков смещается и сами блоки получаются другими. Сдвиг даже на 10 пунктов может сильно изменить конфигурацию блоков, а соответственно форму распределения.
Для чего я так делал. Тут есть 2 причины
1. Сам метода построения блоков очень чувствителен к начальной цене и я хотел посмотреть, как меняется распределение при построении от разных цен. Такой подход позволил посмотреть в динамике и как меняется распредеелние со временем и как меняется распределение от изменения начальной цены.
2. Я делал индикаторо блоков для большого робота и там я использовал именно такой подход, чтобы избежать оптимизации параметров под историю. Та как конфигурации блоков сильно меняются от начальных условий, то сдвиг на 1 день вперед/назад в убивает всю оптимизацию параметров под истори. Так можно избежать грубой подгонки под истори и оценить насколько стабильны выявленные закономерности. Мне важно было сделать робота, который работает на любом торговом инструменте без оптимизации параметров
да, это может показаться подозрительно) Но тут особенность в построении блоков. Блоки строятся не в будущее, а в прошлое от последней даты. Соответственно когда приходит свеча, цена построения блоков смещается и сами блоки получаются другими. Сдвиг даже на 10 пунктов может сильно изменить конфигурацию блоков, а соответственно форму распределения.
Для чего я так делал. Тут есть 2 причины
1. Сам метода построения блоков очень чувствителен к начальной цене и я хотел посмотреть, как меняется распределение при построении от разных цен. Такой подход позволил посмотреть в динамике и как меняется распредеелние со временем и как меняется распределение от изменения начальной цены.
2. Я делал индикаторо блоков для большого робота и там я использовал именно такой подход, чтобы избежать оптимизации параметров под историю. Та как конфигурации блоков сильно меняются от начальных условий, то сдвиг на 1 день вперед/назад в убивает всю оптимизацию параметров под истори. Так можно избежать грубой подгонки под истори и оценить насколько стабильны выявленные закономерности. Мне важно было сделать робота, который работает на любом торговом инструменте без оптимизации параметров
Причину таких скачков понял, но по прежнему не нравится. Где то выложен этот индикатор построения гистограммы? Есть интерес посмотреть вживую, а не на картинке.
Мыслил алгоритмом расчета МА: 1 удалил, 1 прибавил.
Причину таких скачков понял, но по прежнему не нравится. Где то выложен этот индикатор построения гистограммы? Есть интерес посмотреть вживую, а не на картинке.
Нет, я не выкладывал готовый индикатор