O que é o cálculo da diferença?
Pois é:
Δf(xk) = f (xk+1) - f (xk)
Proponho recolher indicadores e especialistas em cálculo de diferenças neste ramo, em código aberto.
Eu reescrevi o indicador em uma variante mais clara como exemplo:
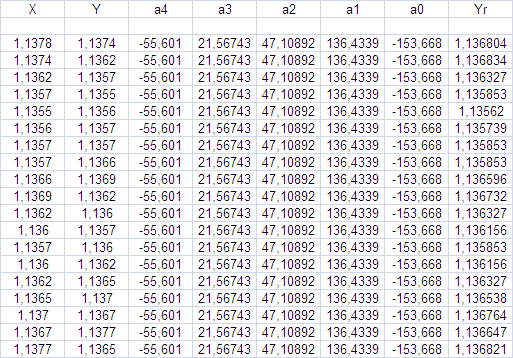
Na tabela parece que é assim:
A linha azul-vermelha é interpolação (encontrando um ponto dentro do intervalo) por um polinômio de 4º grau com uma alavancagem de 72.
a1_Buffer[i]=((open[i] - Znach) +5061600*a1_Buffer[i+1 ]-7489800 *a1_Buffer[i+2 ]+4926624*a1_Buffer[i+3 ]-1215450*a1_Buffer[i+4 ])/1282975;
A fina linha azul é a extrapolação (encontrar um ponto fora do intervalo) pelo polinômio de grau 2 com alavancagem 78.
a2_Buffer[i]= 3160*a1_Buffer[i] -6240 *a1_Buffer[i+1 ] + 3081*a1_Buffer[i+2 ];
A linha vermelha é a linha de construção do polinómio de potência 4. É redesenhado e baseado no último ponto de abertura do bar.
a4_Buffer[i+92]=a1_Buffer[i]; if(i<=10) { for(z=92-1;z>=0;z--){ a4_Buffer[i+0+z]= 5*a4_Buffer[i+1+z] - 10*a4_Buffer[i+2+z] + 10*a4_Buffer[i+3+z] - 5*a4_Buffer[i+4+z] + 1*a4_Buffer[i+5+z]; }}
O que é o cálculo da diferença?
Pois é:
Δf(xk) = f (xk+1) - f (xk)
Sim.
Está directamente relacionado com o binómio de Newton.
É verdade para pontos equidistantes:
1*Y1-2*Y2+1*Y3=0 é a equação da diferença de uma linha reta.
1*Y1-3*Y2+3*Y3-1*Y4=0 - a equação da diferença da parábola de segundo grau.
1*Y1-4*Y2+6*Y3-4*Y4+ 1*Y5=0 - equação da diferença da parábola do terceiro grau.
Também se sobrepõe com os tópicos:
https://www.mql5.com/ru/forum/61389/page48#comment_5633264
https://www.mql5.com/ru/forum/211220/page2#comment_5632736 .

- 2017.07.20
- www.mql5.com
Sim.
Isso é o que todos têm feito... a escrever...
O futuro depende do passado?
Isso é o que todos têm feito... a escrever...
O futuro depende do passado?
Para cada ação, há um traço no presente, que, naturalmente, afeta o futuro. :))))
Sugiro que pulemos a filosofia neste tópico, vamos discutir apenas matemática, programação, testes e otimização.
Sim.
Directamente relacionado com o binómio de Newton.
Para pontos equidistantes, é verdade:
Y1-2*Y2+Y3=0 - equação da diferença de uma linha reta.
Y1-3*Y2+3*Y3-Y4 =0 - a equação da diferença da parábola de segundo grau.
Y1-4*Y2+6*Y3-4*Y4 + Y5 =0 - é a equação da diferença da parábola de terceiro grau.
Já experimentou esta fórmula?
Y = a0 + a1X + a2X^2 + a3X^3 + a4X^4
onde:
X é o preço do bar anterior;
Y - preço do bar actual.
E assim ficamos com a seguinte imagem:
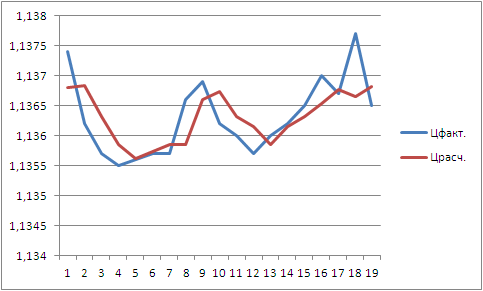
Já experimentou esta fórmula?
Y = a + bX + cX^2 + dX^3 + eX^4
É claro que nesta forma existem X e Y, mas na equação de recorrência, apenas Y e todos os coeficientes (a + bX+ cX^2+ dX^3+ eX^4) são reduzidos e substituídos por cinco valores de Y em si.
Olhei para o código, acertei, é alguma variante de um filtro de feedback? De onde vêm os coeficientes 5061600, 4926624 e outros?
Na verdade, de onde veio o índio, da Internet? ))
1. Olhei para o código, acertei, é alguma variante de filtro com feedback?
2.E de onde vieram os coeficientes 5061600, 4926624 e outros?
3. Em geral, de onde veio o indutor, da internet? ))
1. Sim. Este filtro tem 400 anos de idade e só tem história escrita: Descartes, Newton, Pascal, Taylor, Lagrange.
2. Os coeficientes são calculados. Parece que, no segundo ano, conhecemos os métodos de Lagrange e Taylor. Parece haver muitas variantes para o cálculo de coeficientes.
3. Este em particular foi desenhado hoje. :)))))
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
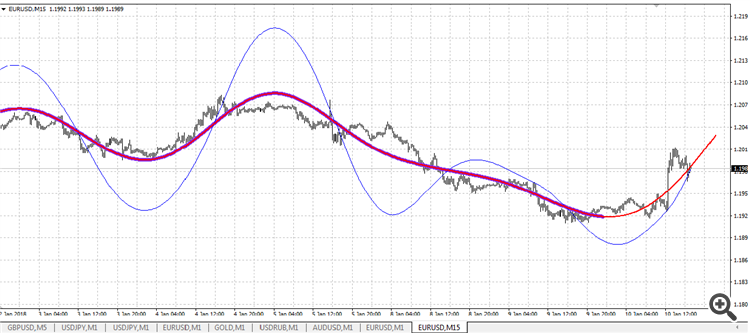
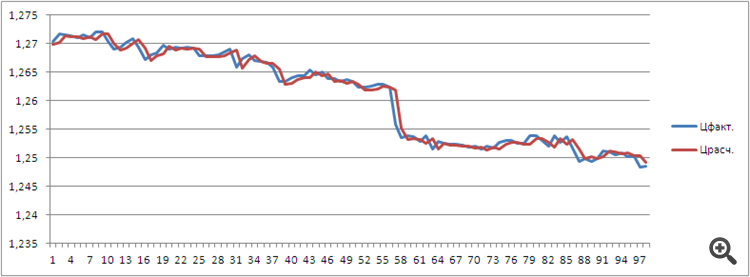
Proponho coletar indicadores e especialistas em cálculo de diferenças neste tópico, no código fonte aberto.
Se houver interesse, eventualmente vamos construir ou desenhar algo útil. :)
Eu reescrevi o indicador em uma versão mais clara como exemplo: